He probado QwQ-32B-Preview: Modelo de razonamiento de Alibaba

¿Qué es QwQ-32B-Preview? 

QwQ-32B-Preview es un modelo construido para manejar tareas de razonamiento avanzadas que van más allá de la simple comprensión de textos. Su objetivo es resolver problemas desafiantes como la codificación y el razonamiento matemático. Como versión "Previa", todavía se está perfeccionando. Tiene acceso de código abierto en plataformas como Hugging Face, ¡así que puedes probar, mejorar y dar tu opinión sobre el modelo si quieres!

Algo a tener en cuenta es que QwQ-32B-Preview es un modelo experimental. Aunque es prometedor, también tiene algunas limitaciones importantes:

• Mezcla de lenguas: El modelo podría cambiar inesperadamente de idioma, haciendo que sus respuestas fueran menos claras.
• Razonamiento circular: A veces, se atasca en bucles de razonamiento repetitivos, lo que da lugar a respuestas largas sin una conclusión clara.
• Cuestiones de seguridad: El modelo aún necesita elementos de seguridad más potentes para garantizar un uso fiable y seguro, por lo que se recomienda precaución al desplegarlo.
• Lagunas de rendimiento: Está demostrado que rinde bien en matemáticas y codificación, pero podría mejorar en áreas como el razonamiento de sentido común y la comprensión de matices sutiles del lenguaje.

¿Cómo acceder a QwQ-32B-Preview?

Puedes acceder a QwQ-32B-Preview a través de HuggingChatdonde actualmente se ejecuta gratuitamente sin cuantizar. Para utilizar QwQ-32B-Preview:

1. Visit HuggingChat: https://huggingface.co/chat/
2. Selecciona QwQ-32B-Vista previa de los modelos disponibles
3. Empieza a interactuar con el modelo

La prueba de la fresa

Empezaremos con la conocida Prueba de la Fresa. La indicación es: "¿Cuántas veces aparece la letra 'r' en 'fresa'?"

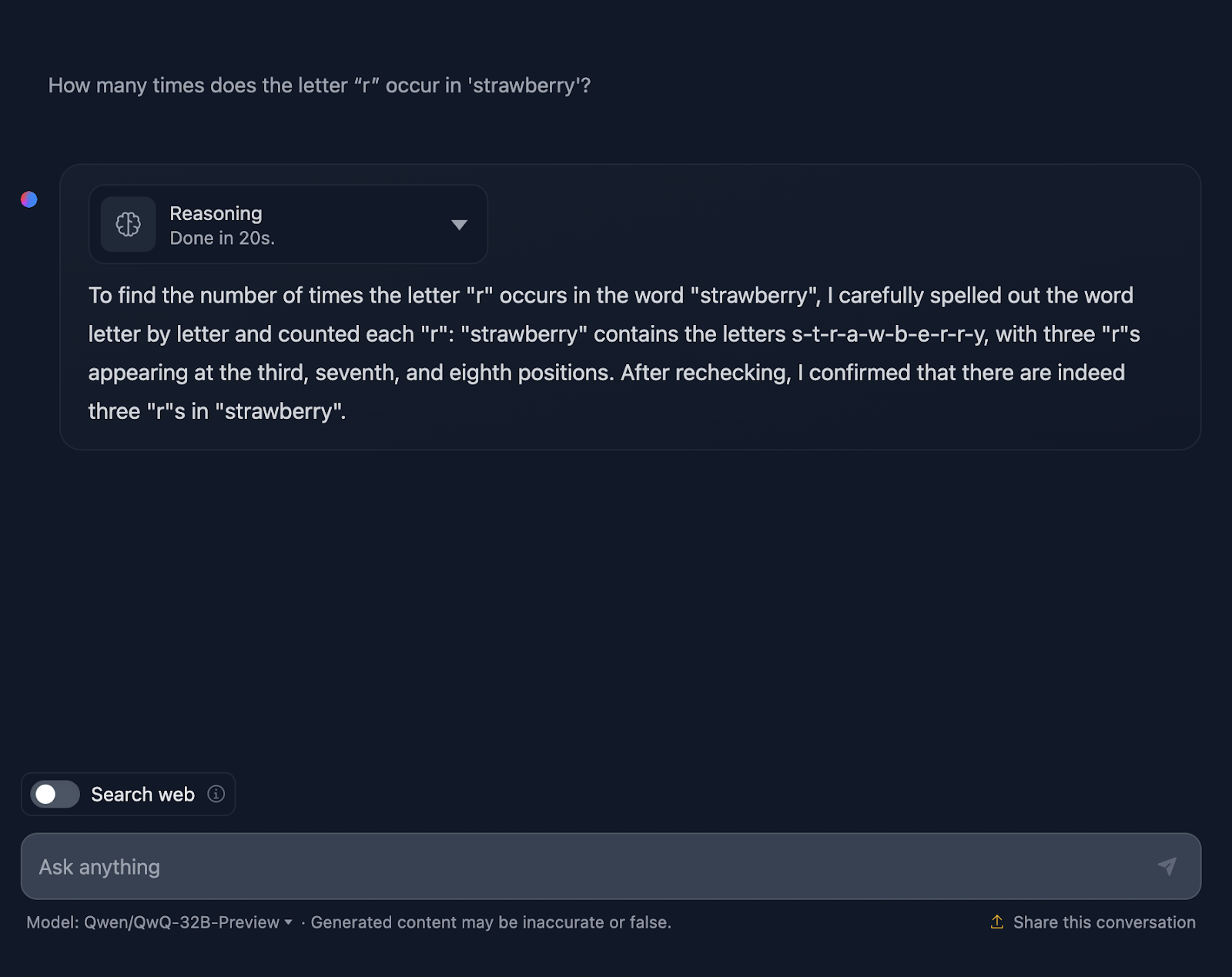
Bien, ¡esto ya se está poniendo interesante! 

Cuenta las letras correctamente, pero afirma erróneamente que las "r" aparecen en las posiciones tercera, séptima y octava, lo que no es cierto. Las posiciones correctas son la tercera, la octava y la novena. Como referencia, esto es algo que DeepSeek manejó correctamente.

Veamos más detenidamente el razonamiento de QwQ-32B-Preview:

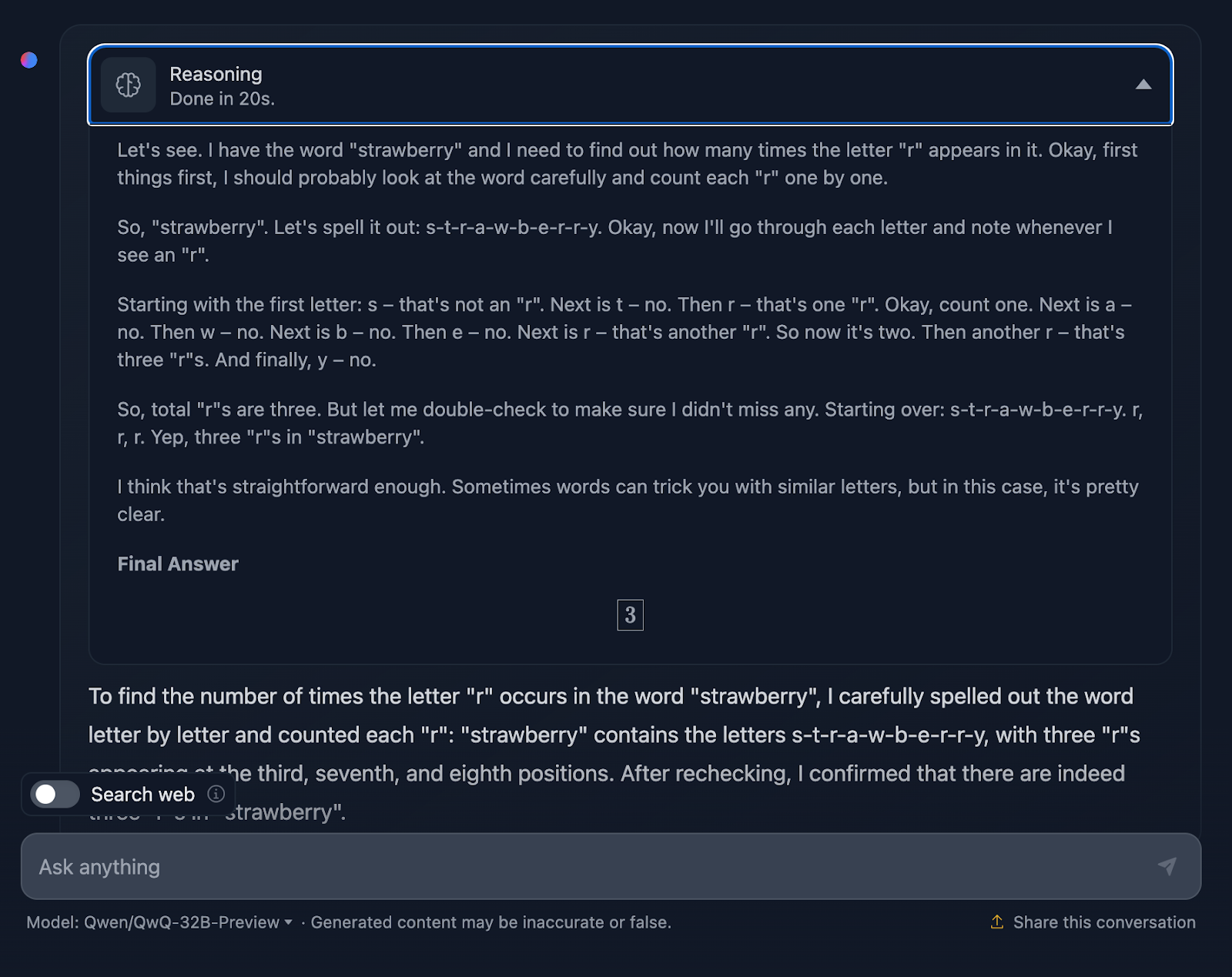
El razonamiento de QwQ-32B-Preview era mucho más corto que el proporcionado por DeepSeek. Sin embargo, en este caso, al contar las letras, no tuvo en cuenta sus posiciones, y supongo que por eso se equivocó. Es interesante porque proporcionó esa información aunque no era necesaria: no pedí las posiciones de las "r", sólo el número de apariciones. Proporcionar información adicional e innecesaria acababa introduciendo errores.

Razonamiento matemático

Para comprobar el razonamiento matemático del modelo realizaremos tres pruebas que varían en complejidad.

Zona triangular

La indicación es: "Si un triángulo tiene lados de longitud 3, 4 y 5, ¿cuál es su área?" Veamos cómo se gestiona esto:

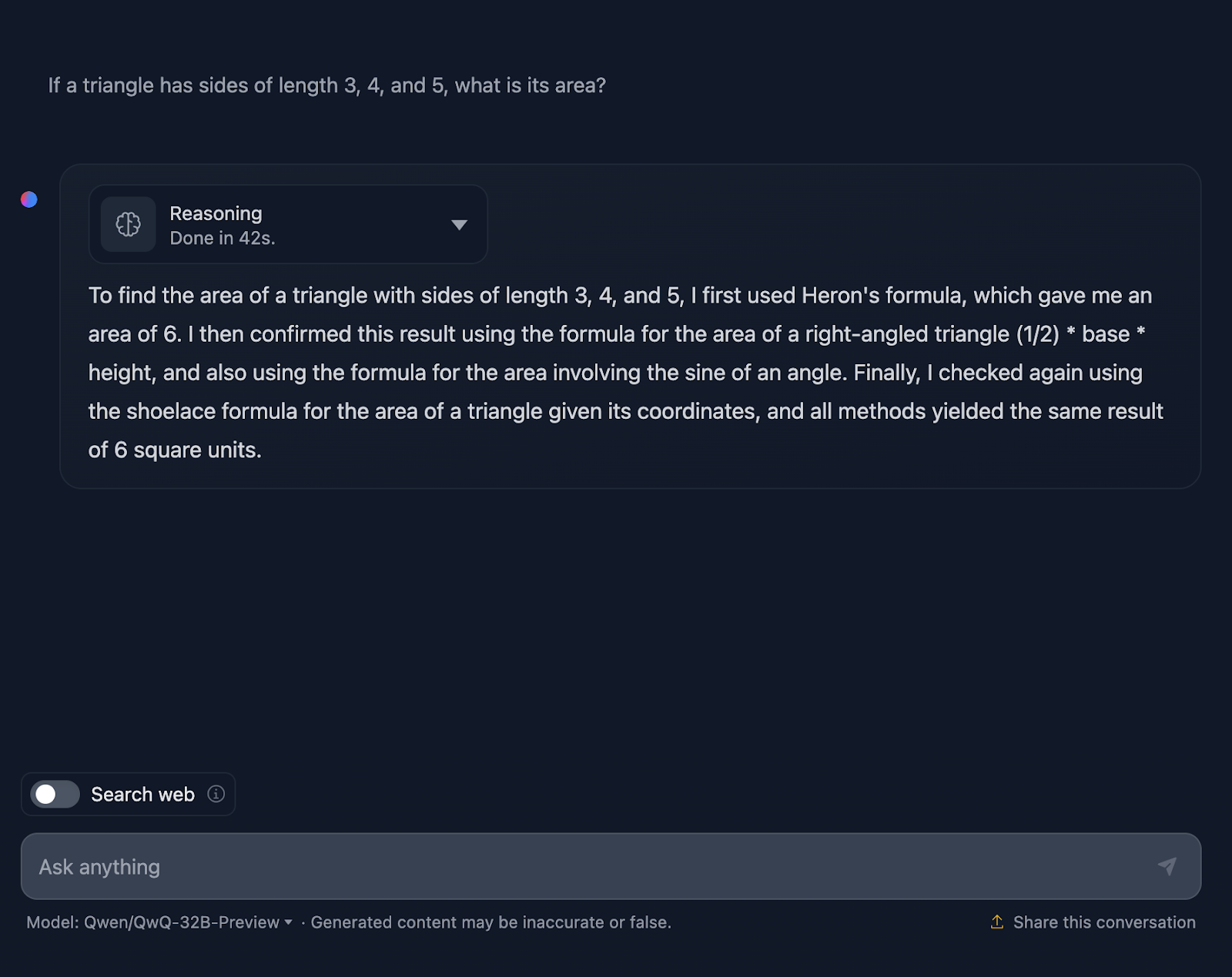
La respuesta es correcta, y explica los métodos utilizados para llegar a la conclusión. Sin embargo, en la solución no se incluye ninguna de las fórmulas o cálculos, lo cual está bien, ya que no era lo que se pedía. Sin embargo, habría sido un buen añadido, algo que DeepSeek sí proporcionó. Veamos ahora el razonamiento:

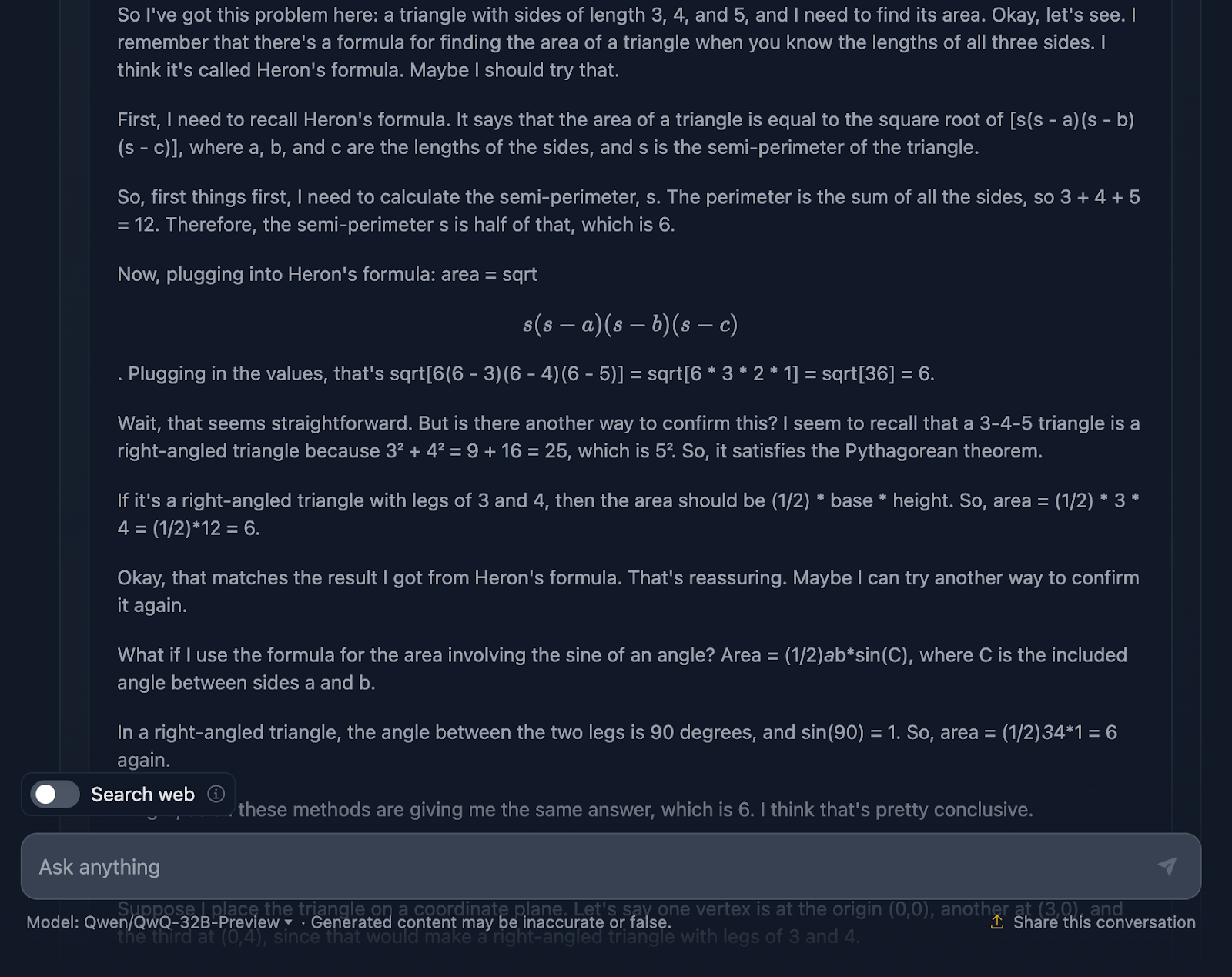
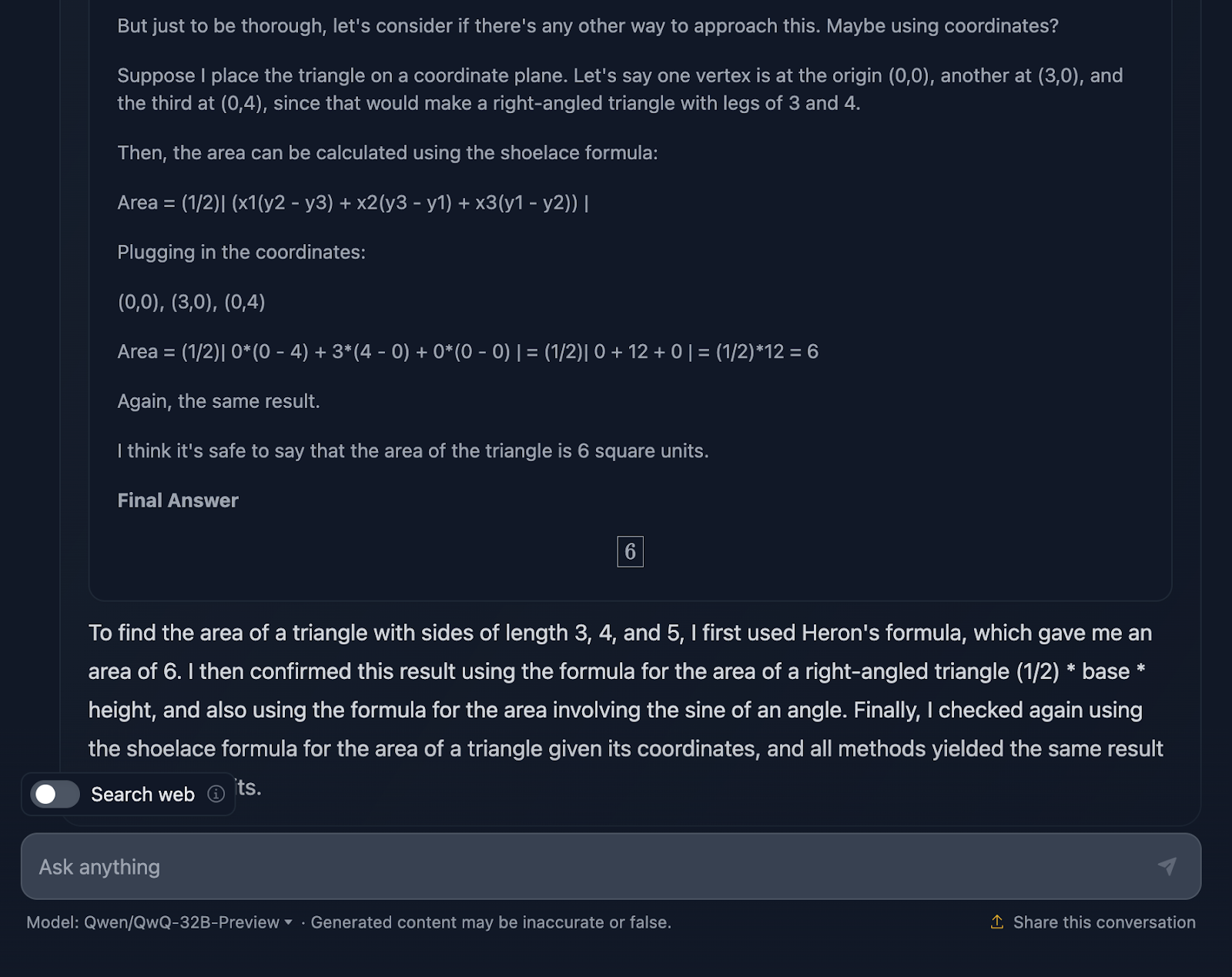
Me parece genial que haya utilizado cuatro enfoques diferentes para llegar a la misma solución, en comparación con DeepSeek, que sólo utilizó tres. El razonamiento es claro y fácil de seguir. El único problema que he observado es que el formato y el estilo de las fórmulas son un poco incoherentes: algunas se analizan correctamente, mientras que otras no. Esto es algo que DeepSeek manejó correctamente.

Prueba matemática

Examinemos una prueba matemática más compleja para ver si hay alguna diferencia en el rendimiento y el proceso de pensamiento. Voy a probar lo siguiente: "Demuestra que la suma de los recíprocos de los números de Fibonacci converge a un valor finito".

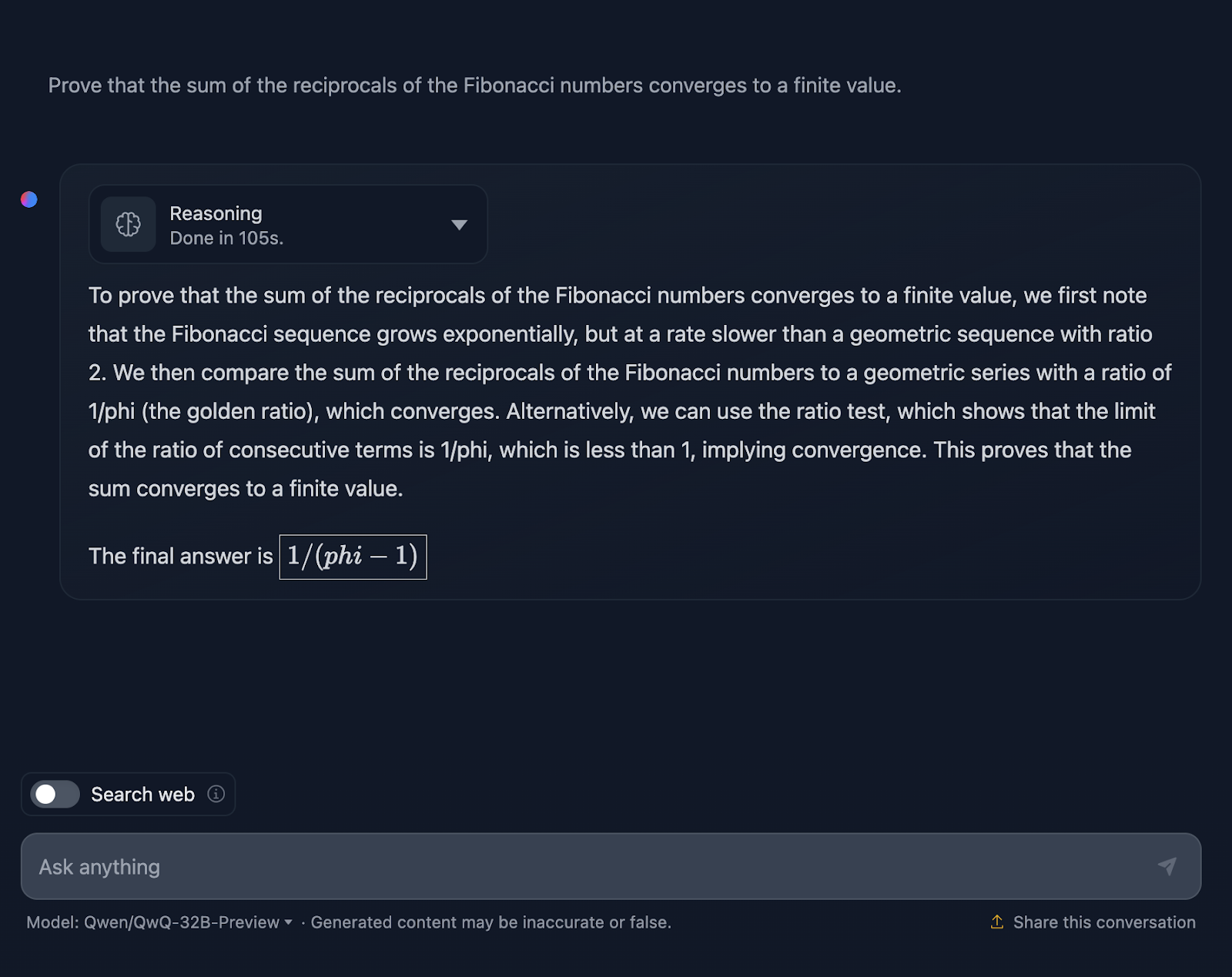
La respuesta no es técnicamente incorrecta, pero hay mucho margen de mejora. En primer lugar, si estoy pidiendo al modelo una demostración, la respuesta final no debe ser sólo un valor; debe incluir una serie de fórmulas o aplicaciones de teoremas para demostrar una hipótesis o afirmación. Intenta esto aquí, pero necesita más elaboración, y la respuesta final no prueba realmente nada. Una vez más, el formato de las fórmulas parece ser un problema recurrente. Un gran ejemplo de una prueba adecuada puede encontrarse en la prueba que realicé con DeepSeek.

Para contextualizar, durante mi doctorado en matemáticas, corregí exámenes de matemáticas, y puedo decirte que esta respuesta no habría recibido la máxima puntuación, ¡pero la de DeepSeek sí!

Veamos ahora el razonamiento (para facilitar la lectura, sólo mostraré la primera y la última parte del largo proceso de razonamiento, pero te animo a que pruebes tú mismo la indicación):

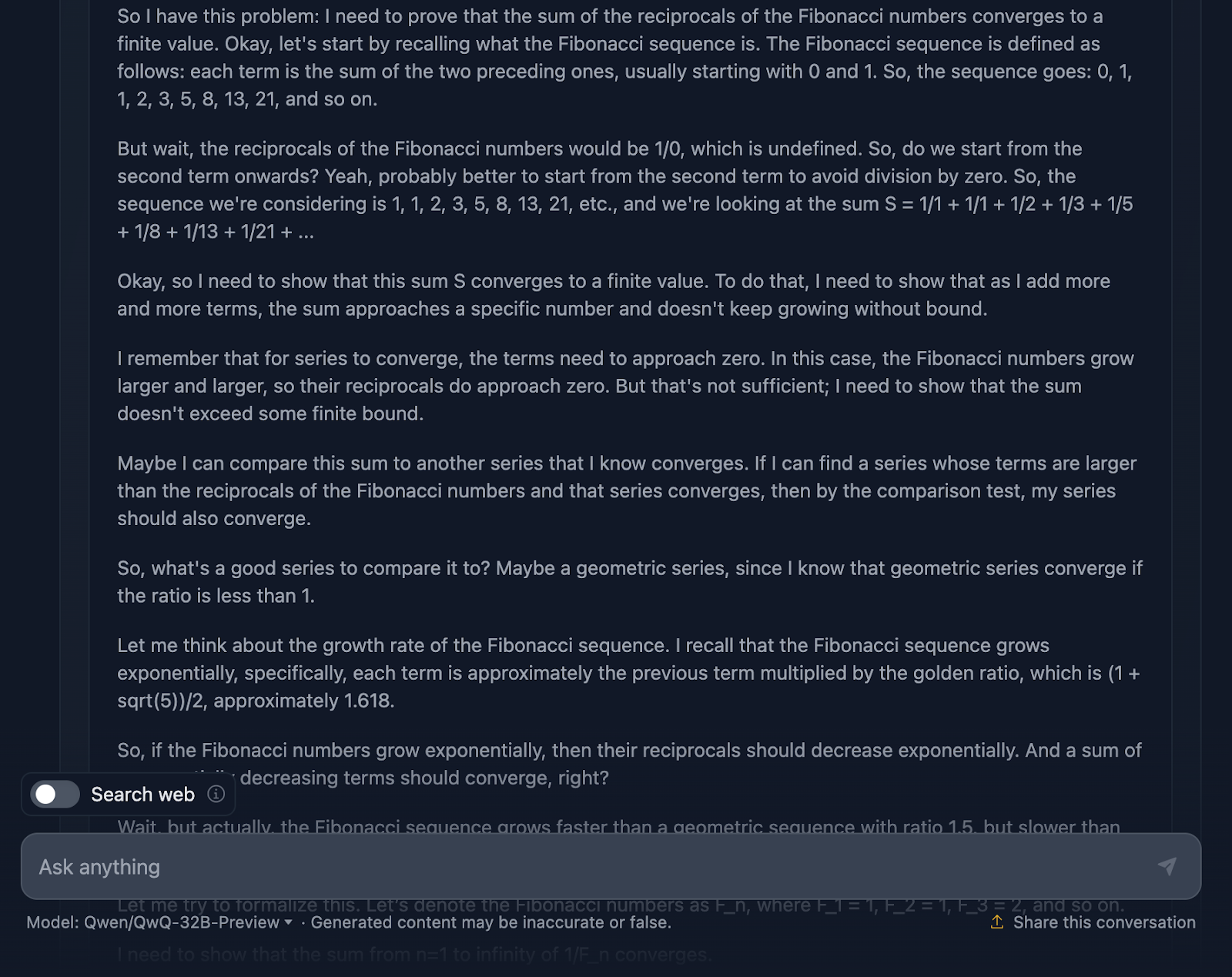
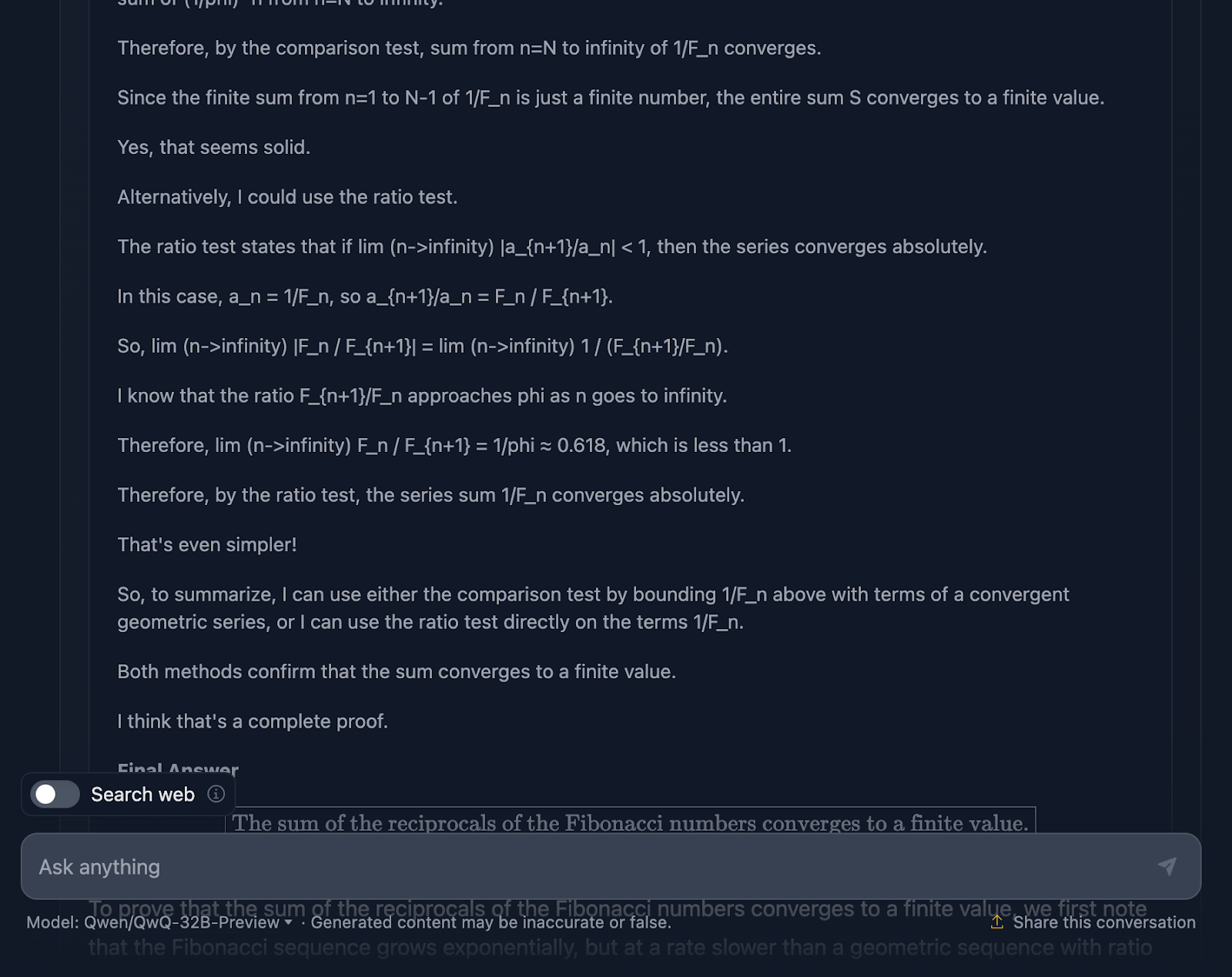
En primer lugar, el modelo empieza fuerte. Recuerda la secuencia de Fibonacci, evita el escollo evidente de dividir por cero y plantea bien el problema. Esa es una base sólida. A continuación, procede a utilizar la prueba de comparación y la prueba de razón, que son pruebas estándar de convergencia de series, e incluso utiliza la fórmula de Binet para aproximar y acotar los números de Fibonacci. También reconoce en algún momento que no necesita calcular el valor exacto, sólo demostrar que la serie converge, lo que demuestra que se ciñe realmente al problema.

Ahora bien, el razonamiento es correcto, de eso no hay duda, pero el camino hacia la respuesta parece un poco enredado. Una vez más, algunas fórmulas están bien formateadas, pero otras no tanto. 

Dicho esto, la prueba final se mantiene. Demuestra que la serie converge, y utiliza métodos válidos para conseguirlo. Pero en comparación con la producción de DeepSeek, a la prueba le habría venido bien un poco más de pulido y consistencia.

También me sorprende mucho que la respuesta final proporcionada en el razonamiento, que es una respuesta final mejor, sea diferente de la que aparece en el resultado final. ¡Debería haberse ceñido a eso!

Geometría diferencial

Intentemos ahora una prueba de geometría diferencial:

Considera una superficie S en ^R3 parametrizada por

φ(u,v) = (u cos v, u sen v, ln u)

para u > 0 y 0 ≤ v < 2π.

a) Calcula la primera forma fundamental de S.

b) Determina si S es una superficie mínima.

c) Halla la curvatura gaussiana K y la curvatura media H de S.

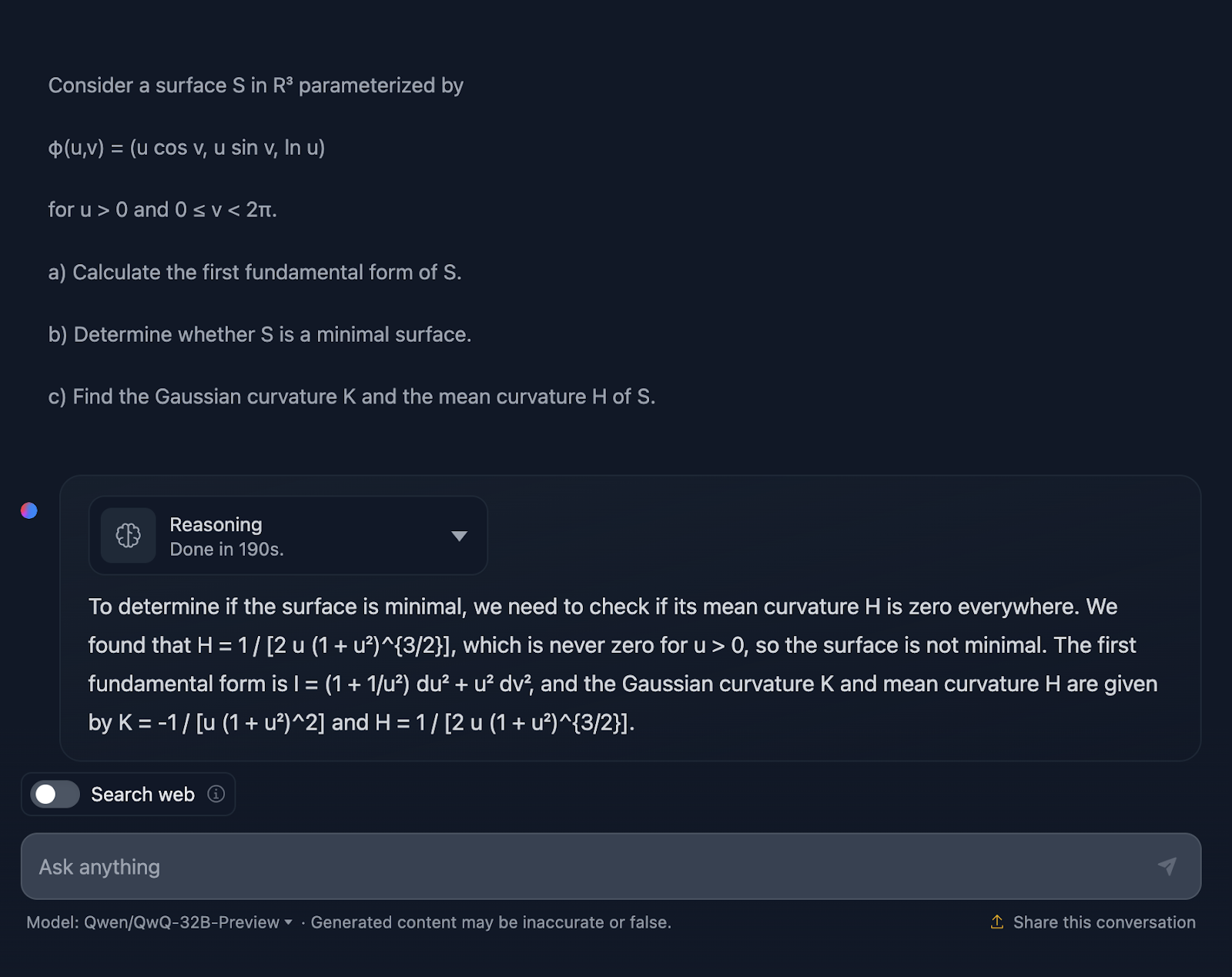
De acuerdo, no me sorprende la respuesta, ya que es bastante similar a la prueba anterior en cuanto al estilo. De nuevo, no es técnicamente incorrecto, pero sin duda se puede mejorar la forma de comunicar la explicación.

La explicación se salta el cómo. No esperaría un enfoque paso a paso, por supuesto, pero sí al menos algunas fórmulas que muestren de dónde proceden los resultados. Además, no divide la respuesta en secciones, y el formato de las fórmulas, una vez más, no es el mejor. DeepSeek hizo un gran trabajo en este sentido.

Una vez más, ¡no toda la puntuación para QwQ, pero sí para DeepSeek!

Veamos el razonamiento (para facilitar la lectura, sólo muestro la primera y la última parte):

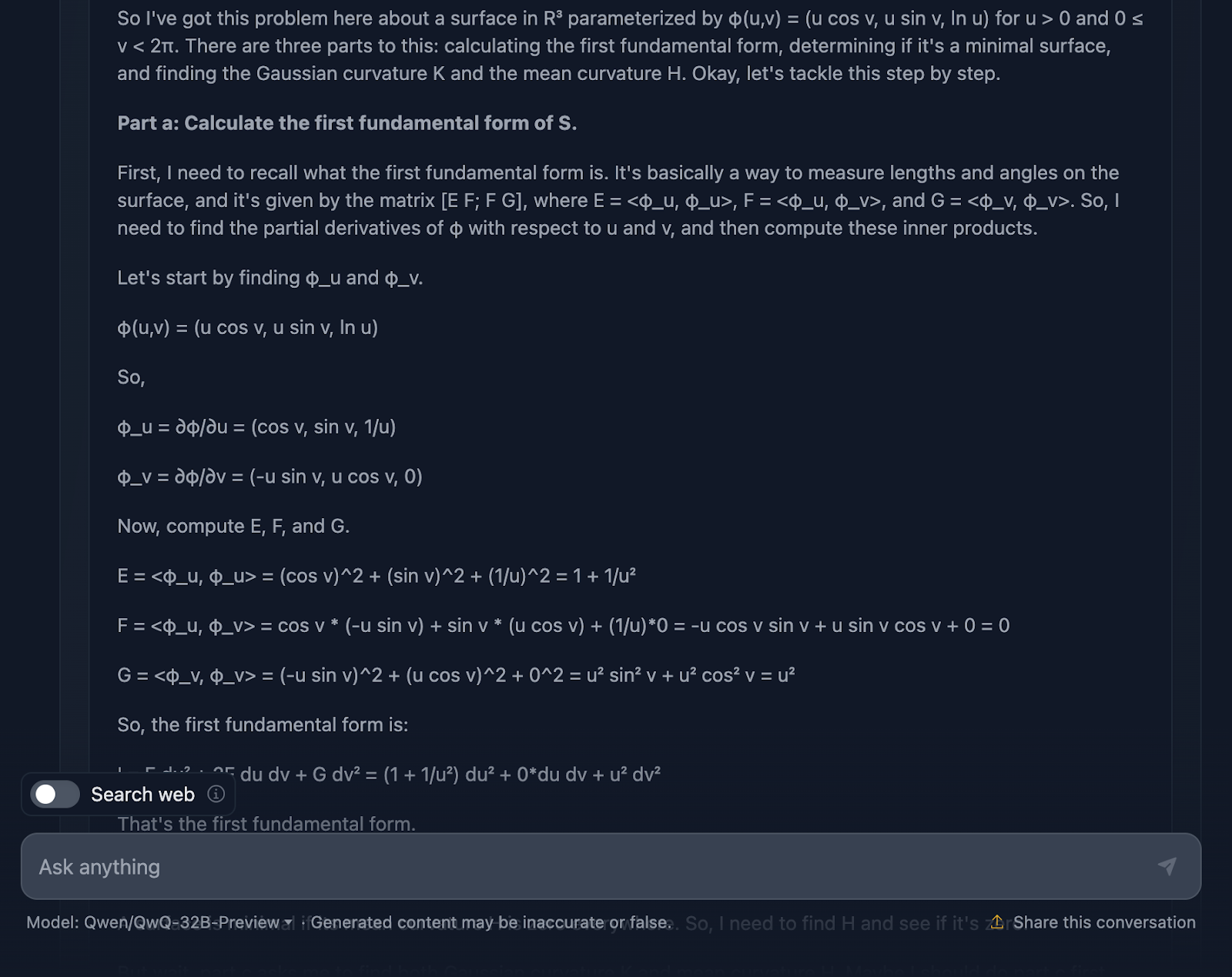
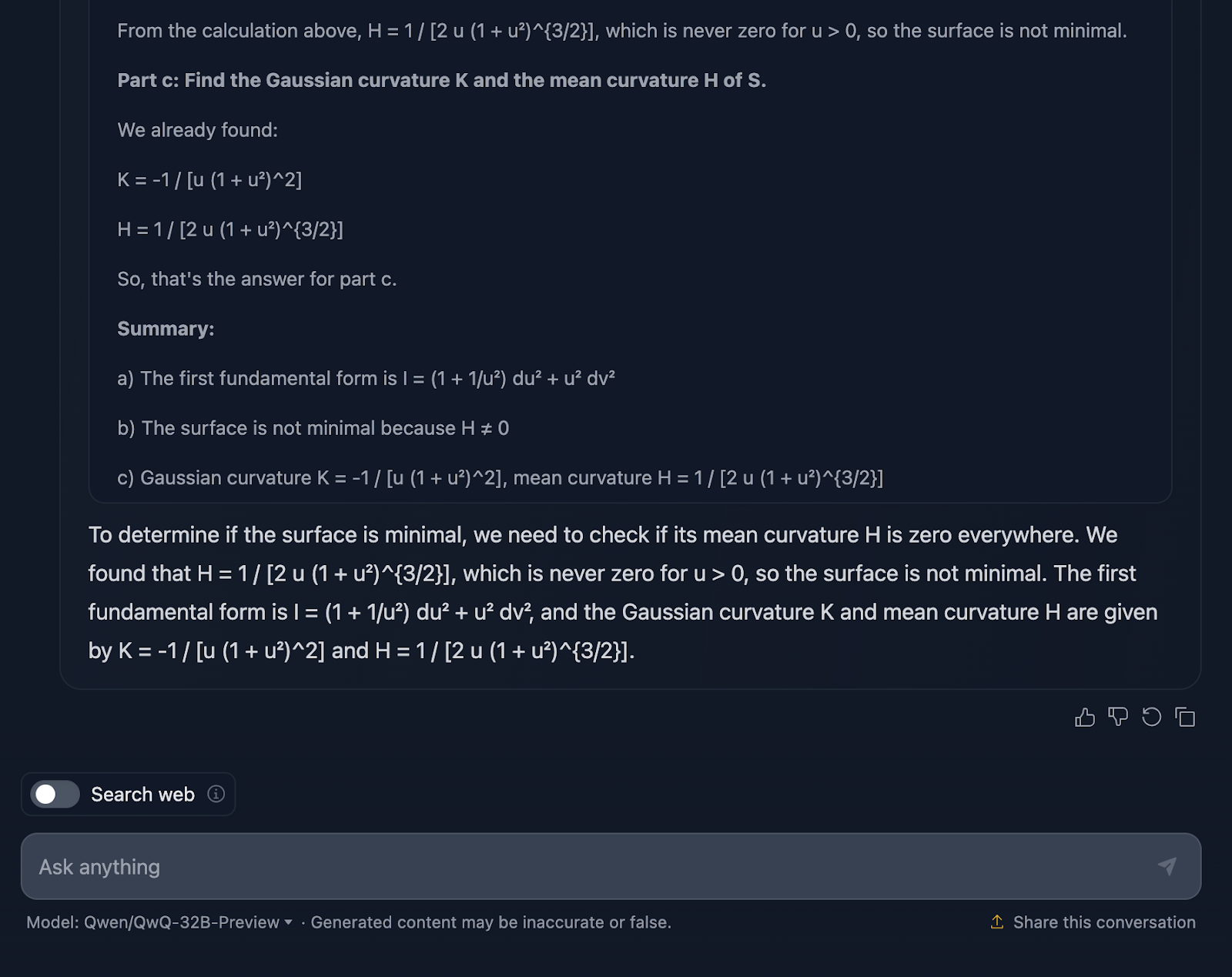
Muy bien, hablemos aquí del razonamiento del modelo. En primer lugar, tengo que reconocer que es minucioso. El desglose en secciones claras -Parte a, Parte b y Parte c- hace que sea fácil de seguir, y hace un trabajo sólido al guiarnos por los pasos. Empieza abordando la primera forma fundamental, calculando cuidadosamente los coeficientes a partir de la parametrización, y luego construye a partir de ahí. Cuando se llega a las curvaturas gaussiana y media en la Parte c, el trabajo preliminar está bastante bien hecho.

Ahora es cuando las cosas empiezan a parecer un poco torpes. Aunque los cálculos son técnicamente correctos, el modelo pasa mucho tiempo volviendo a comprobar los pasos o revisando los cálculos, lo que es estupendo para la precisión, pero no tanto para la legibilidad. 

Hablemos ahora del formato. Las fórmulas están ahí, pero no se presentan de la forma más clara, una vez más. Es un poco desordenado, y para cualquiera que intente seguirlo, eso puede dificultar las cosas más de lo necesario. Un diseño más limpio con los resultados clave resaltados mejoraría mucho esta explicación.

Otra cosa que falta es el contexto. El modelo nos da los resultados, pero no se detiene a explicarnos lo que significan. Por ejemplo, ¿por qué importa aquí la curvatura gaussiana? ¿O qué nos dice sobre la geometría de la superficie? Y cuando concluye que la superficie no es mínima, técnicamente tiene razón, pero pierde la oportunidad de ampliar lo que eso significa en un sentido más amplio.

Pruebas de codificación

Hemos probado el rendimiento de QwQ-32B-Preview en pruebas matemáticas, y no me ha impresionado demasiado... pero quizá soy parcial porque me gustó mucho el resultado de DeepSeek. Veamos cómo se comporta en las pruebas de codificación y si QwQ-32B-Preview puede sorprenderme esta vez.

Python

La primera prueba es:

"Implementa una función en Python que encuentre la subcadena palindrómica más larga de una cadena dada. La función debe tener una complejidad temporal mejor que O(n^3)".

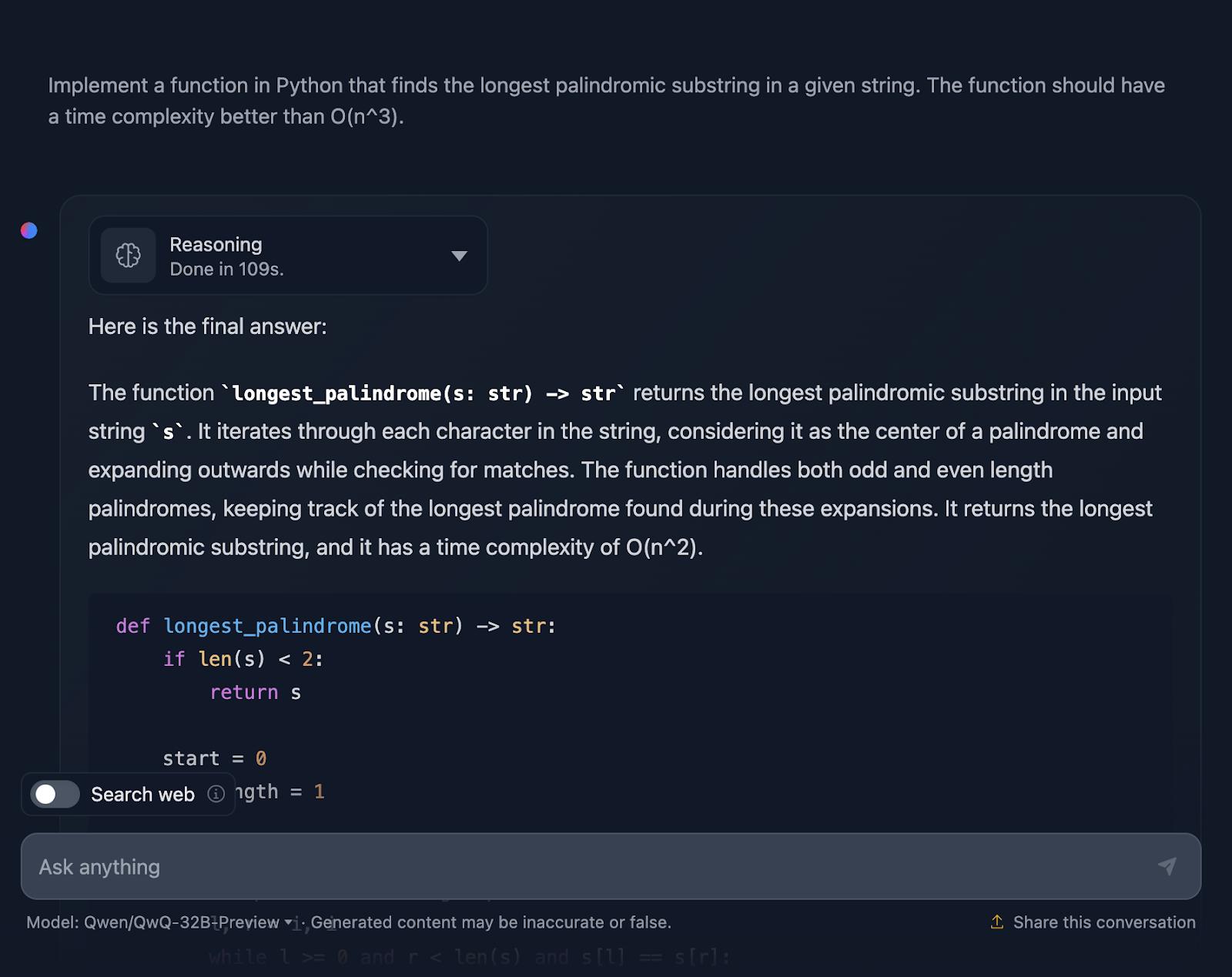
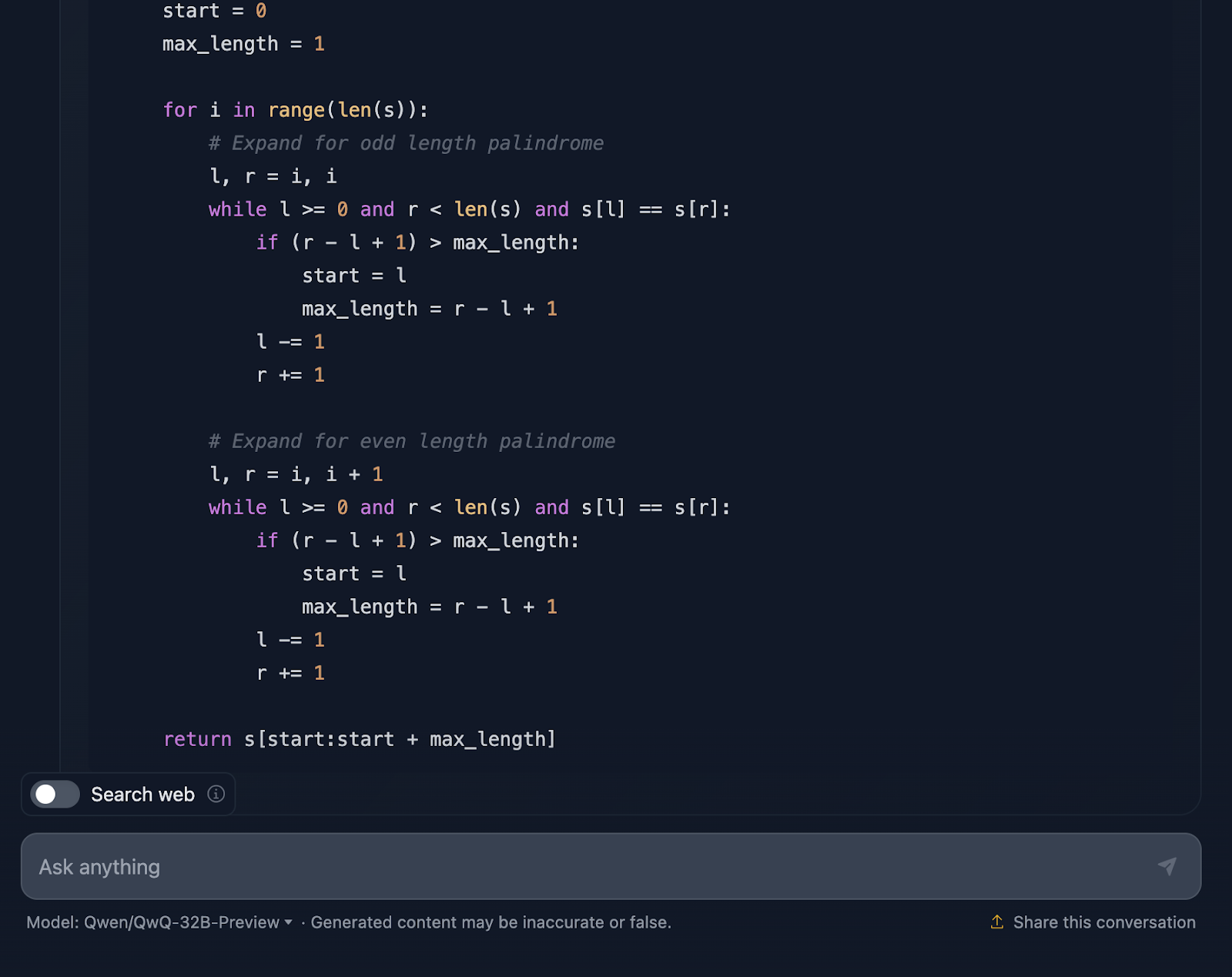
La solución es correcta y proporciona una forma limpia y eficaz de encontrar la subcadena palindrómica más larga con la complejidad requerida. Utiliza un enfoque inteligente expandiéndose alrededor de cada carácter para comprobar si hay palíndromos y maneja bien las longitudes pares e impares. El código es claro y fácil de seguir. Sin embargo, me hubiera gustado ver casos de prueba al final, que es algo que DeepSeek proporcionó. Veamos ahora el razonamiento (sólo mostraré la primera y la última parte para facilitar la lectura):

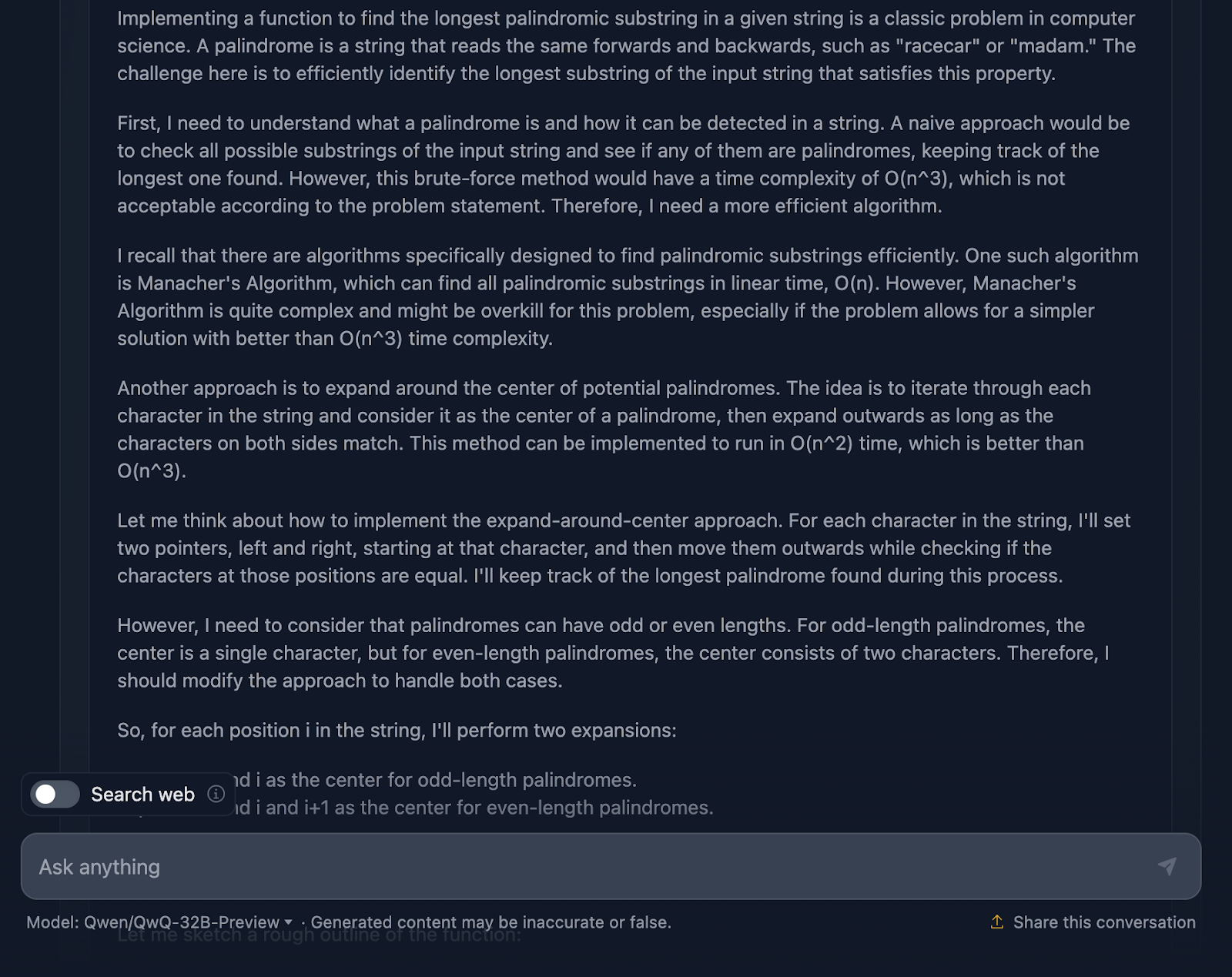
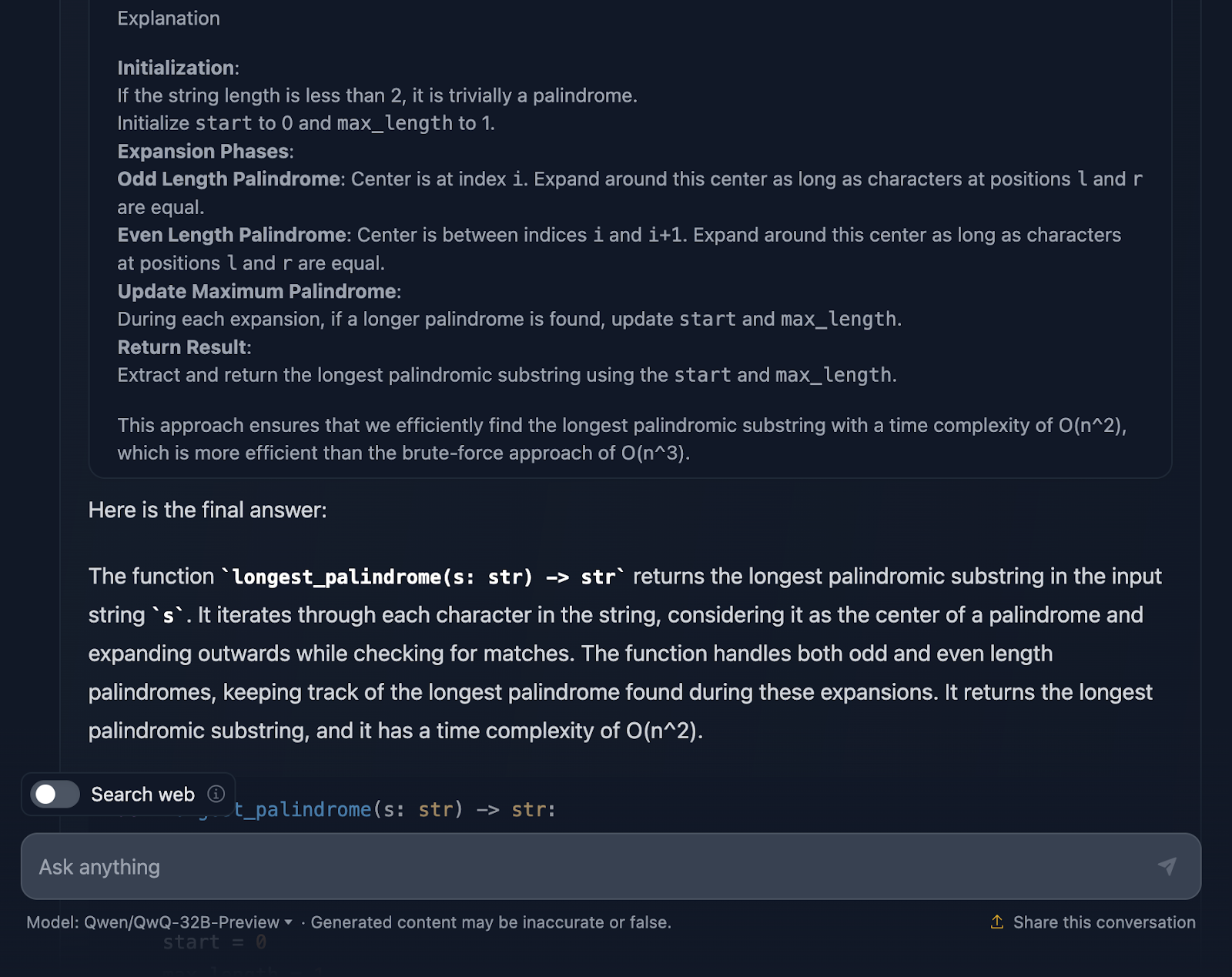
Tengo que decir que es un planteamiento bastante sólido, y de hecho me impresionan algunas partes del razonamiento. Pero hay algunas cosas en las que podría estar un poco más ajustado, así que vamos a hablar de ello.

En primer lugar, el razonamiento comienza abordando lo básico: qué es un palíndromo y por qué un enfoque de fuerza bruta no es el mejor. Luego salta directamente al método de expansión alrededor del centro e incluso menciona el Algoritmo de Manacher con su complejidad O(n). Reconoce que, aunque el de Manacher es más rápido, probablemente sea excesivo para este problema. DeepSeek no mencionó este enfoque, que es algo que esperaba antes de probarlo.  También habla de métodos alternativos, como invertir la cadena u omitir comprobaciones innecesarias, ¡lo cual me parece estupendo!

El método de expansión alrededor del centro se explica con claridad y separa los palíndromos de longitud par de los impares, lo cual es clave para asegurarse de que se cubren todos los casos. 

Destaca la inclusión de casos extremos. Cadenas de un solo carácter, cadenas sin palíndromos, cadenas formadas por todos los caracteres idénticos: todo está ahí. Además, incluso menciona cómo la implementación trata con elegancia las cadenas vacías simplemente devolviéndolas. Ese tipo de minuciosidad es lo que quieres en una explicación.

Me gusta mucho que el resultado final en el razonamiento te ofrezca un desglose del planteamiento, el código de la solución y la explicación, ¡pero me gustaría que esto se incluyera en la respuesta final!

¿Resultó QwQ-32B-Preview mejor que DeepSeek en este caso? Bueno, a pesar de incluir casos de prueba, ¡yo diría que sí!

JavaScript

Ahora voy a probar un reto de codificación en Javascript:

"Escribe una función en JavaScript que determine si un número dado es primo".

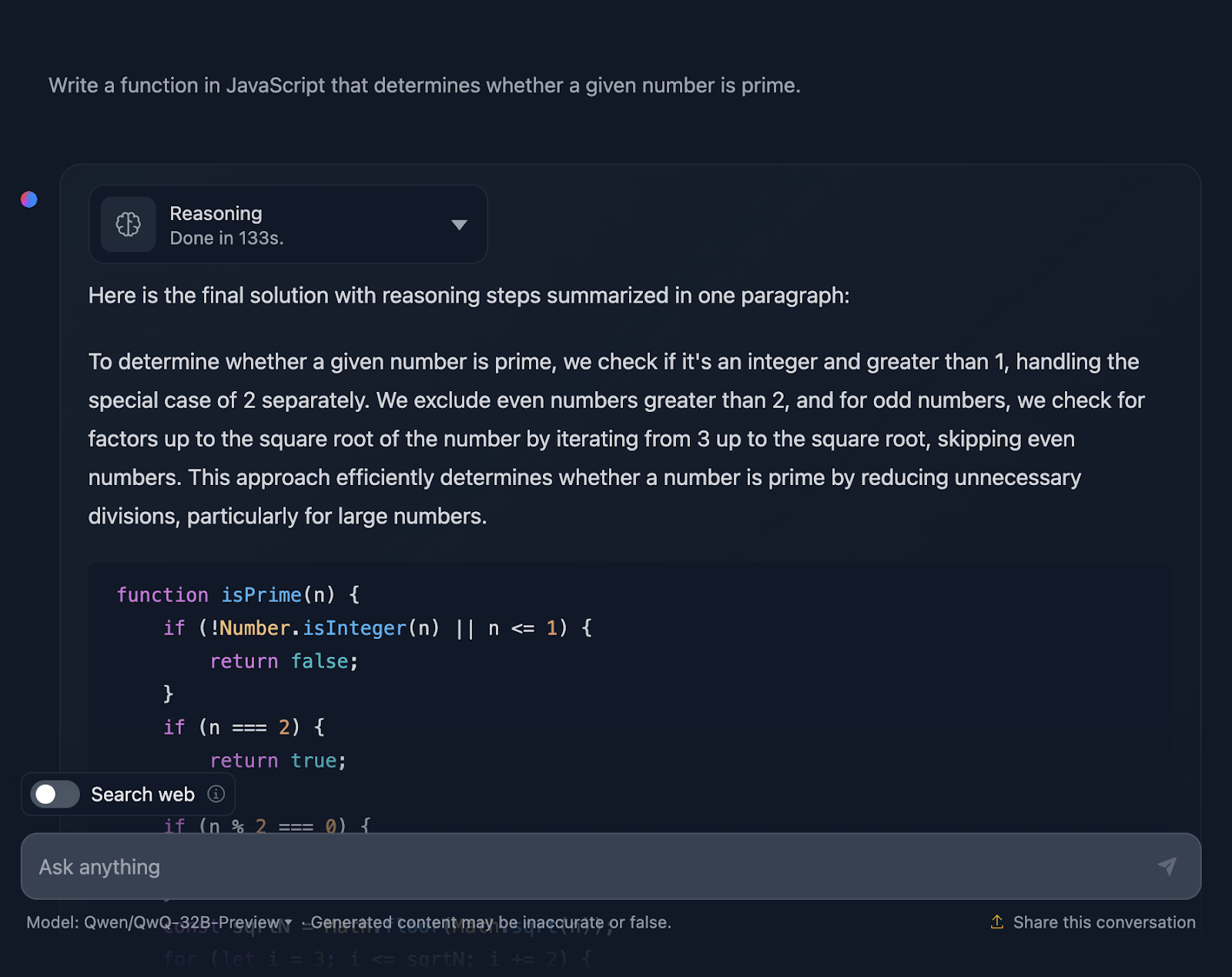
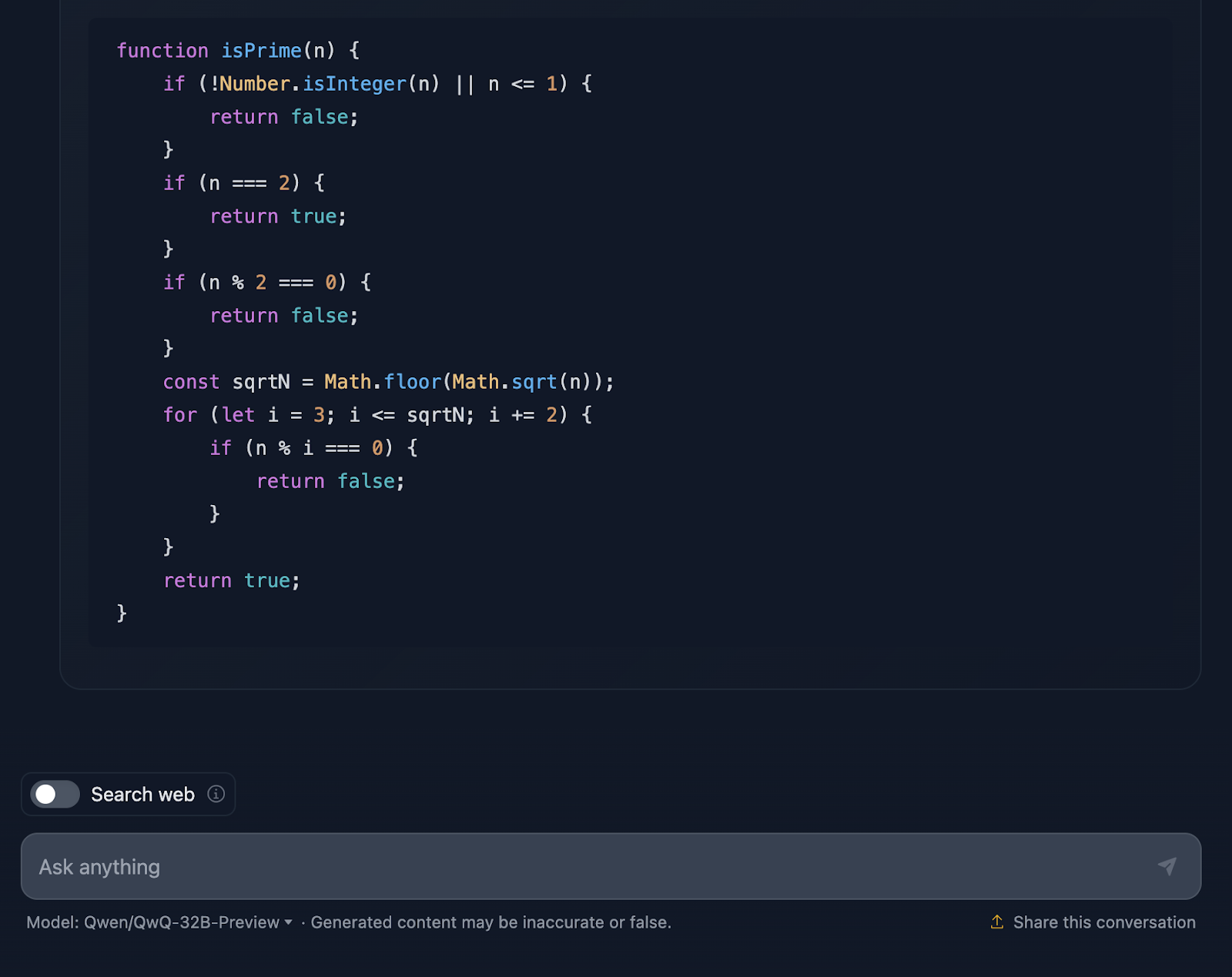
La solución es correcta y muy parecida a la que da DeepSeek. Sin embargo, tardó mucho más en hacer elaltrazonamientoalt, así que veamos cómo ha llegado a esta respuesta (vuelvo a truncar la salida para facilitar la lectura):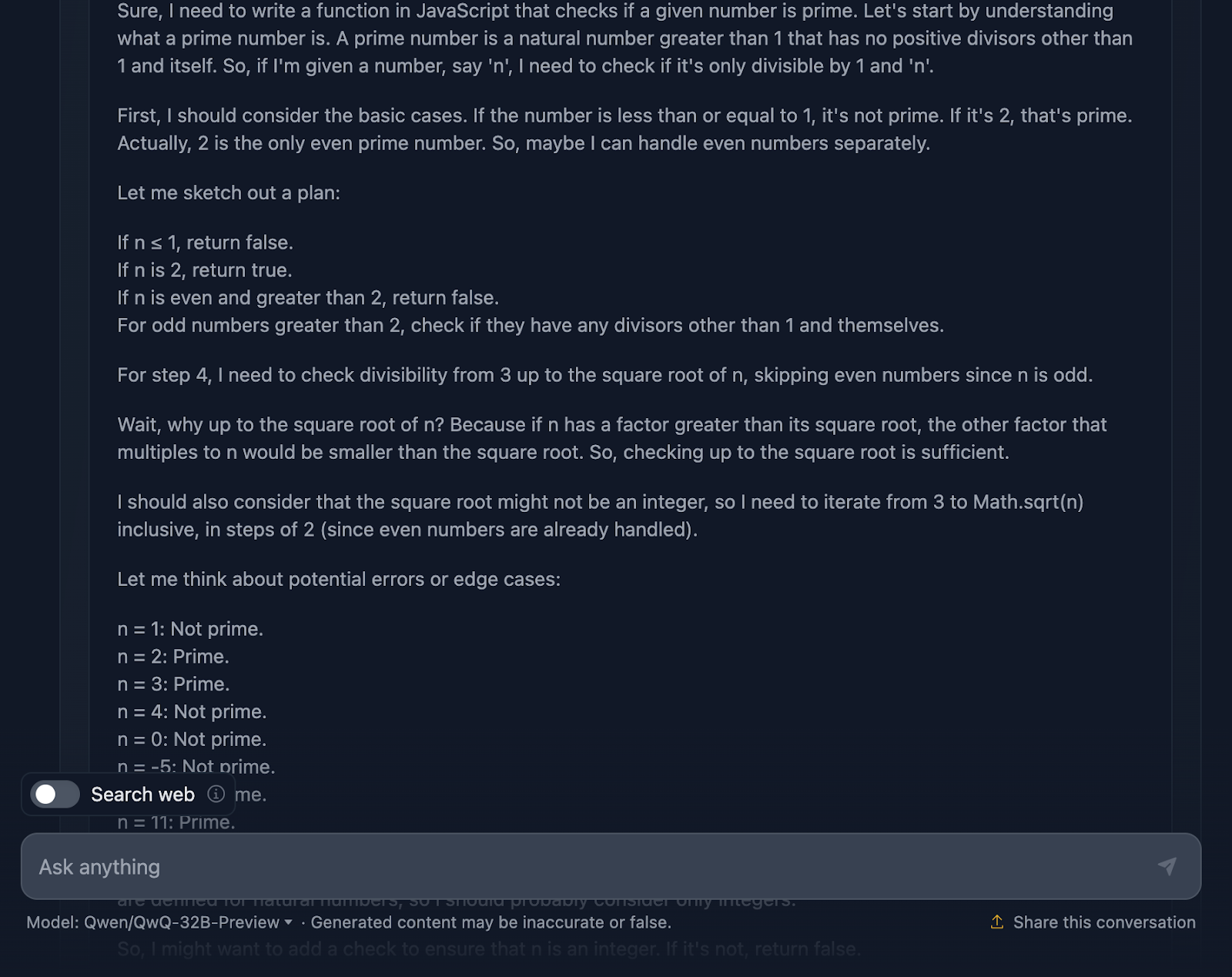

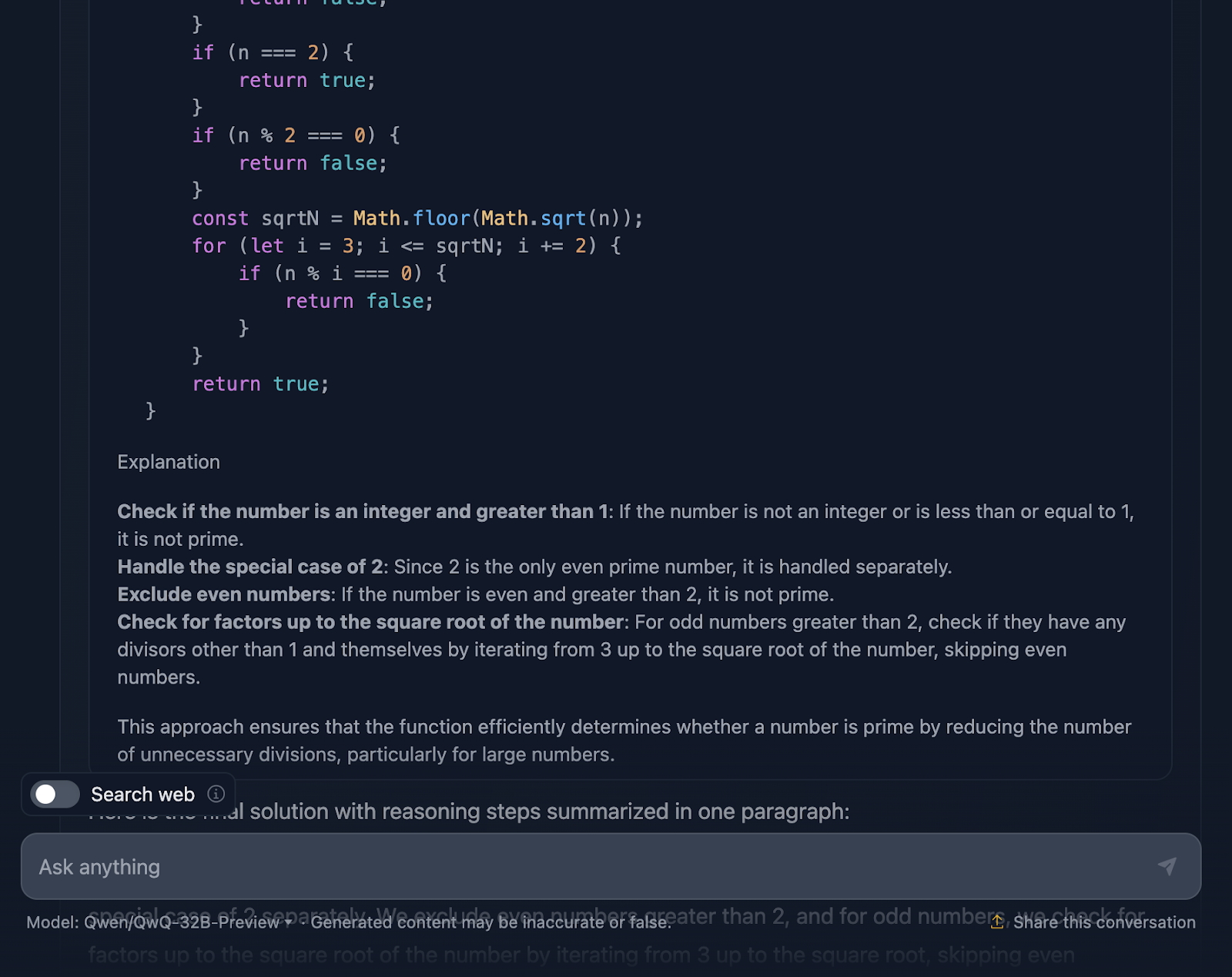
Vale, este razonamiento es especialmente largo comparado con el que proporciona DeepSeek. Veámoslo con más detalle:

En primer lugar, la solución empieza por lo básico. ¿Números menores o iguales que 1? Definitivamente no es de primera. Y el 2 es especial: es el único número primo par. ¿Algún otro número par? Automáticamente, no prima. Esta configuración lógica es clara y tiene mucho sentido cuando se tratan casos límite.

A partir de ahí, llega al meollo de la cuestión: ¿cómo comprobamos eficazmente si un número tiene algún divisor distinto de 1 y de sí mismo? En lugar de comprobar todos los números hasta n, la solución sólo comprueba hasta la raíz cuadrada de n. ¿Por qué? Porque si un número tiene un factor mayor que su raíz cuadrada, su otro factor ya se habrá comprobado por debajo de la raíz cuadrada. Super eficiente, y evita cálculos innecesarios. 

Para agilizar aún más las cosas, la solución se salta todos los números pares después de tratar el 2. Por tanto, sólo comprueba los números impares, empezando por 3 y avanzando de 2 en 2. Se trata de una optimización que reduce el trabajo a la mitad.

A continuación, pasamos a la puesta en práctica. La función comienza validando la entrada. ¿Es un número entero? ¿Es mayor que 1? Si no, es un rápido "no primo". Este tipo de validación es una gran práctica y mantiene la solidez de la función. Comienza entonces la lógica del bucle, comprobando los divisores desde 3 hasta la raíz cuadrada de n. Si cualquier divisor funciona, no es primo. Si no, está todo claro y el número es primo.

Lo mejor es que el razonamiento no se detiene en la aplicación. Se sumerge en casos extremos -como números negativos, no enteros o entradas extrañas como 2,5- y se asegura de que la función los maneja correctamente. Incluso hay un guiño a los límites de JavaScript con los números realmente grandes y una sugerencia de utilizar BigInt para esos escenarios límite, lo que me pareció un gran añadido al razonamiento.

La solución incluye casos de prueba detallados para mostrar exactamente cómo funciona para números como 1, 2, 3, e incluso números más grandes como 13 y 29. Cada prueba se explica paso a paso, para que no haya confusión sobre por qué funciona.

Ahora bien, ¿podría esta solución ir más allá? Claro, siempre se puede mejorar. Por ejemplo, si estuvieras trabajando con números masivos, podrías explorar algoritmos avanzados como Miller-Rabin o la prueba de primalidad de Fermat. Pero para el uso diario, esta solución consigue un gran equilibrio entre sencillez, eficacia y legibilidad.

Entonces, ¿cuál es el veredicto? Este razonamiento es sólido, claro y práctico, y hace un gran trabajo para asegurarse de que el código es robusto, algo que DeepSeek no tuvo muy en cuenta. ¡Creo que gana QwQ-32B-Preview!

Razonamiento lógico

Por último, veamos algunas pruebas de razonamiento lógico.

El problema del lobo, la cabra y la col

Voy a probar un puzzle clásico:

"Un hombre tiene que cruzar un río con un lobo, una cabra y un repollo. Su barco sólo puede transportarse a sí mismo y a otra cosa. Si se le dejara solo, el lobo se comería a la cabra, y la cabra se comería la col. ¿Cómo puede cruzarlo todo de forma segura?"

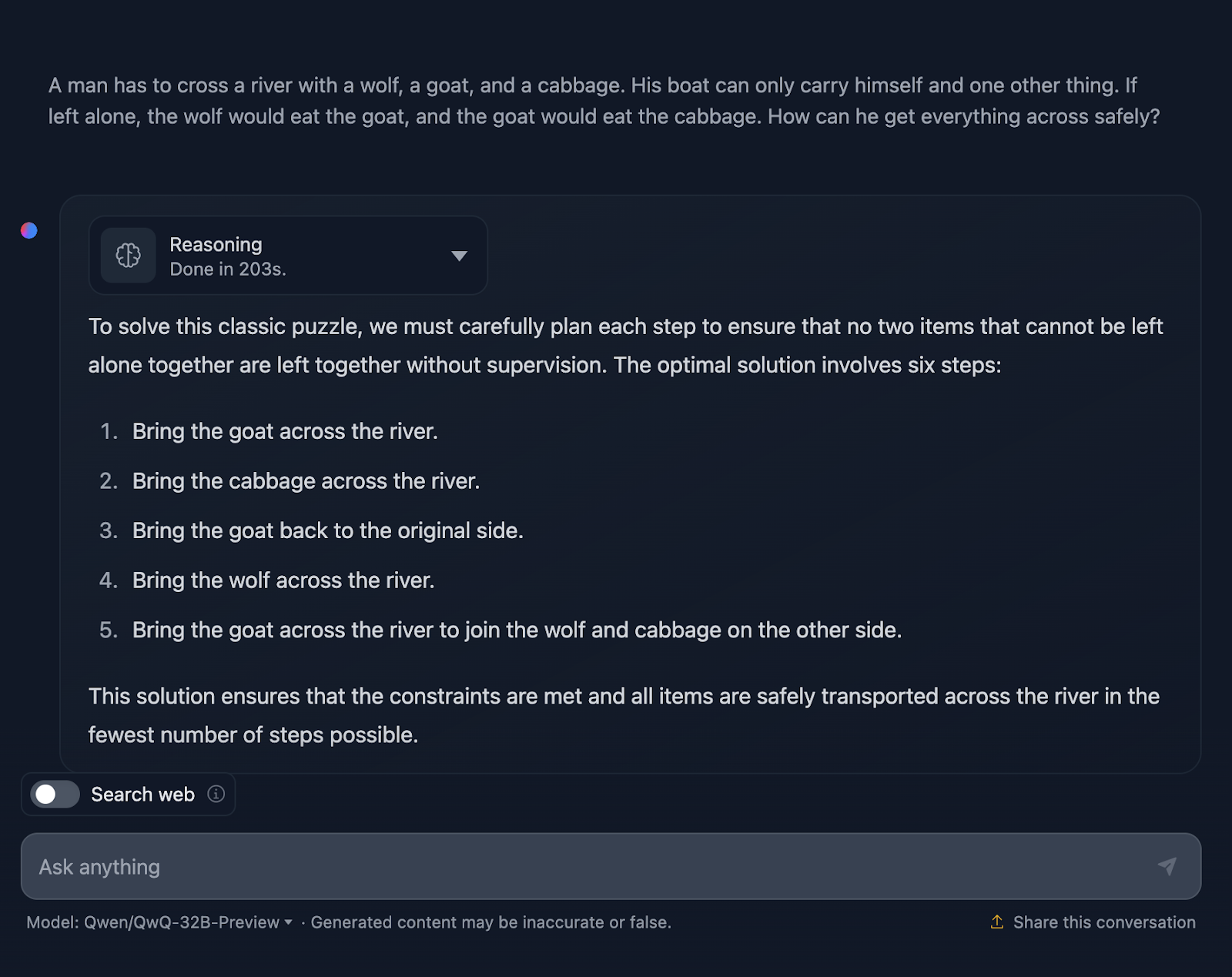
De acuerdo, la solución al problema es correcta, pero hay un par de cosas que deben aclararse. Afirma que la solución óptima implica seis pasos; sin embargo, sólo se proporcionan cinco viñetas. Esto ya es una inexactitud.

Además, puedes pensar que éste es un enfoque mejor en términos de eficacia en comparación con el resultado de DeepSeek, que requería siete pasos. Sin embargo, este planteamiento también consta en realidad de siete pasos. Por alguna razón no se mencionaron los pasos para volver solo. Debería haber salido lo siguiente:

1. Lleva la cabra al otro lado del río.
2. Vuelve solo.
3. Lleva la col al otro lado del río.
4. Vuelve a colocar la cabra en el lado original.
5. Lleva al lobo al otro lado del río.
6. Vuelve solo.
7. Lleva a la cabra al otro lado del río para que se reúna con el lobo y la col al otro lado.

Además, cuando estaba realizando el razonamiento, me di cuenta de esto (¡y conseguí hacer una captura de pantalla!):

Esto me hizo preguntarme si había algo en el razonamiento...

Echemos un vistazo:

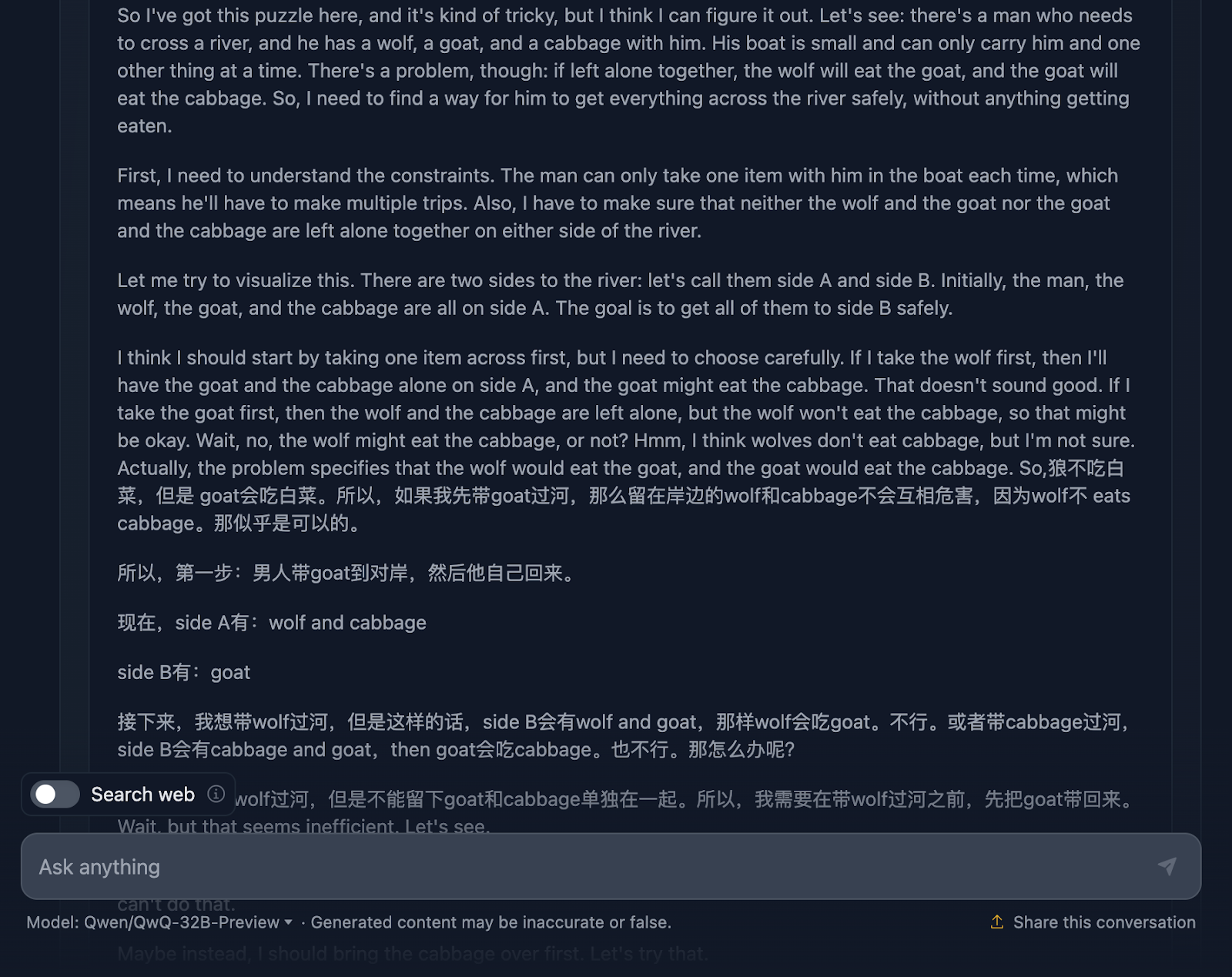
El razonamiento empieza a lo grande, asegurándose a fondo de que comprende el problema, los retos y las limitaciones. Sin embargo, aquí es donde las cosas empiezan a complicarse. Este es un gran ejemplo de las limitaciones de este modelo del que hemos hablado antes, que mezcla dos lenguas. Esto da lugar a razonamientos incomprensibles (al menos para mí, que no entiendo el idioma, ¡supongo que es chino!). Ahora compartiré algunas otras partes del razonamiento para ilustrar esto, pero me saltaré otras partes porque es demasiado largo.

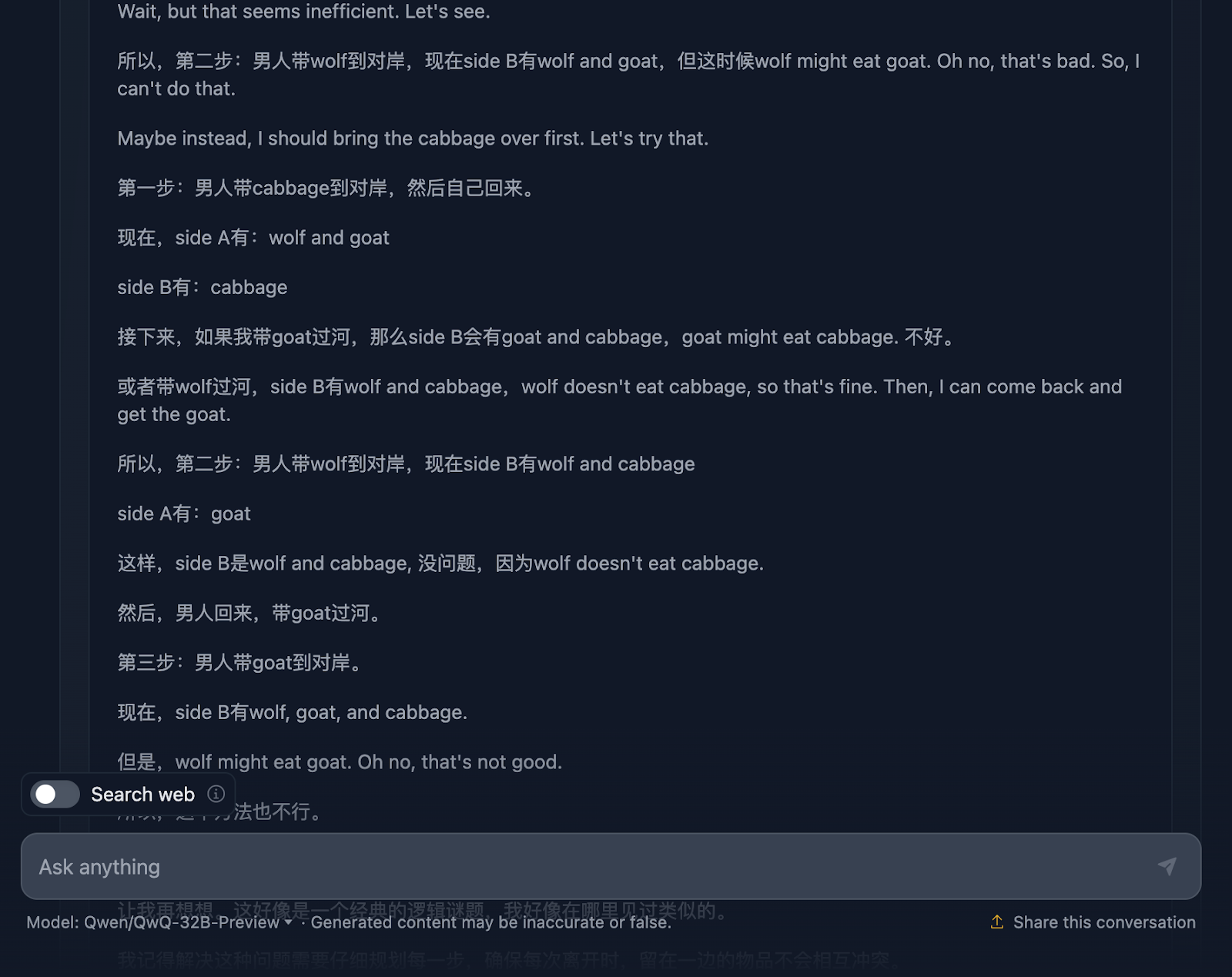
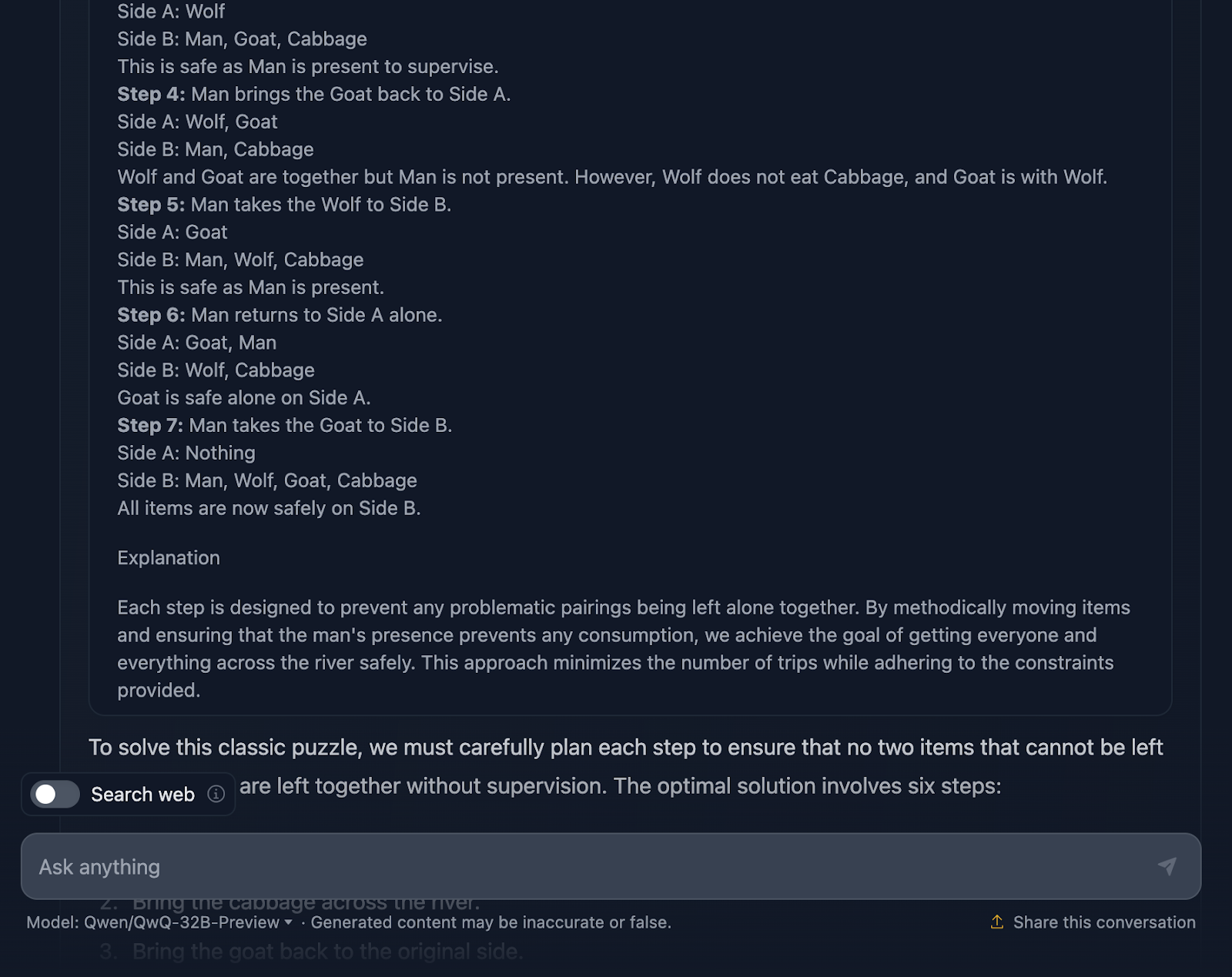
Sin embargo, ¡la solución final es excelente! Esboza la configuración inicial, las limitaciones, el objetivo y la estrategia, junto con un plan de solución muy claro que incluye todos los pasos, curiosamente .

¿Por qué no se reflejó esto en la respuesta final? Incluso añadió una explicación final. Me gustaría que la salida de la respuesta final hubiera coincidido con lo que se mostraba en el razonamiento, ¡y me pregunto por qué no lo hizo!

Puzzle de las bolas de pesaje

Por último, probemos este acertijo lógico clásico que pone a prueba la capacidad del modelo para dar con una estrategia óptima utilizando el razonamiento deductivo.

DESCARGO DE RESPONSABILIDAD: Éste es el resultado que obtuve después de tres intentos: el modelo empezó a generar una respuesta, pero se atascó o produjo un error y no pudo seguir generando. Además, me saltaré el razonamiento de éste, ya que era extremadamente largo, ¡además de que la salida ya es bastante extensa! Echemos un vistazo (la salida también está truncada):

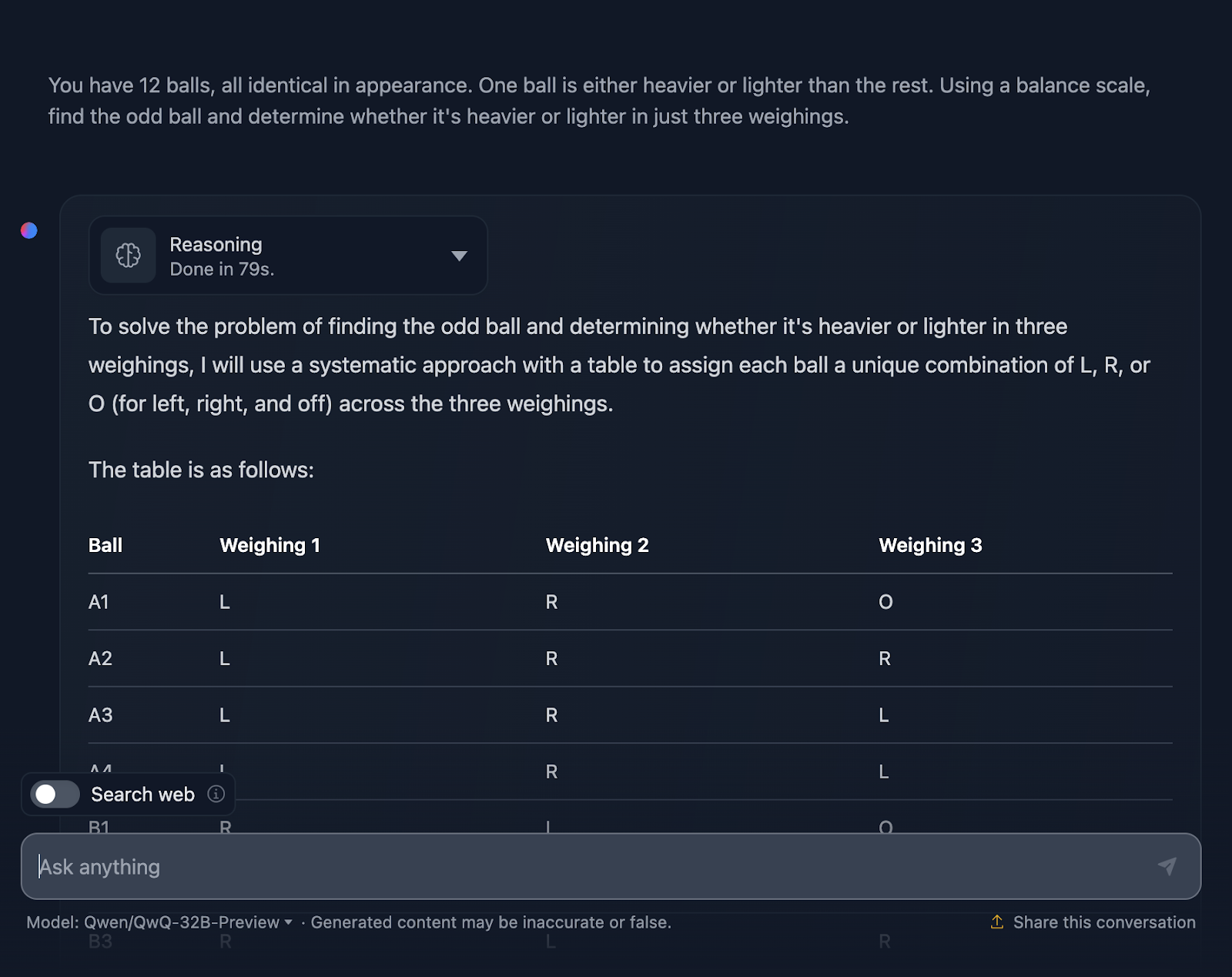
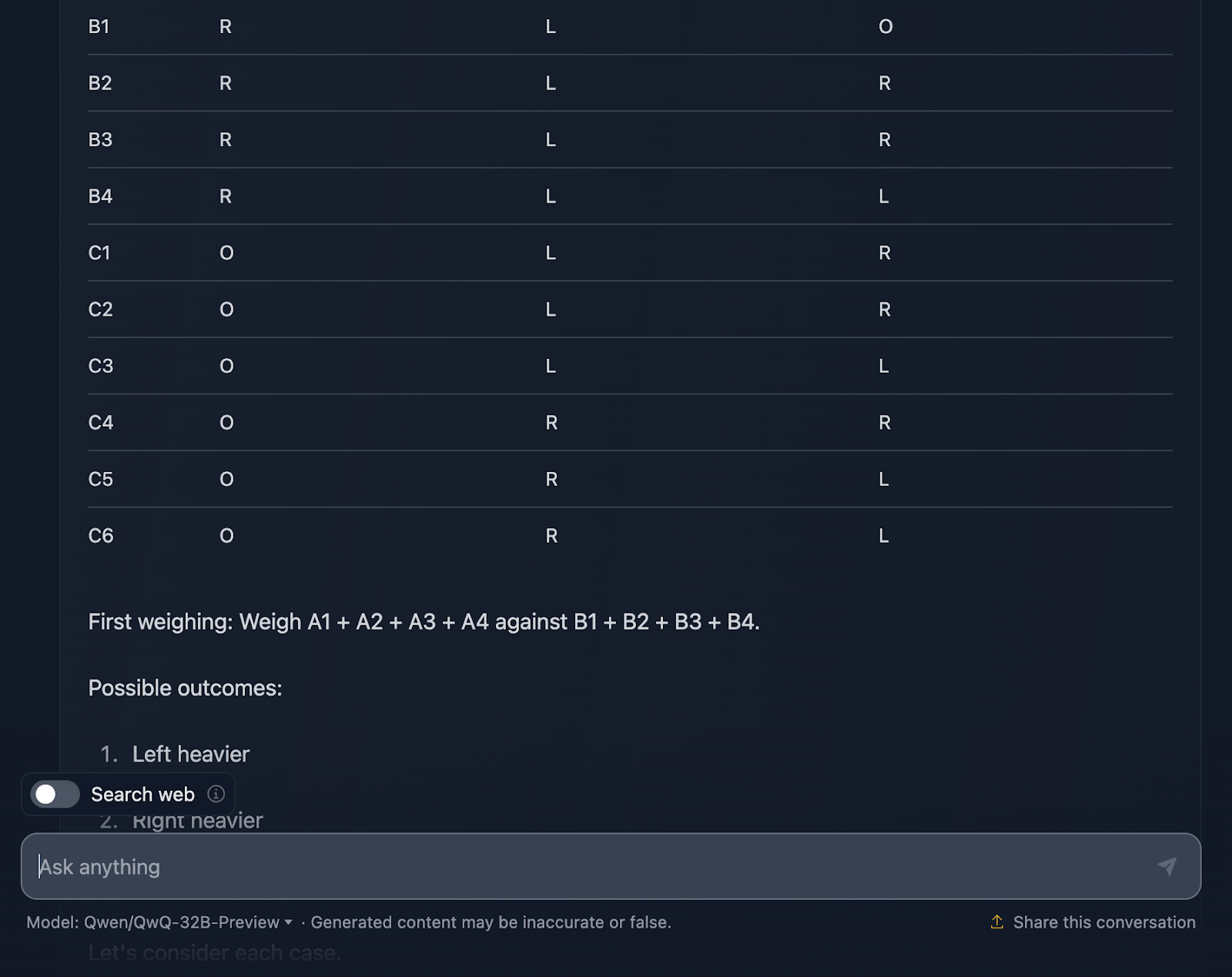
Tengo que decir que estoy muy impresionado con el resultado. La solución comienza con una explicación muy clara del problema y expone un plan mediante una tabla sistemática, lo que me parece muy útil y algo que DeepSeek no incluyó. Cada bola obtiene su propia combinación única en los tres pesajes, asegurándose de que se tienen en cuenta todos los escenarios posibles. 

Me gusta mucho cómo divide el problema en casos y subcasos: "Izquierda más pesada", "Derecha más pesada" e "Igual". Este enfoque incremental toma un problema complejo y lo hace manejable. Cada pesada se basa en los resultados de la anterior. Vas reduciendo la bola extraña paso a paso, a la vez que determinas si es más pesada o más ligera.

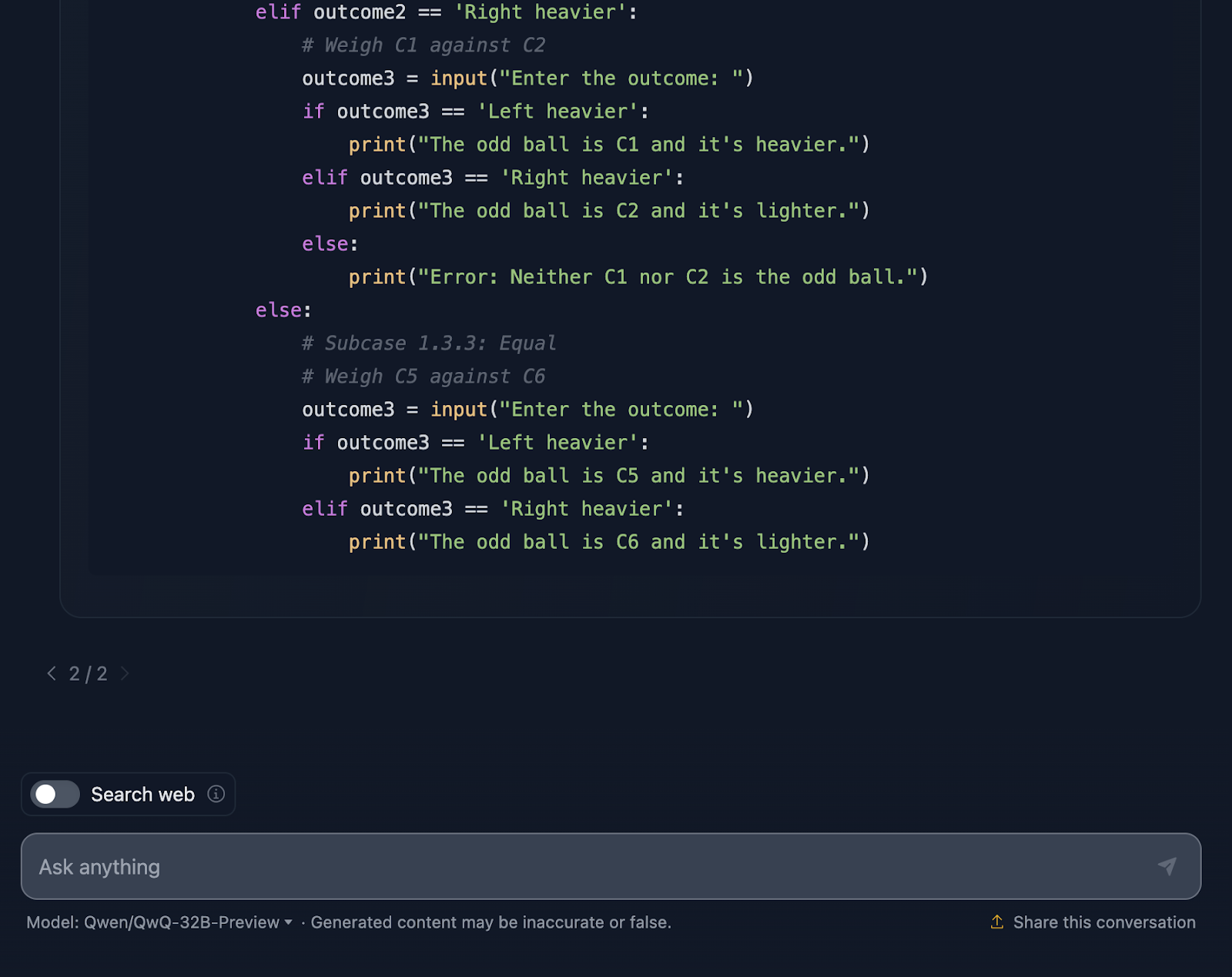
Por último, la solución incluye un fragmento de código Python, ¡que no esperaba!  Es interactivo y permite a los usuarios simular los pesajes, lo que hace que el proceso sea más fácil de seguir e incluso divertido de explorar. Esta solución no deja nada al azar. Se cubren todos y cada uno de los resultados de los pesajes, asegurándose de que ningún bicho raro pueda escapar a la detección. 

Sin embargo, una cosa es que el fragmento de Python supone una entrada perfecta del usuario. Si alguien introduce un resultado de pesaje no válido, el código no tiene tratamiento de errores para detectarlo. Un poco de robustez aquí podría llevarlo al siguiente nivel. 

Yo diría que ésta es una respuesta excelente: supera a la de DeepSeek en cuanto a que la hace más clara y ayuda a los usuarios a visualizarla mejor con las tablas y el código Python.

Comparación de velocidades: DeepSeek vs. QwQ

Por último, voy a comparar la velocidad de cada modelo para cada prueba a la hora de realizar el razonamiento y proporcionar una solución. Algo a tener en cuenta es que los resultados dependerían de muchos factores, y los modelos no siempre rendirían a la misma velocidad, pero me parece interesante que DeepSeek fuera más rápido en todas las tareas que probé.

QwQ-32B-Preview Benchmarks

Las pruebas de QwQ-32B-Preview revelaron lo bien que maneja los difíciles retos matemáticos, de codificación y de razonamiento, ¡aunque algunos eran mejores que otros!

A continuación te mostramos el rendimiento de QwQ en algunas pruebas exigentes:

• GPQA (razonamiento científico de nivel universitario): Puntuación 65,2%, mostrando un sólido razonamiento científico de nivel universitario.
• AIME (temas avanzados de matemáticas): Puntuado 50,0%, demostrando sólidas habilidades en temas matemáticos avanzados como geometría, álgebra y teoría de números.
• MATH-500 (problemas matemáticos de amplio espectro): Consiguió un impresionante 90,6%, demostrando su capacidad para resolver una amplia gama de problemas matemáticos.
• LiveCodeBench (tareas de programación del mundo real): Puntuación 50,0%, mostrando sólidas habilidades de programación en escenarios de codificación del mundo real .

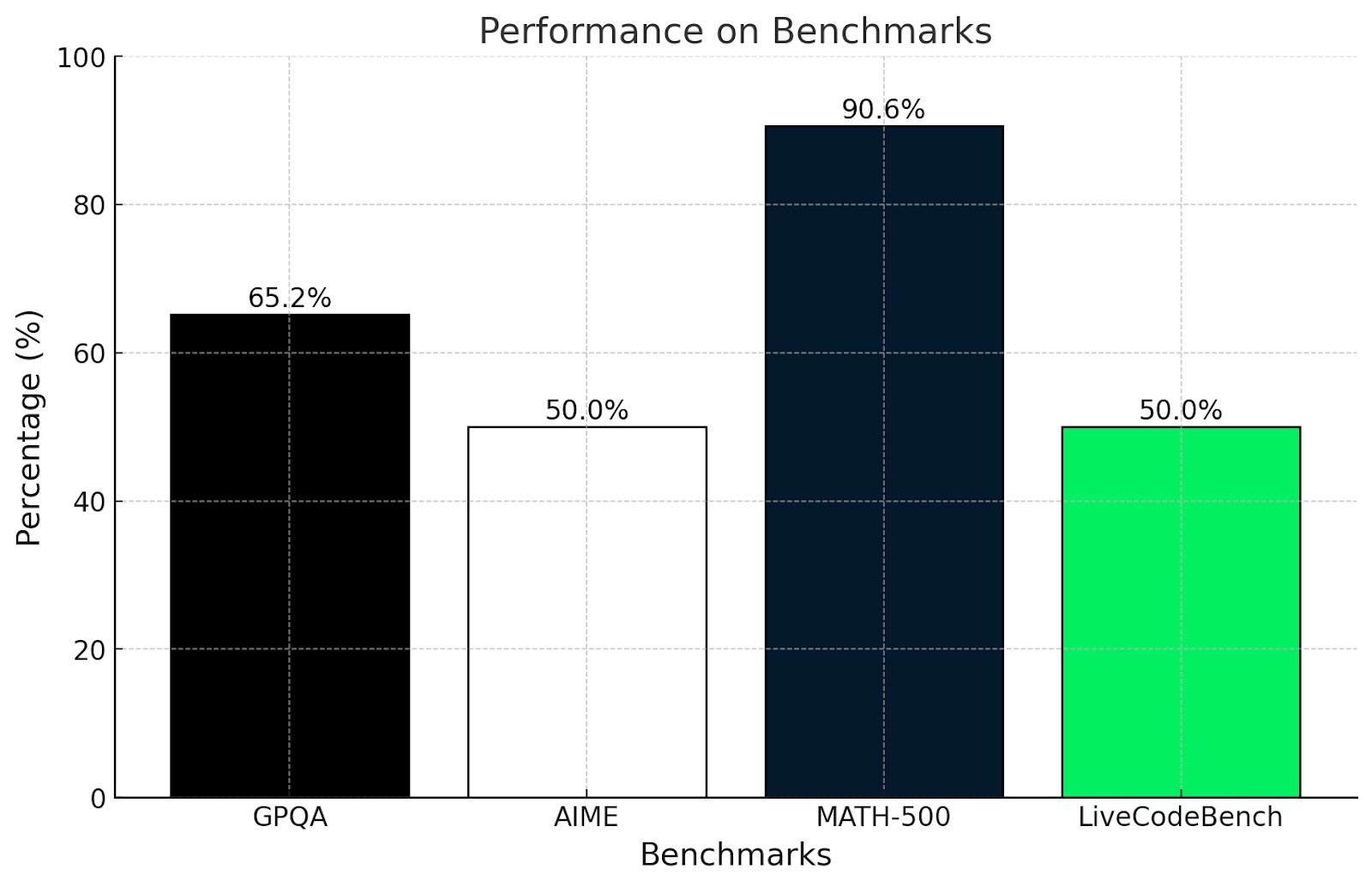
¿Me sorprenden estos resultados? La verdad es que no. Estos resultados coinciden con las pruebas realizadas en este artículo.

El test GPQA mide la comprensión del razonamiento científico a nivel de postgrado. Una puntuación del 65,2% demuestra que es bueno utilizando la lógica y las matemáticas para resolver problemas, pero podría tener dificultades con preguntas muy especializadas o profundamente conceptuales, que hemos visto en las pruebas matemáticas más complejas de este artículo.

Del mismo modo, el examen AIME es conocido por temas de matemáticas avanzadas como geometría y álgebra. Una puntuación del 50% muestra que QwQ-32B-Preview puede resolver algunos de estos problemas, pero tiene dificultades con los realmente inteligentes, que requieren un pensamiento innovador. 

Obtener una puntuación superior al 90% en MATH-500 es muy impresionante y demuestra que QwQ-32B-Preview es excelente para resolver un problema matemático general con una precisión decente.

LiveCodeBench mide la capacidad de programación en escenarios de codificación. Una puntuación del 50% significa que QwQ-32B-Preview puede manejar los conceptos básicos de codificación y seguir instrucciones claras, pero puede tener problemas con tareas más complicadas.

QwQ es realmente fuerte cuando se trata de resolver problemas estructurados y utilizar la lógica, como se ve en las puntuaciones de GPQA y MATH-500. Se desenvuelve bien con las matemáticas y las ciencias, pero encuentra más desafiantes los problemas creativos o poco convencionales, como en AIME. Sus habilidades de programación son decentes, pero podrían ser mejores cuando se trata de tareas de codificación desordenadas o poco claras.

Veamos ahora las métricas de QwQ 32B-preview junto con las métricas de DeepSeek y otros modelos para comparar:

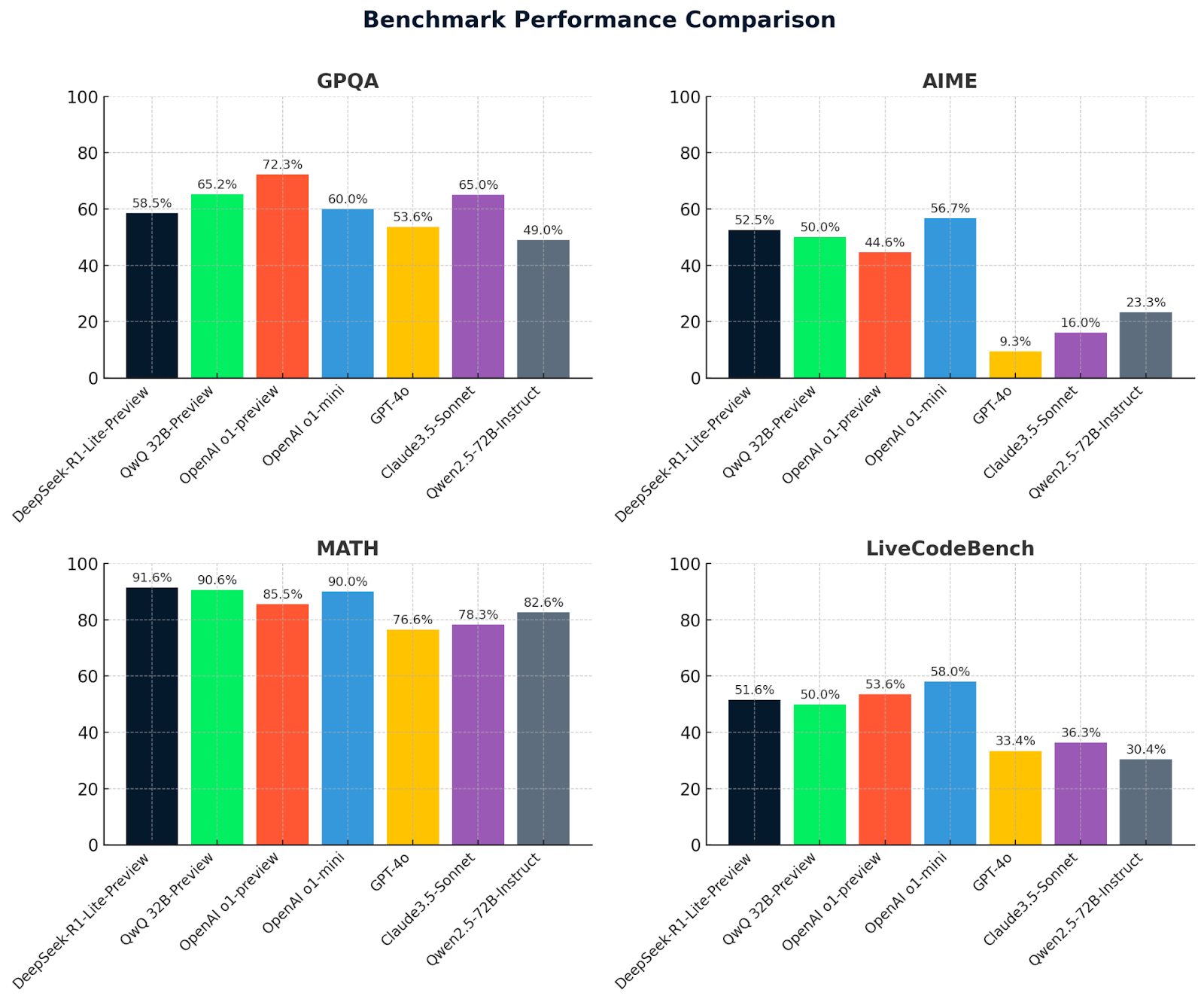
Estos gráficos ofrecen una comparación clara del rendimiento de los modelos en cuatro puntos de referencia: GPQA, AIME, MATH, and LiveCodeBench. DeepSeek-R1-Lite-Preview destaca por sus buenos resultados, especialmente en MATEMÁTICAS (91,6%), mostrando su capacidad en razonamiento avanzado y resolución de problemas.

QwQ-32B-preview obtiene buenos resultados en todas las pruebas de referencia, destacando especialmente en MATEMÁTICAS (90,6%), lo que demuestra sus sólidas capacidades matemáticas y de razonamiento general. Otros modelos como OpenAI O1-preview y Claude 3.5-Sonnet muestran puntos fuertes variados, pero en general quedan por detrás de QwQ-32B-preview y DeepSeek en áreas clave, lo que pone de relieve la ventaja competitiva de estos dos modelos líderes.

Conclusión

Probar QwQ-32B-Preview fue muy divertido, y espero no haber sido demasiado parcial, aunque tengo que admitir que DeepSeek-R1-Lite-Preview me impresionó mucho. 

QwQ-32B-Preview es claramente un modelo fuerte con capacidades asombrosas, pero no es perfecto y la respuesta final dada por el modelo no siempre coincide con la respuesta final en el proceso de razonamiento, que a menudo tenía una solución mejor que la que se presentó realmente.

¿Has probado QwQ? ¿Qué te ha parecido? ¿Te gusta más que DeepSeek? Y quién sabe, quizá el próximo gran modelo sea el que supere a todos los demás en todos los parámetros. ¡Es un momento tan emocionante ver cómo evolucionan estas herramientas!