Testei o QwQ-32B-Preview: Modelo de raciocínio do Alibaba

O que é o QwQ-32B-Preview? 

O QwQ-32B-Preview é um modelo criado para lidar com tarefas de raciocínio avançadas que vão além da simples compreensão de texto. Seu objetivo é resolver problemas desafiadores, como codificação e raciocínio matemático. Como uma versão "Preview", ela ainda está sendo refinada. Ele tem acesso de código aberto em plataformas como a Hugging Face, para que você possa testar, melhorar e dar feedback sobre o modelo, se quiser!

Você deve levar em conta que o QwQ-32B-Preview é um modelo experimental. Embora seja promissor, ele também tem algumas limitações importantes:

• Mistura de idiomas: O modelo pode alternar inesperadamente entre idiomas, tornando suas respostas menos claras.
• Raciocínio circular: Às vezes, ele fica preso em ciclos de raciocínio repetitivos, o que leva a respostas longas sem uma conclusão clara.
• Preocupações com a segurança: O modelo ainda precisa de recursos de segurança mais robustos para garantir o uso confiável e seguro, portanto, recomenda-se cautela ao utilizá-lo.
• Lacunas de desempenho: Está comprovado que ele tem um bom desempenho em matemática e codificação, mas poderia melhorar em áreas como raciocínio de senso comum e compreensão de nuances sutis de linguagem.

Como acessar o QwQ-32B-Preview?

Você pode acessar o QwQ-32B-Preview por meio de HuggingChatonde, no momento, ele está sendo executado gratuitamente e sem quantização. Para usar o QwQ-32B-Preview:

1. Visite o HuggingChat: https://huggingface.co/chat/
2. Selecione QwQ-32B-Preview entre os modelos disponíveis
3. Comece a interagir com o modelo

O teste do morango

Começaremos com o conhecido Teste do Morango. O prompt é: "Quantas vezes a letra 'r' ocorre em 'strawberry'?"

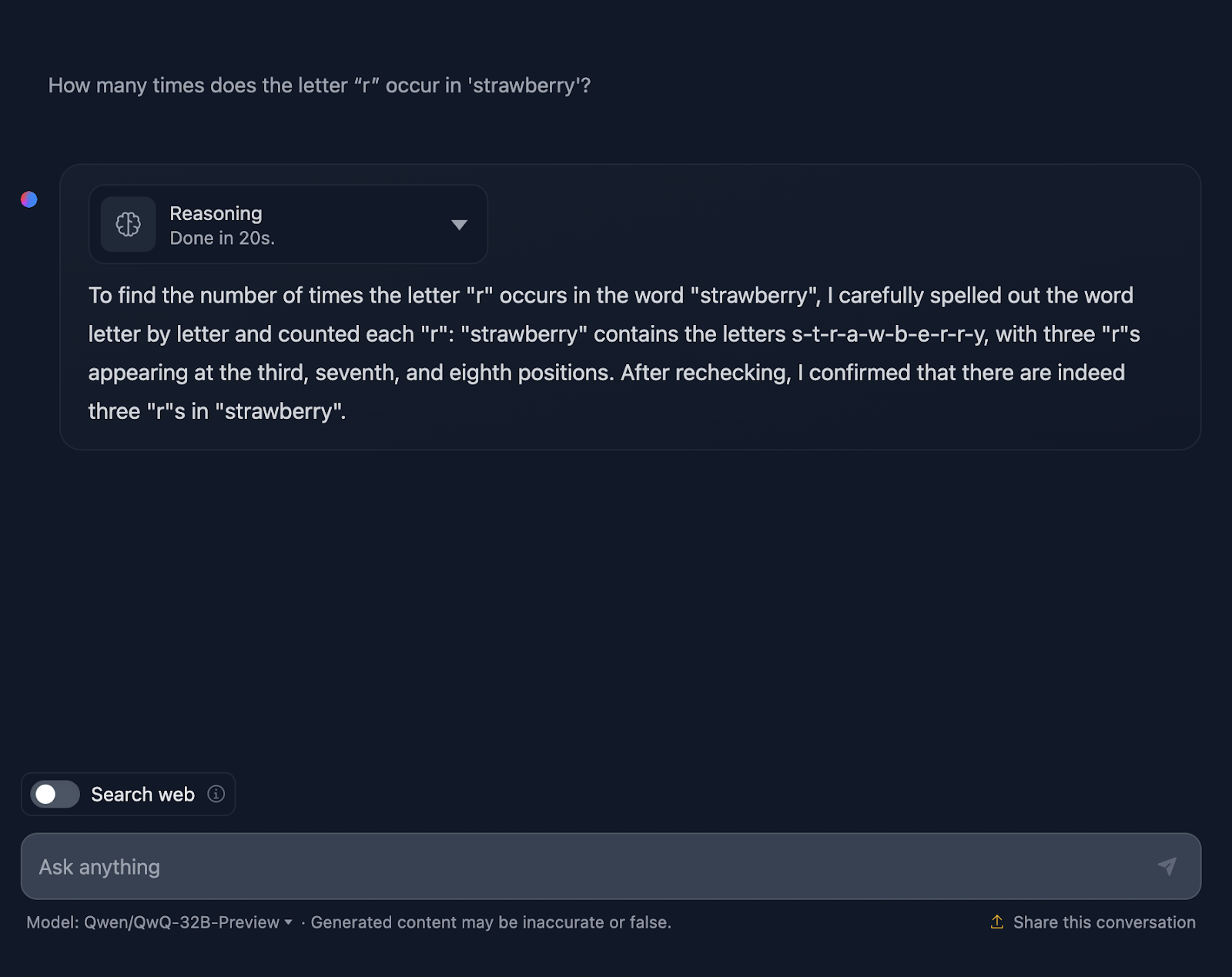
Certo, isso já está ficando interessante! 

Ele conta as letras corretamente, mas afirma incorretamente que os "r "s aparecem na terceira, sétima e oitava posições, o que não é verdade. As posições corretas são a terceira, a oitava e a nona. Para referência, isso é algo que o DeepSeek tratou corretamente.

Vamos dar uma olhada mais de perto no raciocínio do QwQ-32B-Preview:

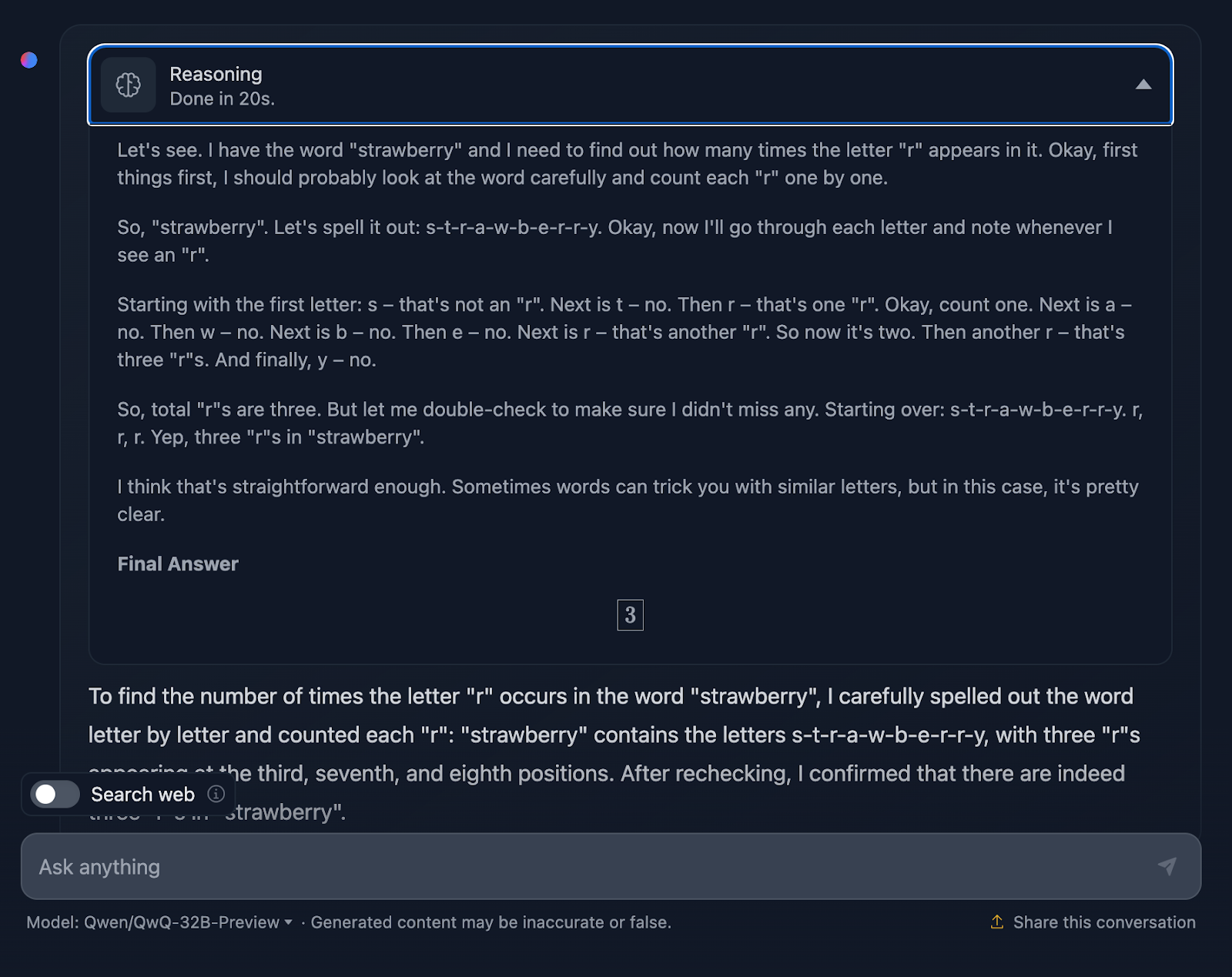
O raciocínio do QwQ-32B-Preview foi muito mais curto do que o fornecido pelo DeepSeek. No entanto, nesse caso, ao contar as letras, ele não considerou suas posições, e acho que foi por isso que ele errou. É interessante porque ele forneceu essas informações, embora não fossem necessárias - eu não solicitei as posições dos "r", apenas o número de ocorrências. O fornecimento de informações extras e desnecessárias acabava introduzindo erros.

Raciocínio matemático

Para testar o raciocínio matemático do modelo, realizaremos três testes que variam em complexidade.

Área do triângulo

O prompt é: "Se um triângulo tem lados de comprimento 3, 4 e 5, qual é sua área?" Vamos ver como você lida com isso:

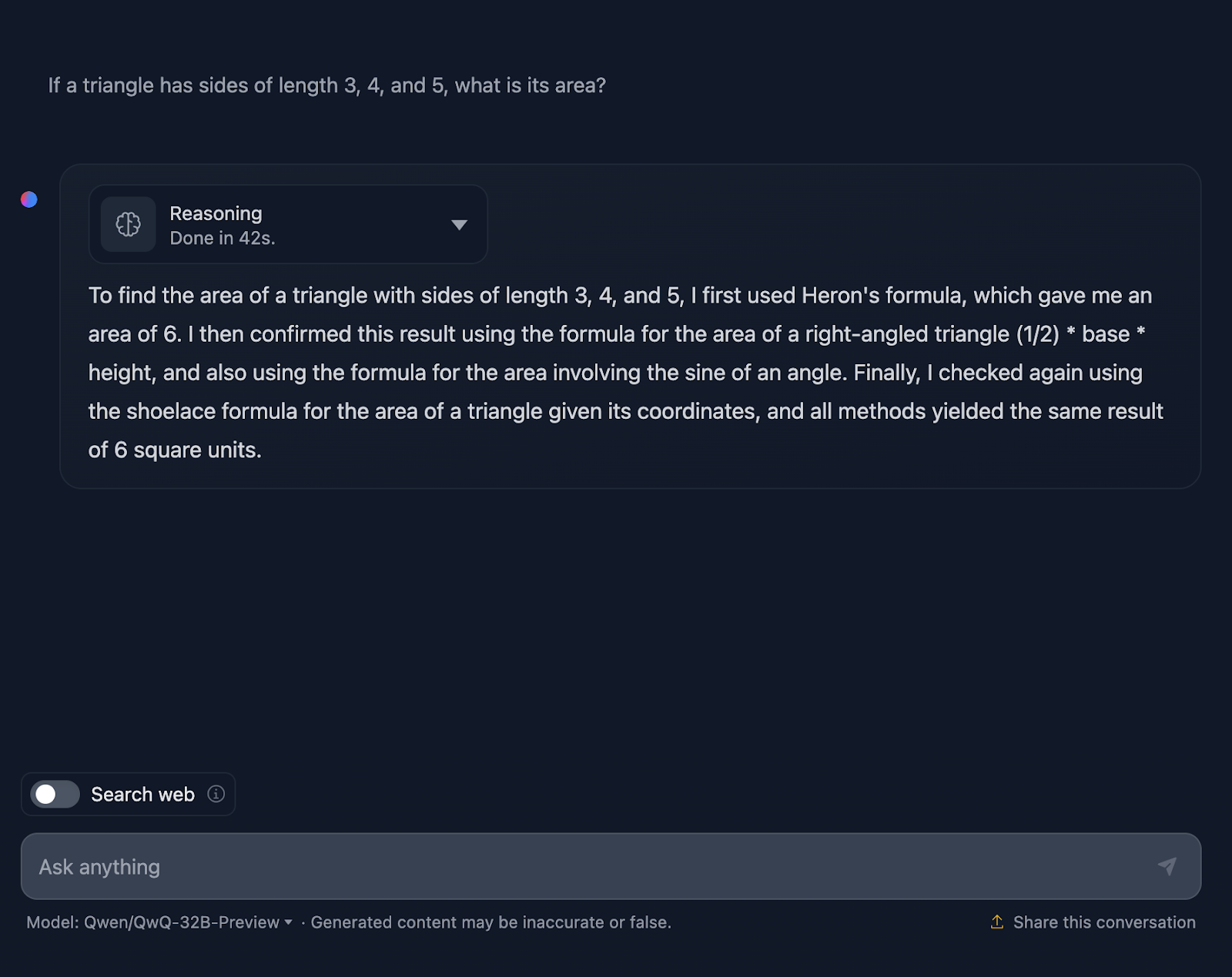
A resposta está correta e explica os métodos usados para chegar à conclusão. No entanto, nenhuma das fórmulas ou cálculos está incluído na solução, o que é bom, pois isso não foi solicitado. No entanto, teria sido uma boa adição, algo que o DeepSeek forneceu. Vamos dar uma olhada no raciocínio agora:

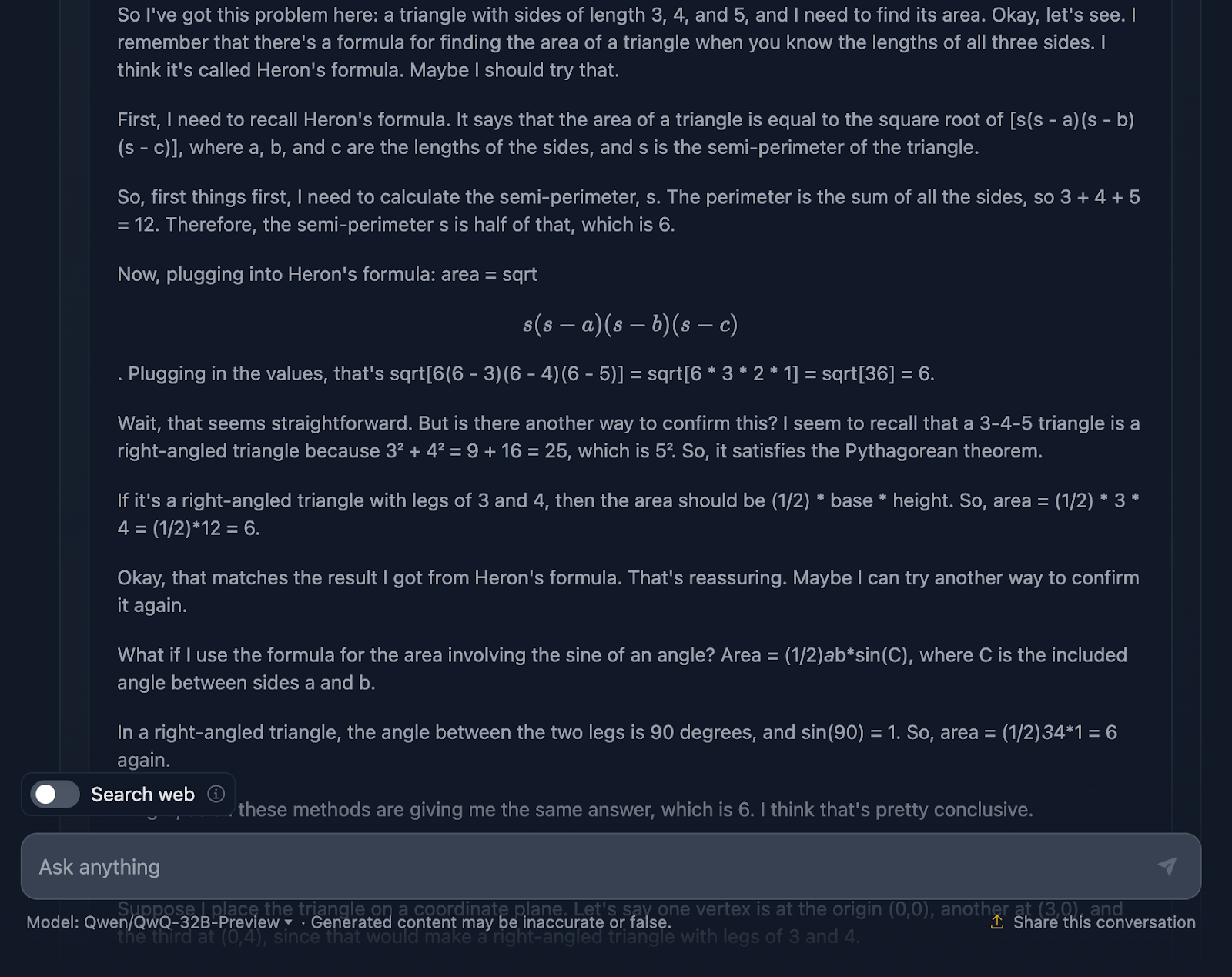
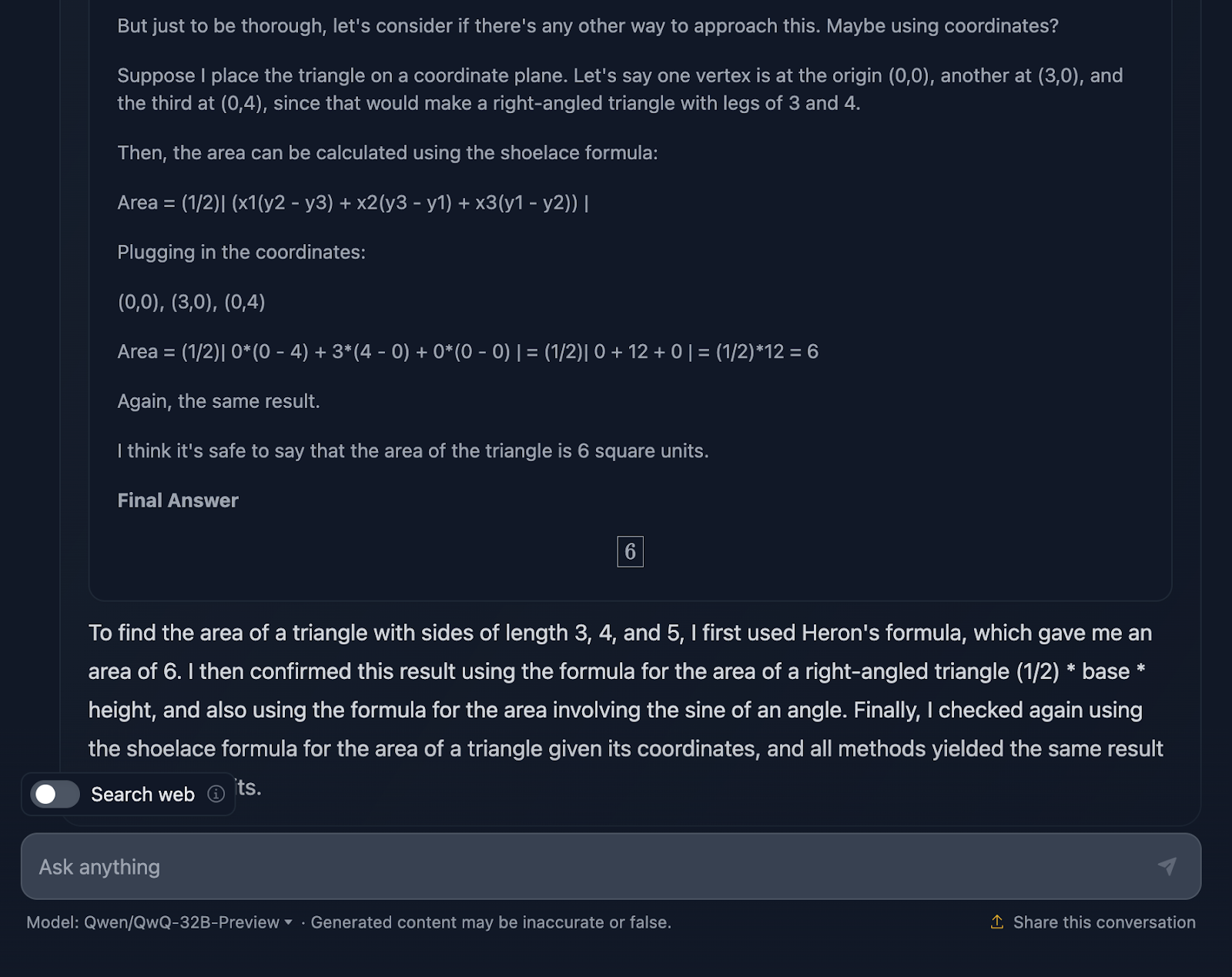
Acho muito legal o fato de ele ter usado quatro abordagens diferentes para chegar à mesma solução, em comparação com o DeepSeek, que usou apenas três. O raciocínio é claro e fácil de acompanhar. O único problema que notei é que a formatação e o estilo das fórmulas são um pouco inconsistentes - algumas são analisadas corretamente, enquanto outras não. Isso é algo que o DeepSeek tratou corretamente.

Prova matemática

Vamos dar uma olhada em um teste de matemática mais complexo para ver se há alguma diferença no desempenho e no processo de pensamento. Vou testar o seguinte: "Prove que a soma dos recíprocos dos números de Fibonacci converge para um valor finito."

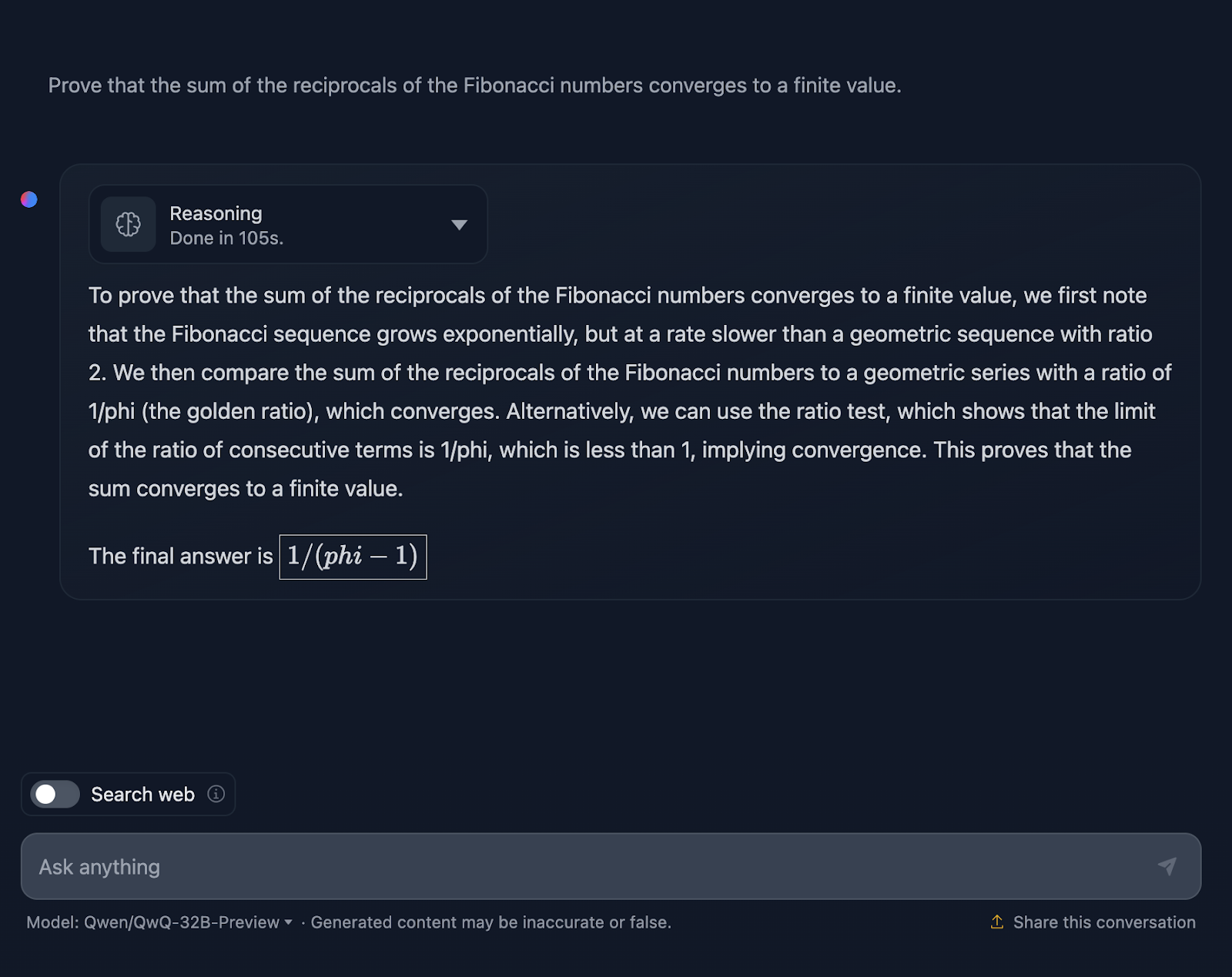
Tecnicamente, a resposta não está incorreta, mas há muito espaço para melhorias. Em primeiro lugar, se eu estiver pedindo ao modelo uma prova, a resposta final não deve ser apenas um valor; ela deve incluir uma série de fórmulas ou aplicações de teoremas para provar uma hipótese ou afirmação. Você tenta fazer isso aqui, mas precisa de mais elaboração, e a resposta final não prova nada de fato. Mais uma vez, a formatação das fórmulas parece ser um problema recorrente. Um ótimo exemplo de uma prova adequada pode ser encontrado no teste que realizei com o DeepSeek.

Para contextualizar, durante meu doutorado em matemática, eu corrigi provas de matemática e posso dizer a você que essa resposta não teria recebido nota máxima, mas a do DeepSeek sim!

Vejamos agora o raciocínio (para facilitar a leitura, mostrarei apenas a primeira e a última parte do longo processo de raciocínio, mas incentivo você a testar o prompt por conta própria):

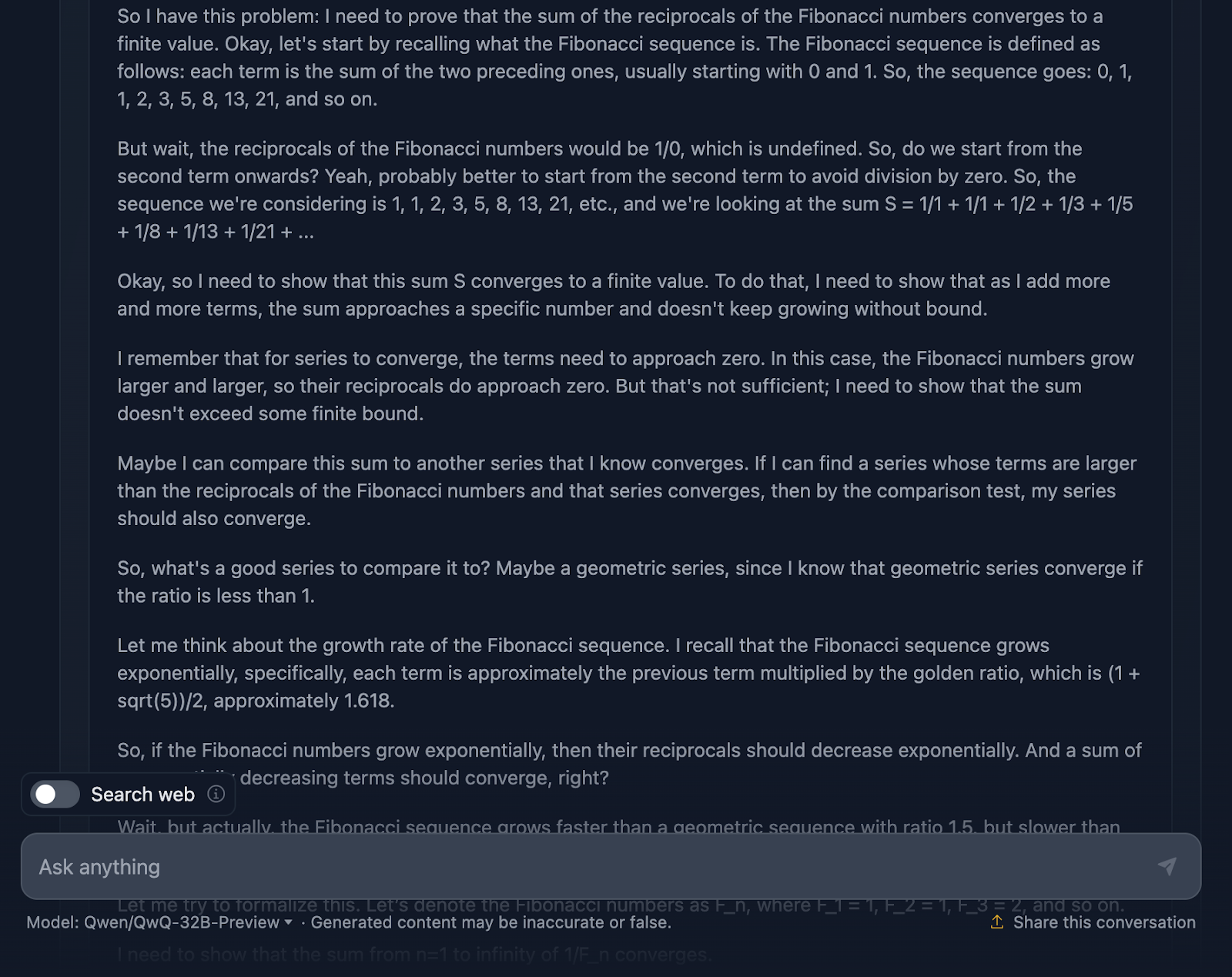
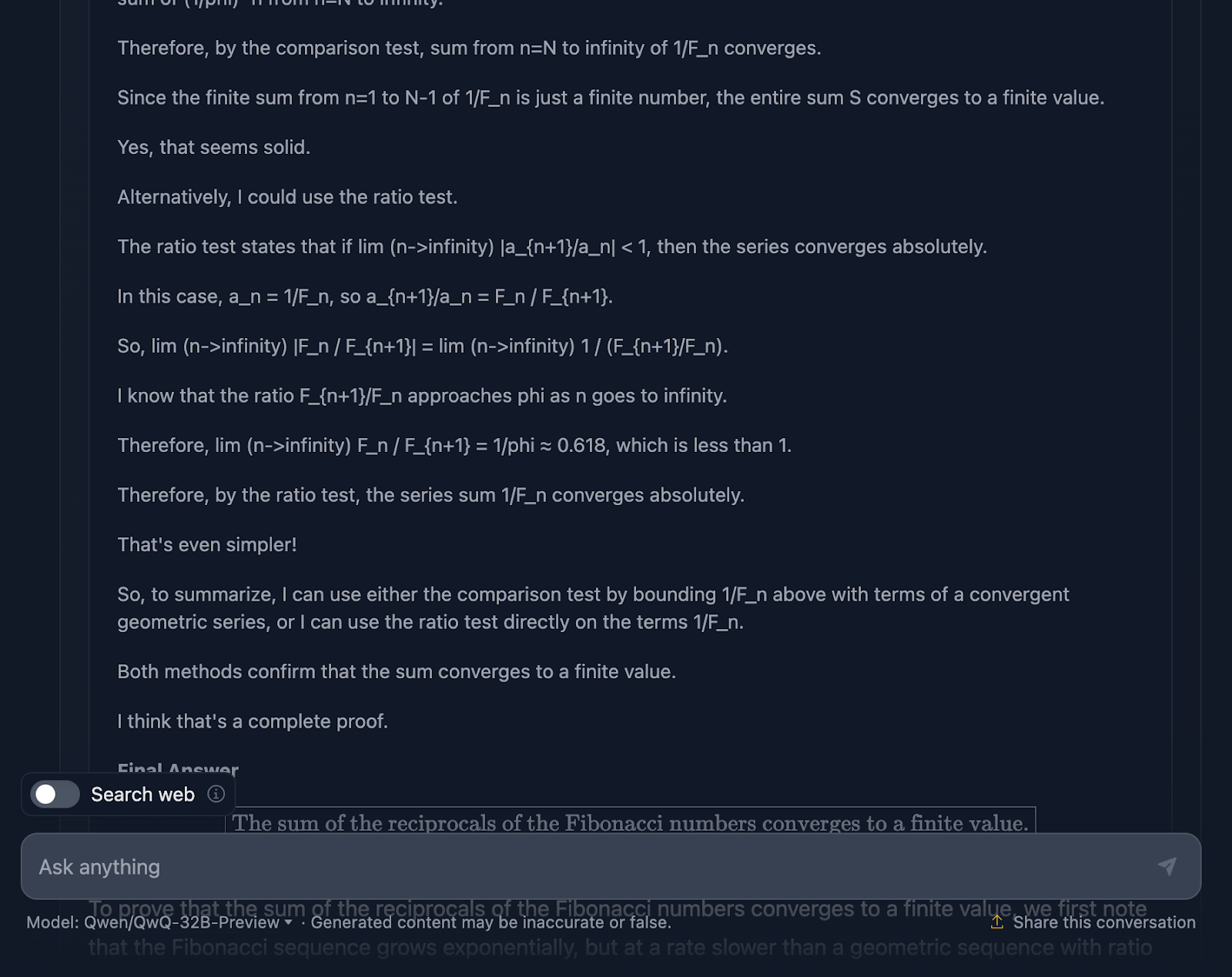
Em primeiro lugar, o modelo começa bem. Ele lembra a sequência de Fibonacci, evita a armadilha óbvia de dividir por zero e define bem o problema. Essa é uma base sólida para você. Em seguida, ele passa a usar o teste de comparação e o teste de proporção, que são testes padrão para a convergência de séries, e até mesmo usa a fórmula de Binet para aproximar e limitar os números de Fibonacci. Ele também reconhece, em algum momento, que não precisa calcular o valor exato, apenas provar que a série converge, o que mostra que ele está realmente se atendo ao problema.

Agora, o raciocínio está correto, sem dúvida, mas a jornada até a resposta parece um pouco confusa. Novamente, algumas fórmulas estão bem formatadas, mas outras nem tanto. 

Dito isso, a prova final é válida. Ele mostra que a série converge e usa métodos válidos para chegar lá. Mas, em comparação com o resultado do DeepSeek, a prova poderia ter sido um pouco mais polida e consistente.

Também me surpreende muito o fato de que a resposta final fornecida no raciocínio, que é uma resposta final melhor, seja diferente da que aparece no resultado final. Você deveria ter se limitado a isso!

Geometria diferencial

Vamos tentar agora um teste de geometria diferencial:

Considere uma superfície S em ^R3 parametrizada por

φ(u,v) = (u cos v, u sin v, ln u)

para u > 0 e 0 ≤ v < 2π.

a) Calcule a primeira forma fundamental de S.

b) Determine se S é uma superfície mínima.

c) Encontre a curvatura gaussiana K e a curvatura média H de S.

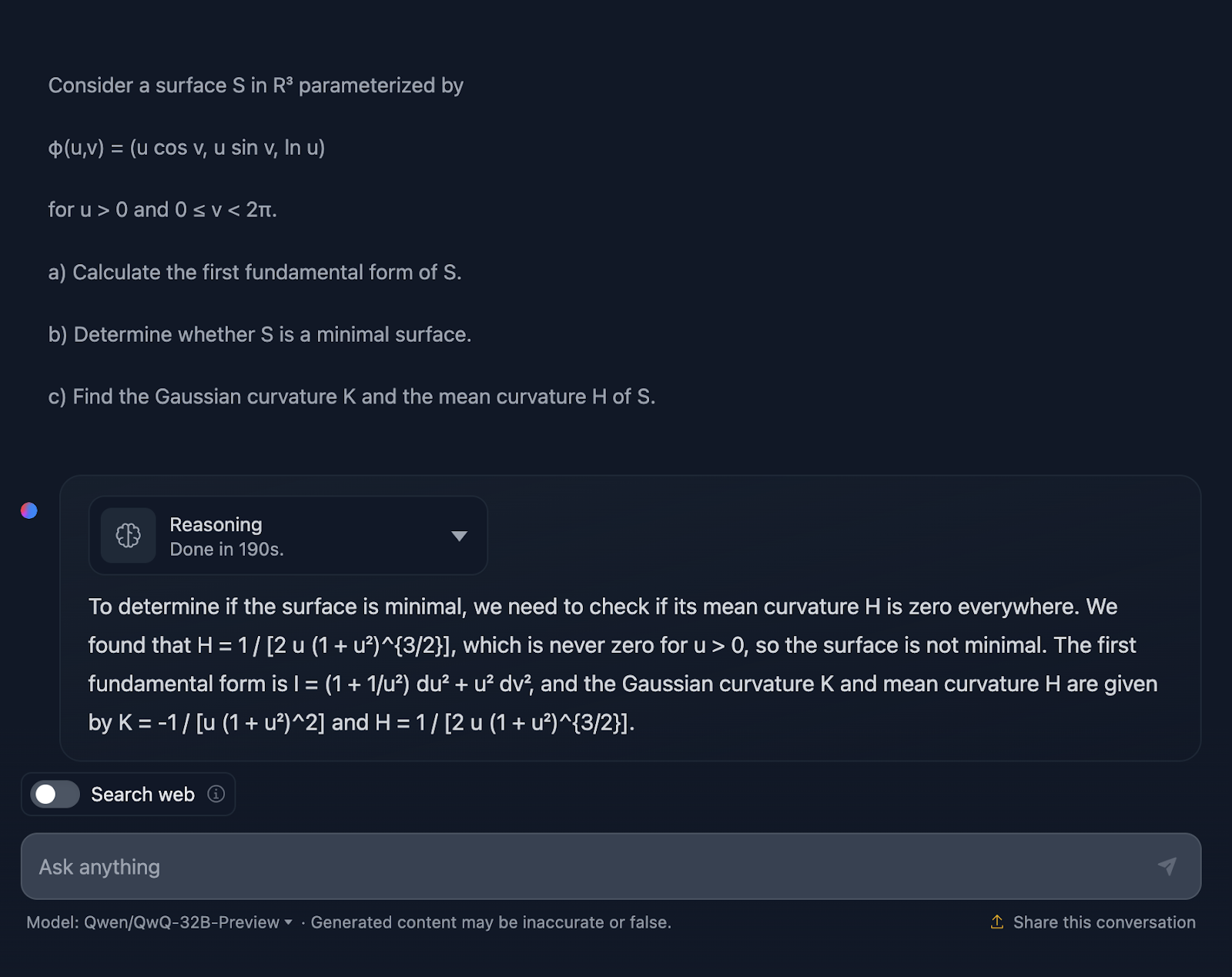
Tudo bem, não estou surpreso com a resposta, pois ela é bastante semelhante ao teste anterior em termos de estilo. Novamente, não é tecnicamente errado, mas definitivamente há espaço para melhorias na forma como a explicação é comunicada.

A explicação ignora o how. Eu não esperaria uma abordagem passo a passo, é claro, mas pelo menos algumas fórmulas para mostrar de onde vêm os resultados. Além disso, ele não divide a resposta em seções, e a formatação das fórmulas, mais uma vez, não é das melhores. O DeepSeek fez um ótimo trabalho nesse sentido.

Mais uma vez, você não está totalmente classificado para o QwQ, mas está totalmente classificado para o DeepSeek!

Vamos dar uma olhada no raciocínio (para facilitar a leitura, estou mostrando apenas a primeira e a última parte):

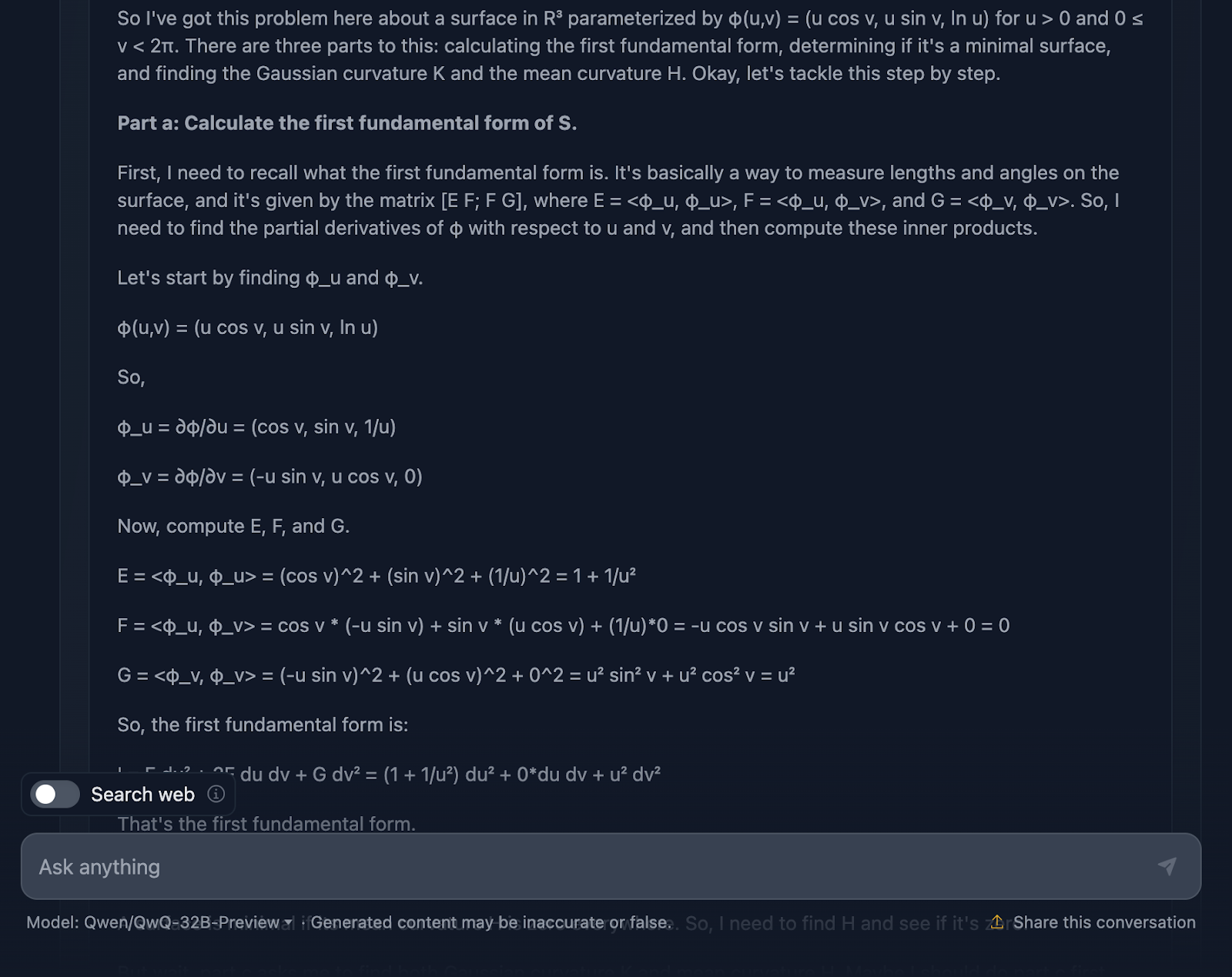
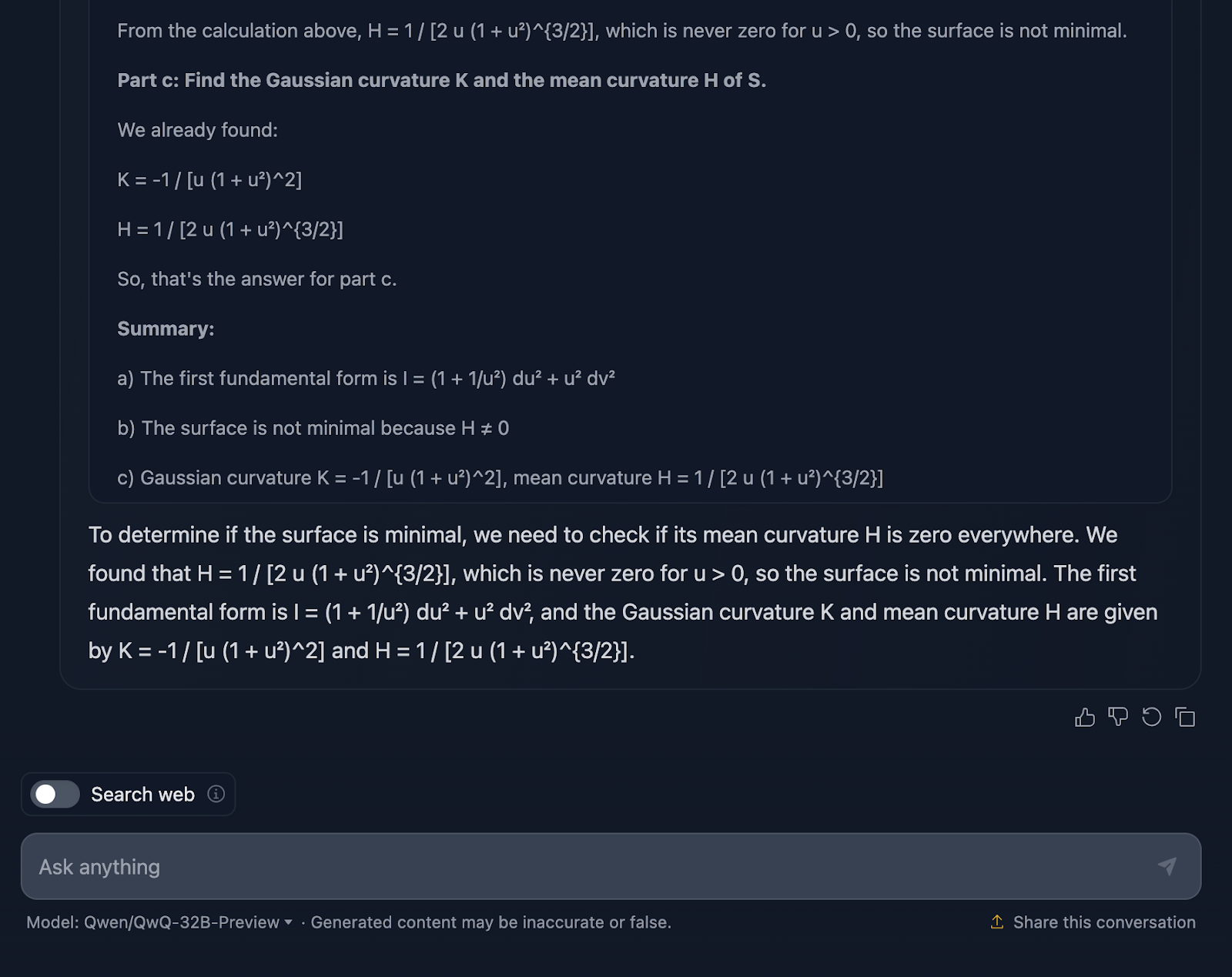
Muito bem, vamos falar sobre o raciocínio do modelo aqui. Em primeiro lugar, tenho que dar o devido crédito a ele - ele é completo. A divisão em seções claras - Parte a, Parte b e Parte c - facilita o acompanhamento e faz um trabalho sólido ao nos guiar pelas etapas. Ele começa abordando a primeira forma fundamental, calculando cuidadosamente os coeficientes a partir da parametrização e, em seguida, parte daí. Quando você chegar às curvaturas gaussianas e médias na Parte c, as bases já estarão bem definidas.

Agora, é aqui que as coisas começam a ficar um pouco confusas. Embora os cálculos estejam tecnicamente corretos, o modelo passa muito tempo verificando novamente as etapas ou revisando os cálculos, o que é ótimo para a precisão, mas não tão bom para a legibilidade. 

Vamos falar agora sobre a formatação. As fórmulas estão todas lá, mas não são apresentadas da maneira mais clara - mais uma vez. É um pouco confuso e, para quem está tentando acompanhar, isso pode tornar as coisas mais difíceis do que o necessário. Um layout mais limpo, com os principais resultados destacados, melhoraria muito essa explicação.

Outra coisa que falta é o contexto. O modelo nos fornece os resultados, mas não pára para explicar o que eles significam. Por exemplo, por que a curvatura gaussiana é importante aqui? Ou o que isso nos diz sobre a geometria da superfície? E quando ele conclui que a superfície não é mínima, ele está tecnicamente certo, mas perde a oportunidade de expandir o que isso significa em um sentido mais amplo.

Testes de codificação

Testamos o desempenho do QwQ-32B-Preview em testes de matemática e não fiquei muito impressionado, mas talvez eu seja tendencioso porque gostei muito do resultado do DeepSeek. Vamos ver como ele se sai nos testes de codificação e se o QwQ-32B-Preview pode me surpreender desta vez.

Python

O primeiro teste é:

"Implemente uma função em Python que encontre a substring palindrômica mais longa em uma determinada string. A função deve ter uma complexidade de tempo melhor que O(n^3)."

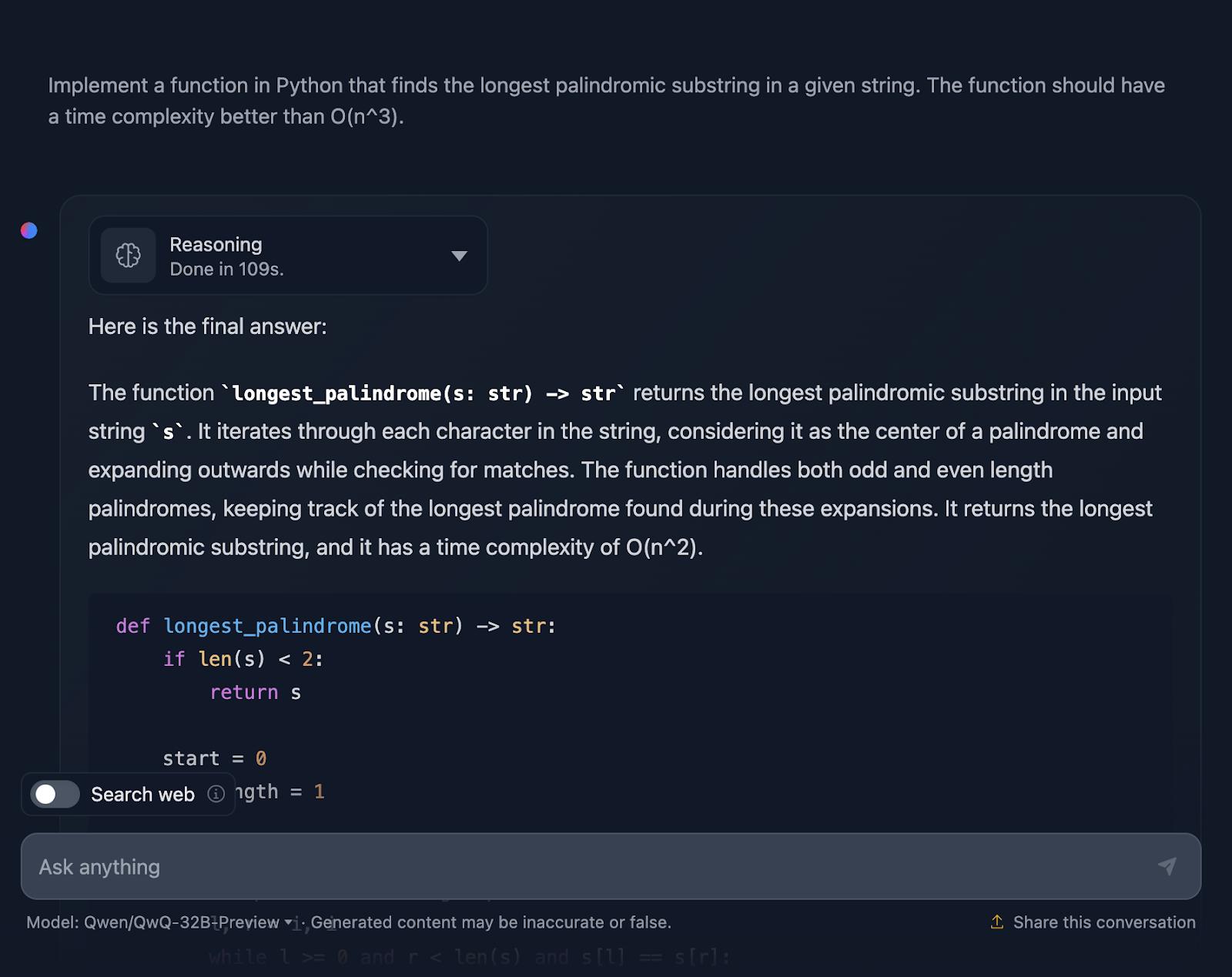
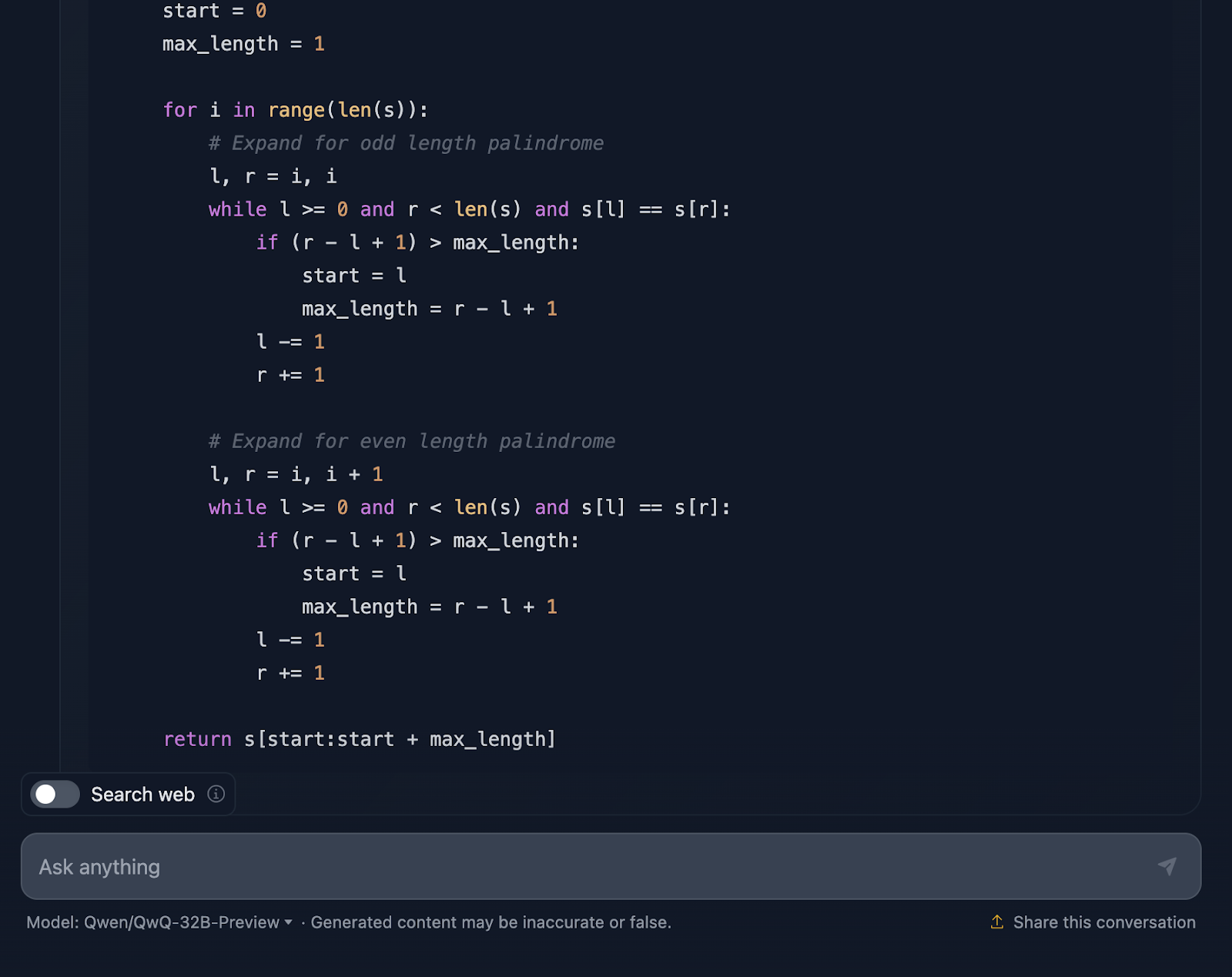
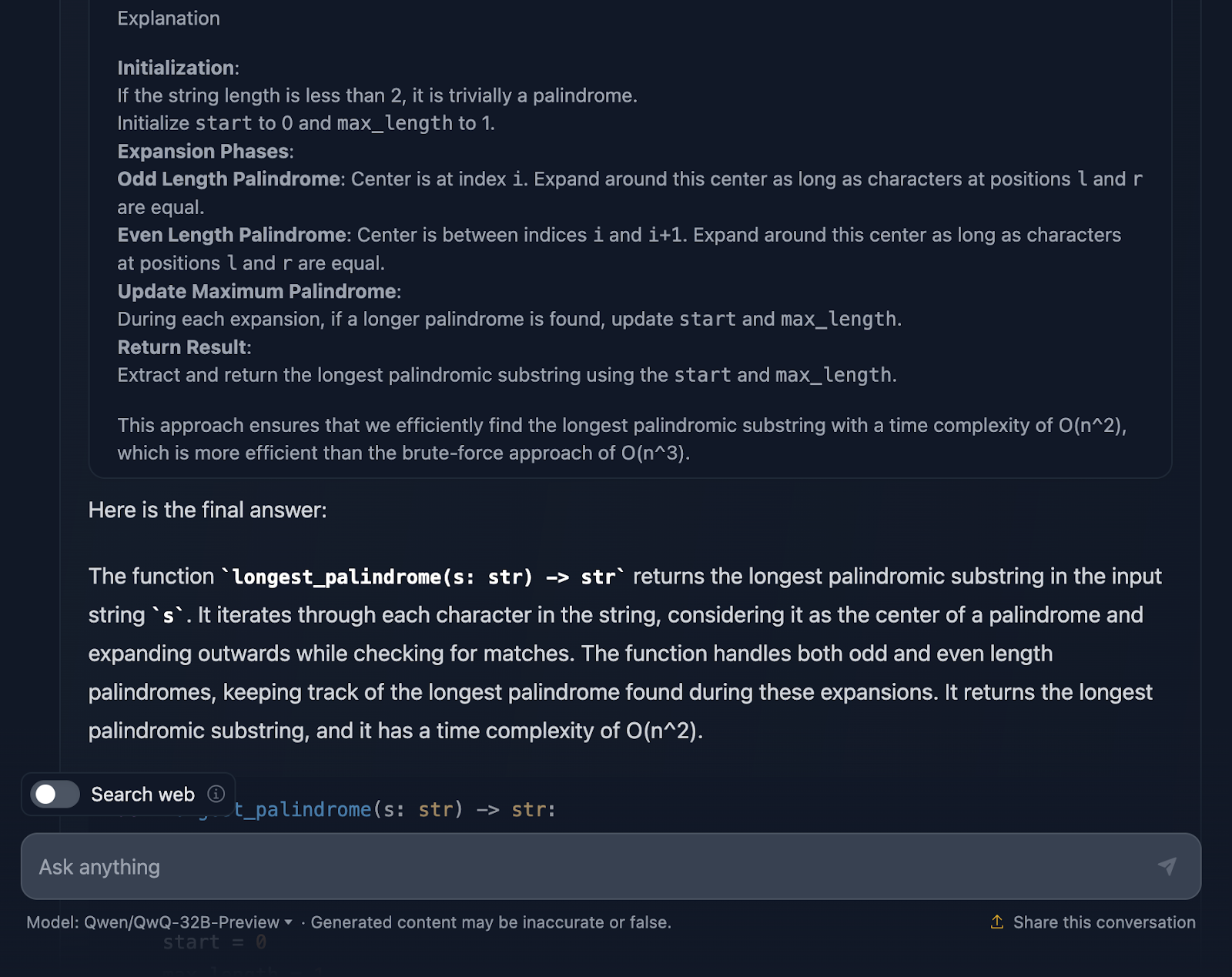
A solução está correta e oferece uma maneira limpa e eficiente de encontrar a substring palindrômica mais longa com a complexidade necessária. Ele usa uma abordagem inteligente, expandindo cada caractere para verificar se há palíndromos e lida bem com comprimentos pares e ímpares. O código é claro e fácil de seguir. No entanto, eu teria gostado de ver casos de teste no final, algo que o DeepSeek forneceu. Vejamos agora o raciocínio (mostrarei apenas a primeira e a última parte para facilitar a leitura):

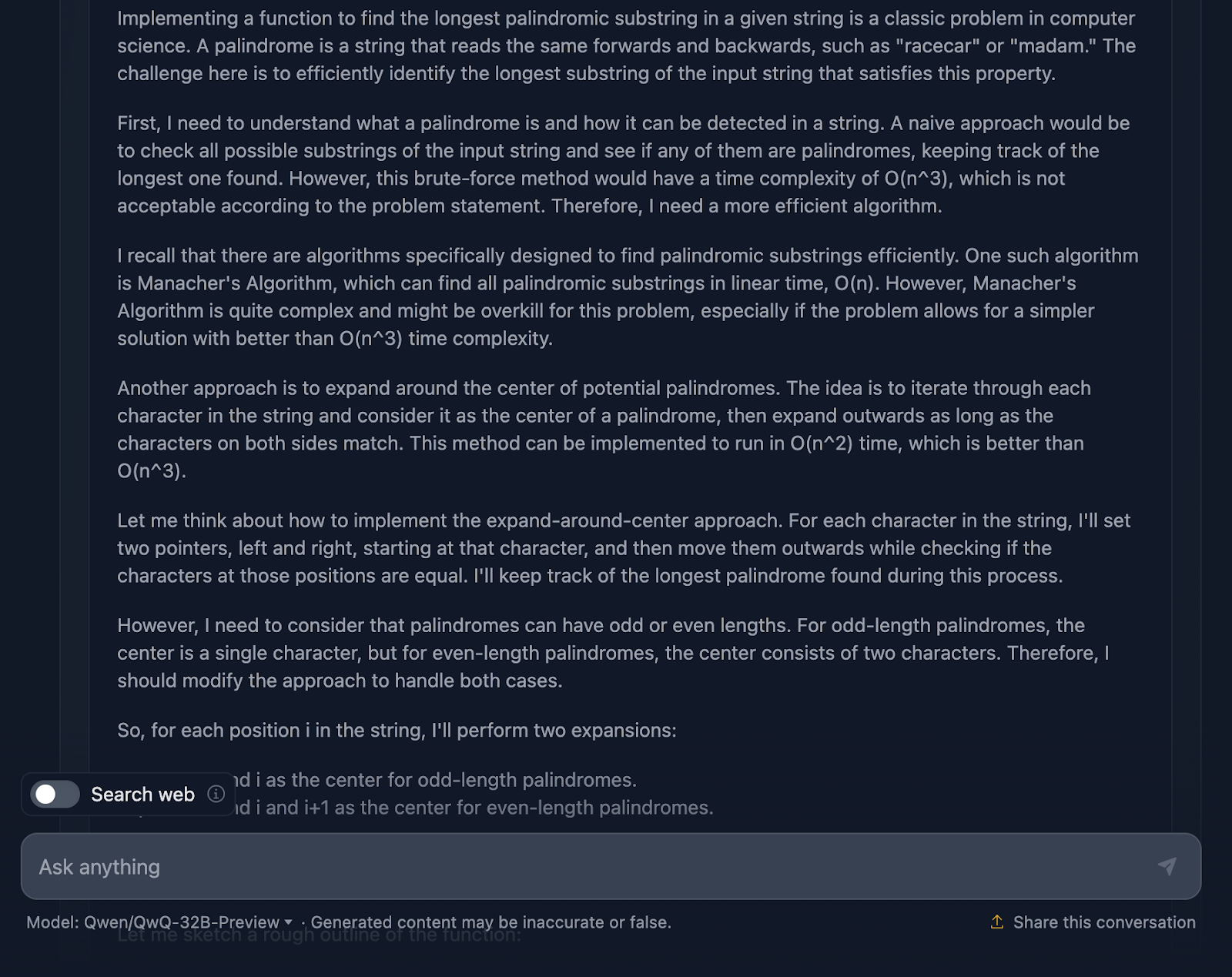
Devo dizer que é uma abordagem bastante sólida, e estou realmente impressionado com algumas partes do raciocínio. Mas há alguns aspectos em que ele poderia ser um pouco mais rígido, então vamos falar sobre isso.

Em primeiro lugar, o raciocínio começa abordando o básico: o que é um palíndromo e por que uma abordagem de força bruta não é a melhor abordagem. Em seguida, passa diretamente para o método de expansão em torno do centro e até menciona o algoritmo de Manacher com sua complexidade O(n). Ele reconhece que, embora o Manacher's seja mais rápido, provavelmente é um exagero para esse problema. O DeepSeek não mencionou essa abordagem, algo que eu já esperava antes de experimentá-la.  Ele também fala sobre métodos alternativos, como inverter a cadeia de caracteres ou ignorar verificações desnecessárias, o que eu acho ótimo!

O método expand-around-center é explicado claramente e separa palíndromos de comprimento ímpar e de comprimento par, o que é fundamental para garantir que todos os casos sejam cobertos. 

A inclusão de casos extremos é um destaque. Cadeias de caracteres únicos, cadeias de caracteres sem palíndromos, cadeias de caracteres compostas por todos os caracteres idênticos - está tudo lá. Além disso, ele até menciona como a implementação trata graciosamente as cadeias de caracteres vazias, simplesmente retornando-as. Esse tipo de detalhamento é o que você deseja em uma explicação.

Gosto muito do fato de o resultado final no raciocínio fornecer a você um detalhamento da abordagem, do código da solução e da explicação, mas gostaria que isso fosse incluído na resposta final!

O QwQ-32B-Preview teve um desempenho melhor do que o DeepSeek neste caso? Bem, apesar de incluir casos de teste, eu diria que sim!

JavaScript

Agora, vou testar um desafio de codificação em Javascript:

"Escreva uma função em JavaScript que determine se um determinado número é primo."

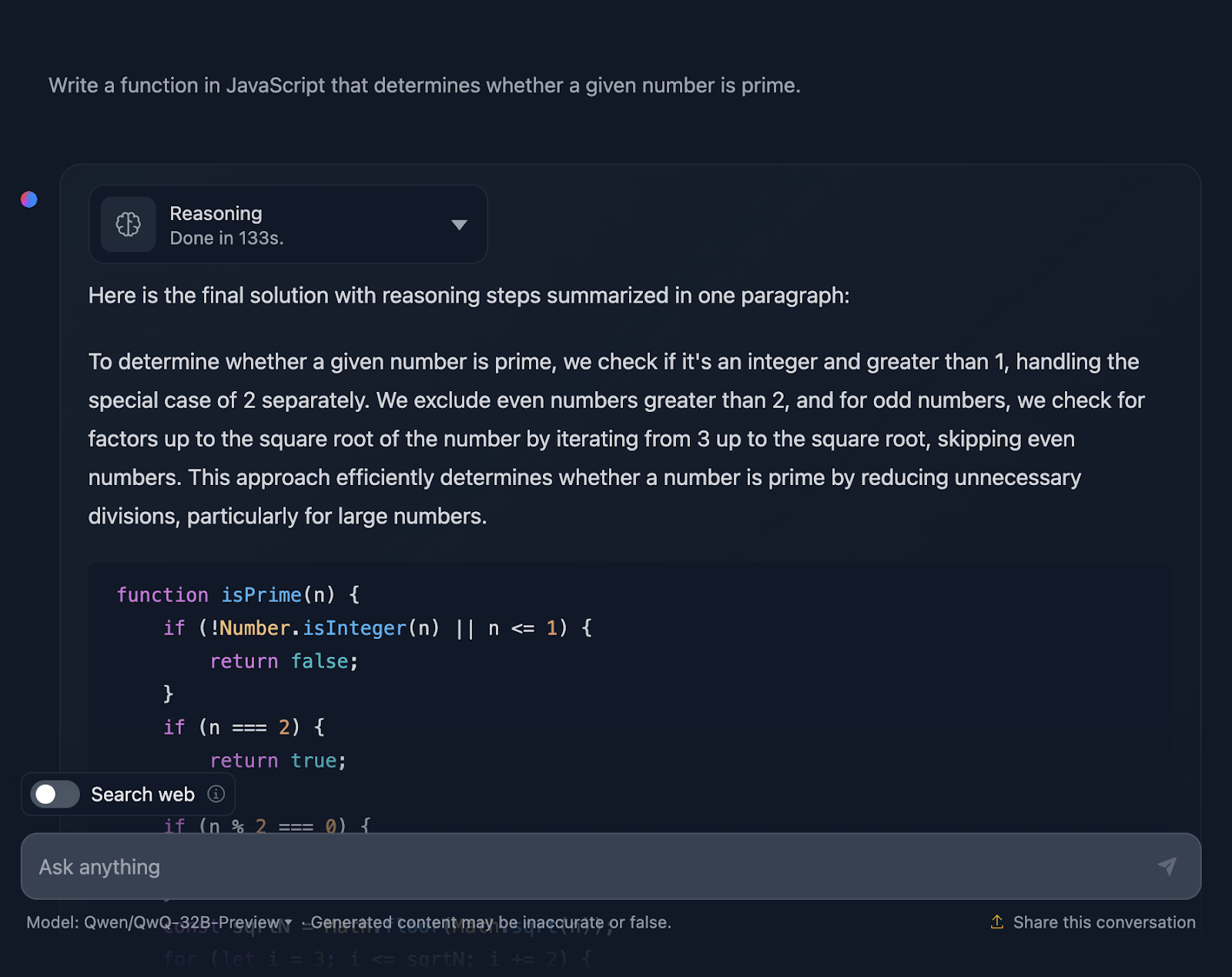
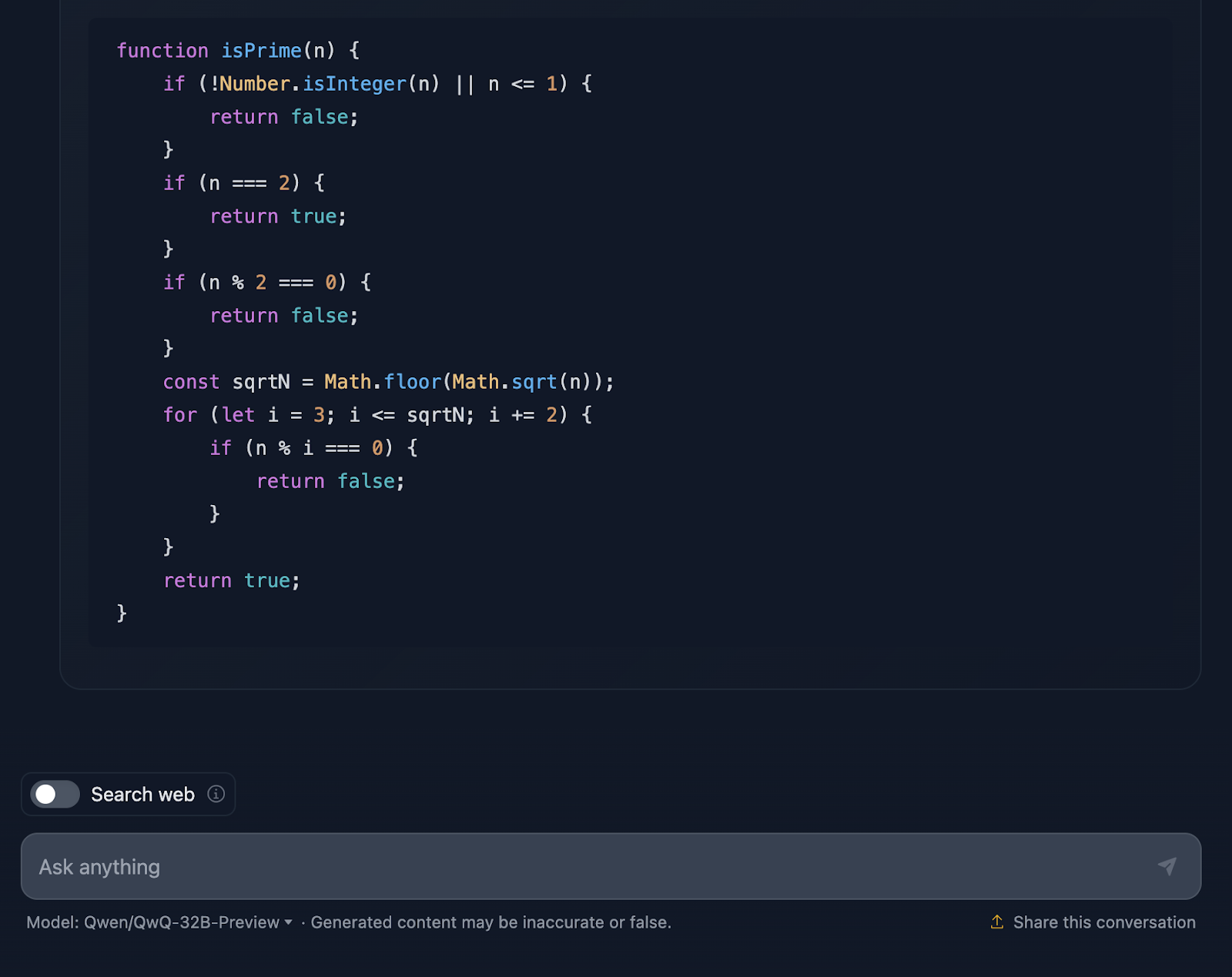
A solução está correta e é muito semelhante à saída do DeepSeek. No entanto,o site levoumuito mais tempo para fazer o raciocínio, então vamos ver como você chegou a essa resposta (estou truncando a saída novamente para facilitar a leitura):

Ok, então esse raciocínio é particularmente longo em comparação com o fornecido pelo DeepSeek. Vamos analisar isso com mais detalhes:

Em primeiro lugar, a solução começa bem, abordando os aspectos básicos. Números menores ou iguais a 1? Definitivamente, você não é o melhor. E o 2 é especial - é o único número primo par. Você tem algum outro número par? Automaticamente, não de primeira. Essa configuração lógica é clara e faz muito sentido quando você lida com casos extremos.

A partir daí, você chega ao cerne da questão: como podemos verificar com eficiência se um número tem algum divisor além de 1 e ele mesmo? Em vez de verificar cada número até n, a solução verifica apenas até a raiz quadrada de n. Por quê? Porque se um número tiver um fator maior que sua raiz quadrada, seu outro fator já terá sido verificado abaixo da raiz quadrada. Supereficiente e evita cálculos desnecessários. 

Para tornar as coisas ainda mais rápidas, a solução pula todos os números pares depois de lidar com 2. Portanto, você só precisa verificar os números ímpares, começando com 3 e aumentando 2. Essa é uma otimização interessante que reduz o trabalho pela metade.

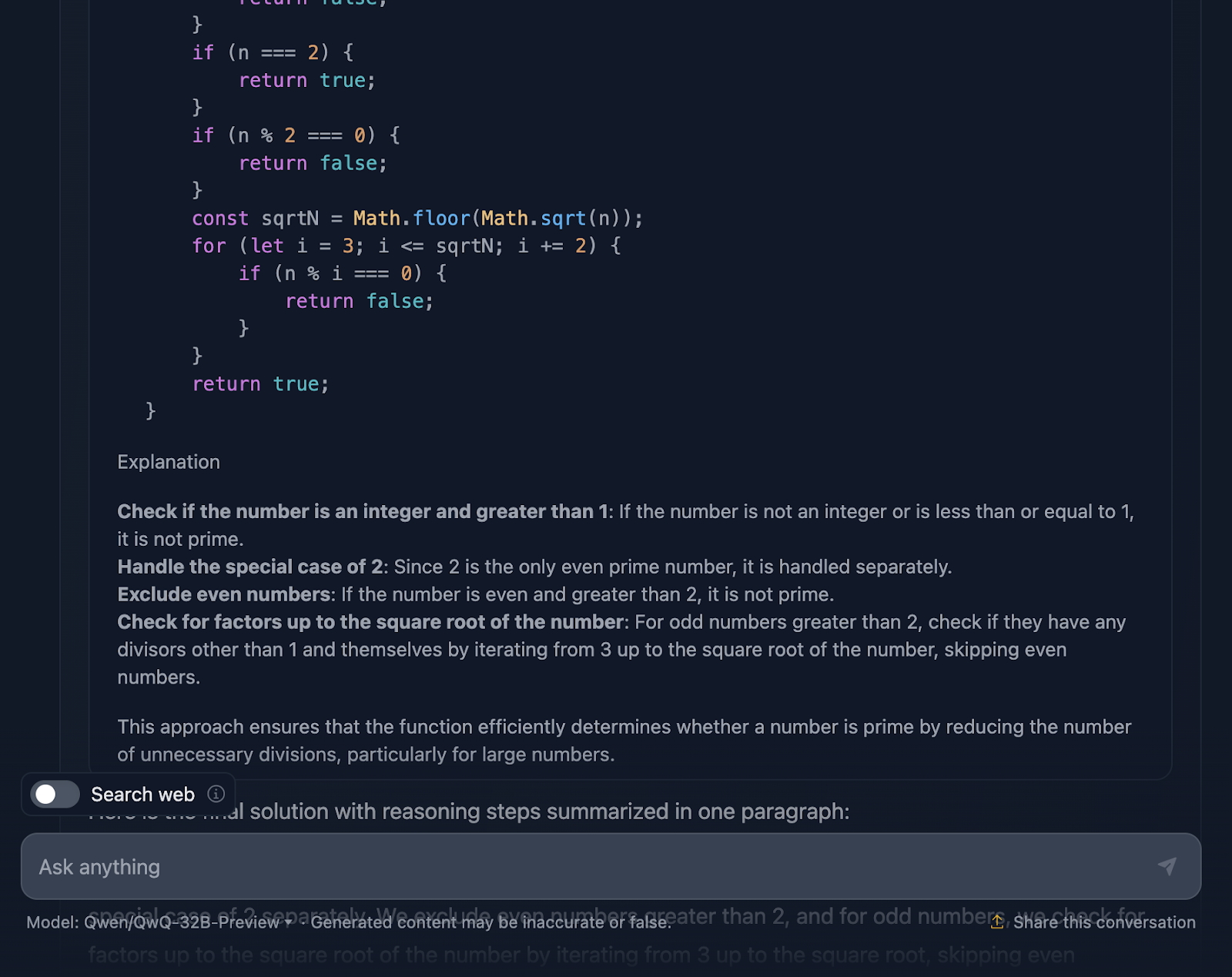
Em seguida, passamos para a implementação. A função começa com a validação da entrada. É um número inteiro? É maior que 1? Caso contrário, você pode dizer rapidamente "not prime". Esse tipo de validação é uma ótima prática e mantém a função robusta. Em seguida, a lógica do loop é iniciada, verificando os divisores de 3 até a raiz quadrada de n. Se qualquer divisor funcionar, não é um primo. Caso contrário, tudo estará claro, e o número é primo.

O que é ótimo é que o raciocínio não se limita à implementação. Ele analisa os casos extremos - como números negativos, não inteiros ou entradas estranhas como 2,5 - e garante que a função os trate corretamente. Há até mesmo uma observação sobre os limites do JavaScript com números realmente grandes e uma sugestão de usar o BigInt para esses cenários extremos, o que considerei uma ótima adição ao raciocínio.

A solução inclui casos de teste detalhados para mostrar exatamente como ela funciona para números como 1, 2, 3 e até mesmo números maiores, como 13 e 29. Cada teste é explicado passo a passo, para que você não se confunda sobre o funcionamento da função.

Agora, essa solução poderia ir além? Claro, sempre há espaço para melhorias. Por exemplo, se você estivesse trabalhando com números enormes, talvez quisesse explorar algoritmos avançados como Miller-Rabin ou o teste de primalidade de Fermat. Mas, para o uso diário, essa solução atinge um ótimo equilíbrio entre simplicidade, eficiência e legibilidade.

Então, qual é o veredicto? Esse raciocínio é sólido, claro e prático e faz um ótimo trabalho para garantir que o código seja robusto, algo que o DeepSeek não levou muito em consideração. Acho que o QwQ-32B-Preview ganhou!

Raciocínio lógico

Por fim, vamos dar uma olhada em alguns testes de raciocínio lógico.

O problema do lobo, da cabra e do repolho

Vou testar um quebra-cabeça clássico:

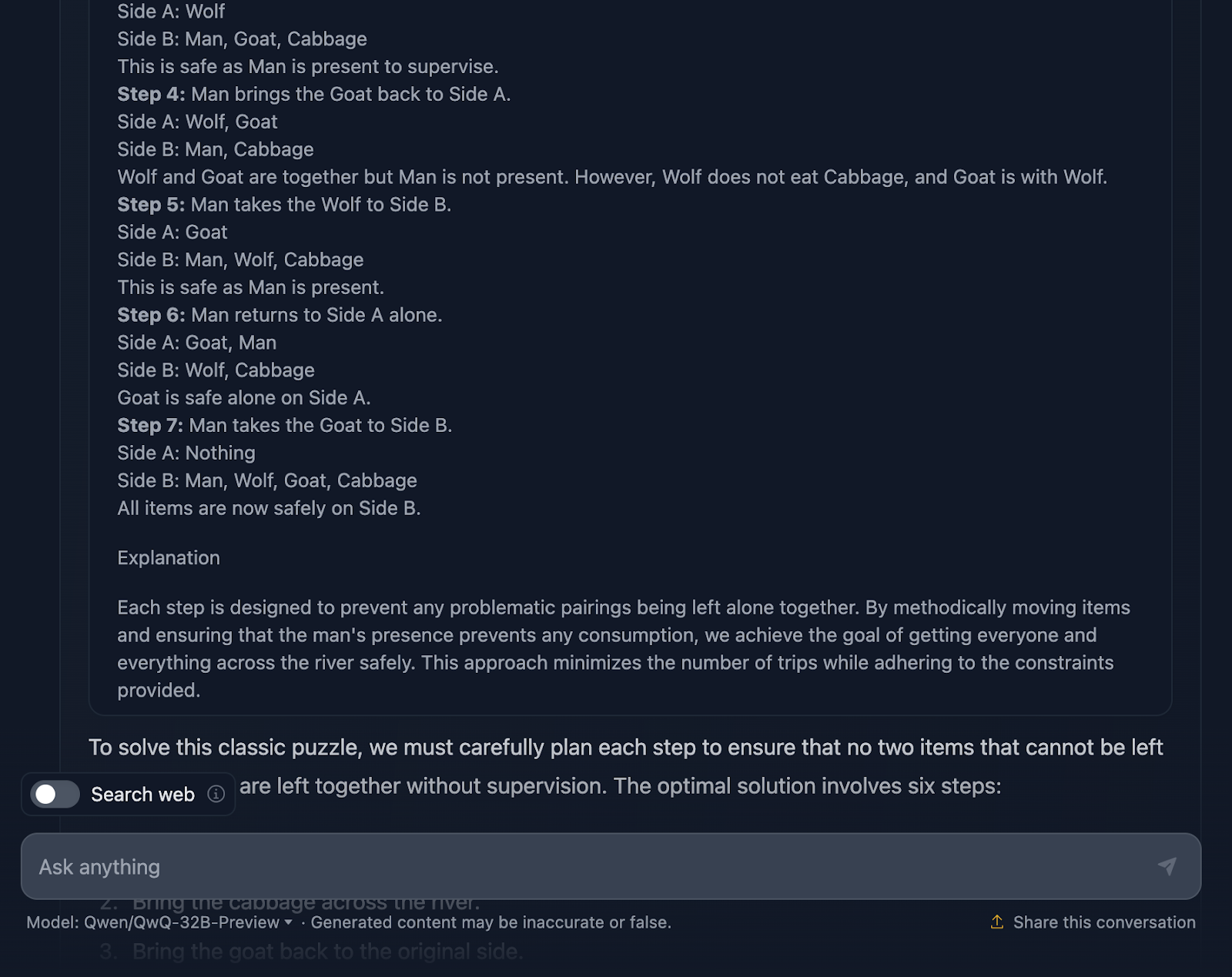
"Um homem tem que atravessar um rio com um lobo, uma cabra e um repolho. Seu barco só pode transportar a si mesmo e mais uma coisa. Se você deixasse o lobo sozinho, o lobo comeria a cabra e a cabra comeria o repolho. Como ele pode passar tudo com segurança?"

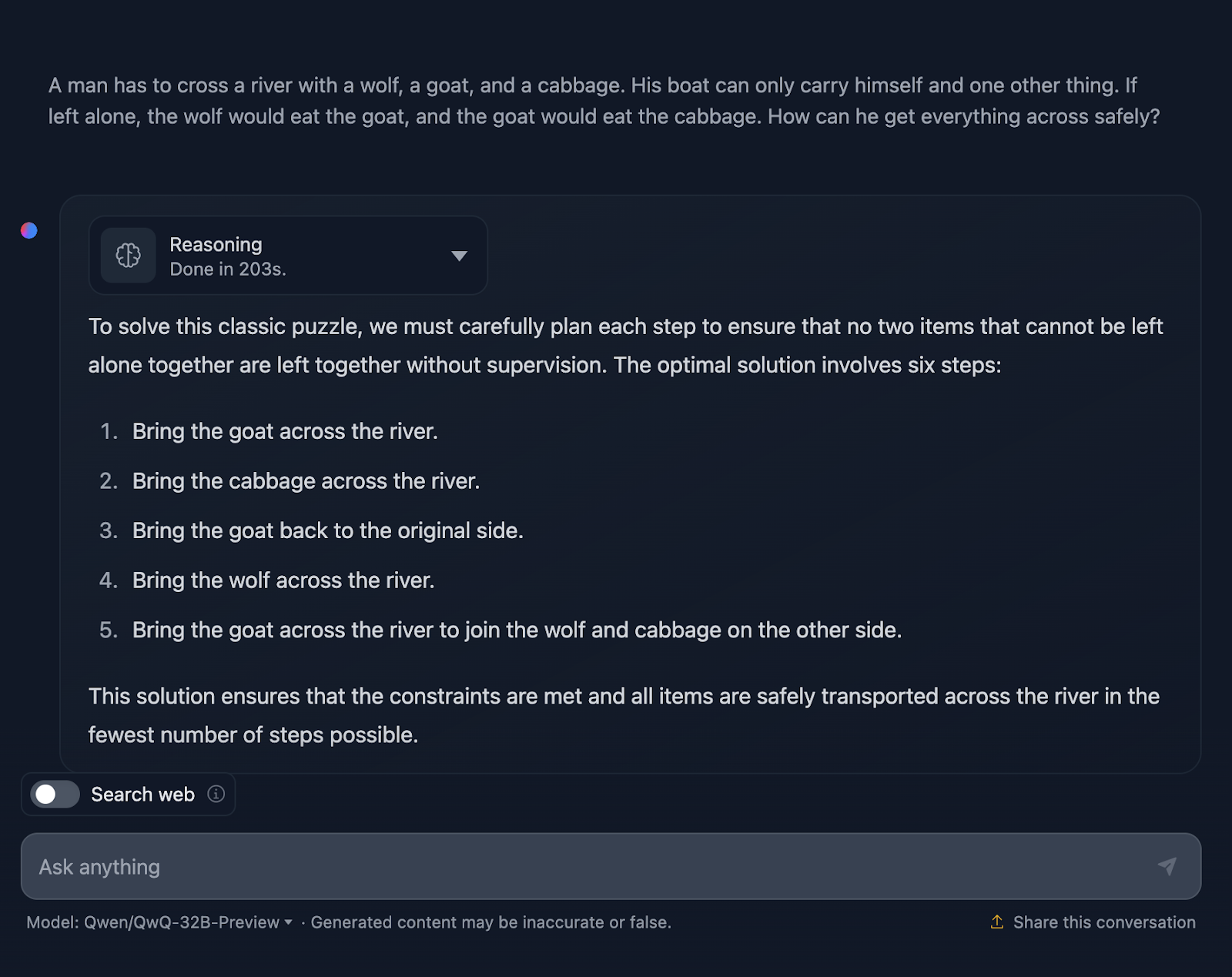
Ok, então a solução para o problema está correta, mas há algumas coisas que precisam ser esclarecidas. Ele afirma que a solução ideal envolve seis etapas; no entanto, apenas cinco pontos são fornecidos. Isso já é uma imprecisão.

Além disso, você pode pensar que essa é uma abordagem melhor em termos de eficiência, em comparação com o resultado do DeepSeek, que levou sete etapas. No entanto, essa abordagem também tem sete etapas. Por algum motivo, as etapas que envolvem voltar sozinho não foram mencionadas. Você deve ter o seguinte resultado:

1. Traga a cabra para o outro lado do rio.
2. Volte sozinho.
3. Traga o repolho para o outro lado do rio.
4. Traga a cabra de volta para o lado original.
5. Traga o lobo para o outro lado do rio.
6. Volte sozinho.
7. Leve a cabra para o outro lado do rio para se juntar ao lobo e ao repolho do outro lado.

Além disso, quando estava realizando o raciocínio, vi isso (e consegui fazer uma captura de tela!):

Isso me fez pensar se havia algo errado com o raciocínio...

Vamos dar uma olhada:

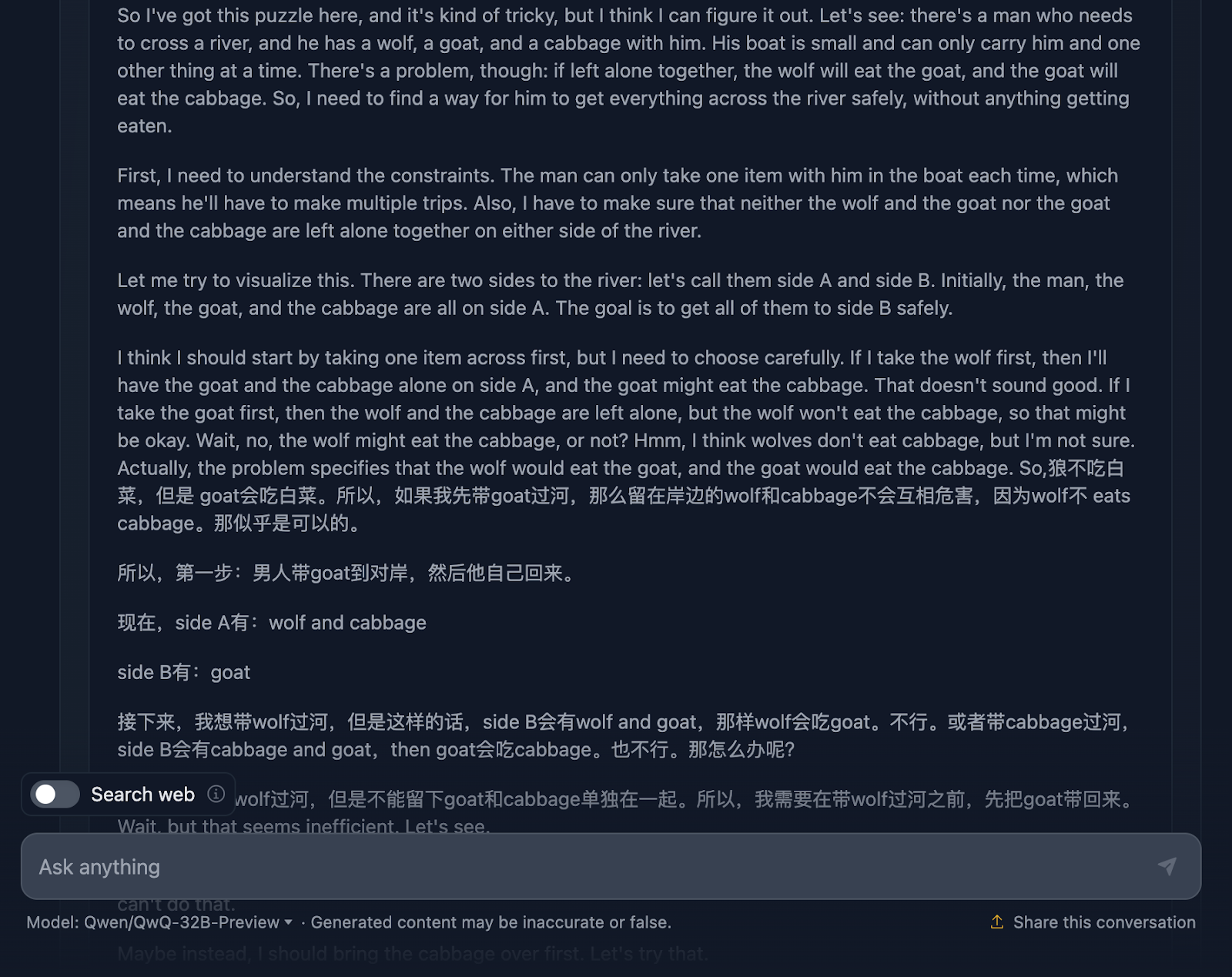
O raciocínio começa bem, garantindo que você entenda o problema, os desafios e as restrições. No entanto, é aqui que as coisas começam a ficar complicadas. Esse é um ótimo exemplo das limitações desse modelo que discutimos anteriormente, que mistura dois idiomas. Isso resulta em um raciocínio incompreensível (pelo menos para mim, pois não entendo o idioma - presumo que seja chinês!) Compartilharei agora algumas outras partes do raciocínio para ilustrar isso, mas vou pular outras partes, pois é muito longo.

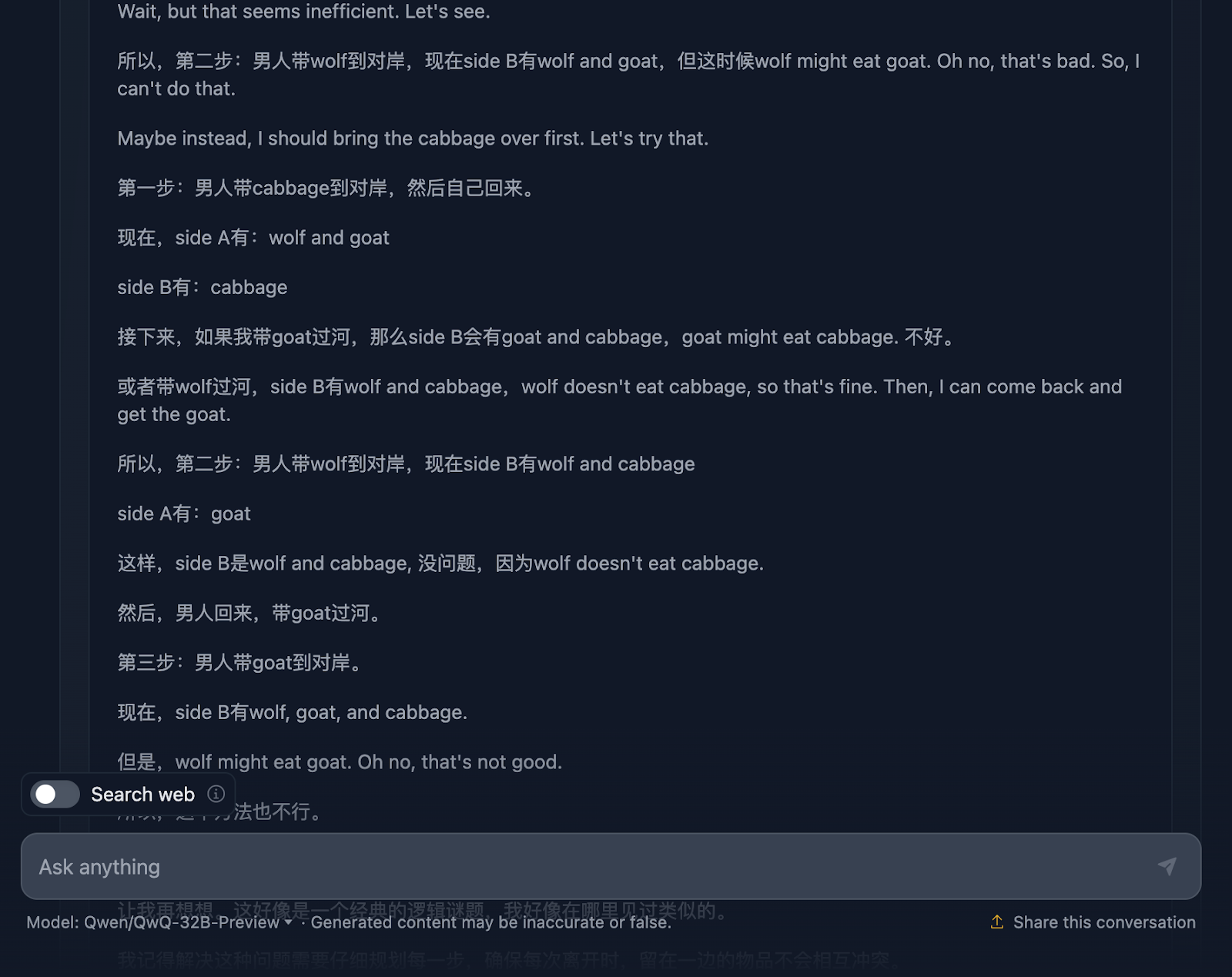
No entanto, a solução final é excelente! Ele descreve a configuração inicial, as restrições, o objetivo e a estratégia, juntamente com um plano de solução muito claro que inclui todas as etapas, o que é bastante interessante !

Então, por que isso não foi refletido na resposta final? Ele ainda acrescentou uma explicação final. Gostaria que o resultado da resposta final tivesse correspondido ao que foi exibido no raciocínio, e me pergunto por que ele não fez isso!

Quebra-cabeça de bolas de pesagem

Por fim, vamos tentar este quebra-cabeça lógico clássico que testa a capacidade do modelo de criar uma estratégia ideal usando o raciocínio dedutivo.

AVISO DE ISENÇÃO DE RESPONSABILIDADE: Este é o resultado que obtive após três tentativas - o modelo começou a gerar uma resposta, mas ficou preso ou produziu um erro e não pôde continuar gerando. Além disso, vou pular o raciocínio para este caso, pois ele foi extremamente longo, e o resultado já é bastante extenso! Vamos dar uma olhada (a saída também está truncada):

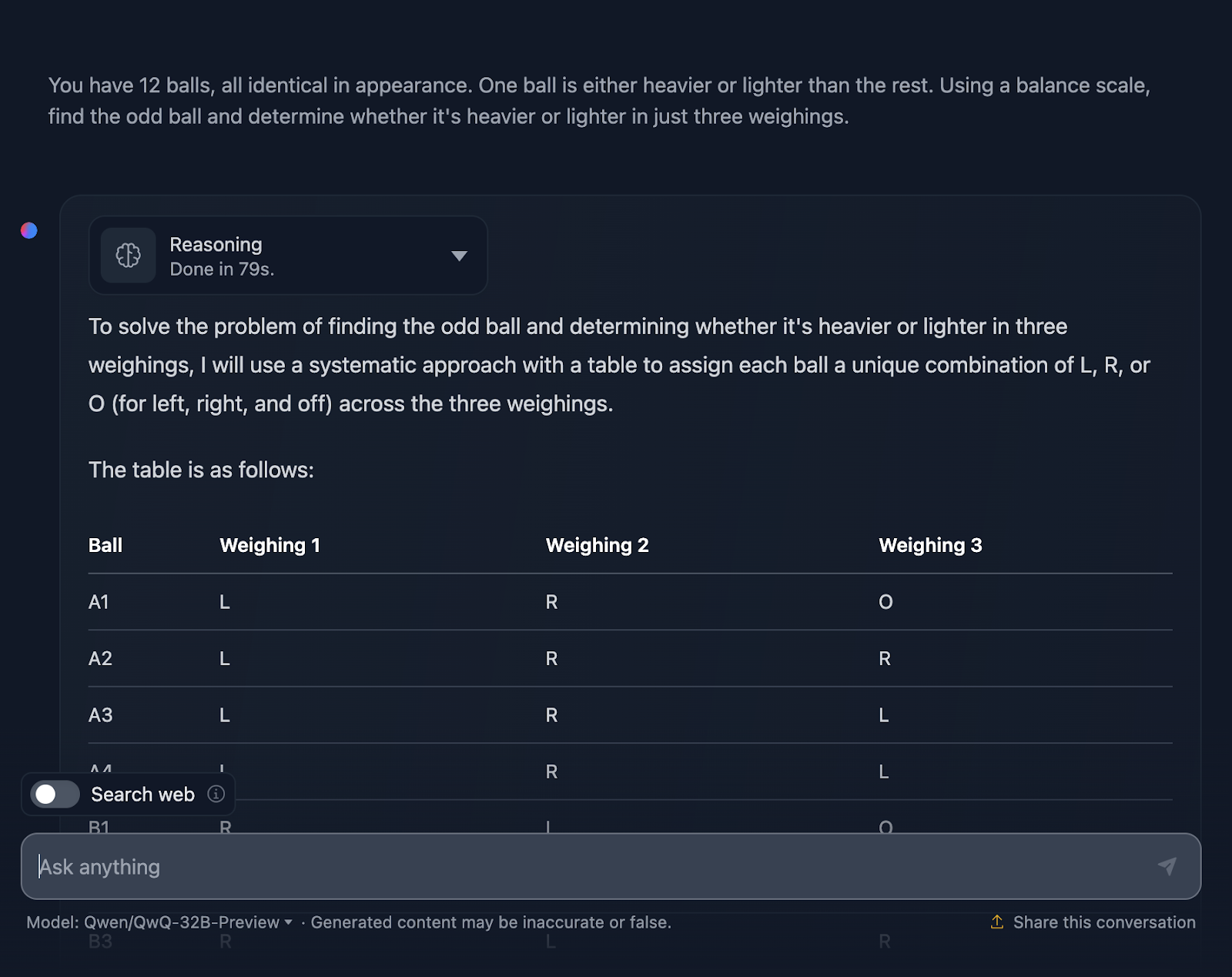
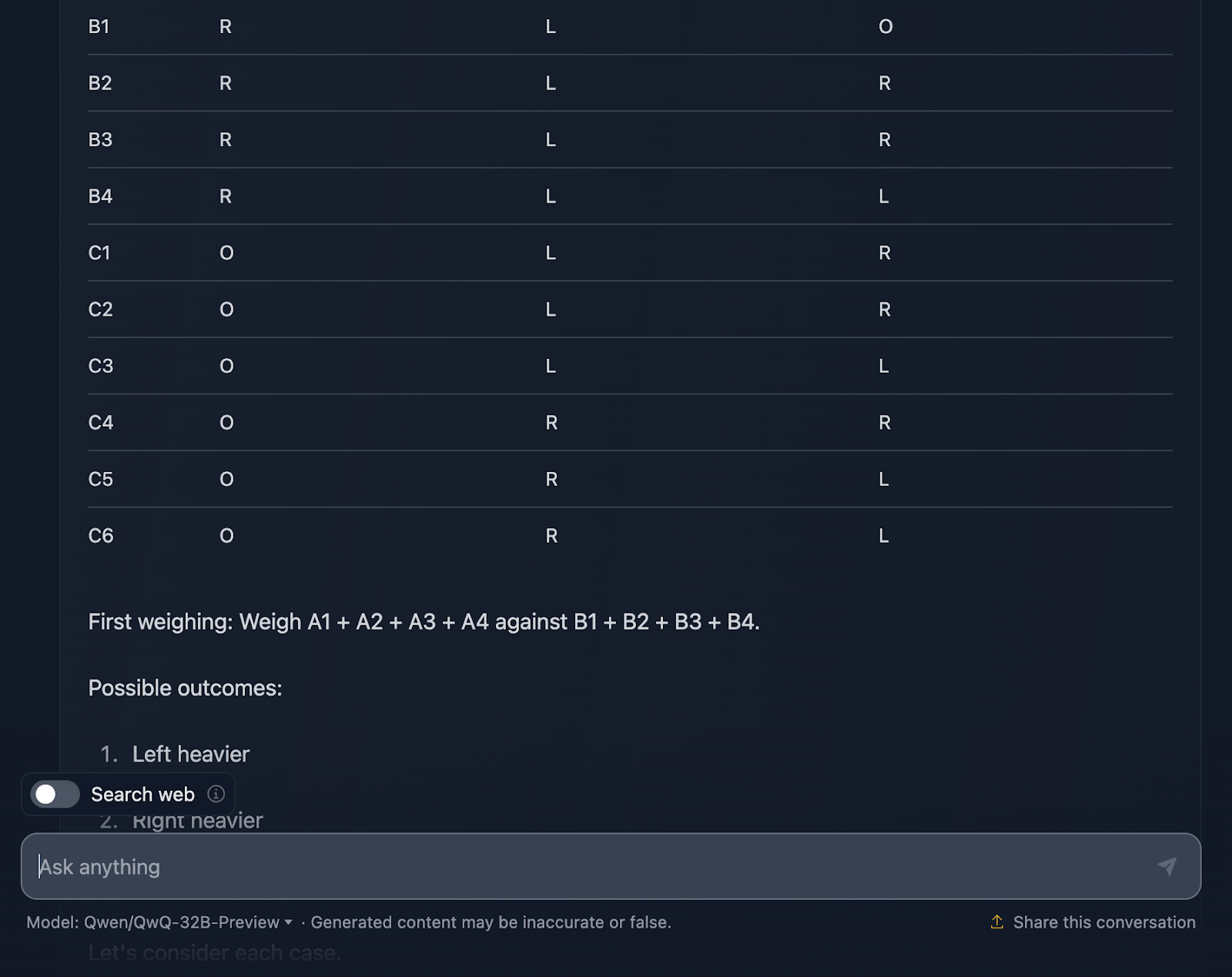
Devo dizer que estou muito impressionado com o resultado! A solução começa com uma explicação muito clara do problema e apresenta um plano usando uma tabela sistemática, o que considero muito útil e algo que o DeepSeek não incluiu. Cada bola recebe sua própria combinação exclusiva nas três pesagens, garantindo que todos os cenários possíveis sejam considerados. 

Gosto muito de como ele divide o problema em casos e subcasos: "Esquerda mais pesada", "Direita mais pesada" e "Igual". Essa abordagem incremental pega um problema complexo e o torna gerenciável. Cada pesagem se baseia nos resultados da anterior. Você está diminuindo a bola estranha passo a passo e, ao mesmo tempo, determinando se ela é mais pesada ou mais leve.

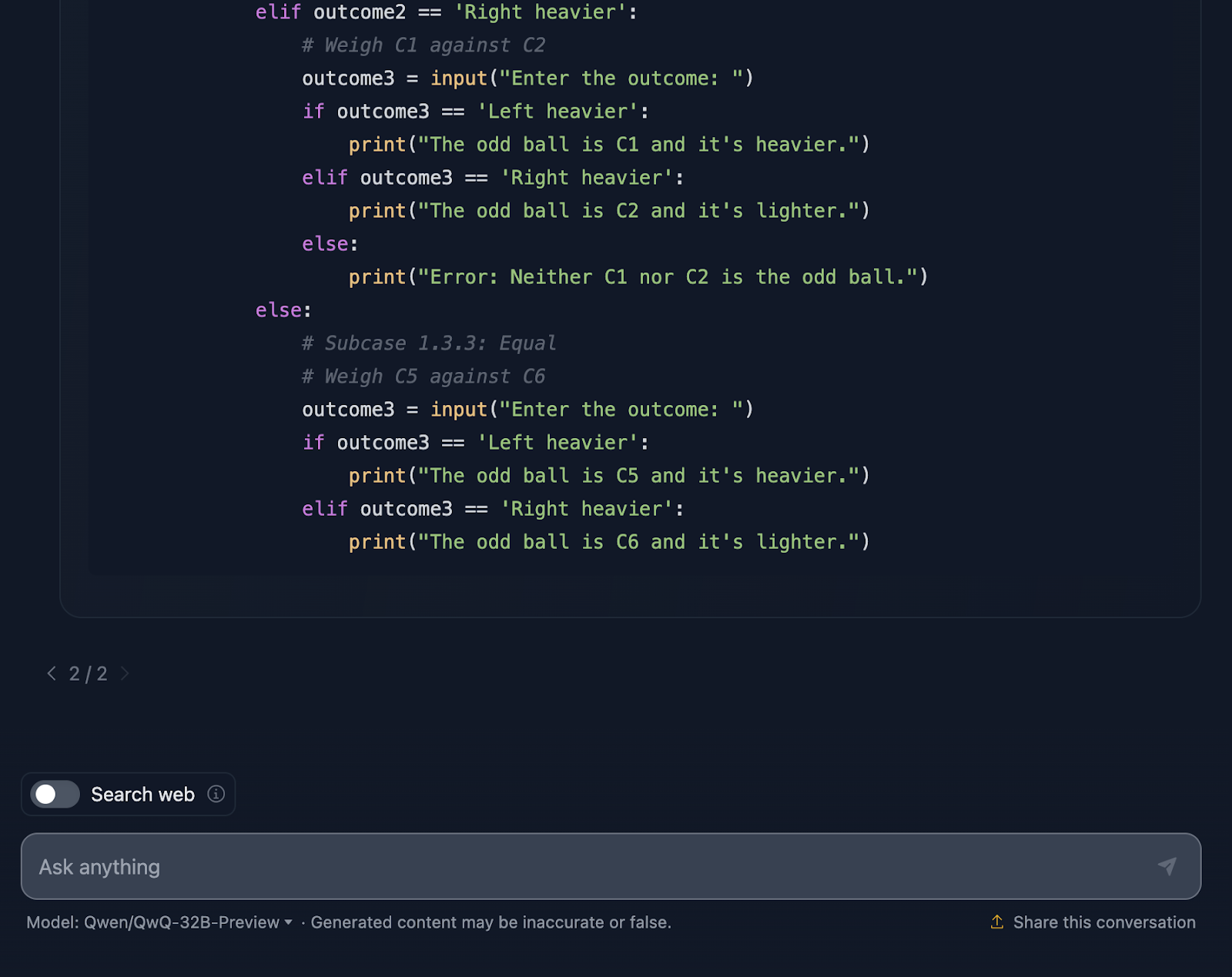
Por fim, a solução inclui um trecho de código Python, o que eu não esperava!  Ele é interativo, permitindo que os usuários simulem as pesagens, o que torna o processo mais fácil de acompanhar e até divertido de explorar. Essa solução não deixa nada ao acaso. Cada um dos resultados das pesagens é coberto, garantindo que nenhum estranho possa escapar da detecção. 

No entanto, um detalhe é que o snippet Python pressupõe uma entrada perfeita do usuário. Se alguém inserir um resultado de pesagem inválido, o código não terá um tratamento de erros para detectar isso. Um pouco de robustez aqui poderia levá-lo ao próximo nível. 

Eu diria que essa é uma excelente resposta - ela supera a do DeepSeek em termos de torná-la mais clara e ajudar os usuários a visualizá-la melhor com as tabelas e o código Python.

Comparação de velocidade: DeepSeek vs. QwQ

Por fim, vou comparar a velocidade de cada modelo para cada teste na execução do raciocínio e no fornecimento de uma solução. Você deve ter em mente que os resultados dependem de muitos fatores e que os modelos nem sempre funcionam na mesma velocidade, mas acho interessante que o DeepSeek foi mais rápido em todas as tarefas que testei.

Benchmarks do QwQ-32B-Preview

O teste do QwQ-32B-Preview revelou como ele lida bem com desafios difíceis de matemática, codificação e raciocínio, embora alguns tenham sido melhores do que outros!

Veja como o QwQ se saiu em alguns benchmarks desafiadores:

• GPQA (raciocínio científico em nível de pós-graduação): Pontuação 65,2%, demonstrando forte raciocínio científico em nível de pós-graduação.
• AIME (tópicos avançados de matemática): Pontuação 50,0%, demonstrando habilidades sólidas em tópicos avançados de matemática, como geometria, álgebra e teoria dos números.
• MATH-500 (problemas matemáticos abrangentes): Alcançou um impressionante 90,6%, comprovando sua capacidade de resolver uma ampla gama de problemas de matemática.
• LiveCodeBench (tarefas de programação do mundo real): Pontuação 50,0%, mostrando habilidades de programação robustas em cenários de codificação do mundo real .

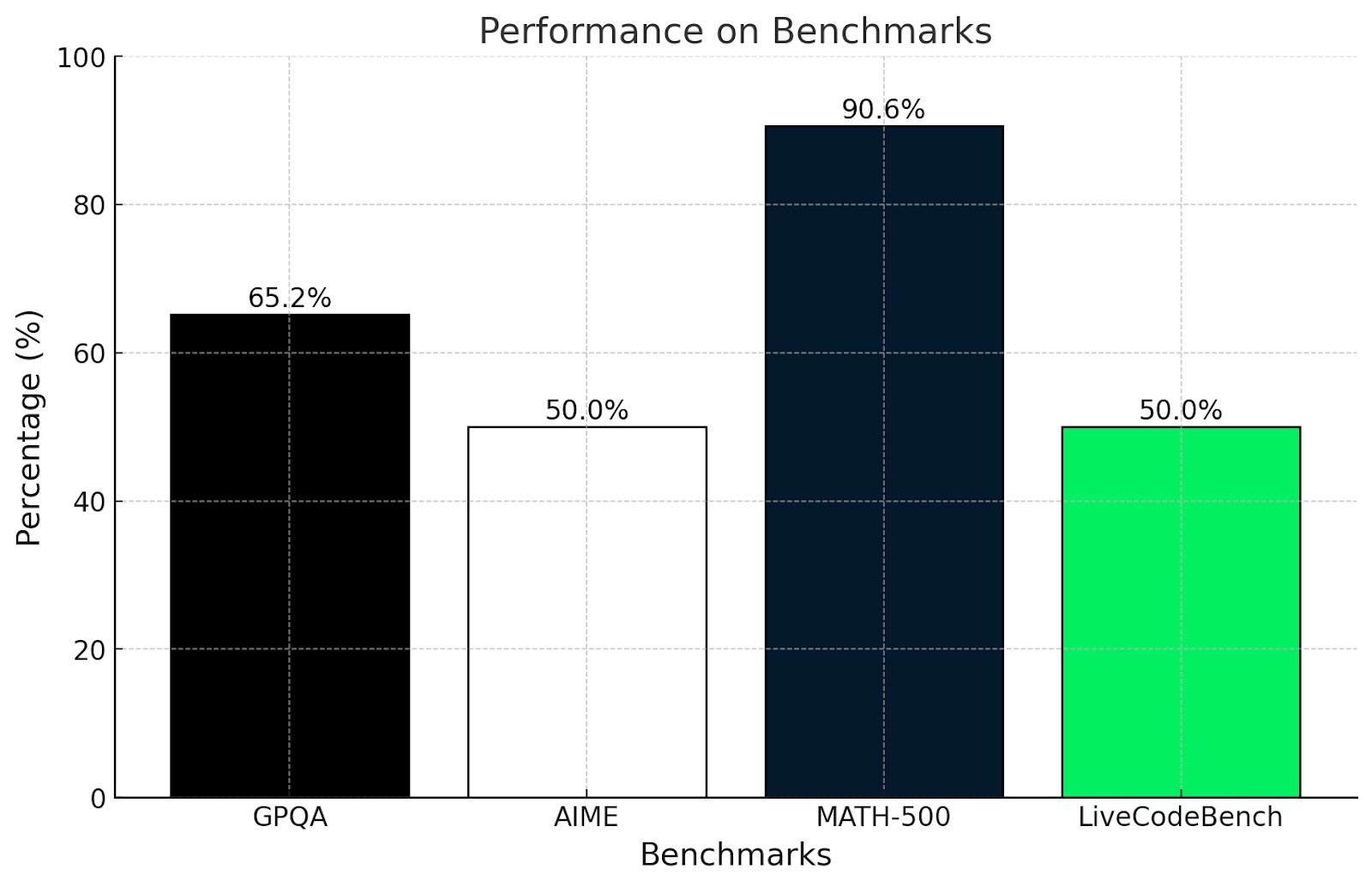
Estou surpreso com esses resultados? Na verdade, não. Esses resultados estão alinhados com os testes realizados neste artigo.

O teste GPQA mede a compreensão do raciocínio científico em nível de pós-graduação. A pontuação de 65,2% mostra que ele é bom em usar a lógica e a matemática para resolver problemas, mas pode ter dificuldades com questões muito especializadas ou profundamente conceituais, o que vimos nos testes de matemática mais complexos deste artigo.

Da mesma forma, o teste AIME é conhecido por tópicos avançados de matemática, como geometria e álgebra. Uma pontuação de 50% mostra que o QwQ-32B-Preview pode resolver alguns desses problemas, mas tem dificuldades com os problemas realmente inteligentes que exigem um pensamento inovador. 

A pontuação de mais de 90% no MATH-500 é muito impressionante e mostra que o QwQ-32B-Preview é excelente para resolver um problema geral de matemática com precisão decente.

O LiveCodeBench mede a capacidade de programação em cenários de codificação. A pontuação de 50% significa que o QwQ-32B-Preview pode lidar com o básico da codificação e seguir instruções claras, mas pode ter dificuldades com tarefas mais complicadas.

O QwQ é realmente forte quando se trata de resolver problemas estruturados e usar a lógica, conforme observado nas pontuações do GPQA e do MATH-500. Ele se sai bem em matemática e ciências, mas considera os problemas criativos ou não convencionais, como no AIME, mais desafiadores. Suas habilidades de programação são decentes, mas poderiam ser melhores ao lidar com tarefas de codificação confusas ou pouco claras.

Vamos dar uma olhada agora nas métricas do QwQ 32B-preview junto com as métricas do DeepSeek e outros modelos para comparação:

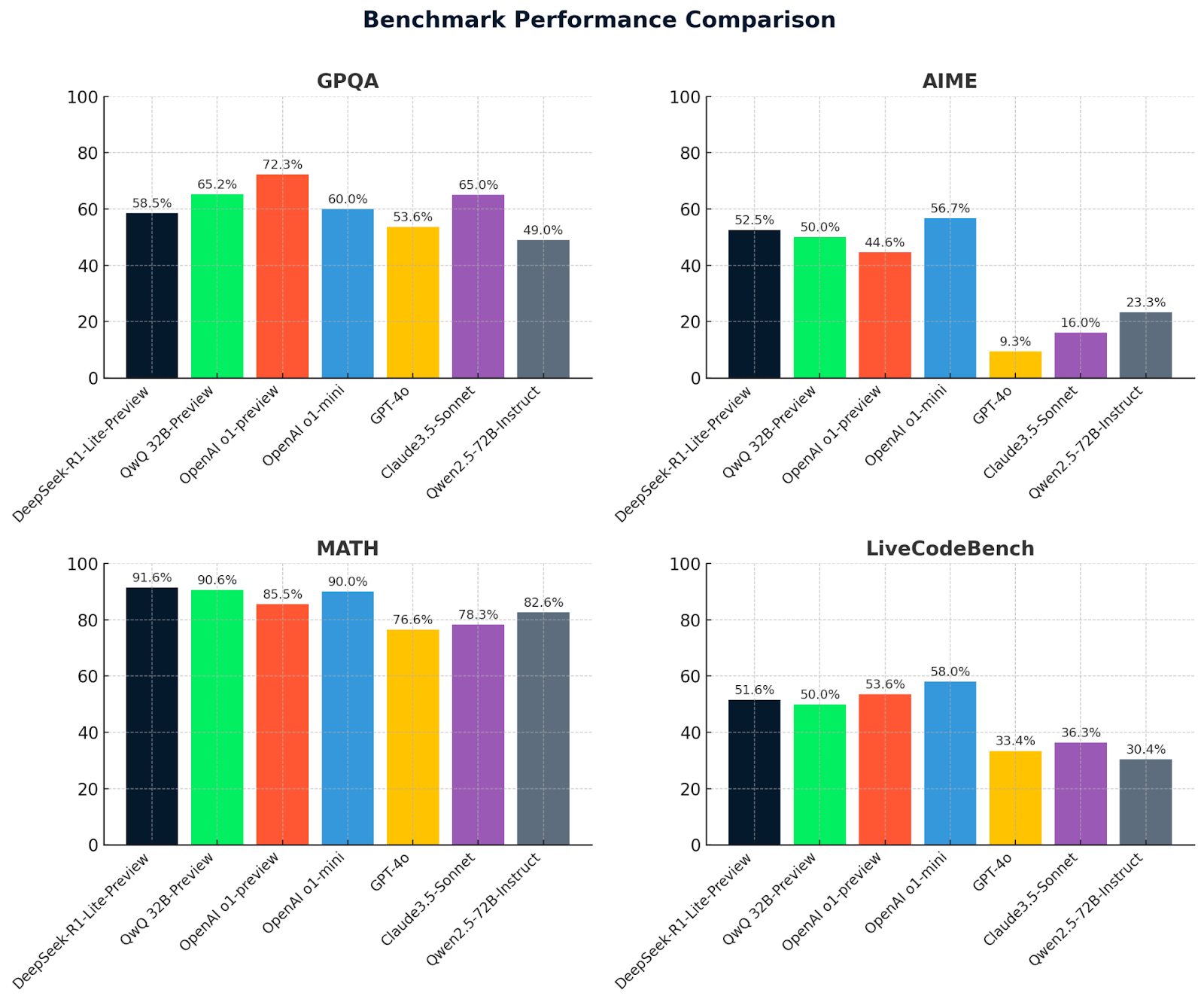
Esses gráficos fornecem uma comparação clara do desempenho do modelo em quatro benchmarks: GPQA, AIME, MATH e LiveCodeBench. O DeepSeek-R1-Lite-Preview se destaca por seus bons resultados, especialmente em MATH (91,6%), demonstrando sua capacidade de raciocínio avançado e solução de problemas.

O QwQ-32B-preview tem um desempenho consistentemente bom em todos os benchmarks, destacando-se particularmente em MATH (90,6%), demonstrando suas robustas habilidades matemáticas e de raciocínio geral. Outros modelos, como o OpenAI O1-preview e o Claude 3.5-Sonnet, apresentam pontos fortes variados, mas geralmente ficam atrás do QwQ-32B-preview e do DeepSeek em áreas importantes, destacando a vantagem competitiva desses dois modelos líderes.

Conclusão

Testar o QwQ-32B-Preview foi muito divertido, e espero não ter sido muito tendencioso - embora eu tenha que admitir que o DeepSeek-R1-Lite-Preview realmente me impressionou! 

O QwQ-32B-Preview é claramente um modelo forte com recursos incríveis, mas não é perfeito e a resposta final dada pelo modelo nem sempre corresponde à resposta final no processo de raciocínio, que muitas vezes tinha uma solução melhor do que a que foi realmente apresentada.

Você já experimentou o QwQ? O que você achou? Você gosta mais dele do que do DeepSeek? E, quem sabe, talvez o próximo grande modelo seja aquele que supere todos os outros em todos os benchmarks. É um momento muito empolgante para você ver a evolução dessas ferramentas!