I Tested QwQ-32B-Preview: Alibabas Begründungsmodell

Was ist QwQ-32B-Preview? 

QwQ-32B-Preview ist ein Modell, das für fortgeschrittene Aufgaben entwickelt wurde, die über einfaches Textverständnis hinausgehen. Es zielt darauf ab, herausfordernde Probleme wie Codierung und mathematisches Denken zu lösen. Als "Preview"-Version wird sie noch verfeinert. Es ist auf Plattformen wie Hugging Face als Open-Source verfügbar, so dass du das Modell testen, verbessern und Feedback geben kannst, wenn du willst!

Du solltest bedenken, dass QwQ-32B-Preview ein experimentelles Modell ist. Sie ist zwar vielversprechend, hat aber auch einige wichtige Einschränkungen:

• Sprachen mischen: Es kann sein, dass das Modell unerwartet zwischen den Sprachen wechselt, wodurch seine Antworten unklarer werden.
• Zirkelschluss: Manchmal bleibt sie in sich wiederholenden Argumentationsschleifen stecken, was zu langen Antworten ohne klare Schlussfolgerung führt.
• Sicherheitsbedenken: Das Modell braucht noch stärkere Sicherheitsmerkmale, um eine zuverlässige und sichere Nutzung zu gewährleisten, daher ist beim Einsatz Vorsicht geboten.
• Leistungslücken: Er ist nachweislich gut in Mathematik und Programmierung, aber er könnte sich in Bereichen wie dem gesunden Menschenverstand und dem Verständnis feiner sprachlicher Nuancen verbessern.

Wie kann ich auf die QwQ-32B-Vorschau zugreifen?

Du kannst auf QwQ-32B-Preview über HuggingChatzugreifen, wo es derzeit kostenlos und ohne Quantisierung läuft. So verwendest du QwQ-32B-Preview:

1. Visit HuggingChat: https://huggingface.co/chat/
2. Wähle QwQ-32B-Vorschau aus den verfügbaren Modellen
3. Beginne mit der Interaktion mit dem Modell

Der Erdbeertest

Wir beginnen mit dem bekannten Erdbeertest. Die Aufforderung lautet: "Wie oft kommt der Buchstabe 'r' in 'Erdbeere' vor?"

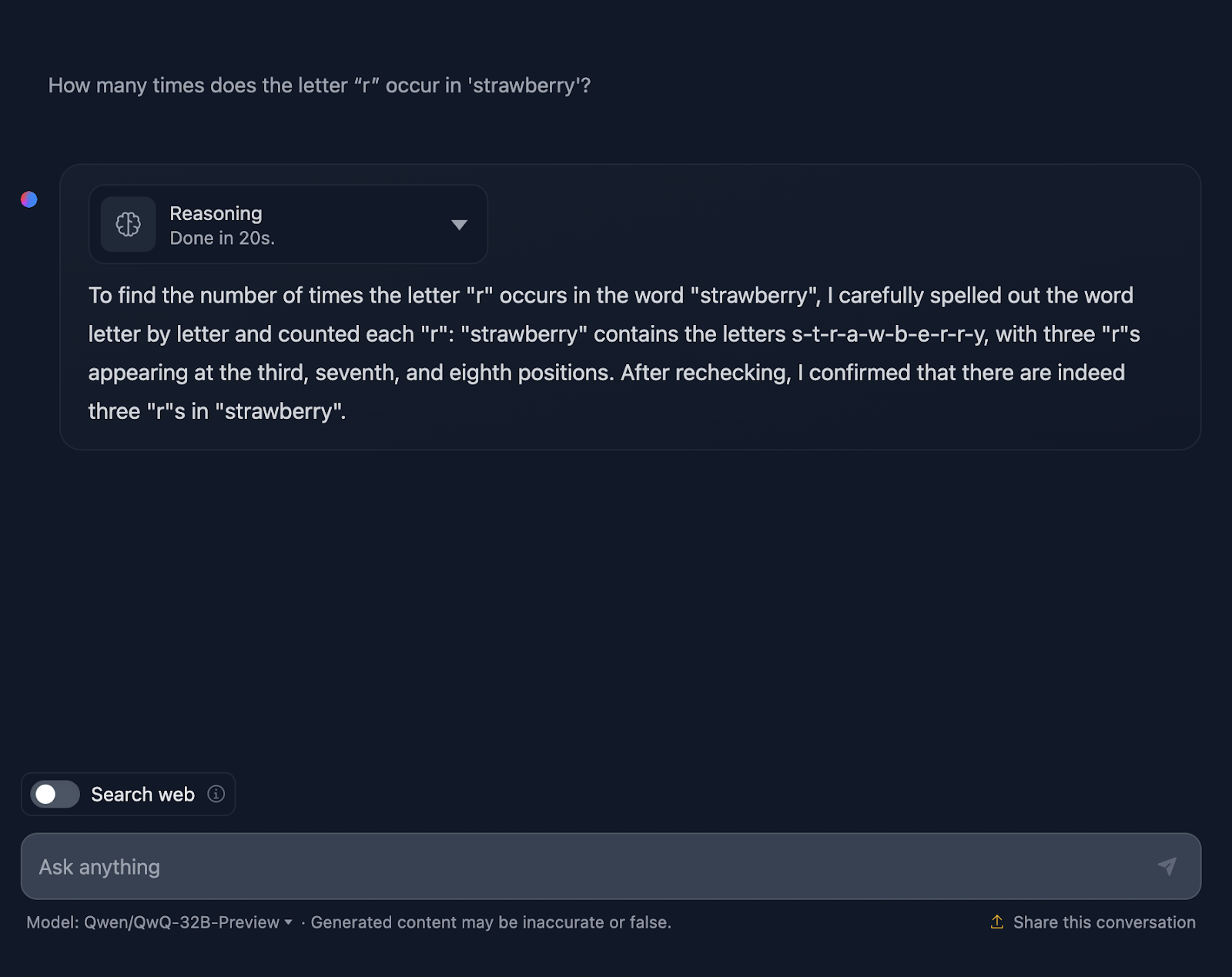
Stimmt, das wird jetzt interessant! 

Er zählt die Buchstaben zwar richtig, aber er gibt fälschlicherweise an, dass die "r "s an der dritten, siebten und achten Stelle stehen, was nicht stimmt. Die richtigen Positionen sind die dritte, achte und neunte. Zum Vergleich: DeepSeek hat dies korrekt gehandhabt.

Schauen wir uns die Argumentation von QwQ-32B-Preview genauer an:

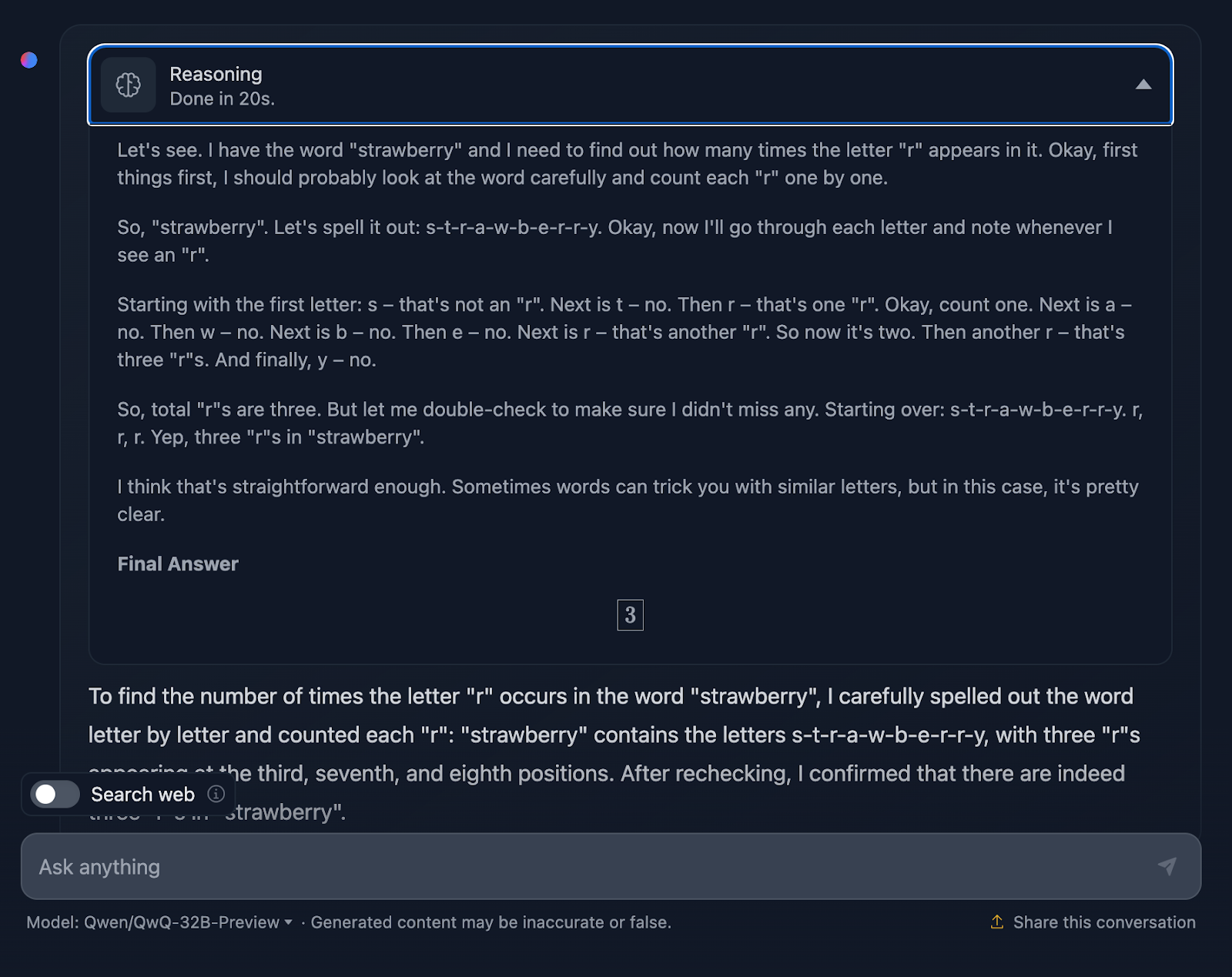
Die Argumentation von QwQ-32B-Preview war viel kürzer als die von DeepSeek. In diesem Fall hat es beim Zählen der Buchstaben jedoch nicht ihre Position berücksichtigt, weshalb es wohl falsch lag. Es ist interessant, weil es diese Information liefert, obwohl sie nicht benötigt wird - ich habe nicht nach der Position der "r "s gefragt, sondern nur nach der Anzahl der Vorkommen. Die Bereitstellung zusätzlicher, unnötiger Informationen führte zu Fehlern.

Rechnen in Mathematik

Um die mathematische Logik des Modells zu testen, werden wir drei unterschiedlich komplexe Tests durchführen.

Dreiecksfläche

Die Aufforderung lautet: "Wenn ein Dreieck die Seitenlängen 3, 4 und 5 hat, wie groß ist dann sein Flächeninhalt?" Mal sehen, wie es damit umgeht:

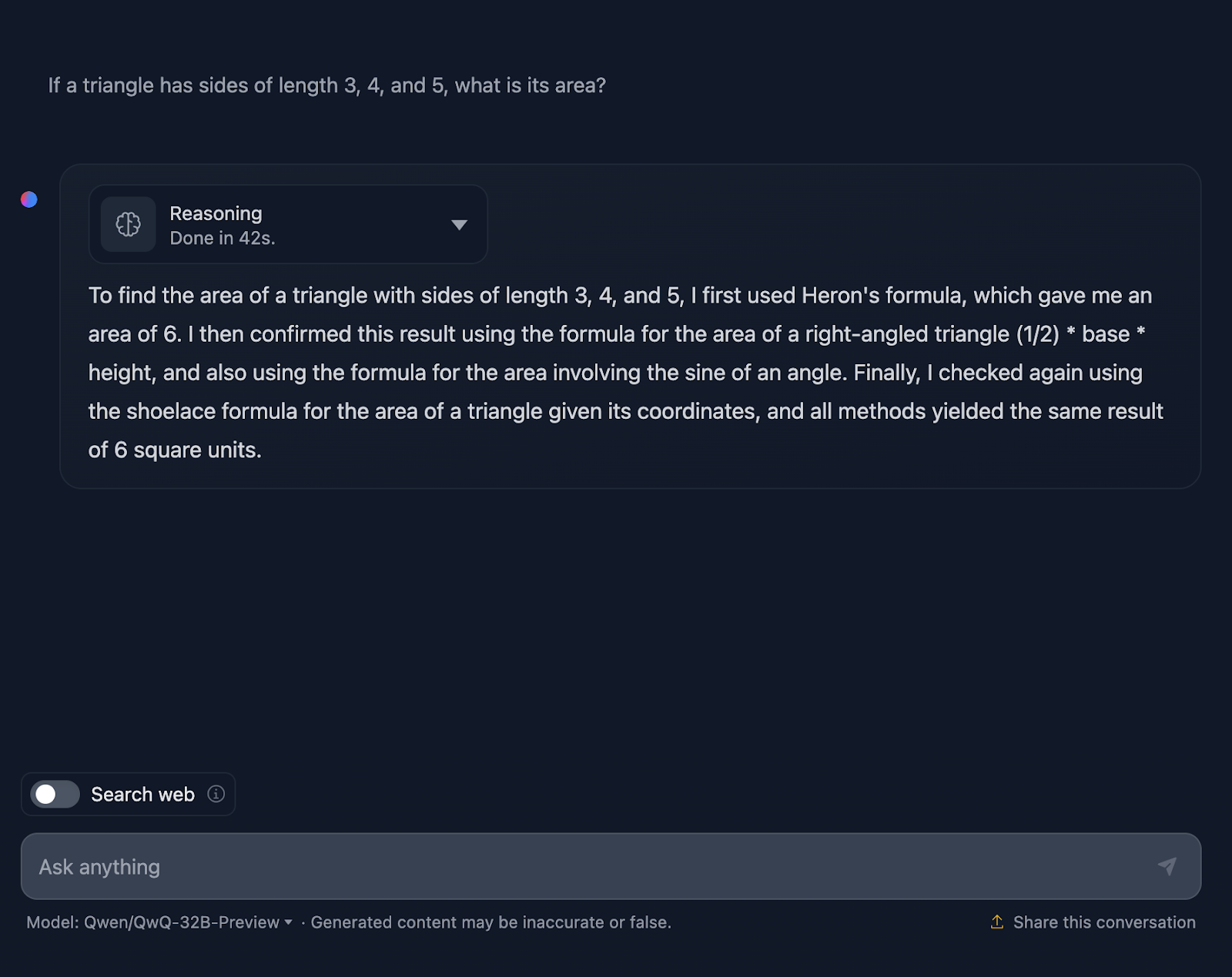
Die Antwort ist richtig und erklärt die Methoden, die verwendet wurden, um zu dieser Schlussfolgerung zu kommen. Allerdings ist keine der Formeln oder Berechnungen in der Lösung enthalten, was in Ordnung ist, da dies nicht verlangt wurde. Es wäre jedoch eine nette Ergänzung gewesen, die DeepSeek zur Verfügung gestellt hat. Schauen wir uns jetzt die Argumentation an:

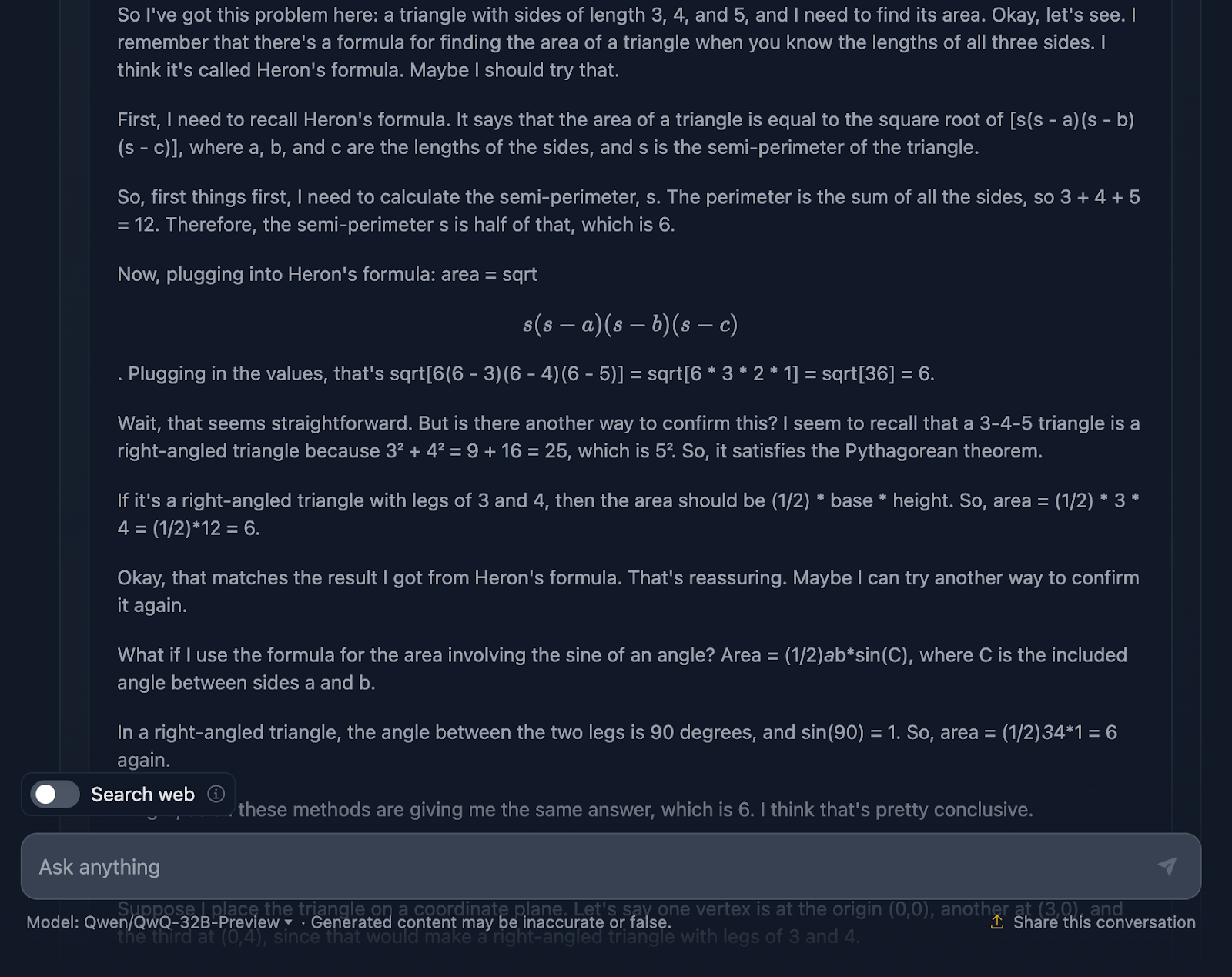
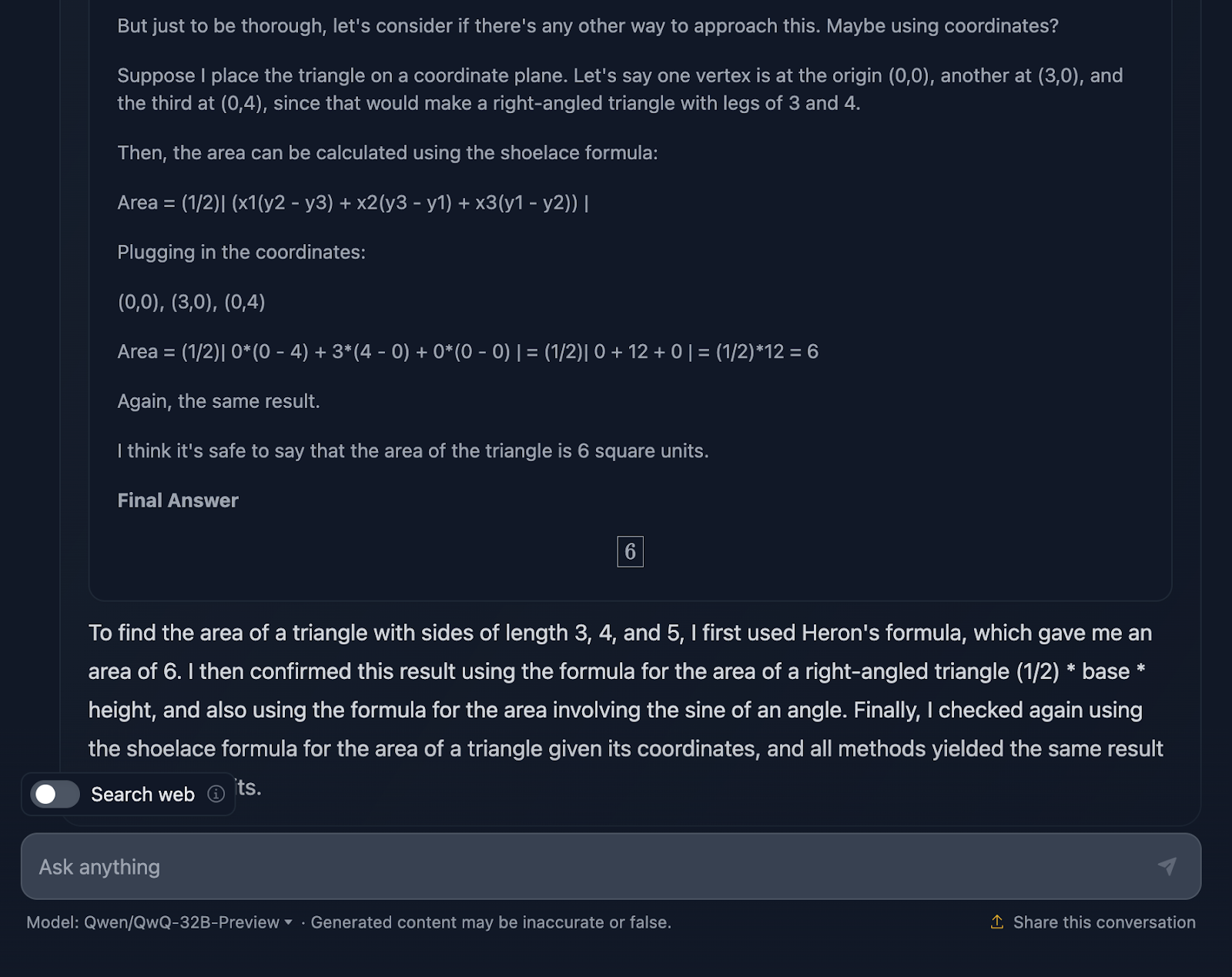
Ich finde es ziemlich cool, dass es vier verschiedene Ansätze verwendet hat, um zur gleichen Lösung zu kommen, im Gegensatz zu DeepSeek, das nur drei verwendet hat. Die Argumentation ist klar und einfach zu verstehen. Das einzige Problem, das mir aufgefallen ist, ist, dass die Formatierung und der Stil der Formeln ein wenig uneinheitlich sind - einige werden richtig analysiert, andere nicht. Das ist etwas, das DeepSeek richtig gemacht hat.

Mathe Beweis

Schauen wir uns einen komplexeren Mathetest an, um zu sehen, ob es einen Unterschied in der Leistung und im Denkprozess gibt. Ich werde das Folgende testen: "Beweise, dass die Summe der Kehrwerte der Fibonacci-Zahlen gegen einen endlichen Wert konvergiert."

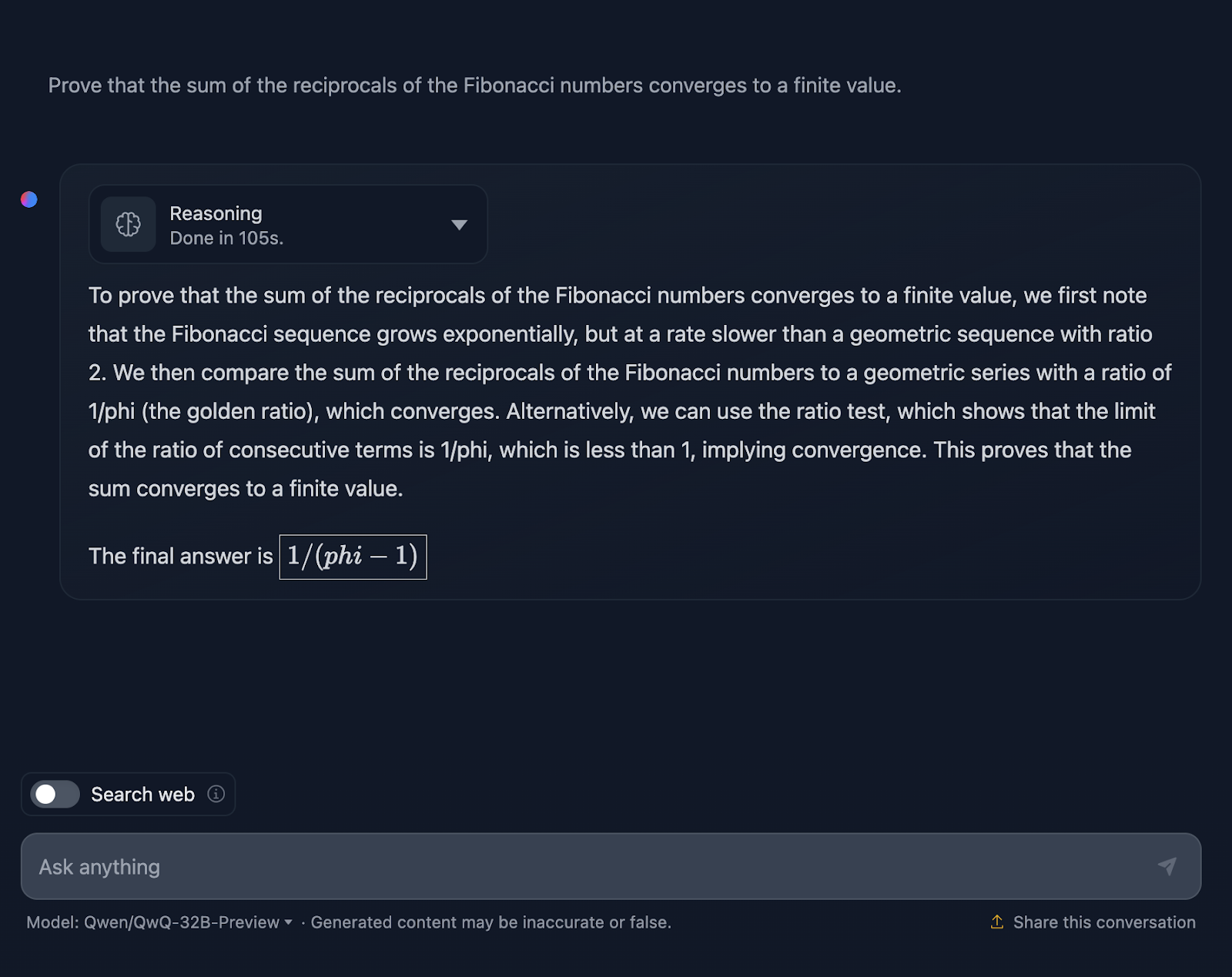
Die Antwort ist technisch nicht falsch, aber es gibt viel Raum für Verbesserungen. Erstens: Wenn ich das Modell um einen Beweis bitte, sollte die endgültige Antwort nicht nur ein Wert sein, sondern eine Reihe von Formeln oder Anwendungen von Theoremen, um eine Hypothese oder Aussage zu beweisen. Das wird hier versucht, aber es braucht mehr Ausarbeitung, und die endgültige Antwort beweist nicht wirklich etwas. Wieder einmal scheint die Formatierung der Formeln ein wiederkehrendes Problem zu sein. Ein großartiges Beispiel für einen richtigen Beweis findest du in dem Test, den ich mit DeepSeek durchgeführt habe.

Während meiner Promotion in Mathematik habe ich Matheprüfungen benotet, und ich kann dir sagen, dass diese Antwort nicht die volle Punktzahl bekommen hätte - aber die von DeepSeek schon!

Schauen wir uns nun die Argumentation an (aus Gründen der Lesbarkeit zeige ich nur den ersten und den letzten Teil des langwierigen Argumentationsprozesses, aber ich ermutige dich, die Aufforderung selbst zu testen):

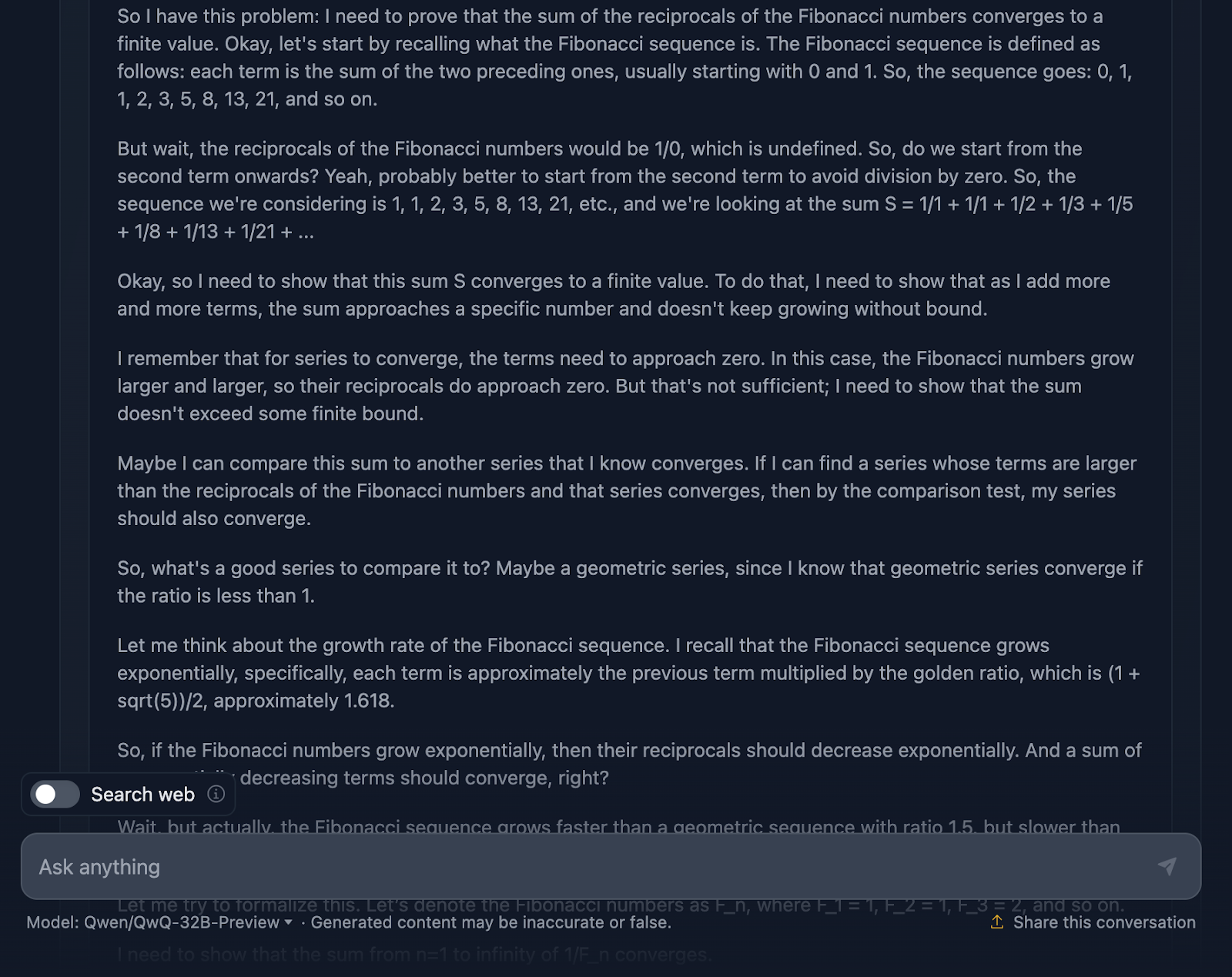
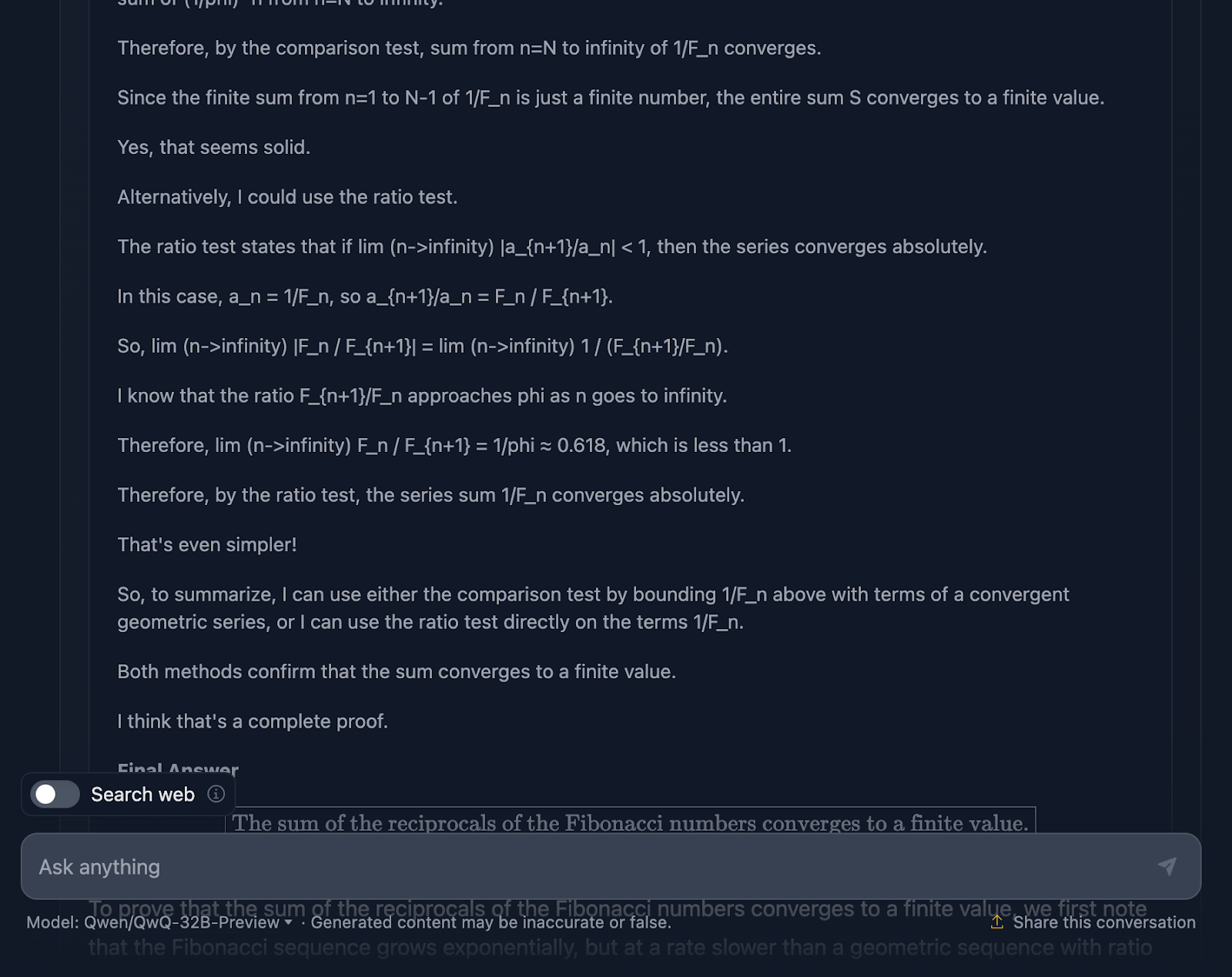
Zunächst einmal beginnt das Modell stark. Sie erinnert an die Fibonacci-Folge, vermeidet den offensichtlichen Fallstrick, durch Null zu teilen, und stellt das Problem gut dar. Das ist eine solide Grundlage. Dann werden der Vergleichstest und der Ratio-Test verwendet, die Standardtests für die Konvergenz von Reihen sind, und es wird sogar die Formel von Binet verwendet, um die Fibonacci-Zahlen zu approximieren und zu begrenzen. An einer Stelle wird auch eingeräumt, dass man nicht den genauen Wert berechnen muss, sondern nur beweisen muss, dass die Reihe konvergiert, was zeigt, dass man sich wirklich an das Problem hält.

Die Argumentation ist zweifellos richtig, aber der Weg zur Antwort ist ein wenig verworren. Auch hier sind einige Formeln schön formatiert, aber andere nicht so sehr. 

Der endgültige Beweis ist jedoch erbracht. Sie zeigt, dass die Reihe konvergiert, und sie verwendet gültige Methoden, um dorthin zu gelangen. Verglichen mit der Leistung von DeepSeek hätte der Nachweis jedoch etwas mehr Feinschliff und Konsistenz vertragen können.

Es überrascht mich auch sehr, dass die endgültige Antwort in der Begründung, die eine bessere endgültige Antwort ist, sich von der in der endgültigen Ausgabe unterscheidet. Daran hätte es sich halten sollen!

Differentialgeometrie

Versuchen wir nun einen Test zur Differentialgeometrie:

Betrachten wir eine Fläche S in^R3, die wie folgt parametrisiert ist

φ(u,v) = (u cos v, u sin v, ln u)

für u > 0 und 0 ≤ v < 2π.

a) Berechne die erste Grundform von S.

b) Bestimme, ob S eine minimale Fläche ist.

c) Finde die Gaußsche Krümmung K und die mittlere Krümmung H von S.

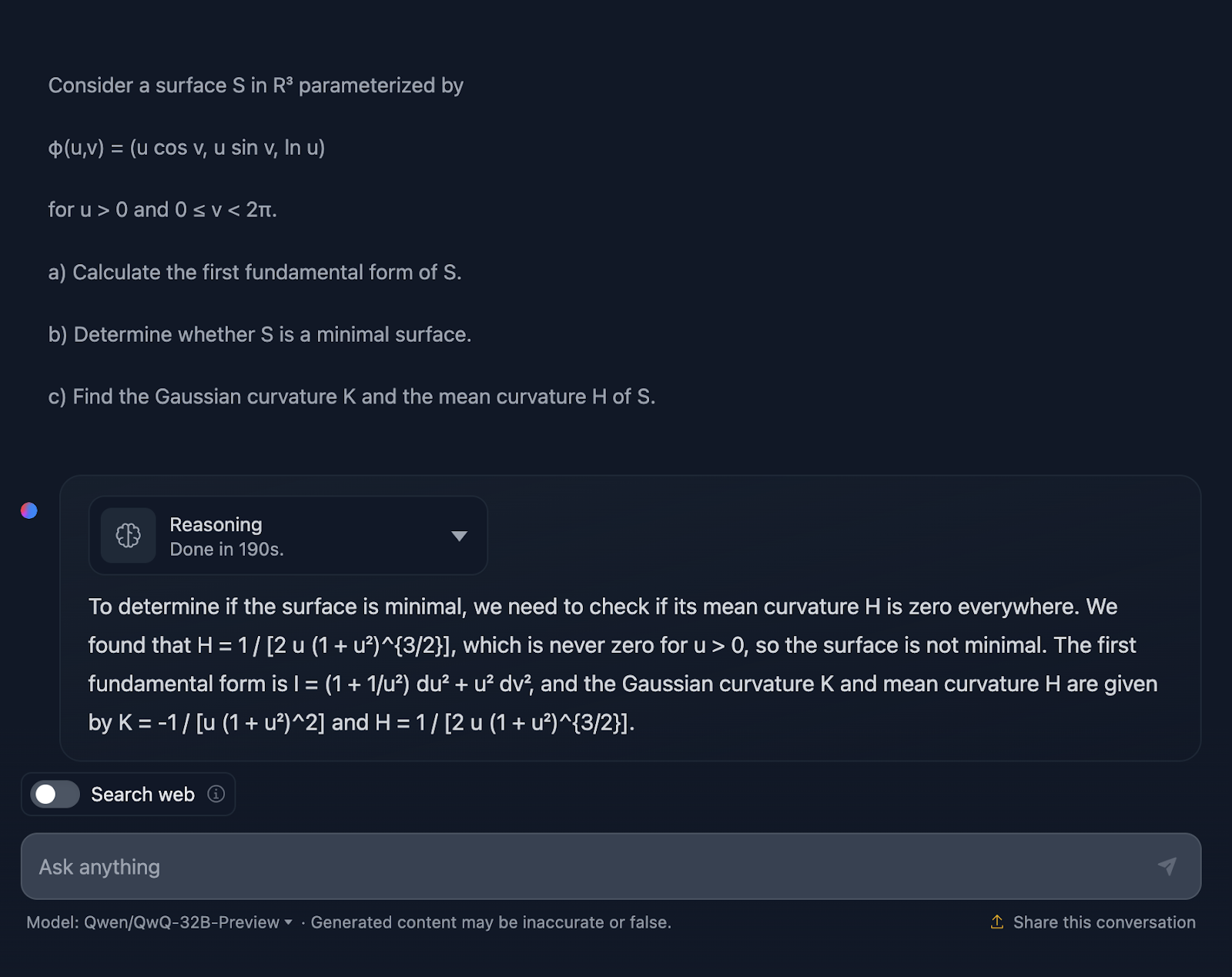
Gut, die Antwort überrascht mich nicht, denn sie ist dem vorherigen Test vom Stil her sehr ähnlich. Auch hier ist es technisch nicht falsch, aber die Art und Weise, wie die Erklärung vermittelt wird, ist definitiv verbesserungswürdig.

Die Erklärung überspringt das Wie. Ich würde natürlich keine Schritt-für-Schritt-Anleitung erwarten, aber zumindest ein paar Formeln, die zeigen, woher die Ergebnisse kommen. Außerdem wird die Antwort nicht in Abschnitte unterteilt, und die Formatierung der Formeln ist auch nicht die beste. DeepSeek hat in dieser Hinsicht gute Arbeit geleistet.

Noch einmal - keine volle Punktzahl für QwQ, aber volle Punktzahl für DeepSeek!

Werfen wir einen Blick auf die Argumentation (aus Gründen der Lesbarkeit zeige ich nur den ersten und den letzten Teil):

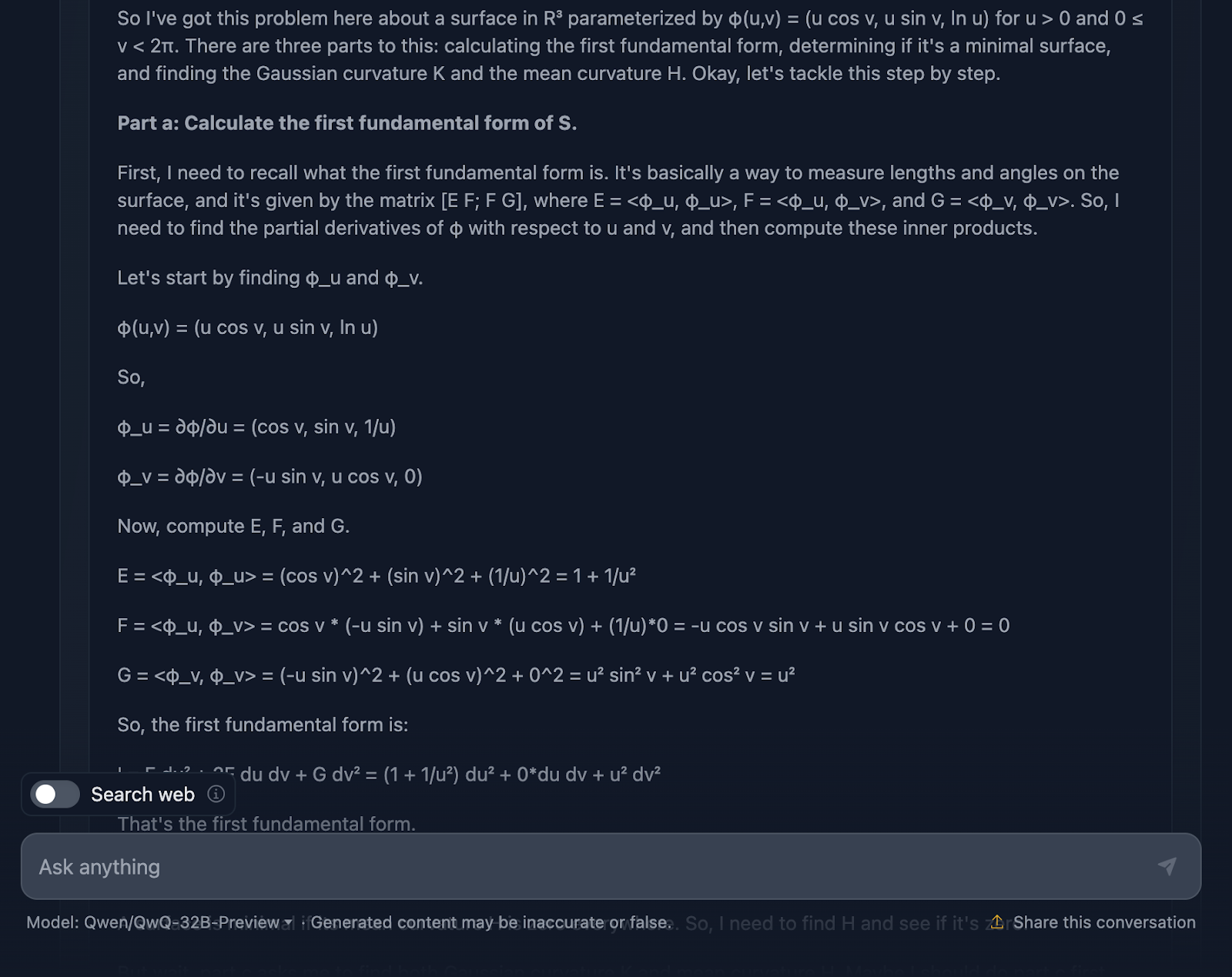
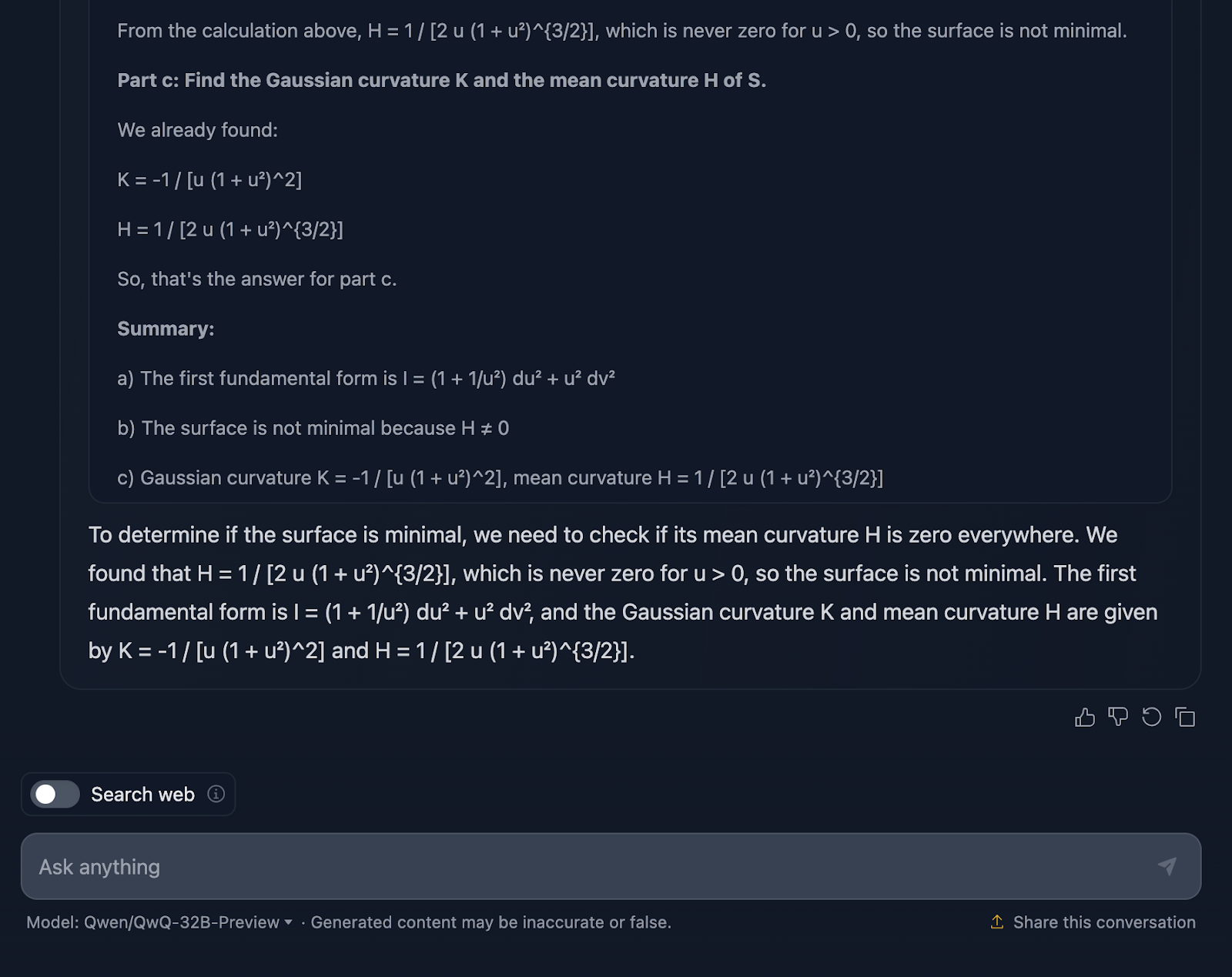
Also gut, lass uns über die Argumentation des Modells sprechen. Zunächst einmal muss ich sagen, dass die Arbeit gründlich ist. Die Aufteilung in klare Abschnitte - Teil a, Teil b und Teil c - macht es einfach, dem Buch zu folgen, und es leistet solide Arbeit, indem es uns durch die Schritte führt. Er beginnt mit der ersten Grundform, berechnet sorgfältig die Koeffizienten aus der Parametrisierung und baut dann darauf auf. Wenn wir in Teil c zu den Gauß'schen und mittleren Krümmungen kommen, sind die Grundlagen schon ziemlich gut gelegt.

Hier fangen die Dinge an, sich ein wenig klobig anzufühlen. Die Berechnungen sind zwar technisch korrekt, aber das Modell verbringt viel Zeit damit, Schritte zu überprüfen oder Berechnungen zu wiederholen, was gut für die Genauigkeit, aber nicht so gut für die Lesbarkeit ist. 

Lass uns jetzt über die Formatierung sprechen. Die Formeln sind alle da, aber sie werden nicht auf die klarste Weise präsentiert - mal wieder. Es ist ein bisschen chaotisch, und für jeden, der versucht, mitzukommen, kann das die Dinge schwieriger machen, als sie sein müssten. Ein übersichtlicheres Layout mit hervorgehobenen Schlüsselergebnissen würde diese Erklärung wirklich verbessern.

Ein weiterer Punkt, der fehlt, ist der Kontext. Das Modell liefert uns die Ergebnisse, aber es hält nicht wirklich an, zu erklären, was sie bedeuten. Warum ist zum Beispiel die Gaußsche Krümmung hier wichtig? Oder was sagt sie uns über die Geometrie der Oberfläche? Und wenn sie zu dem Schluss kommt, dass die Oberfläche nicht minimal ist, hat sie technisch gesehen recht - aber sie verpasst die Gelegenheit, zu erklären, was das im weiteren Sinne bedeutet.

Codierungstests

Wir haben die Leistung von QwQ-32B-Preview in Mathe-Tests getestet und ich bin nicht sonderlich beeindruckt - aber vielleicht bin ich voreingenommen, weil ich die Leistung von DeepSeek wirklich mochte. Mal sehen, wie es bei den Codierungstests abschneidet und ob QwQ-32B-Preview mich dieses Mal überraschen kann.

Python

Der erste Test ist:

"Implementiere eine Funktion in Python, die die längste palindromische Teilzeichenkette in einer gegebenen Zeichenkette findet. Die Funktion sollte eine Zeitkomplexität besser als O(n^3) haben."

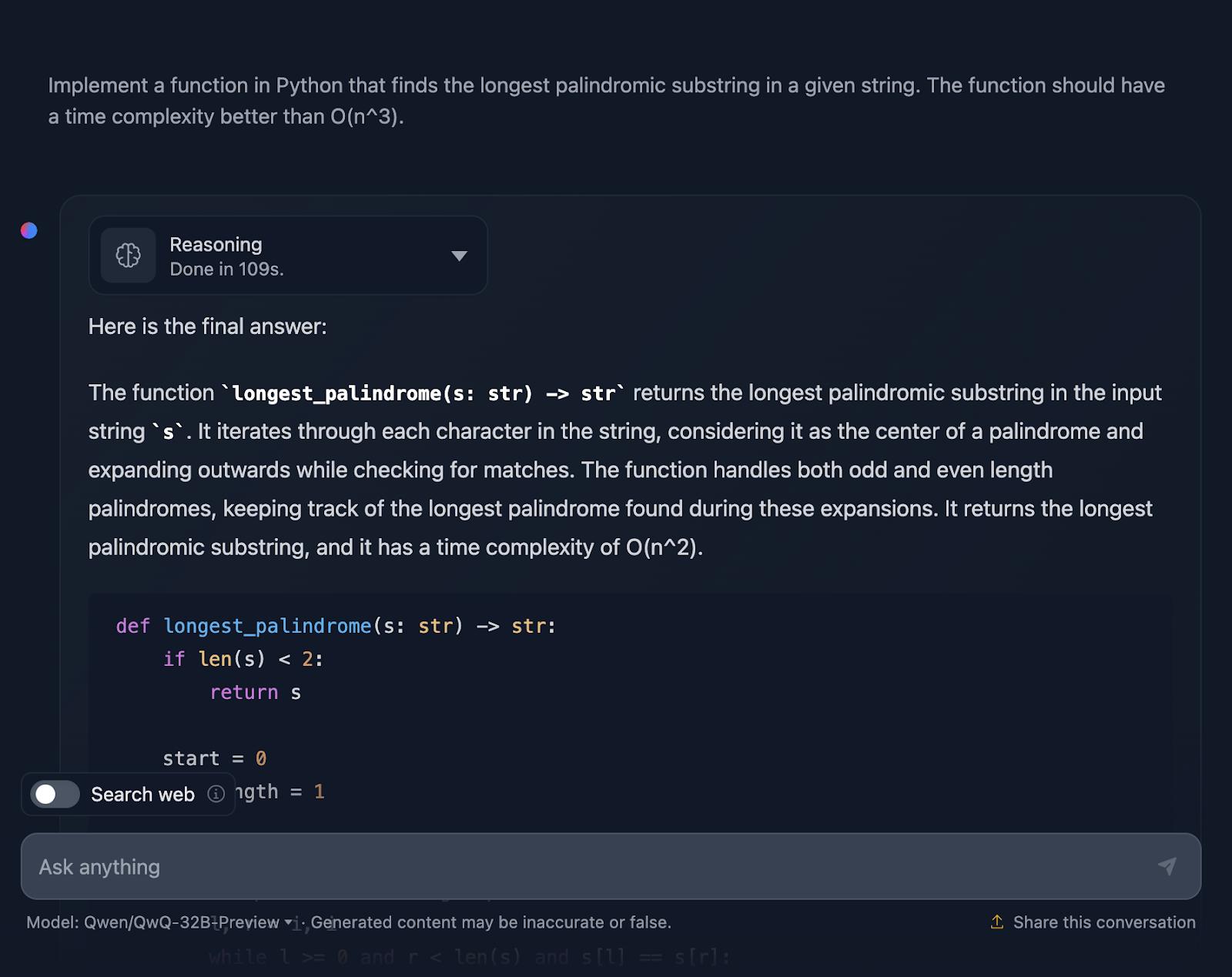
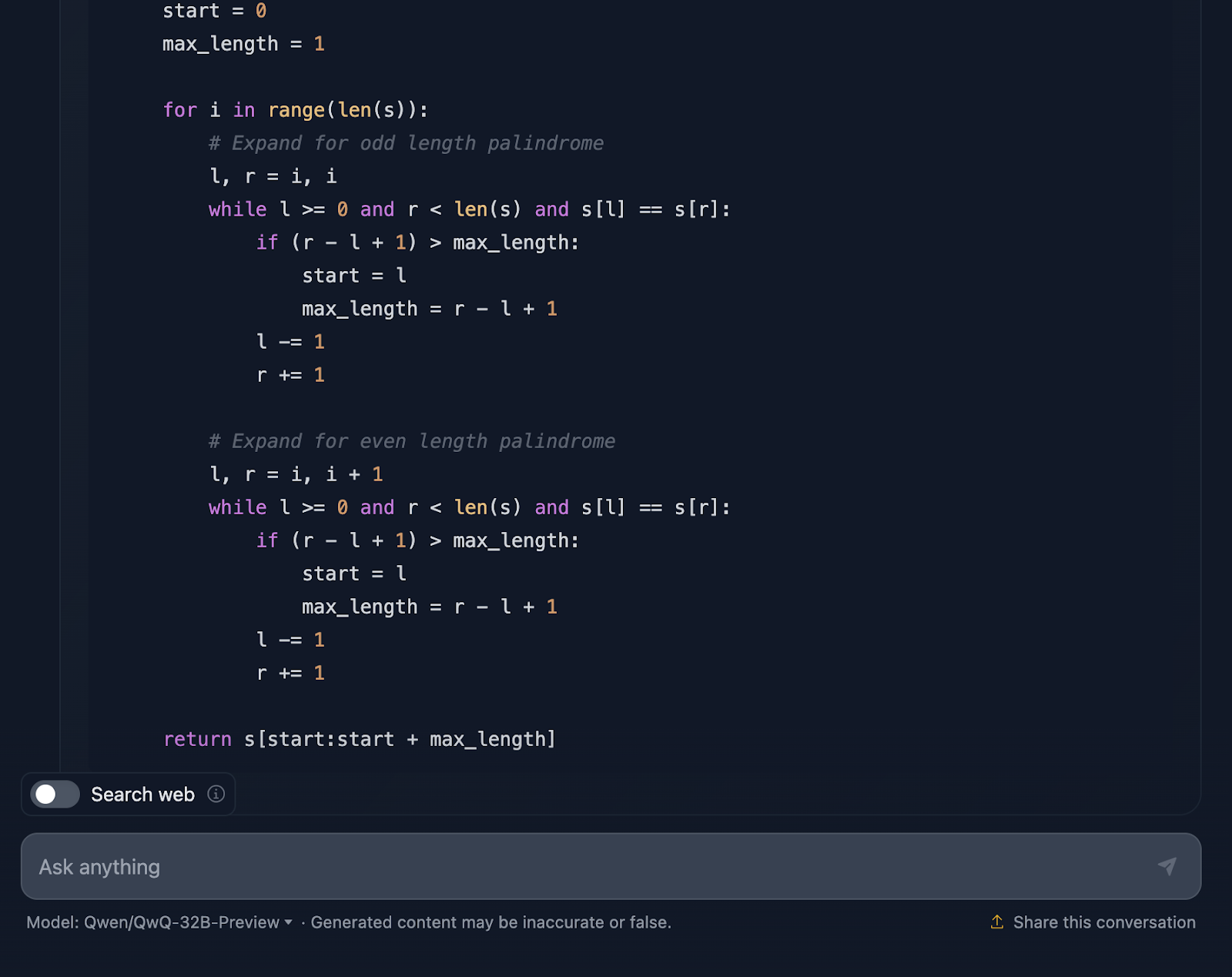
Die Lösung ist korrekt und bietet eine saubere, effiziente Möglichkeit, die längste palindromische Teilzeichenkette mit der erforderlichen Komplexität zu finden. Es verwendet einen intelligenten Ansatz, indem es um jedes Zeichen herum expandiert, um auf Palindrome zu prüfen, und sowohl ungerade als auch gerade Längen gut behandelt. Der Kodex ist klar und leicht zu verstehen. Allerdings hätte ich mir am Ende Testfälle gewünscht, die DeepSeek zur Verfügung gestellt hat. Schauen wir uns jetzt die Argumentation an (ich zeige nur den ersten und den letzten Teil, um die Lesbarkeit zu verbessern):

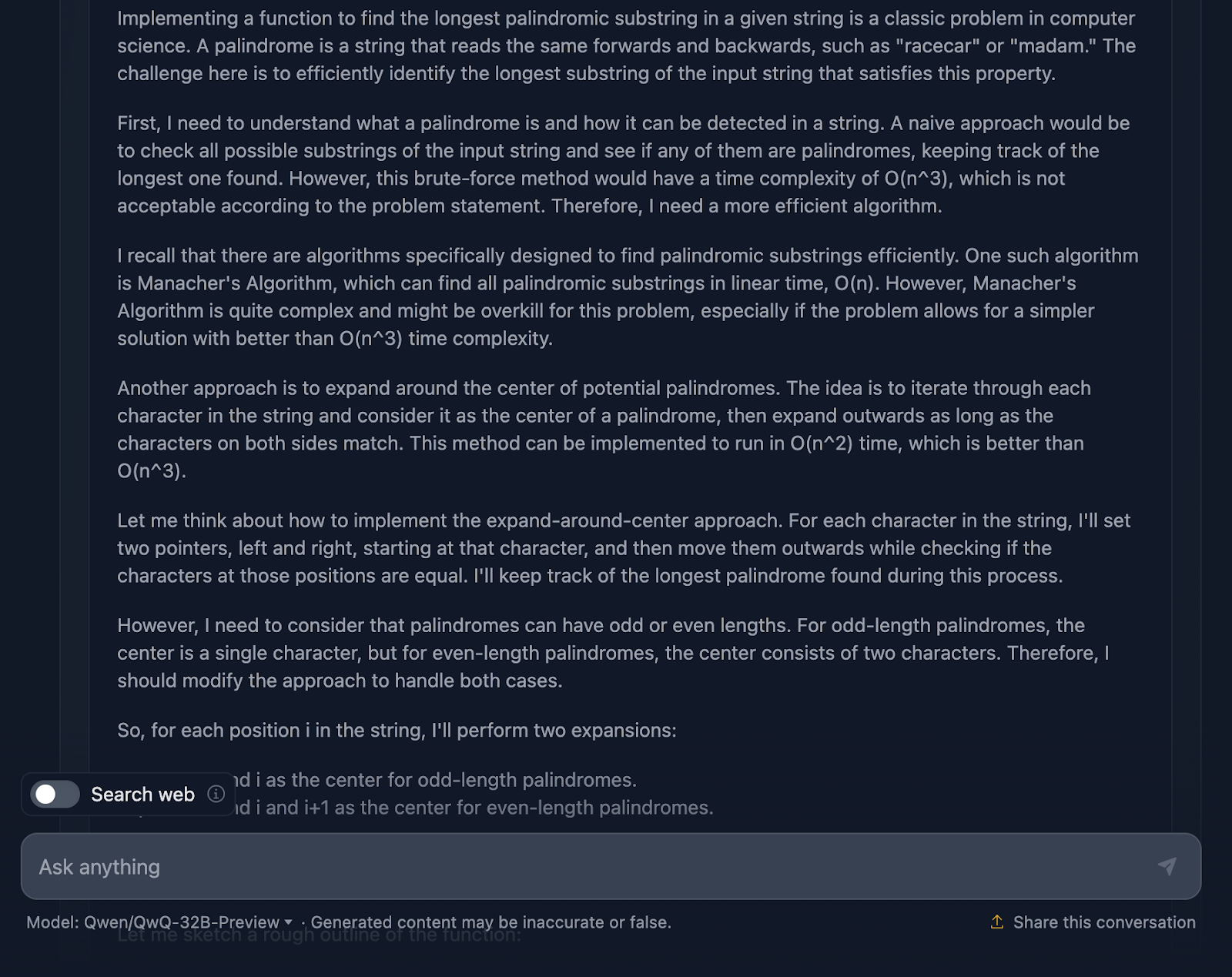
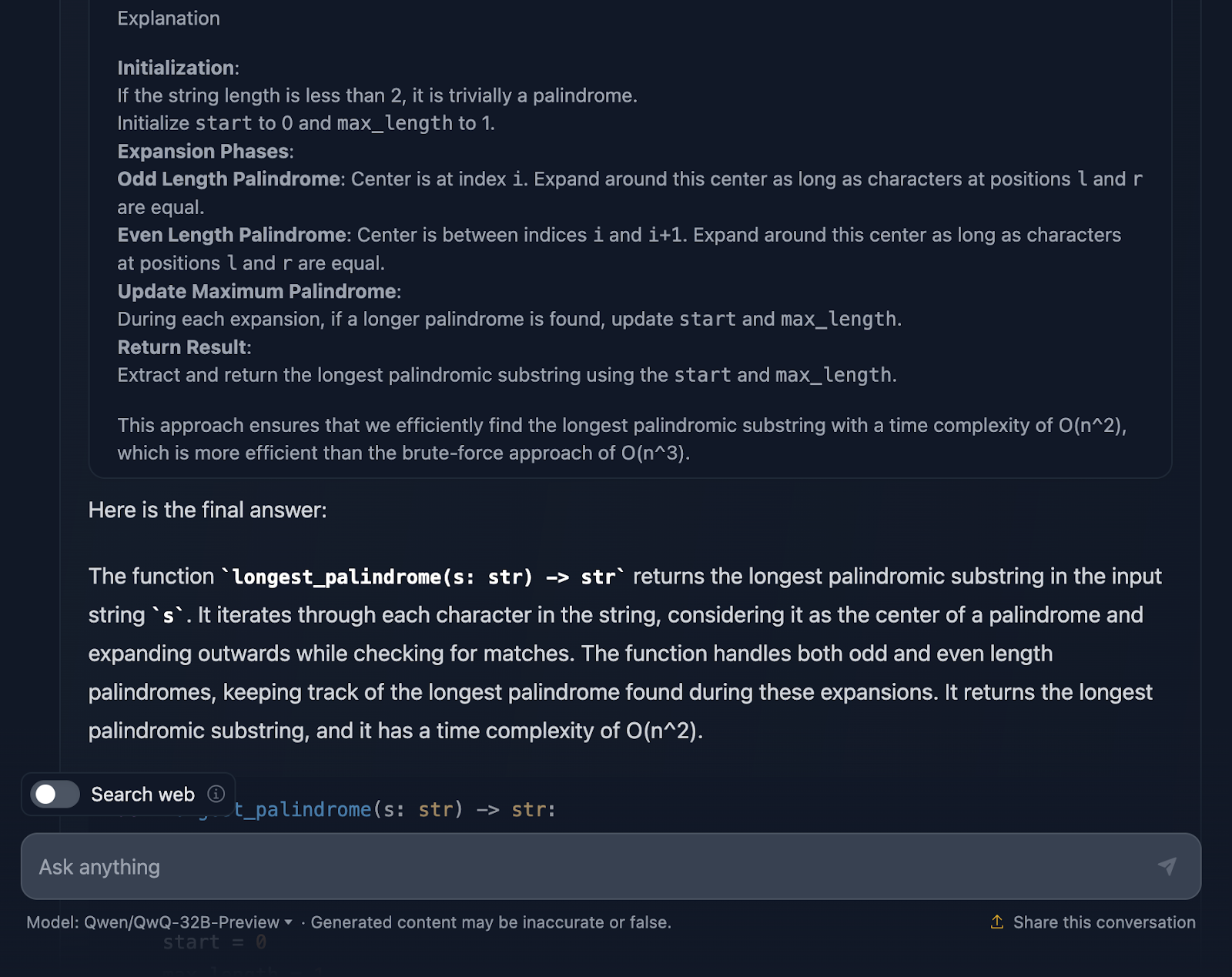
Ich muss sagen, das ist ein ziemlich solider Ansatz, und ich bin von einigen Teilen der Argumentation wirklich beeindruckt. Aber es gibt ein paar Dinge, die noch ein bisschen besser sein könnten - also lass uns darüber reden.

Die Argumentation beginnt mit den Grundlagen: was ein Palindrom ist und warum ein Brute-Force-Ansatz nicht der beste Ansatz ist. Dann springt er direkt zur Expand-around-center-Methode und erwähnt sogar den Manacher-Algorithmus mit seiner O(n)-Komplexität. Er räumt ein, dass das Manacher-System zwar schneller ist, aber für dieses Problem wahrscheinlich zu viel des Guten ist. DeepSeek hat diesen Ansatz nicht erwähnt, was ich auch erwartet hatte, bevor ich ihn ausprobiert habe.  Er spricht auch über alternative Methoden, wie die Umkehrung der Zeichenfolge oder das Überspringen unnötiger Prüfungen, was ich großartig finde!

Die Methode der Erweiterung um den Mittelpunkt wird klar erklärt und trennt zwischen Palindromen mit ungerader und gerader Länge, was wichtig ist, um sicherzustellen, dass alle Fälle abgedeckt sind. 

Die Einbeziehung von Grenzfällen ist ein Highlight. Zeichenketten mit nur einem Zeichen, Zeichenketten ohne Palindrome, Zeichenketten, die nur aus identischen Zeichen bestehen - es ist alles dabei. Es wird sogar erwähnt, wie die Implementierung mit leeren Strings umgeht, indem sie sie einfach zurückgibt. Diese Art von Gründlichkeit ist das, was du von einer Erklärung erwartest.

Ich finde es wirklich gut, dass das Endergebnis in der Begründung eine Aufschlüsselung des Ansatzes, des Lösungscodes und der Erklärung enthält, aber ich wünschte, das wäre auch in der endgültigen Antwort enthalten!

Hat QwQ-32B-Preview in diesem Fall besser abgeschnitten als DeepSeek? Nun, trotz der Testfälle würde ich sagen, ja!

JavaScript

Jetzt werde ich eine Codierungsherausforderung in Javascript testen:

"Schreibe eine Funktion in JavaScript, die feststellt, ob eine bestimmte Zahl eine Primzahl ist."

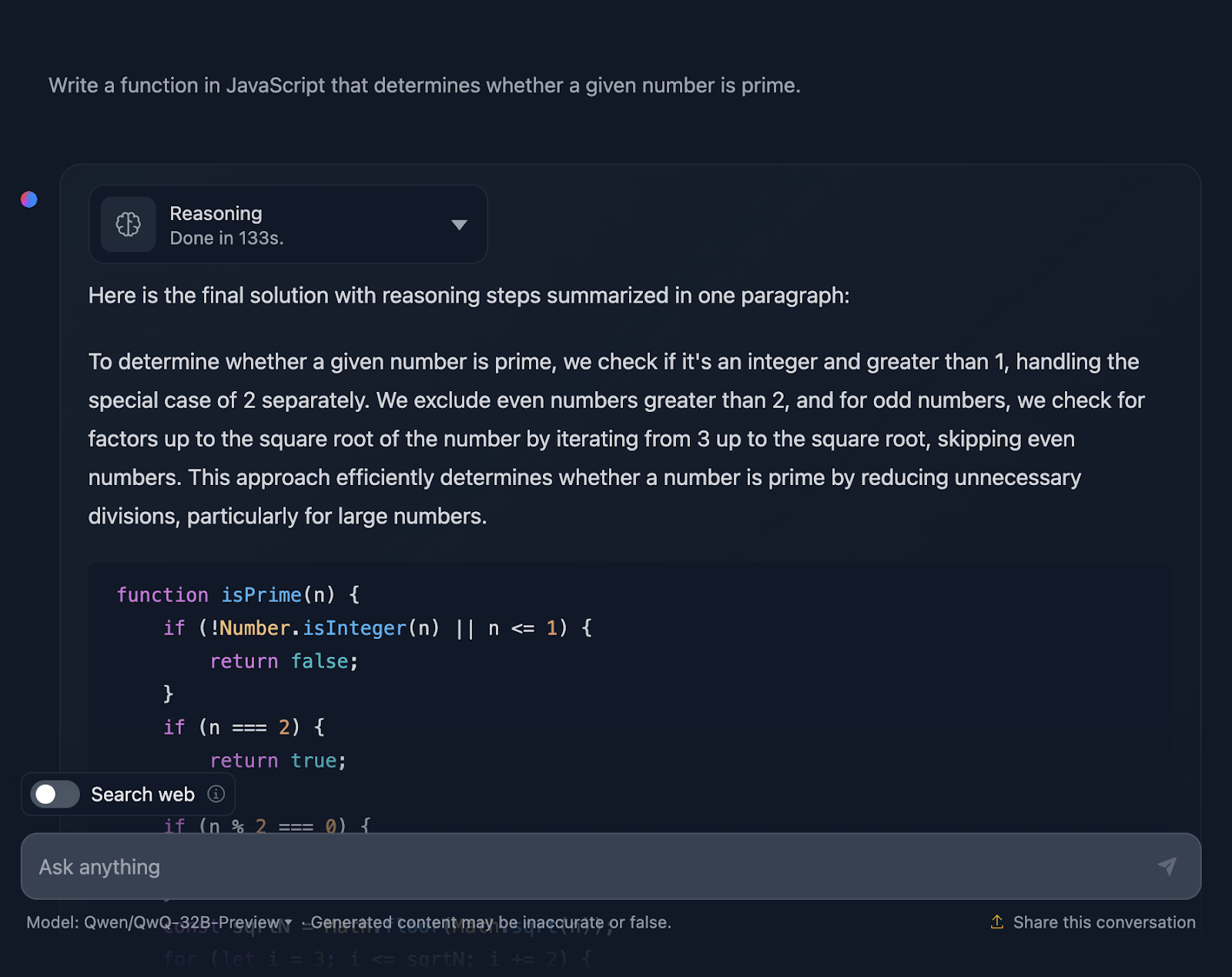
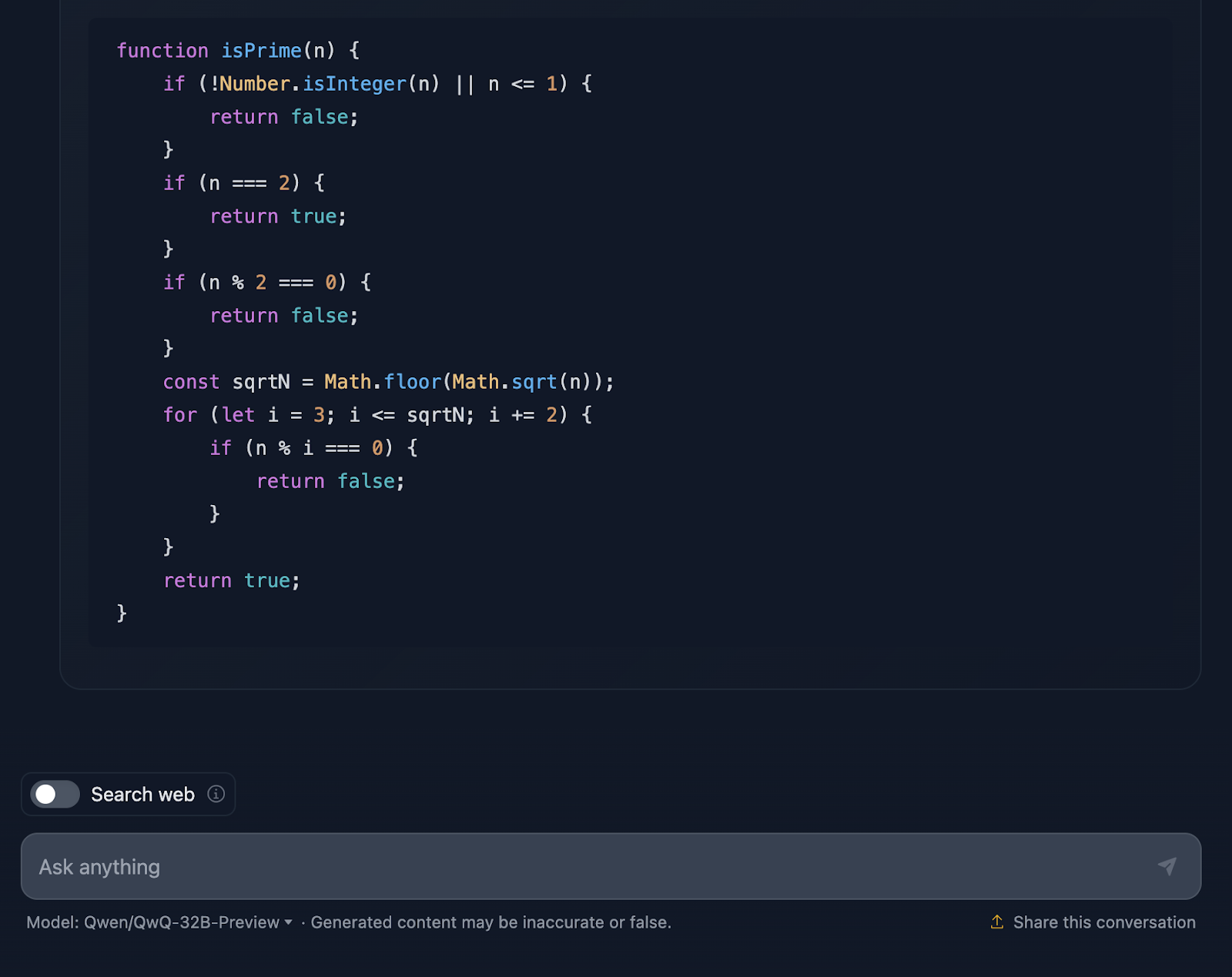
Die Lösung ist korrekt und sehr ähnlich zu der von DeepSeek. Allerdings brauchte viel länger für die Argumentation, also schauen wir mal, wie es zu dieser Antwort gekommen ist (ich kürze die Ausgabe wieder ab, damit sie lesbar ist):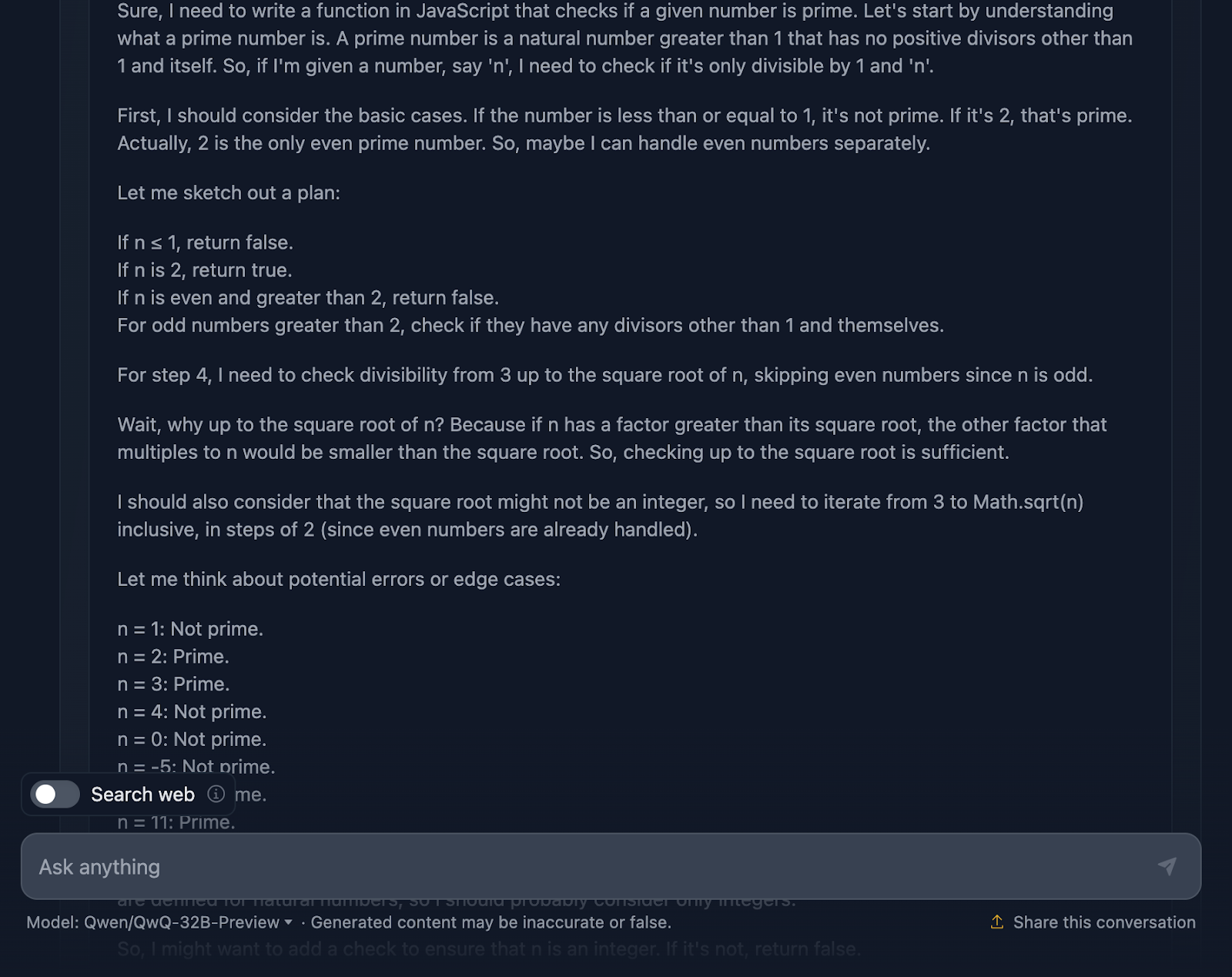

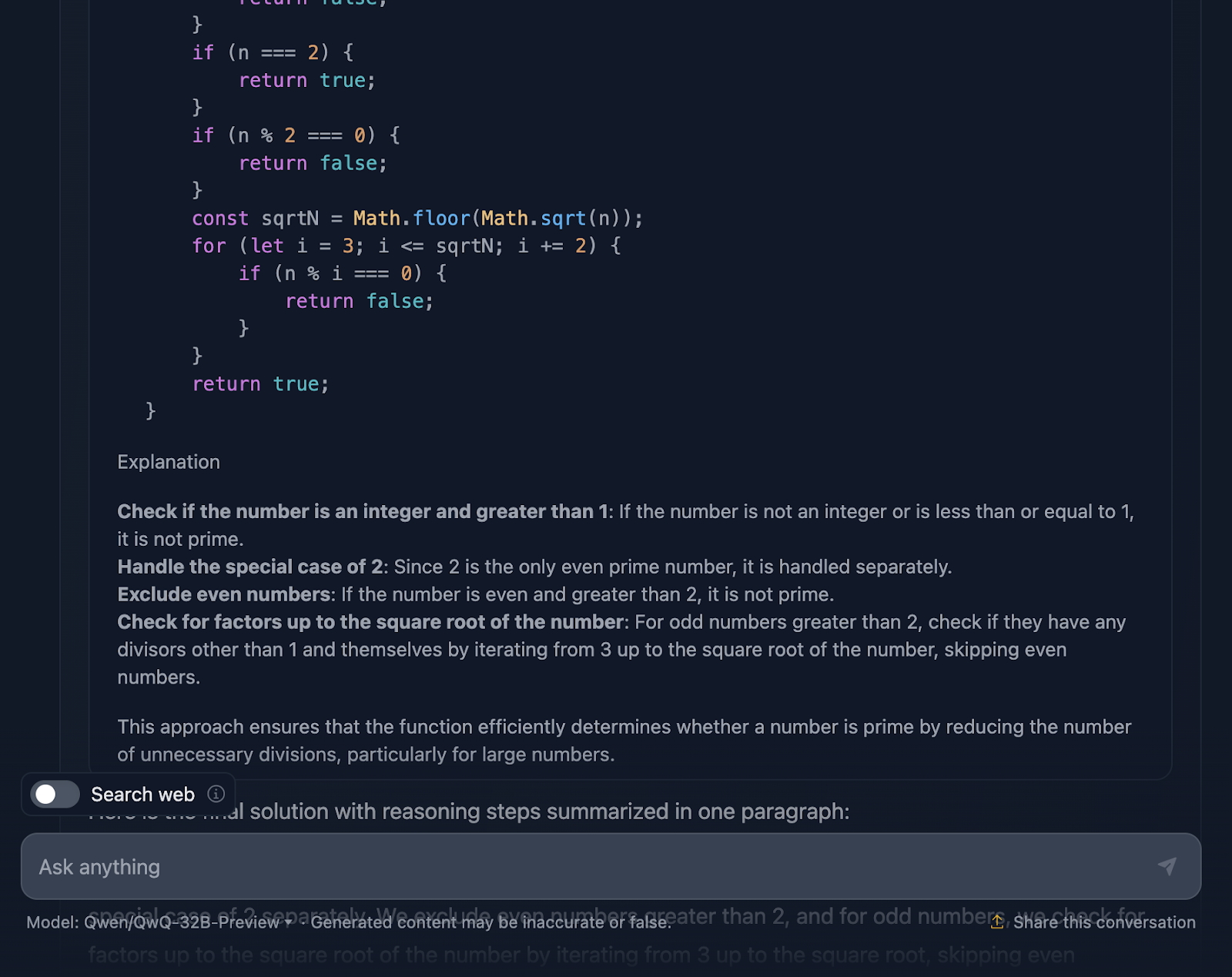
Okay, diese Argumentation ist besonders lang im Vergleich zu der von DeepSeek. Schauen wir uns das genauer an:

Die Lösung fängt damit an, dass sie sich mit den Grundlagen beschäftigt. Zahlen, die kleiner oder gleich 1 sind? Auf jeden Fall nicht erstklassig. Und 2 ist etwas Besonderes - sie ist die einzige gerade Primzahl. Eine andere gerade Zahl? Automatisch, nicht primär. Dieser logische Aufbau ist klar und macht viel Sinn, wenn es um den Umgang mit Grenzfällen geht.

Von dort aus geht es zum Kern der Sache: Wie können wir effizient prüfen, ob eine Zahl andere Teiler als 1 und sich selbst hat? Anstatt jede einzelne Zahl bis n zu prüfen, prüft die Lösung nur bis zur Quadratwurzel aus n. Und warum? Denn wenn eine Zahl einen Faktor hat, der größer als ihre Quadratwurzel ist, wurde der andere Faktor bereits unterhalb der Quadratwurzel geprüft. Das ist super effizient und vermeidet unnötige Berechnungen. 

Um es noch schneller zu machen, überspringt die Lösung alle geraden Zahlen nach der 2. Es geht also nur darum, ungerade Zahlen zu überprüfen, beginnend mit 3 und schrittweise um 2. Das ist eine nette Optimierung, die die Arbeit halbiert.

Als Nächstes wenden wir uns der Umsetzung zu. Die Funktion beginnt mit der Validierung der Eingabe. Ist es eine ganze Zahl? Ist sie größer als 1? Wenn nicht, ist es ein schnelles "nicht prima". Diese Art der Validierung ist eine gute Praxis und hält die Funktion stabil. Dann beginnt die Schleifenlogik und prüft die Teiler von 3 bis zur Quadratwurzel von n. Wenn ein beliebiger Divisor funktioniert, ist es keine Primzahl. Ansonsten ist alles klar und die Zahl ist eine Primzahl.

Das Tolle ist, dass die Überlegungen nicht bei der Umsetzung aufhören. Sie prüft Grenzfälle wie negative Zahlen, nicht-ganzzahlige Werte oder seltsame Eingaben wie 2,5 und stellt sicher, dass die Funktion sie richtig behandelt. Es gibt sogar einen Hinweis auf die Grenzen von JavaScript bei wirklich großen Zahlen und einen Vorschlag, BigInt für solche Grenzszenarien zu verwenden, was ich für eine tolle Ergänzung der Argumentation halte.

Die Lösung enthält detaillierte Testfälle, die genau zeigen, wie sie für Zahlen wie 1, 2, 3 und sogar größere Zahlen wie 13 und 29 funktioniert. Jeder Test wird Schritt für Schritt erklärt, so dass es keine Verwirrung darüber gibt, warum die Funktion funktioniert.

Könnte diese Lösung noch weiter gehen? Sicher, es gibt immer Raum für Verbesserungen. Wenn du zum Beispiel mit großen Zahlen arbeitest, solltest du dich mit fortgeschrittenen Algorithmen wie Miller-Rabin oder dem Fermatschen Primzahltest beschäftigen. Aber für den alltäglichen Gebrauch bietet diese Lösung eine gute Balance zwischen Einfachheit, Effizienz und Lesbarkeit.

Also, wie lautet das Urteil? Diese Argumentation ist solide, klar und praktisch und stellt sicher, dass der Code robust ist - etwas, das DeepSeek nicht so sehr berücksichtigt hat. Ich denke, QwQ-32B-Preview gewinnt!

Logisches Denken

Zum Schluss wollen wir uns noch einige Tests zum logischen Denken ansehen.

Das Wolf-, Ziegen- und Kohlproblem

Ich werde ein klassisches Rätsel testen:

"Ein Mann muss mit einem Wolf, einer Ziege und einem Kohlkopf einen Fluss überqueren. Sein Boot kann nur sich selbst und eine andere Sache tragen. Wenn man ihn in Ruhe lässt, würde der Wolf die Ziege fressen, und die Ziege den Kohl. Wie kann er alles sicher transportieren?"

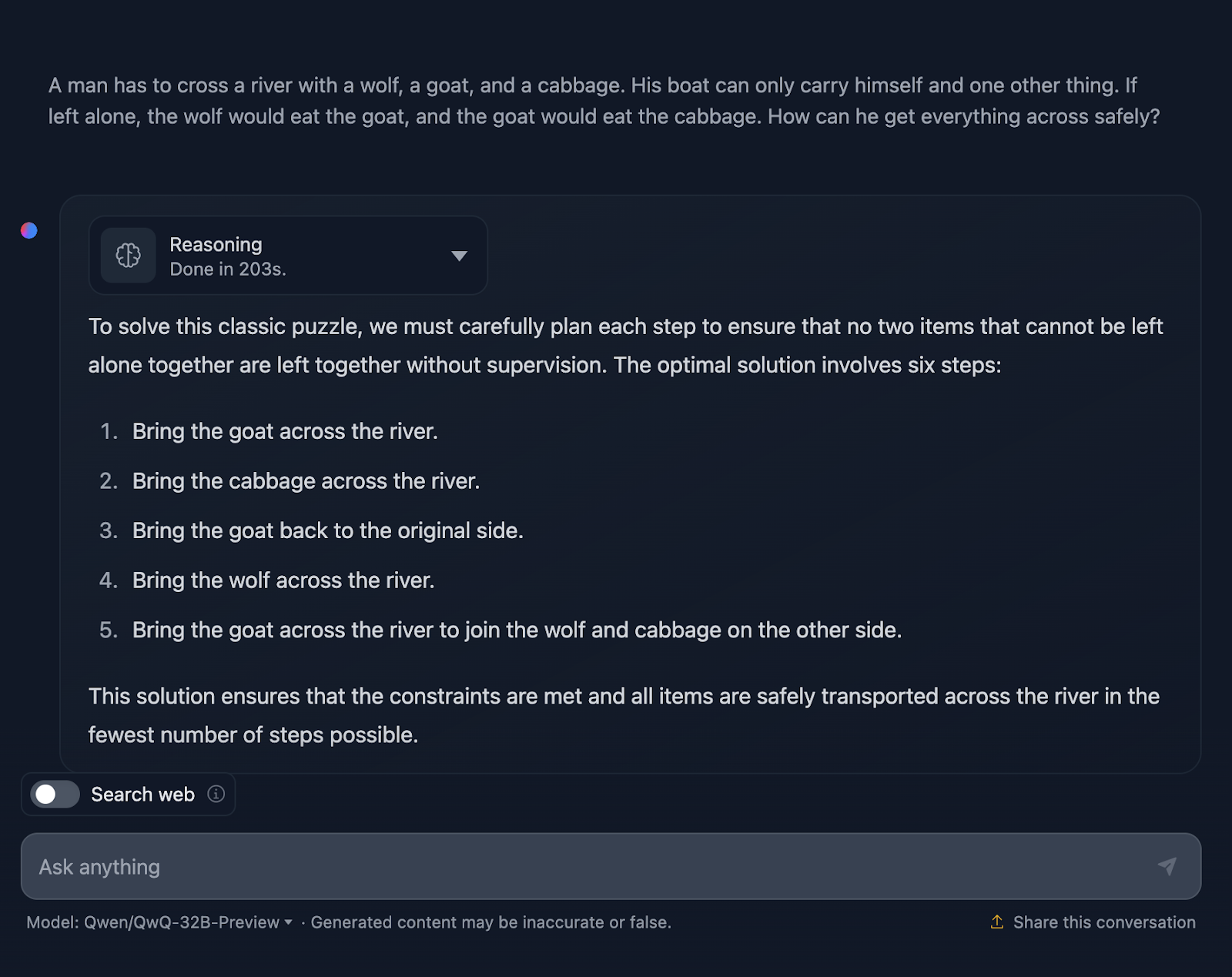
Okay, die Lösung des Problems ist also richtig, aber es gibt ein paar Dinge, die geklärt werden müssen. Darin heißt es, dass die optimale Lösung sechs Schritte umfasst, allerdings werden nur fünf Aufzählungspunkte genannt. Dies ist bereits eine Ungenauigkeit.

Außerdem könnte man meinen, dass dies ein besserer Ansatz in Bezug auf die Effizienz ist als die DeepSeek-Ausgabe, die sieben Schritte benötigte. Aber auch dieser Ansatz besteht eigentlich aus sieben Schritten. Die Schritte, bei denen du alleine zurückkommst, wurden aus irgendeinem Grund nicht erwähnt. Er sollte Folgendes ausgeben:

1. Bring die Ziege über den Fluss.
2. Komm allein zurück.
3. Bringe das Kraut über den Fluss.
4. Bringe die Ziege wieder auf die ursprüngliche Seite.
5. Bring den Wolf über den Fluss.
6. Komm allein zurück.
7. Bringe die Ziege über den Fluss zum Wolf und zum Kraut auf der anderen Seite.

Außerdem habe ich das hier entdeckt (und einen Screenshot davon gemacht!), als ich die Argumentation durchgeführt habe:

Das brachte mich dazu, mich zu fragen, ob etwas mit der Argumentation...

Schauen wir uns das mal an:

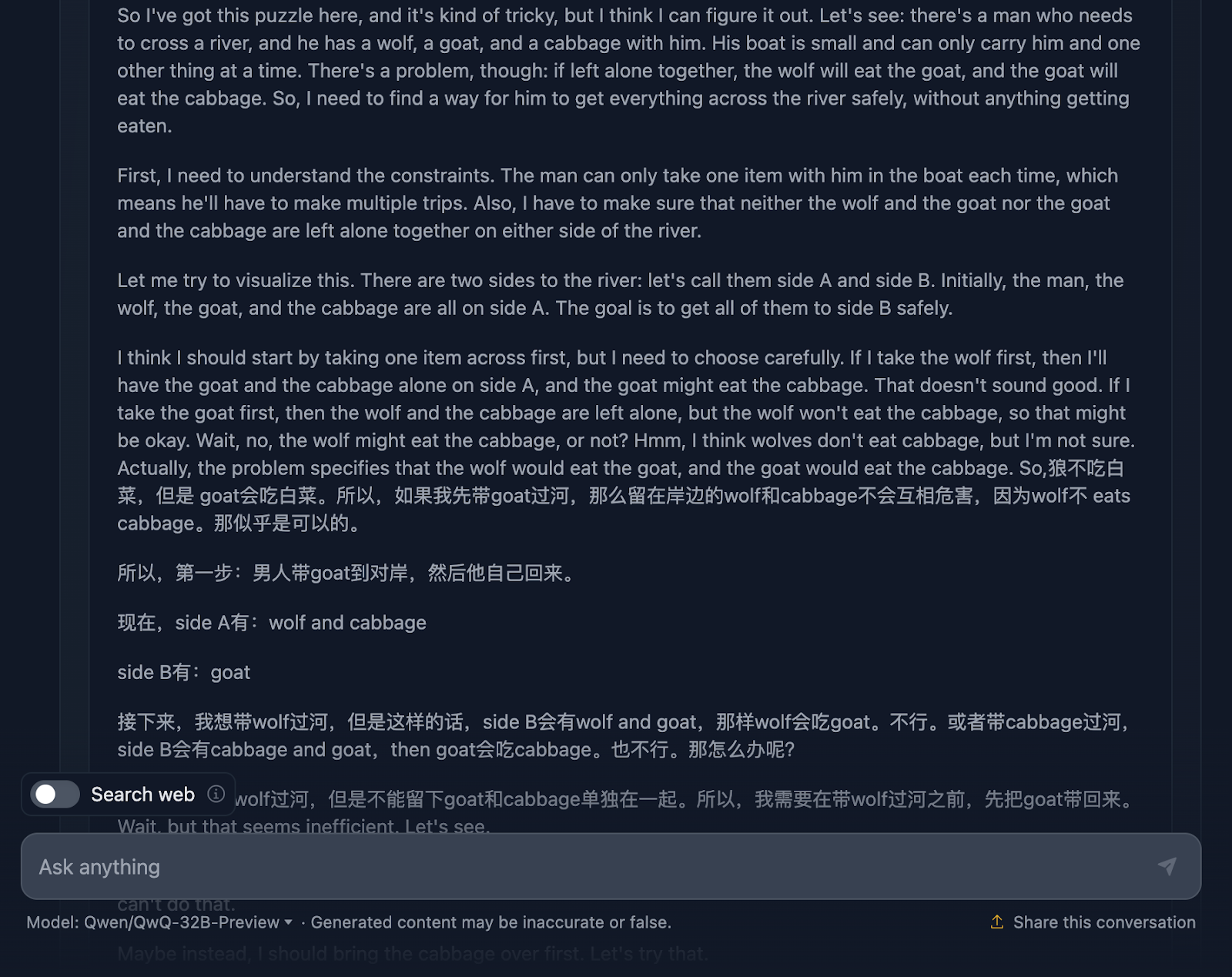
Die Argumentation fängt damit an, dass sie das Problem, die Herausforderungen und die Beschränkungen genau versteht. Doch hier fangen die Dinge an, unübersichtlich zu werden. Dies ist ein großartiges Beispiel für die Grenzen dieses Modells, das wir bereits besprochen haben und das zwei Sprachen vermischt. Das führt zu einer unverständlichen Argumentation (zumindest für mich, da ich die Sprache nicht verstehe - ich nehme an, es ist Chinesisch!). Ich werde nun einige andere Teile der Argumentation teilen, um dies zu veranschaulichen, aber ich überspringe andere Teile, da es zu langwierig ist.

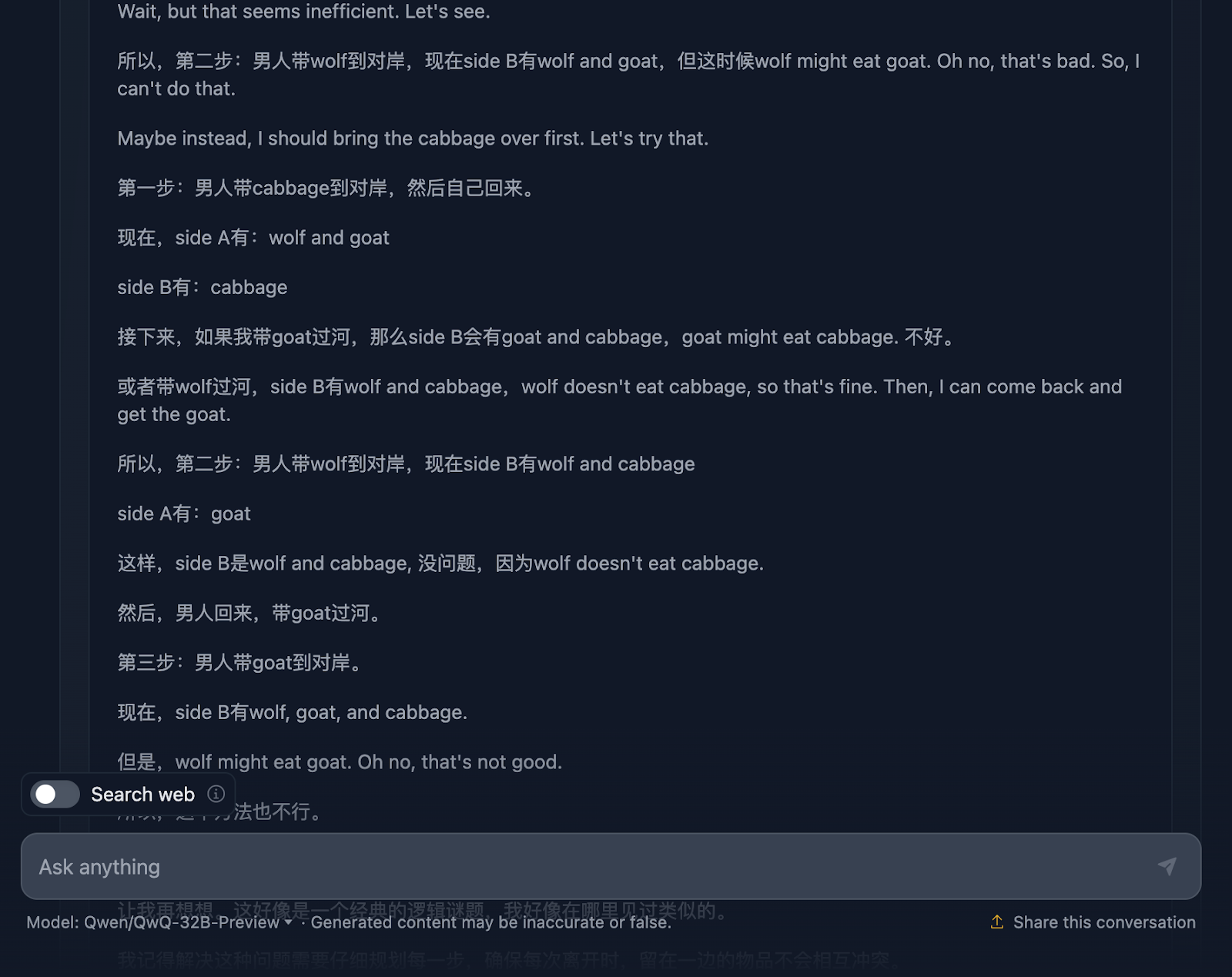
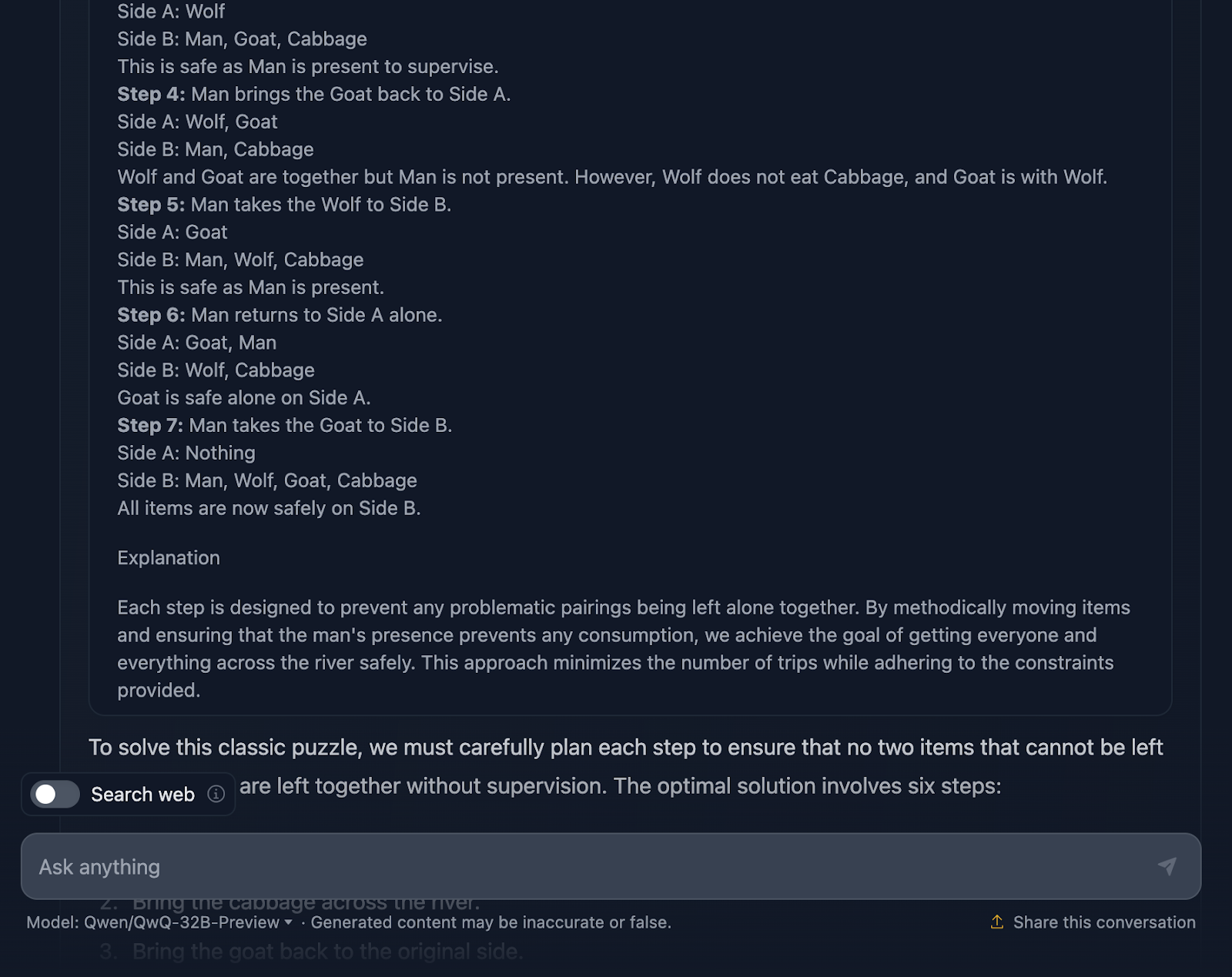
Aber die endgültige Lösung ist hervorragend! Er beschreibt die Ausgangssituation, die Einschränkungen, das Ziel und die Strategie sowie einen sehr klaren Lösungsplan, der interessanterweise alle Schritte enthält!

Warum wurde dies in der endgültigen Antwort nicht berücksichtigt? Es wurde sogar eine letzte Erklärung hinzugefügt. Ich wünschte, die Ausgabe der endgültigen Antwort hätte mit dem übereingestimmt, was in der Argumentation angezeigt wurde, und ich frage mich, warum sie das nicht getan hat!

Rätsel mit gewogenen Bällen

Zum Schluss wollen wir dieses klassische Logikrätsel ausprobieren, bei dem die Fähigkeit des Modells getestet wird, mit Hilfe deduktiver Überlegungen eine optimale Strategie zu finden.

DISCLAIMER: Das ist die Ausgabe, die ich nach drei Versuchen erhalten habe - das Modell begann, eine Antwort zu generieren, blieb aber stecken oder produzierte einen Fehler und konnte die Generierung nicht fortsetzen. Außerdem überspringe ich die Begründung für diesen Artikel, da sie extrem lang war und die Ausgabe bereits ziemlich umfangreich ist! Schauen wir uns das mal an (die Ausgabe ist ebenfalls abgeschnitten):

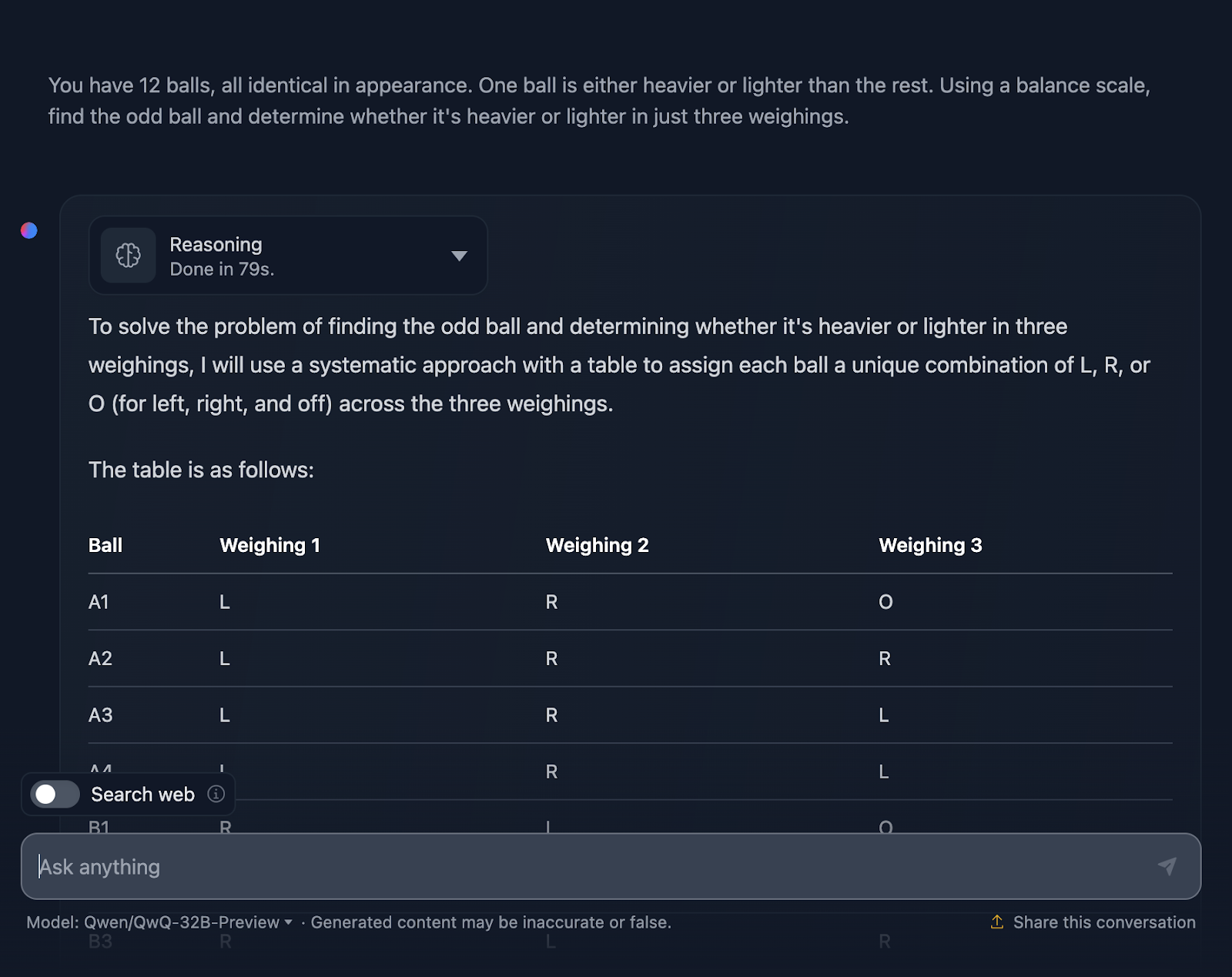
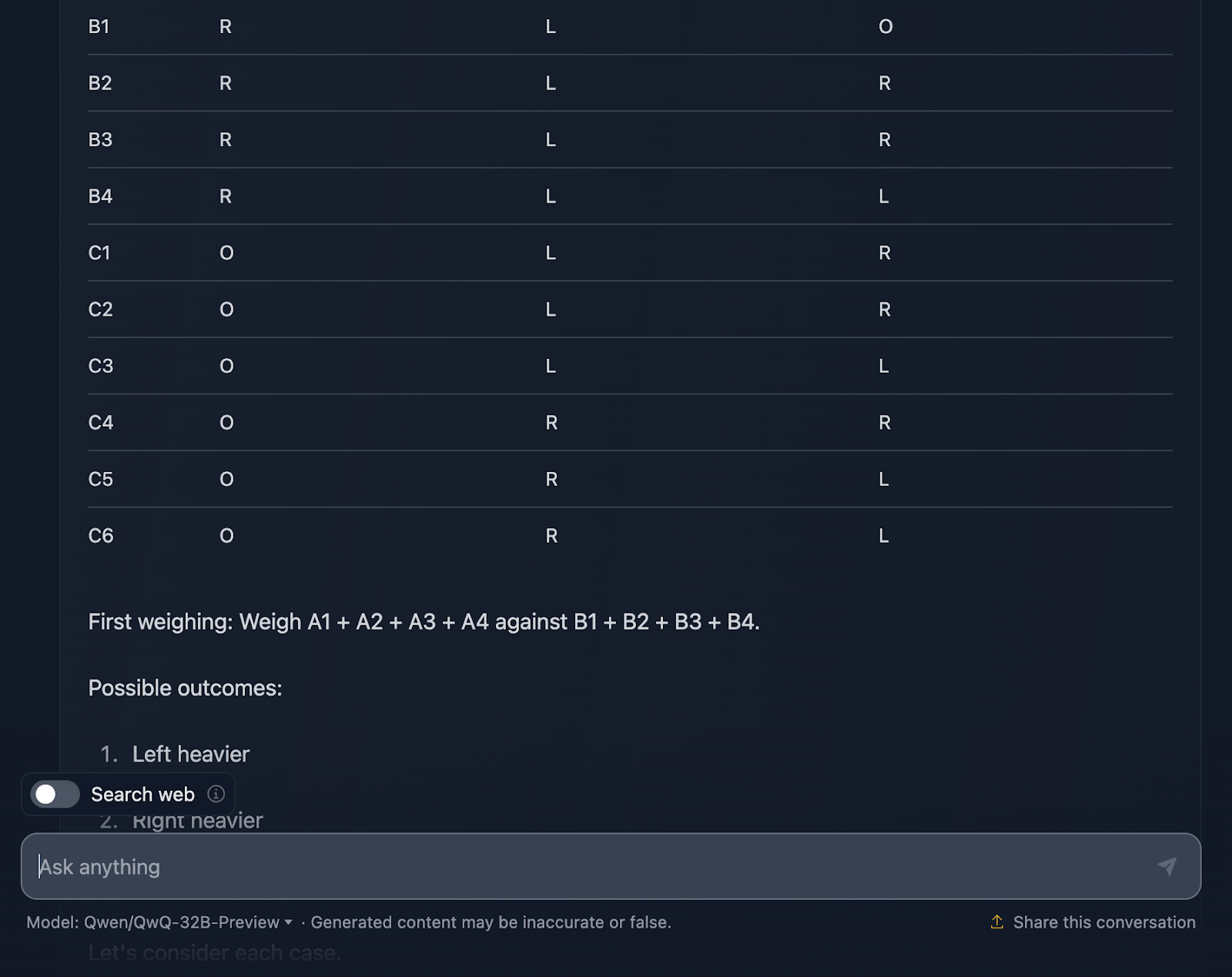
Ich muss sagen, ich bin sehr beeindruckt von der Leistung! Die Lösung beginnt mit einer sehr klaren Erklärung des Problems und legt einen Plan mit einer systematischen Tabelle vor, was ich sehr hilfreich finde und was DeepSeek nicht enthalten hat. Jeder Ball erhält seine eigene Kombination aus den drei Gewichtungen, damit alle möglichen Szenarien berücksichtigt werden. 

Mir gefällt sehr, wie das Problem in Fälle und Unterfälle unterteilt wird: "Schwerer links", "Schwerer rechts" und "Gleich". Dieser schrittweise Ansatz macht ein komplexes Problem überschaubar. Jedes Wiegen baut auf den Ergebnissen des vorherigen Wiegens auf. Du grenzt den ungeraden Ball Schritt für Schritt ein und bestimmst dabei auch, ob er schwerer oder leichter ist.

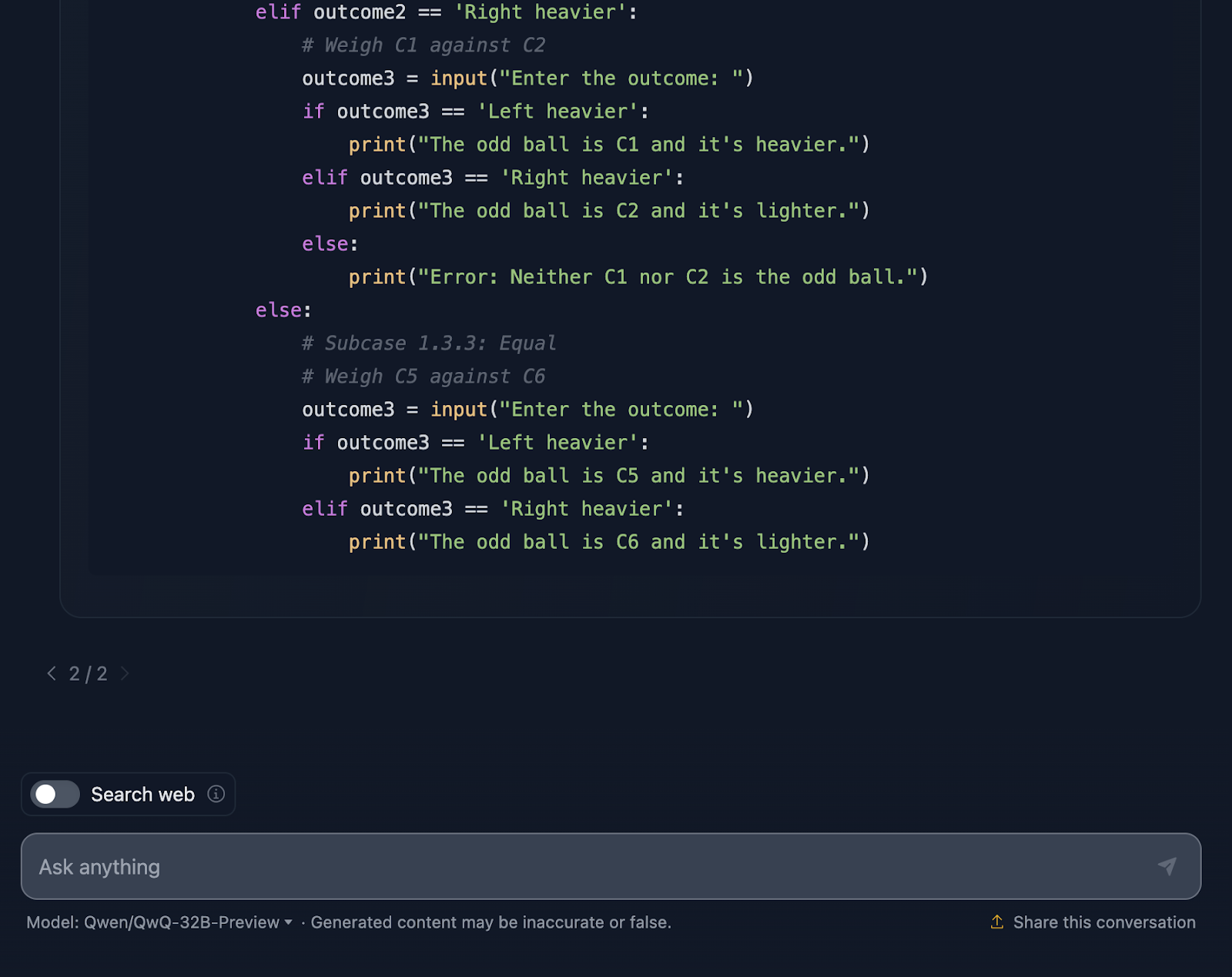
Schließlich enthält die Lösung einen Python-Codeausschnitt, den ich nicht erwartet hatte!  Sie ist interaktiv und ermöglicht es den Nutzern, das Wiegen zu simulieren, was den Prozess leichter nachvollziehbar macht und sogar Spaß macht. Diese Lösung überlässt nichts dem Zufall. Jedes einzelne Ergebnis der Abwägungen wird festgehalten, um sicherzustellen, dass kein Kuriosum unentdeckt bleibt. 

Das Python-Snippet setzt allerdings eine perfekte Benutzereingabe voraus. Wenn jemand ein ungültiges Wiegeergebnis eingibt, hat der Code keine Fehlerbehandlung, um das zu erkennen. Ein bisschen mehr Robustheit könnte es auf die nächste Stufe heben. 

Ich würde sagen, dass dies eine hervorragende Antwort ist - sie übertrifft die von DeepSeek in Bezug auf die Klarheit und die bessere Visualisierung mit den Tabellen und dem Python-Code.

Geschwindigkeitsvergleich: DeepSeek vs. QwQ

Zum Schluss vergleiche ich die Geschwindigkeit jedes Modells bei jedem Test, wenn es darum geht, Schlussfolgerungen zu ziehen und eine Lösung zu finden. Du musst bedenken, dass die Ergebnisse von vielen Faktoren abhängen und die Modelle nicht immer gleich schnell sind, aber ich finde es interessant, dass DeepSeek bei jeder Aufgabe, die ich getestet habe, schneller war.

QwQ-32B-Preview Benchmarks

Der Test von QwQ-32B-Preview hat gezeigt, wie gut es schwierige Mathe-, Programmier- und Denkaufgaben meistert - auch wenn einige besser waren als andere!

Hier siehst du, wie QwQ bei einigen anspruchsvollen Benchmarks abgeschnitten hat:

• GPQA (graduate-level scientific reasoning): 65,2 %, was ein starkes wissenschaftliches Denkvermögen auf Hochschulniveau zeigt.
• AIME (fortgeschrittene mathematische Themen): 50,0 % und beweist damit solide Kenntnisse in fortgeschrittenen mathematischen Themen wie Geometrie, Algebra und Zahlentheorie.
• MATH-500 (umfangreiche mathematische Probleme): Erreichte ein beeindruckendes 90,6% und bewies damit seine Fähigkeit, eine Vielzahl von Matheaufgaben zu lösen.
• LiveCodeBench (reale Programmieraufgaben): 50,0 % der Punkte und zeigt solide Programmierkenntnisse in realen Szenarien .

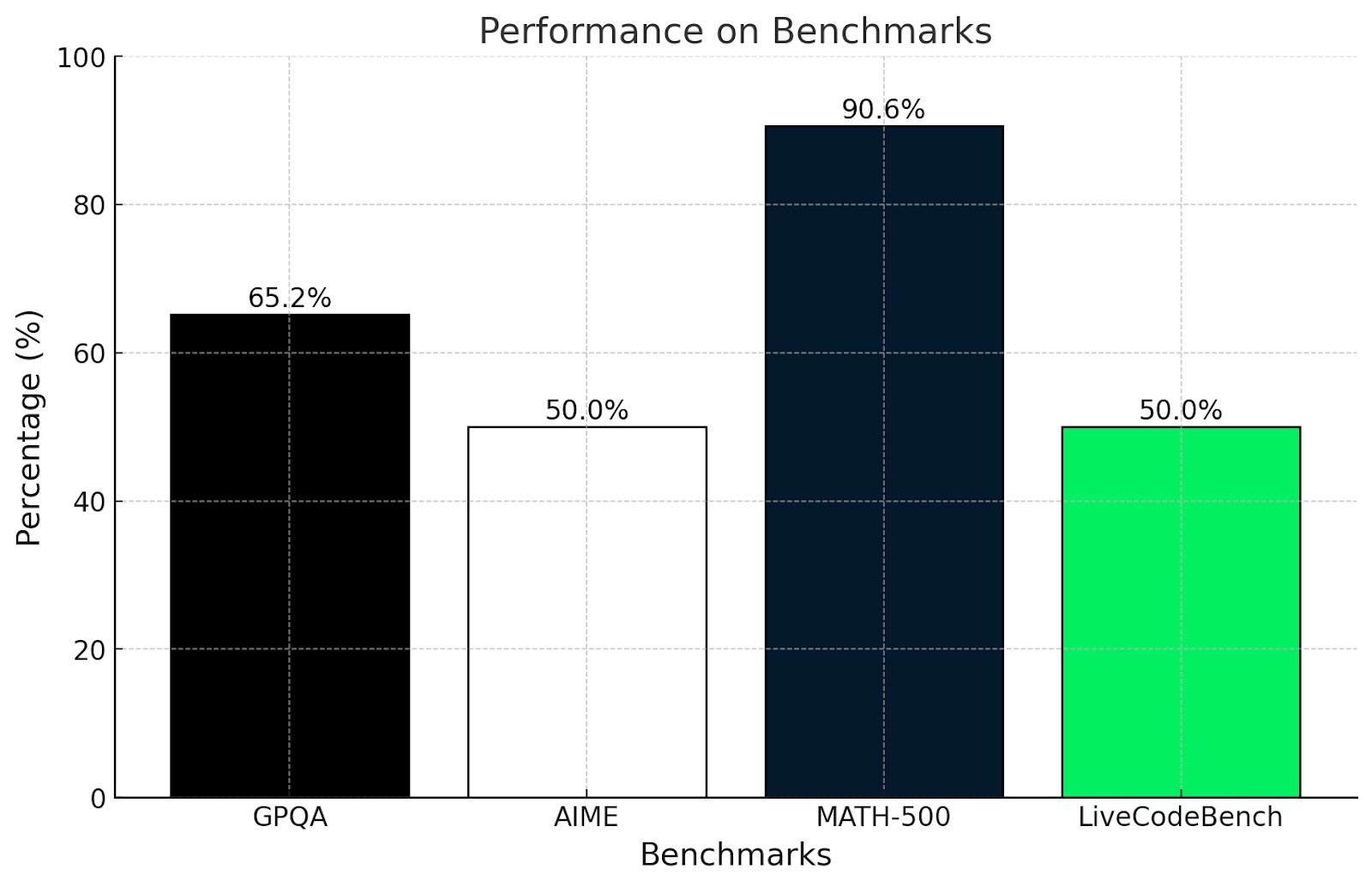
Bin ich von diesen Ergebnissen überrascht? Nicht wirklich. Diese Ergebnisse stimmen mit den in diesem Artikel durchgeführten Tests überein.

Der GPQA-Test misst das Verständnis des wissenschaftlichen Denkens auf Hochschulniveau. Ein Ergebnis von 65,2 % zeigt, dass er gut darin ist, logische und mathematische Probleme zu lösen, aber er könnte Probleme mit sehr spezialisierten oder konzeptionellen Fragen haben, wie wir sie in den komplexeren Mathetests in diesem Artikel gesehen haben.

Ebenso ist der AIME-Test für fortgeschrittene Mathe-Themen wie Geometrie und Algebra bekannt. Eine Punktzahl von 50 % zeigt, dass QwQ-32B-Preview einige dieser Probleme lösen kann, sich aber mit den wirklich cleveren Problemen, für die man über den Tellerrand hinausschauen muss, schwer tut. 

Ein Ergebnis von über 90 % bei MATH-500 ist sehr beeindruckend und zeigt, dass QwQ-32B-Preview ein allgemeines mathematisches Problem mit angemessener Genauigkeit lösen kann.

LiveCodeBench misst die Programmierfähigkeiten in Codeszenarien. Eine Punktzahl von 50 % bedeutet, dass QwQ-32B-Preview die Grundlagen des Codierens beherrscht und klaren Anweisungen folgen kann, aber es könnte bei komplizierteren Aufgaben Schwierigkeiten haben.

QwQ ist wirklich stark, wenn es darum geht, strukturierte Probleme zu lösen und Logik anzuwenden, wie die Ergebnisse von GPQA und MATH-500 zeigen. Er ist gut in Mathematik und Naturwissenschaften, findet aber kreative oder unkonventionelle Probleme, wie in AIME, schwieriger. Seine Programmierfähigkeiten sind anständig, könnten aber besser sein, wenn es um chaotische oder unklare Kodierungsaufgaben geht.

Werfen wir nun einen Blick auf die QwQ 32B-Preview-Metriken zusammen mit den Metriken von DeepSeek und anderen Modellen zum Vergleich:

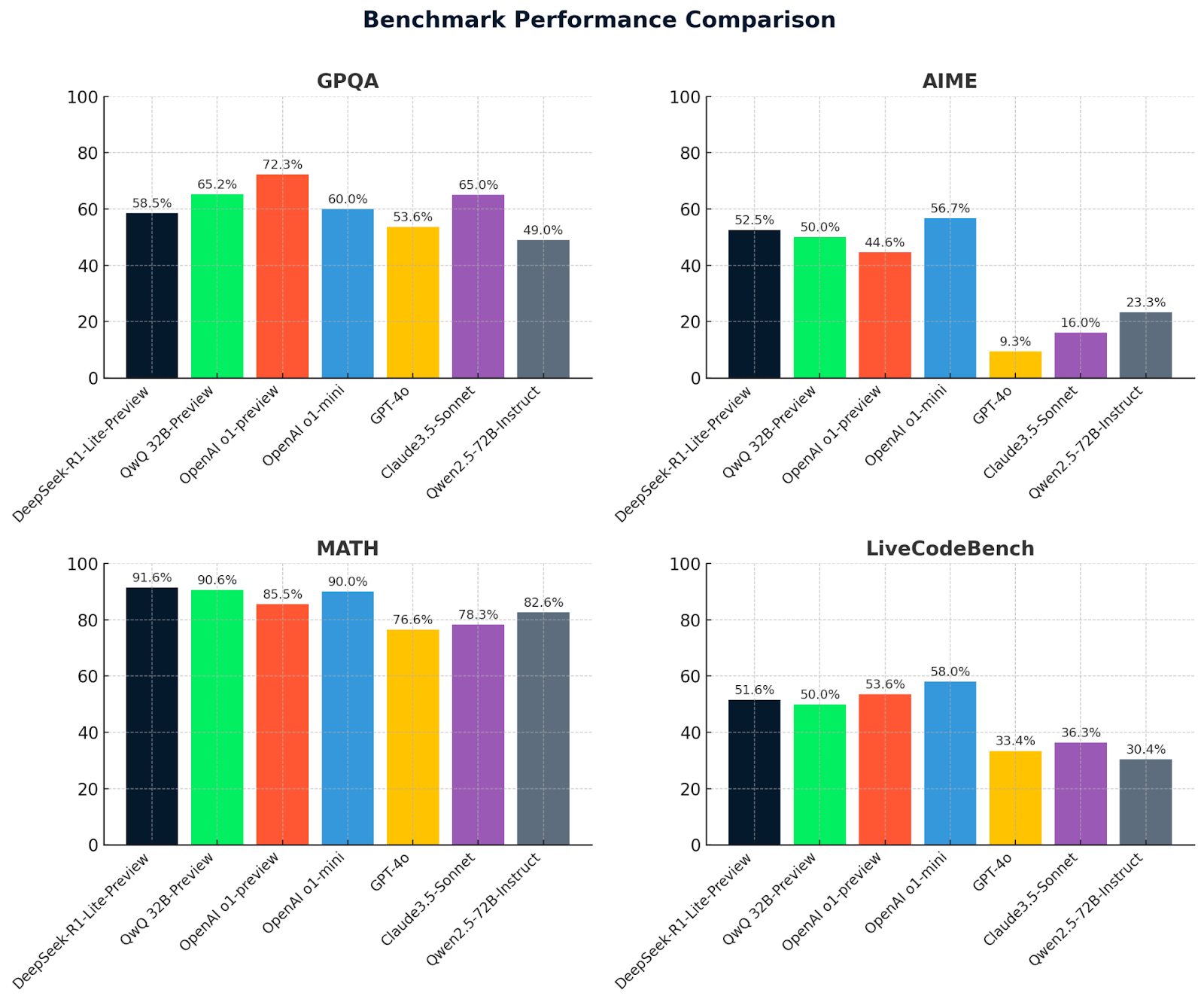
Diese Diagramme bieten einen klaren Vergleich der Modellleistungen bei vier Benchmarks: GPQA, AIME, MATH und LiveCodeBench. DeepSeek-R1-Lite-Preview sticht durch seine starken Ergebnisse hervor, vor allem in MATH (91,6 %), was seine Fähigkeit zu fortgeschrittenem logischen Denken und Problemlösen unterstreicht.

QwQ-32B-preview schneidet in allen Benchmarks durchweg gut ab, besonders gut in MATH (90,6 %), was seine robusten mathematischen und allgemeinen Argumentationsfähigkeiten unter Beweis stellt. Andere Modelle wie OpenAI O1-preview und Claude 3.5-Sonnet zeigen unterschiedliche Stärken, bleiben aber in den wichtigsten Bereichen hinter QwQ-32B-preview und DeepSeek zurück, was den Wettbewerbsvorteil dieser beiden führenden Modelle unterstreicht.

Fazit

Das Testen von QwQ-32B-Preview hat viel Spaß gemacht, und ich hoffe, ich war nicht zu voreingenommen - obwohl ich zugeben muss, dass mich DeepSeek-R1-Lite-Preview wirklich beeindruckt hat! 

QwQ-32B-Preview ist eindeutig ein starkes Modell mit erstaunlichen Fähigkeiten, aber es ist nicht perfekt und die endgültige Antwort, die das Modell gibt, stimmt nicht immer mit der endgültigen Antwort im Denkprozess überein, der oft eine bessere Lösung hatte als die, die tatsächlich präsentiert wurde.

Hast du QwQ schon einmal ausprobiert? Was denkst du? Gefällt er dir besser als DeepSeek? Und wer weiß - vielleicht wird das nächste große Modell dasjenige sein, das alle anderen in allen Benchmarks übertrifft. Es ist eine aufregende Zeit, in der sich diese Werkzeuge weiterentwickeln!