J'ai testé QwQ-32B-Preview : Le modèle de raisonnement d'Alibaba

Qu'est-ce que QwQ-32B-Preview ? 

QwQ-32B-Preview est un modèle conçu pour traiter des tâches de raisonnement avancées qui vont au-delà de la simple compréhension de texte. Il vise à résoudre des problèmes difficiles tels que le codage et le raisonnement mathématique. En tant que version "Preview", elle est encore en cours d'amélioration. Il est en accès libre sur des plateformes comme Hugging Face, ce qui vous permet de tester, d'améliorer et de donner votre avis sur le modèle si vous le souhaitez !

Il faut tenir compte du fait que QwQ-32B-Preview est un modèle expérimental. Bien qu'elle soit prometteuse, elle présente également d'importantes limites :

• Mélanger les langues: Le modèle peut passer inopinément d'une langue à l'autre, ce qui rend ses réponses moins claires.
• Raisonnement circulaire: Parfois, il reste bloqué dans des boucles de raisonnement répétitives, ce qui entraîne de longues réponses sans conclusion claire.
• Préoccupations en matière de sécurité: Le modèle doit encore être doté de dispositifs de sécurité renforcés pour garantir une utilisation fiable et sûre ; la prudence est donc de mise lors de son déploiement.
• Écarts de performance: Il est prouvé qu'il est performant en mathématiques et en codage, mais il pourrait s'améliorer dans des domaines tels que le raisonnement de bon sens et la compréhension des nuances subtiles de la langue.

Comment accéder à QwQ-32B-Preview ?

Vous pouvez accéder à QwQ-32B-Preview via HuggingChatoù il est actuellement disponible gratuitement et non quantifié. Pour utiliser QwQ-32B-Preview :

1. Visitez HuggingChat : https://huggingface.co/chat/
2. Sélectionnez QwQ-32B-Preview parmi les modèles disponibles
3. Commencez à interagir avec le modèle

Le test de la fraise

Nous commencerons par le célèbre test de la fraise. Le message est le suivant : Combien de fois la lettre "r" se trouve-t-elle dans "fraise" ?

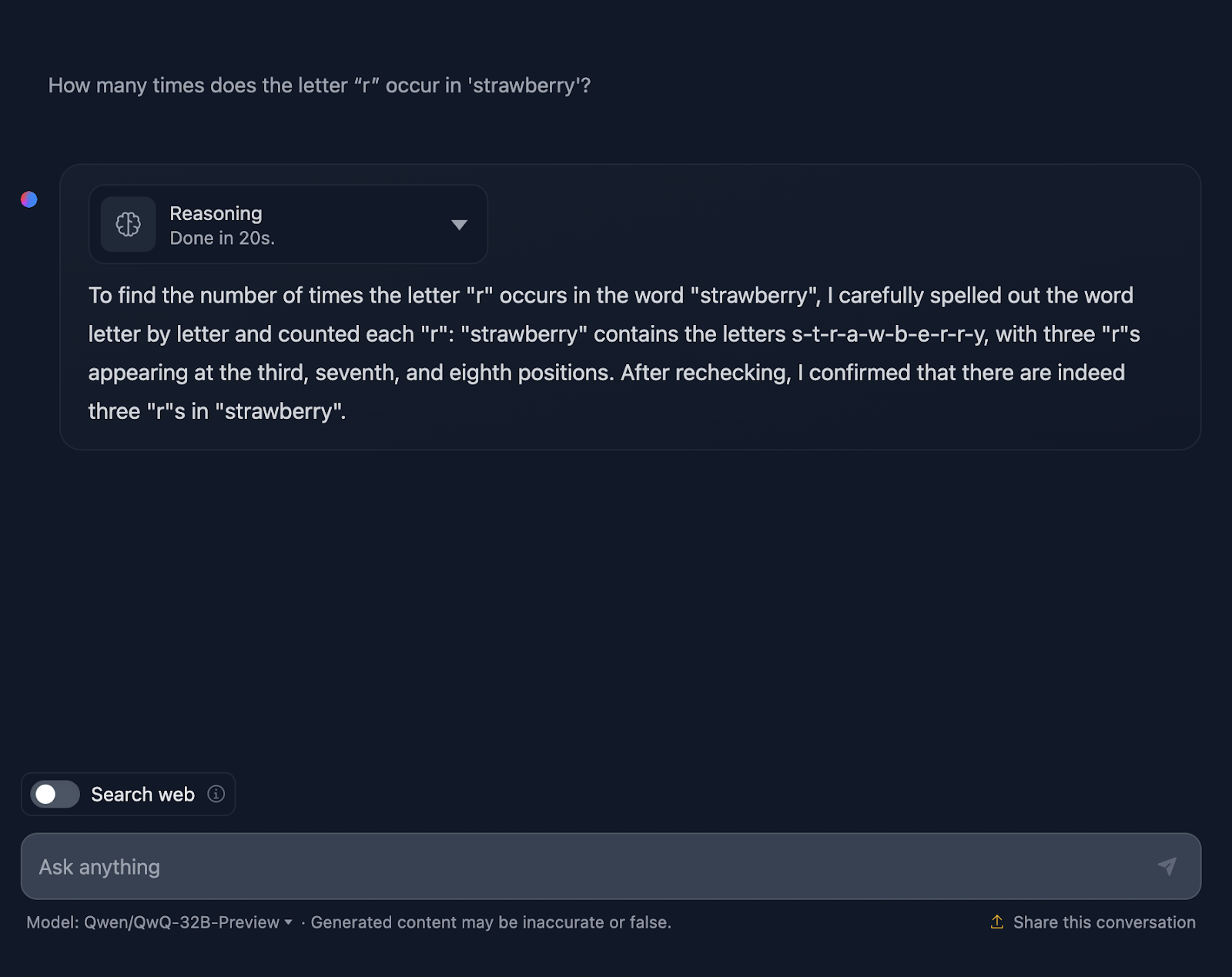
C'est vrai, cela devient déjà intéressant ! 

Il compte correctement les lettres, mais il indique à tort que les "r" apparaissent en troisième, septième et huitième position, ce qui n'est pas vrai. Les positions correctes sont la troisième, la huitième et la neuvième. À titre de référence, DeepSeek a traité cette question correctement.

Examinons de plus près le raisonnement de QwQ-32B-Preview :

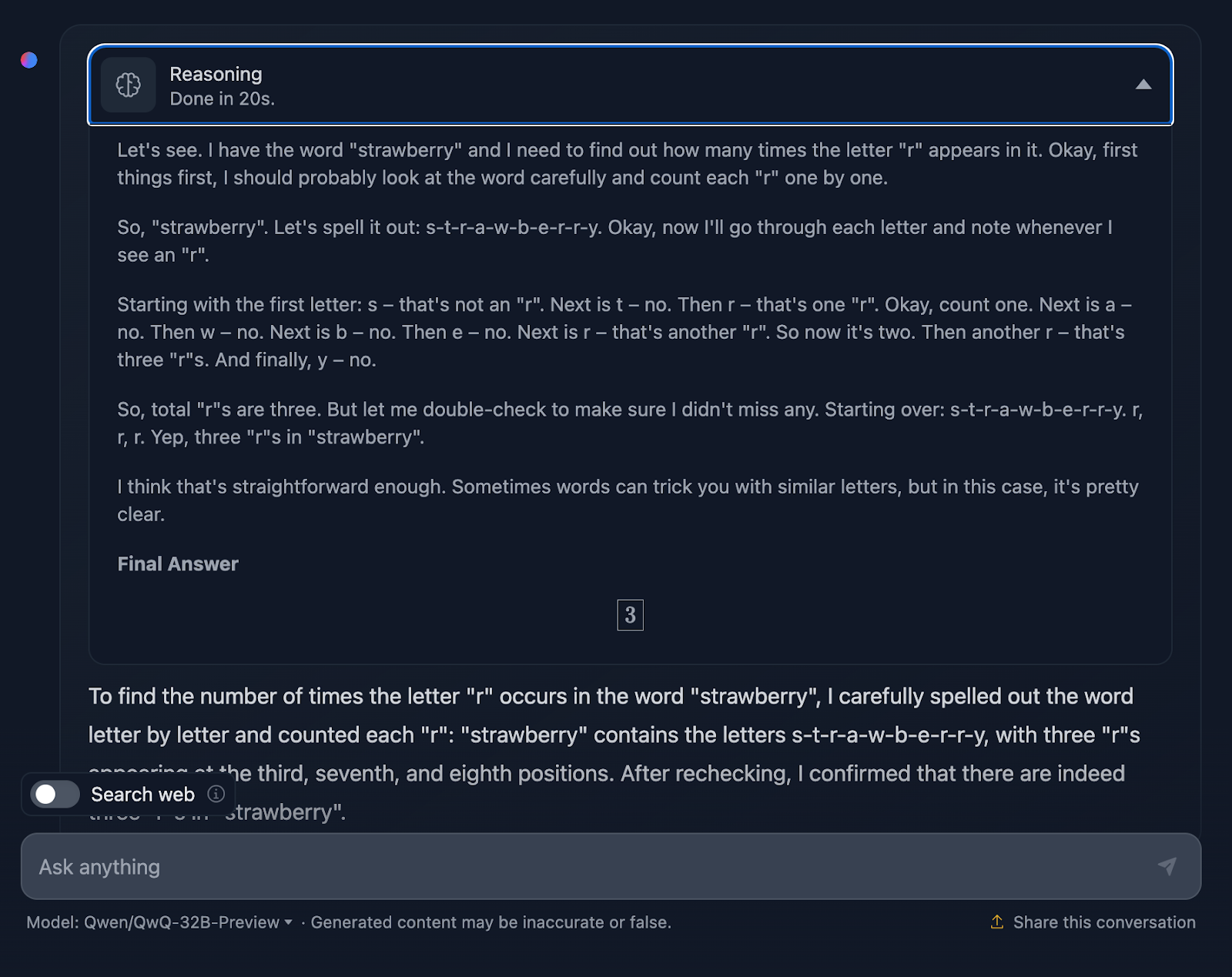
Le raisonnement de QwQ-32B-Preview était beaucoup plus court que celui fourni par DeepSeek. Cependant, dans ce cas, en comptant les lettres, il n'a pas tenu compte de leur position, ce qui explique sans doute pourquoi il s'est trompé. C'est intéressant parce qu'il a fourni cette information même si elle n'était pas nécessaire - je n'ai pas demandé la position des "r", seulement le nombre d'occurrences. Le fait de fournir des informations supplémentaires et inutiles a fini par introduire des erreurs.

Raisonnement mathématique

Pour tester le raisonnement mathématique du modèle, nous effectuerons trois tests plus ou moins complexes.

Zone du triangle

Le message est le suivant : "Si un triangle a des côtés de longueur 3, 4 et 5, quelle est sa surface ? Voyons ce qu'il en est :

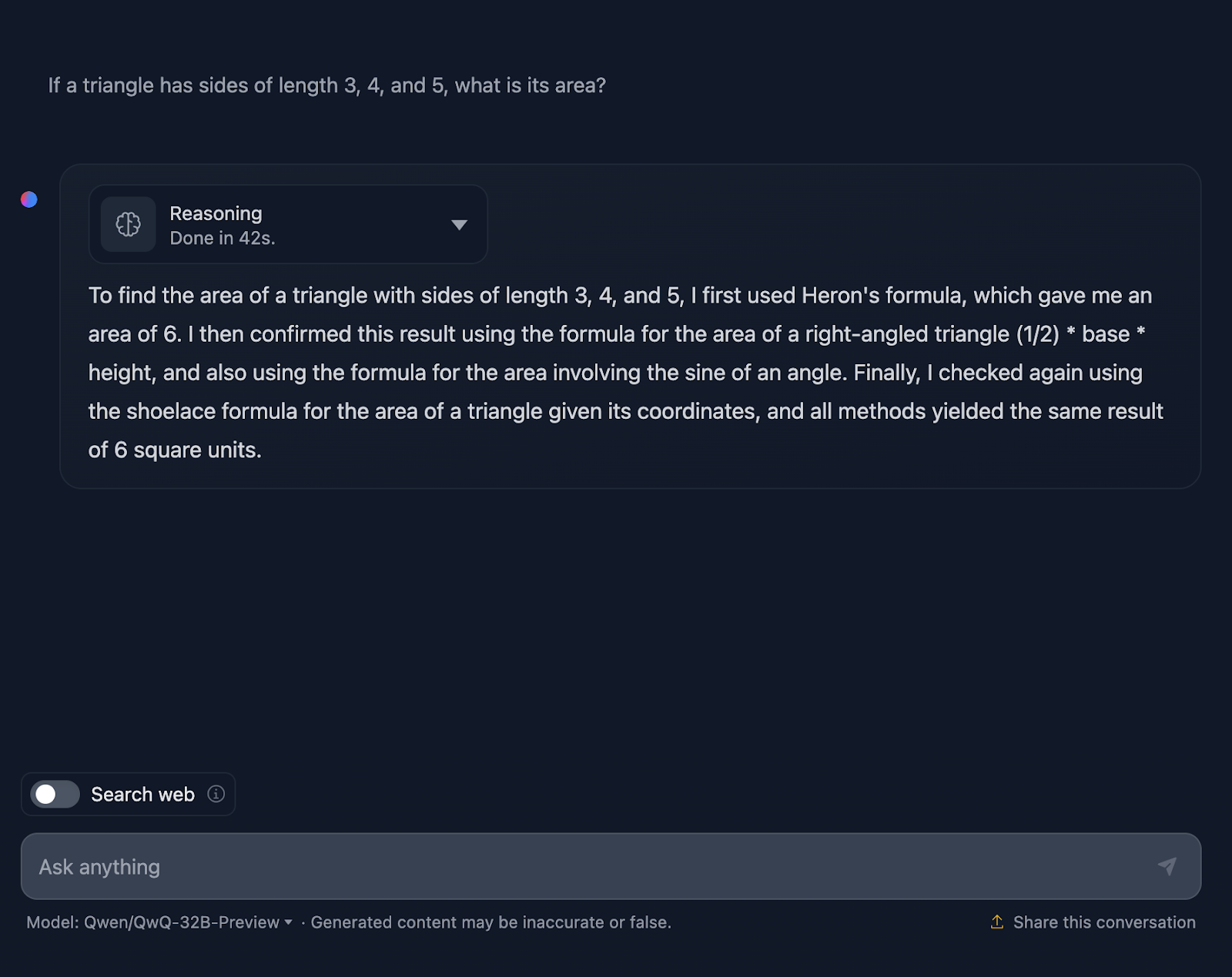
La réponse est correcte et explique les méthodes utilisées pour parvenir à la conclusion. Cependant, aucune formule ni aucun calcul n'est inclus dans la solution, ce qui n'est pas grave puisque cela n'était pas demandé. Cependant, cela aurait été un ajout intéressant, que DeepSeek a fourni. Voyons maintenant le raisonnement :

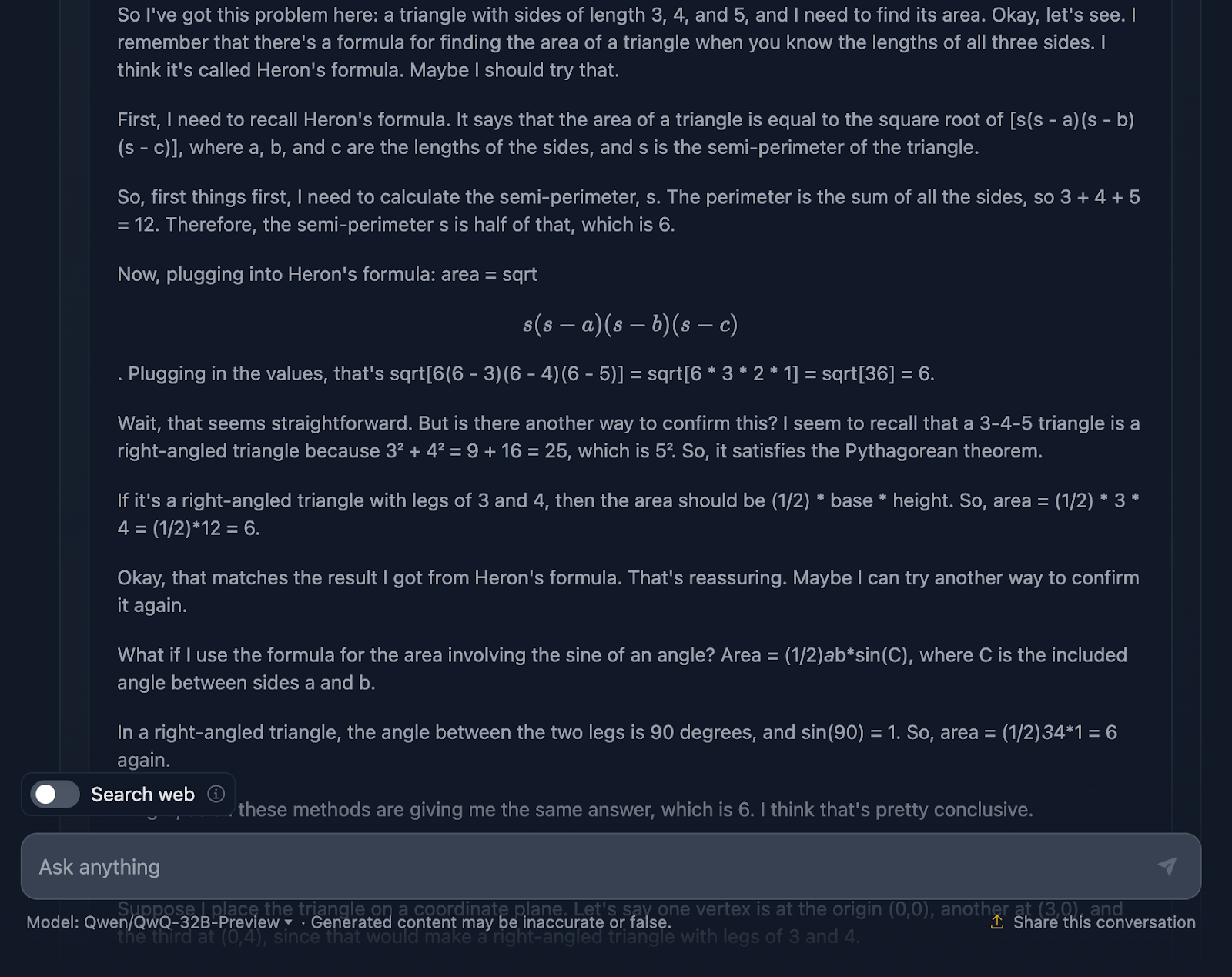
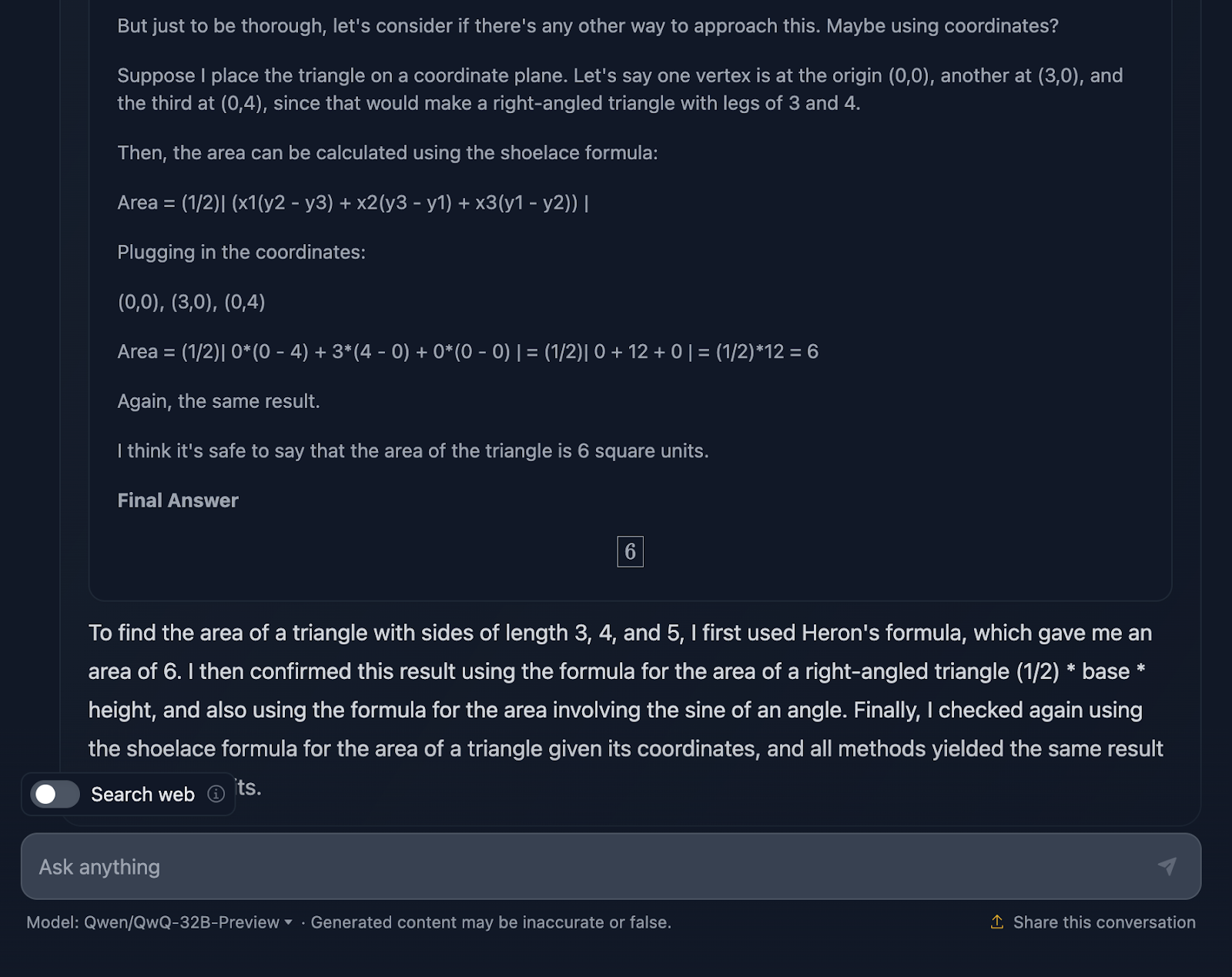
Je trouve assez génial qu'il ait utilisé quatre approches différentes pour parvenir à la même solution, alors que DeepSeek n'en a utilisé que trois. Le raisonnement est clair et facile à suivre. Le seul problème que j'ai remarqué est que le formatage et le style des formules sont un peu incohérents - certaines sont correctement analysées, tandis que d'autres ne le sont pas. C'est un point que DeepSeek a traité correctement.

Preuve mathématique

Examinons un test de mathématiques plus complexe pour voir s'il y a une différence dans les performances et le processus de réflexion. Je testerai les éléments suivants : "Prouvez que la somme des réciproques des nombres de Fibonacci converge vers une valeur finie".

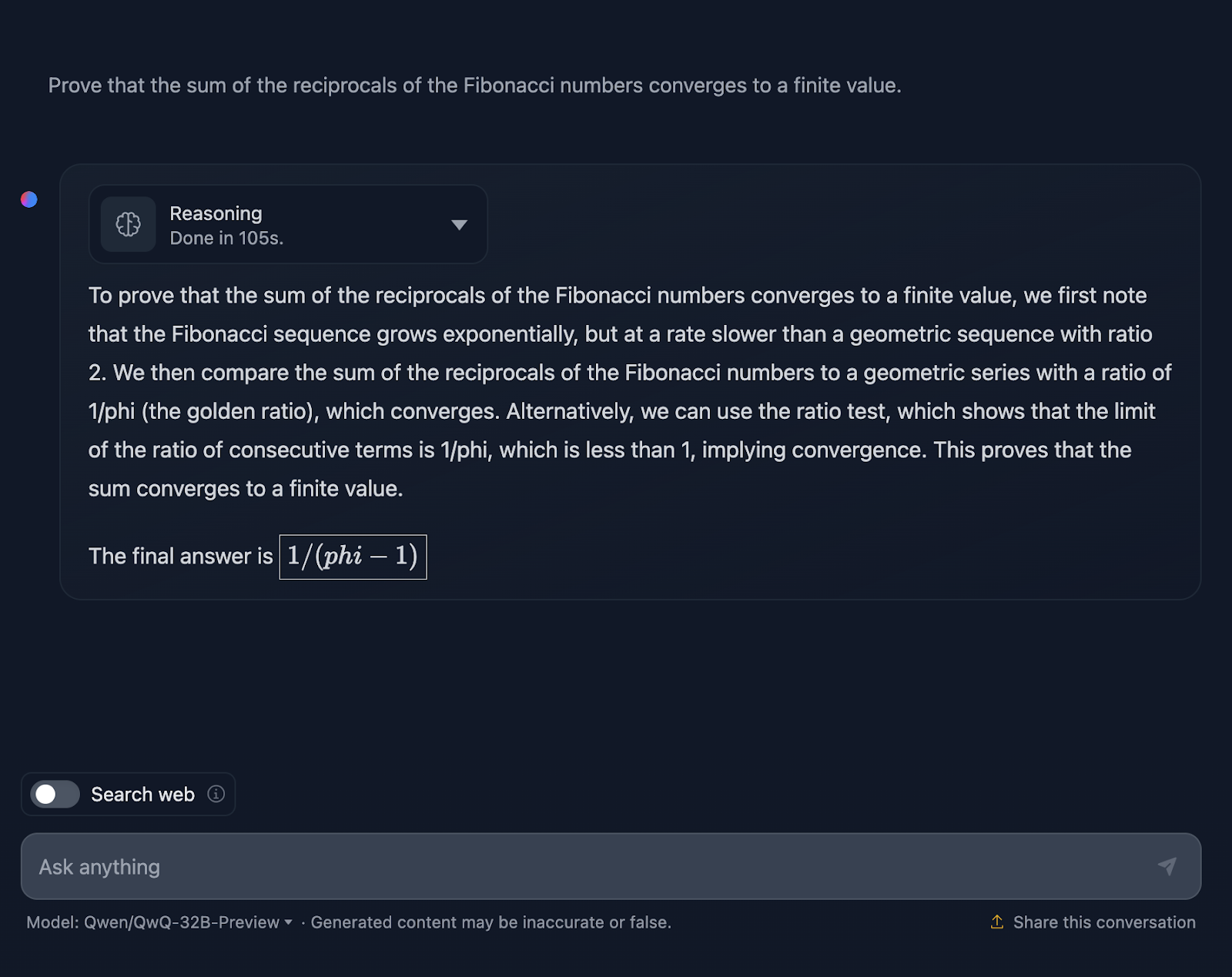
La réponse n'est pas techniquement incorrecte, mais il y a beaucoup de place pour l'amélioration. Tout d'abord, si je demande au modèle une preuve, la réponse finale ne doit pas se limiter à une valeur ; elle doit inclure une série de formules ou d'applications de théorèmes pour prouver une hypothèse ou un énoncé. C'est ce qu'il tente de faire ici, mais il faudrait le développer davantage, et la réponse finale ne prouve pas vraiment quoi que ce soit. Une fois de plus, le formatage des formules semble être un problème récurrent. Le test que j'ai effectué avec DeepSeek est un bon exemple d'une preuve correcte.

À titre d'exemple, pendant mon doctorat en mathématiques, j'ai corrigé des examens de mathématiques et je peux vous dire que cette réponse n'aurait pas été bien notée, mais celle de DeepSeek l'aurait été !

Examinons maintenant le raisonnement (pour des raisons de lisibilité, je ne montrerai que la première et la dernière partie du long processus de raisonnement, mais je vous encourage à tester l'invite vous-même) :

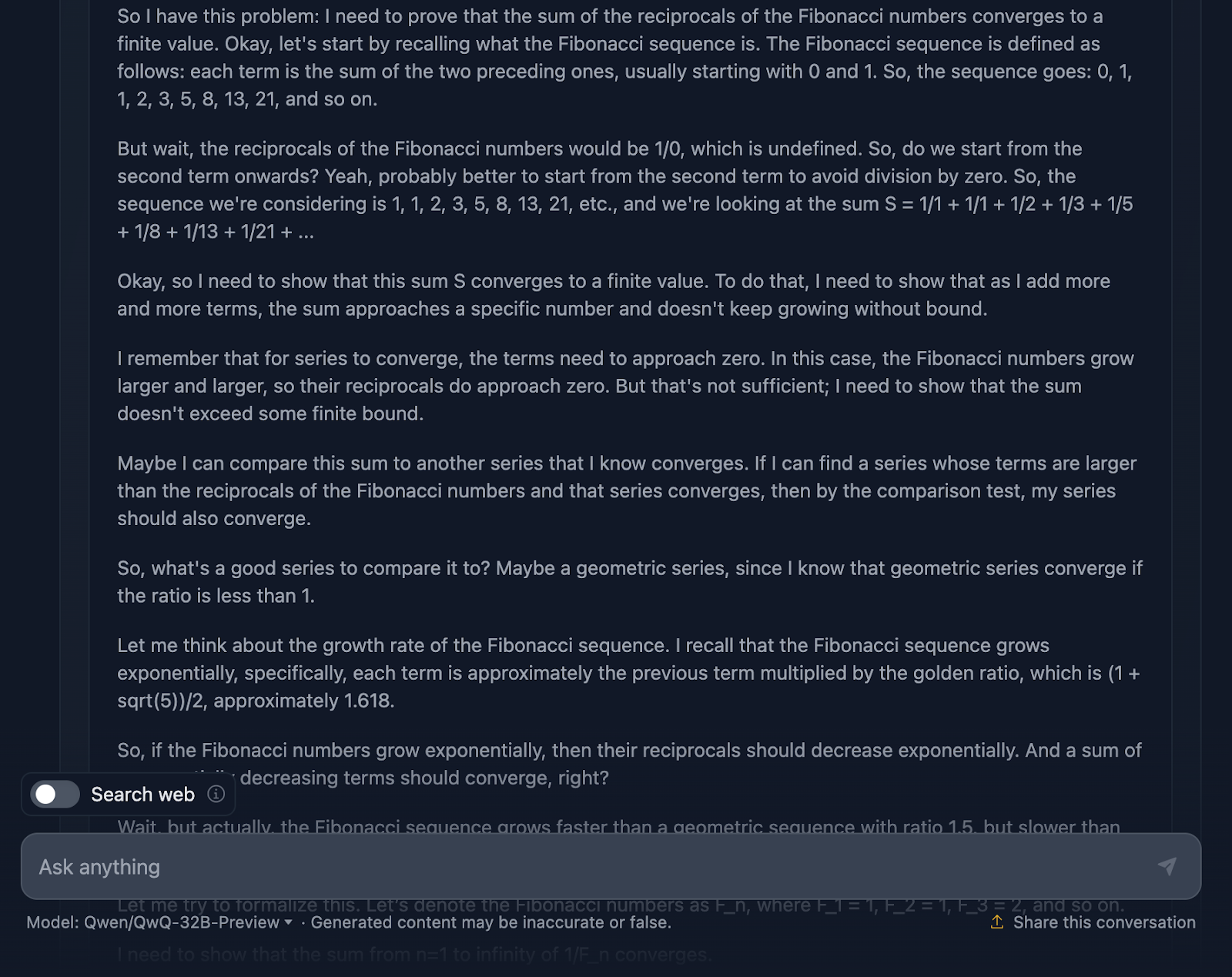
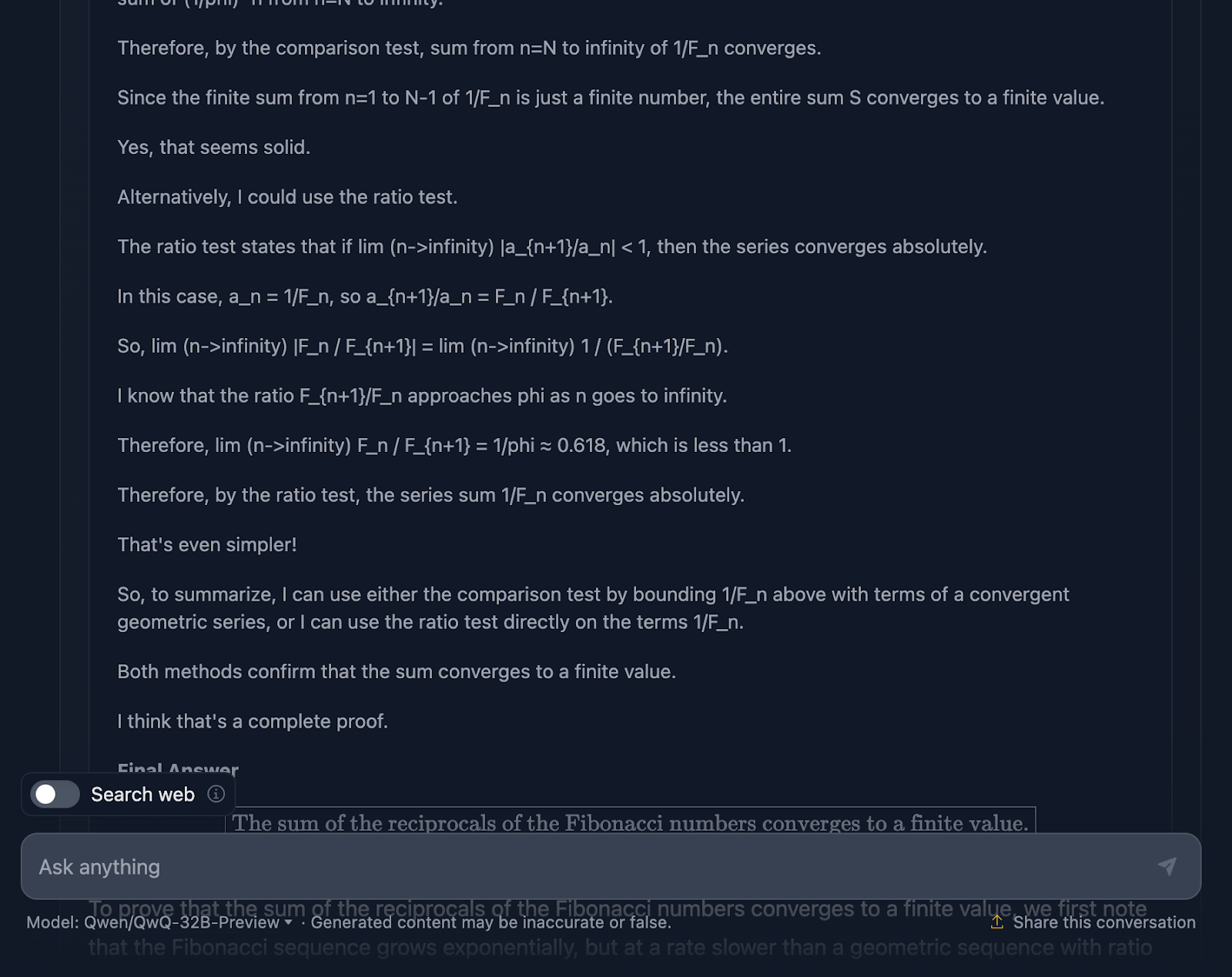
Tout d'abord, le modèle commence fort. Elle rappelle la suite de Fibonacci, évite l'écueil évident de la division par zéro et pose bien le problème. Il s'agit là d'une base solide. Il utilise ensuite le test de comparaison et le test de ratio, qui sont des tests standard pour la convergence des séries, et utilise même la formule de Binet pour approximer et consolider les nombres de Fibonacci. Il reconnaît également à un moment donné qu'il n'a pas besoin de calculer la valeur exacte, mais seulement de prouver que la série converge, ce qui montre qu'il s'en tient vraiment au problème.

Le raisonnement est correct, cela ne fait aucun doute, mais le chemin qui mène à la réponse semble un peu embrouillé. Là encore, certaines formules sont bien formatées, mais d'autres le sont moins. 

Cela dit, la preuve finale tient la route. Il montre que la série converge et utilise des méthodes valables pour y parvenir. Mais par rapport à la production de DeepSeek, la preuve aurait pu être un peu plus soignée et cohérente.

Je suis également très surpris que la réponse finale fournie dans le raisonnement, qui est une meilleure réponse finale, soit différente de celle qui figure dans le résultat final. Il aurait dû s'en tenir à cela !

Géométrie différentielle

Essayons maintenant un test de géométrie différentielle :

Considérons une surface S dans^R3 paramétrée par

φ(u,v) = (u cos v, u sin v, ln u)

pour u > 0 et 0 ≤ v < 2π.

a) Calculez la première forme fondamentale de S.

b) Déterminez si S est une surface minimale.

c) Trouvez la courbure gaussienne K et la courbure moyenne H de S.

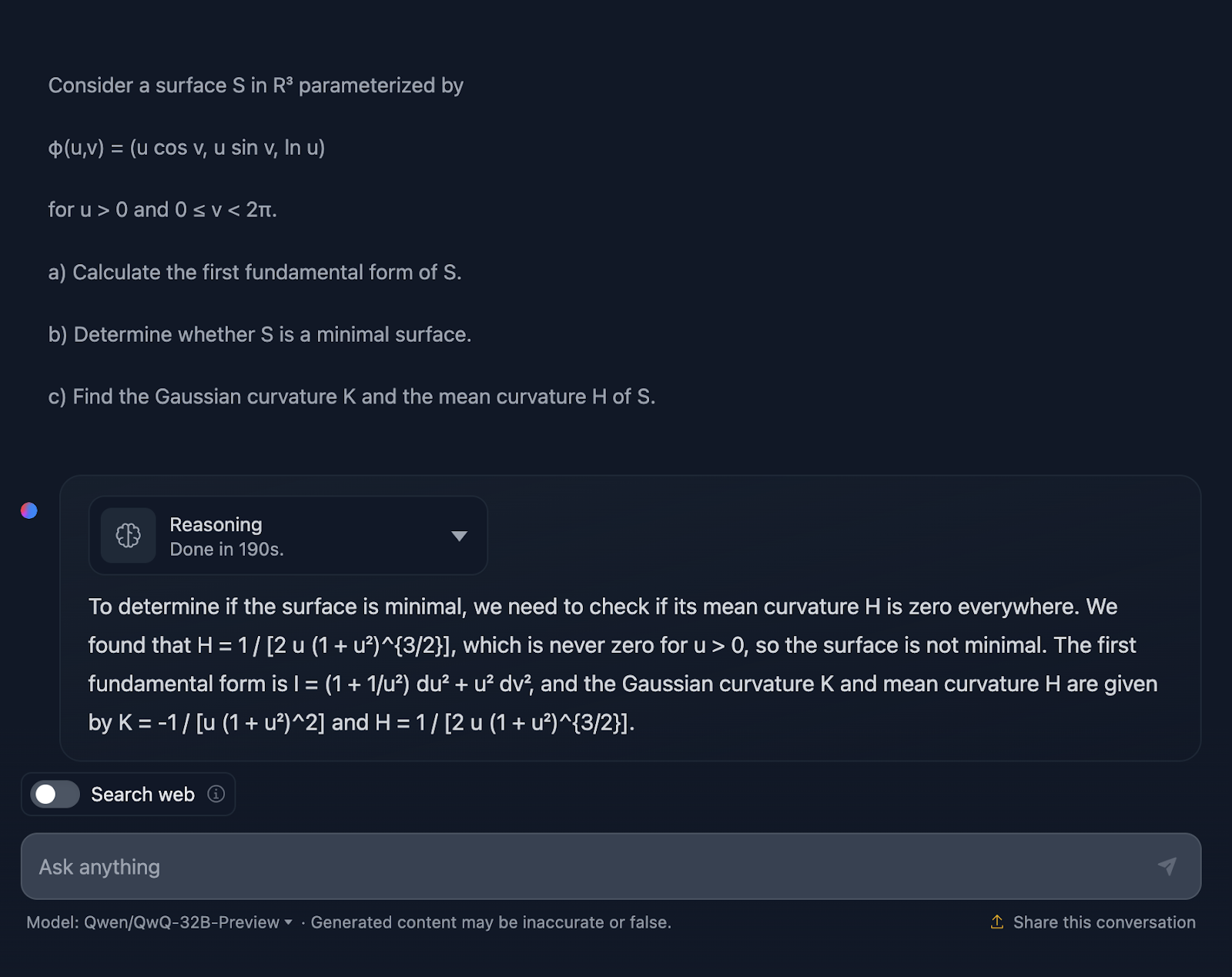
D'accord, la réponse ne m'étonne pas puisqu'elle est assez similaire au test précédent en termes de style. Encore une fois, ce n'est pas techniquement faux, mais il y a certainement une marge d'amélioration dans la façon dont l'explication est communiquée.

L'explication passe sous silence le comment. Je ne m'attends pas à une approche étape par étape, bien sûr, mais au moins à quelques formules pour montrer d'où viennent les résultats. De plus, la réponse n'est pas divisée en sections et le formatage des formules n'est, une fois de plus, pas le meilleur. DeepSeek a fait un excellent travail à cet égard.

Une fois de plus, pas de notes complètes pour QwQ, mais des notes complètes pour DeepSeek !

Examinons le raisonnement (pour des raisons de lisibilité, je ne montre que la première et la dernière partie) :

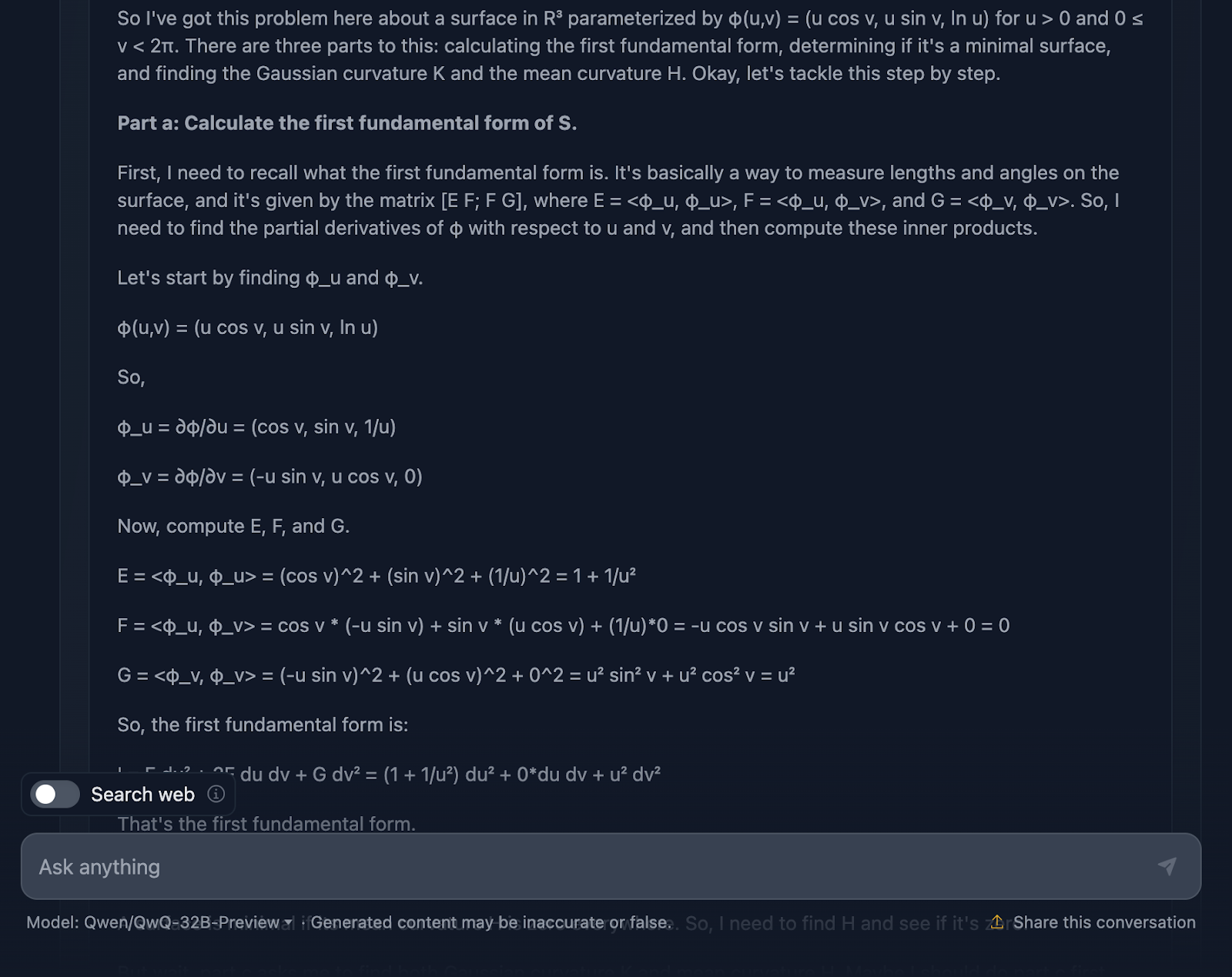
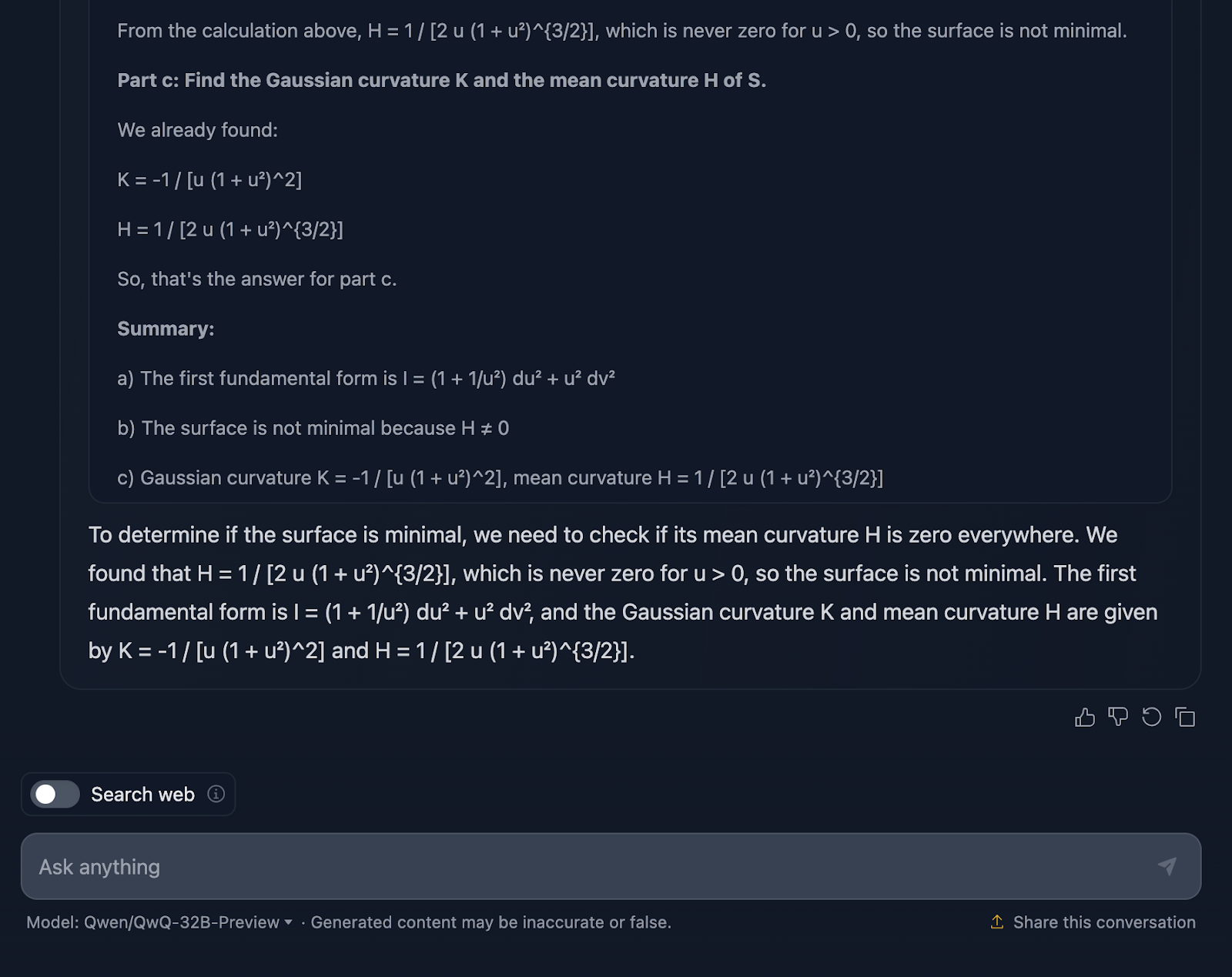
Très bien, parlons du raisonnement du modèle. Tout d'abord, je dois lui reconnaître le mérite d'être exhaustif. La répartition en sections claires - partie a, partie b et partie c - facilite le suivi et permet d'accomplir un travail solide en nous guidant à travers les étapes. Il commence par s'attaquer à la première forme fondamentale, en calculant soigneusement les coefficients de la paramétrisation, puis il poursuit son chemin. Lorsqu'il aborde les courbures gaussiennes et moyennes dans la partie c, les bases sont déjà bien établies.

C'est là que les choses commencent à se gâter. Bien que les calculs soient techniquement corrects, le modèle passe beaucoup de temps à revérifier les étapes ou à revoir les calculs, ce qui est excellent pour la précision mais moins pour la lisibilité. 

Parlons maintenant de la mise en forme. Les formules sont toutes là, mais elles ne sont pas présentées de la manière la plus claire - une fois de plus. C'est un peu désordonné, et pour ceux qui essaient de suivre, cela peut rendre les choses plus difficiles qu'elles ne devraient l'être. Une présentation plus claire, avec des résultats clés mis en évidence, améliorerait vraiment cette explication.

Un autre élément manquant est le contexte. Le modèle nous donne les résultats, mais il ne s'arrête pas vraiment pour expliquer ce qu'ils signifient. Par exemple, pourquoi la courbure gaussienne a-t-elle de l'importance ici ? Ou qu'est-ce que cela nous apprend sur la géométrie de la surface ? Et lorsqu'il conclut que la surface n'est pas minimale, il a techniquement raison, mais il manque une occasion de développer ce que cela signifie dans un sens plus large.

Tests de codage

Nous avons testé les performances de QwQ-32B-Preview sur des tests mathématiques, et je ne suis pas très impressionné - mais peut-être suis-je partial parce que j'ai vraiment aimé les résultats de DeepSeek. Voyons comment il se comporte lors des tests de codage et si QwQ-32B-Preview peut me surprendre cette fois-ci.

Python

Le premier test est le suivant :

" Implémentez une fonction en Python qui trouve la sous-chaîne palindromique la plus longue dans une chaîne donnée. La fonction doit avoir une complexité temporelle supérieure à O(n^3)".

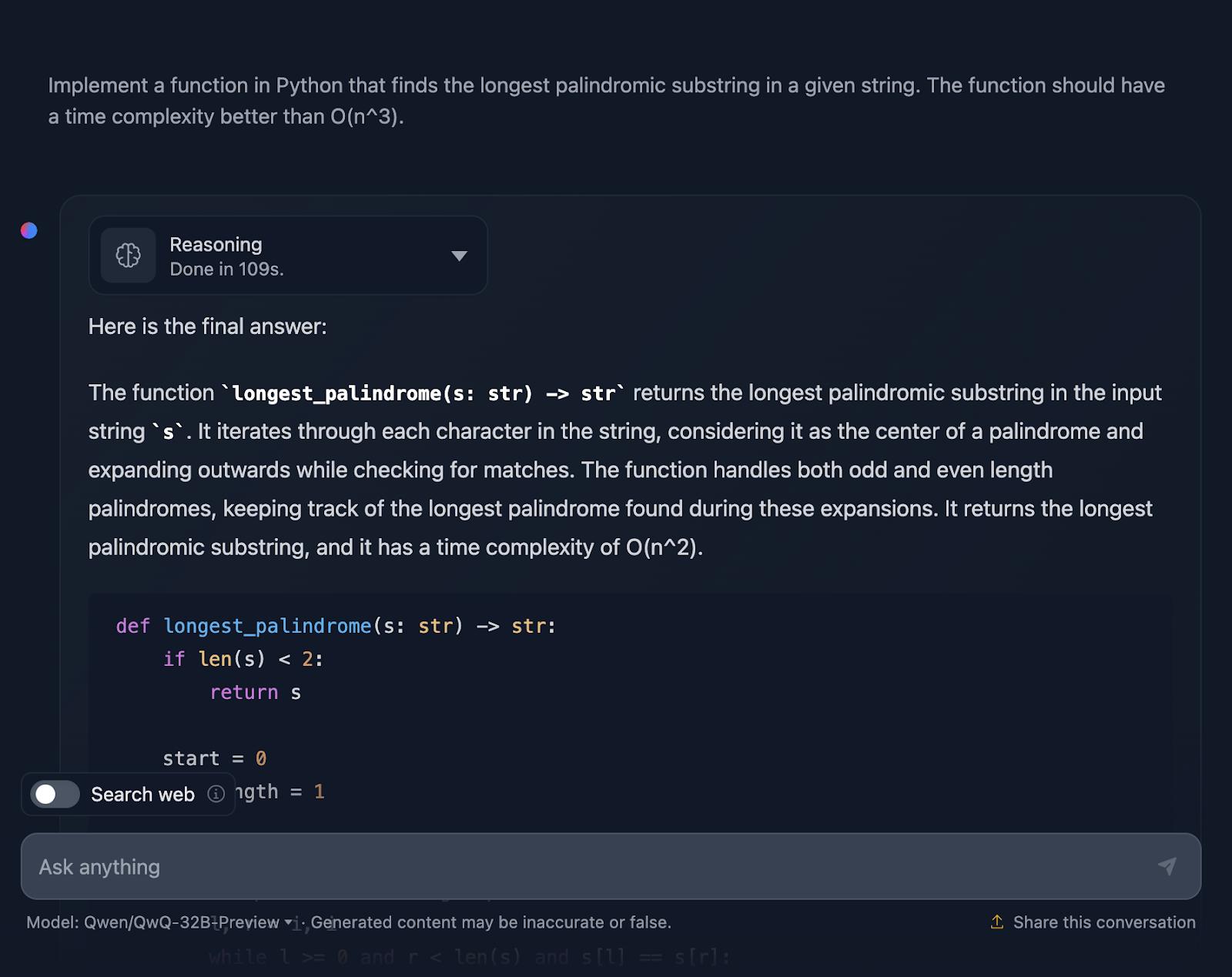
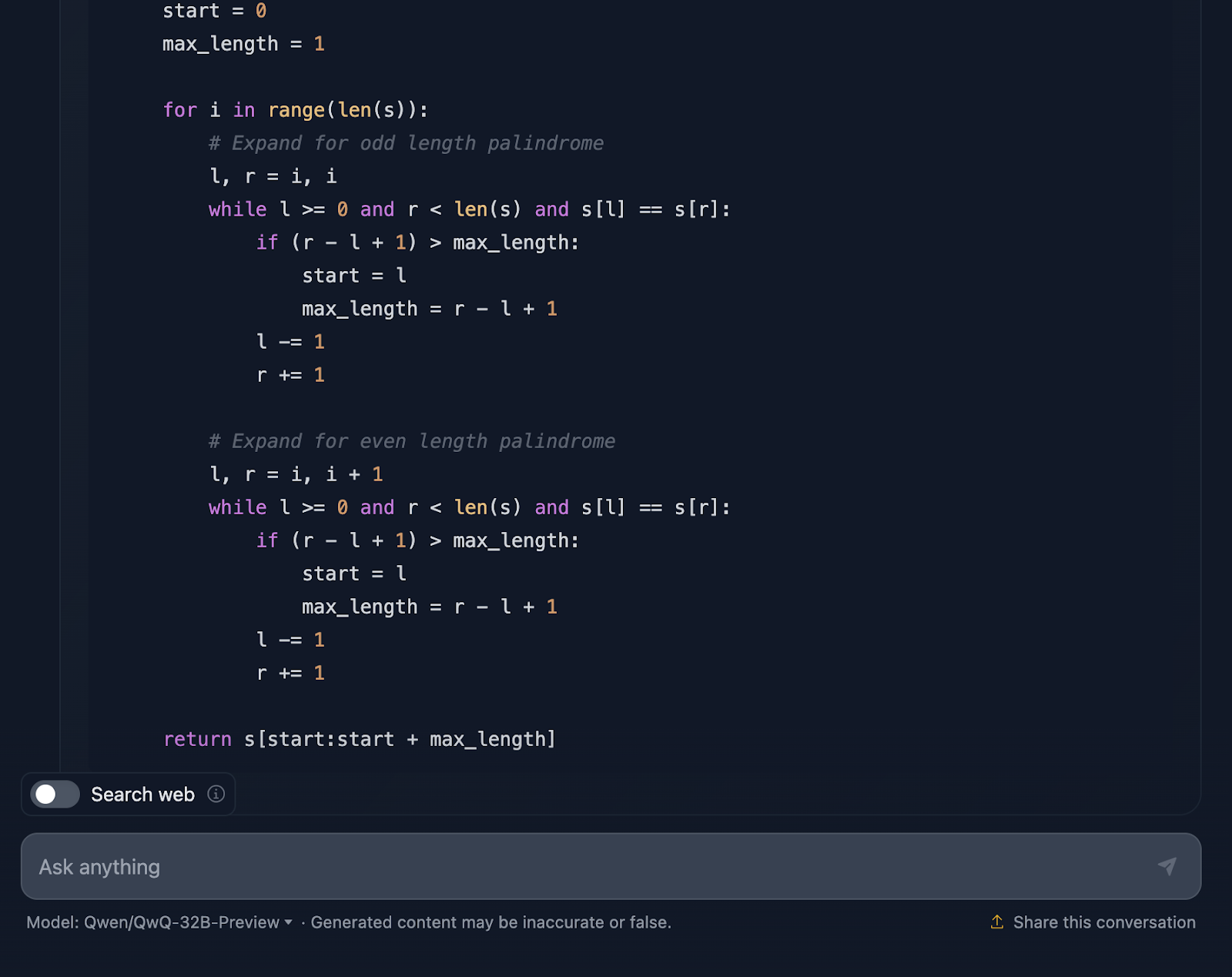
La solution est correcte et fournit un moyen propre et efficace de trouver la plus longue sous-chaîne palindromique avec la complexité requise. Il utilise une approche intelligente en s'étendant autour de chaque caractère pour vérifier les palindromes et gère bien les longueurs paires et impaires. Le code est clair et facile à suivre. Cependant, j'aurais aimé voir des cas de test à la fin, ce que DeepSeek a fourni. Examinons maintenant le raisonnement (je ne montrerai que la première et la dernière partie pour des raisons de lisibilité) :

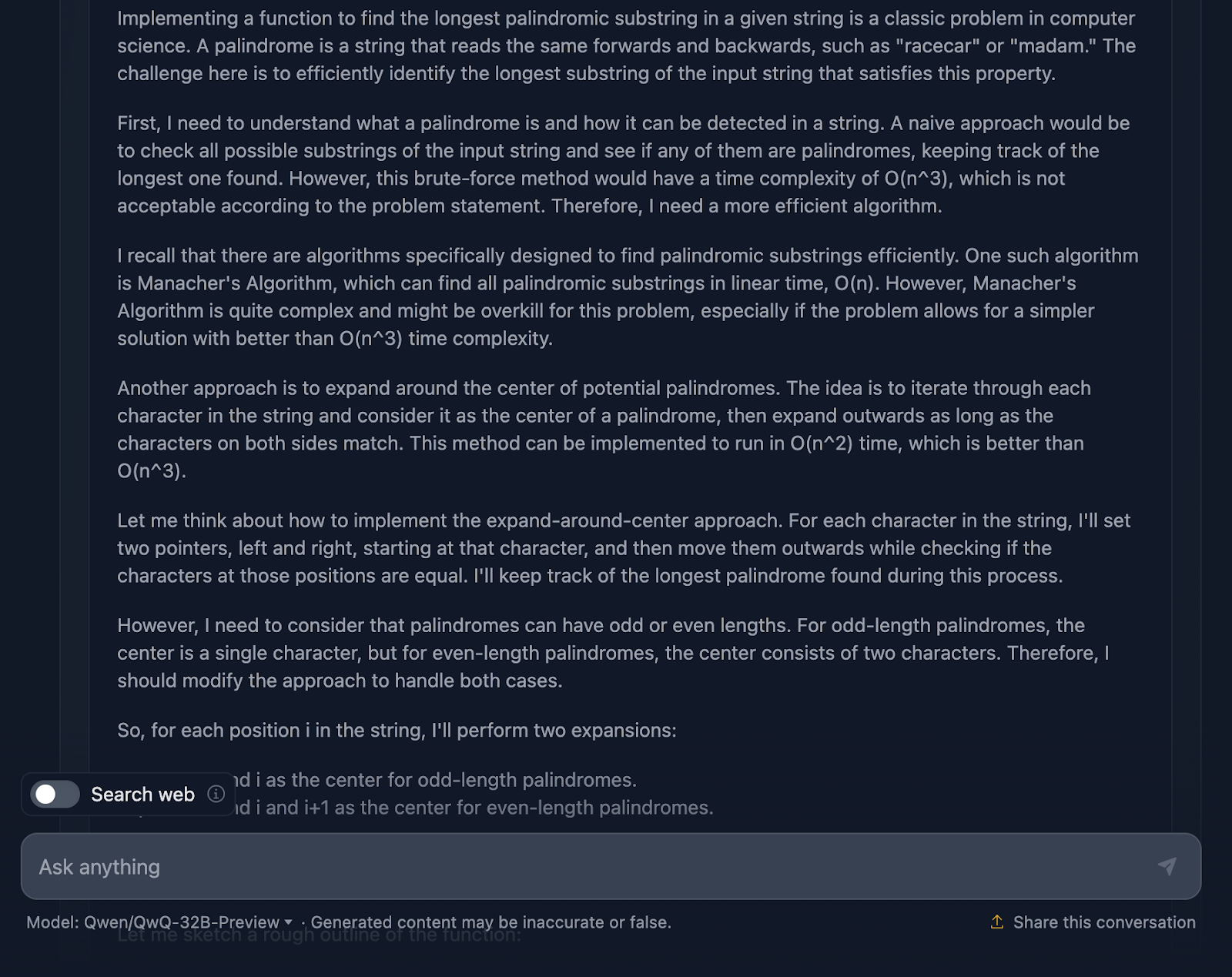
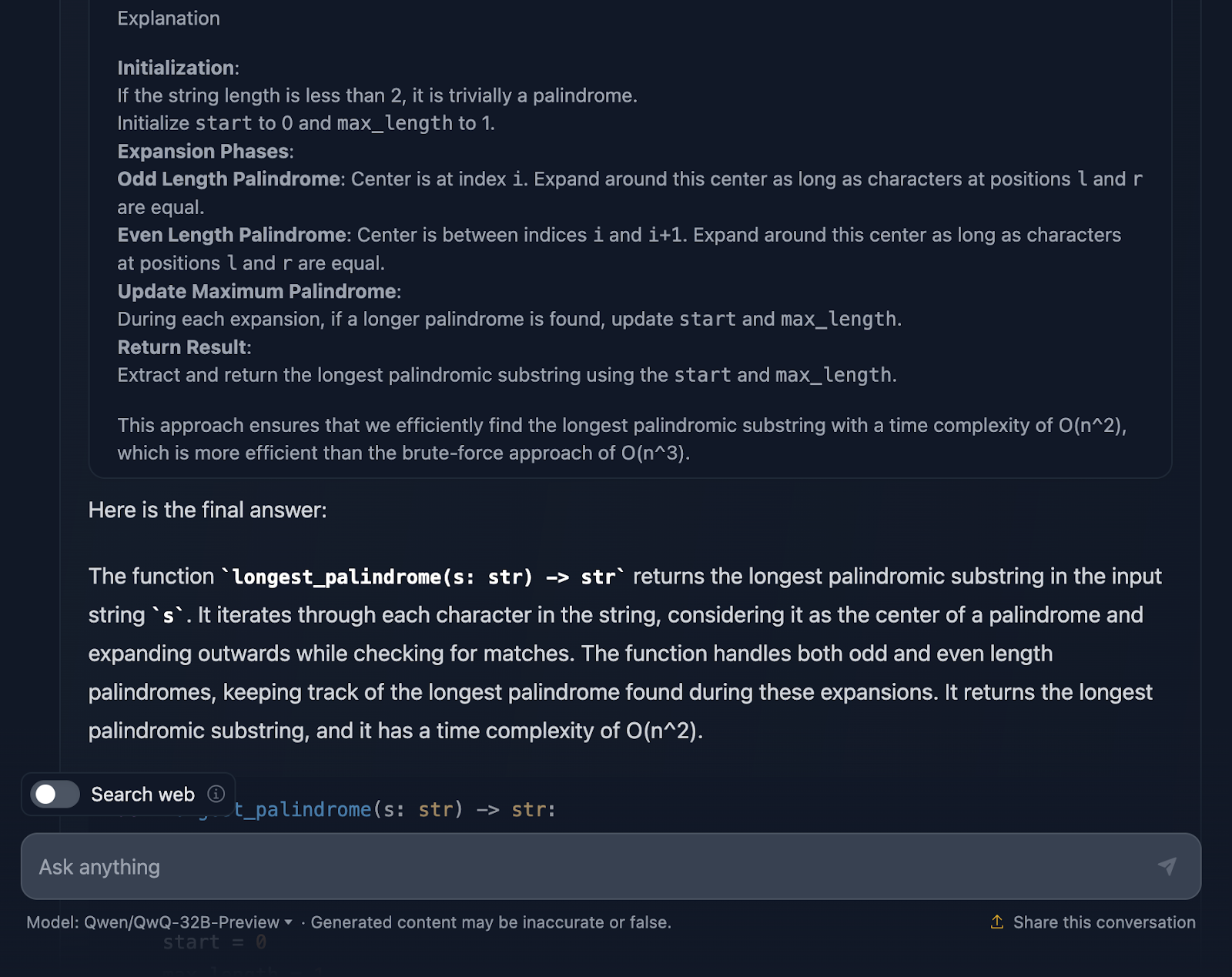
Je dois dire qu'il s'agit d'une approche assez solide et que je suis impressionné par certaines parties du raisonnement. Mais il y a quelques points sur lesquels il pourrait être un peu plus serré - alors parlons-en.

Tout d'abord, le raisonnement commence par aborder les bases : ce qu'est un palindrome et pourquoi une approche par force brute n'est pas la meilleure approche. Il passe ensuite directement à la méthode d'expansion autour du centre et mentionne même l'algorithme de Manacher avec sa complexité O(n). complexité O(n). Il reconnaît que si la méthode de Manacher est plus rapide, elle est probablement excessive pour ce problème. DeepSeek n'a pas mentionné cette approche, ce à quoi je m'attendais avant de l'essayer.  Il évoque également des méthodes alternatives, telles que l'inversion de la chaîne ou l'omission de vérifications inutiles, ce que je trouve très bien !

La méthode d'expansion autour du centre est expliquée clairement et sépare les palindromes de longueur impaire de ceux de longueur paire, ce qui est essentiel pour s'assurer que tous les cas sont couverts. 

L'inclusion des cas limites est un point fort. Chaînes à un seul caractère, chaînes sans palindromes, chaînes composées de tous les caractères identiques : tout est là. De plus, il mentionne même comment l'implémentation gère gracieusement les chaînes vides en les renvoyant simplement. C'est ce genre de rigueur que vous attendez d'une explication.

J'apprécie beaucoup que le résultat final du raisonnement vous donne une ventilation de l'approche, du code de la solution et de l'explication, mais j'aurais aimé que cela soit inclus dans la réponse finale !

QwQ-32B-Preview a-t-il été plus performant que DeepSeek pour cette affaire ? En dépit de l'inclusion de cas de test, je dirais que c'est le cas !

JavaScript

Maintenant, je vais tester un défi de codage en Javascript :

"Ecrivez une fonction en JavaScript qui détermine si un nombre donné est premier.

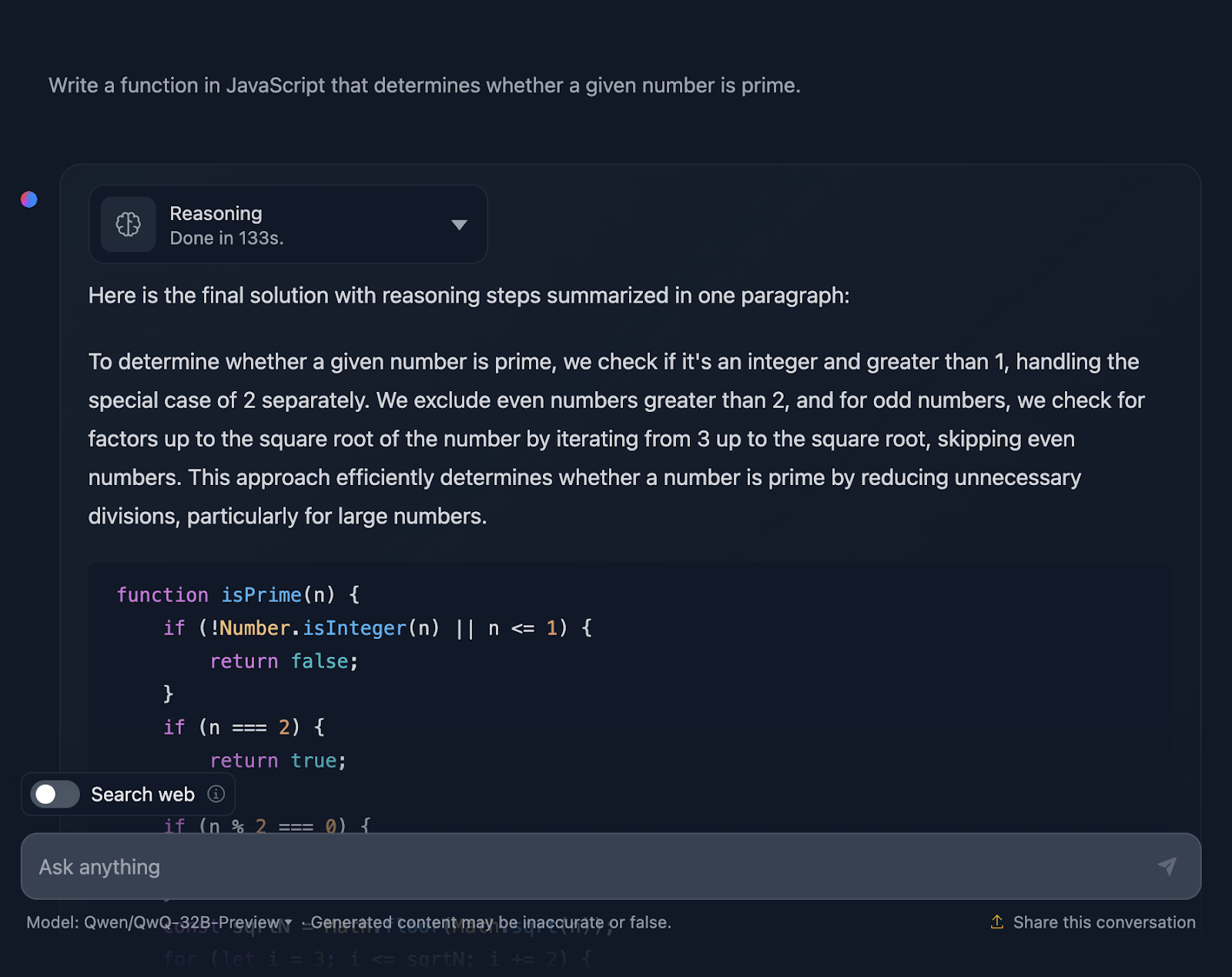
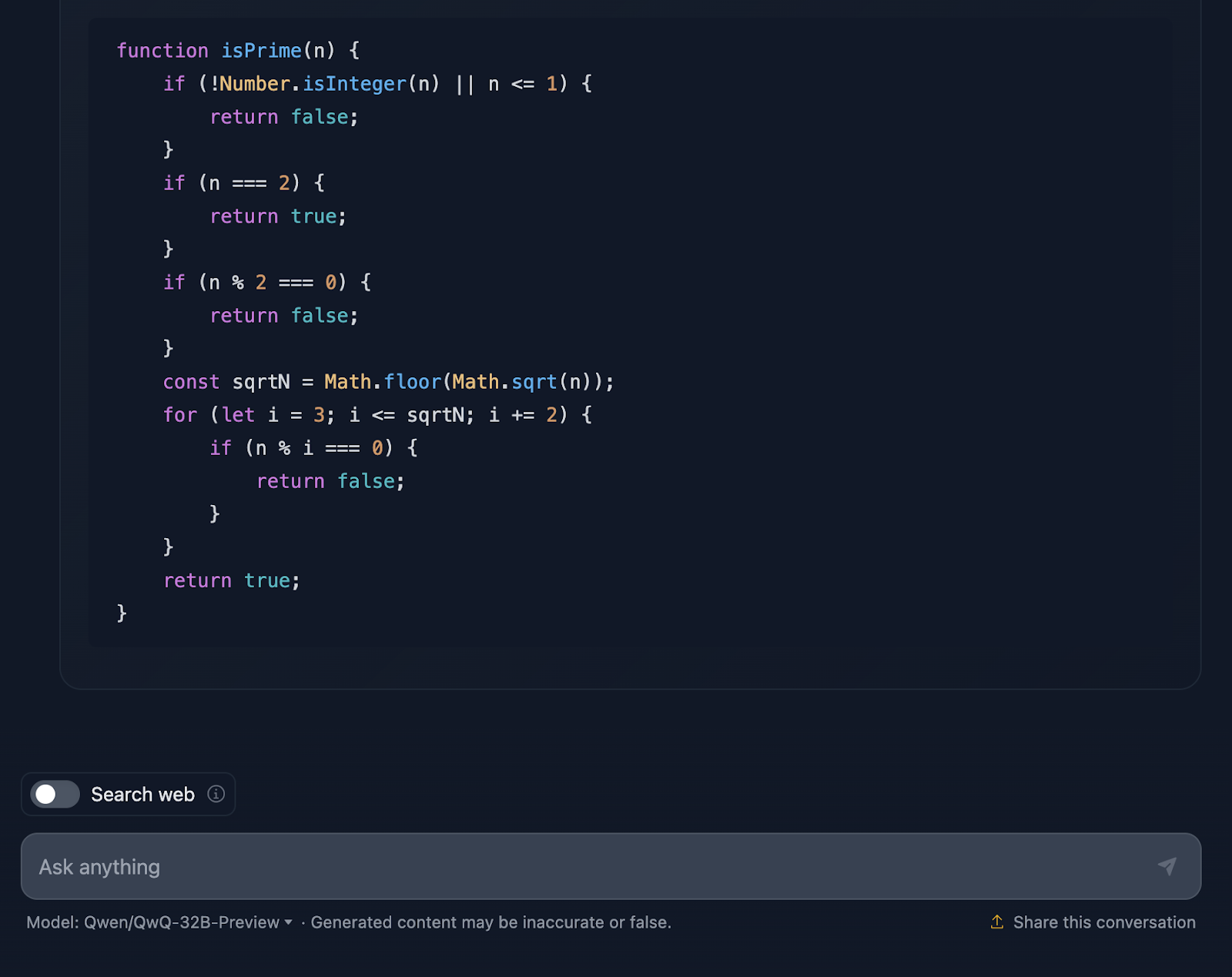
La solution est correcte et très similaire à celle fournie par DeepSeek. Cependant, il a fallubeaucoup plus de temps à pour faire le raisonnement, alors voyons comment il est arrivé à cette réponse (je tronque à nouveau la sortie pour des raisons de lisibilité) :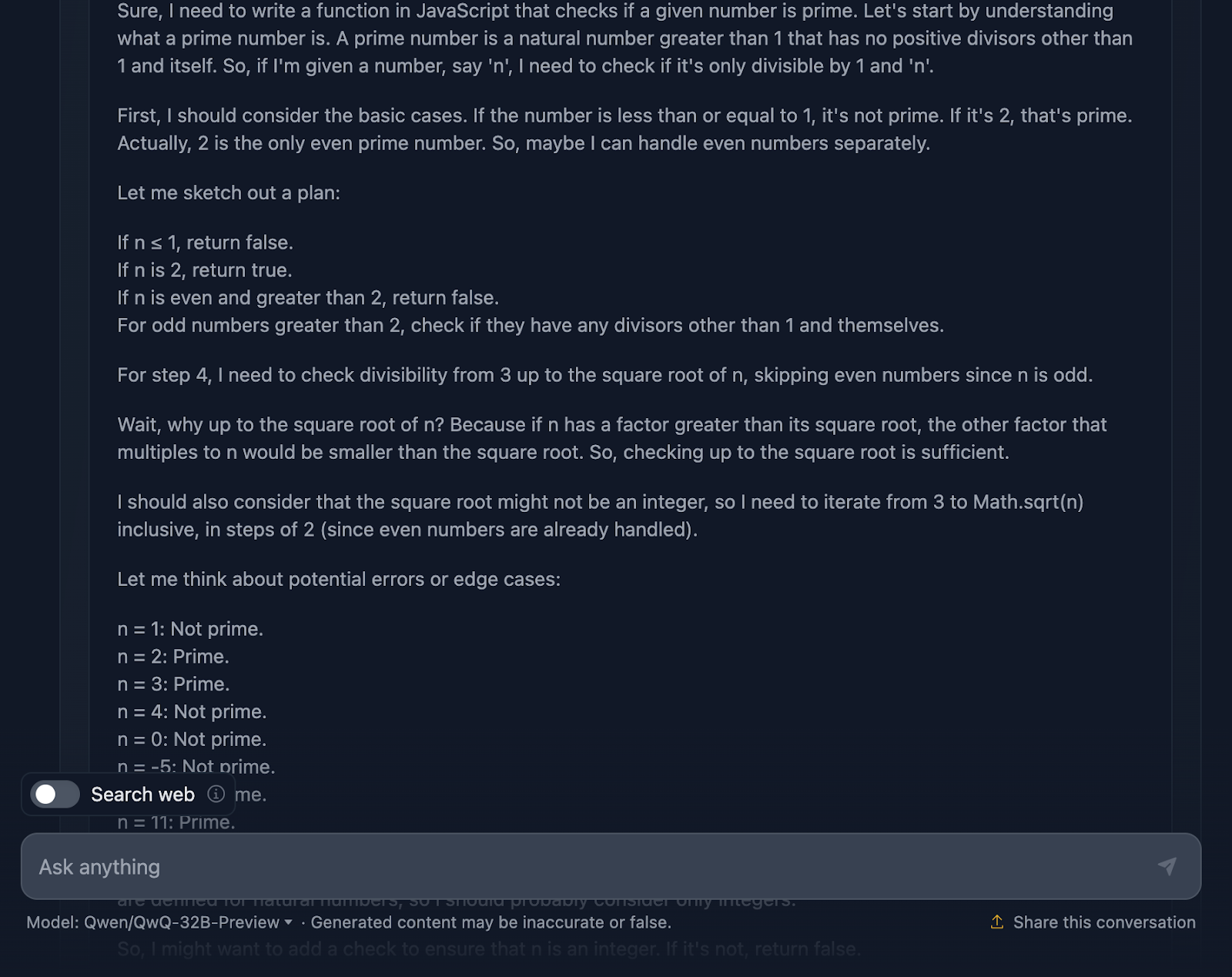

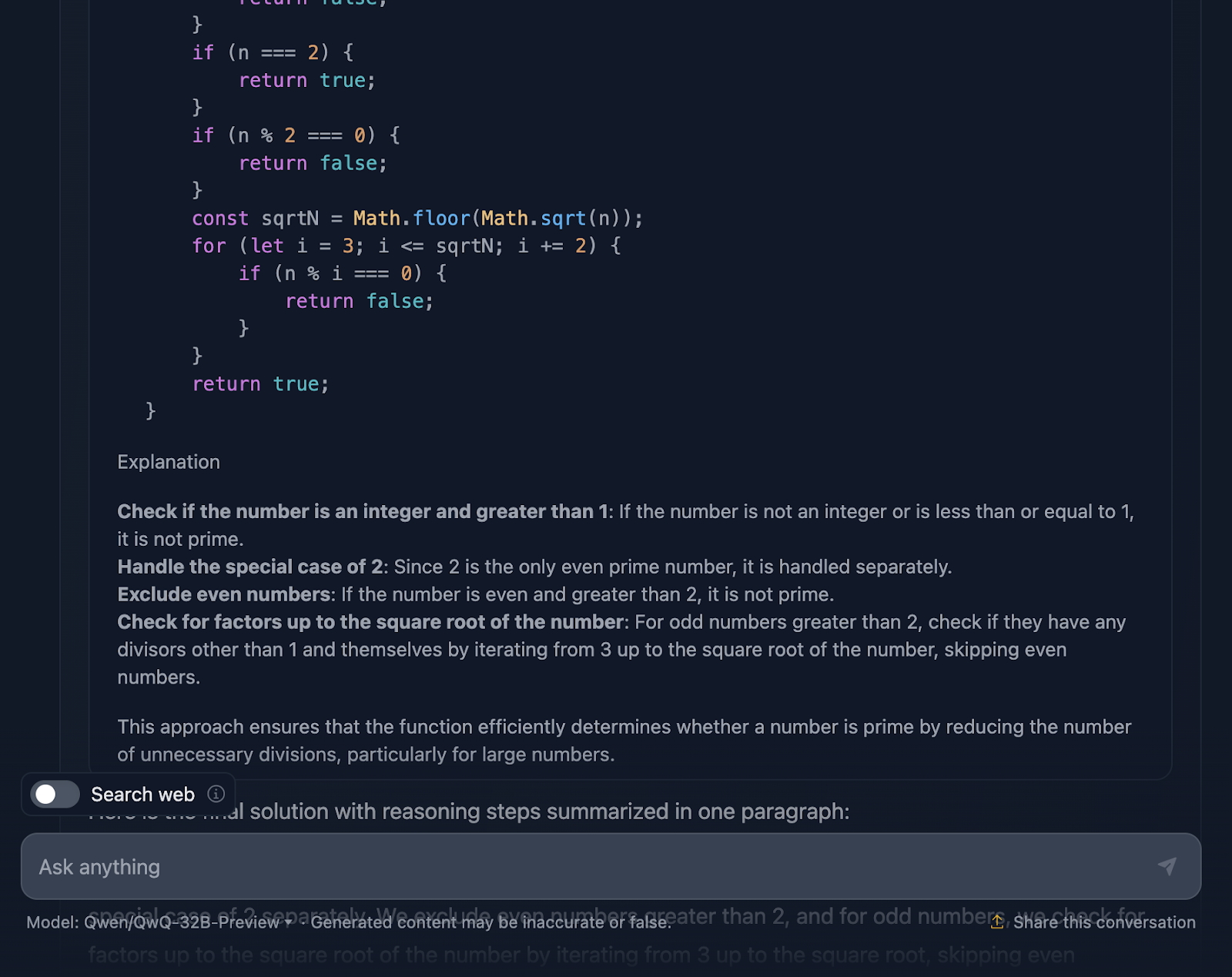
D'accord, ce raisonnement est particulièrement long par rapport à celui fourni par DeepSeek. Examinons-le plus en détail :

Tout d'abord, la solution commence par répondre aux besoins de base. Nombres inférieurs ou égaux à 1 ? Il ne s'agit certainement pas d'une priorité. Et le chiffre 2 est spécial : c'est le seul nombre premier pair. Un autre nombre pair ? Automatiquement, pas prioritairement. Cette configuration logique est claire et a beaucoup de sens lorsque l'on traite des cas particuliers.

À partir de là, on entre dans le vif du sujet : comment vérifier efficacement si un nombre a des diviseurs autres que 1 et lui-même ? Au lieu de vérifier tous les nombres jusqu'à n, la solution ne vérifie que la racine carrée de n. Pourquoi ? En effet, si un nombre a un facteur supérieur à sa racine carrée, son autre facteur aura déjà été vérifié sous la racine carrée. Très efficace, il évite les calculs inutiles. 

Pour aller encore plus vite, la solution saute tous les nombres pairs après avoir traité le 2. Il s'agit donc de vérifier les nombres impairs, en commençant par 3 et en progressant par 2. Il s'agit d'une optimisation intéressante qui réduit le travail de moitié.

Nous passons ensuite à la mise en œuvre. La fonction commence par valider l'entrée. S'agit-il d'un nombre entier ? Est-il supérieur à 1 ? Si ce n'est pas le cas, c'est un rapide "pas de premier choix". Ce type de validation est une excellente pratique qui permet de maintenir la robustesse de la fonction. La logique de la boucle commence alors, vérifiant les diviseurs à partir de 3 jusqu'à la racine carrée de n. Si n'importe quel diviseur fonctionne, il ne s'agit pas d'un nombre premier. Sinon, tout est clair et le nombre est premier.

Ce qui est formidable, c'est que le raisonnement ne s'arrête pas à la mise en œuvre. Il s'intéresse aux cas extrêmes, tels que les nombres négatifs, les nombres non entiers ou les entrées bizarres comme 2,5, et s'assure que la fonction les traite correctement. Il y a même un clin d'œil aux limites de JavaScript avec les très grands nombres et une suggestion d'utiliser BigInt pour ces scénarios limites, ce qui m'a semblé être un excellent ajout au raisonnement.

La solution comprend des cas de test détaillés qui montrent exactement comment elle fonctionne pour des nombres comme 1, 2, 3, et même des nombres plus grands comme 13 et 29. Chaque test est expliqué étape par étape, de sorte qu'il n'y a pas de confusion quant au fonctionnement de la fonction.

Cette solution pourrait-elle aller plus loin ? Bien sûr, il est toujours possible de faire mieux. Par exemple, si vous travaillez avec des nombres massifs, vous pourriez vouloir explorer des algorithmes avancés tels que Miller-Rabin ou le test de primalité de Fermat. Mais pour un usage quotidien, cette solution constitue un excellent équilibre entre simplicité, efficacité et lisibilité.

Quel est le verdict ? Ce raisonnement est solide, clair et pratique et permet de s'assurer que le code est robuste, ce que DeepSeek n'a pas vraiment pris en compte. Je pense que QwQ-32B-Preview l'emporte !

Raisonnement logique

Enfin, examinons quelques tests de raisonnement logique.

Le problème du loup, de la chèvre et du chou

Je vais tester un puzzle classique :

"Un homme doit traverser une rivière avec un loup, une chèvre et un chou. Son bateau ne peut transporter que lui-même et une autre chose. S'il était laissé à lui-même, le loup mangerait la chèvre, et la chèvre mangerait le chou. Comment peut-il tout faire passer en toute sécurité ?"

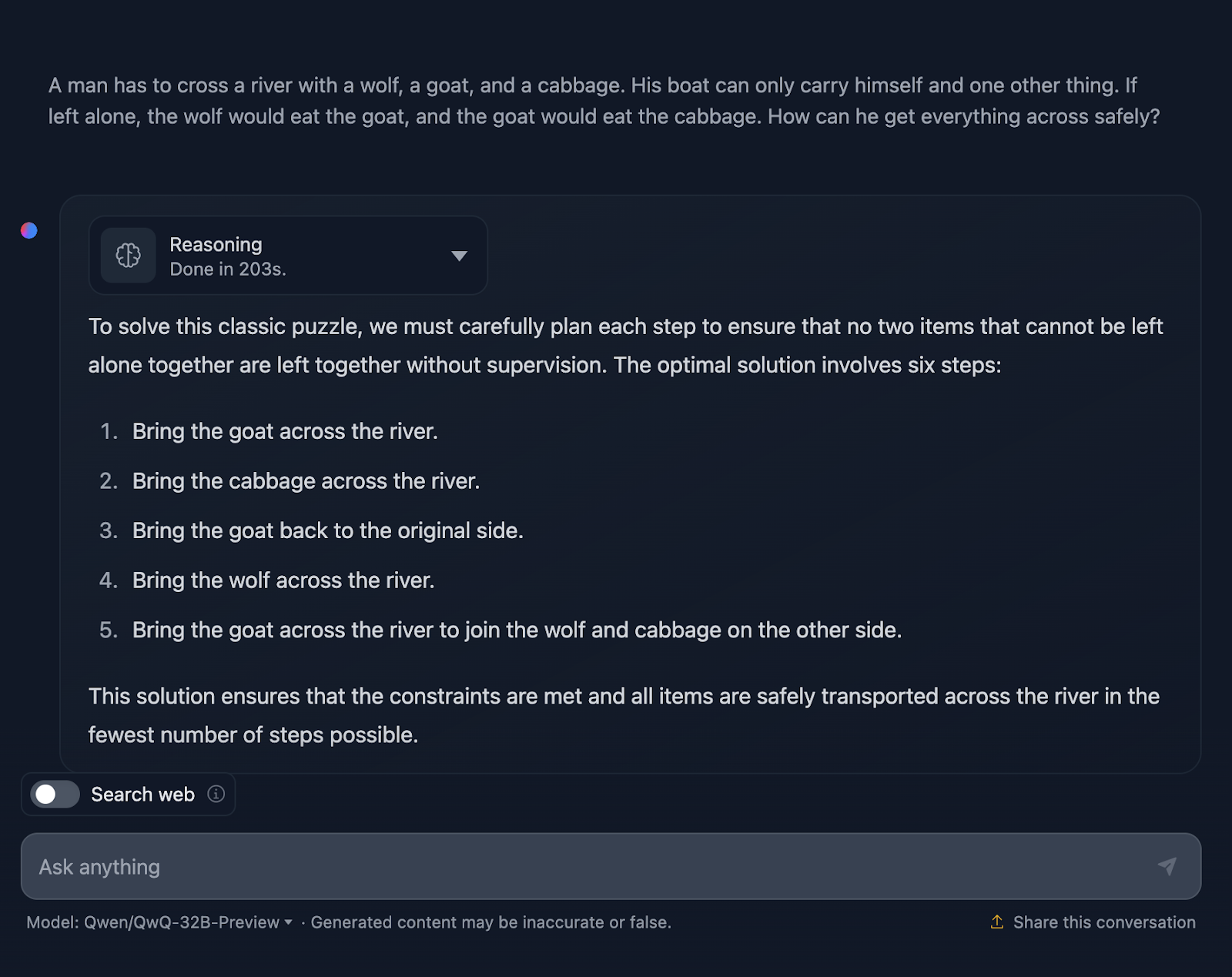
D'accord, la solution au problème est correcte, mais il y a quelques points à clarifier. Il indique que la solution optimale comporte six étapes ; cependant, seules cinq puces sont fournies. Il s'agit déjà d'une inexactitude.

En outre, vous pouvez penser qu'il s'agit d'une meilleure approche en termes d'efficacité par rapport à la sortie de DeepSeek, qui a nécessité sept étapes. Cependant, cette approche comporte en réalité sept étapes. Pour une raison ou une autre, les étapes du retour en solitaire n'ont pas été mentionnées. Il aurait dû produire le résultat suivant :

1. Faites traverser la rivière à la chèvre.
2. Revenez seul.
3. Apportez le chou de l'autre côté de la rivière.
4. Ramenez la chèvre dans sa position initiale.
5. Faire traverser la rivière au loup.
6. Revenez seul.
7. Faites traverser la rivière à la chèvre pour qu'elle rejoigne le loup et le chou de l'autre côté.

De plus, lors de l'exécution du raisonnement, j'ai remarqué ceci (et j'ai réussi à faire une capture d'écran !):

Cela m'a amené à me demander s'il n'y avait pas un problème de raisonnement...

Jetons un coup d'œil :

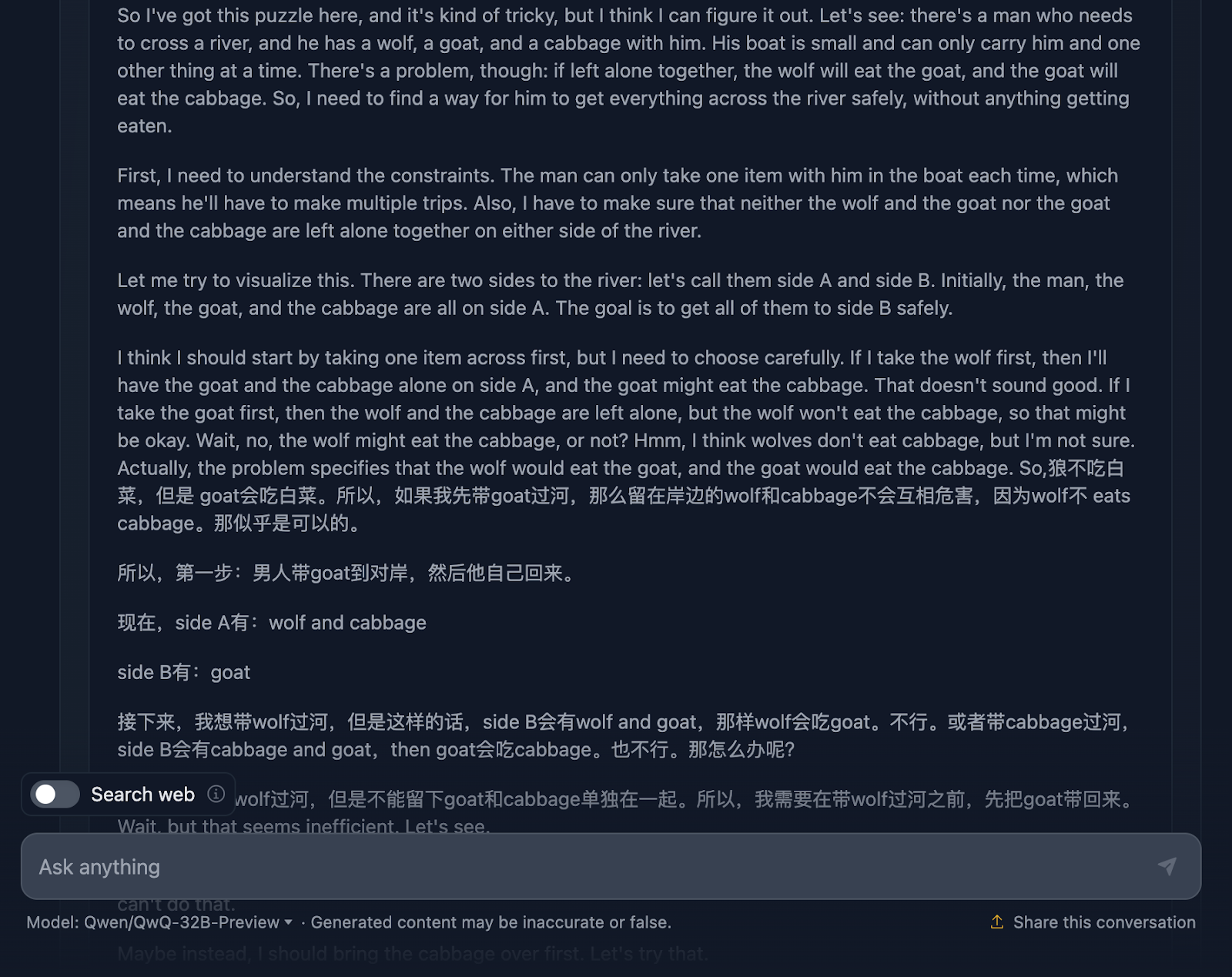
Le raisonnement commence par s'assurer qu'il comprend bien le problème, les défis et les contraintes. Cependant, c'est là que les choses commencent à se gâter. C'est un bon exemple des limites de ce modèle dont nous avons parlé plus haut, qui mélange deux langues. Il en résulte un raisonnement incompréhensible (du moins pour moi, qui ne comprends pas la langue - je suppose qu'il s'agit du chinois !) Je vais maintenant partager d'autres parties du raisonnement pour illustrer ceci, mais je vais sauter d'autres parties car c'est trop long.

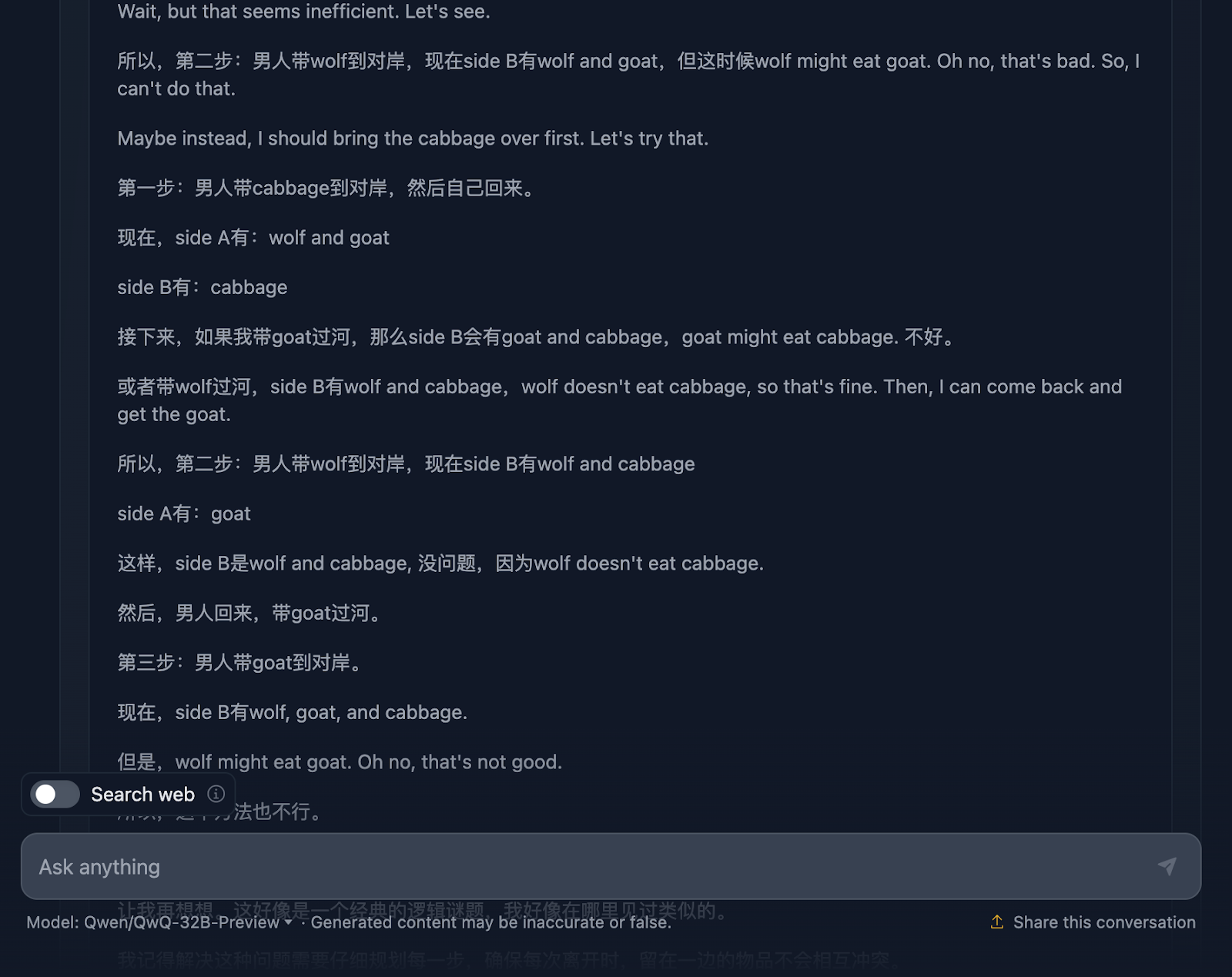
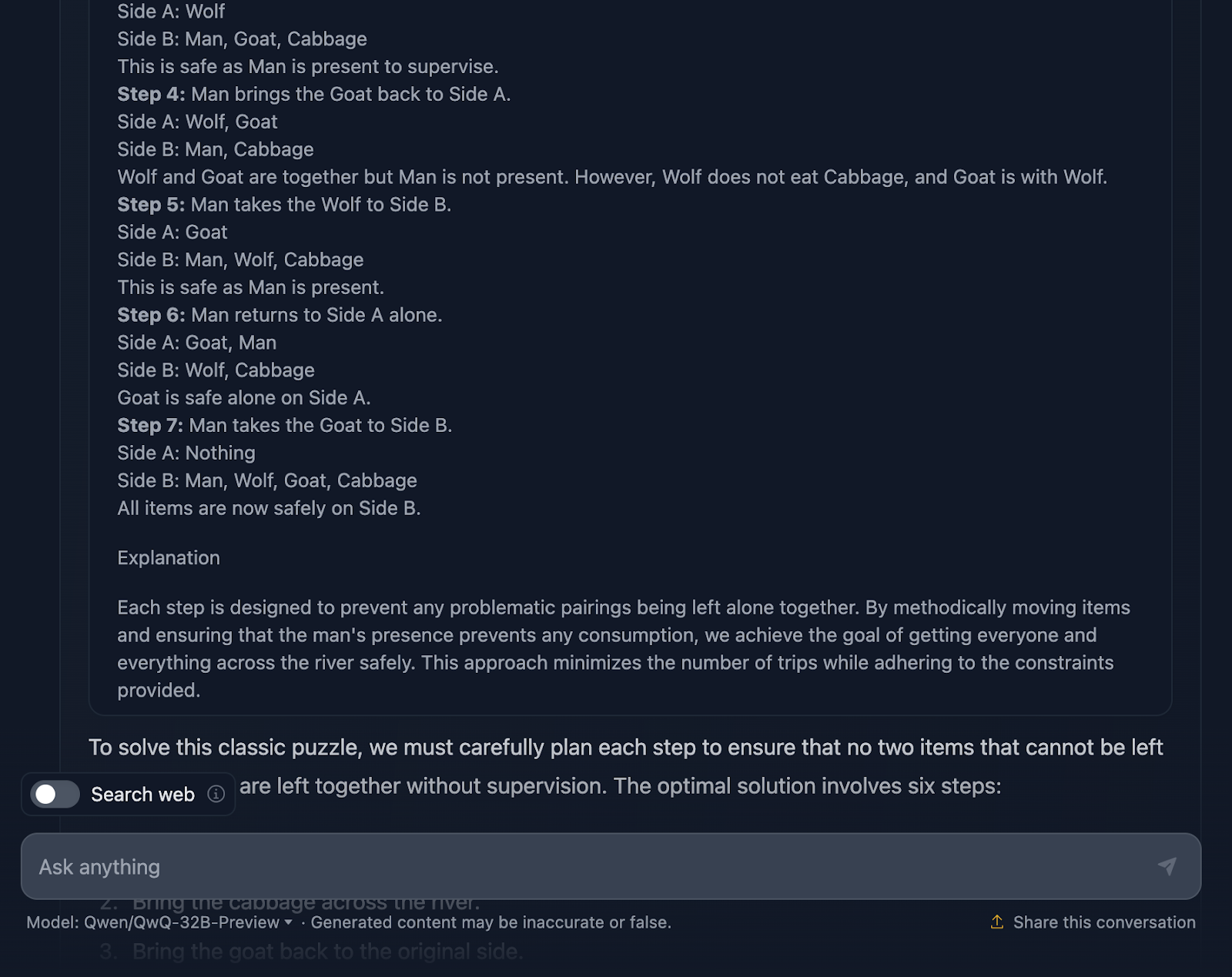
Cependant, la solution finale est excellente ! Il décrit la configuration initiale, les contraintes, l'objectif et la stratégie, ainsi qu'un plan de solution très clair qui inclut toutes les étapes, ce qui est assez intéressant !

Pourquoi cela ne s'est-il pas reflété dans la réponse finale ? Il a même ajouté une explication finale. J'aurais aimé que le résultat de la réponse finale corresponde à ce qui était affiché dans le raisonnement, et je me demande pourquoi cela n'a pas été le cas !

Puzzle de boules de pesée

Enfin, essayons cette énigme logique classique qui teste la capacité du modèle à trouver une stratégie optimale à l'aide d'un raisonnement déductif.

CLAUSE DE NON-RESPONSABILITÉ : Voici le résultat que j'ai obtenu après trois tentatives : le modèle a commencé à générer une réponse, mais s'est bloqué ou a produit une erreur et n'a pas pu continuer à générer. Par ailleurs, je vais passer le raisonnement pour cette fois-ci, car il était extrêmement long, et le résultat est déjà assez important ! Jetons un coup d'œil (la sortie est également tronquée) :

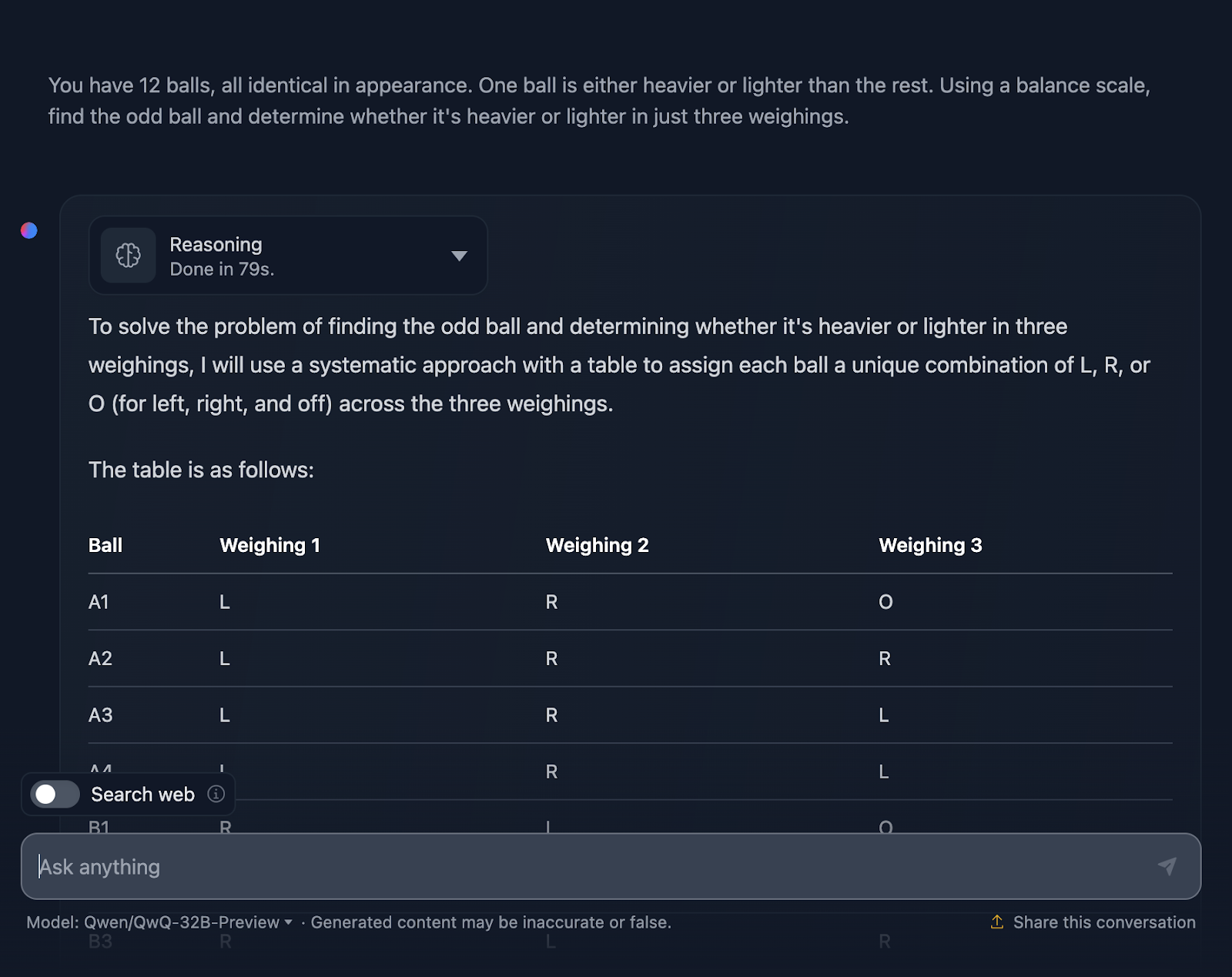
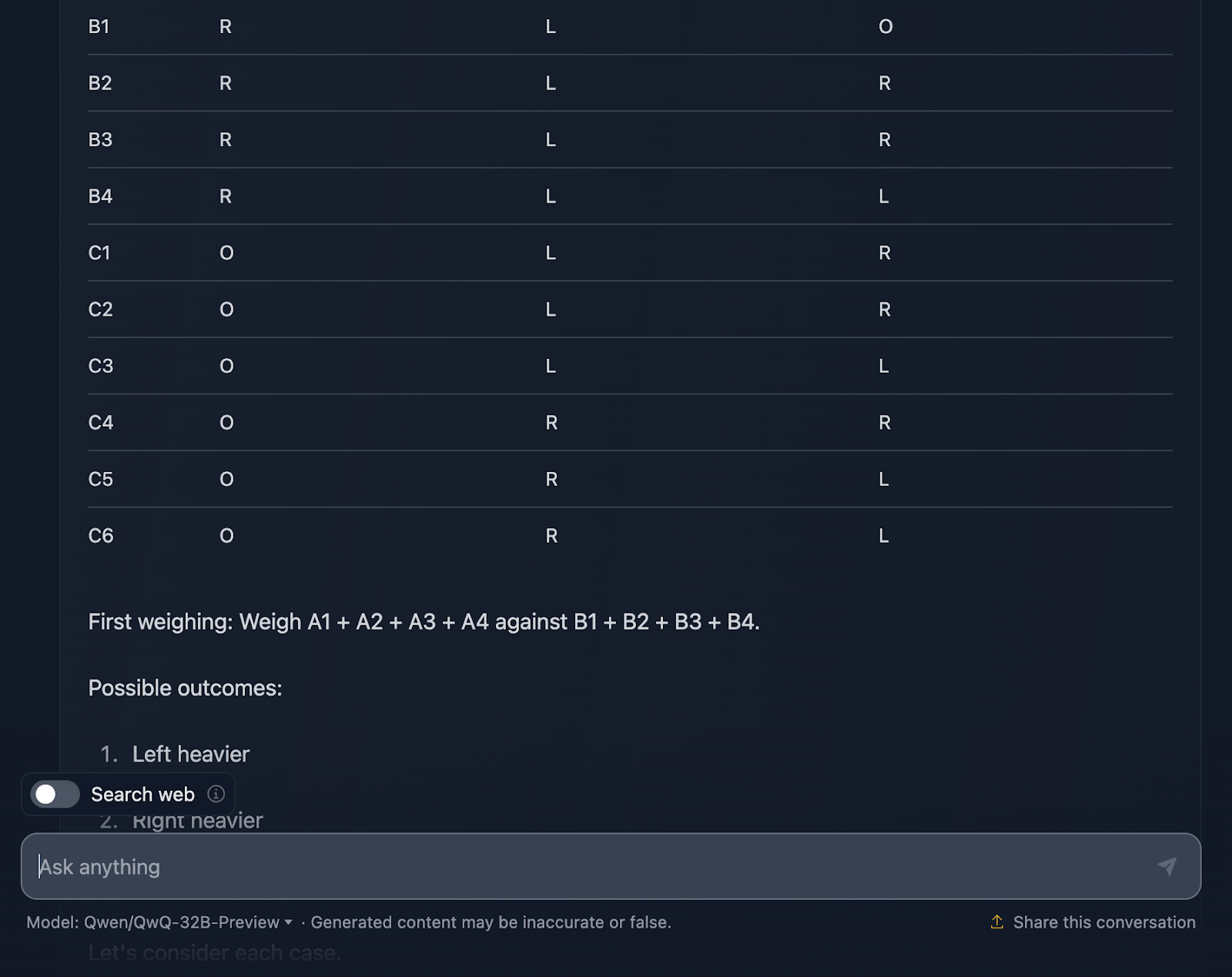
Je dois dire que je suis très impressionné par le résultat ! La solution commence par une explication très claire du problème et présente un plan à l'aide d'un tableau systématique, ce qui me semble très utile et que DeepSeek n'a pas inclus. Chaque balle reçoit une combinaison unique lors des trois pesées, ce qui permet de prendre en compte tous les scénarios possibles. 

J'aime beaucoup la façon dont il décompose le problème en cas et en sous-cas : "Plus lourd à gauche", "Plus lourd à droite" et "Égal". Cette approche progressive permet de gérer un problème complexe. Chaque pesée s'appuie sur les résultats de la précédente. Vous réduisez la taille de la balle bizarre étape par étape tout en déterminant si elle est plus lourde ou plus légère.

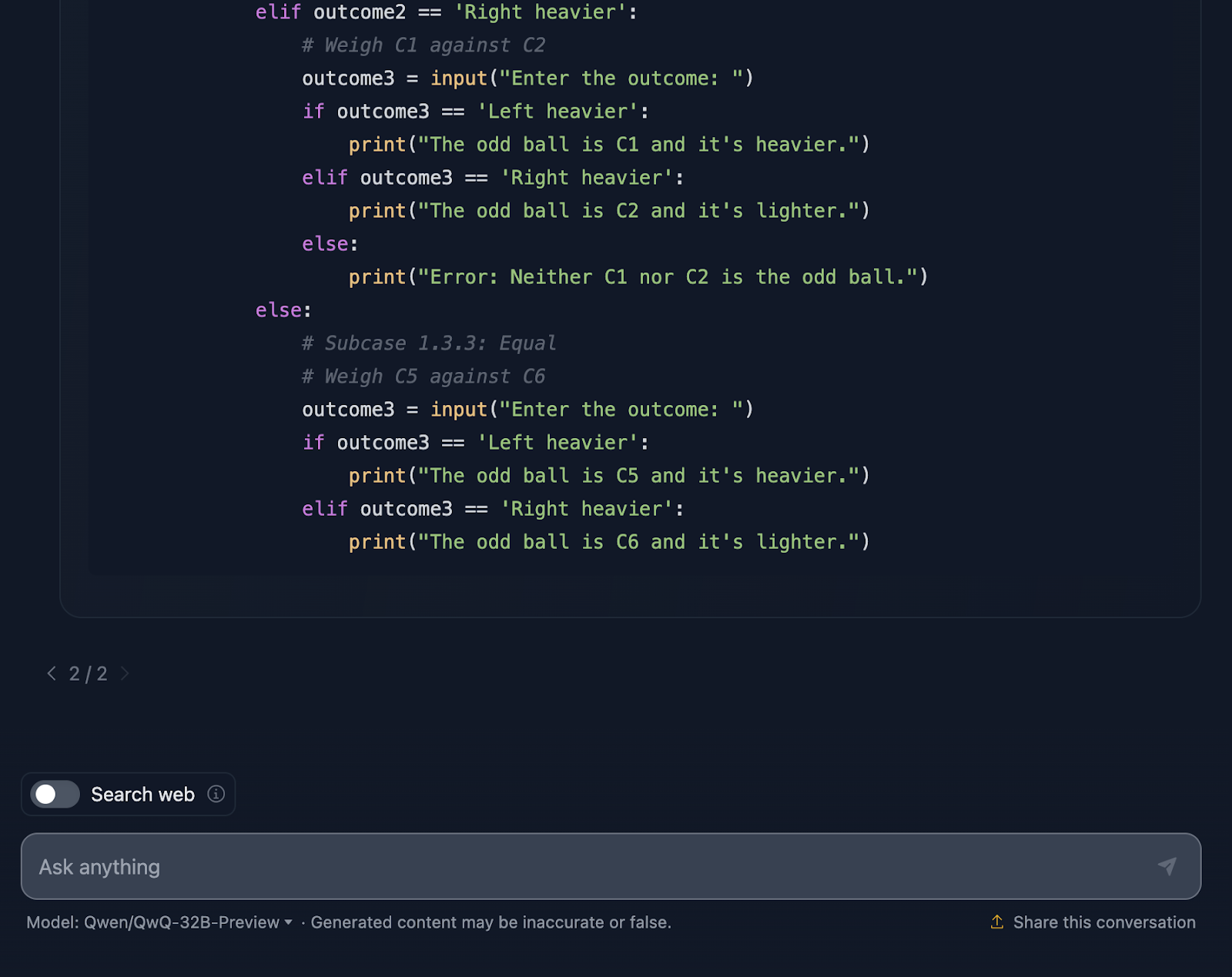
Enfin, la solution comprend un extrait de code Python, ce à quoi je ne m'attendais pas !  Il est interactif et permet aux utilisateurs de simuler les pesées, ce qui rend le processus plus facile à suivre et même amusant à explorer. Cette solution ne laisse rien au hasard. Chaque résultat des pesées est couvert, ce qui permet de s'assurer qu'aucun impair n'échappe à la détection. 

Une chose est sûre : l'extrait de Python suppose une saisie parfaite de la part de l'utilisateur. Si quelqu'un saisit un résultat de pesée non valide, le code ne prévoit pas de gestion des erreurs pour le détecter. Un peu de robustesse pourrait lui permettre d'atteindre un niveau supérieur. 

Je dirais qu'il s'agit d'une excellente réponse, qui surpasse celle de DeepSeek en termes de clarté et d'aide à la visualisation grâce aux tableaux et au code Python.

Comparaison de la vitesse : DeepSeek vs. QwQ

Enfin, je vais comparer la vitesse de chaque modèle pour chaque test en ce qui concerne l'exécution du raisonnement et la fourniture d'une solution. Il faut garder à l'esprit que les résultats dépendent de nombreux facteurs et que les modèles ne fonctionnent pas toujours à la même vitesse, mais je trouve intéressant que DeepSeek ait été plus rapide pour toutes les tâches que j'ai testées.

QwQ-32B-Preview Benchmarks

Le test de QwQ-32B-Preview a révélé à quel point il est capable de relever des défis mathématiques, de codage et de raisonnement, même si certains sont plus difficiles que d'autres !

Voici comment QwQ s'est comporté dans quelques tests de référence difficiles :

• GPQA (raisonnement scientifique de niveau supérieur): Le score de est de 65,2 %, ce qui démontre un raisonnement scientifique de haut niveau.
• AIME (thèmes mathématiques avancés): Le candidat a obtenu un score de50,0 % sur le site , démontrant de solides compétences en mathématiques avancées telles que la géométrie, l'algèbre et la théorie des nombres.
• MATH-500 (problèmes mathématiques très variés): Il a obtenu un score impressionnant de90,6 % sur le site , prouvant ainsi sa capacité à résoudre un large éventail de problèmes mathématiques.
• LiveCodeBench (tâches de programmation réelles): Score 50.0%, démontrant de solides compétences en programmation dans des scénarios de codage du monde réel .

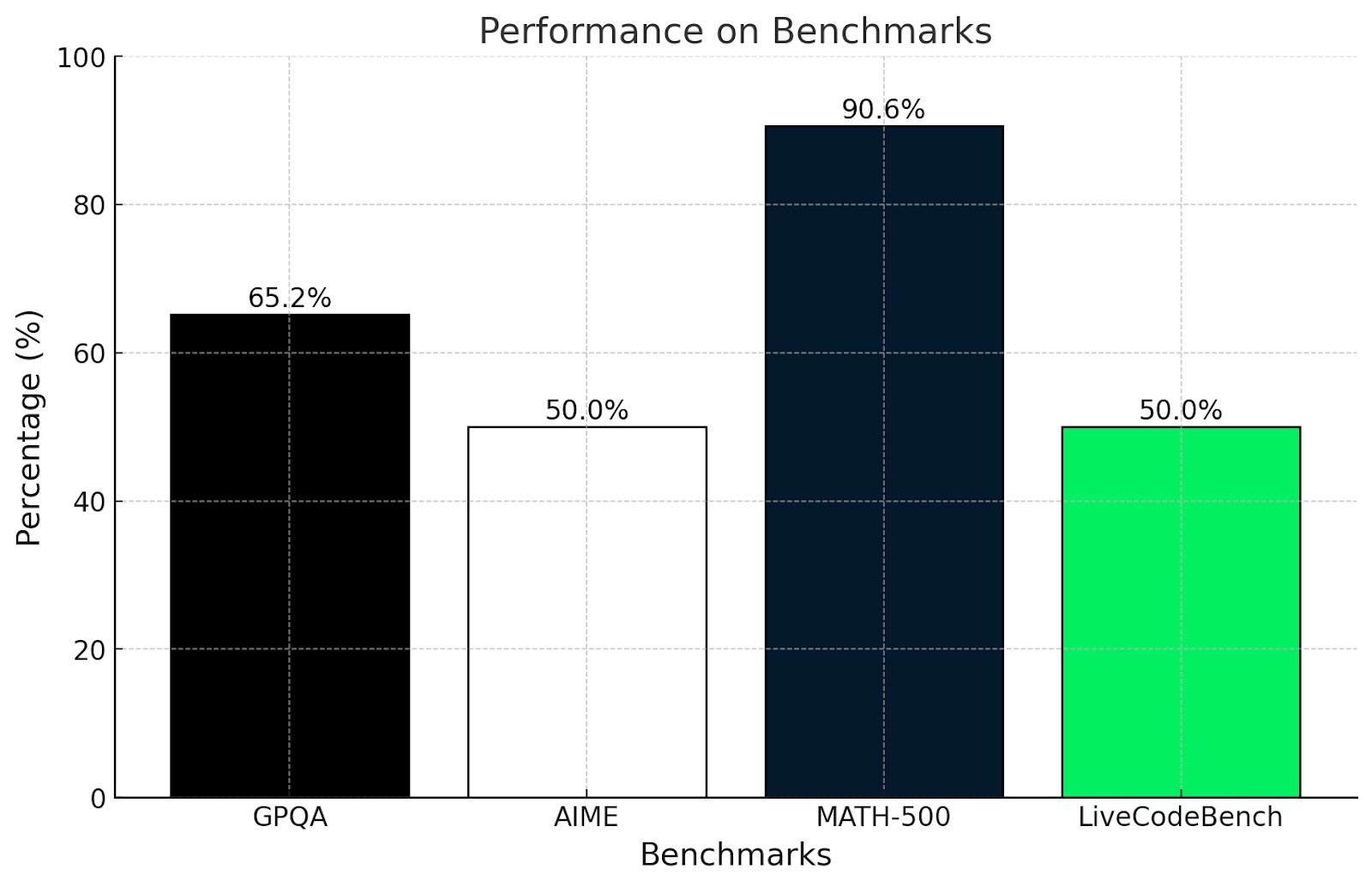
Suis-je surpris par ces résultats ? Pas vraiment. Ces résultats correspondent aux tests effectués dans cet article.

Le test GPQA mesure la compréhension du raisonnement scientifique au niveau de l'enseignement supérieur. Un score de 65,2 % montre qu'il sait utiliser la logique et les mathématiques pour résoudre des problèmes, mais qu'il peut avoir des difficultés avec des questions très spécialisées ou très conceptuelles, comme nous l'avons vu dans les tests de mathématiques plus complexes de cet article.

De même, le test AIME est connu pour ses sujets mathématiques avancés tels que la géométrie et l'algèbre. Un score de 50 % indique que QwQ-32B-Preview peut résoudre certains de ces problèmes, mais qu'il a du mal à résoudre les problèmes les plus complexes, qui nécessitent une réflexion originale. 

Un score de plus de 90 % à MATH-500 est très impressionnant et montre que QwQ-32B-Preview est capable de résoudre un problème mathématique général avec une précision décente.

LiveCodeBench mesure la capacité de programmation dans des scénarios de codage. Un score de 50 % signifie que QwQ-32B-Preview peut gérer les bases du codage et suivre des instructions claires, mais qu'il peut avoir des difficultés avec des tâches plus compliquées.

QwQ est très fort lorsqu'il s'agit de résoudre des problèmes structurés et d'utiliser la logique, comme le montrent les scores obtenus au GPQA et au MATH-500. Il se débrouille bien en mathématiques et en sciences, mais les problèmes créatifs ou non conventionnels, comme ceux de l'AIME, lui posent plus de difficultés. Ses compétences en matière de programmation sont correctes mais pourraient être améliorées lorsqu'il s'agit de tâches de codage compliquées ou peu claires.

Regardons maintenant les métriques de QwQ 32B-preview avec les métriques de DeepSeek et d'autres modèles pour comparaison :

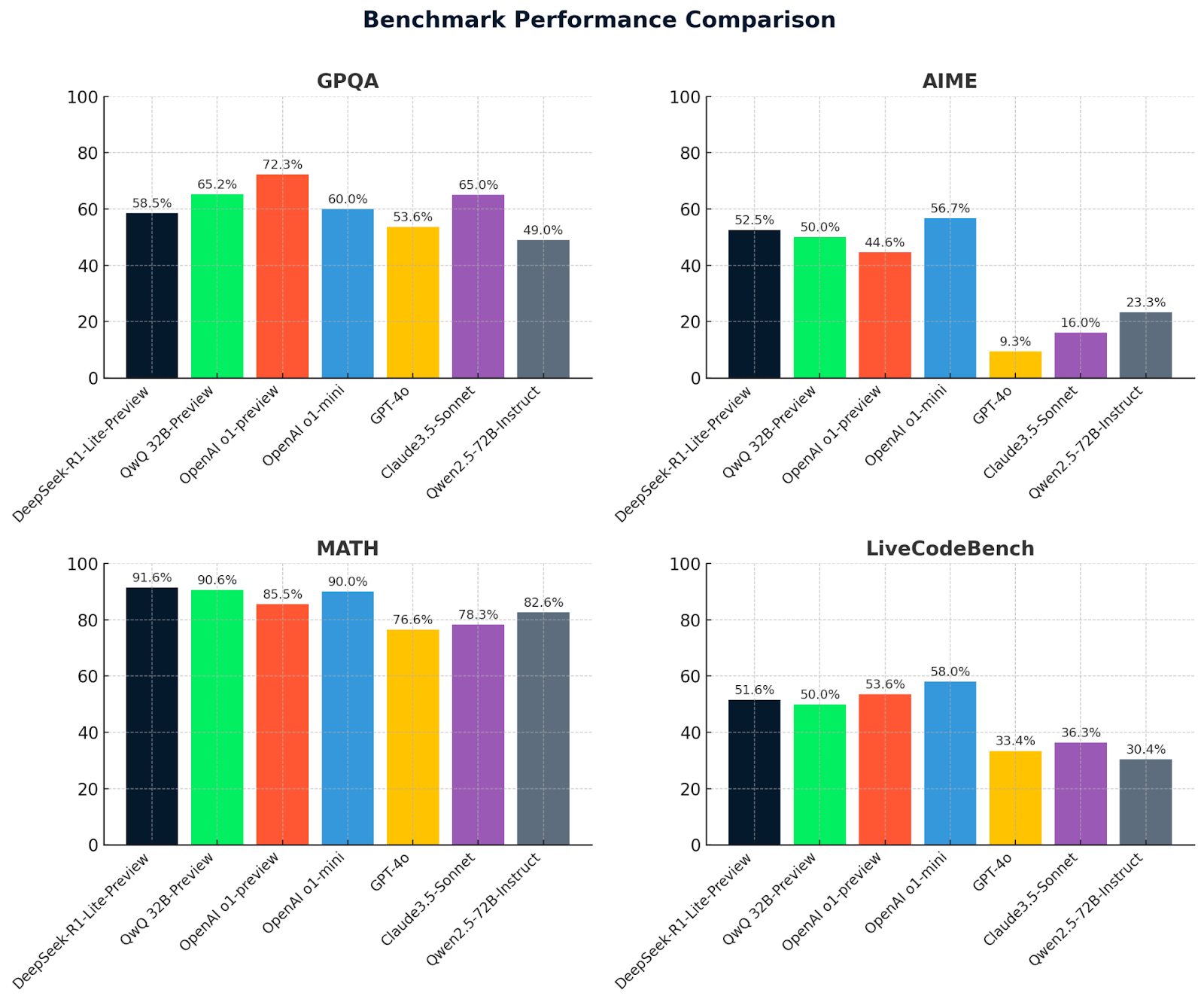
Ces graphiques permettent de comparer clairement les performances des modèles sur quatre critères de référence : GPQA, AIME, MATH et LiveCodeBench. DeepSeek-R1-Lite-Preview se distingue par ses excellents résultats, en particulier en MATH (91,6 %), ce qui témoigne de ses capacités en matière de raisonnement avancé et de résolution de problèmes.

QwQ-32B-preview obtient de bons résultats sur l'ensemble des critères, en particulier en MATH (90,6 %), ce qui démontre ses solides capacités de raisonnement mathématique et général. D'autres modèles comme OpenAI O1-preview et Claude 3.5-Sonnet présentent des forces variées, mais sont généralement derrière QwQ-32B-preview et DeepSeek dans des domaines clés, ce qui met en évidence l'avantage concurrentiel de ces deux modèles de pointe.

Conclusion

Le test de QwQ-32B-Preview a été très amusant, et j'espère ne pas avoir été trop partial - même si je dois admettre que DeepSeek-R1-Lite-Preview m'a vraiment impressionné ! 

QwQ-32B-Preview est clairement un modèle fort avec des capacités étonnantes, mais il n'est pas parfait et la réponse finale donnée par le modèle ne correspond pas toujours à la réponse finale dans le processus de raisonnement, qui avait souvent une meilleure solution que ce qui était réellement présenté.

Avez-vous essayé QwQ ? Qu'en pensez-vous ? Le préférez-vous à DeepSeek ? Et qui sait, peut-être que le prochain grand modèle sera celui qui surpassera tous les autres dans tous les domaines de référence. L'évolution de ces outils est passionnante !