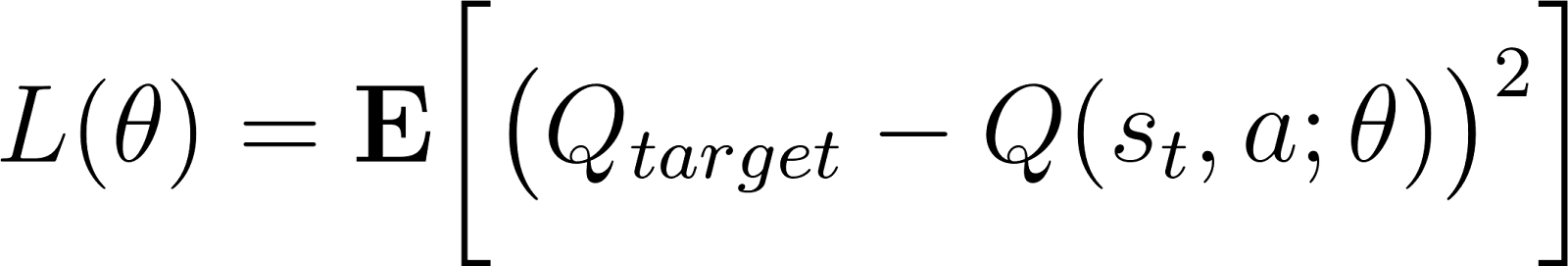programa
El aprendizaje por refuerzo (RL) es un paradigma de machine learning en el que un agente aprende a tomar las decisiones correctas interactuando con un entorno externo. El entorno te recompensa cuando actúas correctamente.
El objetivo del agente es maximizar las recompensas acumuladas. En muchos problemas prácticos, la retroalimentación al agente proviene de un humano; esto se denomina RL con retroalimentación humana (RLHF).
RLHF se utiliza habitualmente para ajustar los LLM con el fin de que sus resultados se ajusten a los valores y preferencias humanos. Cuando se utiliza una IA para proporcionar retroalimentación, se denomina RL con retroalimentación de IA.
El agente utiliza la función acción-valor para evaluar qué acción elegir en cada paso. Una función de valor de acción optimizada ayuda al agente a elegir la mejor acción en cada paso para maximizar sus recompensas acumuladas.
En este tutorial, presentaré la función acción-valor, explicaré su papel en el RL y te mostraré cómo implementarla desde cero.
¿Qué es una función acción-valor?
La función valor-acción (Q) estima la recompensa acumulada esperada (rendimiento) que se obtiene al realizar una acción específica (a) en un estado concreto (s) y siguiendo la política π a a partir de ese momento. Se denota como Qπ(s,a). Cuando es obvio que el agente está siguiendo la política óptima, se expresa de forma más sencilla como Q(s,a).
La función de valor de acción se utiliza para elegir la acción que conduce al mayor rendimiento a partir de un estado dado. La política óptima (π*) maximiza el rendimiento esperado. Así, en cada estado , la política elige la acción que conduce al mayor rendimiento esperado. Esta política óptima se expresa como π* = argmaxa Q(s,a).
La función Q se modela tradicionalmente como una tabla Q. Esta tabla almacena el valor de cada acción posible para cada estado posible del entorno. En entornos complejos, esta tabla se vuelve inmanejable por su gran tamaño y poco eficiente. Por lo tanto, modelamos la tabla Q como una red neuronal en lugar de una tabla para la mayoría de los entornos no triviales. Esta red se aproxima a la función de la tabla Q. Dado un estado, genera los valores de acción correspondientes a ese estado.
Por qué son importantes las funciones de valor de acción en el aprendizaje por refuerzo
Dada la función de valor real de la acción, la política debe elegir la acción que conduzca a las recompensas esperadas más altas. Esta estrategia se conoce como explotación. Sin embargo, la verdadera función del valor de la acción aún no se conoce durante la fase de entrenamiento. Por lo tanto, la elección de la acción se basa en información incompleta. La explotación (maximizar el rendimiento) basada en esta información incompleta puede llevar a no descubrir la verdadera función de valor de la acción y quedar atrapado en un óptimo local.
Por otro lado, una estrategia exploratoria a veces elige acciones subóptimas, que podrían conducir finalmente a un estado con un valor más alto. Esto se implementa como un ε -, donde ε es un valor pequeño. La política elige aleatoriamente una acción subóptima con una probabilidad ε y la acción que maximiza la recompensa con una probabilidad 1 - ε.
Adoptar una estrategia que equilibra la explotación y la exploración permite al agente descubrir caminos alternativos a través del entorno, lo que conduce a mejores recompensas acumulativas.
Fundamentos de los algoritmos RL
Los algoritmos RL se pueden clasificar en dos grandes categorías: 1) basados en modelos y sin modelos, y 2) dentro de la política y fuera de la política.
Algoritmos basados en modelos y sin modelos
En los métodos basados en modelos, se intenta predecir el modelo de distribución de probabilidad del entorno P(r, s' | s, a) , la probabilidad de recibir una recompensa r y alcanzar un estado s' al partir de un estado s y tomando la acción a.
Estos métodos utilizan las interacciones del agente con el entorno para ajustar el modelo (del entorno) y mejorar las recompensas y los estados previstos. De este modo, el agente puede simular el entorno a través del modelo, sin necesidad de interactuar con el entorno en cada paso.
Algunos algoritmos basados en modelos, como Dyna-Q, actualizan la función Q a través de experiencias simuladas. Estos métodos se utilizan cuando resulta caro o poco práctico que un agente sin formación tenga un gran número de interacciones con el entorno. Por ejemplo, es demasiado caro tener un robot sin entrenar que se caiga repetidamente y pueda sufrir daños.
Por el contrario, los métodos sin modelos, como el aprendizaje Q, actualizan directamente Q(s,a) siguiendo un proceso iterativo para converger en la función de valor de acción verdadera sin modelar explícitamente el entorno. El agente interactúa directamente con el entorno en cada paso. Utilizan el método de prueba y error para converger en la política óptima. Al no incluir un modelo del entorno, son más sencillos, pero requieren una gran muestra de interacciones con el entorno.
Los algoritmos sin modelo, como el aprendizaje Q, SARSA (estado-acción-recompensa-estado-acción) y DQN, aprenden explícitamente lafunción Q y la utilizan para estimar el valor de la acción en cada paso.
Algoritmos dentro y fuera de la política
Los algoritmos fuera de política (como DQN y Q-learning) utilizan la repetición de experiencias para aprender el valor de la política óptima. Tienen un amplio conjunto de interacciones (reales o simuladas) con el entorno y extraen muestras aleatorias de estas interacciones para actualizar la función Q. No utilizan la política óptima para determinar la acción en cada paso. Los métodos fuera de la política utilizan la función Q para estimar el valor de la acción para la política objetivo. Su objetivo es maximizar los rendimientos futuros actualizando la función Q en función de la recompensa más alta esperada del siguiente paso.
Algunos algoritmos basados en políticas (como SARSA) utilizan la política para seleccionar la acción en cada paso. De este modo, el agente sigue la misma política que actualiza. La función Q se actualiza en función de la recompensa que recibe el agente por seguir la política. Otros algoritmos basados en políticas, como los gradientes de políticas y el actor-crítico, no utilizan la función Q.
Por lo tanto, las funciones de valor de acción son la base de varios algoritmos de RL.
Selección óptima de acciones
El valor Q Q(s,a) representa el rendimiento esperado de tomar medidas. a en el estado s y siguiendo la política posteriormente. Por lo tanto, dada una tabla Q entrenada, seleccionar la acción que conduce al valor Q máximo en un estado particular conduce a una política óptima basada en una estrategia codiciosa (centrada en la explotación). En cada paso, el agente elige la acción a* = arg max a Q(s,a). Así, a lo largo de todo el episodio, elige el camino que maximiza las recompensas a largo plazo basándose en la explotación de la información disponible.
Métodos como el aprendizaje Q actualizan los valores Q en la tabla Q a lo largo de muchas iteraciones para converger en sus valores óptimos. Así, tras el entrenamiento, el algoritmo alcanza la política óptima que elige la acción óptima en cada estado y la ruta óptima a lo largo del episodio.
Conceptos de Inteligencia Artificial (IA) en Python
Implementación de una función acción-valor
Tras haber analizado los principios básicos y los usos de la función valor-acción, ahora te mostraré los pasos para implementarla en Python.
Paso 1: Define el entorno
Importa los paquetes necesarios, incluyendo Gymnasium y NumPy:
import gymnasium as gym
import numpy as np
import math
import randomInicializa un entorno RL desde Gymnasium. En este artículo, entrenamos a un agente RL para resolver el entorno CartPole.
env = gym.make('CartPole-v1')Paso 2: Inicializar tabla Q
El espacio de observación del CartPole tiene cuatro estados: posición del carro, velocidad del carro, ángulo del poste y velocidad angular del poste.
En este ejemplo, nos centramos únicamente en las observaciones del ángulo del polo y la velocidad angular del polo. De este modo, creamos la tabla Q discreta de la siguiente manera:
- Un estado discreto para la posición del carro: todos los valores posibles se agrupan en este único estado.
- Un estado discreto para la velocidad del carro.
- Seis estados discretos para el ángulo del polo
- Tres estados discretos para la velocidad del polo
El número de columnas se basa en el tamaño del espacio de acción, en este caso, 2.
NUM_BUCKETS = (1, 1, 6, 3)
NUM_ACTIONS = env.action_space.n
q_table = np.zeros(NUM_BUCKETS + (NUM_ACTIONS,))En el entorno CartPole, el espacio de estados es continuo. El ángulo, la velocidad y la posición del poste del carro pueden variar continuamente. El espacio de acción es discreto: puedes empujar el carro hacia la izquierda o hacia la derecha.
El aprendizaje Q utilizando tablas Q solo se puede utilizar en un espacio discreto, ya que es necesario tabular explícitamente el valor Q para un conjunto de estados y acciones. Por lo tanto, el primer paso es discretizar el espacio de estados continuo.
En primer lugar, consideramos los límites superior e inferior de las variables del espacio de estados. Observamos que la velocidad del carro y la velocidad angular del poste tienen límites infinitos. Por lo tanto, establecemos artificialmente límites superiores e inferiores para estas variables de estado.
STATE_BOUNDS = list(zip(env.observation_space.low, env.observation_space.high))
STATE_BOUNDS[1] = [-0.5, 0.5]
STATE_BOUNDS[3] = [-math.radians(50), math.radians(50)]Creamos una función para discretizar los valores de estado continuos en valores discretos:
def discretize_state(state):
discrete_states = []
for i in range(len(state)):
if state[i] <= STATE_BOUNDS[i][0]:
discrete_state = 0
elif state[i] >= STATE_BOUNDS[i][1]:
discrete_state = NUM_BUCKETS[i] - 1
else:
bound_width = STATE_BOUNDS[i][1] - STATE_BOUNDS[i][0]
offset = (NUM_BUCKETS[i] - 1) * STATE_BOUNDS[i][0] / bound_width
scaling = (NUM_BUCKETS[i] - 1) / bound_width
discrete_state = int(round(scaling * state[i] - offset))
discrete_states.append(discrete_state)
return tuple(discrete_states)Paso 3: Actualiza la tabla Q.
Las ecuaciones de Bellman proporcionan la expresión para actualizar los valores Q basándose en la tasa de aprendizaje, la tasa de descuento, la recompensa que se obtiene al pasar al siguiente paso y el valor Q máximo esperado del siguiente estado. Expresa el valor esperado de un estado como la suma de dos partes:
- La recompensa inmediata al pasar al siguiente estado
- El valor esperado descontado del siguiente estado.
La ecuación de Bellman es recursiva. De este modo, es posible escribir un programa iterativo, partiendo de un estado inicial aleatorio, para encontrar la función óptima de valor de acción.
La ecuación para actualizar la tabla Q es:
En la expresión anterior:
- El estado actual es st, indicado como «
state_current» en el código. - El siguiente estado es st+1 (
state_next). - La acción tomada en el estado actual es unat (
action). - P(st, at) es el valor Q actual para el estado st y la acción at
- α es la tasa de aprendizaje.
- γ es el factor de descuento.
- rt+1 es la recompensa tras realizar la acción. at en el paso actual con el estado st. El código siguiente representa esto como
reward. - argmaxa Q(st+1, a) es el valor Q máximo del siguiente estado st+1. En el fragmento de código siguiente, esto se representa en
best_q.
El código siguiente implementa la función para actualizar la tabla Q.
def update_q(state_current, state_next, action, reward, alpha):
best_q = np.amax(q_table[state_next])
q_table[state_current + (action,)] += alpha * (reward + GAMMA*(best_q) - q_table[state_current + (action,)])
return best_qPaso 4: Forma al agente
Declara los parámetros del entrenamiento:
- El número máximo de episodios de entrenamiento
- El número máximo de pasos por episodio proviene de la documentación del entorno. Para CartPole-v1, es 500.
- El número de pasos que debe completar el agente para que el episodio se clasifique como exitoso. Lo hemos puesto a 450.
- El número de episodios correctos que el agente debe completar consecutivamente para que el entrenamiento se considere satisfactorio. Lo hemos fijado en 50.
MAX_EPISODES = 5000
MAX_STEPS = 500
SUCCESS_STEPS = 450
SUCCESS_STREAK = 50Declara los hiperparámetros:
- Los valores mínimo y máximo de la tasa de exploración, ε
- Los valores mínimo y máximo de la tasa de aprendizaje, α
- La tasa de desintegración de α y γ
- El factor de descuento, γ
EPSILON_MIN = 0.01
EPSILON_MAX = 1
ALPHA_MIN = 0.1
ALPHA_MAX = 0.5
GAMMA = 0.99
DECAY_COEFF = 25Antes de entrenar al agente, escribimos dos funciones para reducir gradualmente la tasa de aprendizaje y la tasa de exploración. Estos hiperparámetros disminuyen gradualmente en valor a lo largo del entrenamiento.
def decay_epsilon(step):
return max(EPSILON_MIN, min(EPSILON_MAX, 1.0-math.log10((step+1)/DECAY_COEFF)))
def decay_alpha(step):
return max(ALPHA_MIN, min(ALPHA_MAX, 1.0-math.log10((step+1)/DECAY_COEFF)))También escribimos una función para seleccionar la acción de forma estocástica. Primero generamos un número aleatorio.
- Si este número aleatorio es menor que ε, elegimos aleatoriamente una acción del espacio de acciones. Esta es la estrategia de exploración.
- Si el número aleatorio es mayor que ε, elegimos la acción correspondiente al valor Q máximo. Esta es la estrategia explotadora.
def select_action(state, epsilon):
if random.random() < epsilon:
action = env.action_space.sample()
else:
action = np.argmax(q_table[state])
return actionConstruimos un bucle para entrenar al agente siguiendo estos pasos:
- Obtener los valores decadentes de α, y ε para el episodio actual.
- Restablece el entorno y discretiza el espacio de observación para iniciar un entorno nuevo para el episodio.
- Ejecuta el agente en el entorno hasta que alcance el número máximo de pasos o finalice.
- Para cada paso:
- Selecciona la acción según la función
select_action()declarada anteriormente. - Ejecuta la acción en el entorno para obtener la recompensa y el siguiente estado.
- Obtén el valor Q más alto de la tabla Q.
- Actualiza la tabla Q según la función
update_q()declarada anteriormente.
El código siguiente implementa los pasos del bucle de entrenamiento:
def train():
successful_episodes = 0
for episode in range(MAX_EPISODES):
epsilon = decay_epsilon(episode)
alpha = decay_alpha(episode)
observation, _ = env.reset()
state_current = discretize_state(observation)
for step in range(MAX_STEPS):
action = select_action(state_current, epsilon)
observation, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
state_next = discretize_state(observation)
best_q = update_q(state_current, state_next, action, reward, alpha)
state_current = state_next
if done:
print("Episode %d finished after %d time steps" % (episode, step))
print("best q value: %f" % (float(best_q)))
if (step >= SUCCESS_STEPS):
successful_episodes += 1
print("=============SUCCESS=============")
else:
successful_episodes = 0
print("=============FAIL=============")
break
if successful_episodes > SUCCESS_STREAK:
breakPor último, ejecuta el bucle de entrenamiento, cierra el entorno e imprime el valor final de la tabla Q.
train()
env.close()
print(q_table)Utiliza este cuaderno de trabajo de DataLab como punto de partida para editar y ejecutar el código para Q-Learning.
Ampliación al aprendizaje profundo Q
En la sección anterior, discretizamos el espacio de observación continuo (estado) para utilizar una tabla Q. Una tabla Q grande (para entornos complejos) es ineficiente desde el punto de vista computacional. En tales casos, la función Q puede aproximarse utilizando una red neuronal. Esto se denomina red Q profunda, expresada como Q(s, a; θ), donde el parámetro θ representa los pesos de la red neuronal. Este método se denomina «aprendizaje Q profundo». En términos más generales, el RL que utiliza redes neuronales profundas se denomina aprendizaje por refuerzo profundo.
En lugar de utilizar la tabla Q para elegir la acción para cada estado, la red neuronal DQN toma el estado como entrada y devuelve el valor Q para cada acción posible en ese estado.
La red se entrena mediante métodos tradicionales (como la retropropagación) para minimizar el error de diferencia temporal (TD). El error TD δ es la diferencia entre los valores Q previstos y los valores Q objetivo (calculados como la suma de la recompensa del estado actual y el valor descontado de la recompensa máxima esperada del siguiente estado).
Cuando se implementa como una red neuronal (con parámetros de red θ), el error TD se expresa como:
Ten en cuenta que tanto los valores Q como los valores Q objetivo se calculan utilizando la misma red neuronal.
En cada iteración, se actualizan los parámetros de la red (θ). La actualización de la red (mediante retropropagación) se basa en el valor objetivo calculado utilizando el θ previo a la actualización. Cálculo de los valores objetivo con los mismos resultados actualizados en un objetivo en movimiento continuo. Esto hace que el entrenamiento sea inestable.
Para evitar el problema anterior, creamos una nueva red para calcular los valores Q objetivo. Esta es la red de destino. Se basa en los mismos parámetros que la red de políticas, pero se actualiza con menos frecuencia. Por lo tanto, el proceso de entrenamiento tiene un objetivo estable con respecto al cual aplica la retropropagación.
Si representamos los pesos de la red objetivo con θ-, la ecuación anterior se reescribe como:
Las siguientes secciones mostrarán cómo implementar y entrenar un DQN sencillo en el entorno CartPole.
Ejemplo de implementación
Instala los paquetes necesarios, incluidos Gymnasium y PyTorch.
!pip install gymnasium matplotlib torchImporta los paquetes necesarios en el entorno Python:
import gymnasium as gym
import math
import random
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple, deque
from itertools import count
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as FCrea el entorno CartPole:
env = gym.make("CartPole-v1")Inicializa el entorno y declara las constantes de Python con el tamaño de los espacios de estado y acción del entorno.
state, info = env.reset()
NUM_OBSERVATIONS = len(state)
NUM_ACTIONS = env.action_space.nDeclara una clase Python para una red neuronal simple con una sola capa oculta. El número de capas de entrada es el tamaño del espacio de estado (espacio de observación). El número de capas de salida es el número de acciones posibles que puede realizar el agente RL. Esta red simula internamente la tabla Q y predice los valores de acción dados un estado de entrada.
class DQN(nn.Module):
def __init__(self, NUM_OBSERVATIONS, NUM_ACTIONS):
super(DQN, self).__init__()
self.layer1 = nn.Linear(NUM_OBSERVATIONS, 128)
self.layer2 = nn.Linear(128, 128)
self.layer3 = nn.Linear(128, NUM_ACTIONS)
def forward(self, x):
x = F.relu(self.layer1(x))
x = F.relu(self.layer2(x))
return self.layer3(x)Crea una red de políticas y una red de objetivos. Carga la red de destino con los parámetros de la red de políticas utilizando el diccionario de estados. Inicializa un optimizador para entrenar la red neuronal.
policy_net = DQN(NUM_OBSERVATIONS, NUM_ACTIONS)
target_net = DQN(NUM_OBSERVATIONS, NUM_ACTIONS)
target_net.load_state_dict(policy_net.state_dict())
optimizer = optim.AdamW(policy_net.parameters(), lr=LR, amsgrad=True)Entrenamiento con búfer de reproducción
Los métodos RL sin modelos fuera de política, como el Q-Learning (analizado en la sección anterior) y las DQN, se entrenan utilizando una muestra aleatoria de las interacciones del agente con el entorno. Las acciones del agente y las respuestas del entorno (recompensa y estado siguiente) se recopilan y almacenan. En cada iteración del entrenamiento se selecciona una muestra aleatoria de estas interacciones para formar un lote de entrenamiento.
Declara un objeto tupla para almacenar el estado del entorno (observación) en cada interacción:
Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))Crea una clase Python para el búfer de reproducción:
class ReplayMemory(object):
def __init__(self, capacity):
self.memory = deque([], maxlen=capacity)
def push(self, *args):
self.memory.append(Transition(*args))
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)Crea un objeto de memoria para almacenar un gran número de interacciones. Estas interacciones se utilizan para entrenar al agente.
memory = ReplayMemory(10000)Antes del entrenamiento, declara los parámetros y los hiperparámetros:
- Parámetros:
- Tamaño del lote
- Número máximo de episodios de entrenamiento
- Hiperparámetros:
- Tasa de aprendizaje (
LR) - Factor de descuento (
GAMMA) - La frecuencia de actualización de la red de destino (
TAU) - Valores iniciales y finales de la tasa de exploración y la tasa de decaimiento (
EPS_START,EPS_ENDyEPS_DECAY).
MAX_EPISODES = 600
BATCH_SIZE = 128
GAMMA = 0.99
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 1000
TAU = 0.005
LR = 1e-4Escribe una función para seleccionar la acción en función de la tasa de exploración, siguiendo estos pasos:
- Calcula la tasa de exploración basándote en el número de pasos del episodio (y los valores inicial y final y la tasa de decaimiento de la tasa de exploración).
- Genera un número aleatorio.
- Si el número aleatorio es mayor que la tasa de exploración, elige la acción predicha por la red de políticas.
- Si es inferior a la tasa de exploración, elige una acción aleatoria del espacio de acciones.
steps_done = 0
def select_action(state):
global steps_done
sample = random.random()
eps_threshold = EPS_END + (EPS_START - EPS_END) * \
math.exp(-1. * steps_done / EPS_DECAY)
steps_done += 1
if sample > eps_threshold:
with torch.no_grad():
action = policy_net(state).max(1).indices.view(1, 1)
return action
else:
action = torch.tensor([[env.action_space.sample()]], dtype=torch.long)
return actionEscribe la función para optimizar el modelo basándote en estos pasos:
- Crea un lote utilizando una muestra aleatoria de las interacciones del agente con el entorno. Cada elemento de la muestra corresponde a un intervalo de tiempo. Contiene:
- El estado actual del medio ambiente
- La acción del agente
- La recompensa recibida
- El siguiente estado
- En CartPole, se espera que el agente continúe manipulando el palo del carro sin detenerse (sin golpear los bordes ni caerse). Por lo tanto, solo tenemos en cuenta aquellas interacciones que no conducen a un estado terminal. Creamos una máscara (
non_final_mask) para identificar aquellos estados que no van seguidos de un estado terminal. - Identifica aquellos estados que no van seguidos de un estado terminal (
non_final_next_states). - Obtener los valores de acción del estado para todos los estados actuales st pasando los estados actuales a la red de políticas.
- Obtener los valores de acción esperados para todos los estados siguientes. st+1 pasando los estados siguientes a la red de destino y utilizandola ecuación:
- Calcula la pérdida basándote en la diferencia entre los valores de acción y los valores de acción esperados:
- Retropropaga las pérdidas para calcular losgradientes.
- Recorta los valores del gradiente y actualiza la red de políticas para garantizar un entrenamiento estable.
El siguiente código muestra cómo implementar el optimizador:
batch = 0
def optimize_model():
global batch
if len(memory) < BATCH_SIZE:
return
transitions = memory.sample(BATCH_SIZE)
batch = Transition(*zip(*transitions))
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,
batch.next_state)), dtype=torch.bool)
non_final_next_states = torch.cat([s for s in batch.next_state
if s is not None])
state_batch = torch.cat(batch.state)
action_batch = torch.cat(batch.action)
reward_batch = torch.cat(batch.reward)
state_action_values = policy_net(state_batch).gather(1, action_batch)
next_state_values = torch.zeros(BATCH_SIZE )
with torch.no_grad():
next_state_values[non_final_mask] = target_net(non_final_next_states).max(1).values
expected_state_action_values = (next_state_values * GAMMA) + reward_batch
loss_func = nn.SmoothL1Loss()
loss = loss_func(state_action_values, expected_state_action_values.unsqueeze(1))
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_value_(policy_net.parameters(), 100)
optimizer.step()Escribe un bucle de entrenamiento para entrenar al agente:
- Restablece el entorno y comienza un nuevo episodio.
- Utiliza la función «
select_action()» para decidir la acción del agente. - Obtén la recompensa del entorno y el siguiente estado en función de la acción.
- Añade el estado, la acción, el siguiente estado y la recompensa al búfer de reproducción.
- Ejecuta el optimizador (definido anteriormente). El optimizador calcula los valores Q y la pérdida, aplicando la retropropagación para actualizar la red.
- Actualiza la red de destino según la red de políticas.
- Continúa el episodio hasta que alcance un estado terminal.
El siguiente código implementa estos pasos:
def train():
for episode in range(MAX_EPISODES):
# Initialize the environment and get its state
state, info = env.reset()
state = torch.tensor(state, dtype=torch.float32).unsqueeze(0)
for t in count():
action = select_action(state)
observation, reward, terminated, truncated, _ = env.step(action.item())
reward = torch.tensor([reward])
done = terminated or truncated
if terminated:
next_state = None
else:
next_state = torch.tensor(observation, dtype=torch.float32).unsqueeze(0)
memory.push(state, action, next_state, reward)
state = next_state
optimize_model()
target_net_state_dict = target_net.state_dict()
policy_net_state_dict = policy_net.state_dict()
for key in policy_net_state_dict:
target_net_state_dict[key] = policy_net_state_dict[key]*TAU + target_net_state_dict[key]*(1-TAU)
target_net.load_state_dict(target_net_state_dict)
if done:
episode_durations.append(t + 1)
print('episode -- ', episode)
print('count -- ', t)
#plot_durations()
breakPuedes ver, editar y ejecutar el programa de entrenamiento DQN utilizando este cuaderno de trabajo de DataLab.
Visualización de la función acción-valor
Es útil realizar un seguimiento visual del progreso del proceso de formación. Visualizar los valores de acción ayuda a reconocer dónde está fallando el entrenamiento y qué parámetros o hiperparámetros deben modificarse.
Por ejemplo, si observas visualmente que la mejora en el rendimiento del modelo es demasiado lenta, es posible que desees aumentar la tasa de aprendizaje. Si observas que el modelo está aprendiendo pero aún no se ha entrenado por completo, puede ser útil aumentar el número de episodios de entrenamiento. Si observas que el entrenamiento es inestable, es posible que desees reducir la tasa de aprendizaje o ajustar el coeficiente de exploración o la tasa de actualización de la red objetivo (TAU).
Además de los valores Q, también puede ser útil gráficar el número de pasos exitosos en cada episodio. En el aprendizaje Q utilizando tablas Q, los valores Q se almacenan explícitamente. Sin embargo, cuando se utilizan DQN, los valores Q no se almacenan explícitamente. La red genera la acción en función de sus pesos y del estado. Por lo tanto, realizar un seguimiento del número de pasos correctos en cada episodio puede ser más significativo para el DQN.
Los siguientes pasos describen cómo gráficar los valores Q y el número de pasos exitosos por episodio para entrenar el algoritmo de aprendizaje Q:
- Crea dos arreglos vacíos al inicio del entrenamiento:
q_vals- para almacenar los valores Q en cada paso de cada episodio.success_steps- para almacenar el número de pasos correctos en cada episodio.- En cada paso (en todos los episodios):
- Añade el valor Q de ese paso al arreglo «
q_vals». - Después de que finalice cada episodio, añade al arreglo «
success_steps» el número de pasos completados con éxito en ese episodio. - Grafica ambos arreglos.
El código siguiente muestra el bucle de entrenamiento Q-Learning (utilizando tablas Q) (mostrado en la sección anterior) actualizado para realizar un seguimiento de los valores Q y el número de pasos correctos:
q_vals = []
success_steps = []
def train():
global q_vals
global success_steps
successful_episodes = 0
for episode in range(MAX_EPISODES):
epsilon = decay_epsilon(episode)
alpha = decay_alpha(episode)
observation, _ = env.reset()
state_current = discretize_state(observation)
for step in range(MAX_STEPS):
action = select_action(state_current, epsilon)
observation, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
state_next = discretize_state(observation)
best_q = update_q(state_current, state_next, action, reward, alpha)
q_vals.append(best_q)
state_current = state_next
if done:
q_vals.append(best_q)
success_steps.append(step)
print("Episode %d finished after %d time steps" % (episode, step))
print("best q value: %f" % (float(best_q)))
if (step >= SUCCESS_STEPS):
successful_episodes += 1
else:
successful_episodes = 0
break
if successful_episodes > SUCCESS_STREAK:
print("Training successful")
returnEl siguiente fragmento muestra cómo gráficar los valores Q en cada episodio:
def plot_q():
plt.plot(q_vals)
plt.title('Q-values over training steps')
plt.xlabel('Training steps')
plt.ylabel('Q-value')
plt.show()El siguiente fragmento muestra cómo gráficar el número de pasos exitosos en cada episodio:
def plot_steps():
plt.plot(success_steps)
plt.title('Successful steps over training episodes')
plt.xlabel('Training episode')
plt.ylabel('Successful steps')
plt.show()- El cuaderno de trabajo de DataLab para implementar el aprendizaje Q utilizando funciones de valor de acción también incluye el código para gráficar los valores Q y los pasos exitosos por episodio.
- El cuaderno para implementar DQN también incluye el código para gráficar el número de pasos exitosos por episodio.
Evaluación del rendimiento de los agentes
Es necesario especificar los criterios para decidir si el agente ha sido formado con éxito y en qué momento. En el aprendizaje automático tradicional, el objetivo del entrenamiento es minimizar la pérdida: la diferencia entre los valores previstos y los reales. En RL, el objetivo es maximizar la recompensa acumulada. El entrenamiento se considera exitoso cuando el agente obtiene las máximas recompensas del entorno.
Los entornos como CartPole no terminan hasta que alcanzan una condición terminal, como chocar contra los bordes o permitir que el cartpole se incline excesivamente. En tales casos, un agente entrenado puede continuar interactuando con el entorno de forma indefinida. Por lo tanto, el número máximo de pasos correctos se impone de forma artificial. En el caso de CartPole-v1 de Gymnasium, el episodio finaliza cuando alcanza los 500 pasos de tiempo sin terminar.
Evaluamos el rendimiento del agente a lo largo de episodios consecutivos para determinar si el entrenamiento ha sido satisfactorio. Por ejemplo:
- El agente debe ser capaz de completar más de un número mínimo de pasos (
SUCCESS_STEPS) de media en los últimos N episodios. En los ejemplos de este artículo, hemos establecido este umbral en 450. - El agente puede cruzar el umbral en N episodios consecutivos (
SUCCESS_STREAK). En este ejemplo, establecemos N en 50.
Como ejemplo práctico, considera este fragmento del bucle de entrenamiento DQN mostrado anteriormente.
if done:
episode_durations.append(t + 1)
print('episode -- ', episode)
average_steps = sum(episode_durations[-SUCCESS_STREAK:])/SUCCESS_STREAK
print('average steps over last 50 episodes -- ', average_steps)
if average_steps > SUCCESS_STEPS:
print("training successful.")
return
breakAyuda a evaluar el rendimiento del agente basándose en la ejecución de los siguientes pasos al final (estado terminal) de cada episodio de entrenamiento:
- Añade el número total de pasos de este episodio (antes de que finalizara) a un arreglo. Este arreglo programa el número total de pasos en cada episodio.
- Calcula el promedio de los últimos N valores de este arreglo. En este ejemplo, N (
SUCCESS_STREAK) es 50. Así pues, calculamos el promedio de pasos en los últimos 50 episodios. - Si este promedio es mayor que un umbral (
SUCCESS_STEPS), finalizamos el entrenamiento. En este ejemplo, este umbral se establece en 450 pasos.
Prácticas recomendadas para utilizar funciones de valor de acción
A continuación, se incluyen algunas prácticas recomendadas que puedes seguir para obtener mejores resultados de la implementación de la función de valor de acción.
Equilibrar la exploración y la explotación
Dada la función de valor real de la acción, el agente puede maximizar los rendimientos esperados adoptando una estrategia codiciosa, basada en elegir la acción con el valor más alto en cada paso. Esto se denomina explotación de la información disponible. Sin embargo, el uso de una estrategia codiciosa con una función de valor de acción no entrenada (que aún no representa los valores de acción reales) te llevará a quedarte atascado en un óptimo local.
Durante el entrenamiento, es importante tanto explorar el entorno como aprovechar la información disponible.
En las etapas iniciales del proceso de entrenamiento, la información disponible se basa en una función de valor aleatorio. Por lo tanto, esta información no es muy valiosa (para explotar con una estrategia codiciosa). Es más importante explorar el entorno para descubrir las recompensas de las diversas acciones posibles en diferentes estados.
A medida que se actualiza la tabla Q (o se entrena el DQN), resulta viable explotar parcialmente la información disponible para maximizar las recompensas. Hacia las etapas finales del entrenamiento, el agente converge en la función de valor real; una exploración más profunda puede ser perjudicial. Por lo tanto, el agente da prioridad a explotar la función de valor conocida.
Ajusta los hiperparámetros.
Al igual que con cualquier modelo de machine learning, los hiperparámetros son importantes para entrenar con éxito los algoritmos de RL. En el caso del Q-Learning y las DQN, los hiperparámetros son épsilon (tasa de exploración), alfa (tasa de aprendizaje) y gamma (tasa de descuento).
- ε ( epsilon) controla el equilibrio entre exploración y explotación (como se ha comentado anteriormente). Cuanto mayor sea el valor de épsilon, más importante será la exploración en relación con la explotación. Al inicio de la formación, toma un valor alto, como 0,9, que se reduce gradualmente hasta alcanzar un valor pequeño, como 0,05, hacia el final de la formación.
- α ( alfa) es la tasa de aprendizaje (LR). Controla cuánto cambian los parámetros de la red neuronal (en el caso de las DQN) o los valores de la tabla Q en cada iteración del entrenamiento. Si el LR es demasiado alto, el modelo se vuelve inestable y no converge. Por otro lado, un LR bajo provoca una convergencia lenta. También es habitual comenzar con un valor alto de LR al inicio del proceso de entrenamiento, cuando el agente necesita explorar el entorno. A medida que se acerca a los valores reales de la función Q, el LR se reduce para ayudar a la red a converger.
- γ (gamma) es la tasa de descuento. Decide la importancia de las recompensas en pasos posteriores frente a las recompensas inmediatas. Un valor alto de gamma significa que las recompensas posteriores son importantes. Un valor gamma de 0 significa que solo es importante la recompensa del paso de tiempo actual, y las recompensas posteriores no tienen importancia. En algoritmos como el aprendizaje Q, el rendimiento total se basa en las recompensas obtenidas a lo largo de todo el episodio. Por lo tanto, es habitual utilizar una tasa de descuento elevada, como 0,99.
Por último, ten en cuenta que el entrenamiento RL es sensible a los valores aleatorios iniciales. Si el entrenamiento no converge, suele ser útil utilizar una semilla aleatoria diferente o volver a ejecutar el entrenamiento para que comience con un conjunto diferente de valores iniciales aleatorios.
Empieza con entornos sencillos
Entrenar agentes RL para entornos complejos es todo un reto. Las funciones Q se utilizan en muchos algoritmos diferentes, por lo que es esencial desarrollar cierta intuición para entrenar agentes RL basados en el aprendizaje Q. La mejor manera de hacerlo es practicando las técnicas en entornos más sencillos, como CartPole, antes de aplicar métodos similares en entornos más complejos.
Además, los entornos complejos son más costosos para la formación, por lo que resulta más económico utilizar entornos más sencillos como herramienta de aprendizaje.
Conclusión
Este artículo ha analizado los principios teóricos fundamentales de la función del valor de la acción y su importancia en el RL. Hemos visto cómo se utilizan las funciones de valor de acción en el aprendizaje Q y el aprendizaje Q profundo, y hemos implementado ambos métodos paso a paso en Python.
Para continuar tu aprendizaje, te recomiendo encarecidamenteel curso Deep Reinforcement Learning in Python.
Obtén una certificación superior en IA
Preguntas frecuentes
¿Cuál es la diferencia entre la función de valor y la función de valor de acción en RL?
La función de valor estima el rendimiento esperado de un estado, mientras que la función de valor de acción (función Q) estima el rendimiento de realizar una acción específica en un estado y seguir la política a partir de ese momento. La función de valor de acción proporciona una orientación más detallada para la toma de decisiones.
¿Por qué es importante la función acción-valor en el aprendizaje Q?
El aprendizaje por cuestiones utiliza la función de valor de acción para guiar al agente hacia las acciones que producen las recompensas esperadas más altas. La función permite el aprendizaje fuera de la política y ayuda al agente a converger en la estrategia óptima con el tiempo.
¿Cómo se relaciona la función acción-valor con la ecuación de Bellman?
La ecuación de Bellman proporciona una formulación recursiva para actualizar los valores Q basándose en la recompensa inmediata y la recompensa futura máxima descontada. Es la base para aprender la función acción-valor de forma iterativa.
¿Puedo utilizar la función acción-valor en espacios de estado continuos?
Sí, pero las tablas Q resultan poco prácticas en espacios continuos. En tales casos, se utilizan redes Q profundas (DQN) para aproximar la función de valor de acción con una red neuronal en lugar de tablas explícitas.
¿Cuál es el papel de la exploración en la estimación de la función de valor de acción?
La exploración garantiza que el agente no converja prematuramente en una política subóptima. Ayuda al agente a recopilar experiencias diversas, que son esenciales para estimar con precisión la función de valor de acción durante el entrenamiento.
¿Cómo afecta la estrategia ε-greedy al aprendizaje del valor Q?
La estrategia ε-greedy equilibra la exploración y la explotación. Con una probabilidad ε, el agente explora nuevas acciones y, con 1–ε, aprovecha la mejor acción conocida en ese momento. Esta compensación mejora la estabilidad y la convergencia del aprendizaje.
¿Cuándo se debe cambiar del aprendizaje Q al aprendizaje Q profundo?
Cuando el entorno tiene un espacio de estado grande o continuo, mantener una tabla Q resulta ineficaz. El aprendizaje profundo Q sustituye la tabla por una red neuronal que se adapta mejor a entornos complejos.
¿Cómo puedo visualizar una función de valor de acción durante el entrenamiento?
Puedes gráficar los valores Q máximos a lo largo del tiempo o programar recompensas por episodios para supervisar el progreso del aprendizaje. La visualización ayuda a diagnosticar problemas como una convergencia deficiente o una exploración insuficiente.
¿Cuáles son los principales retos a la hora de entrenar una función de valor de acción?
Entre los retos se incluyen la inestabilidad en la formación debido a objetivos cambiantes, una exploración deficiente y una configuración subóptima de los hiperparámetros. El uso de técnicas como la memoria de reproducción y las redes de objetivos ayuda a mitigar estos problemas.
¿Se utiliza la función de valor de acción en los algoritmos on-policy?
Sí, algoritmos como SARSA utilizan la función de valor de acción, pero la actualizan utilizando la acción realmente tomada por la política actual. Esto contrasta con métodos fuera de la política como el aprendizaje Q, que utilizan el valor Q máximo del siguiente estado.
Arun es un antiguo fundador de startups que disfruta construyendo cosas nuevas. Actualmente explora los fundamentos técnicos y matemáticos de la Inteligencia Artificial. Le encanta compartir lo que ha aprendido, así que escribe sobre ello.
Además de en DataCamp, puedes leer sus publicaciones en Medium, Airbyte y Vultr.