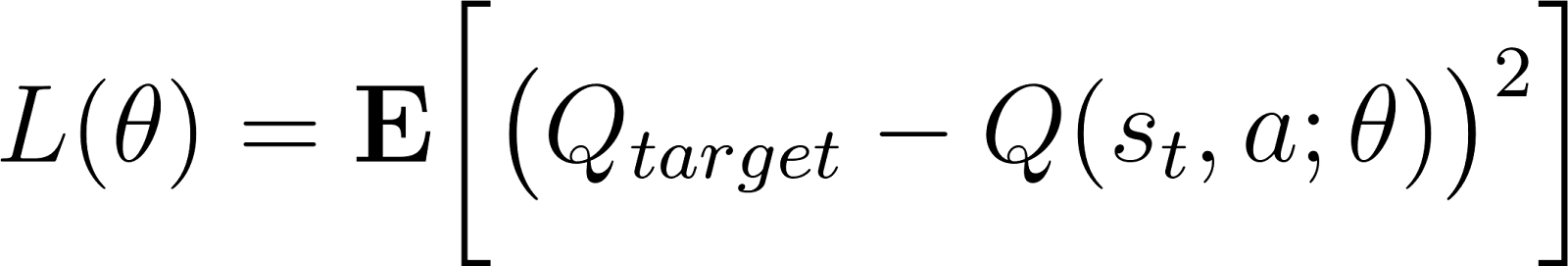Cursus
L'apprentissage par renforcement (RL) est un paradigme d'apprentissage automatique dans lequel un agent apprend à prendre les bonnes décisions en interagissant avec un environnement externe. L'environnement fournit un retour d'information, sous forme de récompenses, lorsque l'on prend les bonnes mesures.
L'objectif de l'agent est de maximiser les récompenses cumulées. Dans de nombreux cas pratiques, le retour d'information à l'agent provient d'un être humain ; on parle alors de RL avec retour d'information humain (RLHF).
Le RLHF est couramment utilisé pour ajuster les LLMs afin qu'ils fournissent des résultats alignés sur les valeurs et les préférences humaines. Lorsqu'une IA est utilisée pour fournir un retour d'information, on parle de RL avec retour d'information IA.
L'agent utilise la fonction action-valeur pour évaluer quelle action choisir à chaque étape. Une fonction de valeur d'action optimisée aide l'agent à choisir la meilleure action à chaque étape afin de maximiser ses récompenses cumulées.
Dans ce tutoriel, je vais vous présenter la fonction action-valeur, vous expliquer son rôle dans le RL et vous montrer comment la mettre en œuvre à partir de zéro.
Qu'est-ce qu'une fonction action-valeur ?
La fonction action-valeur (Q) estime la récompense cumulative attendue (rendement) obtenue en prenant une action spécifique (a) dans un état particulier (s) et en suivant ensuite la politique π . Il est désigné par Qπ(s,a). Lorsqu'il est évident que l'agent suit la politique optimale, cela s'exprime plus simplement comme suit : Q(s,a).
La fonction action-valeur est utilisée pour sélectionner l'action qui conduit au rendement le plus élevé à partir d'un état donné. La politique optimale (π*) maximise le rendement attendu. Ainsi, à chaque état ,, la politique choisit l'action qui conduit au rendement attendu le plus élevé. Cette politique optimale est exprimée par π* = argmaxa Q(s,a).
La fonction Q est traditionnellement modélisée sous la forme d'un tableau Q. Ce tableau stocke la valeur de chaque action possible pour chaque état possible de l'environnement. Dans des environnements complexes, ce tableau devient trop volumineux et inefficace. Ainsi, nous modélisons le tableau Q comme un réseau neuronal plutôt que comme un tableau pour la plupart des environnements non triviaux. Ce réseau se rapproche de la fonction du tableau Q. À partir d'un état, il génère les valeurs d'action correspondant à cet état.
Pourquoi les fonctions action-valeur sont importantes dans le RL
Compte tenu de la fonction de valeur d'action réelle, la politique doit choisir l'action qui conduit aux récompenses attendues les plus élevées. Cette stratégie est connue sous le nom d'exploitation. Cependant, la véritable fonction de valeur d'action n'est pas encore connue pendant la phase d'entraînement. Par conséquent, le choix de l'action repose sur des informations incomplètes. L'exploitation (maximisation du rendement) basée sur ces informations incomplètes peut empêcher de découvrir la véritable fonction de valeur d'action et conduire à un optimum local.
D'un autre côté, une stratégie exploratoire choisit parfois des actions sous-optimales, qui peuvent finalement conduire à un état ayant une valeur plus élevée. Ceci est implémenté comme un ε - gloutonne, où ε est une petite valeur. La politique choisit de manière aléatoire une action sous-optimale avec une probabilité ε et l'action maximisant la récompense avec une probabilité 1 - ε.
Adopter une stratégie qui équilibre l'exploitation et l'exploration permet à l'agent de découvrir d'autres voies dans l'environnement, ce qui conduit à de meilleures récompenses cumulées.
Fondements des algorithmes RL
Les algorithmes RL peuvent être classés en deux grandes catégories : 1) basées sur un modèle et sans modèle, et 2) conformes à la politique et non conformes à la politique.
Algorithmes basés sur des modèles et sans modèles
Dans les méthodes basées sur des modèles, vous essayez de prédire le modèle de distribution de probabilité de l'environnement. P(r, s' | s, a) - la probabilité de recevoir une récompense r et d'atteindre un état s' lorsque l'on part d'un état s et en prenant l'action a.
Ces méthodes utilisent les interactions de l'agent avec l'environnement pour affiner le modèle (de l'environnement) et améliorer les récompenses et les états prédits. Ainsi, l'agent peut simuler l'environnement via le modèle, sans nécessairement avoir à interagir avec l'environnement à chaque étape.
Certains algorithmes basés sur des modèles, tels que Dyna-Q, actualisent la fonction Q à l'aide d'expériences simulées. Ces méthodes sont utilisées lorsqu'il est coûteux ou peu pratique de faire interagir un agent non formé avec l'environnement à de nombreuses reprises. Par exemple, il est trop coûteux de disposer d'un robot non formé qui tombe à plusieurs reprises et risque d'être endommagé.
En revanche, les méthodes sans modèle telles que l'apprentissage par renforcement Q mettent directement à jour Q(s,a) à la suite d'un processus itératif afin de converger vers la véritable fonction de valeur d'action sans modéliser explicitement l'environnement. L'agent interagit directement avec l'environnement à chaque étape. Ils procèdent par essais et erreurs pour aboutir à la politique optimale. Comme elles ne font pas appel à un modèle de l'environnement, elles sont plus simples, mais nécessitent un large échantillon d'interactions avec l'environnement.
Les algorithmes sans modèle, tels que l'apprentissage Q, SARSA (State-Action-Reward-State-Action) et DQN, apprennent explicitement lafonction Q et l'utilisent pour estimer la valeur de l'action à chaque étape.
Algorithmes conformes et non conformes à la politique
Les algorithmes hors politique (tels que les DQN et le Q-learning) utilisent la relecture d'expériences pour apprendre la valeur de la politique optimale. Ils disposent d'un large éventail d'interactions (réelles ou simulées) avec l'environnement et prélèvent des échantillons aléatoires de ces interactions pour mettre à jour la fonction Q. Ils n'utilisent pas la politique optimale pour déterminer l'action à entreprendre à chaque étape. Les méthodes hors politique utilisent la fonction Q pour estimer la valeur de l'action pour la politique cible. Ils visent à maximiser les rendements futurs en mettant à jour la fonction Q en fonction de la récompense la plus élevée attendue à l'étape suivante.
Certains algorithmes basés sur les politiques (tels que SARSA) utilisent la politique pour sélectionner l'action à chaque étape. Ainsi, l'agent suit la même politique qu'il met à jour. La fonction Q est mise à jour en fonction de la récompense que l'agent reçoit pour avoir suivi la politique. D'autres algorithmes basés sur les politiques, tels que les gradients de politique et l'acteur-critique, n'utilisent pas la fonction Q.
Ainsi, les fonctions de valeur d'action constituent la base de divers algorithmes d'apprentissage par renforcement.
Sélection optimale des actions
La valeur Q Q(s,a) représente le rendement attendu d'une action a dans l'état s et en suivant la politique par la suite. Ainsi, à partir d'un tableau Q entraîné, sélectionner l'action qui conduit à la valeur Q maximale dans un état particulier conduit à une politique optimale basée sur une stratégie gloutonne (axée sur l'exploitation). À chaque étape, l'agent choisit l'action a* = arg max a Q(s,a). Ainsi, tout au long de l'épisode, il choisit la voie qui maximise les récompenses à long terme en exploitant les informations disponibles.
Des méthodes telles que l'apprentissage par Q mettent à jour les valeurs Q dans le tableau Q au fil de nombreuses itérations afin de converger vers leurs valeurs optimales. Ainsi, après l'entraînement, l'algorithme atteint la politique optimale qui choisit l'action optimale à partir de chaque état et le chemin optimal tout au long de l'épisode.
Concepts d'intelligence artificielle (IA) en Python
Mise en œuvre d'une fonction action-valeur
Après avoir abordé les principes fondamentaux et les utilisations de la fonction action-valeur, je vais maintenant vous présenter les étapes nécessaires à sa mise en œuvre en Python.
Étape 1 : Définir l'environnement
Veuillez importer les paquets requis, y compris Gymnasium et NumPy :
import gymnasium as gym
import numpy as np
import math
import randomInitialisez un environnement RL à partir de Gymnasium. Dans cet article, nous entraînons un agent RL à résoudre l'environnement CartPole.
env = gym.make('CartPole-v1')Étape 2 : Initialiser le tableau Q
L'espace d'observation CartPole comporte quatre états : la position du chariot, la vitesse du chariot, l'angle du poteau et la vitesse angulaire du poteau.
Dans cet exemple, nous nous concentrons uniquement sur les observations de l'angle polaire et de la vitesse angulaire polaire. Nous créons ainsi le tableau Q discret comme suit :
- Un état distinct pour la position du chariot : toutes les valeurs possibles sont regroupées dans cet état unique.
- Un état discret pour la vitesse du chariot
- Six états distincts pour l'angle du pôle
- Trois états distincts pour la vitesse du pôle
Le nombre de colonnes dépend de la taille de l'espace d'action, dans ce cas, 2.
NUM_BUCKETS = (1, 1, 6, 3)
NUM_ACTIONS = env.action_space.n
q_table = np.zeros(NUM_BUCKETS + (NUM_ACTIONS,))Dans l'environnement CartPole, l'espace d'état est continu. L'angle, la vitesse et la position du poteau du chariot peuvent varier en continu. L'espace d'action est discret : vous pouvez pousser le chariot vers la gauche ou vers la droite.
L'apprentissage par Q-tables ne peut être utilisé que dans un espace discret, car il est nécessaire de tabuler explicitement la valeur Q pour un ensemble d'états et d'actions. La première étape consiste donc à discrétiser l'espace d'états continus.
Nous examinons tout d'abord les limites supérieures et inférieures des variables de l'espace d'état. Nous remarquons que la vitesse du chariot et la vitesse angulaire du poteau ont des limites infinies. Nous avons donc fixé artificiellement des limites supérieures et inférieures pour ces variables d'état.
STATE_BOUNDS = list(zip(env.observation_space.low, env.observation_space.high))
STATE_BOUNDS[1] = [-0.5, 0.5]
STATE_BOUNDS[3] = [-math.radians(50), math.radians(50)]Nous créons une fonction pour discrétiser les valeurs d'état continues en valeurs discrètes :
def discretize_state(state):
discrete_states = []
for i in range(len(state)):
if state[i] <= STATE_BOUNDS[i][0]:
discrete_state = 0
elif state[i] >= STATE_BOUNDS[i][1]:
discrete_state = NUM_BUCKETS[i] - 1
else:
bound_width = STATE_BOUNDS[i][1] - STATE_BOUNDS[i][0]
offset = (NUM_BUCKETS[i] - 1) * STATE_BOUNDS[i][0] / bound_width
scaling = (NUM_BUCKETS[i] - 1) / bound_width
discrete_state = int(round(scaling * state[i] - offset))
discrete_states.append(discrete_state)
return tuple(discrete_states)Étape 3 : Mettre à jour le tableau Q
Les équations de Bellman fournissent l'expression permettant de mettre à jour les valeurs Q en fonction du taux d'apprentissage, du taux d'actualisation, de la récompense obtenue à l'étape suivante et de la valeur Q maximale attendue de l'état suivant. Elle exprime la valeur attendue d'un état comme la somme de deux parties :
- La récompense immédiate pour passer à l'état suivant
- La valeur actualisée attendue de l'état suivant
L'équation de Bellman est récursive. Il est donc possible d'écrire un programme itératif, à partir d'un état initial aléatoire, afin de trouver la fonction de valeur d'action optimale.
L'équation permettant de mettre à jour le tableau Q est la suivante :
Dans l'expression ci-dessus :
- L'état actuel est st, désigné par l'
state_currente dans le code. - L'état suivant est st+1 (
state_next). - L'action entreprise dans l'état actuel est la suivante : unet (
action). - Q(st, at) est la valeur Q actuelle pour l'état st et l'action at
- α est le taux d'apprentissage.
- γ est le facteur d'actualisation.
- rt+1 est la récompense après avoir agi at dans l'étape actuelle avec l'état st. Le code ci-dessous représente cela sous la forme
reward. - argmaxa Q(st+1, a) est la valeur Q maximale de l'état suivant. st+1. Dans l'extrait de code ci-dessous, cela est représenté à l'
best_q.
Le code ci-dessous implémente la fonction permettant de mettre à jour le tableau Q.
def update_q(state_current, state_next, action, reward, alpha):
best_q = np.amax(q_table[state_next])
q_table[state_current + (action,)] += alpha * (reward + GAMMA*(best_q) - q_table[state_current + (action,)])
return best_qÉtape 4 : Former l'agent
Déclarez les paramètres de l'entraînement :
- Le nombre maximal d'épisodes d'entraînement
- Le nombre maximal de pas par épisode est indiqué dans la documentation relative à l'environnement. Pour CartPole-v1, il est de 500.
- Le nombre d'étapes que l'agent doit accomplir pour que l'épisode soit considéré comme réussi. Nous l'avons réglé à 450.
- Le nombre d'épisodes réussis que l'agent doit accomplir consécutivement pour que la formation soit considérée comme réussie. Nous l'avons fixé à 50.
MAX_EPISODES = 5000
MAX_STEPS = 500
SUCCESS_STEPS = 450
SUCCESS_STREAK = 50Déclarez les hyperparamètres :
- Les valeurs minimale et maximale du taux d'exploration, ε
- Les valeurs minimale et maximale du taux d'apprentissage, α
- Le taux de désintégration de α et γ
- Le facteur de réduction, γ
EPSILON_MIN = 0.01
EPSILON_MAX = 1
ALPHA_MIN = 0.1
ALPHA_MAX = 0.5
GAMMA = 0.99
DECAY_COEFF = 25Avant de former l'agent, nous écrivons deux fonctions pour réduire progressivement le taux d'apprentissage et le taux d'exploration. Ces hyperparamètres diminuent progressivement en valeur tout au long de l'entraînement.
def decay_epsilon(step):
return max(EPSILON_MIN, min(EPSILON_MAX, 1.0-math.log10((step+1)/DECAY_COEFF)))
def decay_alpha(step):
return max(ALPHA_MIN, min(ALPHA_MAX, 1.0-math.log10((step+1)/DECAY_COEFF)))Nous écrivons également une fonction pour sélectionner l'action de manière aléatoire. Nous générons tout d'abord un nombre aléatoire.
- Si ce nombre aléatoire est inférieur à ε, nous choisissons aléatoirement une action dans l'espace d'actions. Il s'agit de la stratégie d'exploration.
- Si le nombre aléatoire est supérieur à ε, nous choisissons l'action correspondant à la valeur Q maximale. Il s'agit d'une stratégie d'exploitation.
def select_action(state, epsilon):
if random.random() < epsilon:
action = env.action_space.sample()
else:
action = np.argmax(q_table[state])
return actionNous construisons une boucle pour former l'agent en suivant les étapes suivantes :
- Récupérez les valeurs dégradées de α, et ε pour l'épisode actuel.
- Réinitialisez l'environnement et discrétisez l'espace d'observation afin de démarrer un nouvel environnement pour l'épisode.
- Exécutez l'agent dans l'environnement jusqu'à ce qu'il atteigne le nombre maximal d'étapes ou qu'il se termine.
- Pour chaque étape :
- Sélectionnez l'action en fonction de la fonction d'
select_action()déclarée précédemment. - Exécutez l'action sur l'environnement pour obtenir la récompense et l'état suivant.
- Obtenez la valeur Q la plus élevée dans le tableau Q.
- Mettez à jour le tableau Q conformément à la fonction d'
update_q()déclarée précédemment.
Le code ci-dessous implémente les étapes de la boucle d'entraînement :
def train():
successful_episodes = 0
for episode in range(MAX_EPISODES):
epsilon = decay_epsilon(episode)
alpha = decay_alpha(episode)
observation, _ = env.reset()
state_current = discretize_state(observation)
for step in range(MAX_STEPS):
action = select_action(state_current, epsilon)
observation, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
state_next = discretize_state(observation)
best_q = update_q(state_current, state_next, action, reward, alpha)
state_current = state_next
if done:
print("Episode %d finished after %d time steps" % (episode, step))
print("best q value: %f" % (float(best_q)))
if (step >= SUCCESS_STEPS):
successful_episodes += 1
print("=============SUCCESS=============")
else:
successful_episodes = 0
print("=============FAIL=============")
break
if successful_episodes > SUCCESS_STREAK:
breakEnfin, exécutez la boucle d'apprentissage, fermez l'environnement et affichez la valeur finale du tableau Q.
train()
env.close()
print(q_table)Veuillez utiliser ce classeur DataLab comme point de départ pour modifier et exécuter le code pour l'apprentissage par Q.
Extension à l'apprentissage profond par Q
Dans la section précédente, nous avons discrétisé l'espace d'observation continu (état) afin d'utiliser un tableau Q. Un grand tableau Q (pour les environnements complexes) est inefficace sur le plan informatique. Dans de tels cas, la fonction Q peut être approximée à l'aide d'un réseau neuronal. Ceci est appelé un réseau Q profond, exprimé sous la forme Q(s, a ; θ), où le paramètre θ représente les poids du réseau neuronal. Cette méthode est appelée apprentissage profond par Q. De manière plus générale, l'apprentissage par renforcement utilisant des réseaux neuronaux profonds est appelé apprentissage par renforcement profond.
Au lieu d'utiliser le tableau Q pour choisir l'action pour chaque état, le réseau neuronal DQN prend l'état comme entrée et renvoie la valeur Q pour chaque action possible dans cet état.
Le réseau est formé à l'aide de méthodes traditionnelles (telles que la rétropropagation) afin de minimiser l'erreur de différence temporelle (TD). L'erreur TD δ correspond à la différence entre les valeurs Q prédites et les valeurs Q cibles (calculée comme la somme de la récompense de l'état actuel et de la valeur actualisée de la récompense maximale attendue de l'état suivant).
Lorsqu'elle est mise en œuvre sous forme de réseau neuronal (avec des paramètres de réseau θ), l'erreur TD s'exprime comme suit :
Veuillez noter que les valeurs Q et les valeurs Q cibles sont calculées à l'aide du même réseau neuronal.
À chaque itération, les paramètres du réseau (θ) sont mis à jour. La mise à jour du réseau (via rétropropagation) est basée sur la valeur cible calculée à l'aide du θ pré-mise à jour. Calcul des valeurs cibles avec les mêmes résultats actualisés dans une cible en mouvement continu. Cela rend l'entraînement instable.
Pour éviter ce problème, nous créons un nouveau réseau afin de calculer les valeurs Q cibles. Il s'agit du réseau cible. Il repose sur les mêmes paramètres que le réseau de politiques, mais il est mis à jour moins fréquemment. Ainsi, le processus d'apprentissage dispose d'un objectif stable par rapport auquel il applique la rétropropagation.
Si nous représentons les poids du réseau cible par θ-, l'équation précédente peut être reformulée comme suit :
Les sections suivantes montrent comment implémenter et entraîner un DQN simple dans l'environnement CartPole.
Exemple de mise en œuvre
Veuillez installer les paquets requis, y compris Gymnasium et PyTorch.
!pip install gymnasium matplotlib torchImportez les paquets nécessaires dans l'environnement Python :
import gymnasium as gym
import math
import random
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple, deque
from itertools import count
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as FVeuillez créer l'environnement CartPole :
env = gym.make("CartPole-v1")Initialisez l'environnement et déclarez les constantes Python avec la taille des espaces d'état et d'action de l'environnement.
state, info = env.reset()
NUM_OBSERVATIONS = len(state)
NUM_ACTIONS = env.action_space.nDéclarez une classe Python pour un réseau neuronal simple avec une seule couche cachée. Le nombre de couches d'entrée correspond à la taille de l'espace d'état (espace d'observation). Le nombre de couches de sortie correspond au nombre d'actions possibles que l'agent RL peut effectuer. Ce réseau simule en interne le tableau Q et prédit les valeurs d'action données pour un état d'entrée.
class DQN(nn.Module):
def __init__(self, NUM_OBSERVATIONS, NUM_ACTIONS):
super(DQN, self).__init__()
self.layer1 = nn.Linear(NUM_OBSERVATIONS, 128)
self.layer2 = nn.Linear(128, 128)
self.layer3 = nn.Linear(128, NUM_ACTIONS)
def forward(self, x):
x = F.relu(self.layer1(x))
x = F.relu(self.layer2(x))
return self.layer3(x)Élaborez un réseau de politiques et un réseau cible. Chargez le réseau cible avec les paramètres du réseau de politiques à l'aide du dictionnaire d'états. Initialisez un optimiseur pour entraîner le réseau neuronal.
policy_net = DQN(NUM_OBSERVATIONS, NUM_ACTIONS)
target_net = DQN(NUM_OBSERVATIONS, NUM_ACTIONS)
target_net.load_state_dict(policy_net.state_dict())
optimizer = optim.AdamW(policy_net.parameters(), lr=LR, amsgrad=True)Formation avec tampon de relecture
Les méthodes d'apprentissage par renforcement sans modèle hors politique, telles que l'apprentissage par Q (abordé dans la section précédente) et les DQN, sont entraînées à l'aide d'un échantillon aléatoire des interactions de l'agent avec l'environnement. Les actions de l'agent et les réponses de l'environnement (récompense et état suivant) sont collectées et stockées. Un échantillon aléatoire de ces interactions est sélectionné à chaque itération de l'entraînement afin de former un lot d'entraînement.
Déclarez un objet tuple pour stocker l'état de l'environnement (observation) dans chaque interaction :
Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))Créez une classe Python pour le tampon de relecture :
class ReplayMemory(object):
def __init__(self, capacity):
self.memory = deque([], maxlen=capacity)
def push(self, *args):
self.memory.append(Transition(*args))
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)Créez un objet mémoire pour stocker un grand nombre d'interactions. Ces interactions sont utilisées pour former l'agent.
memory = ReplayMemory(10000)Avant l'entraînement, veuillez déclarer les paramètres et les hyperparamètres :
- Paramètres :
- Taille du lot
- Nombre maximal de séances d'entraînement
- Hyperparamètres :
- Taux d'apprentissage (
LR) - Facteur de réduction (
GAMMA) - Le taux de mise à jour du réseau cible (
TAU) - Valeurs initiales et finales du taux d'exploration et du taux de décroissance (
EPS_START,EPS_ENDetEPS_DECAY)
MAX_EPISODES = 600
BATCH_SIZE = 128
GAMMA = 0.99
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 1000
TAU = 0.005
LR = 1e-4Écrivez une fonction permettant de sélectionner l'action en fonction du taux d'exploration, en suivant les étapes suivantes :
- Calculez le taux d'exploration en fonction du nombre d'étapes dans l'épisode (et des valeurs initiale et finale ainsi que du taux de décroissance du taux d'exploration).
- Générer un nombre aléatoire.
- Si le nombre aléatoire est supérieur au taux d'exploration, veuillez sélectionner l'action prédite par le réseau de politiques.
- Si elle est inférieure au taux d'exploration, veuillez sélectionner une action aléatoire dans l'espace d'action.
steps_done = 0
def select_action(state):
global steps_done
sample = random.random()
eps_threshold = EPS_END + (EPS_START - EPS_END) * \
math.exp(-1. * steps_done / EPS_DECAY)
steps_done += 1
if sample > eps_threshold:
with torch.no_grad():
action = policy_net(state).max(1).indices.view(1, 1)
return action
else:
action = torch.tensor([[env.action_space.sample()]], dtype=torch.long)
return actionÉcrivez la fonction permettant d'optimiser le modèle en suivant ces étapes :
- Créez un lot à partir d'un échantillon aléatoire des interactions de l'agent avec l'environnement. Chaque élément de l'échantillon correspond à un pas de temps. Il contient :
- L'état actuel de l'environnement
- L'action de l'agent
- La récompense reçue
- L'État suivant
- Dans CartPole, l'agent doit continuer à manipuler le poteau du chariot sans s'arrêter (sans heurter les bords ni tomber). Par conséquent, nous ne prenons en compte que les interactions qui ne conduisent pas à un état terminal. Nous créons un masque (
non_final_mask) pour identifier les états qui ne sont pas suivis d'un état terminal. - Identifiez les états qui ne sont pas suivis d'un état terminal (
non_final_next_states). - Obtenir les valeurs d'action d'état pour tous les états actuels st en transmettant les états actuels au réseau de politiques.
- Obtenir les valeurs d'action attendues pour tous les états suivants st+1 en transmettant les états suivants au réseau cible et en utilisantl'équation suivante :
- Calculez la perte en fonction de la différence entre les valeurs d'action et les valeurs d'action attendues :
- Rétropropagation des pertes pour calculer lesgradients.
- Clipez les valeurs de gradient et mettez à jour le réseau de politiques pour garantir un apprentissage stable.
Le code ci-dessous montre comment implémenter l'optimiseur :
batch = 0
def optimize_model():
global batch
if len(memory) < BATCH_SIZE:
return
transitions = memory.sample(BATCH_SIZE)
batch = Transition(*zip(*transitions))
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,
batch.next_state)), dtype=torch.bool)
non_final_next_states = torch.cat([s for s in batch.next_state
if s is not None])
state_batch = torch.cat(batch.state)
action_batch = torch.cat(batch.action)
reward_batch = torch.cat(batch.reward)
state_action_values = policy_net(state_batch).gather(1, action_batch)
next_state_values = torch.zeros(BATCH_SIZE )
with torch.no_grad():
next_state_values[non_final_mask] = target_net(non_final_next_states).max(1).values
expected_state_action_values = (next_state_values * GAMMA) + reward_batch
loss_func = nn.SmoothL1Loss()
loss = loss_func(state_action_values, expected_state_action_values.unsqueeze(1))
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_value_(policy_net.parameters(), 100)
optimizer.step()Écrivez une boucle d'entraînement pour former l'agent :
- Réinitialisez l'environnement et commencez un nouvel épisode.
- Veuillez utiliser la fonction «
select_action()» pour déterminer l'action de l'agent. - Obtenez la récompense de l'environnement et l'état suivant en fonction de l'action.
- Ajoutez l'état, l'action, l'état suivant et la récompense au tampon de relecture.
- Exécutez l'optimiseur (défini ci-dessus). L'optimiseur calcule les valeurs Q et la perte, en appliquant la rétropropagation pour mettre à jour le réseau.
- Mettre à jour le réseau cible en fonction du réseau de politiques.
- Veuillez poursuivre l'épisode jusqu'à ce qu'il atteigne un état terminal.
Le code suivant met en œuvre ces étapes :
def train():
for episode in range(MAX_EPISODES):
# Initialize the environment and get its state
state, info = env.reset()
state = torch.tensor(state, dtype=torch.float32).unsqueeze(0)
for t in count():
action = select_action(state)
observation, reward, terminated, truncated, _ = env.step(action.item())
reward = torch.tensor([reward])
done = terminated or truncated
if terminated:
next_state = None
else:
next_state = torch.tensor(observation, dtype=torch.float32).unsqueeze(0)
memory.push(state, action, next_state, reward)
state = next_state
optimize_model()
target_net_state_dict = target_net.state_dict()
policy_net_state_dict = policy_net.state_dict()
for key in policy_net_state_dict:
target_net_state_dict[key] = policy_net_state_dict[key]*TAU + target_net_state_dict[key]*(1-TAU)
target_net.load_state_dict(target_net_state_dict)
if done:
episode_durations.append(t + 1)
print('episode -- ', episode)
print('count -- ', t)
#plot_durations()
breakVous pouvez afficher, modifier et exécuter le programme de formation DQN à l'aide de ce classeur DataLab.
Visualisation de la fonction action-valeur
Il est utile de suivre visuellement la progression du processus de formation. La visualisation des valeurs d'action permet d'identifier les lacunes de la formation et les paramètres ou hyperparamètres à modifier.
Par exemple, si vous constatez visuellement que l'amélioration des performances du modèle est trop lente, vous pouvez augmenter le taux d'apprentissage. Si vous remarquez que le modèle apprend mais n'est pas encore entièrement formé, il peut être utile d'augmenter le nombre d'épisodes d'entraînement. Si vous constatez que l'entraînement est instable, vous pouvez réduire le taux d'apprentissage ou ajuster le coefficient d'exploration ou le taux de mise à jour du réseau cible (TAU).
En plus des valeurs Q, il peut également être utile de représenter graphiquement le nombre d'étapes réussies dans chaque épisode. Dans l'apprentissage par Q utilisant des tables Q, les valeurs Q sont explicitement stockées. Cependant, lors de l'utilisation des DQN, les valeurs Q ne sont pas explicitement enregistrées. Le réseau génère l'action en fonction de ses poids et de l'état. Ainsi, le suivi du nombre d'étapes réussies dans chaque épisode peut être plus significatif pour le DQN.
Les étapes suivantes décrivent comment représenter graphiquement les valeurs Q et le nombre d'étapes réussies par épisode pour l'entraînement de l'algorithme d'apprentissage Q :
- Au début de l'entraînement, créez deux tableaux vides :
q_vals- pour stocker les valeurs Q à chaque étape de chaque épisode.success_steps- pour enregistrer le nombre d'étapes réussies dans chaque épisode.- À chaque étape (dans tous les épisodes) :
- Ajoutez la valeur Q pour cette étape au tableau d'
q_vals. - À la fin de chaque épisode, ajoutez au tableau d'
success_stepss le nombre d'étapes réussies dans cet épisode. - Veuillez représenter graphiquement les deux tableaux.
Le code ci-dessous montre la boucle d'apprentissage Q-Learning (utilisant des tableaux Q) (illustrée dans la section précédente) mise à jour pour suivre les valeurs Q et le nombre d'étapes réussies :
q_vals = []
success_steps = []
def train():
global q_vals
global success_steps
successful_episodes = 0
for episode in range(MAX_EPISODES):
epsilon = decay_epsilon(episode)
alpha = decay_alpha(episode)
observation, _ = env.reset()
state_current = discretize_state(observation)
for step in range(MAX_STEPS):
action = select_action(state_current, epsilon)
observation, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
state_next = discretize_state(observation)
best_q = update_q(state_current, state_next, action, reward, alpha)
q_vals.append(best_q)
state_current = state_next
if done:
q_vals.append(best_q)
success_steps.append(step)
print("Episode %d finished after %d time steps" % (episode, step))
print("best q value: %f" % (float(best_q)))
if (step >= SUCCESS_STEPS):
successful_episodes += 1
else:
successful_episodes = 0
break
if successful_episodes > SUCCESS_STREAK:
print("Training successful")
returnL'extrait ci-dessous montre comment représenter graphiquement les valeurs Q dans chaque épisode :
def plot_q():
plt.plot(q_vals)
plt.title('Q-values over training steps')
plt.xlabel('Training steps')
plt.ylabel('Q-value')
plt.show()L'extrait suivant montre comment représenter graphiquement le nombre d'étapes réussies dans chaque épisode :
def plot_steps():
plt.plot(success_steps)
plt.title('Successful steps over training episodes')
plt.xlabel('Training episode')
plt.ylabel('Successful steps')
plt.show()- Le classeur DataLab pour la mise en œuvre de l'apprentissage Q à l'aide de fonctions de valeur d'action comprend également le code permettant de représenter graphiquement les valeurs Q et les étapes réussies par épisode.
- Le cahier pour la mise en œuvre de DQN comprend également le code permettant de représenter graphiquement le nombre d'étapes réussies par épisode.
Évaluation de la performance des agents
Il est nécessaire de préciser les critères permettant de déterminer si et quand l'agent a été formé avec succès. Dans le ML traditionnel, l'objectif de l'entraînement est de minimiser la perte : la différence entre les valeurs prédites et les valeurs réelles. Dans RL, l'objectif est de maximiser la récompense cumulative. La formation est considérée comme réussie lorsque l'agent obtient le maximum de récompenses de l'environnement.
Les environnements tels que CartPole ne se terminent pas avant d'atteindre une condition terminale, comme heurter les bords ou permettre au chariot de s'incliner excessivement. Dans de tels cas, un agent qualifié peut continuer à interagir avec l'environnement indéfiniment. Ainsi, le nombre maximal de pas réussis est imposé artificiellement. Dans le cas du CartPole-v1 de Gymnasium, l'épisode se termine lorsqu'il atteint 500 étapes sans s'arrêter.
Nous évaluons les performances de l'agent au cours d'épisodes consécutifs afin de déterminer si la formation est efficace. Par exemple :
- L'agent doit être capable d'effectuer en moyenne plus qu'un nombre seuil d'étapes (
SUCCESS_STEPS) au cours des N derniers épisodes. Dans les exemples présentés dans cet article, nous avons défini ce seuil à 450. - L'agent peut franchir le seuil au cours de N épisodes consécutifs (
SUCCESS_STREAK). Dans cet exemple, nous avons défini N à 50.
À titre d'exemple pratique, considérons cet extrait de la boucle d'entraînement DQN présentée précédemment.
if done:
episode_durations.append(t + 1)
print('episode -- ', episode)
average_steps = sum(episode_durations[-SUCCESS_STREAK:])/SUCCESS_STREAK
print('average steps over last 50 episodes -- ', average_steps)
if average_steps > SUCCESS_STEPS:
print("training successful.")
return
breakIl est utile d'évaluer les performances de l'agent en fonction de l'exécution des étapes suivantes à la fin (état terminal) de chaque épisode d'entraînement :
- Ajoutez le nombre total de pas effectués dans cet épisode (avant qu'il ne se termine) à un tableau. Ce tableau suit le nombre total d'étapes dans chaque épisode.
- Calculez la moyenne des N dernières valeurs de ce tableau. Dans cet exemple, N (
SUCCESS_STREAK) est égal à 50. Nous calculons donc la moyenne des étapes parcourues au cours des 50 derniers épisodes. - Si cette moyenne est supérieure à un seuil (
SUCCESS_STEPS), nous mettons fin à l'entraînement. Dans cet exemple, ce seuil est fixé à 450 pas.
Meilleures pratiques pour l'utilisation des fonctions action-valeur
Voici quelques bonnes pratiques que vous pouvez suivre pour obtenir de meilleurs résultats lors de la mise en œuvre de votre fonction de valeur d'action.
Équilibrer exploration et exploitation
Compte tenu de la fonction de valeur d'action réelle, l'agent peut maximiser les rendements attendus en adoptant une stratégie avide, basée sur le choix de l'action ayant la valeur la plus élevée à chaque étape. Ceci est appelé « exploitation des informations disponibles ». Cependant, l'utilisation d'une stratégie avide avec une fonction de valeur d'action non entraînée (qui ne représente pas encore les valeurs d'action réelles) conduira à rester bloqué dans un optimum local.
Au cours de la formation, il est important d'explorer l'environnement et d'exploiter les informations disponibles.
Au début du processus de formation, les informations disponibles sont basées sur une fonction de valeur aléatoire. Par conséquent, ces informations ne sont pas très utiles (à exploiter avec une stratégie avide). Il est plus important d'explorer l'environnement afin de découvrir les avantages de différentes actions possibles dans différents états.
Au fur et à mesure que le tableau Q est mis à jour (ou que le DQN est entraîné), il devient possible d'exploiter partiellement les informations disponibles afin de maximiser les récompenses. Vers la fin de la formation, l'agent converge vers la fonction de valeur réelle ; toute exploration supplémentaire peut être préjudiciable. Par conséquent, l'agent privilégie l'exploitation de la fonction de valeur connue.
Régler les hyperparamètres
Comme pour tout modèle d'apprentissage automatique, les hyperparamètres sont essentiels à la réussite de l'entraînement des algorithmes RL. Dans le cas du Q-Learning et des DQN, les hyperparamètres sont epsilon (taux d'exploration), alpha (taux d'apprentissage) et gamma (taux d'actualisation).
- ε ( epsilon) contrôle l'équilibre entre exploration et exploitation (voir ci-dessus). Plus la valeur epsilon est élevée, plus l'exploration est importante par rapport à l'exploitation. Au début de la formation, elle prend une valeur élevée telle que 0,9, qui est progressivement réduite à une valeur faible telle que 0,05 vers la fin de la formation.
- α ( alpha) est le taux d'apprentissage (LR). Il contrôle la variation des paramètres du réseau neuronal (dans le cas des DQN) ou des valeurs du tableau Q à chaque itération de l'entraînement. Si le LR est trop élevé, le modèle devient instable et ne parvient pas à converger. D'autre part, un LR faible entraîne une convergence lente. Il est également courant de commencer avec une valeur élevée de LR au début du processus d'entraînement, lorsque l'agent doit explorer l'environnement. À mesure qu'il se rapproche des valeurs réelles de la fonction Q, le LR est réduit afin de faciliter la convergence du réseau.
- γ (gamma) est le taux d'actualisation. Il détermine l'importance des récompenses à long terme par rapport aux récompenses immédiates. Une valeur gamma élevée signifie que les récompenses ultérieures sont importantes. Une valeur gamma de 0 signifie que seule la récompense de l'étape temporelle actuelle est importante, et que les récompenses ultérieures n'ont aucune importance. Dans des algorithmes tels que l'apprentissage par Q, le rendement total est basé sur les récompenses obtenues tout au long de l'épisode. Il est donc courant d'utiliser un taux d'actualisation élevé, tel que 0,99.
Enfin, il est important de comprendre que l'entraînement RL est sensible aux valeurs aléatoires initiales. Si l'entraînement ne converge pas, il est souvent utile d'utiliser une graine aléatoire différente ou de relancer l'entraînement afin qu'il commence avec un ensemble différent de valeurs initiales aléatoires.
Commencez par des environnements simples
La formation d'agents RL pour des environnements complexes représente un défi. Les fonctions Q sont utilisées dans de nombreux algorithmes différents. Il est donc essentiel de développer une certaine intuition pour former des agents RL basés sur l'apprentissage Q. Il est préférable de s'exercer à ces techniques dans des environnements plus simples, tels que CartPole, avant d'appliquer des méthodes similaires à des environnements plus complexes.
De plus, les environnements complexes sont plus coûteux à former, il est donc plus économique d'utiliser des environnements plus simples comme outil d'apprentissage.
Conclusion
Cet article a abordé les principes théoriques fondamentaux de la fonction de valeur d'action et son importance dans l'apprentissage par renforcement. Nous avons abordé l'utilisation des fonctions de valeur d'action dans l'apprentissage Q et l'apprentissage Q profond, et avons implémenté ces deux méthodes étape par étape en Python.
Pour approfondir vos connaissances, je vous recommande vivementle cours Deep Reinforcement Learning in Python.
Obtenez une certification de haut niveau en matière d'IA
Foire aux questions
Quelle est la différence entre la fonction de valeur et la fonction de valeur d'action dans le RL ?
La fonction de valeur estime le rendement attendu d'un état, tandis que la fonction de valeur d'action (fonction Q) estime le rendement obtenu en prenant une action spécifique dans un état et en suivant la politique par la suite. La fonction valeur-action fournit des indications plus précises pour la prise de décision.
Pourquoi la fonction action-valeur est-elle importante dans l'apprentissage par renforcement Q-learning ?
L'apprentissage par Q utilise la fonction action-valeur pour guider l'agent vers les actions qui rapportent les récompenses attendues les plus élevées. Cette fonction permet l'apprentissage hors politique et aide l'agent à converger vers la stratégie optimale au fil du temps.
Quel est le lien entre la fonction action-valeur et l'équation de Bellman ?
L'équation de Bellman fournit une formulation récursive pour mettre à jour les valeurs Q en fonction de la récompense immédiate et de la récompense future maximale actualisée. C'est la base pour apprendre la fonction action-valeur de manière itérative.
Puis-je utiliser la fonction action-valeur dans des espaces d'états continus ?
Oui, mais les tableaux Q deviennent peu pratiques dans les espaces continus. Dans de tels cas, les réseaux Q profonds (DQN) sont utilisés pour approximer la fonction valeur-action à l'aide d'un réseau neuronal plutôt que de tableaux explicites.
Quel est le rôle de l'exploration dans l'estimation de la fonction de valeur d'action ?
L'exploration garantit que l'agent ne converge pas prématurément vers une politique sous-optimale. Cela aide l'agent à accumuler diverses expériences, qui sont essentielles pour estimer avec précision la fonction de valeur d'action pendant l'entraînement.
Comment la stratégie ε-greedy influence-t-elle l'apprentissage de la valeur Q ?
La stratégie ε-greedy équilibre exploration et exploitation. Avec une probabilité ε, l'agent explore de nouvelles actions, et avec 1–ε, il exploite la meilleure action connue à ce moment-là. Ce compromis améliore la stabilité et la convergence de l'apprentissage.
Quand faut-il passer du Q-learning au Deep Q-learning ?
Lorsque l'environnement présente un espace d'états vaste ou continu, la gestion d'un tableau Q devient inefficace. L'apprentissage profond Q remplace le tableau par un réseau neuronal qui s'adapte mieux aux environnements complexes.
Comment puis-je visualiser une fonction action-valeur pendant l'entraînement ?
Vous pouvez représenter graphiquement les valeurs Q maximales au fil du temps ou suivre les récompenses par épisode afin de surveiller les progrès de l'apprentissage. La visualisation facilite le diagnostic de problèmes tels qu'une convergence insuffisante ou une exploration insuffisante.
Quels sont les principaux défis liés à l'entraînement d'une fonction de valeur d'action ?
Les défis à relever comprennent l'instabilité de la formation due à des cibles mobiles, une exploration insuffisante et des paramètres hyperparamétriques sous-optimaux. L'utilisation de techniques telles que la mémoire de relecture et les réseaux cibles contribue à atténuer ces problèmes.
La fonction action-valeur est-elle utilisée dans les algorithmes on-policy ?
Oui, les algorithmes tels que SARSA utilisent la fonction valeur-action, mais la mettent à jour en fonction de l'action réellement prise par la politique actuelle. Cela contraste avec les méthodes hors politique telles que l'apprentissage Q, qui utilisent la valeur Q maximale de l'état suivant.
Arun est un ancien fondateur de startup qui aime construire de nouvelles choses. Il étudie actuellement les fondements techniques et mathématiques de l'intelligence artificielle. Il aime partager ce qu'il a appris, alors il écrit à ce sujet.
En plus de DataCamp, vous pouvez lire ses publications sur Medium, Airbyte et Vultr.