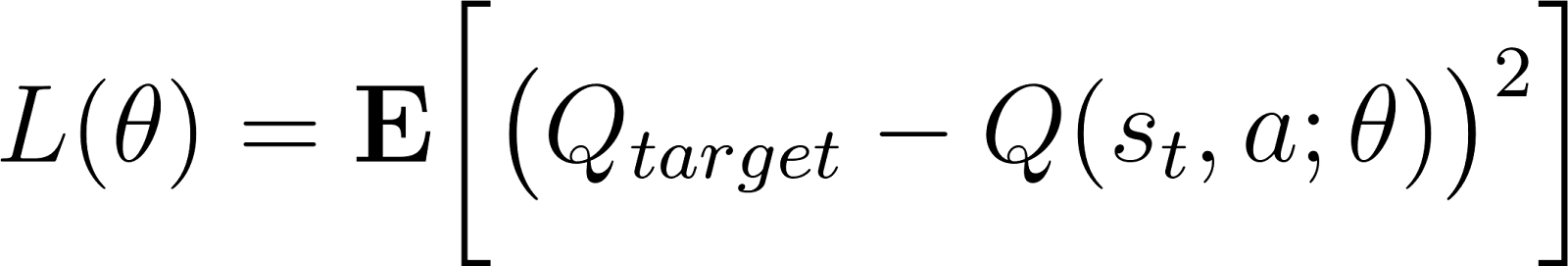Programa
Aprendizagem por reforço (RL) é um jeito de machine learning em que um agente aprende a tomar as decisões certas interagindo com um ambiente externo. O ambiente dá um feedback, tipo recompensas, por fazer a coisa certa.
O objetivo do agente é maximizar as recompensas acumuladas. Em muitos problemas práticos, o feedback para o agente vem de um humano; isso é chamado de RL com feedback humano (RLHF).
RLHF é normalmente usado pra ajustar LLMs pra dar resultados que combinem com os valores e preferências das pessoas. Quando uma IA é usada pra dar feedback, isso é chamado de RL com feedback de IA.
O agente usa a função ação-valor para avaliar qual ação escolher em cada etapa. Uma função de valor de ação otimizada ajuda o agente a escolher a melhor ação em cada etapa para maximizar suas recompensas acumuladas.
Neste tutorial, vou apresentar a função ação-valor, explicar o papel dela na RL e mostrar como implementá-la do zero.
O que é uma Função Ação-Valor?
A função valor-ação (Q) estima a recompensa acumulada esperada (retorno) obtida ao realizar uma ação específica (a) em um estado específico (s) e seguindo a política π depois disso. É denotado como Qπ(s,a). Quando é óbvio que o agente está seguindo a política ideal, isso é expresso de forma mais simples como Q(s,a).
A função valor-ação é usada pra escolher a ação que leva ao maior retorno a partir de um estado dado. A política ideal (π*) maximiza o retorno esperado. Então, em cada estado ,, a política escolhe a ação que leva ao maior retorno esperado. Essa política ideal é expressa como π* = argmaxa Q(s,a).
A função Q é normalmente representada como uma tabela Q. Essa tabela guarda o valor de cada ação possível para cada estado possível do ambiente. Para ambientes complexos, essa tabela se torna grande demais para ser gerenciada e ineficiente. Assim, modelamos a tabela Q como uma rede neural em vez de uma tabela para a maioria dos ambientes não triviais. Essa rede é parecida com a função da tabela Q. Dado um estado, ele mostra os valores de ação que combinam com esse estado.
Por que as funções de valor de ação são importantes na RL
Com a função de valor de ação real, a política deve escolher a ação que leva às recompensas esperadas mais altas. Essa estratégia é conhecida como exploração. Mas, a verdadeira função do valor da ação ainda não é conhecida durante a fase de treinamento. Então, a escolha da ação é baseada em informações incompletas. A exploração (maximizar o retorno) com base nessas informações incompletas pode fazer com que a gente não descubra a verdadeira função de valor da ação e fique preso em um ótimo local.
Por outro lado, uma estratégia exploratória às vezes escolhe ações que não são as melhores, mas que podem acabar levando a um resultado melhor. Isso é implementado como um ε -, onde ε é um valor pequeno. A política escolhe aleatoriamente uma ação subótima com uma probabilidade ε e a ação que maximiza a recompensa com probabilidade 1 - ε.
Adotar uma estratégia que equilibra exploração e exploração permite que o agente descubra caminhos alternativos pelo ambiente, levando a melhores recompensas acumuladas.
Fundamentos dos algoritmos RL
Os algoritmos RL podem ser classificados em duas grandes categorias: 1) baseado em modelo e sem modelo, e 2) dentro da política e fora da política.
Algoritmos baseados em modelos e sem modelos
Nos métodos baseados em modelos, você tenta prever o modelo de distribuição de probabilidade do ambiente P(r, s' | s, a) - a probabilidade de receber uma recompensa r e chegar a um estado s' ao começar de um estado s e tomando uma ação a.
Esses métodos usam as interações do agente com o ambiente para ajustar o modelo (do ambiente) e melhorar as recompensas e os estados previstos. Assim, o agente pode simular o ambiente através do modelo, sem necessariamente ter que interagir com o ambiente em cada etapa.
Alguns algoritmos baseados em modelos, como o Dyna-Q, atualizam a função Q por meio de experiências simuladas. Esses métodos são usados quando é caro ou impraticável ter um agente não treinado tendo um monte de interações com o ambiente. Por exemplo, é muito caro ter um robô sem treinamento caindo várias vezes e podendo se danificar.
Por outro lado, métodos sem modelo, como o aprendizado Q, atualizam diretamente Q(s,a) após um processo iterativo para convergir na função de valor de ação verdadeira sem modelar explicitamente o ambiente. O agente interage diretamente com o ambiente em cada etapa. Eles usam tentativa e erro para chegar à política ideal. Como não envolvem um modelo do ambiente, são mais simples, mas precisam de muitas interações com o ambiente.
Algoritmos sem modelo, como Q-learning, SARSA (State-Action-Reward-State-Action) e DQNs, aprendem explicitamente afunção Q e a usam para estimar o valor da ação em cada etapa.
Algoritmos dentro e fora da política
Algoritmos fora da política (como DQNs e Q-learning) usam a repetição da experiência para aprender o valor da política ideal. Eles têm um monte de interações (reais ou simuladas) com o ambiente e pegam amostras aleatórias dessas interações para atualizar a função Q. Eles não usam a política ideal para decidir o que fazer em cada etapa. Os métodos fora da política usam a função Q para estimar o valor da ação para a política alvo. O objetivo é maximizar os retornos futuros atualizando a função Q com base na maior recompensa esperada do próximo passo.
Alguns algoritmos on-policy (como o SARSA) usam a política para escolher a ação em cada etapa. Assim, o agente segue a mesma política que atualiza. A função Q é atualizada com base na recompensa que o agente recebe por seguir a política. Outros algoritmos on-policy, como gradientes de política e ator-crítico, não usam a função Q.
Então, as funções de valor de ação são a base de vários algoritmos de RL.
Escolha da ação ideal
O valor Q Q(s,a) representa o retorno esperado ao tomar uma ação a no estado s e seguir a política depois disso. Assim, com uma tabela Q treinada, escolher a ação que leva ao valor Q máximo em um estado específico leva a uma política ideal com base em uma estratégia gananciosa (focada na exploração). Em cada etapa, o agente escolhe a ação a* = arg max a Q(s,a). Então, durante todo o episódio, ele escolhe o caminho que maximiza as recompensas a longo prazo com base nas informações disponíveis.
Métodos como o aprendizado Q atualizam os valores Q na tabela Q ao longo de muitas iterações para convergir para seus valores ideais. Assim, depois do treinamento, o algoritmo chega à política ideal que escolhe a ação ideal em cada situação e o caminho ideal ao longo do episódio.
Conceitos de inteligência artificial (IA) em Python
Implementando uma função ação-valor
Depois de falar sobre os princípios básicos e os usos da função valor-ação, agora vou mostrar os passos para implementá-la em Python.
Passo 1: Defina o ambiente
Importa os pacotes necessários, incluindo Gymnasium e NumPy:
import gymnasium as gym
import numpy as np
import math
import randomInicialize um ambiente RL a partir do Gymnasium. Neste artigo, a gente treina um agente RL pra resolver o ambiente CartPole.
env = gym.make('CartPole-v1')Passo 2: Inicializar tabela Q
O espaço de observação do CartPole tem quatro estados: posição do carrinho, velocidade do carrinho, ângulo do poste e velocidade angular do poste.
Neste exemplo, vamos focar só nas observações do ângulo do polo e da velocidade angular do polo. Assim, criamos a tabela Q discreta da seguinte forma:
- Um estado discreto para a posição do carrinho - todos os valores possíveis são agrupados nesse único estado.
- Um estado discreto para a velocidade do carrinho
- Seis estados diferentes para o ângulo do polo
- Três estados diferentes para a velocidade do polo
O número de colunas depende do tamanho do espaço de ação, que aqui é 2.
NUM_BUCKETS = (1, 1, 6, 3)
NUM_ACTIONS = env.action_space.n
q_table = np.zeros(NUM_BUCKETS + (NUM_ACTIONS,))No ambiente CartPole, o espaço de estado é contínuo. O ângulo, a velocidade e a posição do poste do carrinho podem mudar o tempo todo. O espaço de ação é discreto - você pode empurrar o carrinho para a esquerda ou para a direita.
O Q-Learning usando tabelas Q só pode ser usado em um espaço discreto, porque você precisa tabular explicitamente o valor Q para um conjunto de estados e ações. Então, o primeiro passo é discretizar o espaço de estado contínuo.
Primeiro, vamos pensar nos limites superior e inferior das variáveis do espaço de estado. A gente percebe que a velocidade do carrinho e a velocidade angular do poste não têm limites. Então, a gente definiu limites superiores e inferiores artificiais para essas variáveis de estado.
STATE_BOUNDS = list(zip(env.observation_space.low, env.observation_space.high))
STATE_BOUNDS[1] = [-0.5, 0.5]
STATE_BOUNDS[3] = [-math.radians(50), math.radians(50)]Criamos uma função para discretizar os valores contínuos do estado em valores discretos:
def discretize_state(state):
discrete_states = []
for i in range(len(state)):
if state[i] <= STATE_BOUNDS[i][0]:
discrete_state = 0
elif state[i] >= STATE_BOUNDS[i][1]:
discrete_state = NUM_BUCKETS[i] - 1
else:
bound_width = STATE_BOUNDS[i][1] - STATE_BOUNDS[i][0]
offset = (NUM_BUCKETS[i] - 1) * STATE_BOUNDS[i][0] / bound_width
scaling = (NUM_BUCKETS[i] - 1) / bound_width
discrete_state = int(round(scaling * state[i] - offset))
discrete_states.append(discrete_state)
return tuple(discrete_states)Passo 3: Atualize a tabela Q.
As equações de Bellman mostram como atualizar os valores Q com base na taxa de aprendizagem, na taxa de desconto, na recompensa que vai para a próxima etapa e no valor Q máximo esperado do próximo estado. É o valor esperado de um estado como a soma de duas partes:
- A recompensa imediata ao passar para o próximo estado
- O valor esperado descontado do próximo estado
A equação de Bellman é recursiva. Assim, dá pra escrever um programa iterativo, começando de um estado inicial aleatório, pra achar a função de valor de ação ideal.
A equação para atualizar a tabela Q é:
Na expressão acima:
- O estado atual é st, indicado como “
state_current” no código. - O próximo estado é st+1 (
state_next). - A ação tomada no estado atual é umat (
action). - P(st, at) é o valor Q atual para o estado st e ação at
- α é a taxa de aprendizagem.
- γ é o fator de desconto.
- rt+1 é a recompensa depois de agir at na etapa atual com o estado st. O código abaixo mostra isso como
reward. - argmaxa Q(st+1, a) é o valor Q máximo do próximo estado st+1. No trecho de código abaixo, isso é mostrado em
best_q.
O código abaixo implementa a função para atualizar a tabela Q.
def update_q(state_current, state_next, action, reward, alpha):
best_q = np.amax(q_table[state_next])
q_table[state_current + (action,)] += alpha * (reward + GAMMA*(best_q) - q_table[state_current + (action,)])
return best_qPasso 4: Treinar o agente
Declara os parâmetros do treinamento:
- O máximo de episódios de treinamento
- O número máximo de etapas por episódio vem da documentação do ambiente. Para o CartPole-v1, é 500.
- O número de etapas que o agente precisa fazer para que o episódio seja considerado um sucesso. A gente colocou em 450.
- O número de episódios que o agente precisa completar de uma vez só para que o treinamento seja considerado um sucesso. A gente colocou em 50.
MAX_EPISODES = 5000
MAX_STEPS = 500
SUCCESS_STEPS = 450
SUCCESS_STREAK = 50Declara os hiperparâmetros:
- Os valores mínimo e máximo da taxa de exploração, ε
- Os valores mínimo e máximo da taxa de aprendizagem, α
- A taxa de decaimento de α e γ
- O fator de desconto, γ
EPSILON_MIN = 0.01
EPSILON_MAX = 1
ALPHA_MIN = 0.1
ALPHA_MAX = 0.5
GAMMA = 0.99
DECAY_COEFF = 25Antes de treinar o agente, a gente escreve duas funções pra diminuir a taxa de aprendizado e a taxa de exploração aos poucos. Esses hiperparâmetros diminuem de valor gradualmente ao longo do treinamento.
def decay_epsilon(step):
return max(EPSILON_MIN, min(EPSILON_MAX, 1.0-math.log10((step+1)/DECAY_COEFF)))
def decay_alpha(step):
return max(ALPHA_MIN, min(ALPHA_MAX, 1.0-math.log10((step+1)/DECAY_COEFF)))Também criamos uma função pra escolher a ação de forma aleatória. Primeiro, a gente gera um número aleatório.
- Se esse número aleatório for menor que ε, a gente escolhe aleatoriamente uma ação do espaço de ações. Essa é a estratégia de exploração.
- Se o número aleatório for maior que ε, escolhemos a ação que corresponde ao valor Q máximo. Essa é a estratégia de exploração.
def select_action(state, epsilon):
if random.random() < epsilon:
action = env.action_space.sample()
else:
action = np.argmax(q_table[state])
return actionA gente cria um loop pra treinar o agente seguindo esses passos:
- Pega os valores de α, e ε que estão meio velhos para o episódio atual.
- Reinicie o ambiente e discretize o espaço de observação para começar um ambiente novo para o episódio.
- Execute o agente no ambiente até que ele atinja o número máximo de etapas ou seja encerrado.
- Para cada etapa:
- Escolha a ação de acordo com a função
select_action()que falamos antes. - Execute a ação no ambiente para obter a recompensa e o próximo estado.
- Pega o valor Q mais alto da tabela Q.
- Atualize a tabela Q de acordo com a função
update_q()declarada anteriormente.
O código abaixo mostra como funciona o loop de treinamento:
def train():
successful_episodes = 0
for episode in range(MAX_EPISODES):
epsilon = decay_epsilon(episode)
alpha = decay_alpha(episode)
observation, _ = env.reset()
state_current = discretize_state(observation)
for step in range(MAX_STEPS):
action = select_action(state_current, epsilon)
observation, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
state_next = discretize_state(observation)
best_q = update_q(state_current, state_next, action, reward, alpha)
state_current = state_next
if done:
print("Episode %d finished after %d time steps" % (episode, step))
print("best q value: %f" % (float(best_q)))
if (step >= SUCCESS_STEPS):
successful_episodes += 1
print("=============SUCCESS=============")
else:
successful_episodes = 0
print("=============FAIL=============")
break
if successful_episodes > SUCCESS_STREAK:
breakPor fim, execute o loop de treinamento, feche o ambiente e imprima o valor final da tabela Q.
train()
env.close()
print(q_table)Use esta pasta de trabalho do DataLab como ponto de partida para editar e executar o código para o Q-Learning.
Estendendo para o Deep Q-Learning
Na seção anterior, a gente discretizou o espaço de observação contínuo (estado) pra usar uma tabela Q. Uma tabela Q grande (para ambientes complexos) é ineficiente em termos computacionais. Nesses casos, a função Q pode ser aproximada usando uma rede neural. Isso é chamado de Deep Q-Network, que é tipo um Q(s, a; θ), onde o parâmetro θ representa os pesos da rede neural. Esse método é chamado de Deep Q-learning. De um jeito mais geral, RL usando redes neurais profundas é chamado de Aprendizado por Reforço Profundo.
Em vez de usar a Tabela Q para escolher a ação para cada estado, a rede neural DQN pega o estado como entrada e mostra o valor Q para cada ação possível nesse estado.
A rede é treinada usando métodos tradicionais (como retropropagação) para minimizar o erro de diferença temporal (TD). O erro TD δ é a diferença entre os valores Q previstos e os valores Q alvo (calculados como a soma da recompensa do estado atual e o valor descontado da recompensa máxima esperada do próximo estado).
Quando implementado como uma rede neural (com parâmetros de rede θ), o erro TD é expresso como:
Observe que tanto os valores Q quanto os valores Q alvo são calculados usando a mesma rede neural.
Em cada repetição, os parâmetros da rede (θ) são atualizados. A atualização da rede (via backprop) é baseada no valor alvo calculado usando o θ pré-atualização. Calcular os valores alvo com os mesmos resultados atualizados em um alvo em movimento contínuo. Isso deixa o treino meio instável.
Para evitar o problema acima, criamos uma nova rede para calcular os valores Q desejados. Essa é a rede que a gente quer. É baseada nos mesmos parâmetros da rede de políticas, mas é atualizada com menos frequência. Então, o processo de treinamento tem um objetivo fixo em relação ao qual aplica a retropropagação.
Se representarmos os pesos da rede alvo com θ-, a equação anterior é reescrita como:
As seções a seguir mostram como implementar e treinar um DQN simples no ambiente CartPole.
Exemplo de implementação
Instale os pacotes necessários, incluindo Gymnasium e PyTorch.
!pip install gymnasium matplotlib torchImporta os pacotes necessários no ambiente Python:
import gymnasium as gym
import math
import random
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple, deque
from itertools import count
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as FCrie o ambiente CartPole:
env = gym.make("CartPole-v1")Inicialize o ambiente e declare as constantes Python com o tamanho dos espaços de estado e ação do ambiente.
state, info = env.reset()
NUM_OBSERVATIONS = len(state)
NUM_ACTIONS = env.action_space.nDeclare uma classe Python para uma rede neural simples com uma única camada oculta. O número de camadas de entrada é o tamanho do espaço de estado (espaço de observação). O número de camadas de saída é o número de ações possíveis que o agente RL pode realizar. Essa rede simula internamente a tabela Q e prevê os valores de ação para um estado de entrada.
class DQN(nn.Module):
def __init__(self, NUM_OBSERVATIONS, NUM_ACTIONS):
super(DQN, self).__init__()
self.layer1 = nn.Linear(NUM_OBSERVATIONS, 128)
self.layer2 = nn.Linear(128, 128)
self.layer3 = nn.Linear(128, NUM_ACTIONS)
def forward(self, x):
x = F.relu(self.layer1(x))
x = F.relu(self.layer2(x))
return self.layer3(x)Crie uma rede de políticas e uma rede de metas. Carregue a rede de destino com os parâmetros da rede de políticas usando o dicionário de estados. Inicialize um otimizador para treinar a rede neural.
policy_net = DQN(NUM_OBSERVATIONS, NUM_ACTIONS)
target_net = DQN(NUM_OBSERVATIONS, NUM_ACTIONS)
target_net.load_state_dict(policy_net.state_dict())
optimizer = optim.AdamW(policy_net.parameters(), lr=LR, amsgrad=True)Treino com buffer de repetição
Os métodos RL sem modelo fora da política, como Q-Learning (falado na seção anterior) e DQNs, são treinados usando uma amostra aleatória das interações do agente com o ambiente. As ações do agente e as respostas do ambiente (recompensa e próximo estado) são coletadas e armazenadas. Uma amostra aleatória dessas interações é escolhida em cada iteração do treinamento para formar um lote de treinamento.
Declare um objeto tupla para guardar o estado do ambiente (observação) em cada interação:
Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))Crie uma classe Python para o buffer de reprodução:
class ReplayMemory(object):
def __init__(self, capacity):
self.memory = deque([], maxlen=capacity)
def push(self, *args):
self.memory.append(Transition(*args))
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)Crie um objeto de memória pra guardar um monte de interações. Essas interações são usadas para treinar o agente.
memory = ReplayMemory(10000)Antes de treinar, declare os parâmetros e hiperparâmetros:
- Parâmetros:
- Tamanho do lote
- Número máximo de episódios de treinamento
- Hiperparâmetros:
- Taxa de aprendizagem (
LR) - Fator de desconto (
GAMMA) - A taxa de atualização da rede de destino (
TAU) - Valores iniciais e finais da taxa de exploração e da taxa de decaimento (
EPS_START,EPS_ENDeEPS_DECAY)
MAX_EPISODES = 600
BATCH_SIZE = 128
GAMMA = 0.99
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 1000
TAU = 0.005
LR = 1e-4Escreva uma função para escolher a ação com base na taxa de exploração, seguindo esses passos:
- Calcule a taxa de exploração com base no número de etapas do episódio (e nos valores inicial e final e na taxa de decaimento da taxa de exploração).
- Gerar um número aleatório.
- Se o número aleatório for maior que a taxa de exploração, escolha a ação prevista pela rede de políticas.
- Se for menor que a taxa de exploração, escolha uma ação aleatória do espaço de ação.
steps_done = 0
def select_action(state):
global steps_done
sample = random.random()
eps_threshold = EPS_END + (EPS_START - EPS_END) * \
math.exp(-1. * steps_done / EPS_DECAY)
steps_done += 1
if sample > eps_threshold:
with torch.no_grad():
action = policy_net(state).max(1).indices.view(1, 1)
return action
else:
action = torch.tensor([[env.action_space.sample()]], dtype=torch.long)
return actionEscreva a função para otimizar o modelo com base nessas etapas:
- Crie um lote usando uma amostra aleatória das interações do agente com o ambiente. Cada item da amostra é igual a um passo de tempo. Tem:
- Como tá o meio ambiente hoje em dia?
- A ação do agente
- A recompensa recebida
- O próximo estado
- No CartPole, o agente deve continuar a manipular o poste do carrinho sem parar (sem bater nas bordas ou cair). Então, a gente só considera as interações que não levam a um estado final. Criamos uma máscara (
non_final_mask) pra identificar os estados que não são seguidos por um estado terminal. - Identifique os estados que não são seguidos por um estado terminal (
non_final_next_states). - Pega os valores de ação do estado para todos os estados atuais st passando os estados atuais para a rede de políticas.
- Pega os valores de ação esperados para todos os próximos estados st+1 passando os próximos estados para a rede de destino e usandoa equação:
- Calcule a perda com base na diferença entre os valores da ação e os valores esperados da ação:
- Propaga as perdas pra calcular osgradientes.
- Corte os valores do gradiente e atualize a rede de políticas para garantir um treinamento estável.
O código abaixo mostra como implementar o otimizador:
batch = 0
def optimize_model():
global batch
if len(memory) < BATCH_SIZE:
return
transitions = memory.sample(BATCH_SIZE)
batch = Transition(*zip(*transitions))
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,
batch.next_state)), dtype=torch.bool)
non_final_next_states = torch.cat([s for s in batch.next_state
if s is not None])
state_batch = torch.cat(batch.state)
action_batch = torch.cat(batch.action)
reward_batch = torch.cat(batch.reward)
state_action_values = policy_net(state_batch).gather(1, action_batch)
next_state_values = torch.zeros(BATCH_SIZE )
with torch.no_grad():
next_state_values[non_final_mask] = target_net(non_final_next_states).max(1).values
expected_state_action_values = (next_state_values * GAMMA) + reward_batch
loss_func = nn.SmoothL1Loss()
loss = loss_func(state_action_values, expected_state_action_values.unsqueeze(1))
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_value_(policy_net.parameters(), 100)
optimizer.step()Escreva um loop de treinamento para treinar o agente:
- Reinicie o ambiente e comece um novo episódio.
- Use a função
select_action()para decidir o que o agente vai fazer. - Pega a recompensa do ambiente e o próximo estado com base na ação.
- Adicione o estado, a ação, o próximo estado e a recompensa ao buffer de repetição.
- Execute o otimizador (definido acima). O otimizador calcula os valores Q e a perda, aplicando retropropagação para atualizar a rede.
- Atualize a rede de destino com base na rede de políticas.
- Continue o episódio até chegar a um estado final.
O código a seguir implementa essas etapas:
def train():
for episode in range(MAX_EPISODES):
# Initialize the environment and get its state
state, info = env.reset()
state = torch.tensor(state, dtype=torch.float32).unsqueeze(0)
for t in count():
action = select_action(state)
observation, reward, terminated, truncated, _ = env.step(action.item())
reward = torch.tensor([reward])
done = terminated or truncated
if terminated:
next_state = None
else:
next_state = torch.tensor(observation, dtype=torch.float32).unsqueeze(0)
memory.push(state, action, next_state, reward)
state = next_state
optimize_model()
target_net_state_dict = target_net.state_dict()
policy_net_state_dict = policy_net.state_dict()
for key in policy_net_state_dict:
target_net_state_dict[key] = policy_net_state_dict[key]*TAU + target_net_state_dict[key]*(1-TAU)
target_net.load_state_dict(target_net_state_dict)
if done:
episode_durations.append(t + 1)
print('episode -- ', episode)
print('count -- ', t)
#plot_durations()
breakVocê pode ver, editar e rodar o programa de treinamento DQN usando essa pasta de trabalho do DataLab.
Visualizando a função ação-valor
É legal acompanhar visualmente o progresso do treinamento. Visualizar os valores da ação ajuda a ver onde o treinamento está falhando e quais parâmetros ou hiperparâmetros precisam ser alterados.
Por exemplo, se você perceber que o modelo está demorando muito pra melhorar, pode ser uma boa ideia aumentar a taxa de aprendizado. Se você perceber que o modelo está aprendendo, mas ainda não foi totalmente treinado, pode ser uma boa ideia aumentar o número de episódios de treinamento. Se você achar que o treinamento está instável, pode ser uma boa ideia reduzir a taxa de aprendizagem ou ajustar o coeficiente de exploração ou a taxa de atualização da rede de destino (TAU).
Além dos valores Q, também pode ser útil traçar o número de etapas bem-sucedidas em cada episódio. No Q-Learning usando tabelas Q, os valores Q são guardados explicitamente. Mas, quando usamos DQNs, os valores Q não ficam guardados de forma explícita. A rede mostra a ação dependendo dos pesos e do estado. Então, acompanhar o número de etapas bem-sucedidas em cada episódio pode ser mais útil para o DQN.
Os passos a seguir mostram como plotar os valores Q e o número de passos bem-sucedidos por episódio para treinar o algoritmo de aprendizado Q:
- Crie duas matrizes vazias no começo do treinamento:
q_vals- pra guardar os valores Q em cada etapa de cada episódio.success_steps- pra guardar o número de passos que deram certo em cada episódio.- Em cada etapa (em todos os episódios):
- Adicione o valor Q dessa etapa à matriz
q_vals. - Depois que cada episódio terminar, acrescente à matriz “
success_steps” o número de etapas bem-sucedidas nesse episódio. - Plotamos as duas matrizes.
O código abaixo mostra o loop de treinamento do Q-Learning (usando tabelas Q) (mostrado na seção anterior) atualizado para acompanhar os valores Q e o número de etapas bem-sucedidas:
q_vals = []
success_steps = []
def train():
global q_vals
global success_steps
successful_episodes = 0
for episode in range(MAX_EPISODES):
epsilon = decay_epsilon(episode)
alpha = decay_alpha(episode)
observation, _ = env.reset()
state_current = discretize_state(observation)
for step in range(MAX_STEPS):
action = select_action(state_current, epsilon)
observation, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
state_next = discretize_state(observation)
best_q = update_q(state_current, state_next, action, reward, alpha)
q_vals.append(best_q)
state_current = state_next
if done:
q_vals.append(best_q)
success_steps.append(step)
print("Episode %d finished after %d time steps" % (episode, step))
print("best q value: %f" % (float(best_q)))
if (step >= SUCCESS_STEPS):
successful_episodes += 1
else:
successful_episodes = 0
break
if successful_episodes > SUCCESS_STREAK:
print("Training successful")
returnO trecho abaixo mostra como plotar os valores Q em cada episódio:
def plot_q():
plt.plot(q_vals)
plt.title('Q-values over training steps')
plt.xlabel('Training steps')
plt.ylabel('Q-value')
plt.show()O trecho a seguir mostra como plotar o número de etapas bem-sucedidas em cada episódio:
def plot_steps():
plt.plot(success_steps)
plt.title('Successful steps over training episodes')
plt.xlabel('Training episode')
plt.ylabel('Successful steps')
plt.show()- A pasta de trabalho do DataLab para implementar o aprendizado Q usando funções de valor de ação também inclui o código para plotar os valores Q e as etapas bem-sucedidas por episódio.
- O caderno para implementar o DQN também inclui o código para plotar o número de etapas bem-sucedidas por episódio.
Avaliando o desempenho dos agentes
É preciso definir os critérios para saber se e quando o agente foi treinado com sucesso. No aprendizado de máquina tradicional, o objetivo do treinamento é minimizar a perda: a diferença entre os valores previstos e os valores reais. Na RL, o objetivo é maximizar a recompensa acumulada. O treinamento é considerado bem-sucedido quando o agente consegue o máximo de recompensas do ambiente.
Ambientes como o CartPole não acabam até chegarem a uma condição final, tipo bater nas bordas ou deixar o cartpole inclinar demais. Nesses casos, um agente treinado pode continuar interagindo com o ambiente por tempo ilimitado. Então, o número máximo de passos que dá certo é meio que imposto de um jeito artificial. No caso do CartPole-v1 do Gymnasium, o episódio termina quando chega a 500 passos de tempo sem terminar.
A gente avalia o desempenho do agente em episódios seguidos pra ver se o treinamento deu certo. Por exemplo:
- O agente deve conseguir completar mais do que um número mínimo de etapas (
SUCCESS_STEPS) em média nos últimos N episódios. Nos exemplos deste artigo, definimos esse limite em 450. - O agente pode passar do limite em N episódios seguidos (
SUCCESS_STREAK). Neste exemplo, definimos N como 50.
Como exemplo prático, dá uma olhada nesse trecho do loop de treinamento DQN que mostramos antes.
if done:
episode_durations.append(t + 1)
print('episode -- ', episode)
average_steps = sum(episode_durations[-SUCCESS_STREAK:])/SUCCESS_STREAK
print('average steps over last 50 episodes -- ', average_steps)
if average_steps > SUCCESS_STEPS:
print("training successful.")
return
breakIsso ajuda a avaliar o desempenho do agente com base na execução das seguintes etapas no final (estado terminal) de cada episódio de treinamento:
- Adicione o número total de passos deste episódio (antes de terminar) a uma matriz. Esse array controla o número total de passos em cada episódio.
- Calcule a média dos últimos N valores neste array. Neste exemplo, N (
SUCCESS_STREAK) é 50. Então, a gente calcula a média de passos nos últimos 50 episódios. - Se essa média for maior que um limite (
SUCCESS_STEPS), a gente encerra o treinamento. Neste exemplo, esse limite está definido em 450 passos.
Melhores práticas para usar funções de valor de ação
Aqui estão algumas dicas que você pode seguir pra ter melhores resultados com a implementação da função valor-ação.
Equilíbrio entre exploração e aproveitamento
Com a função de valor de ação real, o agente pode maximizar os retornos esperados usando uma estratégia gananciosa, que é escolher a ação com o maior valor em cada etapa. Isso é chamado de exploração das informações disponíveis. Mas, usar uma estratégia gananciosa com uma função de valor de ação não treinada (que ainda não representa os valores de ação reais) vai fazer com que a gente fique preso em um ótimo local.
Durante o treinamento, é importante tanto explorar o ambiente quanto usar as informações disponíveis.
Nas primeiras etapas do processo de treinamento, as informações disponíveis são baseadas em uma função de valor aleatório. Então, essa informação não é muito valiosa (para usar com uma estratégia gananciosa). É mais importante explorar o ambiente para descobrir as recompensas de várias ações possíveis em diferentes situações.
À medida que a tabela Q é atualizada (ou o DQN é treinado), torna-se possível usar parcialmente as informações disponíveis para maximizar as recompensas. Nas fases finais do treinamento, o agente converge para a função de valor real; explorar mais pode ser ruim. Então, o agente prioriza explorar a função de valor conhecida.
Ajustar hiperparâmetros
Como em qualquer modelo de machine learning, os hiperparâmetros são importantes para treinar algoritmos de RL com sucesso. No caso do Q-Learning e das DQNs, os hiperparâmetros são epsilon (taxa de exploração), alfa (taxa de aprendizagem) e gama (taxa de desconto).
- ε ( epsilon) controla o equilíbrio entre exploração e exploração (discutido acima). Quanto maior o valor epsilon, mais importante é a exploração em relação à exploração. No começo do treinamento, ele tem um valor alto, tipo 0,9, que vai diminuindo até chegar a um valor bem baixo, tipo 0,05, no final do treinamento.
- α ( alfa) é a taxa de aprendizagem (LR). Ele controla o quanto os parâmetros da rede neural (no caso de DQNs) ou os valores da Tabela Q mudam em cada iteração do treinamento. Se o LR estiver muito alto, o modelo fica instável e não consegue convergir. Por outro lado, um LR baixo faz com que a convergência seja lenta. Também é comum começar com um valor alto de LR no início do processo de treinamento, quando o agente precisa explorar o ambiente. À medida que se aproxima dos valores reais da função Q, o LR é reduzido para ajudar a rede a convergir.
- γ (gama) é a taxa de desconto. Ele decide a importância das recompensas em etapas posteriores em relação às recompensas imediatas. Um valor alto de gama significa que as recompensas posteriores são importantes. Um valor gama de 0 quer dizer que só a recompensa do passo atual é importante, e as recompensas depois disso não têm importância. Em algoritmos como o Q-learning, o retorno total é baseado nas recompensas obtidas ao longo de todo o episódio. Então, usar uma taxa de desconto alta, tipo 0,99, é bem comum.
Por fim, entenda que o treinamento RL é sensível aos valores aleatórios iniciais. Se o treinamento não convergir, muitas vezes é útil usar uma semente aleatória diferente ou refazer o treinamento para que ele comece com um conjunto diferente de valores iniciais aleatórios.
Comece com ambientes simples
Treinar agentes RL para ambientes complexos é um desafio. As funções Q são usadas em vários algoritmos diferentes, então é essencial ter uma boa intuição pra treinar agentes RL baseados em Q-learning. A melhor maneira de fazer isso é praticando as técnicas em ambientes mais simples, como CartPole, antes de tentar métodos parecidos em ambientes mais complexos.
Além disso, ambientes complexos são mais caros para treinar, então é mais econômico usar ambientes mais simples como ferramenta de aprendizagem.
Conclusão
Esse artigo falou sobre os princípios teóricos básicos da função de valor de ação e sua importância na RL. A gente falou sobre como as funções de valor de ação são usadas no Q-learning e no Deep Q-learning e implementou esses dois métodos passo a passo em Python.
Para continuar aprendendo, recomendo muitoo curso Deep Reinforcement Learning em Python.
Obtenha uma das melhores certificações de IA
Perguntas frequentes
Qual é a diferença entre função de valor e função de valor de ação em RL?
A função de valor estima o retorno esperado de um estado, enquanto a função de valor de ação (função Q) estima o retorno de tomar uma ação específica em um estado e seguir a política a partir daí. A função valor-ação dá uma orientação mais detalhada para a tomada de decisões.
Por que a função valor-ação é importante no aprendizado Q?
O Q-learning usa a função ação-valor para guiar o agente em direção às ações que geram as maiores recompensas esperadas. A função permite o aprendizado fora da política e ajuda o agente a chegar na estratégia ideal com o tempo.
Como a função valor-ação se relaciona com a equação de Bellman?
A equação de Bellman dá uma fórmula recursiva pra atualizar os valores Q com base na recompensa imediata e na recompensa futura máxima descontada. É a base para aprender a função ação-valor de forma iterativa.
Posso usar a função ação-valor em espaços de estado contínuos?
Sim, mas as tabelas Q ficam meio complicadas em espaços contínuos. Nesses casos, as Deep Q-Networks (DQNs) são usadas para aproximar a função de valor de ação com uma rede neural em vez de tabelas explícitas.
Qual é o papel da exploração na estimativa da função de valor da ação?
A exploração garante que o agente não se concentre muito cedo numa política que não é a melhor. Isso ajuda o agente a juntar várias experiências, que são essenciais pra estimar com precisão a função de valor de ação durante o treinamento.
Como a estratégia ε-greedy afeta o aprendizado do valor Q?
A estratégia ε-greedy equilibra exploração e exploração. Com uma probabilidade ε, o agente tenta novas ações e, com 1–ε, usa a melhor ação que conhece no momento. Essa troca melhora a estabilidade e a convergência do aprendizado.
Quando você deve trocar o Q-learning pelo Deep Q-learning?
Quando o ambiente tem um espaço de estado grande ou contínuo, manter uma tabela Q se torna ineficiente. O Deep Q-learning troca a tabela por uma rede neural que se adapta melhor a ambientes complexos.
Como posso visualizar uma função de valor de ação durante o treinamento?
Você pode traçar os valores Q máximos ao longo do tempo ou acompanhar as recompensas dos episódios para monitorar o progresso da aprendizagem. A visualização ajuda a diagnosticar problemas como convergência ruim ou exploração insuficiente.
Quais são os principais desafios no treinamento de uma função de valor de ação?
Os desafios incluem instabilidade no treinamento por causa de alvos que mudam, exploração ruim e configurações de hiperparâmetros que não são as melhores. Usar técnicas como memória de repetição e redes de destino ajuda a resolver esses problemas.
A função valor-ação é usada em algoritmos on-policy?
Sim, algoritmos como o SARSA usam a função valor-ação, mas atualizam ela usando a ação realmente tomada pela política atual. Isso é diferente de métodos fora da política, como o aprendizado Q, que usa o valor Q máximo do próximo estado.
Arun é um ex-fundador de startup que gosta de criar coisas novas. Atualmente, ele está explorando os fundamentos técnicos e matemáticos da Inteligência Artificial. Ele adora compartilhar o que aprendeu, por isso escreve sobre isso.
Além do DataCamp, você pode ler as publicações dele no Medium, Airbyte e Vultr.