Guía sobre el algoritmo de agrupamiento DBSCAN

En la ciencia de datos y el machine learning, la capacidad de descubrir patrones ocultos y agrupar puntos de datos similares es una habilidad importante. Los algoritmos de agrupamiento desempeñan un papel fundamental en este proceso. 

La agrupación es una técnica fundamental del machine learning y la ciencia de datos que consiste en agrupar puntos de datos similares. Es un método de aprendizaje no supervisado, lo que significa que no requiere datos etiquetados para encontrar patrones. 

El objetivo principal de la agrupación es:

• Simplifica grandes conjuntos de datos en subgrupos significativos.
• Identificar agrupaciones naturales dentro de los datos
• Revela patrones y estructuras ocultos.

Aunque existen numerosos algoritmos de agrupamiento (quizás hayas oído hablar de K-means o del agrupamiento jerárquico), DBSCAN ofrece ventajas únicas. Como método basado en la densidad, DBSCAN tiene varias ventajas:

1. Flexibilidad en la forma del clúster
2. Sin número predefinido de clústeres
3. Gestión del ruido
4. Información basada en la densidad

En este artículo, veremos qué es el algoritmo DBSCAN, cómo funciona, cómo implementarlo en Python y cuándo utilizarlo en tus proyectos de ciencia de datos.

¿Qué es DBSCAN?

DBSCAN, siglas en inglés de «agrupamiento espacial basado en la densidad de aplicaciones con ruido», es un potente algoritmo de agrupamiento que agrupa puntos que están muy juntos en el espacio de datos. A diferencia de otros algoritmos de agrupamiento, DBSCAN no requiere que especifiques el número de agrupamientos de antemano, lo que lo hace especialmente útil para el análisis exploratorio de datos.

El algoritmo funciona definiendo los clústeres como regiones densas separadas por regiones de menor densidad. Este enfoque permite a DBSCAN descubrir clústeres de forma arbitraria e identificar valores atípicos como ruido.

DBSCAN gira en torno a tres conceptos clave:

1. Puntos clave: Estos son puntos que tienen al menos un número mínimo de otros puntos (MinPts) dentro de una distancia especificada (ε o épsilon).
2. Puntos fronterizos: Son puntos que se encuentran dentro de la distancia ε de un punto central, pero que no tienen vecinos MinPts.
3. Puntos de ruido: Estos son puntos que no son ni puntos centrales ni puntos fronterizos. No están lo suficientemente cerca de ningún cúmulo como para ser incluidos.

Imagen del autor.

El diagrama anterior ilustra estos conceptos. Los puntos centrales (azules) forman el núcleo de los clústeres, los puntos fronterizos (naranjas) se encuentran en el borde de los clústeres y los puntos de ruido (rojos) están aislados.

DBSCAN utiliza dos parámetros principales:

• ε (epsilon): La distancia máxima entre dos puntos para que se consideren vecinos.
• Puntos mínimos: El número mínimo de puntos necesarios para formar una región densa.

Al ajustar estos parámetros, puedes controlar cómo define el algoritmo los clústeres, lo que le permite adaptarse a diferentes tipos de conjuntos de datos y requisitos de agrupación.

En la siguiente sección, veremos cómo funciona el algoritmo DBSCAN, explorando su proceso paso a paso para identificar clústeres en los datos.

¿Cómo funciona DBSCAN?

DBSCAN funciona examinando el vecindario de cada punto del conjunto de datos. El algoritmo sigue un proceso paso a paso para identificar grupos basándose en la densidad de los puntos de datos. Analicemos cómo funciona DBSCAN:

1. Selección de parámetros
• Elige ε (epsilon): La distancia máxima entre dos puntos para que se consideren vecinos.
• Elige MinPts: El número mínimo de puntos necesarios para formar una región densa.
2. Selecciona un punto de partida
• El algoritmo comienza con un punto arbitrario no visitado en el conjunto de datos.
3. Examina el vecindario
• Recupera todos los puntos que se encuentran dentro de la distancia ε del punto de partida.
• Si el número de puntos vecinos es inferior a MinPts, el punto se etiqueta como ruido (por ahora).
• Si hay al menos MinPts puntos dentro de la distancia ε, el punto se marca como punto central y se forma un nuevo clúster.
4. Expandir el clúster
• Todos los vecinos del punto central se añaden al clúster.
• Para cada uno de estos vecinos:
• Si se trata de un punto central, sus vecinos se añaden al clúster de forma recursiva.
• Si no es un punto central, se marca como punto fronterizo y la expansión se detiene.
5. Repite el proceso.
• El algoritmo pasa al siguiente punto no visitado del conjunto de datos.
• Los pasos 3 y 4 se repiten hasta que se hayan visitado todos los puntos.
6. Finalizar clústeres
• Una vez procesados todos los puntos, el algoritmo identifica todos los clústeres.
• Los puntos inicialmente etiquetados como ruido ahora pueden ser puntos fronterizos si se encuentran a una distancia ε de un punto central.
7. Manejo del ruido
• Los puntos que no pertenecen a ningún clúster siguen clasificándose como ruido.

Este proceso permite a DBSCAN formar clústeres de formas arbitrarias e identificar valores atípicos de manera eficaz. La capacidad del algoritmo para encontrar clústeres sin especificar previamente el número de clústeres es una de sus principales ventajas.

Es importante tener en cuenta que la elección de ε y MinPts puede afectar significativamente a los resultados de la agrupación. En la siguiente sección, analizaremos cómo elegir estos parámetros de forma eficaz y presentaremos métodos como el gráfico de distancia k para la selección de parámetros.

Conceptos y parámetros clave de DBSCAN

Para comprender plenamente cómo DBSCAN forma clústeres, es importante entender dos conceptos clave: accesibilidad de densidad y conectividad de densidad.

Accesibilidad de densidad

Un punto q es accesible en densidad desde un punto p si:

1. p es un punto central (tiene al menos MinPts dentro de la distancia ε).

2. Hay una cadena de puntos p = p₁, ..., p_n = q en la que cada p_i+1 es directamente accesible en densidad desde p_i.

En términos más sencillos, puedes llegar a q desde p pasando por puntos centrales, donde cada paso no es mayor que ε.

Conectividad de densidad

Dos puntos p y q están conectados por densidad si existe un punto o tal que tanto p como q son accesibles por densidad desde o.

La conectividad de densidad es la base para formar clústeres en DBSCAN. Todos los puntos de un clúster están conectados entre sí por densidad, y si un punto está conectado por densidad a cualquier punto del clúster, también pertenece a ese clúster.

Selección de los parámetros DBSCAN

La eficacia de DBSCAN depende en gran medida de la elección de sus dos parámetros principales: ε (epsilon) y MinPts. A continuación, se explica cómo seleccionar estos parámetros:

Selección de ε (Epsilon)

El parámetro ε determina la distancia máxima entre dos puntos para que se consideren vecinos. Para elegir un ε adecuado:

1. Utiliza el conocimiento del dominio: Si tienes una idea clara de qué distancia es significativa para tu problema específico, utilízala como punto de partida.

2. Gráfico de distancia K: Este es un enfoque más sistemático:

• Calcula la distancia al k-ésimo vecino más cercano para cada punto (donde k = MinPts).
• Realiza gráficos de estas distancias k en orden ascendente.
• Busca un «codo» en el gráfico, es decir, un punto en el que la curva comienza a aplanarse.
• El valor ε en este codo suele ser una buena opción.

Seleccionar MinPts

MinPts determina el número mínimo de puntos necesarios para formar una región densa. Aquí tienes algunas pautas:

1. Regla general: Un buen punto de partida es establecer MinPts = 2 * num_features, donde num_features es el número de dimensiones de tu conjunto de datos.

2. Consideraciones sobre el ruido: Si tus datos contienen ruido o deseas detectar clústeres más pequeños, es posible que desees reducir el valor de MinPts.

3. Tamaño del conjunto de datos: Para conjuntos de datos más grandes, es posible que tengas que aumentar MinPts para evitar crear demasiados clústeres pequeños.

Recuerda que la elección de los parámetros puede afectar significativamente a los resultados. A menudo resulta útil probar diferentes valores y evaluar los clústeres resultantes para encontrar el que mejor se adapta a tu conjunto de datos y problema específicos.

Selección de una métrica de distancia

La elección de la métrica de distancia en DBSCAN puede afectar significativamente a los resultados de la agrupación. Por defecto, DBSCAN utiliza la distancia euclídea, que funciona bien para clústeres compactos y esféricos. Sin embargo, es posible que esto no sea ideal para todos los tipos de datos.

Puedes especificar métricas alternativas, tales como:

• Manhattan (norma L1) para datos en forma de cuadrícula
• Cosinusos para vectores dispersos de alta dimensión (por ejemplo, incrustaciones de texto)
• Haversine para coordenadas de latitud/longitud

Ajustar la métrica de distancia a la estructura de tus datos garantiza que la agrupación basada en la densidad refleje la similitud real.

En scikit-learn, el parámetro metric te permite configurarlo explícitamente (por ejemplo, metric='cosine'). Algunas métricas personalizadas pueden requerir una matriz de distancias precalculada.

Escalado de características

Dado que DBSCAN se basa en valores de distancia absolutos, las características sin escalar pueden dar lugar a resultados distorsionados. Las variables con rangos más amplios dominarán el cálculo de la distancia, aunque no sean más importantes. Esto puede impedir que el algoritmo identifique correctamente las regiones densas en los datos.

Para evitarlo, es fundamental escalar tus funciones para que contribuyan por igual. Los enfoques comunes incluyen:

• Estandarización: Los centros se sitúan en torno a cero con una varianza unitaria utilizando StandardScaler.

• Escalado mínimo-máximo: Reescala las características a un rango fijo (normalmente [0, 1]) utilizando MinMaxScaler.

Elige un método de escalado que se ajuste a la distribución de tus datos. Sin un preprocesamiento adecuado, DBSCAN puede no detectar clústeres significativos, incluso si tus parámetros epsilon y MinPts están bien ajustados.

Implementación de DBSCAN en Python

En esta sección, veremos la implementación de DBSCAN utilizando Python y la biblioteca scikit-learn. Utilizaremos el conjunto de datos Make Moons para mostrar el proceso.

Configuración del entorno

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
from sklearn.neighbors import NearestNeighbors

Estas importaciones proporcionan las herramientas necesarias para la manipulación de datos, la visualización, la creación de conjuntos de datos y la implementación del algoritmo DBSCAN.

Generación de datos de muestra

X, _ = make_moons(n_samples=200, noise=0.05, random_state=42)

Este código crea un conjunto de datos sintéticos utilizando la función « make_moons » de scikit-learn. A continuación, se ofrece una breve descripción del conjunto de datos:

La función make_moons genera una clasificación binaria. con un que se asemeja a dos medias lunas entrelazadas. En nuestro caso:

• Creamos 200 muestras (n_samples=200)
• Añadimos una pequeña cantidad de ruido gaussiano (noise=0.05) para que el conjunto de datos sea más realista.
• Establecemos random_state=42 la reproducibilidad

Este conjunto de datos es especialmente útil para demostrar DBSCAN porque:

1. Tiene una forma no convexa que muchos algoritmos de agrupamiento (como K-means) tendrían dificultades para
2. Los dos grupos están claramente separados, pero tienen una forma compleja.
3. El ruido añadido proporciona un escenario más realista en el que algunos puntos podrían clasificarse como valores atípicos.

Visualicemos este conjunto de datos para comprender mejor su estructura:

# Visualize the dataset
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1])
plt.title('Moon-shaped Dataset')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Esto te mostrará las dos formas de media luna entrelazadas en nuestro conjunto de datos, como se muestra a continuación.

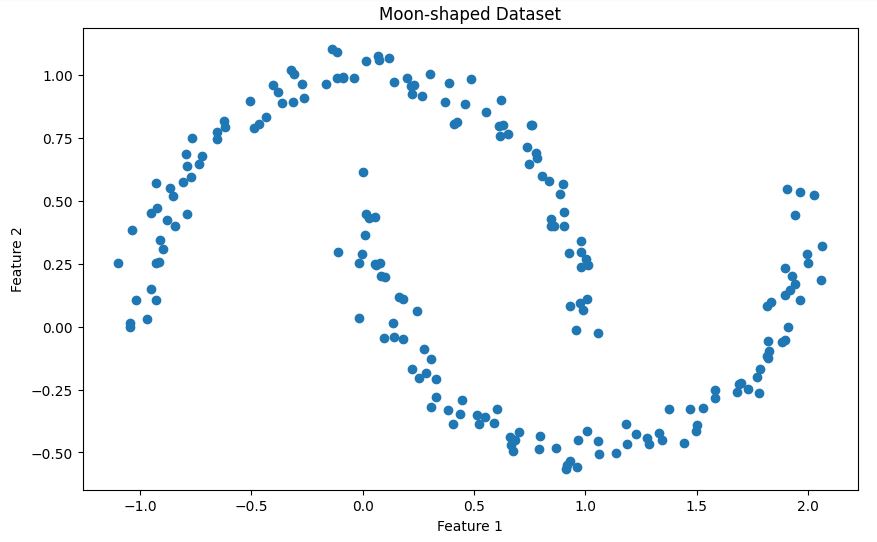
Determinación del parámetro épsilon

Utilizamos el método del gráfico de distancia k para ayudar a elegir un valor épsilon adecuado:

1. Definimos una función plot_k_distance_graph que calcula la distancia al k-ésimo vecino más cercano para cada punto.
2. Las distancias se ordenan y se gráfican.
3. Buscamos un «codo» en el gráfico resultante para elegir epsilon.

# Function to plot k-distance graph
def plot_k_distance_graph(X, k):
    neigh = NearestNeighbors(n_neighbors=k)
    neigh.fit(X)
    distances, _ = neigh.kneighbors(X)
    distances = np.sort(distances[:, k-1])
    plt.figure(figsize=(10, 6))
    plt.plot(distances)
    plt.xlabel('Points')
    plt.ylabel(f'{k}-th nearest neighbor distance')
    plt.title('K-distance Graph')
    plt.show()
# Plot k-distance graph
plot_k_distance_graph(X, k=5)

Salida

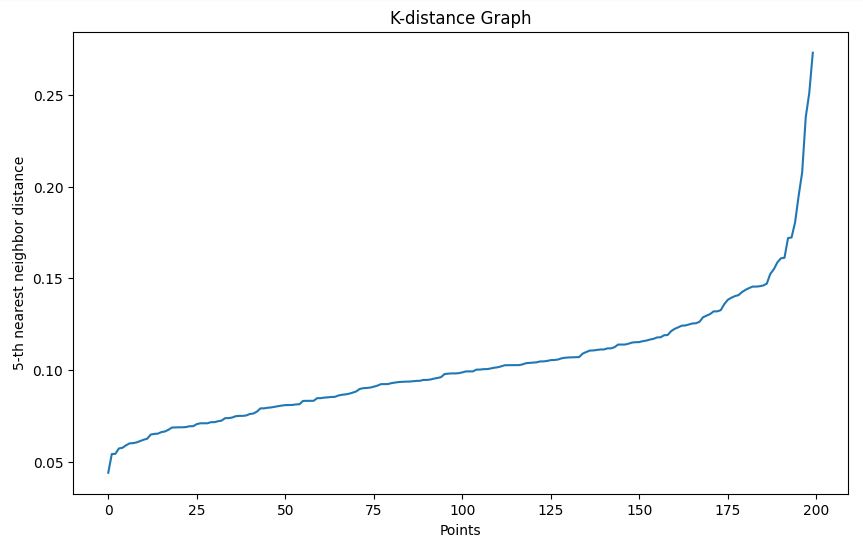
En nuestro ejemplo, basado en el gráfico de distancia k, elegimos un épsilon de 0,15.

Realización de agrupamientos DBSCAN

Utilizamos la implementación DBSCAN de scikit-learn:

1. Establecemos epsilon=0.15 basándonos en nuestro gráfico de distancia k.
2. Establecemos min_samples=5 (2 * num_features, ya que nuestros datos son 2D).
3. Ajustamos el modelo a vuestros datos y predecimos los clústeres.

# Perform DBSCAN clustering
epsilon = 0.15  # Chosen based on k-distance graph
min_samples = 5  # 2 * num_features (2D data)
dbscan = DBSCAN(eps=epsilon, min_samples=min_samples)
clusters = dbscan.fit_predict(X)

Visualización de los resultados

Creamos un gráfico de dispersión de nuestros puntos de datos, coloreándolos según los clústeres asignados. Los puntos clasificados como ruido suelen tener un color diferente (a menudo negro).

# Visualize the results
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='viridis')
plt.colorbar(scatter)
plt.title('DBSCAN Clustering Results')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Salida

Interpretación de los resultados

Por último, imprimimos el número de clústeres encontrados y el número de puntos clasificados como ruido. Esto nos ofrece un breve resumen de los resultados de la agrupación.

# Print number of clusters and noise points
n_clusters = len(set(clusters)) - (1 if -1 in clusters else 0)
n_noise = list(clusters).count(-1)
print(f'Number of clusters: {n_clusters}')
print(f'Number of noise points: {n_noise}')

Salida

Número de grupos: 2

Número de puntos de ruido: 5

Esta implementación proporciona un flujo de trabajo completo, desde la generación de datos hasta la interpretación de los resultados. Es importante tener en cuenta que, en situaciones reales, sustituirías la generación de datos de muestra por la carga y el preprocesamiento de tu conjunto de datos real.

Recuerda que la clave para el éxito del agrupamiento DBSCAN suele residir en la selección adecuada de los parámetros. No dudes en probar diferentes valores de epsilon y min_samples para encontrar el que mejor se adapte a tu conjunto de datos específico.

DBSCAN frente a K-Means

Aunque tanto DBSCAN como K-Means son algoritmos de agrupamiento muy populares, tienen características distintas que los hacen adecuados para diferentes tipos de datos y casos de uso. Comparemos estos dos algoritmos para entender cuándo usar cada uno.

Comparación visual

Para ilustrar estas diferencias, apliquemos ambos algoritmos a nuestro conjunto de datos con forma de luna.

from sklearn.cluster import KMeans

# DBSCAN clustering
dbscan = DBSCAN(eps=0.15, min_samples=5)
dbscan_labels = dbscan.fit_predict(X)

# K-Means clustering
kmeans = KMeans(n_clusters=2, random_state=42)
kmeans_labels = kmeans.fit_predict(X)

# Visualize the results
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

ax1.scatter(X[:, 0], X[:, 1], c=dbscan_labels, cmap='viridis')
ax1.set_title('DBSCAN Clustering')

ax2.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='viridis')
ax2.set_title('K-Means Clustering')

plt.show()

Este código aplica tanto DBSCAN como K-Means a nuestro conjunto de datos y visualiza los resultados uno al lado del otro.

Salida

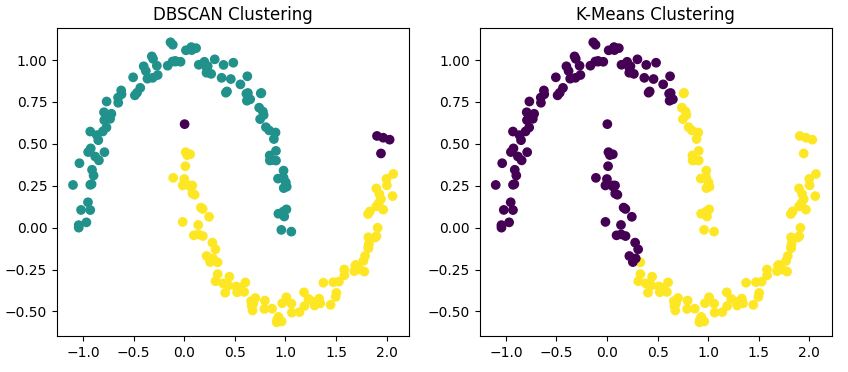
Notarás que

1. DBSCAN identifica correctamente las dos formas de media luna como grupos separados.
2. K-Means tiene dificultades con las formas no convexas, ya que a menudo divide una luna en dos grupos o combina partes de ambas lunas en un solo grupo.
3. DBSCAN puede identificar algunos puntos como ruido (normalmente con un color diferente), mientras que K-Means asigna cada punto a un clúster.

¿Cuándo utilizar DBSCAN?

Ahora que hemos visto cómo funciona DBSCAN y lo hemos comparado con K-Means, veamos cuándo DBSCAN es la opción adecuada para nuestras necesidades de agrupación. Las propiedades únicas de DBSCAN lo hacen especialmente adecuado para ciertos tipos de datos y ámbitos problemáticos.

Formas complejas de los cúmulos 

Basándonos en nuestra comparación anterior, DBSCAN realmente destaca cuando se trata de formas de clústeres no globulares. Si tus datos forman patrones arbitrarios como las medias lunas que hemos visto anteriormente, es probable que DBSCAN supere a algoritmos tradicionales como K-Means. 

Por ejemplo, en el análisis geográfico, las formaciones naturales como los sistemas fluviales o la expansión urbana suelen formar figuras irregulares que DBSCAN puede identificar eficazmente.

Número desconocido de clústeres

Una de las principales ventajas de DBSCAN es su capacidad para determinar automáticamente el número de clústeres. Esto resulta especialmente útil en el análisis exploratorio de datos, en el que es posible que no tengas conocimientos previos sobre la estructura subyacente de tus datos. 

Considera un problema de segmentación de mercado: es posible que no sepas de antemano cuántos grupos de clientes distintos existen. DBSCAN puede ayudar a descubrir estos segmentos sin necesidad de adivinar el número de clústeres.

Conjuntos de datos con ruido 

El enfoque de DBSCAN para manejar los puntos ruidosos lo hace robusto frente a los valores atípicos. Esto es crucial en muchos conjuntos de datos del mundo real, en los que son habituales los errores de medición o las anomalías.

Por ejemplo, en los sistemas de detección de anomalías para la seguridad de la red, DBSCAN puede separar eficazmente los patrones normales de tráfico de red de las posibles amenazas de seguridad.

Densidades variables de los clústeres

A diferencia de K-Means, que asume clústeres de densidad similar, DBSCAN puede identificar clústeres de densidades variables. Esto resulta especialmente útil en situaciones en las que algunos grupos de tus datos están más agrupados que otros.

Un ejemplo podría ser el análisis de la distribución de las galaxias en astronomía, donde diferentes regiones del espacio tienen densidades variables de objetos celestes.

Limitaciones de DBSCAN y alternativas

Ahora que ya sabemos cuándo utilizar DBSCAN, veamos cuáles son sus puntos débiles y echemos un vistazo a dos alternativas: OPTICS y HDBSCAN.

Limitaciones

Aunque DBSCAN es potente, es importante tener en cuenta sus limitaciones:

1. Sensibilidad de los parámetros: Como hemos comentado anteriormente, es fundamental elegir los valores adecuados para ε y MinPts. Las malas decisiones pueden dar lugar a resultados de agrupamiento subóptimos.
2. Datos de alta dimensión: El rendimiento de DBSCAN puede verse afectado con datos de alta dimensión debido a la «maldición de la dimensionalidad».
3. Densidades variables: Aunque DBSCAN puede manejar clústeres de diferentes densidades, las densidades extremadamente variables en el mismo conjunto de datos pueden seguir planteando retos.
4. Escalabilidad: Para conjuntos de datos muy grandes, DBSCAN puede resultar computacionalmente costoso en comparación con algoritmos como K-Means.

Para mejorar la agrupación, aplica técnicas de reducción de dimensionalidad como PCA, t-SNE o UMAP antes de utilizar DBSCAN. Esto reduce el ruido y mejora la capacidad del algoritmo para detectar regiones densas.

ÓPTICA

Una alternativa útil a DBSCAN es OPTICS (Ordenación de puntos para identificar la estructura de agrupamiento). Aborda la limitación de DBSCAN de utilizar un valor epsilon fijo ajustando dinámicamente los umbrales de vecindad.

OPTICS es más eficaz en conjuntos de datos con clústeres de diferentes densidades y puede revelar estructuras de clústeres que DBSCAN puede pasar por alto. Scikit-learn incluye OPTICS en su módulo de agrupamiento y utiliza la misma interfaz que DBSCAN.

HDBSCAN

HDBSCAN (Hierarchical DBSCAN) es una extensión moderna de DBSCAN que construye una jerarquía de clústeres basada en diferentes niveles de densidad. Elimina la necesidad de elegir manualmente el épsilon y, a menudo, proporciona mejores resultados con menos ajustes de parámetros.

HDBSCAN tiende a superar a DBSCAN en conjuntos de datos reales, ruidosos o desequilibrados. Está disponible como un paquete independiente de Python (hdbscan) y se integra bien con scikit-learn.

Ejemplos prácticos de DBSCAN

DBSCAN tiene aplicaciones en diversos ámbitos.

Análisis de datos espaciales

En los sistemas de información geográfica (SIG), DBSCAN puede identificar áreas de alta actividad o interés. Por ejemplo, un estudio titulado «Descubriendo la movilidad humana urbana a partir de datos GPS de taxis a gran escala» demuestra cómo DBSCAN puede detectar puntos de interés urbanos a partir de datos GPS de taxis. 

Esta aplicación muestra la capacidad de DBSCAN para identificar regiones de actividad densa en datos espaciales, lo cual es crucial para la planificación urbana y la gestión del transporte.

Procesamiento de imágenes 

DBSCAN puede agrupar píxeles en objetos distintos para tareas como el reconocimiento de objetos en imágenes. Un estudio titulado «Segmentación de tumores cerebrales a partir de imágenes de resonancia magnética: análisis de agrupamiento K-means y DBSCAN» demuestra la eficacia de DBSCAN en el análisis de imágenes médicas. 

Los investigadores utilizaron DBSCAN para segmentar con precisión los tumores cerebrales en resonancias magnéticas, lo que demuestra su potencial en el diagnóstico asistido por ordenador y en el campo de la imagen médica.

Detección de anomalías 

En la detección de fraudes o la supervisión del estado del sistema, DBSCAN puede aislar patrones inusuales. Un estudio titulado «Detección incremental eficiente de valores atípicos basada en la densidad y los clústeres en flujos de datos» demuestra la aplicación de un algoritmo DBSCAN modificado para la detección de anomalías en tiempo real. 

Los investigadores aplicaron una versión incremental de DBSCAN para detectar valores atípicos en datos de streaming, lo que tiene aplicaciones potenciales en la detección de fraudes y la supervisión del estado del sistema. 

Este estudio muestra cómo se puede adaptar DBSCAN para identificar patrones inusuales en flujos de datos continuos, una capacidad crucial para los sistemas de detección de fraudes en tiempo real.

Sistemas de recomendación

DBSCAN puede agrupar a usuarios con preferencias similares, lo que ayuda a generar recomendaciones más precisas. Por ejemplo, un estudio titulado «Sistema de recomendación de servicios basado en múltiples nubes que utiliza el algoritmo DBSCAN» muestra la aplicación de DBSCAN en la mejora del filtrado colaborativo para sistemas de recomendación. Los investigadores utilizaron DBSCAN como parte de un enfoque de agrupación para clasificar a los usuarios en función de sus preferencias y valoraciones cinematográficas, lo que mejoró la precisión de las recomendaciones de películas.

Este enfoque muestra cómo DBSCAN puede mejorar las recomendaciones personalizadas en ámbitos como los servicios de streaming de entretenimiento.

Conclusión

DBSCAN es una herramienta poderosa en el kit de herramientas del científico de datos, especialmente valiosa cuando se trata de conjuntos de datos complejos y ruidosos en los que se desconoce el número de clústeres. Sin embargo, como cualquier algoritmo, no es una solución válida para todos los casos. 

La clave para lograr una agrupación satisfactoria reside en comprender los datos, las ventajas y limitaciones de los diferentes algoritmos, y elegir la herramienta adecuada para cada tarea. En muchos casos, probar varios enfoques de agrupamiento, incluidos DBSCAN y K-Means, y comparar sus resultados puede proporcionar información valiosa sobre la estructura de tus datos.

Con la práctica y la experiencia, desarrollarás una intuición para saber cuándo es probable que DBSCAN revele los patrones ocultos en tus datos.

Puedes obtener más información sobre las diversas tecnologías y métodos que hemos tratado en esta publicación en DataCamp con los siguientes recursos: 

• Científico especializado en machine learning con Python
• Hoja de referencia sobre machine learning no supervisado
• Curso de aprendizaje no supervisado en Python