Um guia para o algoritmo de agrupamento DBSCAN

Na ciência de dados e no machine learning, a capacidade de descobrir padrões ocultos e agrupar pontos de dados semelhantes é uma habilidade importante. Os algoritmos de agrupamento são super importantes nesse processo. 

O agrupamento é uma técnica fundamental de machine learning e ciência de dados que envolve juntar pontos de dados parecidos. É um método de aprendizado sem supervisão, ou seja, não precisa de dados rotulados para encontrar padrões. 

O principal objetivo do agrupamento é:

• Simplifique grandes conjuntos de dados em subgrupos significativos
• Identifique agrupamentos naturais nos dados
• Descubra padrões e estruturas escondidos

Embora existam vários algoritmos de agrupamento (talvez você já tenha ouvido falar do K-means ou do agrupamento hierárquico), o DBSCAN oferece vantagens únicas. Como método baseado em densidade, o DBSCAN tem várias vantagens:

1. Flexibilidade na forma do cluster
2. Sem número pré-definido de clusters
3. Tratamento do ruído
4. Informações baseadas na densidade

Neste artigo, vamos ver o que é o algoritmo DBSCAN, como ele funciona, como implementá-lo em Python e quando usá-lo nos seus projetos de ciência de dados.

O que é DBSCAN?

DBSCAN, que significa Agrupamento Espacial Baseado em Densidade de Aplicações com Ruído, é um algoritmo de agrupamento bem poderoso que junta pontos que estão bem próximos uns dos outros no espaço de dados. Diferente de outros algoritmos de agrupamento, o DBSCAN não precisa que você diga antes quantos grupos quer, o que o torna bem útil para fazer análises exploratórias de dados.

O algoritmo funciona definindo os clusters como regiões densas separadas por regiões de menor densidade. Essa abordagem permite que o DBSCAN descubra clusters de formas arbitrárias e identifique outliers como ruído.

O DBSCAN gira em torno de três conceitos principais:

1. Pontos principais: São pontos que têm pelo menos um número mínimo de outros pontos (MinPts) dentro de uma distância específica (ε ou épsilon).
2. Pontos de fronteira: São pontos que estão dentro da distância ε de um ponto central, mas que não têm vizinhos MinPts.
3. Pontos de ruído: Esses são pontos que não são nem pontos centrais nem pontos de fronteira. Eles não estão perto o suficiente de nenhum aglomerado para serem incluídos.

Imagem do autor

O diagrama acima mostra esses conceitos. Os pontos centrais (azuis) são o coração dos clusters, os pontos de borda (laranja) ficam na borda dos clusters e os pontos de ruído (vermelhos) ficam isolados.

O DBSCAN usa dois parâmetros principais:

• ε (epsilon): A distância máxima entre dois pontos para que eles sejam considerados vizinhos.
• MinPts: O número mínimo de pontos necessários para formar uma região densa.

Ao ajustar esses parâmetros, você pode controlar como o algoritmo define os clusters, permitindo que ele se adapte a diferentes tipos de conjuntos de dados e requisitos de agrupamento.

Na próxima seção, vamos ver como o algoritmo DBSCAN funciona, explorando seu processo passo a passo para identificar clusters nos dados.

Como funciona o DBSCAN?

O DBSCAN funciona examinando a vizinhança de cada ponto no conjunto de dados. O algoritmo segue um processo passo a passo para identificar agrupamentos com base na densidade dos pontos de dados. Vamos ver como o DBSCAN funciona:

1. Seleção de parâmetros
• Escolha ε (epsilon): A distância máxima entre dois pontos para que eles sejam considerados vizinhos.
• Escolha MinPts: O número mínimo de pontos necessários para formar uma região densa.
2. Escolha um ponto de partida
• O algoritmo começa com um ponto aleatório não visitado no conjunto de dados.
3. Dá uma olhada na vizinhança
• Ele pega todos os pontos que estão a uma distância ε do ponto inicial.
• Se o número de pontos vizinhos for menor que MinPts, o ponto é marcado como ruído (por enquanto).
• Se tiver pelo menos MinPts pontos dentro da distância ε, o ponto é marcado como um ponto central e um novo agrupamento é formado.
4. Expanda o cluster
• Todos os vizinhos do ponto central são adicionados ao cluster.
• Para cada um desses vizinhos:
• Se for um ponto central, seus vizinhos são adicionados ao cluster de forma recursiva.
• Se não for um ponto central, ele é marcado como um ponto de fronteira e a expansão para.
5. Repita o processo
• O algoritmo vai para o próximo ponto não visitado no conjunto de dados.
• Os passos 3 e 4 são repetidos até que todos os pontos tenham sido visitados.
6. Finalizar Clusters
• Depois que todos os pontos forem processados, o algoritmo identifica todos os clusters.
• Pontos inicialmente rotulados como ruído agora podem ser pontos de fronteira se estiverem dentro da distância ε de um ponto central.
7. Lidando com o barulho
• Quaisquer pontos que não pertençam a nenhum agrupamento continuam classificados como ruído.

Esse processo permite que o DBSCAN forme grupos de formas aleatórias e identifique valores atípicos de forma eficaz. A capacidade do algoritmo de encontrar agrupamentos sem precisar especificar o número de agrupamentos antes é um dos seus principais pontos fortes.

É importante notar que a escolha de ε e MinPts pode afetar bastante os resultados do agrupamento. Na próxima seção, vamos falar sobre como escolher esses parâmetros de forma eficaz e apresentar métodos como o gráfico de distância k para a seleção de parâmetros.

Conceitos e parâmetros principais do DBSCAN

Para entender completamente como o DBSCAN forma clusters, é importante compreender dois conceitos-chave: acessibilidade de densidade e conectividade de densidade.

Alcance da densidade

Um ponto q é alcançável em termos de densidade a partir de um ponto p se:

1. p é um ponto central (tem pelo menos MinPts dentro da distância ε)

2. Tem uma cadeia de pontos p = p₁, ..., p_n = q onde cada p_i+1 é diretamente alcançável em densidade a partir de p_i.

Em termos mais simples, você pode chegar a q a partir de p passando por pontos centrais, onde cada passo não é maior que ε.

Conectividade de densidade

Dois pontos p e q são densamente conectados se existe um ponto o tal que tanto p quanto q são densamente alcançáveis a partir de o.

A conectividade de densidade é a base para formar clusters no DBSCAN. Todos os pontos em um agrupamento estão conectados entre si por densidade, e se um ponto está conectado por densidade a qualquer ponto no agrupamento, ele também faz parte desse agrupamento.

Escolhendo os parâmetros do DBSCAN

A eficácia do DBSCAN depende muito da escolha dos seus dois parâmetros principais: ε (epsilon) e MinPts. Veja como selecionar esses parâmetros:

Selecionando ε (Epsilon)

O parâmetro ε determina a distância máxima entre dois pontos para que eles sejam considerados vizinhos. Para escolher um ε adequado:

1. Use o conhecimento do domínio: Se você sabe qual distância é importante para o seu problema específico, use isso como ponto de partida.

2. Gráfico de distância K: Essa é uma abordagem mais sistemática:

• Calcule a distância até o k-ésimo vizinho mais próximo para cada ponto (onde k = MinPts).
• Plote essas distâncias k em ordem crescente.
• Procure um “cotovelo” no gráfico – um ponto em que a curva começa a se estabilizar.
• O valor ε neste cotovelo costuma ser uma boa escolha.

Selecionando MinPts

MinPts determina o número mínimo de pontos necessários para formar uma região densa. Aqui vão algumas dicas:

1. Regra geral: Um bom ponto de partida é definir MinPts = 2 * num_features, onde num_features é o número de dimensões no seu conjunto de dados.

2. Considerações sobre ruído: Se seus dados tiverem ruído ou você quiser detectar clusters menores, talvez seja uma boa ideia diminuir o MinPts.

3. Tamanho do conjunto de dados: Para conjuntos de dados maiores, talvez você precise aumentar o parâmetro ` MinPts ` para evitar a criação de muitos clusters pequenos.

Lembre-se de que a escolha dos parâmetros pode afetar bastante os resultados. Muitas vezes, é legal testar valores diferentes e ver os agrupamentos que saem pra achar o que funciona melhor pro seu conjunto de dados e problema.

Escolhendo uma métrica de distância

A escolha da métrica de distância no DBSCAN pode afetar bastante os resultados do agrupamento. Por padrão, o DBSCAN usa a distância euclidiana, que funciona bem para clusters compactos e esféricos. Mas isso pode não ser ideal para todos os tipos de dados.

Você pode especificar métricas alternativas, como:

• Manhattan (norma L1) para dados em forma de grade
• Cosseno para vetores esparsos de alta dimensão (por exemplo, incorporações de texto)
• Haversine para coordenadas de latitude/longitude

Combinar a métrica de distância com a estrutura dos seus dados garante que o agrupamento baseado em densidade reflita a semelhança real.

Em scikit-learn, o parâmetro metric permite definir isso explicitamente (por exemplo, metric='cosine'). Algumas métricas personalizadas podem precisar de uma matriz de distância pré-calculada.

Escalonamento de recursos

Como o DBSCAN depende de valores de distância absolutos, características não escalonadas podem levar a resultados distorcidos. Variáveis com intervalos maiores vão dominar o cálculo da distância, mesmo que não sejam mais importantes. Isso pode impedir que o algoritmo identifique corretamente regiões densas nos dados.

Para evitar isso, é essencial dimensionar seus recursos para que eles contribuam igualmente. Abordagens comuns incluem:

• Padronização: Centros com valor próximo de zero e variância unitária usando StandardScaler.

• Escalonamento Mínimo-Máximo: Redimensiona os recursos para um intervalo fixo (normalmente [0, 1]) usando MinMaxScaler.

Escolha um método de dimensionamento que combine com a distribuição dos seus dados. Sem um pré-processamento adequado, o DBSCAN pode não conseguir detectar clusters significativos, mesmo que seus parâmetros epsilon e MinPts estejam bem ajustados.

Implementando DBSCAN em Python

Nesta seção, vamos ver como implementar o DBSCAN usando Python e a biblioteca scikit-learn. Vamos usar o conjunto de dados Make Moons para mostrar como funciona.

Configurando o ambiente

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
from sklearn.neighbors import NearestNeighbors

Essas importações fornecem as ferramentas necessárias para manipulação de dados, visualização, criação de conjuntos de dados e implementação do algoritmo DBSCAN.

Gerando dados de amostra

X, _ = make_moons(n_samples=200, noise=0.05, random_state=42)

Esse código cria um conjunto de dados sintéticos usando a função ` make_moons ` do scikit-learn. Aqui vai uma breve descrição do conjunto de dados:

A função make_moons gera uma classificação binária classificação que lembra duas meias-luas entrelaçadas. No nosso caso:

• Criamos 200 amostras (n_samples=200)
• A gente adiciona um pouco de ruído gaussiano (noise=0.05) para tornar o conjunto de dados mais realista.
• Definimos random_state=42 para a reprodutibilidade

Esse conjunto de dados é super útil pra mostrar como funciona o DBSCAN porque:

1. Tem uma forma não convexa que muitos algoritmos de agrupamento (como o K-means) teriam dificuldade em lidar
2. Os dois aglomerados estão bem separados, mas têm um formato complicado.
3. O ruído adicionado cria um cenário mais realista, onde alguns pontos podem ser classificados como outliers.

Vamos visualizar esse conjunto de dados para entender melhor sua estrutura:

# Visualize the dataset
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1])
plt.title('Moon-shaped Dataset')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Isso vai mostrar as duas formas de meia-lua entrelaçadas no nosso conjunto de dados, como mostrado abaixo.

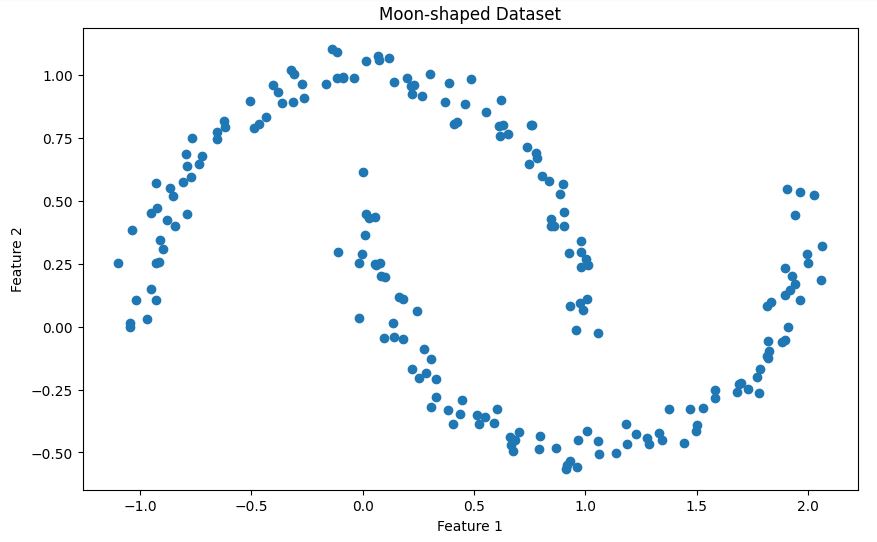
Determinando o parâmetro epsilon

Usamos o método do gráfico de distância k para ajudar a escolher um valor epsilon apropriado:

1. A gente define uma função plot_k_distance_graph que calcula a distância até o k-ésimo vizinho mais próximo para cada ponto.
2. As distâncias são organizadas e plotadas.
3. A gente procura um “cotovelo” no gráfico resultante para escolher o epsilon.

# Function to plot k-distance graph
def plot_k_distance_graph(X, k):
    neigh = NearestNeighbors(n_neighbors=k)
    neigh.fit(X)
    distances, _ = neigh.kneighbors(X)
    distances = np.sort(distances[:, k-1])
    plt.figure(figsize=(10, 6))
    plt.plot(distances)
    plt.xlabel('Points')
    plt.ylabel(f'{k}-th nearest neighbor distance')
    plt.title('K-distance Graph')
    plt.show()
# Plot k-distance graph
plot_k_distance_graph(X, k=5)

Saída

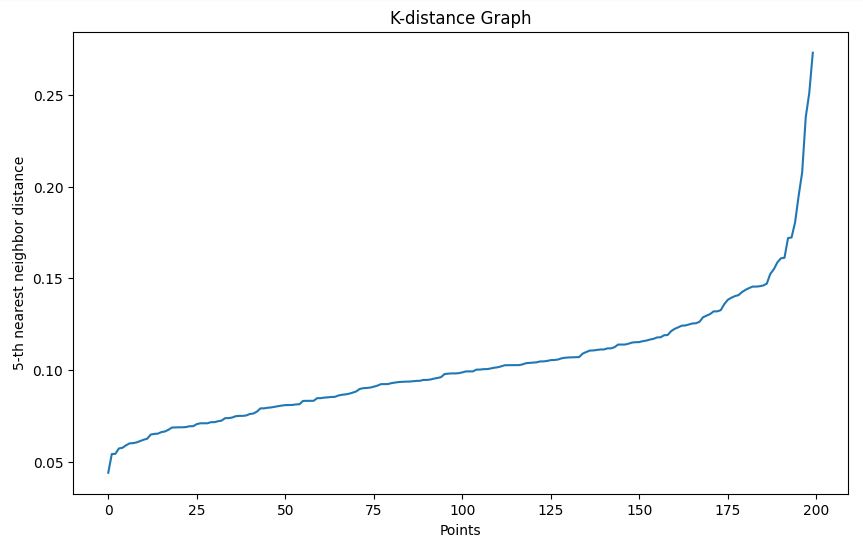
No nosso exemplo, com base no gráfico de distância k, escolhemos um epsilon de 0,15.

Fazendo agrupamento DBSCAN

Usamos a implementação DBSCAN do scikit-learn:

1. Definimos epsilon=0.15 com base no nosso gráfico de distância k.
2. Definimos min_samples=5 (2 * num_features, já que nossos dados são 2D).
3. A gente ajusta o modelo aos nossos dados e prevê os clusters.

# Perform DBSCAN clustering
epsilon = 0.15  # Chosen based on k-distance graph
min_samples = 5  # 2 * num_features (2D data)
dbscan = DBSCAN(eps=epsilon, min_samples=min_samples)
clusters = dbscan.fit_predict(X)

Visualizando os resultados

Fazemos um gráfico de dispersão dos nossos pontos de dados, colorindo-os de acordo com os grupos que lhes foram atribuídos. Os pontos classificados como ruído geralmente têm uma cor diferente (muitas vezes preta).

# Visualize the results
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='viridis')
plt.colorbar(scatter)
plt.title('DBSCAN Clustering Results')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Saída

Interpretando os resultados

Por fim, imprimimos o número de clusters encontrados e o número de pontos classificados como ruído. Isso nos dá um resumo rápido dos resultados do agrupamento.

# Print number of clusters and noise points
n_clusters = len(set(clusters)) - (1 if -1 in clusters else 0)
n_noise = list(clusters).count(-1)
print(f'Number of clusters: {n_clusters}')
print(f'Number of noise points: {n_noise}')

Saída

Número de grupos: 2

Número de pontos de ruído: 5

Essa implementação oferece um fluxo de trabalho completo, desde a geração de dados até a interpretação dos resultados. É importante notar que, em cenários reais, você substituiria a geração de dados de amostra pelo carregamento e pré-processamento do seu conjunto de dados real.

Lembre-se, o segredo para um agrupamento DBSCAN bem-sucedido geralmente está na escolha certa dos parâmetros. Não hesite em experimentar diferentes valores de epsilon e min_samples para encontrar o mais adequado para o seu conjunto de dados específico.

DBSCAN vs. K-Means

Embora tanto o DBSCAN quanto o K-Means sejam algoritmos de agrupamento bem conhecidos, eles têm características diferentes que os tornam adequados para diferentes tipos de dados e casos de uso. Vamos comparar esses dois algoritmos para entender quando usar cada um deles.

Comparação visual

Para mostrar essas diferenças, vamos usar os dois algoritmos no nosso conjunto de dados em forma de lua.

from sklearn.cluster import KMeans

# DBSCAN clustering
dbscan = DBSCAN(eps=0.15, min_samples=5)
dbscan_labels = dbscan.fit_predict(X)

# K-Means clustering
kmeans = KMeans(n_clusters=2, random_state=42)
kmeans_labels = kmeans.fit_predict(X)

# Visualize the results
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

ax1.scatter(X[:, 0], X[:, 1], c=dbscan_labels, cmap='viridis')
ax1.set_title('DBSCAN Clustering')

ax2.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='viridis')
ax2.set_title('K-Means Clustering')

plt.show()

Esse código usa o DBSCAN e o K-Means no nosso conjunto de dados e mostra os resultados lado a lado.

Saída

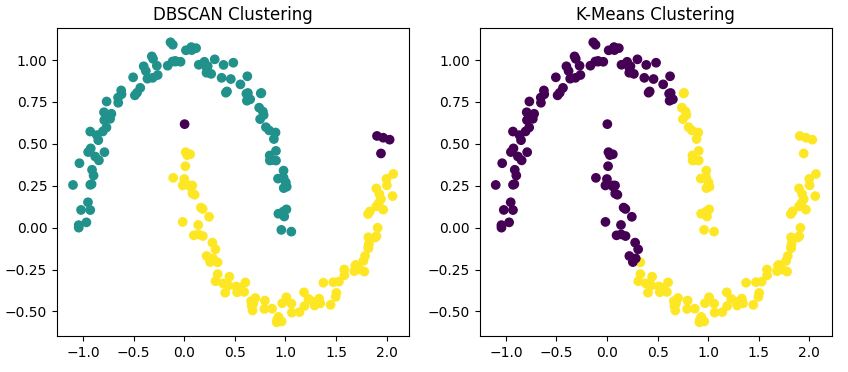
Você vai perceber que

1. O DBSCAN identifica corretamente as duas formas de meia-lua como agrupamentos separados.
2. O K-Means tem dificuldade com a forma não convexa, muitas vezes dividindo uma lua em dois agrupamentos ou juntando partes das duas luas em um único agrupamento.
3. O DBSCAN pode identificar alguns pontos como ruído (geralmente com cores diferentes), enquanto o K-Means coloca cada ponto em um cluster.

Quando usar o DBSCAN?

Agora que vimos como o DBSCAN funciona e comparamos com o K-Means, vamos ver quando o DBSCAN é a escolha certa para nossas necessidades de agrupamento. As propriedades únicas do DBSCAN fazem com que ele seja especialmente bom para certos tipos de dados e áreas de problemas.

Formas complexas de aglomerados 

Com base na nossa comparação anterior, o DBSCAN realmente se destaca quando lida com formas de agrupamentos não globulares. Se seus dados formam padrões aleatórios, como as meias-luas que vimos antes, o DBSCAN provavelmente vai funcionar melhor do que os algoritmos tradicionais, como o K-Means. 

Por exemplo, na análise geográfica, formações naturais como sistemas fluviais ou expansão urbana geralmente têm formas irregulares que o DBSCAN consegue identificar direitinho.

Número desconhecido de clusters

Uma das principais vantagens do DBSCAN é a capacidade de determinar automaticamente o número de clusters. Isso é super útil na análise exploratória de dados, onde você pode não ter conhecimento prévio sobre a estrutura subjacente dos seus dados. 

Pense num problema de segmentação de mercado: você pode não saber de antemão quantos grupos distintos de clientes existem. O DBSCAN pode ajudar a descobrir esses segmentos sem que você precise adivinhar o número de clusters.

Conjuntos de dados com ruído 

A maneira como o DBSCAN lida com pontos ruidosos o torna resistente a valores atípicos. Isso é super importante em muitos conjuntos de dados do mundo real, onde erros de medição ou anomalias são comuns.

Por exemplo, em sistemas de detecção de anomalias para segurança de rede, o DBSCAN consegue separar bem os padrões normais de tráfego de rede das possíveis ameaças à segurança.

Densidades variáveis dos aglomerados

Ao contrário do K-Means, que assume clusters de densidade semelhante, o DBSCAN consegue identificar clusters de densidades diferentes. Isso é super útil quando alguns grupos nos seus dados estão mais compactados do que outros.

Um exemplo poderia ser a análise da distribuição das galáxias na astronomia, onde diferentes regiões do espaço têm densidades variadas de objetos celestes.

Limitações do DBSCAN e alternativas

Agora que já sabemos quando usar o DBSCAN, vamos ver quais são os pontos fracos dele e dar uma olhada rápida em duas alternativas: OPTICS e HDBSCAN.

Limitações

Embora o DBSCAN seja poderoso, é importante estar ciente de suas limitações:

1. Sensibilidade dos parâmetros: Como falamos antes, escolher valores certos para ε e MinPts é super importante. Escolhas ruins podem levar a resultados de agrupamento abaixo do ideal.
2. de dados de alta dimensão: O desempenho do DBSCAN pode piorar com dados de alta dimensão por causa da “maldição da dimensionalidade”.
3. : Embora o DBSCAN consiga lidar com clusters de densidades diferentes, densidades muito variadas no mesmo conjunto de dados ainda podem ser um desafio.
4. Escalabilidade: Para conjuntos de dados muito grandes, o DBSCAN pode ser computacionalmente caro em comparação com algoritmos como o K-Means.

Para melhorar o agrupamento, use técnicas de redução de dimensionalidade como PCA, t-SNE ou UMAP antes de usar o DBSCAN. Isso reduz o ruído e melhora a capacidade do algoritmo de detectar regiões densas.

ÓPTICA

Uma alternativa útil ao DBSCAN é o OPTICS (Ordering Points To Identify the Clustering Structure). Ele resolve a limitação do DBSCAN de usar um valor epsilon fixo, ajustando dinamicamente os limites de vizinhança.

O OPTICS é mais eficaz em conjuntos de dados com clusters de diferentes densidades e pode revelar estruturas de clusters que o DBSCAN pode deixar passar. O Scikit-learn inclui o OPTICS no seu módulo de agrupamento e usa a mesma interface que o DBSCAN.

HDBSCAN

O HDBSCAN (Hierarchical DBSCAN) é uma versão mais moderna do DBSCAN que cria uma hierarquia de clusters com base em diferentes níveis de densidade. Isso elimina a necessidade de escolher manualmente o epsilon e, muitas vezes, dá resultados melhores com menos ajustes de parâmetros.

O HDBSCAN costuma ter um desempenho melhor do que o DBSCAN básico em conjuntos de dados reais, ruidosos ou desequilibrados. Está disponível como um pacote Python independente (hdbscan) e se integra bem com scikit-learn.

Exemplos práticos do DBSCAN

O DBSCAN tem aplicações em vários domínios.

Análise de dados espaciais

Nos sistemas de informação geográfica (SIG), o DBSCAN consegue identificar áreas de muita atividade ou interesse. Por exemplo, um estudo chamado “Descobrindo a mobilidade humana urbana a partir de dados GPS de táxis em grande escala” mostra como o DBSCAN consegue detectar pontos de interesse urbanos a partir de dados de GPS de táxis. 

Esse aplicativo mostra como o DBSCAN consegue identificar áreas com muita atividade em dados espaciais, o que é super importante para o planejamento urbano e a gestão do transporte.

Processamento de imagens 

O DBSCAN pode juntar pixels em objetos diferentes para tarefas como reconhecimento de objetos em imagens. Um estudo chamado “Segmentação de tumor cerebral a partir de imagem de ressonância magnética – Análise de agrupamento K-means e DBSCAN” mostra como o DBSCAN é eficiente na análise de imagens médicas. 

Os pesquisadores usaram o DBSCAN para segmentar com precisão tumores cerebrais em exames de ressonância magnética, mostrando seu potencial no diagnóstico assistido por computador e em imagens médicas.

Detecção de anomalias 

Na detecção de fraudes ou no monitoramento da saúde do sistema, o DBSCAN pode isolar padrões incomuns. Um estudo chamado “Detecção eficiente de outliers incrementais baseada em densidade e cluster em fluxos de dados” mostra como usar um algoritmo DBSCAN modificado para detectar anomalias em tempo real. 

Os pesquisadores usaram uma versão melhorada do DBSCAN para achar dados fora do normal em fluxos de dados, o que pode ser útil para detectar fraudes e monitorar a saúde do sistema. 

Esse estudo mostra como o DBSCAN pode ser adaptado para identificar padrões incomuns em fluxos de dados contínuos, uma capacidade essencial para sistemas de detecção de fraudes em tempo real.

Sistemas de recomendação

O DBSCAN pode juntar usuários com gostos parecidos, ajudando a gerar recomendações mais precisas. Por exemplo, um estudo chamado “Sistema de recomendação de serviços baseado em múltiplas nuvens usando o algoritmo DBSCAN” mostra como o DBSCAN pode melhorar a filtragem colaborativa em sistemas de recomendação. Os pesquisadores usaram o DBSCAN como parte de uma abordagem de agrupamento para classificar os usuários com base em suas preferências e avaliações de filmes, o que melhorou a precisão das recomendações de filmes.

Essa abordagem mostra como o DBSCAN pode melhorar as recomendações personalizadas em áreas como serviços de streaming de entretenimento.

Conclusão

O DBSCAN é uma ferramenta poderosa no kit de ferramentas do cientista de dados, especialmente útil quando se lida com conjuntos de dados complexos e ruidosos, onde o número de clusters é desconhecido. Mas, como qualquer algoritmo, não é uma solução que serve para todos. 

O segredo para um agrupamento bem-sucedido está em entender seus dados, os pontos fortes e as limitações dos diferentes algoritmos e escolher a ferramenta certa para o trabalho. Em muitos casos, experimentar várias abordagens de agrupamento, incluindo DBSCAN e K-Means, e comparar seus resultados pode fornecer informações valiosas sobre a estrutura dos seus dados.

Com prática e experiência, você vai desenvolver uma intuição para saber quando o DBSCAN provavelmente revelará os padrões ocultos em seus dados.

Você pode saber mais sobre as várias tecnologias e métodos que falamos neste post no DataCamp com os seguintes recursos: 

• Cientista de Machine Learning em Python
• Folha de dicas sobre machine learning não supervisionado
• Curso de Aprendizado Não Supervisionado em Python