Guide de l'algorithme de regroupement DBSCAN

Dans le domaine de la science des données et de l'apprentissage automatique, la capacité à découvrir des modèles cachés et à regrouper des points de données similaires est une compétence importante. Les algorithmes de regroupement jouent un rôle essentiel dans ce processus. 

Le regroupement est une technique fondamentale de l'apprentissage automatique et de la science des données qui consiste à regrouper des points de données similaires. Il s'agit d'une méthode d'apprentissage non supervisée, ce qui signifie qu'elle ne nécessite pas de données étiquetées pour identifier des modèles. 

L'objectif principal du regroupement est de :

• Simplifier les grands ensembles de données en sous-groupes significatifs
• Identifier les regroupements naturels au sein des données
• Révéler les modèles et les structures cachés

Bien qu'il existe de nombreux algorithmes de regroupement (vous avez peut-être entendu parler des algorithmes K-means ou de regroupement hiérarchique), DBSCAN offre des avantages uniques. En tant que méthode basée sur la densité, DBSCAN présente plusieurs atouts :

1. Flexibilité dans la forme des clusters
2. Aucun nombre prédéfini de clusters
3. Gestion du bruit
4. Perspective fondée sur la densité

Dans cet article, nous examinerons ce qu'est l'algorithme DBSCAN, comment il fonctionne, comment l'implémenter en Python et quand l'utiliser dans vos projets de science des données.

Qu'est-ce que DBSCAN ?

DBSCAN, acronyme de Density-Based Spatial Clustering of Applications with Noise (regroupement spatial basé sur la densité des applications avec bruit), est un algorithme de regroupement puissant qui regroupe les points étroitement rapprochés dans l'espace de données. Contrairement à certains autres algorithmes de clustering, DBSCAN ne nécessite pas de spécifier le nombre de clusters à l'avance, ce qui le rend particulièrement utile pour l'analyse exploratoire des données.

L'algorithme fonctionne en définissant les clusters comme des régions denses séparées par des régions de densité plus faible. Cette approche permet à DBSCAN de détecter des clusters de forme arbitraire et d'identifier les valeurs aberrantes comme du bruit.

DBSCAN s'articule autour de trois concepts clés :

1. Points essentiels: Il s'agit de points qui possèdent au moins un nombre minimum d'autres points (MinPts) à une distance spécifiée (ε ou epsilon).
2. Points frontaliers: Il s'agit de points qui se trouvent à une distance ε d'un point central, mais qui n'ont pas eux-mêmes de voisins MinPts.
3. Points relatifs au bruit: Il s'agit de points qui ne sont ni des points centraux ni des points frontaliers. Ils ne sont pas suffisamment proches d'un groupe pour être inclus.

Image par l'auteur

Le diagramme ci-dessus illustre ces concepts. Les points centraux (en bleu) constituent le cœur des grappes, les points périphériques (en orange) se trouvent à la périphérie des grappes et les points parasites (en rouge) sont isolés.

DBSCAN utilise deux paramètres principaux :

• ε (epsilon): La distance maximale entre deux points pour qu'ils soient considérés comme voisins.
• MinPts: Le nombre minimum de points requis pour former une région dense.

En ajustant ces paramètres, vous pouvez contrôler la manière dont l'algorithme définit les clusters, ce qui lui permet de s'adapter à différents types d'ensembles de données et d'exigences en matière de clustering.

Dans la section suivante, nous examinerons le fonctionnement de l'algorithme DBSCAN, en explorant son processus étape par étape pour identifier les clusters dans les données.

Comment fonctionne DBSCAN ?

DBSCAN fonctionne en examinant le voisinage de chaque point dans l'ensemble de données. L'algorithme suit un processus étape par étape pour identifier les clusters en fonction de la densité des points de données. Analysons le fonctionnement de DBSCAN :

1. Sélection des paramètres
• Veuillez sélectionner ε (epsilon) : La distance maximale entre deux points pour qu'ils soient considérés comme voisins.
• Veuillez sélectionner MinPts : Le nombre minimum de points requis pour former une région dense.
2. Veuillez sélectionner un point de départ
• L'algorithme commence par un point arbitraire non visité dans l'ensemble de données.
3. Veuillez examiner le quartier.
• Il récupère tous les points situés à une distance ε du point de départ.
• Si le nombre de points voisins est inférieur à MinPts, le point est étiqueté comme bruit (pour l'instant).
• Si au moins MinPts points se trouvent à une distance ε, le point est marqué comme point central et un nouveau cluster est formé.
4. Développer le cluster
• Tous les voisins du point central sont inclus dans le cluster.
• Pour chacun de ces voisins :
• S'il s'agit d'un point central, ses voisins sont ajoutés au cluster de manière récursive.
• Si ce n'est pas un point central, il est marqué comme point frontalier et l'expansion s'arrête.
5. Veuillez répéter le processus.
• L'algorithme se déplace vers le point suivant non visité dans l'ensemble de données.
• Les étapes 3 et 4 sont répétées jusqu'à ce que tous les points aient été visités.
6. Finaliser les clusters
• Une fois tous les points traités, l'algorithme identifie tous les clusters.
• Les points initialement considérés comme du bruit peuvent désormais être des points frontaliers s'ils se trouvent à une distance ε d'un point central.
7. Gestion du bruit
• Les points n'appartenant à aucun cluster sont classés comme du bruit.

Ce processus permet à DBSCAN de former des clusters de formes arbitraires et d'identifier efficacement les valeurs aberrantes. La capacité de l'algorithme à identifier des clusters sans spécifier au préalable leur nombre constitue l'un de ses principaux atouts.

Il est important de noter que le choix de ε et MinPts peut considérablement influencer les résultats du regroupement. Dans la section suivante, nous aborderons la manière de choisir efficacement ces paramètres et présenterons des méthodes telles que le graphe de distance k pour la sélection des paramètres.

Concepts et paramètres clés de DBSCAN

Pour bien comprendre comment DBSCAN forme des clusters, il est essentiel de saisir deux concepts clés : l'accessibilité de densité et la connectivité de densité.

Accessibilité de la densité

Un point q est accessible en densité à partir d'un point p si :

1. p est un point central (possède au moins MinPts à une distance ε)

2. Il existe une chaîne de points p = p₁, ..., p_n = q où chaque p_i+1 est directement accessible en densité à partir de p_i.

En termes plus simples, vous pouvez atteindre q à partir de p en passant par des points centraux, chaque étape n'étant pas supérieure à ε.

Connectivité de densité

Deux points p et q sont denses-connectés s'il existe un point o tel que p et q sont tous deux denses-accessibles depuis o.

La connectivité de densité constitue la base de la formation de clusters dans DBSCAN. Tous les points d'un cluster sont mutuellement connectés en termes de densité, et si un point est connecté en termes de densité à n'importe quel point du cluster, il appartient également à ce cluster.

Sélection des paramètres DBSCAN

L'efficacité de DBSCAN dépend fortement du choix de ses deux paramètres principaux : ε (epsilon) et MinPts. Voici comment procéder pour sélectionner ces paramètres :

Sélectionner ε (Epsilon)

Le paramètre ε détermine la distance maximale entre deux points pour qu'ils soient considérés comme voisins. Pour sélectionner un ε approprié :

1. Utiliser l' s issues de la connaissance du domaine : Si vous avez une idée de la distance qui est pertinente pour votre problème spécifique, veuillez l'utiliser comme point de départ.

2. s graphiques K-distance : Il s'agit d'une approche plus systématique :

• Calculez la distance jusqu'au k-ième voisin le plus proche pour chaque point (où k = MinPts).
• Veuillez réaliser un graphique pour représenter ces distances k par ordre croissant.
• Recherchez un « coude » dans le graphique, c'est-à-dire un point où la courbe commence à se stabiliser.
• La valeur ε à ce coude constitue souvent un choix judicieux.

Sélectionner MinPts

MinPts détermine le nombre minimal de points requis pour former une région dense. Voici quelques directives :

1. Règle générale: Un bon point de départ consiste à définir MinPts = 2 * num_features, où num_features correspond au nombre de dimensions de votre ensemble de données.

2. Considérations relatives au bruit: Si vos données contiennent du bruit ou si vous souhaitez détecter des clusters plus petits, il peut être judicieux de réduire l'MinPts.

3. s relatives à la taille de l'ensemble de données : Pour les ensembles de données plus volumineux, il peut être nécessaire d'augmenter la valeur de MinPts afin d'éviter la création d'un nombre excessif de petits clusters.

Veuillez noter que le choix des paramètres peut influencer considérablement les résultats. Il est souvent utile d'expérimenter différentes valeurs et d'évaluer les clusters obtenus afin de trouver celui qui correspond le mieux à votre ensemble de données et à votre problème spécifiques.

Sélection d'une métrique de distance

Le choix de la métrique de distance dans DBSCAN peut avoir un impact significatif sur les résultats du regroupement. Par défaut, DBSCAN utilise la distance euclidienne, qui fonctionne bien pour les clusters compacts et sphériques. Cependant, cela peut ne pas convenir à tous les types de données.

Vous pouvez spécifier d'autres mesures, telles que :

• Manhattan (norme L1) pour les données de type grille
• Cosinus pour les vecteurs clairsemés à haute dimension (par exemple, les plongements de texte)
• Haversine pour les coordonnées de latitude/longitude

L'adaptation de la métrique de distance à la structure de vos données garantit que le regroupement basé sur la densité reflète une similitude réelle.

Dans scikit-learn, le paramètre metric vous permet de définir cela explicitement (par exemple, metric='cosine'). Certaines mesures personnalisées peuvent nécessiter une matrice de distance précalculée.

Mise à l'échelle des fonctionnalités

Étant donné que DBSCAN s'appuie sur des valeurs de distance absolues, les caractéristiques non mises à l'échelle peuvent entraîner des résultats faussés. Les variables ayant des plages plus larges domineront le calcul de la distance, même si elles ne sont pas plus importantes. Cela peut empêcher l'algorithme d'identifier correctement les régions denses dans les données.

Pour éviter cela, il est essentiel d'adapter vos fonctionnalités afin qu'elles contribuent de manière égale. Les approches courantes comprennent :

• Normalisation: Centres caractéristiques autour de zéro avec variance unitaire à l'aide de StandardScaler.

• Mise à l'échelle min-max: Redimensionne les caractéristiques à une plage fixe (généralement [0, 1]) à l'aide de la fonction MinMaxScaler.

Veuillez sélectionner une méthode de mise à l'échelle qui correspond à la distribution de vos données. Sans un prétraitement adéquat, DBSCAN peut ne pas détecter les clusters significatifs, même si vos paramètres d'epsilon et d'MinPts s sont bien réglés.

Mise en œuvre de DBSCAN en Python

Dans cette section, nous examinerons la mise en œuvre de DBSCAN à l'aide de Python et de la bibliothèque scikit-learn. Nous utiliserons l'ensemble de données Make Moons pour illustrer le processus.

Configuration de l'environnement

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
from sklearn.neighbors import NearestNeighbors

Ces importations fournissent les outils nécessaires à la manipulation des données, à la visualisation, à la création d'ensembles de données et à la mise en œuvre de l'algorithme DBSCAN.

Génération de données d'exemple

X, _ = make_moons(n_samples=200, noise=0.05, random_state=42)

Ce code génère un ensemble de données synthétiques à l'aide de la fonction ` make_moons ` de scikit-learn. Voici une brève description de l'ensemble de données :

La fonction make_moons génère une classification binaire. classification qui ressemble à deux demi-lunes entrelacées. Dans notre cas :

• Nous créons 200 échantillons (n_samples=200)
• Nous ajoutons une petite quantité de bruit gaussien (noise=0.05) afin de rendre l'ensemble de données plus réaliste.
• Nous avons défini random_state=42 pour la reproductibilité

Cet ensemble de données est particulièrement utile pour illustrer le DBSCAN pour les raisons suivantes :

1. Il présente une forme non convexe que de nombreux algorithmes de regroupement (tels que K-means) auraient des difficultés à traiter.
2. Les deux groupes sont clairement séparés mais présentent une forme complexe.
3. Le bruit ajouté offre un scénario plus réaliste dans lequel certains points peuvent être classés comme des valeurs aberrantes.

Veuillez visualiser cet ensemble de données afin de mieux appréhender sa structure :

# Visualize the dataset
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1])
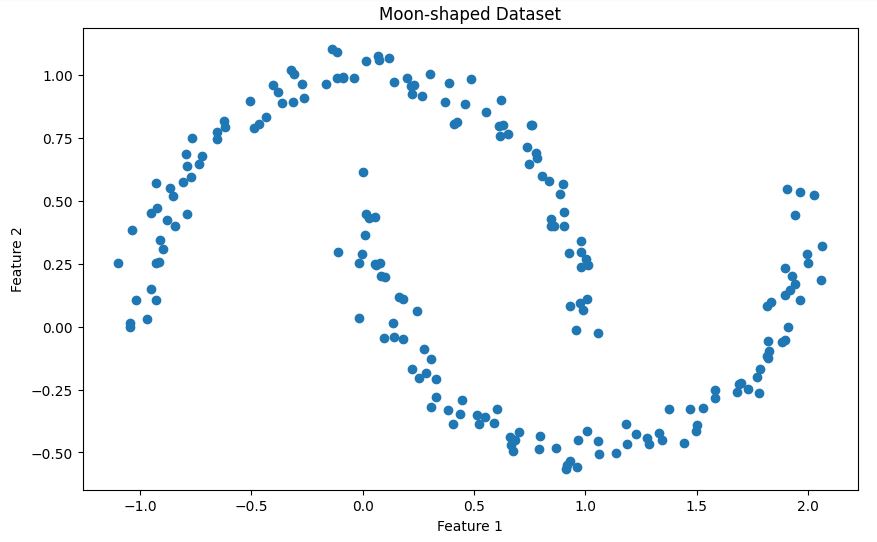
plt.title('Moon-shaped Dataset')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Cela vous permettra de visualiser les deux formes en demi-lune entrelacées dans notre ensemble de données, comme illustré ci-dessous.

Détermination du paramètre epsilon

Nous utilisons la méthode du graphe de distance k pour faciliter le choix d'une valeur epsilon appropriée :

1. Nous définissons une fonction plot_k_distance_graph qui calcule la distance au k-ième voisin le plus proche pour chaque point.
2. Les distances sont triées et présentées sous forme graphique.
3. Nous recherchons un « coude » dans le graphique obtenu afin de sélectionner epsilon.

# Function to plot k-distance graph
def plot_k_distance_graph(X, k):
    neigh = NearestNeighbors(n_neighbors=k)
    neigh.fit(X)
    distances, _ = neigh.kneighbors(X)
    distances = np.sort(distances[:, k-1])
    plt.figure(figsize=(10, 6))
    plt.plot(distances)
    plt.xlabel('Points')
    plt.ylabel(f'{k}-th nearest neighbor distance')
    plt.title('K-distance Graph')
    plt.show()
# Plot k-distance graph
plot_k_distance_graph(X, k=5)

Sortie

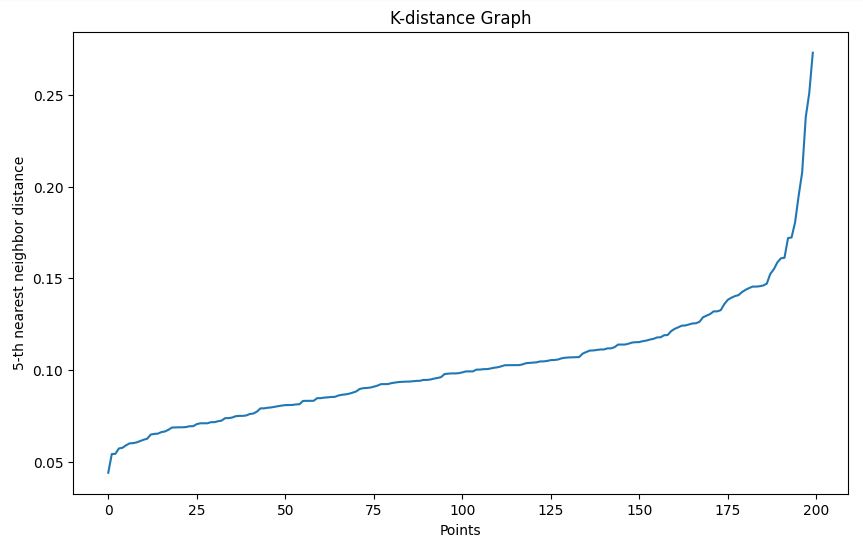
Dans notre exemple, sur la base du graphique de distance k, nous choisissons un epsilon de 0,15.

Réalisation du regroupement DBSCAN

Nous utilisons l'implémentation DBSCAN de scikit-learn :

1. Nous avons défini epsilon=0.15 en fonction de notre graphique de distance k.
2. Nous définissons min_samples=5 (2 * num_features, car nos données sont en 2D).
3. Nous ajustons le modèle à nos données et prédisons les clusters.

# Perform DBSCAN clustering
epsilon = 0.15  # Chosen based on k-distance graph
min_samples = 5  # 2 * num_features (2D data)
dbscan = DBSCAN(eps=epsilon, min_samples=min_samples)
clusters = dbscan.fit_predict(X)

Visualisation des résultats

Nous créons un graphique à nuage de points à partir de nos points de données, en les colorant en fonction des clusters qui leur ont été attribués. Les points classés comme bruit sont généralement représentés par une couleur différente (souvent le noir).

# Visualize the results
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='viridis')
plt.colorbar(scatter)
plt.title('DBSCAN Clustering Results')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Sortie

Interprétation des résultats

Enfin, nous imprimons le nombre de clusters trouvés et le nombre de points classés comme bruit. Ceci nous fournit un résumé rapide des résultats du regroupement.

# Print number of clusters and noise points
n_clusters = len(set(clusters)) - (1 if -1 in clusters else 0)
n_noise = list(clusters).count(-1)
print(f'Number of clusters: {n_clusters}')
print(f'Number of noise points: {n_noise}')

Sortie

Nombre de groupes : 2

Nombre de points de bruit : 5

Cette implémentation offre un flux de travail complet, de la génération des données à l'interprétation des résultats. Il est important de noter que dans des scénarios réels, il serait nécessaire de remplacer la génération de données échantillons par le chargement et le prétraitement de votre ensemble de données réel.

Veuillez noter que la clé d'un regroupement DBSCAN réussi réside souvent dans le choix approprié des paramètres. N'hésitez pas à tester différentes valeurs pour epsilon et min_samples afin de déterminer celles qui conviennent le mieux à votre ensemble de données spécifique.

DBSCAN vs. K-Means

Bien que DBSCAN et K-Means soient tous deux des algorithmes de clustering populaires, ils présentent des caractéristiques distinctes qui les rendent adaptés à différents types de données et cas d'utilisation. Comparons ces deux algorithmes afin de déterminer quand utiliser chacun d'eux.

Comparaison visuelle

Pour illustrer ces différences, appliquons les deux algorithmes à notre ensemble de données en forme de lune.

from sklearn.cluster import KMeans

# DBSCAN clustering
dbscan = DBSCAN(eps=0.15, min_samples=5)
dbscan_labels = dbscan.fit_predict(X)

# K-Means clustering
kmeans = KMeans(n_clusters=2, random_state=42)
kmeans_labels = kmeans.fit_predict(X)

# Visualize the results
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

ax1.scatter(X[:, 0], X[:, 1], c=dbscan_labels, cmap='viridis')
ax1.set_title('DBSCAN Clustering')

ax2.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='viridis')
ax2.set_title('K-Means Clustering')

plt.show()

Ce code applique à la fois DBSCAN et K-Means à notre ensemble de données et permet de visualiser les résultats côte à côte.

Sortie

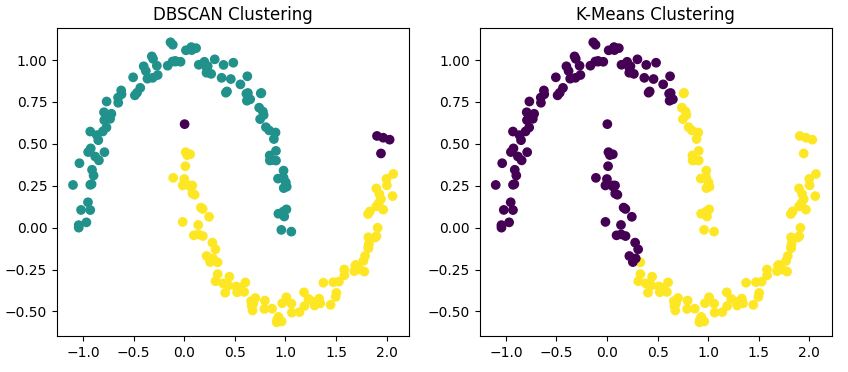
Vous remarquerez que

1. DBSCAN identifie correctement les deux formes en demi-lune comme des clusters distincts.
2. K-Means rencontre des difficultés avec les formes non convexes, divisant souvent une lune en deux groupes ou combinant des parties des deux lunes en un seul groupe.
3. DBSCAN peut identifier certains points comme du bruit (généralement de couleur différente), tandis que K-Means attribue chaque point à un cluster.

Quand utiliser DBSCAN ?

Maintenant que nous avons examiné le fonctionnement de DBSCAN et l'avons comparé à K-Means, nous allons déterminer dans quels cas DBSCAN constitue le choix approprié pour nos besoins en matière de clustering. Les propriétés uniques de DBSCAN le rendent particulièrement adapté à certains types de données et domaines problématiques.

Formes complexes des grappes 

En nous appuyant sur notre comparaison précédente, DBSCAN se distingue particulièrement lorsqu'il s'agit de formes de grappes non globulaires. Si vos données forment des motifs arbitraires tels que les demi-lunes que nous avons examinées précédemment, DBSCAN est susceptible de surpasser les algorithmes traditionnels tels que K-Means. 

Par exemple, dans le cadre d'une analyse géographique, les formations naturelles telles que les réseaux fluviaux ou l'étalement urbain présentent souvent des formes irrégulières que DBSCAN est en mesure d'identifier efficacement.

Nombre inconnu de clusters

L'un des principaux avantages de DBSCAN réside dans sa capacité à déterminer automatiquement le nombre de clusters. Cela est particulièrement utile dans le cadre d'une analyse exploratoire des données, où vous ne disposez pas nécessairement d'informations préalables sur la structure sous-jacente de vos données. 

Considérons un problème de segmentation du marché : il est possible que vous ne sachiez pas à l'avance combien de groupes de clients distincts existent. DBSCAN peut vous aider à identifier ces segments sans que vous ayez à estimer le nombre de clusters.

Ensembles de données contenant du bruit 

L'approche de DBSCAN pour traiter les points parasites le rend robuste face aux valeurs aberrantes. Ceci est essentiel dans de nombreux ensembles de données réels où les erreurs de mesure ou les anomalies sont courantes.

Par exemple, dans les systèmes de détection d'anomalies pour la sécurité des réseaux, DBSCAN peut efficacement distinguer les modèles de trafic réseau normaux des menaces potentielles pour la sécurité.

Densités de grappes variables

Contrairement à K-Means, qui suppose des clusters de densité similaire, DBSCAN peut identifier des clusters de densités variables. Cela s'avère particulièrement utile dans les cas où certains groupes de vos données sont plus compacts que d'autres.

Un exemple pourrait être l'analyse de la répartition des galaxies en astronomie, où différentes régions de l'espace présentent des densités variables d'objets célestes.

Limites de DBSCAN et alternatives

Maintenant que nous avons appris quand utiliser DBSCAN, examinons ses faiblesses et jetons un bref coup d'œil à deux alternatives, OPTICS et HDBSCAN.

Restrictions

Bien que DBSCAN soit un outil puissant, il est important de connaître ses limites :

1. s de sensibilité aux paramètres: Comme nous l'avons mentionné précédemment, il est essentiel de choisir des valeurs appropriées pour ε et MinPts. De mauvais choix peuvent conduire à des résultats de regroupement non optimaux.
2. s de données à haute dimension: Les performances de DBSCAN peuvent être affectées par les données à haute dimension en raison de la « malédiction de la dimensionnalité ».
3. s de densités variables: Bien que DBSCAN puisse traiter des clusters de densités différentes, des densités extrêmement variables dans un même ensemble de données peuvent néanmoins poser des difficultés.
4. s de l'évolutivité: Pour les ensembles de données très volumineux, DBSCAN peut s'avérer coûteux en termes de calcul par rapport à des algorithmes tels que K-Means.

Afin d'améliorer le regroupement, veuillez appliquer des techniques de réduction de dimensionnalité telles que PCA, t-SNE ou UMAP avant d'utiliser DBSCAN. Cela permet de réduire le bruit et d'améliorer la capacité de l'algorithme à détecter les zones denses.

OPTIQUE

Une alternative utile à DBSCAN est OPTICS (Ordering Points To Identify the Clustering Structure). Il remédie à la limitation de DBSCAN qui consiste à utiliser une valeur epsilon fixe en ajustant dynamiquement les seuils de voisinage.

OPTICS est plus efficace sur les ensembles de données comportant des clusters de densités différentes et peut révéler des structures de clusters que DBSCAN pourrait ne pas détecter. Scikit-learn intègre OPTICS dans son module de clustering et utilise la même interface que DBSCAN.

HDBSCAN

HDBSCAN (Hierarchical DBSCAN) est une extension moderne de DBSCAN qui établit une hiérarchie de clusters en fonction de différents niveaux de densité. Il élimine la nécessité de choisir manuellement epsilon et fournit souvent de meilleurs résultats avec moins de réglages des paramètres.

HDBSCAN tend à surpasser DBSCAN standard sur des ensembles de données réels, bruités ou déséquilibrés. Il est disponible sous forme de package Python autonome (hdbscan) et s'intègre parfaitement à scikit-learn.

Exemples pratiques de DBSCAN

DBSCAN trouve des applications dans divers domaines.

Analyse des données spatiales

Dans les systèmes d'information géographique (SIG), DBSCAN permet d'identifier les zones à forte activité ou présentant un intérêt particulier. Par exemple, une étude intitulée «Découvrir la mobilité humaine urbaine à partir de données GPS de taxis à grande échelle» (Découvrir la mobilité humaine urbaine à partir de données GPS de taxis à grande échelle) montre comment DBSCAN peut détecter les points chauds urbains à partir des données GPS des taxis. 

Cette application démontre la capacité de DBSCAN à identifier les zones d'activité dense dans les données spatiales, ce qui est essentiel pour l'urbanisme et la gestion des transports.

Traitement d'images 

DBSCAN peut regrouper des pixels en objets distincts pour des tâches telles que la reconnaissance d'objets dans des images. Une étude intitulée «Segmentation des tumeurs cérébrales à partir d'images IRM – Analyse du regroupement par la méthode des K-moyennes et DBSCAN» démontre l'efficacité de DBSCAN dans l'analyse d'images médicales. 

Les chercheurs ont utilisé DBSCAN pour segmenter avec précision les tumeurs cérébrales dans les IRM, démontrant ainsi son potentiel dans le domaine du diagnostic assisté par ordinateur et de l'imagerie médicale.

Détection d'anomalies 

Dans le cadre de la détection des fraudes ou de la surveillance de l'état du système, DBSCAN est capable d'isoler les modèles inhabituels. Une étude intitulée «Détection incrémentielle efficace des valeurs aberrantes dans les flux de données, basée sur la densité et les clusters» démontre l'application d'un algorithme DBSCAN modifié pour la détection d'anomalies en temps réel. 

Les chercheurs ont appliqué une version incrémentielle de DBSCAN pour détecter les valeurs aberrantes dans les données en continu, ce qui présente des applications potentielles dans la détection des fraudes et la surveillance de l'état des systèmes. 

Cette étude démontre comment DBSCAN peut être adapté pour identifier des modèles inhabituels dans des flux de données continus, une capacité essentielle pour les systèmes de détection de fraude en temps réel.

Systèmes de recommandation

DBSCAN peut regrouper les utilisateurs ayant des préférences similaires, ce qui contribue à générer des recommandations plus précises. Par exemple, une étude intitulée «Système de recommandation de services multi-cloud utilisant l'algorithme DBSCAN» démontre l'application de DBSCAN dans l'amélioration du filtrage collaboratif pour les systèmes de recommandation. Les chercheurs ont utilisé DBSCAN dans le cadre d'une approche de regroupement visant à classer les utilisateurs en fonction de leurs préférences et de leurs évaluations cinématographiques, ce qui a amélioré la précision des recommandations de films.

Cette approche démontre comment DBSCAN peut améliorer les recommandations personnalisées dans des domaines tels que les services de streaming de divertissement.

Conclusion

DBSCAN est un outil puissant dans la boîte à outils du data scientist, particulièrement utile lorsqu'il s'agit de traiter des ensembles de données complexes et bruités dont le nombre de clusters est inconnu. Cependant, comme tout algorithme, il ne s'agit pas d'une solution universelle. 

La clé d'un regroupement réussi réside dans la compréhension de vos données, des forces et des limites des différents algorithmes, ainsi que dans le choix de l'outil approprié pour la tâche à accomplir. Dans de nombreux cas, essayer plusieurs approches de regroupement, notamment DBSCAN et K-Means, et comparer leurs résultats peut fournir des informations précieuses sur la structure de vos données.

Avec de la pratique et de l'expérience, vous développerez une intuition pour déterminer quand DBSCAN est susceptible de révéler les modèles cachés dans vos données.

Vous pouvez approfondir vos connaissances sur les différentes technologies et méthodes abordées dans cet article sur DataCamp grâce aux ressources suivantes : 

• Chercheur en apprentissage automatique avec Python
• Aide-mémoire sur l'apprentissage automatique non supervisé
• Cours sur l'apprentissage non supervisé en Python