Ein Leitfaden zum DBSCAN-Clustering-Algorithmus

In der Datenwissenschaft und im maschinellen Lernen ist es echt wichtig, versteckte Muster zu erkennen und ähnliche Datenpunkte zu gruppieren. Clustering-Algorithmen sind echt wichtig in diesem Prozess. 

Clustering ist eine grundlegende Technik im Bereich des maschinellen Lernens und der Datenwissenschaft, bei der ähnliche Datenpunkte zusammengefasst werden. Es ist eine Methode des unüberwachten Lernens, was bedeutet, dass keine gekennzeichneten Daten nötig sind, um Muster zu finden. 

Das Hauptziel von Clustering ist:

• Große Datensätze in sinnvolle Untergruppen aufteilen
• Identifiziere natürliche Gruppierungen innerhalb der Daten
• Versteckte Muster und Strukturen aufdecken

Es gibt zwar viele Clustering-Algorithmen (vielleicht hast du schon mal von K-Means oder hierarchischem Clustering gehört), aber DBSCAN hat ein paar coole Vorteile. Als dichtebasierte Methode hat DBSCAN ein paar Vorteile:

1. Flexibilität bei der Clusterform
2. Keine festgelegte Anzahl von Clustern
3. Umgang mit Lärm
4. Dichtebasierte Erkenntnis

In diesem Artikel schauen wir uns an, was der DBSCAN-Algorithmus ist, wie DBSCAN funktioniert, wie man ihn in Python umsetzt und wann man ihn in deinen Data-Science-Projekten verwenden kann.

Was ist DBSCAN?

DBSCAN, das für „Density-Based Spatial Clustering of Applications with Noise” steht, ist ein starker Clustering-Algorithmus, der Punkte gruppiert, die im Datenraum dicht beieinander liegen. Anders als bei manchen anderen Clustering-Algorithmen musst du bei DBSCAN nicht vorher die Anzahl der Cluster festlegen, was es besonders praktisch für die explorative Datenanalyse macht.

Der Algorithmus funktioniert so, dass er Cluster als dichte Bereiche definiert, die durch Bereiche mit geringerer Dichte getrennt sind. Mit diesem Ansatz kann DBSCAN Cluster beliebiger Form erkennen und Ausreißer als Rauschen identifizieren.

DBSCAN dreht sich um drei Hauptideen:

1. Wichtige Punkte: Das sind Punkte, die mindestens eine bestimmte Anzahl anderer Punkte (MinPts) innerhalb einer bestimmten Entfernung (ε oder Epsilon) haben.
2. Grenzpunkte: Das sind Punkte, die innerhalb der ε-Distanz zu einem Kernpunkt liegen, aber selbst keine MinPts-Nachbarn haben.
3. Lärm-Punkte: Das sind Punkte, die weder Kernpunkte noch Randpunkte sind. Sie sind nicht nah genug an einem Cluster, um dazuzugehören.

Bild vom Autor

Das Diagramm oben zeigt diese Konzepte. Die Kernpunkte (blau) sind das Herz der Cluster, die Randpunkte (orange) sind am Rand der Cluster und die Rauschenpunkte (rot) sind isoliert.

DBSCAN nutzt zwei Hauptparameter:

• ε (Epsilon): Die maximale Entfernung zwischen zwei Punkten, damit sie als Nachbarn gelten.
• MinPts: Die Mindestanzahl an Punkten, die man braucht, um einen dichten Bereich zu bilden.

Durch das Anpassen dieser Einstellungen kannst du steuern, wie der Algorithmus Cluster definiert, sodass er sich an verschiedene Arten von Datensätzen und Clustering-Anforderungen anpassen kann.

Im nächsten Abschnitt schauen wir uns an, wie der DBSCAN-Algorithmus funktioniert, und gehen Schritt für Schritt durch, wie er Cluster in Daten findet.

Wie funktioniert DBSCAN?

DBSCAN checkt die Umgebung von jedem Punkt im Datensatz. Der Algorithmus geht Schritt für Schritt vor, um Cluster anhand der Dichte der Datenpunkte zu erkennen. Schauen wir uns mal an, wie DBSCAN funktioniert:

1. Parameterauswahl
• Wähle ε (Epsilon): Die maximale Entfernung zwischen zwei Punkten, damit sie als Nachbarn gelten.
• Wähle MinPts: Die Mindestanzahl an Punkten, die man braucht, um einen dichten Bereich zu bilden.
2. Wähle einen Startpunkt aus
• Der Algorithmus fängt mit einem beliebigen, noch nicht besuchten Punkt im Datensatz an.
3. Schau dir die Nachbarschaft an
• Es werden alle Punkte innerhalb der ε-Entfernung vom Startpunkt geholt.
• Wenn die Anzahl der benachbarten Punkte kleiner als MinPts ist, wird der Punkt (vorerst) als Rauschen markiert.
• Wenn es mindestens MinPts Punkte innerhalb der ε-Entfernung gibt, wird der Punkt als Kernpunkt markiert und ein neuer Cluster gebildet.
4. Erweitere den Cluster
• Alle Nachbarn des Kernpunkts werden zum Cluster hinzugefügt.
• Für jeden dieser Nachbarn:
• Wenn es ein Kernpunkt ist, werden seine Nachbarn rekursiv zum Cluster hinzugefügt.
• Wenn es kein Kernpunkt ist, wird er als Randpunkt markiert und die Erweiterung hört auf.
5. Mach das Ganze nochmal
• Der Algorithmus geht zum nächsten Punkt im Datensatz, den er noch nicht besucht hat.
• Die Schritte 3 und 4 machst du so lange, bis du alle Punkte besucht hast.
6. Cluster fertigstellen
• Nachdem alle Punkte verarbeitet wurden, findet der Algorithmus alle Cluster.
• Punkte, die zuerst als Rauschen gekennzeichnet wurden, könnten jetzt Grenzpunkte sein, wenn sie innerhalb der ε-Entfernung von einem Kernpunkt liegen.
7. Umgang mit Lärm
• Alle Punkte, die zu keinem Cluster gehören, werden weiterhin als Rauschen eingestuft.

Mit diesem Verfahren kann DBSCAN Cluster beliebiger Formen bilden und Ausreißer effektiv erkennen. Die Fähigkeit des Algorithmus, Cluster zu finden, ohne vorher die Anzahl der Cluster festzulegen, ist eine seiner größten Stärken.

Es ist wichtig zu wissen, dass die Wahl von ε und MinPts die Clustering-Ergebnisse stark beeinflussen kann. Im nächsten Abschnitt schauen wir uns an, wie man diese Parameter effektiv auswählt, und stellen Methoden wie den k-Distanz-Graphen für die Parameterauswahl vor.

Wichtige Konzepte und Parameter von DBSCAN

Um zu verstehen, wie DBSCAN Cluster bildet, muss man zwei wichtige Sachen kennen: Dichteerreichbarkeit und Dichtekonnektivität.

Erreichbarkeit der Dichte

Ein Punkt q ist von einem Punkt p aus dichteerreichbar, wenn:

1. p ist ein Kernpunkt (hat mindestens MinPts innerhalb der ε-Distanz).

2. Es gibt eine Kette von Punkten p = p₁, ..., p_n = q, wobei jedes p_i+1 direkt von p_i

Einfacher gesagt: Du kommst von p zu q, indem du Kernpunkte durchläufst, wobei jeder Schritt nicht größer als ε ist.

Dichte der Konnektivität

Zwei Punkte p und q sind dichteverbunden, wenn es einen Punkt o gibt, von dem aus sowohl p als auch q dichterreichbar sind.

Die Dichtekonnektivität ist die Grundlage für die Bildung von Clustern in DBSCAN. Alle Punkte in einem Cluster sind miteinander dichteverbunden, und wenn ein Punkt mit irgendeinem Punkt im Cluster dichteverbunden ist, gehört er auch zu diesem Cluster.

Auswahl der DBSCAN-Parameter

Die Effektivität von DBSCAN hängt stark von der Wahl seiner beiden Hauptparameter ab: ε (Epsilon) und MinPts. So gehst du bei der Auswahl dieser Parameter vor:

Auswahl von ε (Epsilon)

Der Parameter ε sagt, wie weit zwei Punkte maximal voneinander entfernt sein dürfen, damit sie als Nachbarn gelten. Um ein passendes ε zu wählen:

1. Nutze dein Fachwissen: Wenn du weißt, welche Entfernung für dein spezielles Problem wichtig ist, fang damit an.

2. K-Distanz-Graphen: Das ist ein systematischerer Ansatz:

• Berechne für jeden Punkt die Entfernung zum k-ten nächsten Nachbarn (wobei k = MinPts ist).
• Zeichne diese k-Abstände in aufsteigender Reihenfolge auf.
• Such in der Grafik nach einem „Knickpunkt“ – einem Punkt, an dem die Kurve flacher wird.
• Der ε-Wert an diesem Winkelstück ist oft eine gute Wahl.

MinPts auswählen

MinPts bestimmt die Mindestanzahl an Punkten, die man braucht, um einen dichten Bereich zu bilden. Hier sind ein paar Tipps:

1. Allgemeine Regel: Ein guter Anfang ist, MinPts = 2 * num_features festzulegen, wobei num_features die Anzahl der Dimensionen in deinem Datensatz ist.

2. Lärmschutz: Wenn deine Daten Rauschen haben oder du kleinere Cluster erkennen möchtest, solltest du vielleicht den Wert für „ MinPts “ verringern.

3. Datensatzgröße: Bei größeren Datensätzen musst du vielleicht den Wert „ MinPts “ erhöhen, um zu viele kleine Cluster zu vermeiden.

Denk dran, dass die Wahl der Parameter die Ergebnisse stark beeinflussen kann. Es ist oft hilfreich, mit verschiedenen Werten rumzuexperimentieren und die resultierenden Cluster zu checken, um die beste Lösung für deinen spezifischen Datensatz und dein Problem zu finden.

Auswahl einer Distanzmetrik

Die Wahl der Distanzmetrik in DBSCAN kann die Clustering-Ergebnisse stark beeinflussen. Standardmäßig nutzt DBSCAN die euklidische Distanz, die bei kompakten, kugelförmigen Clustern gut funktioniert. Das ist aber vielleicht nicht für alle Datentypen das Beste.

Du kannst auch andere Metriken angeben, wie zum Beispiel:

• Manhattan (L1-Norm) für gitterartige Daten
• Cosinus für hochdimensionale spärliche Vektoren (z. B. Text-Embeddings)
• Haversine für Breiten- und Längengradkoordinaten

Wenn du die Distanzmetrik an die Struktur deiner Daten anpasst, stellst du sicher, dass das dichtebasierte Clustering die tatsächliche Ähnlichkeit widerspiegelt.

In „ scikit-learn “ kannst du das über den Parameter „ metric “ direkt einstellen (z. B. „ metric='cosine' “). Manche benutzerdefinierten Metriken brauchen vielleicht eine im Voraus berechnete Distanzmatrix.

Feature-Skalierung

Weil DBSCAN auf absoluten Entfernungswerten basiert, können nicht skalierte Merkmale zu verzerrten Ergebnissen führen. Variablen mit größeren Bereichen werden die Entfernungsberechnung dominieren, auch wenn sie nicht wichtiger sind. Das kann dazu führen, dass der Algorithmus dichte Bereiche in den Daten nicht richtig erkennt.

Um das zu vermeiden, musst du deine Funktionen so anpassen, dass sie gleich viel beitragen. Zu den gängigen Ansätzen gehören:

• Standardisierung: Die Mittelwerte liegen bei Null mit einer Varianz von eins, wenn man „ StandardScaler “ benutzt.

• Min-Max-Skalierung: Skaliert die Werte auf einen festen Bereich (normalerweise [0, 1]) mit der Funktion „ MinMaxScaler “.

Such dir eine Skalierungsmethode aus, die zu deiner Datenverteilung passt. Ohne die richtige Vorverarbeitung kann DBSCAN möglicherweise keine sinnvollen Cluster erkennen – selbst wenn deine Parameter „ epsilon “ und „ MinPts “ gut abgestimmt sind.

DBSCAN in Python umsetzen

In diesem Abschnitt schauen wir uns die Umsetzung von DBSCAN mit Python und der scikit-learn-Bibliothek an. Wir zeigen dir den Ablauf am Beispiel des Datensatzes „Make Moons “.

Einrichten der Umgebung

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
from sklearn.neighbors import NearestNeighbors

Diese Importe bieten die Tools, die man für die Datenbearbeitung, Visualisierung, Erstellung von Datensätzen und die Implementierung des DBSCAN-Algorithmus braucht.

Beispieldaten erstellen

X, _ = make_moons(n_samples=200, noise=0.05, random_state=42)

Dieser Code erstellt einen synthetischen Datensatz mit der Funktion „ make_moons ” aus scikit-learn. Hier ist eine kurze Beschreibung des Datensatzes:

Die Funktion make_moons macht eine binäre Klassifizierung Datensatz, der wie zwei ineinander verschachtelte Halbmonde aussieht. In unserem Fall:

• Wir machen 200 Proben (n_samples=200)
• Wir fügen ein bisschen Gaußsches Rauschen hinzu (noise=0.05), um den Datensatz realistischer zu machen.
• Wir haben random_state=42 auf Reproduzierbarkeit

Dieser Datensatz ist besonders nützlich, um DBSCAN zu zeigen, weil:

1. Es hat eine nicht konvexe Form, die viele Clustering-Algorithmen Algorithmen (wie K-Means) Probleme bereiten würde.
2. Die beiden Cluster sind klar voneinander getrennt, haben aber eine komplizierte Form.
3. Das zusätzliche Rauschen macht das Szenario realistischer, sodass manche Punkte als Ausreißer eingestuft werden könnten.

Lass uns diesen Datensatz mal anschauen, um besser zu verstehen, wie er aufgebaut ist:

# Visualize the dataset
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1])
plt.title('Moon-shaped Dataset')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Hier siehst du die beiden ineinander verschachtelten Halbmondformen in unserem Datensatz, wie unten gezeigt.

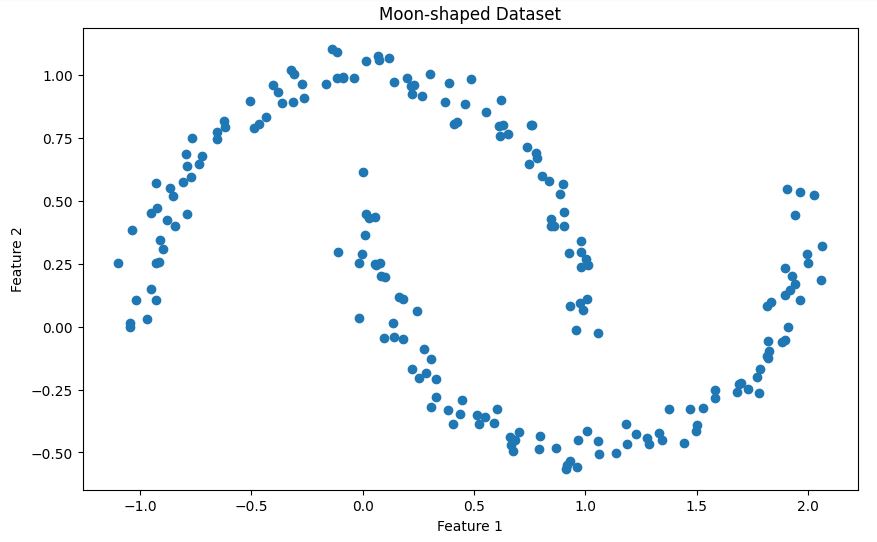
Den Epsilon-Parameter bestimmen

Wir nutzen die k-Distanz-Graph-Methode, um einen passenden Epsilon-Wert zu finden:

1. Wir definieren eine Funktion plot_k_distance_graph , die für jeden Punkt den Abstand zum k-ten nächsten Nachbarn berechnet.
2. Die Entfernungen sind sortiert und eingezeichnet.
3. Wir suchen nach einer „Knickstelle“ im resultierenden Diagramm, um Epsilon auszuwählen.

# Function to plot k-distance graph
def plot_k_distance_graph(X, k):
    neigh = NearestNeighbors(n_neighbors=k)
    neigh.fit(X)
    distances, _ = neigh.kneighbors(X)
    distances = np.sort(distances[:, k-1])
    plt.figure(figsize=(10, 6))
    plt.plot(distances)
    plt.xlabel('Points')
    plt.ylabel(f'{k}-th nearest neighbor distance')
    plt.title('K-distance Graph')
    plt.show()
# Plot k-distance graph
plot_k_distance_graph(X, k=5)

Ausgabe

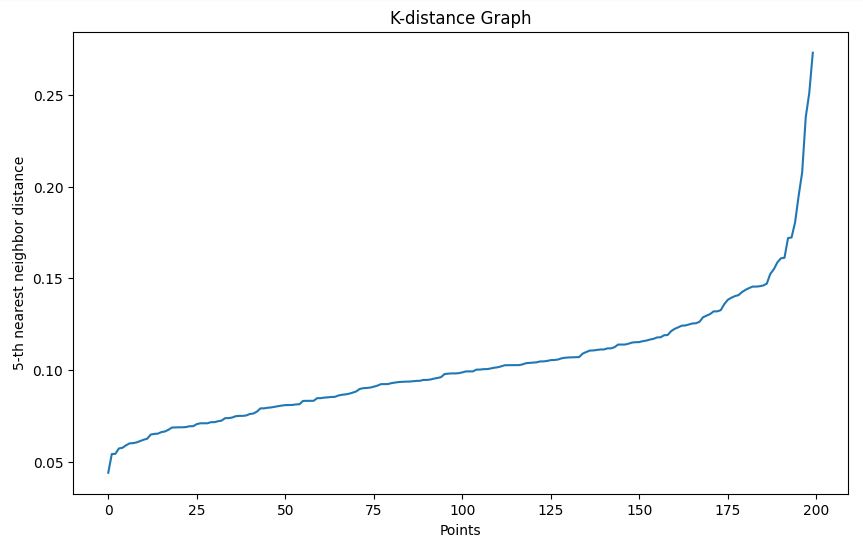
In unserem Beispiel, das auf dem k-Distanz-Graphen basiert, nehmen wir ein Epsilon von 0,15.

DBSCAN-Clustering durchführen

Wir nutzen die DBSCAN-Implementierung von scikit-learn:

1. Wir haben epsilon=0.15 basierend auf unserem k-Distanz-Diagramm.
2. Wir setzen min_samples=5 (2 * Anzahl_Merkmale, weil unsere Daten 2D sind).
3. Wir passen das Modell an unsere Daten an und sagen die Cluster voraus.

# Perform DBSCAN clustering
epsilon = 0.15  # Chosen based on k-distance graph
min_samples = 5  # 2 * num_features (2D data)
dbscan = DBSCAN(eps=epsilon, min_samples=min_samples)
clusters = dbscan.fit_predict(X)

Die Ergebnisse anschaulich machen

Wir machen ein Streudiagramm aus unseren Datenpunkten und färben sie je nach den Clustern, zu denen sie gehören. Punkte, die als Rauschen eingestuft werden, sind normalerweise anders gefärbt (oft schwarz).

# Visualize the results
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='viridis')
plt.colorbar(scatter)
plt.title('DBSCAN Clustering Results')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Ausgabe

Die Ergebnisse verstehen

Zum Schluss drucken wir die Anzahl der gefundenen Cluster und die Anzahl der als Rauschen eingestuften Punkte aus. Das gibt uns einen schnellen Überblick über die Clustering-Ergebnisse.

# Print number of clusters and noise points
n_clusters = len(set(clusters)) - (1 if -1 in clusters else 0)
n_noise = list(clusters).count(-1)
print(f'Number of clusters: {n_clusters}')
print(f'Number of noise points: {n_noise}')

Ausgabe

Anzahl der Cluster: 2

Anzahl der Geräuschpunkte: 5

Diese Lösung bietet einen kompletten Arbeitsablauf von der Datengenerierung bis zur Interpretation der Ergebnisse. Es ist wichtig zu beachten, dass du in echten Szenarien die Generierung von Beispieldaten durch das Laden und die Vorverarbeitung deines tatsächlichen Datensatzes ersetzen würdest.

Denk dran, dass der Schlüssel zum erfolgreichen DBSCAN-Clustering oft in der richtigen Auswahl der Parameter liegt. Probier ruhig verschiedene Werte für epsilon und min_samples aus, um die beste Lösung für deinen Datensatz zu finden.

DBSCAN vs. K-Means

Obwohl sowohl DBSCAN als auch K-Means beliebte Clustering-Algorithmen sind, haben sie unterschiedliche Eigenschaften, die sie für verschiedene Arten von Daten und Anwendungsfälle geeignet machen. Vergleichen wir diese beiden Algorithmen, um zu verstehen, wann man welchen verwendet.

Visueller Vergleich

Um diese Unterschiede zu zeigen, probieren wir beide Algorithmen mal auf unseren mondförmigen Datensatz aus.

from sklearn.cluster import KMeans

# DBSCAN clustering
dbscan = DBSCAN(eps=0.15, min_samples=5)
dbscan_labels = dbscan.fit_predict(X)

# K-Means clustering
kmeans = KMeans(n_clusters=2, random_state=42)
kmeans_labels = kmeans.fit_predict(X)

# Visualize the results
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

ax1.scatter(X[:, 0], X[:, 1], c=dbscan_labels, cmap='viridis')
ax1.set_title('DBSCAN Clustering')

ax2.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='viridis')
ax2.set_title('K-Means Clustering')

plt.show()

Dieser Code wendet sowohl DBSCAN als auch K-Means auf unseren Datensatz an und zeigt die Ergebnisse nebeneinander.

Ausgabe

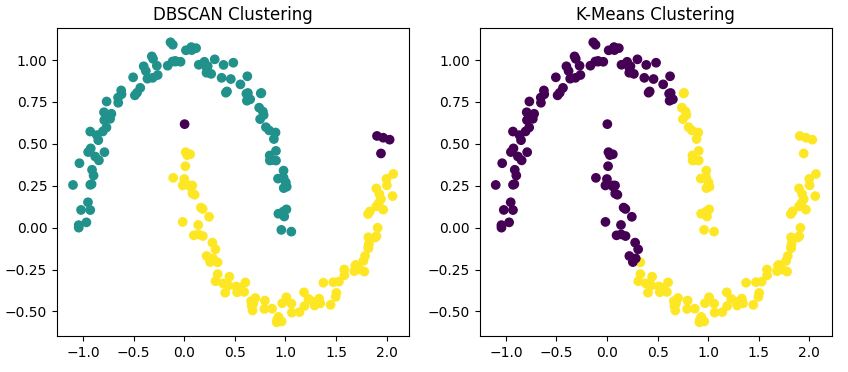
Du wirst feststellen, dass

1. DBSCAN erkennt die beiden Halbmondformen richtig als separate Cluster.
2. K-Means hat Probleme mit der nicht konvexen Form und teilt oft einen Mond in zwei Cluster auf oder kombiniert Teile beider Monde zu einem Cluster.
3. DBSCAN kann manche Punkte als Rauschen erkennen (die sind normalerweise anders gefärbt), während K-Means jeden Punkt einem Cluster zuordnet.

Wann sollte man DBSCAN verwenden?

Nachdem wir uns angesehen haben, wie DBSCAN funktioniert, und es mit K-Means verglichen haben, schauen wir mal, wann DBSCAN die richtige Wahl für unsere Clustering-Anforderungen ist. Die einzigartigen Eigenschaften von DBSCAN machen es besonders gut für bestimmte Arten von Daten und Problembereiche geeignet.

Komplexe Clusterformen 

Wenn wir auf unseren vorherigen Vergleich zurückkommen, zeigt DBSCAN seine Stärken vor allem bei nicht-kugelförmigen Clusterformen. Wenn deine Daten willkürliche Muster wie die zuvor untersuchten Halbmonde bilden, ist es wahrscheinlich, dass DBSCAN traditionelle Algorithmen wie K-Means übertrifft. 

In der Geografieanalyse zum Beispiel bilden natürliche Strukturen wie Flusssysteme oder Zersiedelung oft unregelmäßige Formen, die DBSCAN gut erkennen kann.

Unbekannte Anzahl von Clustern

Einer der Hauptvorteile von DBSCAN ist, dass es die Anzahl der Cluster automatisch bestimmen kann. Das ist besonders nützlich bei der explorativen Datenanalyse, wo du vielleicht noch keine Ahnung von der zugrunde liegenden Struktur deiner Daten hast. 

Stell dir mal ein Problem mit der Marktsegmentierung vor: Du weißt vielleicht vorher nicht, wie viele verschiedene Kundengruppen es gibt. DBSCAN kann dir dabei helfen, diese Segmente zu finden, ohne dass du die Anzahl der Cluster schätzen musst.

Datensätze mit Rauschen 

Der Ansatz von DBSCAN zum Umgang mit Rauschpunkten macht es robust gegenüber Ausreißern. Das ist bei vielen Datensätzen aus der Praxis echt wichtig, wo Messfehler oder Anomalien oft vorkommen.

Zum Beispiel kann DBSCAN in Systemen zur Erkennung von Anomalien für die Netzwerksicherheit normale Netzwerkverkehrsmuster effektiv von potenziellen Sicherheitsbedrohungen trennen.

Unterschiedliche Clusterdichten

Anders als K-Means, das von Clustern mit ähnlicher Dichte ausgeht, kann DBSCAN Cluster mit unterschiedlichen Dichten erkennen. Das ist besonders nützlich, wenn manche Gruppen in deinen Daten dichter beieinander liegen als andere.

Ein Beispiel könnte die Analyse der Verteilung von Galaxien in der Astronomie sein, wo verschiedene Regionen des Weltraums unterschiedliche Dichten an Himmelsobjekten aufweisen.

Einschränkungen von DBSCAN und Alternativen

Nachdem wir jetzt wissen, wann man DBSCAN einsetzt, schauen wir uns mal seine Schwächen an und werfen einen kurzen Blick auf zwei Alternativen, OPTICS und HDBSCAN.

Einschränkungen

Obwohl DBSCAN echt leistungsstark ist, sollte man seine Grenzen im Auge behalten:

1. Parameterempfindlichkeits: Wie wir schon gesagt haben, ist es echt wichtig, die richtigen Werte für ε und MinPts zu finden. Schlechte Entscheidungen können zu nicht optimalen Clustering-Ergebnissen führen.
2. Hochdimensionale Daten: Die Leistung von DBSCAN kann bei hochdimensionalen Daten wegen dem „Fluch der Dimensionalität” schlechter werden.
3. Unterschiedliche Dichten: Obwohl DBSCAN mit Clustern unterschiedlicher Dichte umgehen kann, können extrem unterschiedliche Dichten im selben Datensatz trotzdem Probleme bereiten.
4. Skalierbarkeit: Bei richtig großen Datensätzen kann DBSCAN im Vergleich zu Algorithmen wie K-Means ziemlich rechenintensiv sein.

Um das Clustering zu verbessern, solltest du vor der Verwendung von DBSCAN Techniken zur Dimensionsreduktion wie PCA, t-SNE oder UMAP anwenden. Das reduziert das Rauschen und macht den Algorithmus besser darin, dichte Bereiche zu erkennen.

OPTIK

Eine coole Alternative zu DBSCAN ist OPTICS (Ordering Points To Identify the Clustering Structure). Es löst das Problem von DBSCAN, dass man einen festen Epsilon-Wert nehmen muss, indem es die Nachbarschaftsschwellenwerte dynamisch anpasst.

OPTICS ist bei Datensätzen mit Clustern unterschiedlicher Dichte effektiver und kann Clusterstrukturen aufdecken, die DBSCAN möglicherweise übersieht. Scikit-learn hat OPTICS in sein Clustering-Modul eingebaut und nutzt die gleiche Schnittstelle wie DBSCAN.

HDBSCAN

HDBSCAN (Hierarchical DBSCAN) ist eine moderne Erweiterung von DBSCAN, die eine Hierarchie von Clustern auf der Grundlage unterschiedlicher Dichtewerte aufbaut. Man muss Epsilon nicht mehr manuell auswählen und kriegt oft bessere Ergebnisse mit weniger Parametereinstellungen.

HDBSCAN ist bei realen, verrauschten oder unausgewogenen Datensätzen meistens besser als das normale DBSCAN. Es ist als eigenständiges Python-Paket (hdbscan) verfügbar und lässt sich gut mit scikit-learn integrieren.

Praktische Beispiele für DBSCAN

DBSCAN findet in vielen Bereichen Anwendung.

Raumdatenanalyse

In Geografischen Informationssystemen (GIS) kann DBSCAN Bereiche mit hoher Aktivität oder großem Interesse erkennen. Zum Beispiel hat eine Studie mit dem Titel „Aufdeckung der städtischen Mobilität anhand von groß angelegten GPS-Daten von Taxis” zeigt, wie DBSCAN anhand von Taxi-GPS-Daten urbane Hotspots erkennen kann. 

Diese Anwendung zeigt, wie DBSCAN dichte Aktivitätsbereiche in räumlichen Daten erkennen kann, was für die Stadtplanung und das Verkehrsmanagement echt wichtig ist.

Bildverarbeitung 

DBSCAN kann Pixel zu einzelnen Objekten gruppieren, zum Beispiel für die Objekterkennung in Bildern. Eine Studie mit dem Titel „Segmentierung von Hirntumoren aus MRT-Bildern – Analyse von K-Means- und DBSCAN-Clustering“ zeigt, wie gut DBSCAN bei der Analyse medizinischer Bilder funktioniert. 

Die Forscher haben DBSCAN benutzt, um Hirntumore in MRT-Scans genau zu segmentieren, und damit gezeigt, wie nützlich das Verfahren bei der computergestützten Diagnose und medizinischen Bildgebung sein kann.

Anomalieerkennung 

Bei der Betrugserkennung oder der Überwachung des Systemzustands kann DBSCAN ungewöhnliche Muster herausfiltern. Eine Studie mit dem Titel „Effiziente dichte- und clusterbasierte inkrementelle Ausreißererkennung in Datenströmen” zeigt, wie man einen modifizierten DBSCAN-Algorithmus für die Echtzeit-Anomalieerkennung nutzen kann. 

Die Forscher haben eine inkrementelle Version von DBSCAN benutzt, um Ausreißer in Streaming-Daten zu finden, was bei der Betrugsaufdeckung und der Überwachung des Systemzustands nützlich sein könnte. 

Diese Studie zeigt, wie DBSCAN angepasst werden kann, um ungewöhnliche Muster in kontinuierlichen Datenströmen zu erkennen – eine wichtige Funktion für Echtzeit-Betrugserkennungssysteme.

Empfehlungssysteme

DBSCAN kann Leute mit ähnlichen Vorlieben zusammenfassen und so dabei helfen, genauere Empfehlungen zu machen. Zum Beispiel eine Studie mit dem Titel „Multi-Cloud-basiertes Serviceempfehlungssystem mit DBSCAN-Algorithmus” zeigt, wie man DBSCAN nutzen kann, um das kollaborative Filtern für Empfehlungssysteme zu verbessern. Die Forscher haben DBSCAN als Teil eines Clustering-Ansatzes benutzt, um Nutzer nach ihren Filmvorlieben und Bewertungen zu gruppieren, was die Genauigkeit der Filmempfehlungen verbessert hat.

Dieser Ansatz zeigt, wie DBSCAN personalisierte Empfehlungen in Bereichen wie Streaming-Diensten für Unterhaltungsangebote verbessern kann.

Fazit

DBSCAN ist ein echt starkes Tool im Werkzeugkasten von Datenwissenschaftlern und besonders nützlich, wenn man mit komplizierten, verrauschten Datensätzen zu tun hat, bei denen man nicht weiß, wie viele Cluster es gibt. Aber wie bei jedem Algorithmus ist es keine Lösung, die für alle passt. 

Der Schlüssel zum erfolgreichen Clustering liegt darin, deine Daten zu verstehen, die Stärken und Grenzen verschiedener Algorithmen zu kennen und das richtige Tool für die jeweilige Aufgabe auszuwählen. Oft kann es echt hilfreich sein, verschiedene Clustering-Ansätze wie DBSCAN und K-Means auszuprobieren und die Ergebnisse zu vergleichen, um wertvolle Einblicke in die Struktur deiner Daten zu bekommen.

Mit etwas Übung und Erfahrung wirst du ein Gefühl dafür entwickeln, wann DBSCAN wahrscheinlich die versteckten Muster in deinen Daten aufdeckt.

Du kannst mehr über die verschiedenen Technologien und Methoden erfahren, die wir in diesem Beitrag auf DataCamp behandelt haben, mit den folgenden Ressourcen: 

• Wissenschaftler für maschinelles Lernen in Python
• Spickzettel zum unüberwachten maschinellen Lernen
• Kurs „Unüberwachtes Lernen in Python”