Curso
Merece la pena aprender la regresión MCO (mínimos cuadrados ordinarios) porque es una parte importante de la estadística y el aprendizaje automático. Se utiliza para predecir resultados o analizar relaciones entre variables, y las aplicaciones de esos dos usos incluyen desde la comprobación de hipótesis hasta la previsión.
En este artículo, te ayudaré a comprender los fundamentos de la regresión MCO, sus aplicaciones, supuestos y cómo se puede implementar en Excel, R y Python. Hay mucho que aprender, así que cuando termines, sigue nuestros cursos designados de regresión, como Introducción a la regres ión en Python e Introducción a la regresión en R, y lee nuestros tutoriales, como Regresión lineal en Excel.
¿Qué es la regresión OLS?
La regresión MCO estima la relación entre una o varias variables independientes (predictores) y una variable dependiente (respuesta). Lo consigue ajustando una ecuación lineal a los datos observados. He aquí cómo es esa ecuación:
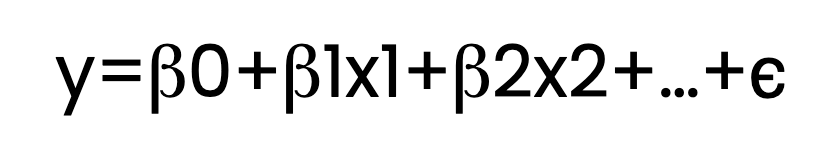
Toma:
- y es la variable dependiente.
- x1, x2,..., son variables independientes.
- β0 es la intercepción.
- β1, β2, .... son los coeficientes.
- ϵ representa el término de error.
En la ecuación anterior, muestro varios términos β , como β1 y β2. Pero para que quede claro, la ecuación de regresión podría contener sólo un término β además de β0, en cuyo caso la llamaríamos regresión lineal simple. Con dos o más predictores, como β1 y β2 , lo llamaríamos regresión lineal múltiple. Ambas se calificarían de regresión MCO si se utilizara un estimador de mínimos cuadrados ordinarios.
¿Qué es el problema de minimización OLS?
En el núcleo de la regresión MCO se encuentra un reto de optimización: encontrar la línea (o hiperplano en dimensiones superiores) que mejor se ajuste a los datos. Pero, ¿qué significa "mejor ajuste"? "Mejor ajuste" significa aquí minimizar la suma de los residuos al cuadrado.
Voy a intentar explicar el problema de minimización, explicando también la idea de residuos.
- Explicación de los residuos: Los residuos son las diferencias entre los valores reales observados y los valores predichos por el modelo de regresión. Para cada punto de datos, el residuo nos indica lo alejada que estaba nuestra predicción.
- ¿Por qué cuadrar los residuos? Al elevar al cuadrado cada residuo, nos aseguramos de que las diferencias positivas y negativas no se anulan entre sí. La cuadratura también da más peso a los errores más grandes, lo que significa que el modelo da prioridad a reducir los errores más grandes.
Al minimizar la suma de los residuos al cuadrado, la recta de regresión se convierte en una representación exacta de la relación entre las variables independiente y dependiente. De hecho, al minimizar la suma de los residuos al cuadrado, nuestro modelo tiene el menor error global posible en sus predicciones. Para saber más sobre los residuos y la descomposición de la regresión, lee nuestro tutorial, Comprender la suma de cuadrados: Guía de la TSM, la TSS y la TSE.
¿Qué es el estimador de mínimos cuadrados ordinarios?
En el contexto de la regresión, los estimadores se utilizan para calcular los coeficientes que describen la relación entre las variables independientes y la variable dependiente. El estimador de mínimos cuadrados ordinarios (MCO) es uno de esos métodos. Encuentra los valores de los coeficientes que minimizan la suma de las diferencias al cuadrado entre los valores observados y los predichos por el modelo.
Traigo esto a colación para que queden claros los términos. La regresión puede hacerse con otros estimadores, cada uno de los cuales ofrece distintas ventajas según los datos y los objetivos del análisis. Por ejemplo, algunos estimadores son más robustos frente a los valores atípicos, mientras que otros ayudan a evitar el sobreajuste regularizando los parámetros del modelo.
¿Cómo se estiman los parámetros de la regresión MCO?
Para determinar los coeficientes que mejor se ajustan al modelo de regresión, el estimador MCO emplea técnicas matemáticas para minimizar la suma de los residuos al cuadrado. Un método posible es la ecuación normal, que proporciona una solución directa estableciendo un sistema de ecuaciones basado en los datos y resolviendo los coeficientes que consiguen la menor suma posible de diferencias al cuadrado entre los valores observados y los predichos.
Sin embargo, resolver la ecuación normal puede llegar a ser exigente desde el punto de vista informático, especialmente con grandes conjuntos de datos. Para solucionar esto, se suele utilizar otra técnica llamada descomposición QR. La descomposición QR descompone la matriz de variables independientes en dos matrices más sencillas: una matriz ortogonal (Q) y una matriz triangular superior (R). Esta simplificación hace que los cálculos sean más eficaces y también mejora la estabilidad numérica.
Cuándo utilizar la regresión OLS
¿Cómo decidimos utilizar la regresión MCO? Al tomar esa decisión, tenemos que evaluar tanto las características de nuestro conjunto de datos como definir el problema concreto que intentamos resolver.
Supuestos de la regresión MCO
Antes de aplicar la regresión MCO, debemos asegurarnos de que nuestros datos cumplen los siguientes supuestos, para obtener resultados fiables:
- Linealidad: La relación entre las variables independiente y dependiente debe ser lineal.
- Independencia de los errores: Los residuos no deben estar correlacionados entre sí.
- Homocedasticidad: Los residuos deben tener una varianza constante en todos los niveles de las variables independientes.
- Normalidad de los errores: Los residuos deben tener una distribución normal.
Las violaciones graves de estos supuestos pueden dar lugar a estimaciones sesgadas o predicciones poco fiables. Por tanto, tenemos que evaluar y abordar cualquier problema potencial antes de seguir adelante.
Aplicaciones de la regresión MCO
Una vez satisfechos los supuestos, la regresión MCO puede utilizarse para distintos fines:
- Modelización predictiva: Previsión de resultados, como ventas, ingresos o tendencias.
- Análisis de relaciones: Comprender la influencia de las variables independientes en una variable dependiente.
- Comprobación de hipótesis: Evaluar si los predictores específicos influyen significativamente en la variable de resultado.
Regresión OLS en R, Python y Excel
Veamos ahora cómo realizar la regresión MCO en R, Python y Excel.
Regresión OLS en R
R proporciona la función lm() para la regresión MCO. He aquí un ejemplo:
# Let's create sample data
predictor_variable <- c(1, 2, 3, 4, 5)
response_variable <- c(2, 4, 5, 4, 5)
# We now fit the OLS regression model using the lm() function from base R
ols_regression_model <- lm(response_variable ~ predictor_variable)
# OLS regression model summary
summary(ols_regression_model)Observa que no tenemos que importar ningún paquete adicional para realizar la regresión MCO en R.
Regresión OLS en Python
Python ofrece bibliotecas como statsmodels y scikit-learn para la regresión OLS. Probemos un ejemplo utilizando statsmodels:
import statsmodels.api as sm
# We can create some sample data
ols_regression_predictor = [1, 2, 3, 4, 5]
ols_regression_response = [2, 4, 5, 4, 5]
# Adding a constant for the intercept
ols_regression_predictor = sm.add_constant(ols_regression_predictor)
# We now fit our OLS regression model
ols_regression_model = sm.OLS(ols_regression_response, ols_regression_predictor).fit()
# Summary of our OLS regression
print(ols_regression_model.summary())Regresión OLS en Excel
Excel también proporciona una forma de hacer la regresión MCO a través de sus herramientas incorporadas. Sólo tienes que seguir estos pasos:
Prepara tus datos
Organiza tus datos en dos columnas: una para la(s) variable(s) independiente(s) y otra para la variable dependiente. Asegúrate de que no hay celdas en blanco en tu conjunto de datos.
Activar el Paquete de Herramientas de Análisis de Datos
Ve a Archivo > Opciones > Complementos. En el cuadro Gestionar, selecciona Excel Complementosy haz clic en Ir a. Marca la casilla de Análisis ToolPak y pulsa OK.
Ejecuta el análisis de regresión
Ve a Datos > Análisis de datos y selecciona Regresión de la lista de opciones. Haz clic en OK.
En el cuadro de diálogo Regresión:
- Ajusta el Rango Y de entrada a tu columna de variable dependiente.
- Ajusta el Rango X de entrada a tu(s) variable(s) independiente(s).
- Consulta Etiquetas si tu rango de entrada incluye cabeceras de columna.
- Selecciona un rango de salida o una nueva hoja de cálculo para los resultados.
Cómo evaluar los modelos de regresión OLS
Ahora hemos creado un modelo de regresión MCO. El siguiente paso es ver si es eficaz mirando los diagnósticos del modelo y las estadísticas del modelo.
Parcelas de diagnóstico
Podemos evaluar un modelo de regresión MCO utilizando herramientas visuales para evaluar los supuestos del modelo y la calidad del ajuste. Algunas opciones incluyen ungráfico residuales frente a valores ajustados, que busca patrones que podrían indicar no linealidad o heteroscedasticidad, o el gráfico Q-Q gráfico Q-Qque examina si los residuos siguen una distribución normal.
Estadísticas del modelo
También podemos evaluar nuestro modelo con métricas estadísticas que proporcionan información sobre el rendimiento del modelo y la importancia de los predictores. Las estadísticas comunes de los modelos incluyen R -cuadrado y R cuadrado ajustadoque miden la proporción de varianza explicada por el modelo. También podemos observar los estadísticos F y los valores p, que prueban la significación global del modelo y de los predictores individuales .
Flujo de trabajo de formación/prueba
Por último, debemos decir que a los analistas de datos también les gusta seguir un proceso estructurado para validar las capacidades predictivas de un modelo. Esto incluye un proceso de división de datos, en el que los datos se dividen en subconjuntos de entrenamiento y de prueba, un proceso de entrenamiento para ajustar el modelo, y luego un proceso de prueba para evaluar el rendimiento del modelo en datos de prueba no vistos. Este proceso también puede incluir pasos de validación cruzada como la validación cruzada k-fold.
Profundizar en la regresión OLS
Ahora que hemos explorado los fundamentos de la regresión MCO, vamos a explorar algunos conceptos más avanzados.
Regresión MCO y estimación de máxima verosimilitud
La estimación de máxima verosimilitud (MLE) es otro concepto del que se habla junto a la regresión MCO, y con razón. Hasta ahora hemos dedicado tiempo a hablar de cómo la MCO minimiza la suma de los residuos al cuadrado para estimar los coeficientes. Demos ahora un paso atrás para hablar de la MLE.
El MLE maximiza la probabilidad de observar los datos dados según nuestro modelo. Funciona asumiendo una distribución de probabilidad específica para el término de error. Esta distribución de probabilidad suele ser una distribución normal, o gaussiana. Utilizando nuestra distribución de probabilidad, encontramos los valores de los parámetros que hacen más probables los datos observados.
La razón por la que menciono ahora la estimación de máxima verosimilitud es porque, en el contexto de la regresión MCO, el enfoque MLE conduce a las mismas estimaciones de coeficientes que obtenemos minimizando la suma de errores cuadrados, siempre que los errores se distribuyan normalmente.
Interpretar la regresión OLS como media ponderada
Otra perspectiva fascinante de la regresión MCO es su interpretación como media ponderada. El profesor Andrew Gelman expone la idea de que los coeficientes de una regresión MCO pueden considerarse una media ponderada de los puntos de datos observados, en la que las ponderaciones vienen determinadas por la varianza de los predictores y la estructura del modelo.
Este punto de vista permite comprender cómo funciona el proceso de regresión y por qué se comporta como lo hace, porque La regresión MCO en realidad está dando más peso a las observaciones que tienen menos varianza o que están más cerca de las predicciones del modelo. También puedes tune en nuestro episodio del podcast DataFramed, Election Forecasting and Polling, para escuchar lo que dice el profesor Gelman sobre el uso de la regresión en los sondeos electorales.
Regresión OLS vs. Métodos de regresión similares
Otros métodos de regresión tienen nombres que pueden sonar parecidos, pero sirven para fines distintos o funcionan con supuestos diferentes. Echemos un vistazo a algunos que suenan parecido:
MCO frente a mínimos cuadrados ponderados (MPP)
WLS es una extensión de OLS que asigna diferentes ponderaciones a cada punto de datos en función de la varianza de sus observaciones. El WLS es especialmente útil cuando se incumple el supuesto de varianza constante de los residuos. Al ponderar las observaciones inversamente a su varianza, WLS proporciona estimaciones más fiables cuando se trata de datos heteroscedásticos.
Regresión OLS frente amínimos cuadrados parciales(PLS)
El PLS combina características del análisis de componentes principales y de la regresión múltiple mediante la extracción de variables latentes que capturan la máxima covarianza entre los predictores y la variable de respuesta. El PLS es ventajoso en situaciones de multicolinealidad o cuando el número de predictores supera al de observaciones. Reduce la dimensionalidad al tiempo que maximiza el poder predictivo, algo que OLS no aborda de forma inherente.
MCO frente amínimos cuadrados generalizados (mcg)
Al igual que el WLS, el GLS generaliza el OLS al permitir una varianza correlacionada y/o no constante de los residuos. GLS ajusta el proceso de estimación para tener en cuenta las violaciones de los supuestos OLS relativos a los residuos, proporcionando estimaciones más eficientes e insesgadas en tales escenarios.
MCO vs. mínimos cuadrados totales (TLS)
También conocida como regresión ortogonal, la TLS minimiza las distancias perpendiculares de los puntos de datos a la recta de regresión, en lugar de las distancias verticales minimizadas por la OLS. La TLS es útil cuando hay error tanto en la variable independiente como en la dependiente, mientras que la OLS supone que sólo la variable dependiente tiene error de medición.
Alternativas a la regresión OLS
Cuando la relación entre variables es compleja o no lineal, los métodos de regresión no paramétricos ofrecen alternativas flexibles a los MCO, al permitir que los datos determinen la forma de la función de regresión. Todos los ejemplos anteriores (los que "suenan parecido") pertenecen a la categoría de modelos paramétricos. Pero los modelos no paramétricos también podrían utilizarse cuando quieras modelizar patrones sin las limitaciones de los supuestos paramétricos.
| Método | Descripción | Ventajas | Casos de uso habituales |
|---|---|---|---|
| Regresión kernel | Utiliza medias ponderadas con un núcleo para suavizar los datos. | Capta las relaciones no lineales Suavizado flexible |
Análisis exploratorio Relaciones entre variables desconocidas |
| Regresión local | Ajusta polinomios locales a subconjuntos de datos para una curva suave. | Maneja patrones complejos Suavidad adaptable |
Visualización de tendencias Suavizado de gráficas de dispersión |
| Árboles de regresión | Divide los datos en ramas para ajustar modelos sencillos en cada segmento. | Fácil de interpretar Maneja las interacciones |
Segmentar los datos Identificar distintos regímenes de datos |
| Regresión Spline | Utiliza polinomios a trozos con continuidad en los nudos para modelizar los datos. | Modela tendencias no lineales suaves Ajuste flexible |
Series temporales Curvas de crecimiento |
Reflexiones finales
La regresión MCO es una herramienta fundamental para comprender las relaciones entre los datos y hacer predicciones. Al dominar OLS, construirás una base sólida para explorar modelos y técnicas avanzados. Explora los cursos de DataCamp sobre regresión en R y Python para ampliar tu conjunto de habilidades: Introducción a la Regresión con statsmodels en Python e Introducción a la Regresión en R). Considera también nuestra popular carrera de Científico de Aprendizaje Automático en Python.
Conviértete en un Científico ML


