Coeficiente de determinación: Lo que nos dice el R cuadrado

Imagina que intentas predecir la nota que obtendrá alguien en un examen basándote en cuántas horas ha estudiado. Ahora bien, ¿en qué medida coinciden tus predicciones con los resultados reales? Eso es lo que nos indica el coeficiente de determinación, también conocido como^R² (R cuadrado).

Nos indica en qué medida el cambio en una variable (por ejemplo, las notas de un examen) puede explicarse por los cambios en otra (por ejemplo, las horas de estudio). De esta forma, podrás comprender en qué medida tu modelo «se ajusta» a los datos.

En este artículo, te ayudaremos a comprender qué significa^R², por qué es importante y cómo calcularlo e interpretarlo, incluso si eres nuevo en el mundo de la estadística. 

¿Qué es el coeficiente de determinación?

El coeficiente de determinación, que normalmente se escribe como^R² (R al cuadrado), es un número que nos indica en qué medida un modelo de regresión explica lo que ocurre en los datos. Muestra en qué medida el cambio en el resultado (variable dependiente) puede explicarse por los elementos que utilizamos para predecirlo (variable(s) independiente(s)). 

Supongamos que quieres predecir el peso de una persona basándote en su altura. Si^R² es cercano a 1, tu predicción es muy acertada. La mayor parte de las diferencias de peso pueden atribuirse a diferencias de altura. Si^R² es cercano a 0, entonces tu predicción es básicamente una suposición, ya que, en ese caso, la altura no explica gran parte del cambio en el peso.

Esperamos valores de^R² entre 0 y 1:

• 0 significa que el modelo no explica ninguna de la variabilidad en los datos.

• 1 significa que el modelo explica toda la variabilidad.

• Los valores más cercanos a 1 significan un mejor ajuste, lo que demuestra que tu modelo está captando mejor el patrón de los datos.

Regresión lineal simple

Cuando trabajas con una sola variable independiente, el modelo se denomina regresión lineal simple. En este caso,^R² tiene una relación clara con el coeficiente de correlación de Pearson (r): R^² = r^²

Esto significa que si existe una fuerte correlación positiva o negativa entre tu predictor y el resultado,^R² será alto.

Nota: En modelos con más de un predictor (denominados regresión múltiple),^R² sigue indicando cuánta varianza se explica, pero ya no es solo^r², porque ahora se combinan los efectos de múltiples variables.

¿Puede el coeficiente de determinación ser negativo?

^R² suele oscilar entre 0 y 1. Pero a veces, es posible que veas un R² negativo^. Esto puede suceder si:

• Tu modelo no incluye un intercepto (un valor inicial constante).
• Estás utilizando un tipo de modelo inadecuado para los datos.

Un^R² negativo significa que tu modelo está funcionando peor que adivinando la media. En otras palabras, se ajusta tan mal a los datos que, en realidad, resulta engañoso.

Cómo calcular el coeficiente de determinación

Hay dos formas habituales de calcular^R²:

1. Usando la suma de cuadrados
2. Utilizando el coeficiente de correlación (r)

Repasemos ambos casos.

Usando la suma de cuadrados

La fórmula más común para^R² es:

Aquí, la suma residual de cuadrados (la parte no explicada) mide la distancia entre los valores reales y los valores previstos por tu modelo. Es el error que comete tu modelo.

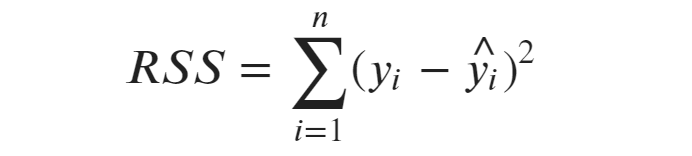
La suma total de los cuadrados es la variación total en los datos observados. Nos indica cuánto se alejan los valores reales de la media (promedio) de la variable dependiente.

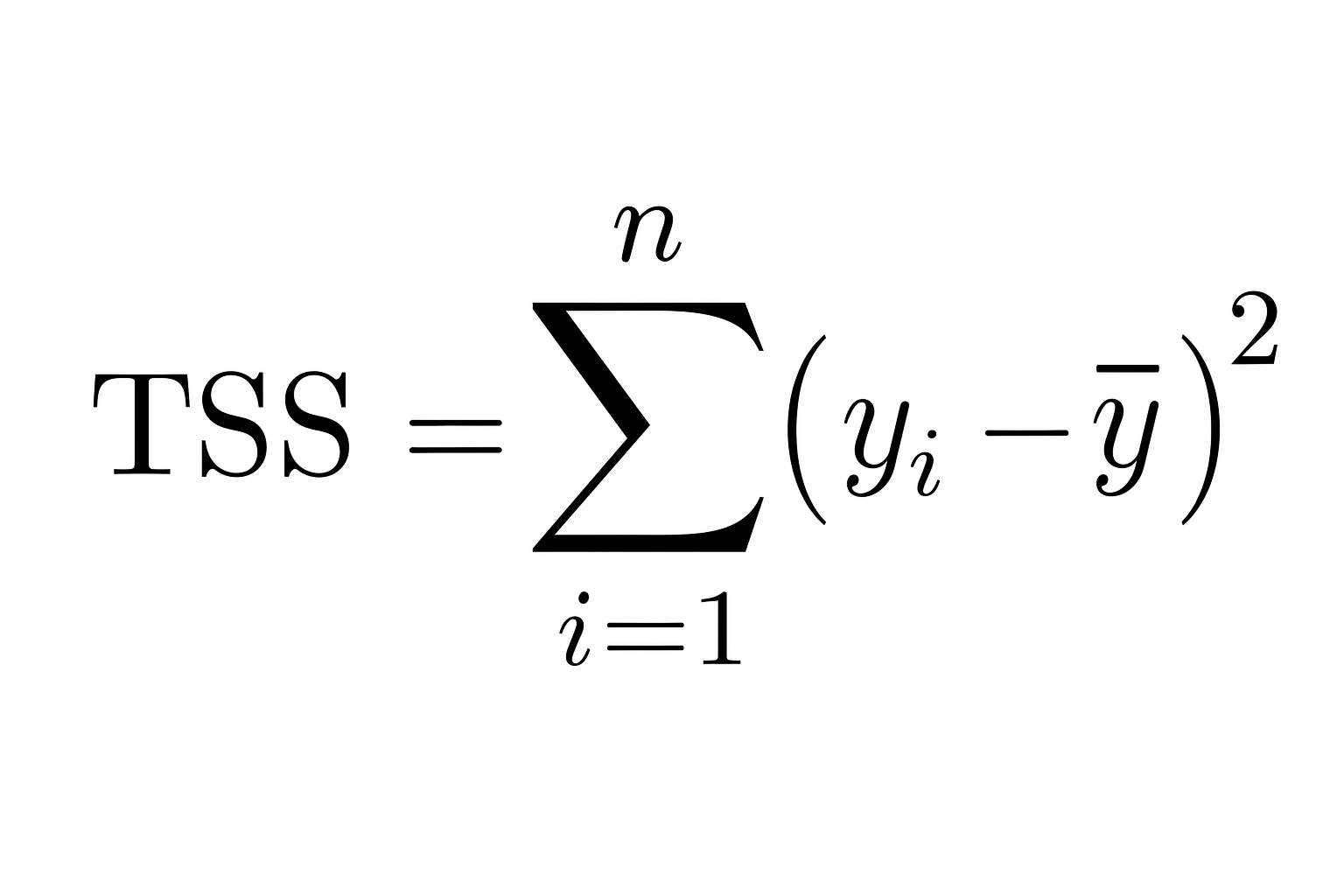
Por lo tanto, cuanto menor sea la suma de cuadrados residuales en comparación con la suma de cuadrados total, mejor se ajustará tu modelo a los datos y más se acercará^R² a 1.

Entendamos esto con un ejemplo: 

Supongamos que tienes un pequeño conjunto de datos con los siguientes valores:

Primero, calcula la media de los valores reales:

• y = (10+12+14)/3 = 12

A continuación, calcula la suma de los cuadrados totales (la distancia entre los valores reales y la media):

• suma de cuadrados total = (10 − 12)² + (12 − 12)² + (14 − 12)² = 4 + 0 + 4 = 8

A continuación, calcula la suma de cuadrados residuales (la distancia entre los valores reales y los valores previstos):

• suma residual de cuadrados = (10 − 12)² + (12 − 11)² + (14 − 13)² = 4 + 1 + 1 = 6

Ahora añade esto a la fórmula:

• ^R² = 1 − ( suma de cuadrados residuales / suma total de cuadrados) = 1 − (6/8) = 1 − 0,75 = 0,25

Por lo tanto,^R² = 0,25, lo que significa que el modelo explica el 25 % de la variación en los datos.

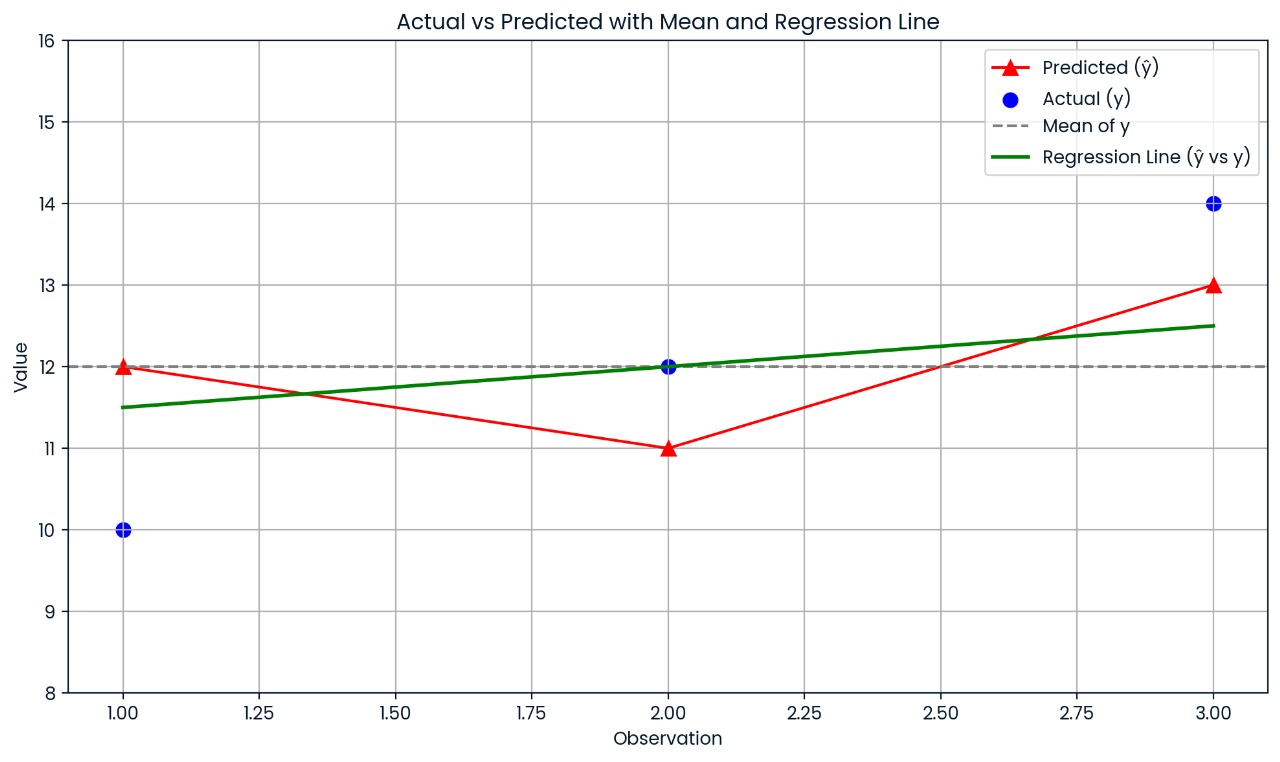
Este gráfico muestra la distancia entre cada valor real y su valor previsto. Las predicciones del modelo son bastante inexactas, por lo que el R² es solo de 0,25; solo se explica el 25 % de la variación.

Uso del coeficiente de correlación

Si estás utilizando una regresión lineal simple (una sola variable independiente), utiliza esta fórmula:

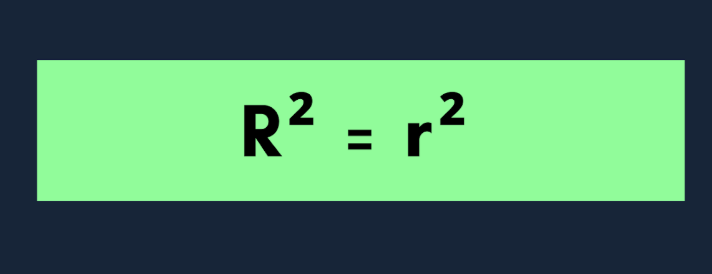
Aquí r es el coeficiente de correlación de Pearson entre los valores reales y los valores previstos. Este atajo solo funciona cuando hay un único predictor.

Supongamos que la correlación entre X e Y es: r = −0,8

Aunque la correlación es negativa (lo que significa que las variables se mueven en direcciones opuestas),^R² es positivo: R^² = (−0.8)^² = 0.64

Por lo tanto, el 64 % de la variación en el resultado aún puede explicarse por el predictor, incluso si la relación es negativa. Por eso^R² siempre es positivo o cero; representa la cantidad de variación explicada, no la dirección.

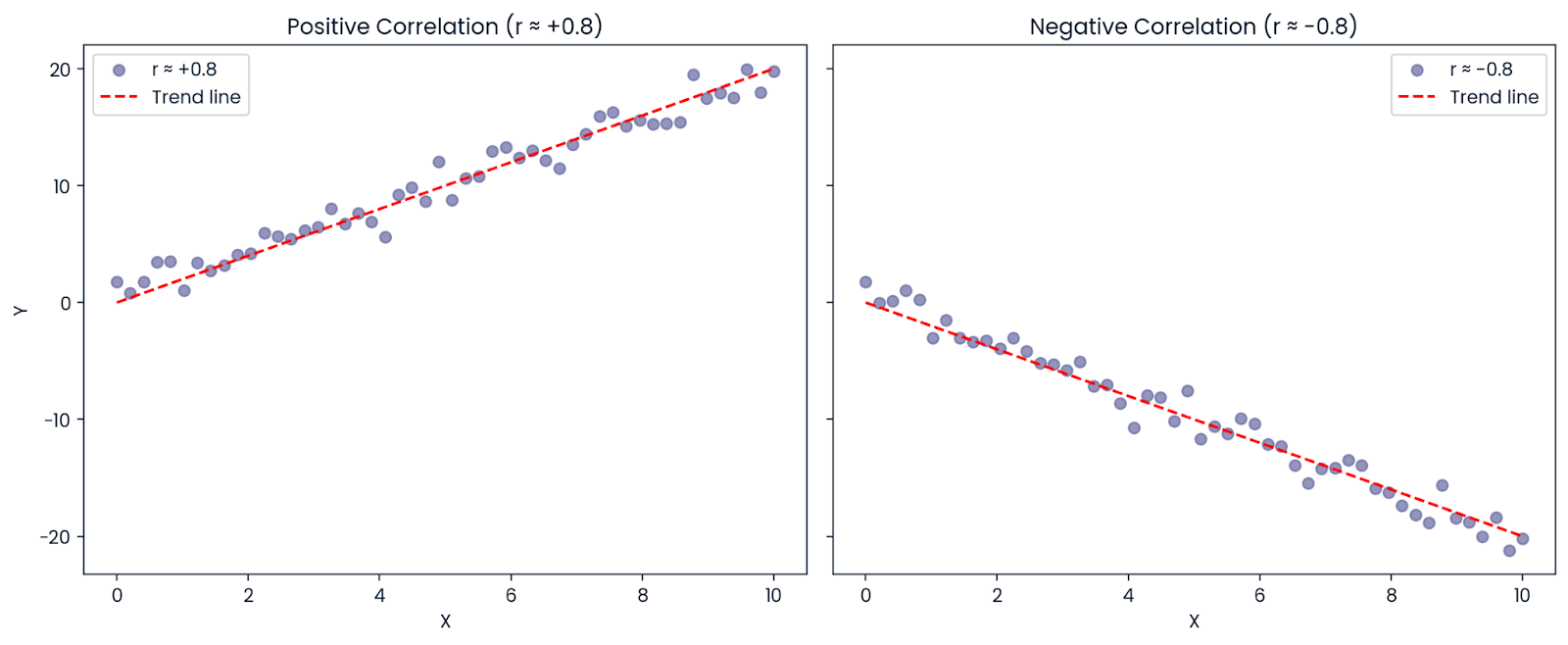
Correlación positiva y negativa. Imagen del autor.

Cómo interpretar el coeficiente de determinación

El coeficiente de determinación nos indica qué parte de la variación en el resultado (variable dependiente) se explica mediante nuestro modelo. En términos sencillos, es como preguntar: «¿En qué medida los cambios que intento predecir pueden explicarse con los datos que estoy utilizando?».

Supongamos que estás creando un modelo para predecir las calificaciones de los alumnos en un examen en función de las horas que estudian. Si tu modelo te da: ^R² = 0,90

Esto significa que el 90 % de las diferencias en las calificaciones de los exámenes pueden explicarse por las diferencias en el tiempo de estudio. El 10 % restante proviene de otros factores que tu modelo no incluyó, como el sueño, la capacidad natural, los conocimientos previos o la dificultad de la prueba.

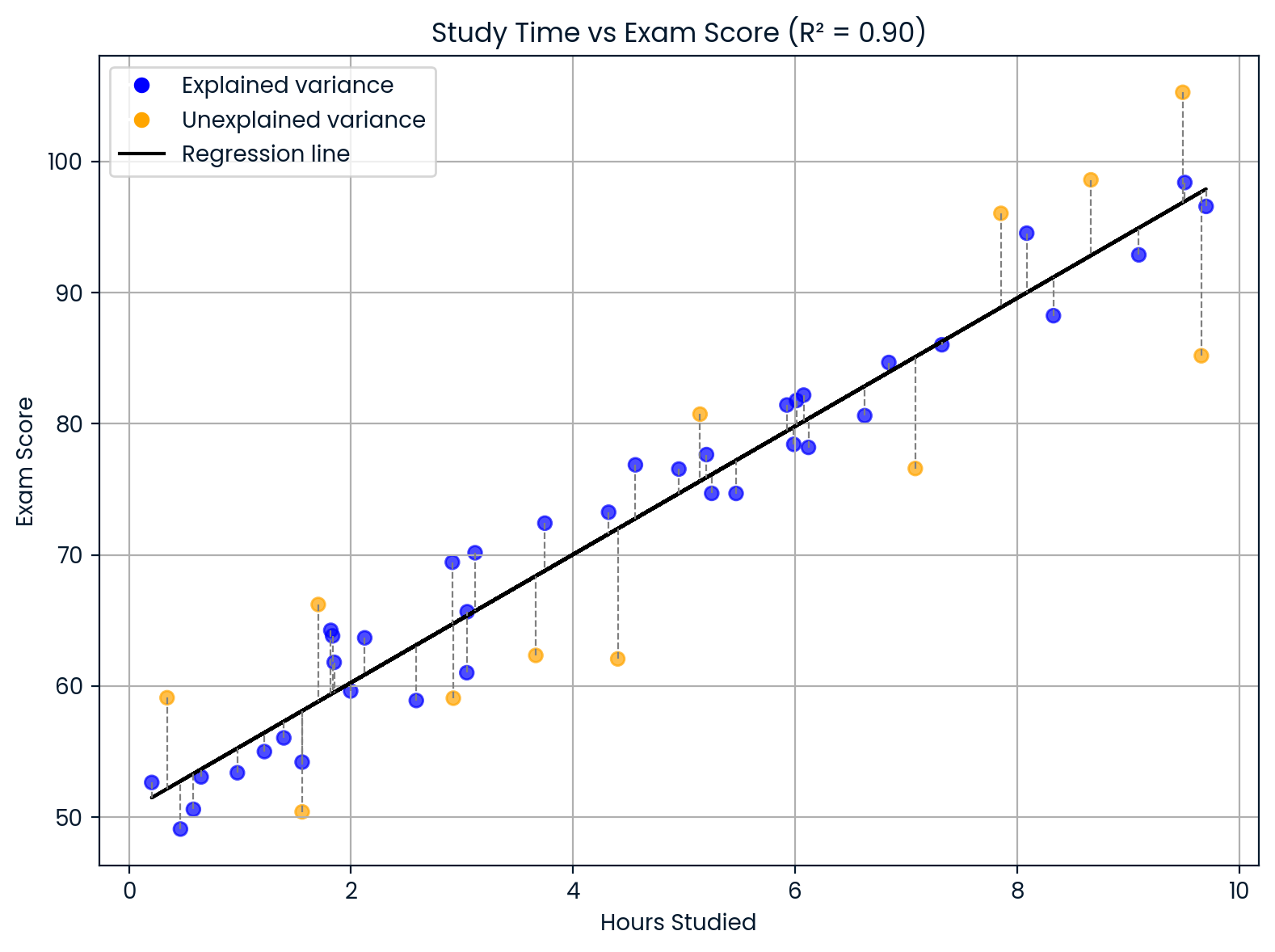
Interpretación del coeficiente de determinación. Imagen del autor.

Este gráfico muestra cómo el tiempo de estudio afecta a las calificaciones de los exámenes. 

• La línea negra es la predicción del modelo. 
• Los puntos azules son puntuaciones que el modelo ha explicado bien utilizando el tiempo de estudio. 
• Los puntos naranjas representan puntuaciones que no encajan, probablemente debido a otros factores como el sueño, la dificultad de la prueba o los conocimientos previos del estudiante. Dado que^R² = 0,90, la mayoría de las puntuaciones siguen el patrón, pero no todas.

Directrices de Cohen

Jacob Cohen creó una guía muy utilizada para ayudarnos a comprender qué pueden significar los diferentes valores^{de R²} a la hora de interpretar la fuerza de una relación.

A continuación se muestran los puntos de referencia aproximados de Cohen para^R²:

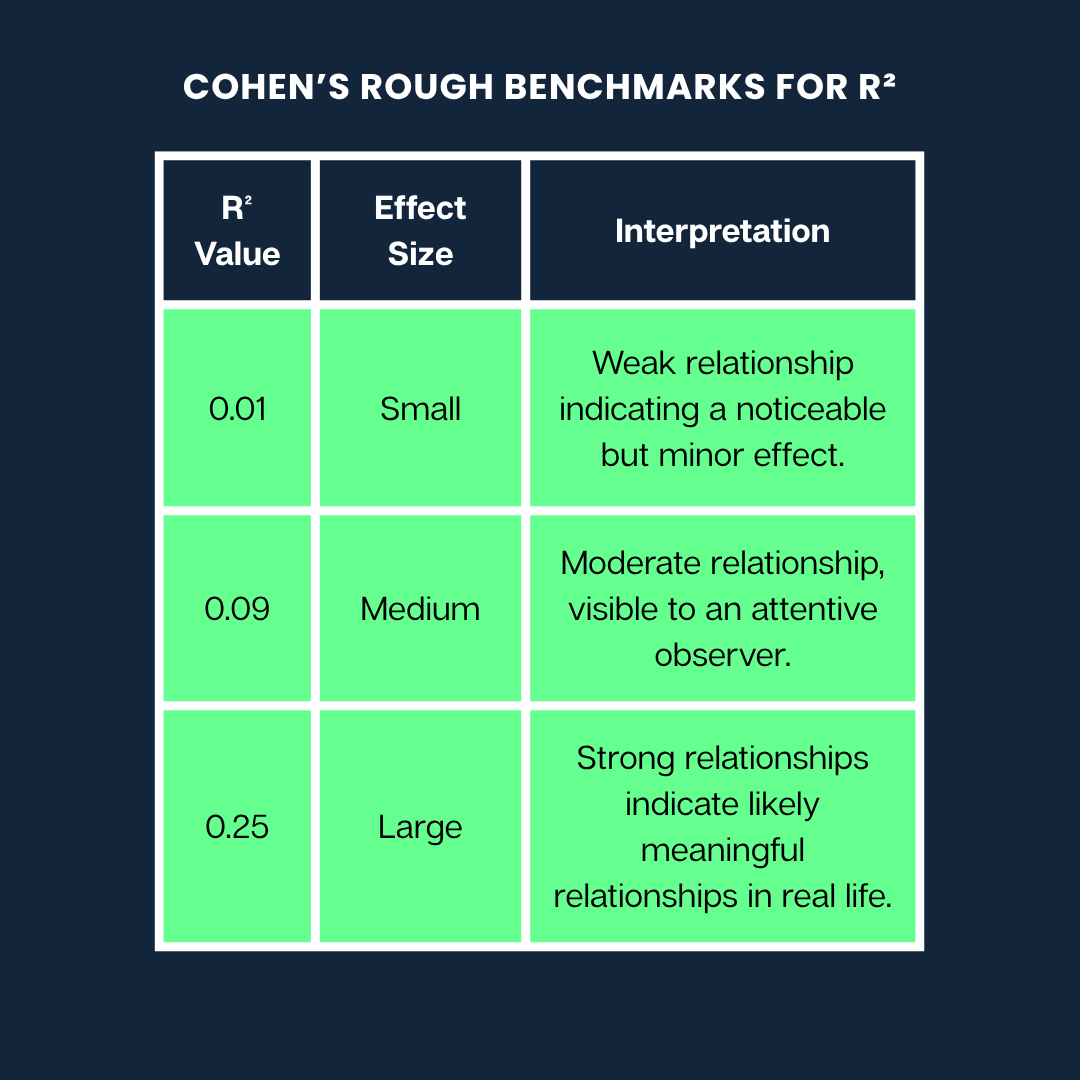
Puntos de referencia aproximados de Cohen. Imagen del autor

Nota: Estas son pautas generales. Lo que se considera un efecto «grande» o «pequeño» puede variar mucho dependiendo de tu campo (por ejemplo, psicología frente a ingeniería) y del contexto de la investigación.

Limitaciones y conceptos erróneos comunes

Aunque^R² es útil, debes comprender lo que puede y no puede decirte. A continuación, se indican algunos malentendidos y limitaciones comunes a los que debes prestar atención:

Mito 1: Un coeficiente de determinación alto significa un mejor modelo.

Puede parecer que un^R² más alto siempre significa un mejor modelo, pero eso no es necesariamente cierto. ^R² siempre aumenta o permanece igual cuando añades más variables a un modelo, incluso si esas variables son completamente irrelevantes. 

¿Por qué? 

Porque el modelo tiene más flexibilidad para ajustarse a los datos de entrenamiento, aunque solo se ajuste a ruido aleatorio. Esto puede provocar un sobreajuste, por el que tu modelo parece excelente con los datos con los que se ha entrenado, pero funciona mal con datos nuevos.

Consejo: Ue R² ajustado al comparar modelos con diferentes números de predictores. Penaliza la complejidad innecesaria y puede ayudar a detectar el sobreajuste. 

Mito 2: Un coeficiente de determinación alto significa predicciones precisas sobre nuevos datos o causalidad.

^R² solo mide lo bien que el modelo describe los datos que ya tienes. No te dice:

• Si el modelo realizará buenas predicciones sobre nuevos datos.
• Si una variable causa la otra

Un^R² alto puede darse incluso por casualidad si utilizas muchos predictores. Por lo tanto, siempre hay que fijarse en otras métricas de evaluación de modelos (como RMSE o MAE para la calidad de la predicción) y recordar que la correlación no implica causalidad.

Mito 3: Un R cuadrado bajo significa que el modelo es inútil.

A veces, en sistemas complejos (como la predicción del comportamiento humano o los mercados financieros), se espera un^R² bajo.

Por ejemplo, si estás modelando algo influenciado por muchos factores impredecibles o inconmensurables, tu modelo puede seguir siendo útil, incluso con un^R² bajo^. Puede capturar una tendencia significativa o proporcionar información valiosa, aunque no explique una gran parte de la varianza.

En la investigación médica o psicológica, es habitual encontrar valores bajos^{de R²}, ya que los resultados dependen de muchas variables que interactúan entre sí.

Otras variantes: R cuadrado parcial y generalizaciones

Si bien^R² ayuda a comprender cómo se ajusta el modelo en la regresión lineal, existen otras variantes y generalizaciones que ayudan en diferentes contextos de modelado.

R cuadrado ajustado

Al igual que el^R² normal,^{el R²} ajustado nos indica qué proporción de la variación de la variable dependiente se explica mediante el modelo. Pero va un paso más allá al penalizar la complejidad innecesaria. En otras palabras, te disuade de llenar tu modelo con predictores adicionales que no ayudan.

Su fórmula es:

Adjusted R² = 1 - [ (1 - R²) × (n - 1) / (n - p - 1) ]

Aquí:

• n es el número de observaciones (puntos de datos)

• p es el número de predictores (variables independientes)

La fórmula ajusta^R² a la baja si una nueva variable no mejora el modelo. Esta penalización se hace más severa a medida que se añaden más predictores.

Por ejemplo, si añades una nueva variable que mejora la precisión de tu modelo,^{el R²} ajustado aumentará. Pero si esa variable apenas cambia algo o solo ayuda por casualidad,^{el R²} ajustado bajará, lo que te alertará de un posible sobreajuste.

Esto hace que^{el R²} ajustado sea útil para comparar modelos.

Supongamos que quieres elegir entre un modelo más sencillo con tres predictores y otro más complejo con seis. Incluso si el modelo complejo tiene un^R² ligeramente superior, el^R² ajustado podría ser inferior, lo que indicaría que no merece la pena añadir complejidad.

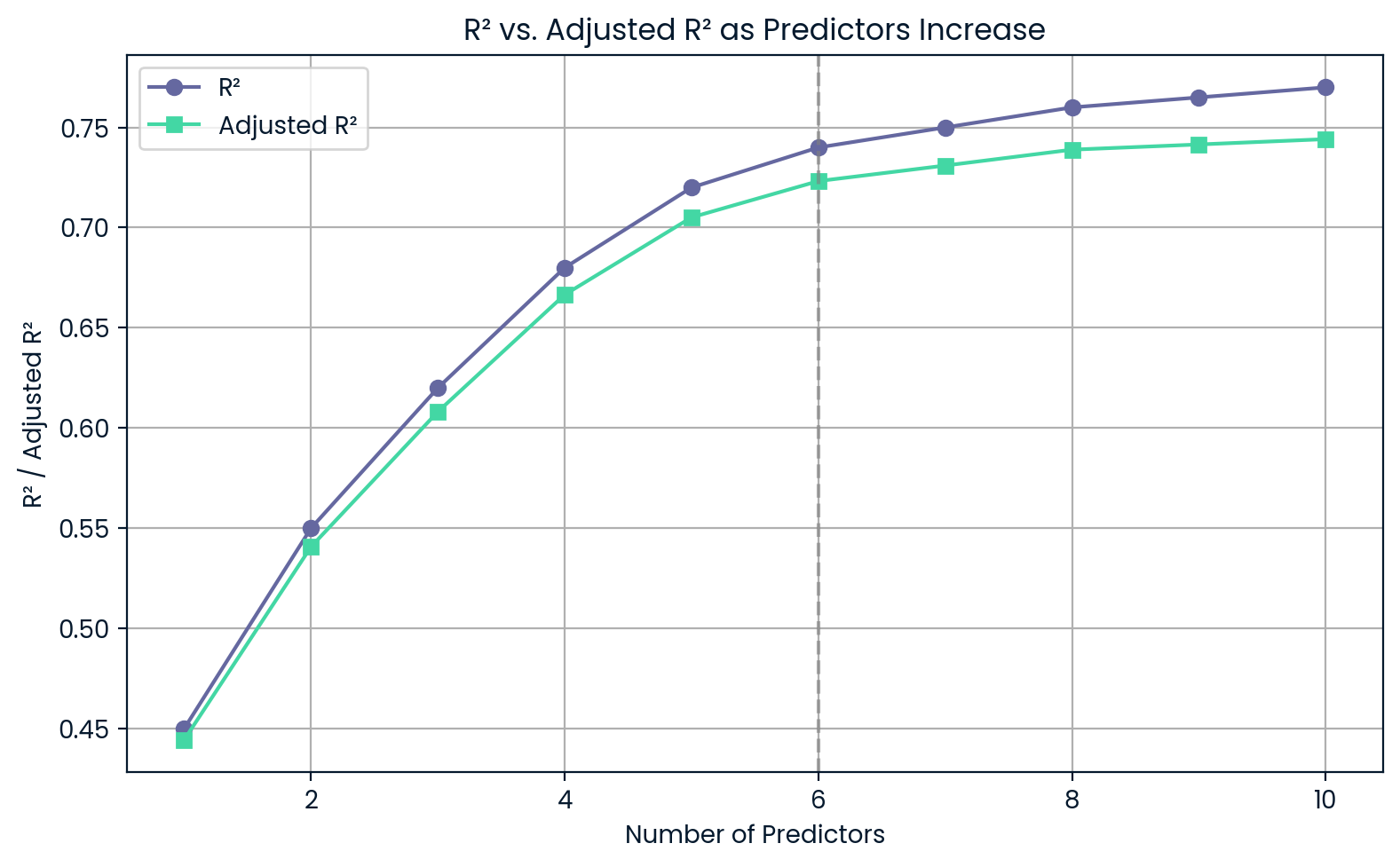
R² frente a R² ajustado a medida que aumentan los predictores. Imagen del autor.

Este gráfico muestra que, a medida que añades más predictores,^R² sigue aumentando, incluso si esos predictores no son muy útiles. Por otro lado,^{el R²} ajustado disminuye si añades demasiado, lo que te advierte sobre el sobreajuste.

Coeficiente de determinación parcial

^{El R²} parcial (o coeficiente de determinación parcial) nos indica cuánta varianza adicional en la variable dependiente se explica al añadir un predictor específico a un modelo que ya incluye otros.

Para calcular^{el R²} parcial, comparamos dos modelos:

• El modelo reducido, que excluye el predictor en cuestión.
• El modelo completo, que incluye todos los predictores.

La fórmula para^{el R²} parcial se basa en la reducción de la suma de los errores al cuadrado (SSE) cuando se añade la nueva variable. Una forma habitual es:

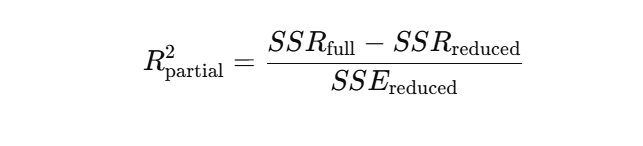
O en términos de sumas de cuadrados de regresión:

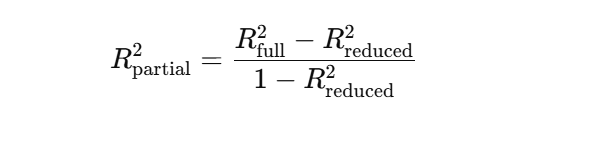
Supongamos que estás creando un modelo para predecir las ventas de un producto. 

Ya tienes «precio del producto» y «temporada» en el modelo. Ahora, quieres ver si añadir «gasto en marketing» mejora las predicciones. El R² parcial indica cuánta variación adicional en las ventas se explica al incluir el «gasto en marketing».

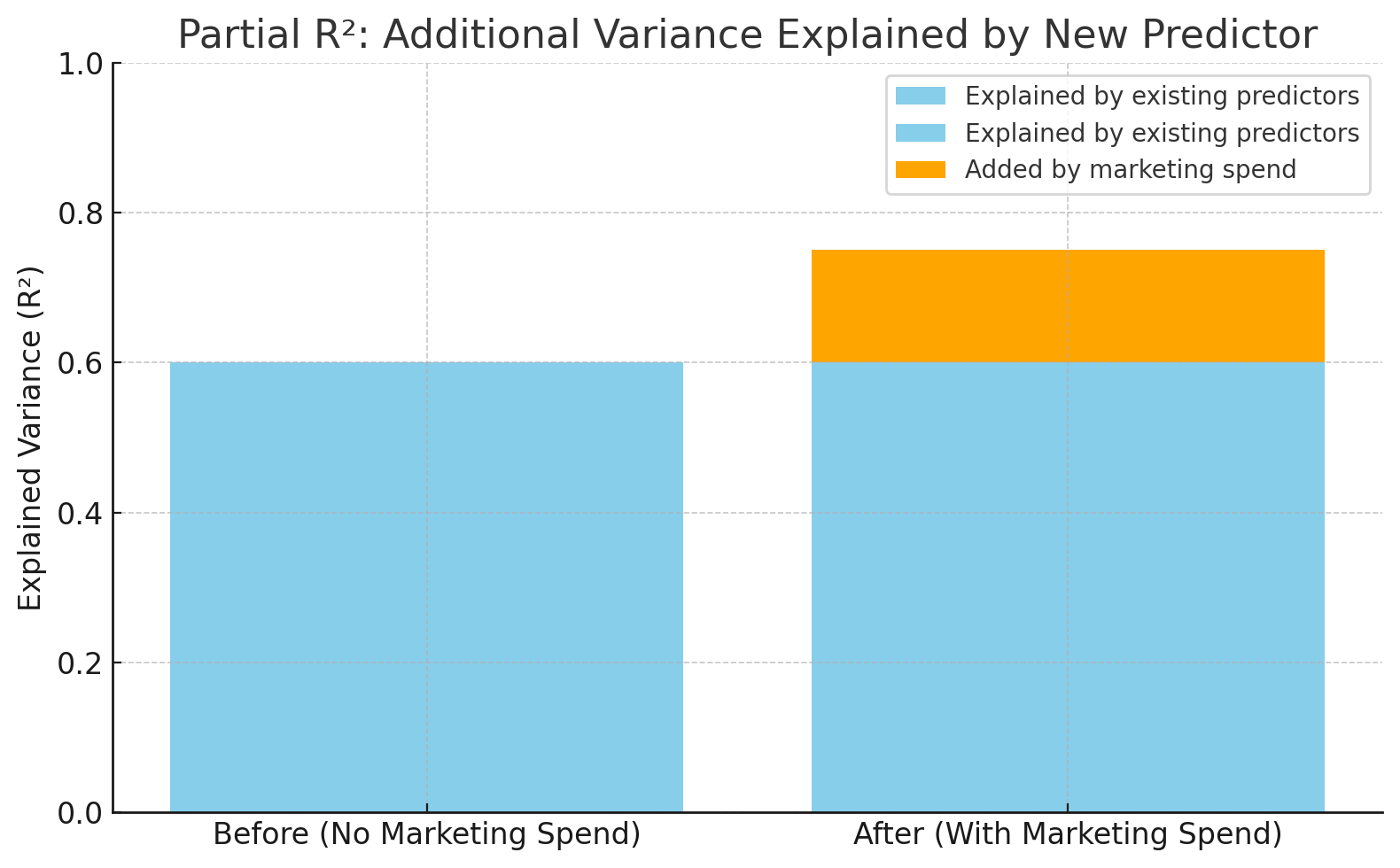
^{El R²} aumentó de 0,60 a 0,75 tras añadir el gasto en marketing. Imagen del autor.

Este gráfico muestra cuánto aumenta la precisión del modelo cuando se añade el «gasto en marketing». ^R² pasa de 0,60 a 0,75, lo que significa que la nueva variable explica un 15 % más de la variación en las ventas: ese es el R^² parcial^.

Coeficiente de determinación en regresión logística

En la regresión logística, la variable de resultado es categórica, como sí/no, aprobado/suspenso, por lo que no se aplica^{el R²} tradicional. En su lugar, utilizamos métricas^pseudo-R², que tienen una finalidad similar: estimar en qué medida el modelo explica la variación en los resultados.

Dos valores^pseudo-R² comunes son:

• Cox y Snell^R²: Las estimaciones explicaron la varianza, pero su valor máximo es inferior a 1, incluso para un modelo perfecto.
• Nagelkerke^R²: Una versión corregida de Cox & Snell^R² que se escala hasta 1, lo que facilita su interpretación al igual que el^R² tradicional^.

Supongamos que estás modelando si un cliente hará clic en un anuncio (sí/no). Dado que el resultado es binario, no puedes utilizar el R² habitual^. Sin embargo, los valores^pseudo-R² como el de Nagelkerke ayudan a comparar modelos logísticos y evaluar su capacidad predictiva, aunque no sean directamente equivalentes al^R² en la regresión lineal.

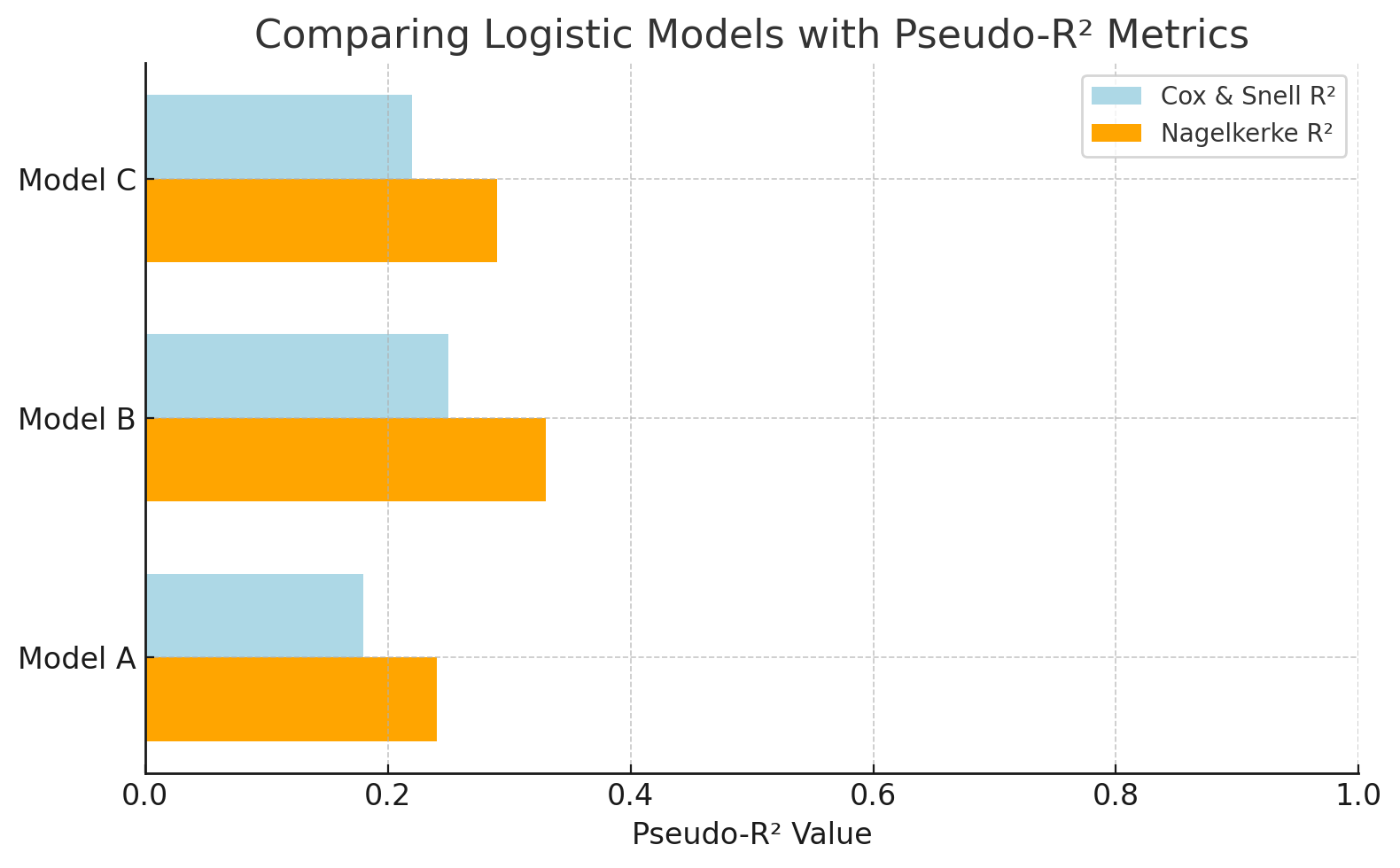
Compara modelos logísticos con métricas^pseudo-R ². Imagen del autor.

Este gráfico compara modelos de regresión logística utilizando valores^pseudo-R ². Nagelkerke^R² ofrece una escala más interpretable que Cox & Snell. Esto facilita la evaluación de la eficacia de cada modelo a la hora de explicar el resultado (por ejemplo, predecir los clics en anuncios).

Coeficiente de determinación frente a otras métricas de ajuste del modelo

Aunque^R² es útil para comprender cuánta variación se explica, no mide cuánto se alejan tus predicciones. Para eso sirven las métricas basadas en errores, como RMSE, MAE y MAPE.

Aquí tienes una breve comparación:

Aplicaciones prácticas en distintos campos

Ahora, veamos algunos de los innumerables casos en los que se ha utilizado el coeficiente de determinación. 

Economía: Explicación de las fluctuaciones del PIB

En economía,^R² se utiliza para explicar cambios en indicadores generales como el producto interior bruto (PIB). Por ejemplo, un modelo puede incluir variables como los tipos de interés, el gasto de los consumidores y las balanzas comerciales para predecir el PIB.

Si dicho modelo arroja un^R² de 0.83, significa que el 83 % de la variación del PIB puede explicarse por estos factores económicos. Esto ayuda a los economistas a comprender en qué medida las fluctuaciones del PIB pueden atribuirse a factores conocidos.

Un estudio de investigación de la Asociación Nacional de Fabricantes de Productos de Limpieza ( ) utilizó datos de la Encuesta de o del PIB como variable independiente para predecir el índice S&P 500 y se obtuvo un^R² de 0.83. Esto demostró una fuerte relación entre la actividad económica y las tendencias del mercado bursátil.

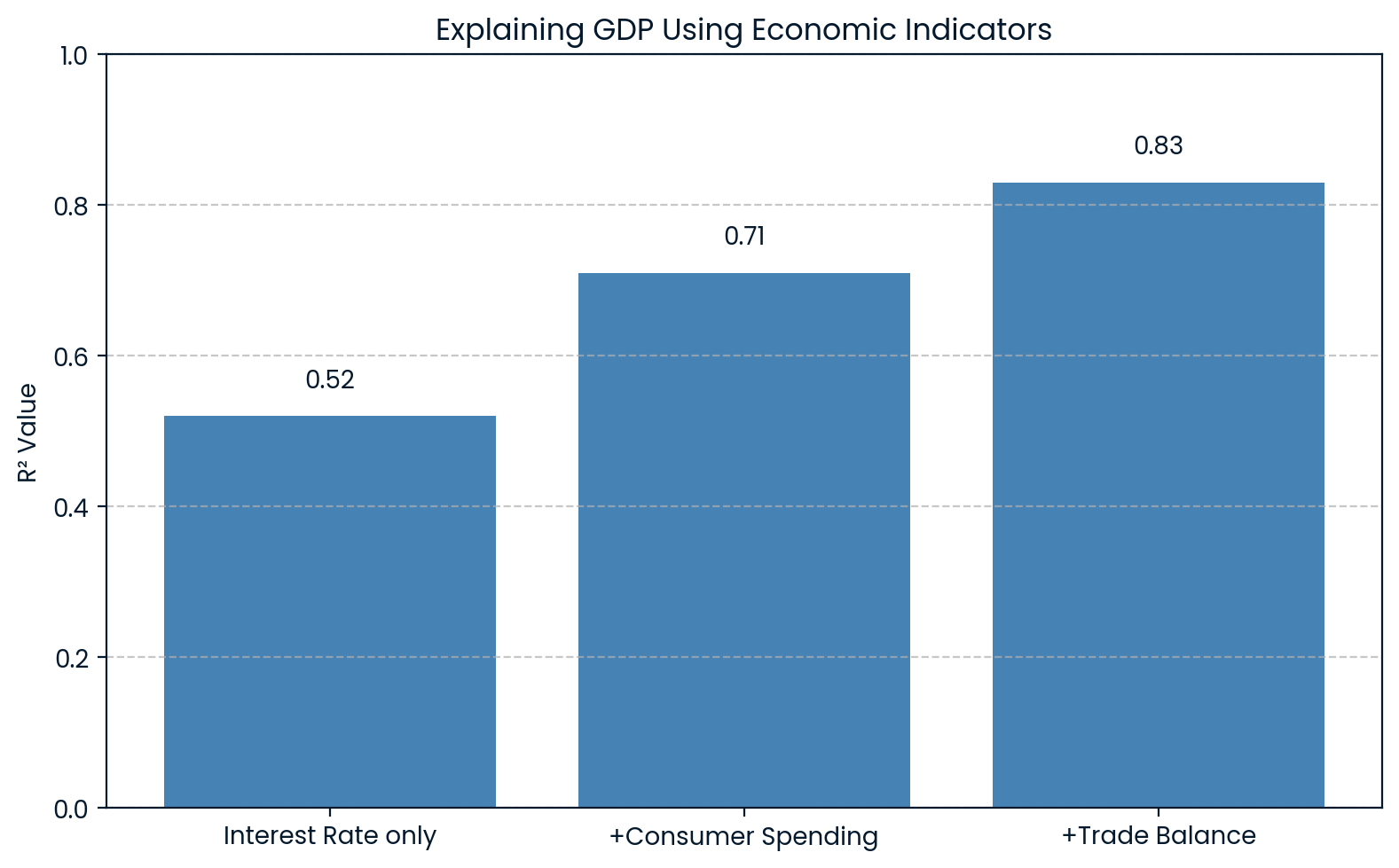
^R² que explica la economía del PIB. Imagen del autor.

El gráfico muestra que, a medida que se añaden más indicadores económicos al modelo, el^R² aumenta, pasando de 0.52 a 0.83 con las tres variables. Esto deja claro que cada factor añadido explica mejor las fluctuaciones del PIB.

Finanzas: Movimientos del precio de las acciones frente al índice bursátil

En finanzas,^R² se utiliza para medir en qué medida los rendimientos de una acción se explican por los movimientos generales del mercado. Esto se hace comparando los rendimientos de una acción con un índice bursátil como el S&P 500.

Por ejemplo, si regresas los rendimientos de Apple (AAPL) frente al S&P 500 y obtienes^R² = 0.82, significa que el 85 % de los movimientos de rendimiento de Apple se explican por el mercado en general.

• Un^R² alto sugiere que las acciones están estrechamente vinculadas al mercado.
• Un^R² bajo implica que las acciones son más independientes.

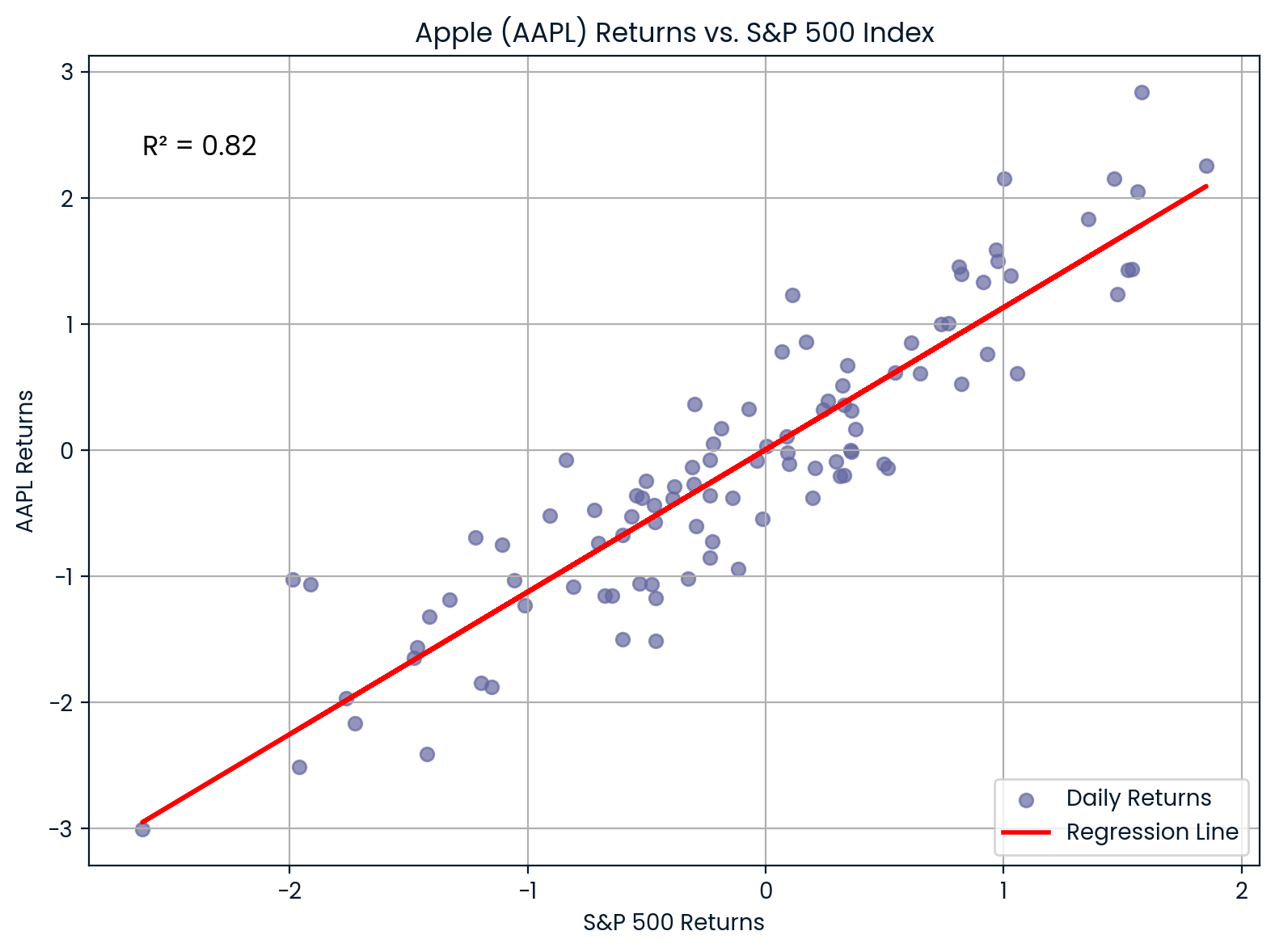
Correlación entre AAPL y S&P 500. Imagen del autor.

El gráfico muestra la fuerte correlación entre Apple (AAPL) y el S&P 500. Con un^R² del 0.82, la mayoría de los movimientos de precios de Apple se alinean estrechamente con las tendencias del mercado, lo que indica una alta sensibilidad al mercado.

Marketing: Gasto publicitario y conversiones

En marketing,^R² muestra en qué medida el gasto en publicidad explica las tasas de conversión de los clientes.

Supongamos que trabajas en una empresa de comercio electrónico y deseas saber si aumentar el gasto mensual en publicidad mejora las tasas de conversión. Realizas una regresión lineal y obtienes^R² = 0,98. Esto significa que el 98 % de la variación en la tasa de conversión se explica por tu inversión publicitaria, lo que sugiere una relación muy fuerte.

Esta información ayuda a los profesionales del marketing a:

• Resultados previstos de la conversión
• Justificar los presupuestos publicitarios
• Predice el retorno de la inversión (ROI)

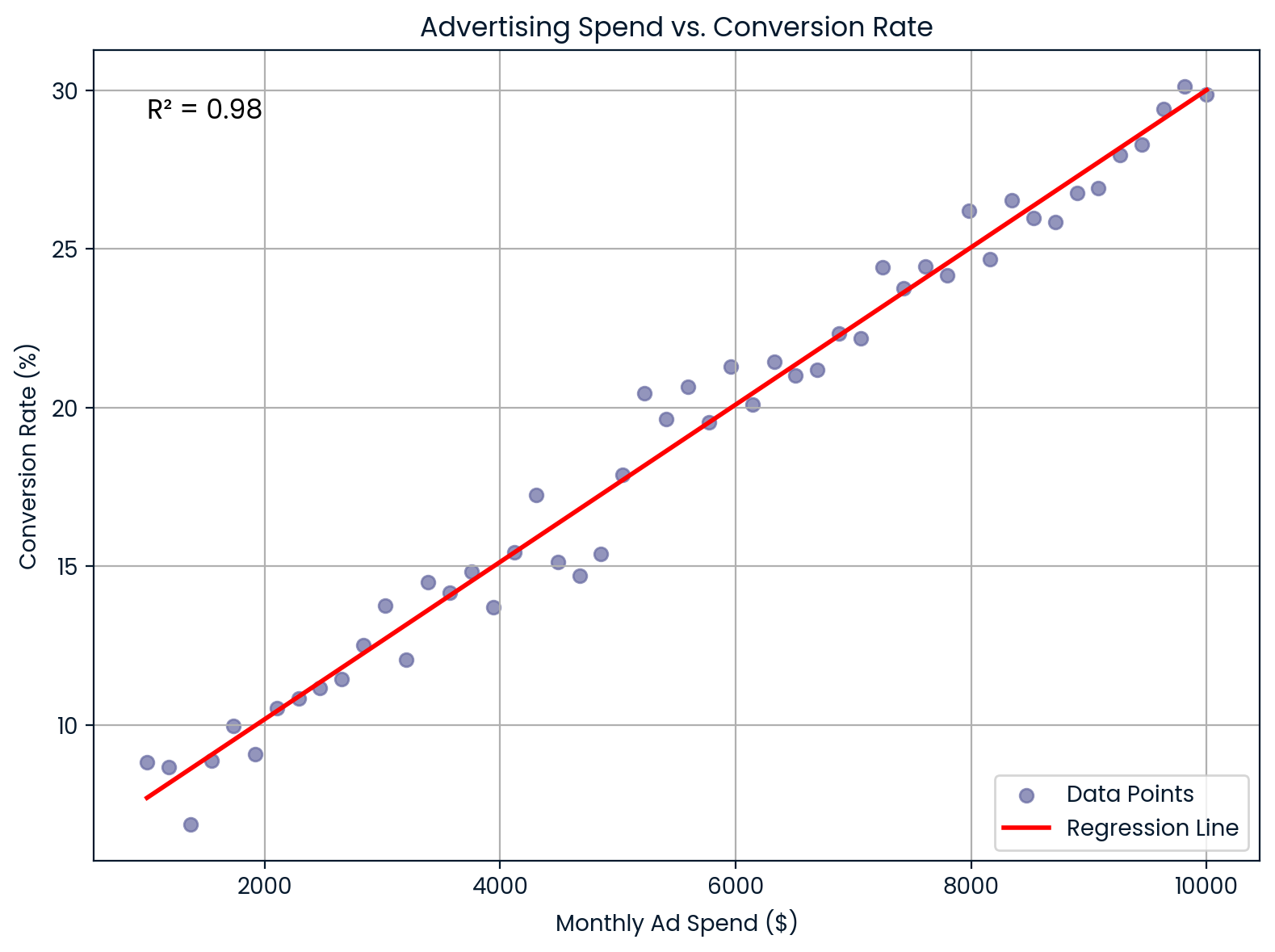
Gasto mensual en publicidad frente a tasa de conversión. Imagen del autor.

Este gráfico ilustra una relación lineal casi perfecta entre el gasto mensual en publicidad y la tasa de conversión. Ofrece un gran valor predictivo para el retorno de la inversión y la planificación presupuestaria.

Machine learning: Evalúa los modelos de regresión

En machine learning,^R² se utiliza como métrica de rendimiento para tareas de regresión. Las bibliotecas como scikit-learn ofrecen la función r2_score() para calcularlo.

Te indica en qué medida tu modelo explica la variabilidad de los datos:

• ^{Un R²} cercano a 1 significa un buen ajuste y un error bajo.

• ^{Un R²} cercano a 0,000 ( 0 ) significa un ajuste deficiente.

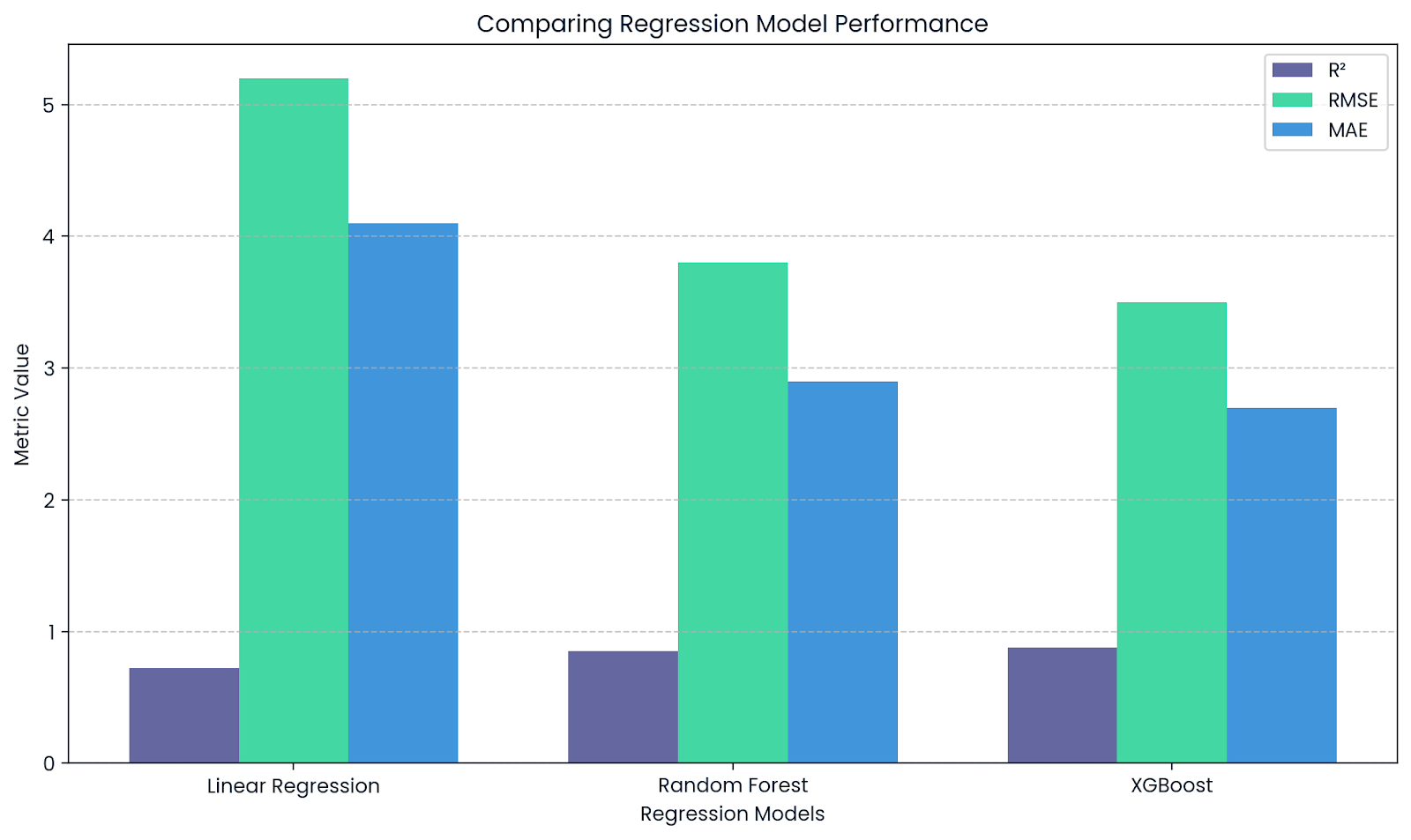
^R² complementa RMSE y MAE. Imagen del autor.

Este gráfico destaca cómo R² complementa otras métricas como RMSE y MAE al evaluar modelos de regresión. Mientras que^R² muestra el poder explicativo, RMSE y MAE proporcionan información sobre el tamaño real de los errores de predicción.

Cómo informar sobre el coeficiente de determinación en la investigación

Si vas a incluir^R² en un trabajo de investigación o proyecto, hay algunas reglas de formato que debes tener en cuenta:

• Asegúrate de poner en cursiva^R² y sí, debe ser una R mayúscula, no minúscula. 
• No utilices un cero delante del decimal. Así que, en lugar de escribir^R² = 0,73, escribe^R² = 0,73. Y, a menos que realmente necesites más detalles, redondéalo a dos decimales.

Si estás utilizando^R² como parte de un análisis de regresión o ANOVA, y comprobando si tu modelo es significativo, incluye algunos datos más: la estadística F, los grados de libertad y el valor p. Estos indican al lector el grado de confianza que podemos tener en que tu modelo explica algo significativo.

Por lo tanto, cuando informes los resultados, podría verse algo así:

«El modelo explicó una parte significativa de la varianza en las ventas,^R² = 0,73, F(2, 97) = 25,42, p < 0,001».

Sin embargo, si no estás realizando una prueba de hipótesis, supongamos que estás llevando a cabo un análisis exploratorio o evaluando el rendimiento de un modelo con validación cruzada, entonces está perfectamente bien informar el valor R² por sí solo.

El coeficiente de determinación en Python, R y Excel

Veamos cómo calcular^R² utilizando tres métodos diferentes: Python, R y Excel a través de un miniproyecto en el que predicen las calificaciones de los alumnos en función de su tiempo de estudio.

Usaremos el siguiente conjunto de datos para los tres ejemplos:

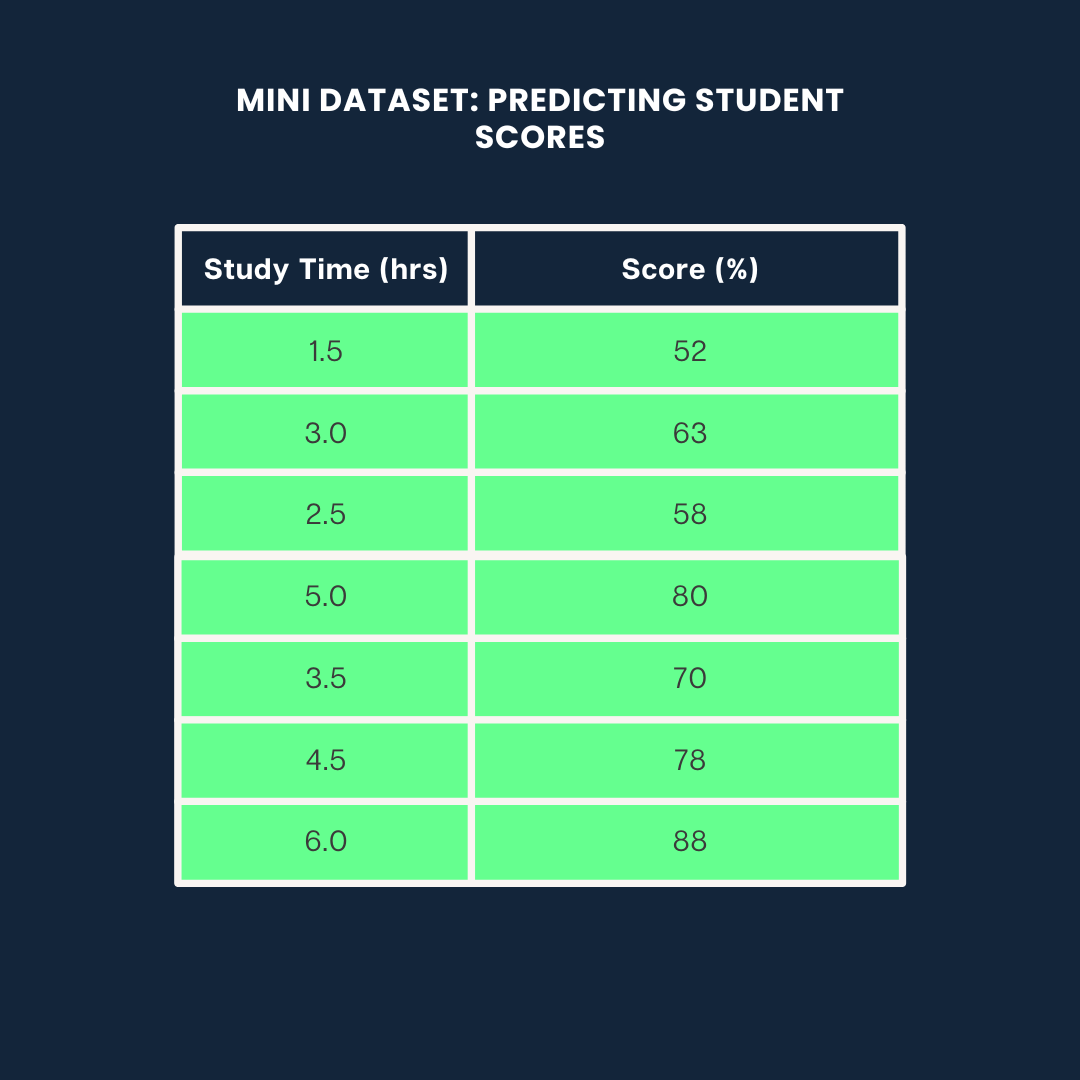
Conjunto de datos de ejemplo. Imagen del autor

Coeficiente de determinación en Python

A continuación se explica cómo calcular^R² en Python utilizando scikit-learn:

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

# Data
study_time = np.array([1.5, 3.0, 2.5, 5.0, 3.5, 4.5, 6.0]).reshape(-1, 1)
scores = np.array([52, 63, 58, 80, 70, 78, 88])

# Model
model = LinearRegression()
model.fit(study_time, scores)
predicted_scores = model.predict(study_time)

# R² score
r2 = r2_score(scores, predicted_scores)
print(f"R² = {r2:.2f}")

0.99

Esto significa que el 99 % de la variación en las puntuaciones se explica por el tiempo de estudio.

Si deseas obtener más información sobre los modelos de regresión y estadística, puedes consultar nuestra guía Introducción a la regresión con statsmodels en Python. 

Coeficiente de determinación en R

En R, puedes calcular R² con unas pocas líneas utilizando la función lm():

# Data
study_time <- c(1.5, 3.0, 2.5, 5.0, 3.5, 4.5, 6.0)
scores <- c(52, 63, 58, 80, 70, 78, 88)

# Linear model
model <- lm(scores ~ study_time)

# R-squared
summary(model)$r.squared

0.9884718

Alrededor del 98 % de la variación en las puntuaciones se explica por el tiempo de estudio. Si deseas obtener más información sobre la regresión en R, consulta nuestro curso Introducción a la regresión en R.

Coeficiente de determinación en Excel

En Excel, puedes calcular R² utilizando la función integrada « RSQ() » (R cuadrado). Suponiendo que:

• El tiempo de estudio está en las celdas A2:A8

• Las puntuaciones están en las celdas. B2:B8

La sintaxis es:

RSQ(known_y's,known_x's)

Utilicé la siguiente fórmula:

=RSQ(B2:B8,A2:A8)

Esto le indica a Excel que calcule el valor^R² entre la variable dependiente (puntuaciones) y la variable independiente (tiempo de estudio).

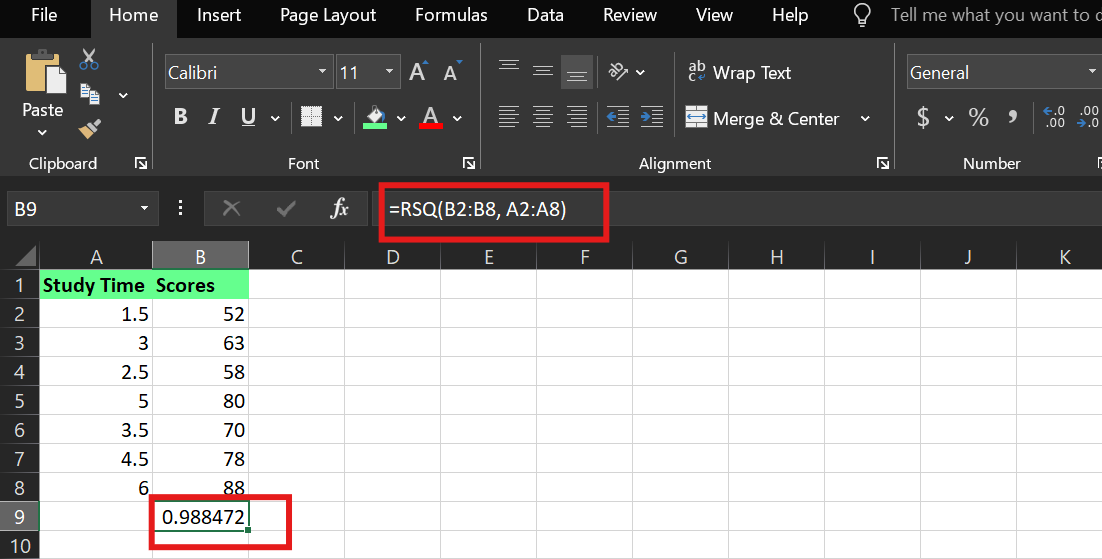
Ejemplo de^R² en Excel. Imagen del autor.  

Puntos clave

Ya sea que estés prediciendo las calificaciones de los estudiantes, el rendimiento de las acciones o el comportamiento de los clientes, el coeficiente de determinación te indica qué parte del resultado comprende realmente tu modelo. 

Un coeficiente de determinación alto puede parecer impresionante, pero no te dejes engañar pensando que el modelo es perfecto o que demuestra una relación causa-efecto. Y un coeficiente de determinación bajo no siempre significa fracaso; podría significar que tu sistema es complejo o que tus variables son incompletas.

Por lo tanto, si estás creando o analizando modelos, pregúntate lo siguiente:

• ¿Qué es lo que estoy explicando bien?
• ¿Qué me estoy perdiendo?
• ¿Y mi modelo es útil, no solo preciso?

Empieza con esa mentalidad y utilizarás el coeficiente de determinación como lente para tomar mejores decisiones.