Probabilidad conjunta: Teoría, ejemplos y aplicaciones de la ciencia de datos

Cuando un analista meteorológico predice una tormenta severa, no solo está pronosticando lluvias intensas o vientos fuertes de forma independiente, sino que está evaluando la probabilidad de que ambas condiciones meteorológicas se den al mismo tiempo. Este escenario ilustrauna probabilidad conjunta e : la probabilidad de que dos eventos ocurran simultáneamente.

En este artículo, exploraremos cómo funciona la probabilidad conjunta, examinaremos fórmulas para eventos dependientes e independientes, trabajaremos con ejemplos prácticos y veremos cómo se aplica este concepto en la ciencia de datos y machine learning. Para obtener una referencia práctica sobre las definiciones y reglas básicas de probabilidad, consulta DataCamp's Introducción a la hoja de referencia de reglas de probabilidad de DataCamp. 

¿Qué es la probabilidad conjunta?

La probabilidad conjunta representa la probabilidad de que dos (o más) eventos ocurran al mismo tiempo. Matemáticamente, lo denotamos como P(A∩B), que se lee como «la probabilidad de A intersección B» o, simplemente, «la probabilidad de A y B».

Para entender la probabilidad conjunta, primero hay que establecer un contexto:

• Espacio muestral: El conjunto de todos los resultados posibles en un experimento.
• Evento: Un subconjunto de resultados del espacio muestral.
• Probabilidad marginal: Probabilidad de que ocurra un solo evento, independientemente de otros eventos.
• Probabilidad condicional: Probabilidad de que ocurra un evento dado que ya ha ocurrido otro evento.

La probabilidad conjunta difiere significativamente entre eventos independientes y dependientes:

• Eventos independientes: Eventos en los que la ocurrencia de uno no tiene ningún efecto sobre la probabilidad del otro. Por ejemplo, al lanzar dos monedas, el resultado del primer lanzamiento no influye en el segundo.
• Eventos dependientes: Eventos en los que la ocurrencia de uno afecta la probabilidad del otro. Por ejemplo, robar cartas sin reemplazo: al retirar una carta, cambia la composición del mazo restante.

Podemos visualizar la probabilidad conjunta utilizando un diagrama de Venn, en el que la región superpuesta representa la intersección de los eventos, es decir, los escenarios en los que ambos eventos ocurren simultáneamente:

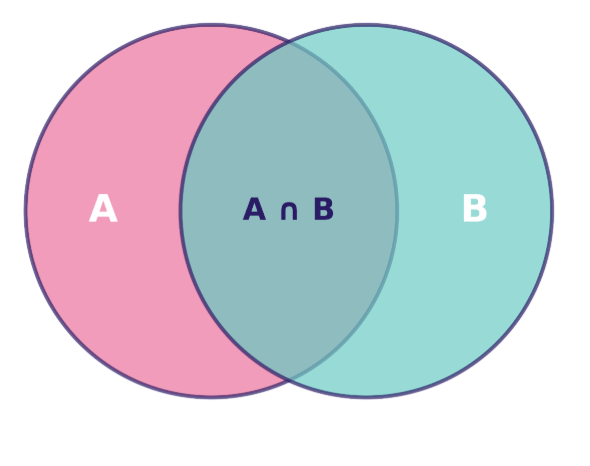
Diagrama de Venn que muestra la relación entre los conjuntos A y B, con su intersección A ∩ B resaltada. Imagen del autor.

El área de esta región superpuesta, en relación con el espacio muestral total, nos da P(A∩B), la probabilidad conjunta que queremos calcular.

La fórmula de probabilidad conjunta y sus propiedades clave

Para comprender cómo calcular la probabilidad conjunta, se requieren diferentes enfoques dependiendo de si los eventos son independientes o dependientes. Examinemos ambos escenarios y exploremos las reglas que rigen estos cálculos.

Probabilidad conjunta para eventos independientes

Cuando dos eventos son independientes, calcular su probabilidad conjunta resulta sencillo. Dado que ninguno de los dos eventos influye en el otro, podemos simplemente multiplicar sus probabilidades individuales:

P(A∩B) = P(A) × P(B)

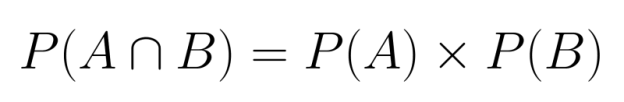
Esta regla de multiplicación se aplica porque la independencia significa que saber que ocurrió un evento no proporciona información sobre la probabilidad de que ocurra el otro evento.

Ejemplo: Considera lanzar dos monedas justas. La probabilidad de que salga cara en la primera moneda es de 1/2, y la probabilidad de que salga cara en la segunda moneda también es de 1/2. Dado que estos eventos son independientes (el primer lanzamiento no afecta al segundo), la probabilidad de obtener cara en ambas monedas es:

Esto significa que hay un 25 % de probabilidades de sacar dos caras seguidas.

Probabilidad conjunta para eventos dependientes

Cuando los eventos son dependientes, debemos tener en cuenta cómo el primer evento afecta a la probabilidad del segundo. Esto requiere utilizar la probabilidad condicional en nuestro cálculo:

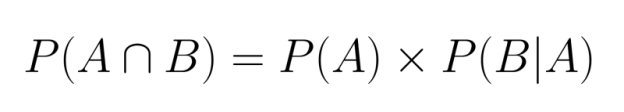
Aquí, P(B|A) representa la probabilidad de que ocurra el evento B dado que el evento A ya ha ocurrido.

Ejemplo: Imagina que sacas dos cartas de una baraja estándar sin reemplazo. ¿Cuál es la probabilidad de sacar dos ases?

• La probabilidad de sacar un as en la primera jugada es P(As₁) = 4/52 = 1/13.
• Después de sacar un as, solo quedan 3 ases en una baraja de 51 cartas, por lo que P(As₂|As₁) = 3/51 = 1/17.
• Por lo tanto:

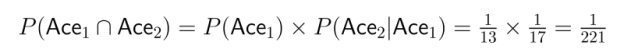
Esto ilustra cómo la dependencia afecta significativamente al cálculo de la probabilidad conjunta.

Regla de multiplicación y regla de la cadena

Los cálculos anteriores demuestran la regla de multiplicación de la probabilidad. Esta regla se extiende a más de dos eventos, lo que nos permite calcular probabilidades conjuntas para múltiples eventos utilizando una cadena de probabilidades condicionales:

Esto se conoce como la regla de la cadena, que proporciona una forma sistemática de descomponer probabilidades conjuntas complejas en partes manejables.

Ejemplo: Considera la probabilidad de sacar tres corazones seguidos de una baraja estándar sin reemplazo:

• P(Corazón₁) = 13/52 = 1/4
• P(Heart₂|Heart₁) = 12/51
• P(Corazón₃|Corazón₁ ∩ Corazón₂) = 11/50
• P(Corazón₁ ∩ Corazón₂ ∩ Corazón₃) = 1/4 × 12/51 × 11/50 = 11/850

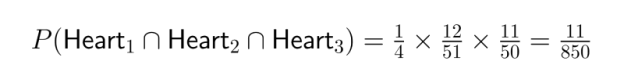
La regla de la cadena resulta especialmente valiosa en la ciencia de datos a la hora de modelar secuencias de eventos o trabajar con procesos de varias etapas.

Ejemplos para ilustrar la probabilidad conjunta

Para consolidar nuestra comprensión de la probabilidad conjunta, veamos algunos ejemplos clásicos y exploremos aplicaciones prácticas que demuestran cómo funcionan estos conceptos en diversos contextos.

Ejemplos clásicos

Tiradas de dados

Imagina que lanzas dos dados de seis caras. ¿Cuál es la probabilidad de sacar un 4 en el primer dado y un 6 en el segundo?

Dado que el resultado del primer lanzamiento no afecta al segundo, se trata de eventos independientes:

• P(Primer dado = 4) = 1/6
• P(Segundo dado = 6) = 1/6
• P(Primer dado = 4 ∩ Segundo dado = 6) = 1/6 × 1/6 = 1/36

Esto nos indica que hay aproximadamente un 2,78 % de probabilidades de que se produzca esta combinación específica.

Robar cartas

Calculemos la probabilidad de sacar una carta roja seguida de un as de una baraja estándar de 52 cartas sin reemplazo.

Dado que estamos extrayendo sin reemplazo, estos eventos son dependientes:

• P(tarjeta roja en el primer sorteo) = 26/52 = 1/2
• P(As en la segunda carta | Carta roja en la primera carta) = 3/51 si la primera carta era un as rojo, o 4/51 si la primera carta no era un as.

Para manejar esto adecuadamente, debemos considerar ambos escenarios:

• P(Rojo sin as y luego as) = P(Rojo sin as) × P(As | Rojo sin as) = 24/52 × 4/51 = 24/663
• P(As rojo y luego otro as) = P(As rojo) × P(As | As rojo) = 2/52 × 3/51 = 1/442

Por lo tanto, la probabilidad conjunta total es: P(Carta roja ∩ As en la segunda jugada) = 24/663 + 1/442 = (24×2 + 3)/1326 = 51/1326 = 1/26

La probabilidad es de aproximadamente el 3,85 %.

Canicas en una bolsa

Considera una bolsa que contiene 5 canicas azules y 3 canicas verdes. Calculemos la probabilidad de sacar dos canicas azules en dos escenarios diferentes.

Con sustitución:

• P(Azul en la primera jugada) = 5/8
• P(Azul en la segunda tirada) = 5/8 (sin cambios porque se reemplaza la primera canica)
• P(Azul ∩ Azul) = 5/8 × 5/8 = 25/64 ≈ 39,06 %

Sin reemplazo:

• P(Azul en la primera jugada) = 5/8
• P(Azul en la segunda tirada | Azul en la primera tirada) = 4/7
• P(Azul ∩ Azul) = 5/8 × 4/7 = 20/56 = 5/14 ≈ 35,71 %

Esta comparación pone de relieve cómo la dependencia creada por no reemplazar las canicas reduce la probabilidad conjunta.

Aplicaciones en el mundo real

Diagnóstico médico

La probabilidad conjunta es fundamental en contextos médicos a la hora de evaluar múltiples síntomas o resultados de pruebas. Considera un escenario diagnóstico en el que los médicos deben evaluar a pacientes con los síntomas A y B para detectar una afección específica.

Basado en datos históricos:

• P(Síntoma A) = 0,30 (el 30 % de la población presenta el síntoma A)
• P(Síntoma B) = 0,25 (el 25 % de la población presenta el síntoma B)
• P(Síntoma A ∩ Síntoma B) = 0,12 (el 12 % presenta ambos síntomas)

Esta probabilidad conjunta ayuda a los médicos a evaluar la probabilidad de diferentes afecciones. Cabe señalar que P(A ∩ B) no es igual a P(A) × P(B) = 0,30 × 0,25 = 0,075, lo que indica que estos síntomas no son independientes: saber que un paciente tiene un síntoma aumenta la probabilidad de que tenga el otro.

Modelización de riesgos financieros

Los analistas de inversiones a menudo necesitan evaluar la probabilidad conjunta de que se den varias condiciones de mercado al mismo tiempo. Considera el caso de un analista que evalúa el riesgo tanto de una caída del mercado bursátil como de un aumento de los tipos de interés en el próximo trimestre.

Si sus modelos sugieren:

• P(Caída del mercado bursátil) = 0,35
• P (Aumento de los tipos de interés) = 0,60
• P(Caída del mercado bursátil | Aumento de los tipos de interés) = 0,45

El cálculo de la probabilidad conjunta sería: P(Caída del mercado bursátil ∩ Aumento de los tipos de interés) = 0,60 × 0,45 = 0,27

Esta probabilidad del 27 % ayuda a cuantificar el riesgo del portafolio y orienta las estrategias de cobertura para protegerse frente a este escenario.

Estos ejemplos demuestran cómo la probabilidad conjunta constituye una poderosa herramienta para cuantificar la incertidumbre en diversos campos, ya sea para analizar simples juegos de azar o para tomar decisiones complejas en medicina y finanzas.

Probabilidad conjunta y probabilidad condicional

Las probabilidades conjuntas y condicionales son conceptos estrechamente relacionados que nos permiten analizar escenarios complejos que implican múltiples eventos. Comprender vuestra relación proporciona herramientas poderosas para el razonamiento probabilístico.

La relación fundamental

La relación entre la probabilidad conjunta y la probabilidad condicional se expresa mediante la fórmula:

P(A|B) = P(A∩B) / P(B)

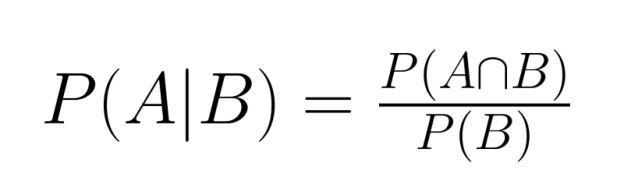
Reorganizando esta ecuación, podemos expresar la probabilidad conjunta en términos de probabilidad condicional:

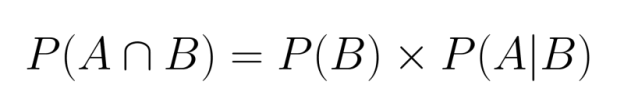
Esta relación muestra que podemos calcular la probabilidad conjunta si conocemos la probabilidad marginal de un evento y la probabilidad condicional del otro dado el primero.

Del mismo modo, también podríamos escribir:

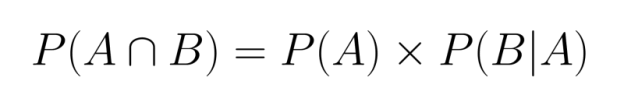
Ambas formulaciones son válidas y equivalentes, lo que demuestra la naturaleza simétrica de la probabilidad conjunta.

Relevancia para el teorema de Bayes

La relación entre la probabilidad conjunta y la probabilidad condicional es fundamental para el teorema de Bayes, una herramienta básica en la inferencia probabilística:

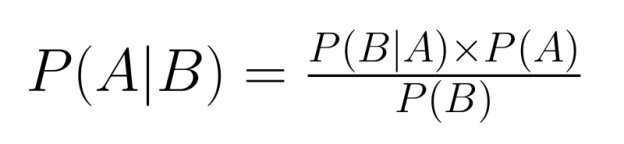
El teorema de Bayes nos permite «invertir» las probabilidades condicionales: si conocemos P(B|A), podemos calcular P(A|B). Esto resulta muy valioso cuando tenemos información sobre una relación condicional, pero necesitamos razonar sobre la relación inversa.

Por ejemplo, las pruebas médicas suelen proporcionar información sobre P(prueba positiva|enfermedad), pero los médicos necesitan determinar P(enfermedad|prueba positiva). El teorema de Bayes salva esta diferencia incorporando la probabilidad conjunta:

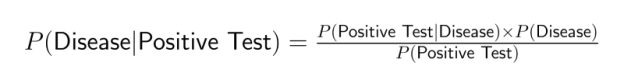
Aplicaciones en ciencia de datos

La probabilidad conjunta constituye la base de numerosas técnicas y aplicaciones de la ciencia de datos. Comprender cómo interactúan múltiples eventos ayuda a los científicos de datos a crear modelos más precisos y realizar mejores predicciones en diversos ámbitos.

Modelización predictiva

La probabilidad conjunta es fundamental para muchos algoritmos de clasificación, en particular para los clasificadores Naive Bayes. Estos populares modelos de machine learning calculan la probabilidad de diferentes resultados basándose en la presencia de múltiples características.

El enfoque Naive Bayes aplica el teorema de Bayes con una suposición «ingenua» de que las características son condicionalmente independientes. Esto simplifica los cálculos de probabilidad conjunta:

A pesar de esta simplificación, los clasificadores Naive Bayes funcionan muy bien para:

• Clasificación de textos y filtrado de spam
• Análisis de sentimientos
• Diagnóstico médico
• Segmentación de clientes

Este enfoque es computacionalmente eficiente y, a menudo, funciona sorprendentemente bien incluso cuando la hipótesis de independencia no se cumple estrictamente.

Evaluación de riesgos

La probabilidad conjunta desempeña un papel crucial en los sistemas de detección de fraudes, en los que es necesario evaluar conjuntamente múltiples factores de riesgo. Los algoritmos modernos de detección de fraudes analizan combinaciones de comportamientos sospechosos para identificar transacciones potencialmente fraudulentas.

Considera un sistema de pago en línea que supervisa varias señales:

• Importe de la transacción
• Ubicación geográfica
• Hora de la transacción
• Información del dispositivo
• Patrones de comportamiento de los usuarios

Aunque cada señal por sí sola puede no indicar fraude, ciertas combinaciones específicas (su aparición conjunta) pueden aumentar significativamente las sospechas. Por ejemplo, una transacción de gran cuantía, realizada desde un dispositivo nuevo, en un país extranjero y a una hora inusual, representa un evento conjunto con una probabilidad de fraude potencialmente alta.

Esta evaluación conjunta de probabilidades permite una puntuación de riesgos más sofisticada que la evaluación aislada de cada factor, lo que reduce tanto los falsos positivos como los falsos negativos.

Aprendizaje automático

Los conceptos de probabilidad conjunta son fundamentales para muchos modelos avanzados de machine learning, entre los que se incluyen:

Redes bayesianas: Estos modelos gráficos representan variables y sus relaciones probabilísticas. Permiten razonar sobre distribuciones de probabilidad conjuntas complejas descomponiéndolas en probabilidades condicionales más simples. Las redes bayesianas se utilizan ampliamente en:

• Sistemas de diagnóstico médico
• Análisis genético
• Sistemas de apoyo a la toma de decisiones
• Modelización de causalidad

Modelos ocultos de Markov (HMM): Estos modelos secuenciales utilizan probabilidades conjuntas para modelar sistemas en los que el estado subyacente está oculto, pero produce resultados observables. Las aplicaciones incluyen:

• Reconocimiento de voz
• Procesamiento del lenguaje natural
• Análisis de secuencias biológicas
• Modelización de series temporales financieras

Modelos gráficos probabilísticos: Estos abarcan una clase más amplia de modelos que utilizan estructuras gráficas para codificar distribuciones de probabilidad conjuntas complejas. Son herramientas esenciales para:

• Reconocimiento de imágenes
• Sistemas de recomendación
• Detección de anomalías
• Aprendizaje por refuerzo

A través de estas aplicaciones, la probabilidad conjunta permite a los científicos de datos crear modelos que capturan las complejas interdependencias de los datos del mundo real, lo que conduce a predicciones más precisas y a una mejor toma de decisiones en situaciones de incertidumbre.

Cómo se puede malinterpretar la probabilidad conjunta

A pesar de su utilidad, la probabilidad conjunta a menudo se malinterpreta o se aplica incorrectamente. Examinemos algunos conceptos erróneos comunes y cómo evitarlos.

Confundir probabilidad conjunta con probabilidad condicional

Uno de los errores más frecuentes es confundir P(A∩B) con P(A|B). Aunque están relacionados, representan conceptos diferentes:

• Probabilidad conjunta P(A∩B) responde: «¿Cuál es la probabilidad de que ocurran tanto A como B?».
• La probabilidad condicional P(A|B) responde: «Dado que B ha ocurrido, ¿cuál es la probabilidad de que ocurra A?».

Por ejemplo, la probabilidad de que una persona tenga diabetes y sea mayor de 65 años (conjunta) es diferente de la probabilidad de que una persona tenga diabetes dado que es mayor de 65 años (condicional).

Esta distinción es importante en muchos contextos analíticos. Por ejemplo, cuando un científico de datos informa que «el 5 % de los usuarios hicieron clic en un anuncio y realizaron una compra», esta probabilidad conjunta es muy diferente de «el 40 % de los usuarios que hicieron clic en un anuncio realizaron una compra», que es una probabilidad condicional.

Suponer erróneamente la independencia

Otro error común es asumir automáticamente que P(A∩B) = P(A) × P(B) sin verificar que los eventos sean realmente independientes. Esta suposición puede dar lugar a errores significativos cuando los eventos son realmente dependientes.

Por ejemplo, en el análisis de mercado, suponer que la compra del producto A y la del producto B son independientes puede llevar a una planificación incorrecta del inventario si estos productos son complementarios (como impresoras y tinta) o sustitutos (como diferentes marcas del mismo artículo).

Es fundamental comprobar la independencia: si P(A∩B) ≠ P(A) × P(B), los eventos son dependientes y es necesario realizar cálculos de probabilidad conjunta más precisos.

Ignorar las probabilidades marginales

Cuando trabajas con probabilidades conjuntas, a veces os centráis exclusivamente en la intersección, ignorando la frecuencia global de los eventos individuales. Esto puede llevar a conclusiones erróneas sobre la solidez de las relaciones.

Por ejemplo, descubrir que el 90 % de los clientes que compraron los productos A y B también compraron el producto C puede parecer impresionante. Sin embargo, si el 89 % de todos los clientes compran el producto C independientemente, la relación aparente es mucho más débil de lo que parecía inicialmente.

Compara siempre las probabilidades conjuntas con las probabilidades marginales relevantes para evitar exagerar las relaciones entre los eventos. La razón de elevación —la relación entre la probabilidad conjunta y el producto de las probabilidades marginales— ofrece una medida más precisa de la asociación:

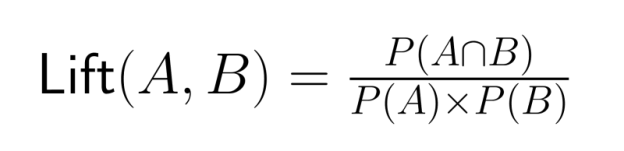
Un valor de elevación superior a 1 indica que los eventos ocurren juntos con más frecuencia de lo que cabría esperar si fueran independientes.

Comprender estos errores comunes ayuda a los científicos de datos a aplicar correctamente la probabilidad conjunta y obtener información significativa a partir del análisis probabilístico.

Temas avanzados y consideraciones adicionales

A medida que los científicos de datos avanzan en sus carreras, se encontrarán con aplicaciones más sofisticadas de la probabilidad conjunta. Exploremos algunos conceptos avanzados que se basan en los fundamentos que hemos establecido.

Probabilidad conjunta en espacios de alta dimensión

Cuando se enfrentan a problemas modernos de machine learning, los científicos de datos suelen trabajar con docenas o incluso cientos de variables simultáneamente. En estos espacios de alta dimensión, calcular y representar probabilidades conjuntas se convierte en un reto.

El número de parámetros necesarios para especificar una distribución conjunta crece exponencialmente con el número de variables, un fenómeno conocido como «la maldición de la dimensionalidad». Por ejemplo, una distribución conjunta de 10 variables binarias requiere 2¹⁰ - 1 = 1023 parámetros para especificarse por completo.

Para gestionar esta complejidad, los científicos de datos emplean técnicas como:

• Reducción de dimensionalidad
• Selección de variables
• Supuestos de independencia condicional
• Representaciones factorizadas (como las redes bayesianas)

Estos enfoques facilitan los cálculos de probabilidad conjunta de alta dimensión para aplicaciones prácticas en áreas como la visión artificial, la genómica y el procesamiento del lenguaje natural.

Distribuciones de probabilidad conjuntas

Hasta ahora, nuestros ejemplos han versado principalmente sobre sucesos discretos, pero la probabilidad conjunta se extiende de forma natural a las variables continuas a través de las distribuciones de probabilidad conjunta.

Para variables discretas, trabajamos con funciones de masa de probabilidad conjunta (PMF), que especifican la probabilidad de que cada combinación de variables aleatorias adopte valores específicos:

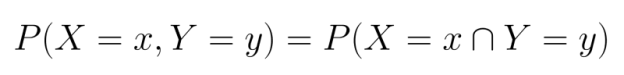
Para las variables continuas, utilizamos funciones de densidad de probabilidad conjunta (PDF). A diferencia de las PMF, las PDF no proporcionan probabilidades directamente, sino que deben integrarse en regiones para hallar la probabilidad de que las variables se encuentren dentro de esas regiones:

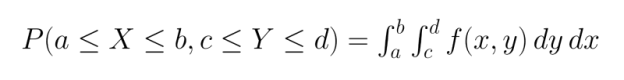
Las distribuciones conjuntas comunes incluyen:

• Distribución normal multivariante
• Distribución t multivariante
• Distribución de Dirichlet
• Distribución multinomial

Comprender estas distribuciones permite realizar modelos más sofisticados de las relaciones entre variables continuas en campos como la economía, la bioinformática y las ciencias ambientales.

Herramientas prácticas para calcular la probabilidad conjunta

Varias herramientas de software y lenguajes de programación ofrecen funciones y bibliotecas para trabajar con probabilidades conjuntas:

Python:

• NumPy y SciPy proporcionan funciones para distribuciones de probabilidad multivariantes.
• Pandas ofrece potentes herramientas para cálculos empíricos de probabilidad conjunta.
• Bibliotecas como PyMC3 y PyStan implementan modelos bayesianos con distribuciones conjuntas.

R:

• Base R incluye muchas funciones de distribución multivariante.
• Paquetes como «copula» permiten modelar estructuras de dependencia complejas.
• «bnlearn» admite el análisis de redes bayesianas.

SQL:

• Las cláusulas GROUP BY con funciones COUNT pueden calcular probabilidades conjuntas empíricas.
• Las funciones de ventana permiten realizar análisis probabilísticos más complejos.
• Las bases de datos modernas admiten funciones estadísticas para cálculos de probabilidad.

Estas herramientas permiten aplicar conceptos de probabilidad conjunta a grandes conjuntos de datos, lo que permite a los científicos de datos crear modelos probabilísticos sofisticados para problemas complejos.

Para profundizar en tu comprensión de la probabilidad conjunta y sus aplicaciones en el análisis bayesiano, DataCamp ofrece varios cursos excelentes:

• Fundamentos del análisis bayesiano de datos en R - Aprende a aplicar métodos bayesianos a problemas comunes de análisis de datos.
• Modelado bayesiano con RJAGS - Domina las técnicas prácticas de modelado bayesiano utilizando el marco JAGS en R.
• Análisis bayesiano de datos en Python - Desarrolla habilidades para implementar enfoques bayesianos en el análisis de datos utilizando Python.

Estos cursos te ayudarán a desarrollar los conceptos tratados en este artículo y a aplicar técnicas de probabilidad conjunta para resolver problemas reales de ciencia de datos.

Conclusión

Como hemos visto a lo largo de este artículo, la probabilidad conjunta es un concepto estadístico fundamental con amplias aplicaciones en numerosos campos de la ciencia de datos. Los recursos de DataCamp, como los que se comparten en los Más de 40 recursos de estadística Python para ciencia de datos, proporcionan excelentes vías para reforzar tu comprensión. Esta completa colección incluye recomendaciones específicas para aprender teoría de la probabilidad, pensamiento bayesiano y otros conceptos estadísticos que se basan en la probabilidad conjunta.

Para aquellos que se preparan para puestos relacionados con la ciencia de datos, nuestras guía con las 35 preguntas y respuestas más frecuentes en entrevistas sobre estadística ofrece una valiosa práctica con preguntas sobre probabilidad conjunta, junto con otros conceptos estadísticos importantes.  También creo que nuestros Rompecabezas de probabilidad en R es una opción divertida.