Probabilité conjointe : Théorie, exemples et applications de la science des données

Lorsqu'un analyste météorologique prévoit une tempête violente, il ne se contente pas de prévoir séparément de fortes pluies ou des vents violents, il évalue également la probabilité que ces deux conditions météorologiques se produisent simultanément. Ce scénario illustrela probabilité conjointe d' , c'est-à-dire la probabilité que deux événements se produisent simultanément.

Dans cet article, nous explorerons le fonctionnement de la probabilité conjointe, examinerons les formules pour les événements dépendants et indépendants, étudierons des exemples pratiques et verrons comment ce concept est appliqué dans la science des données et l'apprentissage automatique. Pour une référence pratique sur les définitions et les règles de base des probabilités, veuillez consulter le document de DataCamp intitulé « Introduction aux règles de probabilité ». Introduction aux règles de probabilité de DataCamp. 

Qu'est-ce que la probabilité conjointe ?

La probabilité conjointe représente la probabilité que deux événements (ou plus) se produisent simultanément. Mathématiquement, nous notons cela P(A∩B), qui se lit « la probabilité de l'intersection de A et B » ou simplement « la probabilité de A et B ».

Pour appréhender la probabilité conjointe, il est nécessaire de définir le contexte :

• s de l'espace d'échantillonnage: L'ensemble de tous les résultats possibles dans une expérience.
• s sur l'événement: Un sous-ensemble de résultats issus de l'espace d'échantillonnage.
• s de probabilité marginale: La probabilité qu'un événement unique se produise, indépendamment d'autres événements.
• Probabilité conditionnelle: La probabilité qu'un événement se produise étant donné qu'un autre événement s'est déjà produit.

La probabilité conjointe diffère considérablement entre les événements indépendants et dépendants :

• Événements indépendants: Événements dont la survenue de l'un n'a aucune incidence sur la probabilité de l'autre. Par exemple, lancer deux pièces de monnaie : le résultat du premier lancer n'influence pas le second.
• Événements dépendants: Événements où la survenue de l'un affecte la probabilité de l'autre. Par exemple, tirer des cartes sans les remplacer : retirer une carte modifie la composition du paquet restant.

Nous pouvons visualiser la probabilité conjointe à l'aide d'un diagramme de Venn, où la zone de chevauchement représente l'intersection des événements, c'est-à-dire les scénarios dans lesquels les deux événements se produisent simultanément :

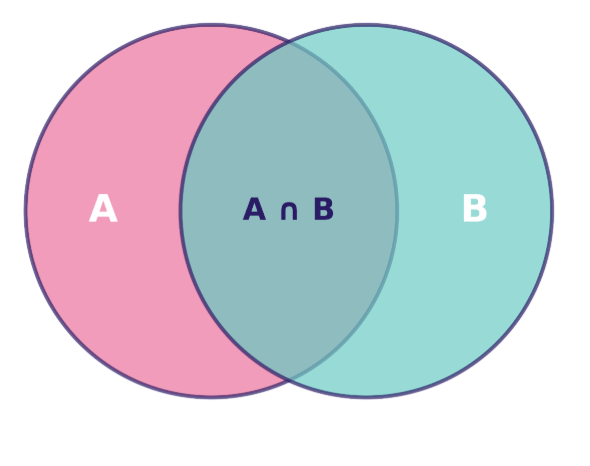
Diagramme de Venn illustrant la relation entre les ensembles A et B, avec leur intersection A ∩ B mise en évidence. Image fournie par l'auteur.

La superficie de cette région de chevauchement, par rapport à l'espace d'échantillonnage total, nous donne P(A∩B), c'est-à-dire la probabilité conjointe que nous cherchons à calculer.

La formule de probabilité conjointe et ses propriétés clés

Pour comprendre comment calculer la probabilité conjointe, il est nécessaire d'adopter différentes approches selon que les événements sont indépendants ou dépendants. Examinons les deux scénarios et explorons les règles qui régissent ces calculs.

Probabilité conjointe pour des événements indépendants

Lorsque deux événements sont indépendants, le calcul de leur probabilité conjointe devient simple. Étant donné qu'aucun des deux événements n'influence l'autre, nous pouvons simplement multiplier leurs probabilités individuelles :

P(A∩B) = P(A) × P(B)

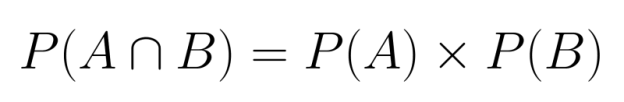
Cette règle de multiplication s'applique car l'indépendance signifie que le fait de savoir qu'un événement s'est produit ne fournit aucune information sur la probabilité de l'autre événement.

Exemple: Envisagez de lancer deux pièces équitables. La probabilité d'obtenir pile lors du premier lancer est de 1/2, et la probabilité d'obtenir pile lors du deuxième lancer est également de 1/2. Étant donné que ces événements sont indépendants (le premier lancer n'affecte pas le second), la probabilité d'obtenir pile sur les deux pièces est :

Cela signifie qu'il y a 25 % de chances d'obtenir deux faces consécutives.

Probabilité conjointe pour des événements dépendants

Lorsque des événements sont dépendants, il est nécessaire de prendre en compte la manière dont le premier événement influence la probabilité du second. Cela nécessite l'utilisation de la probabilité conditionnelle dans notre calcul :

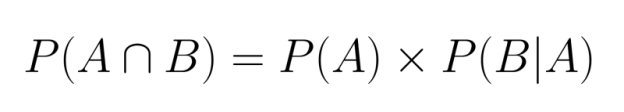
Ici, P(B|A) représente la probabilité que l'événement B se produise étant donné que l'événement A s'est déjà produit.

Exemple: Veuillez imaginer que vous piochez deux cartes d'un jeu standard sans les remettre en place. Quelle est la probabilité de tirer deux as ?

• La probabilité de tirer un as lors du premier tirage est P(As₁) = 4/52 = 1/13.
• Après avoir tiré un as, il ne reste que 3 as dans un jeu de 51 cartes, donc P(As₂|As₁) = 3/51 = 1/17
• Par conséquent :

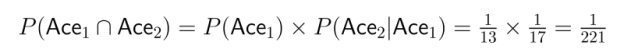
Cela montre à quel point la dépendance influe considérablement sur le calcul de la probabilité conjointe.

Règle de multiplication et règle de la chaîne

Les calculs ci-dessus illustrent la règle de multiplication des probabilités. Cette règle s'applique à plus de deux événements, ce qui nous permet de calculer les probabilités conjointes pour plusieurs événements à l'aide d'une chaîne de probabilités conditionnelles :

Ceci est connu sous le nom de règle de dérivation en chaîne, qui fournit une méthode systématique pour décomposer des probabilités conjointes complexes en éléments plus faciles à gérer.

Exemple: Considérons la probabilité de tirer trois cœurs consécutifs d'un jeu de cartes standard sans remplacement :

• P(Cœur₁) = 13/52 = 1/4
• P(Cœur₂|Cœur₁) = 12/51
• P(Cœur₃|Cœur₁ ∩ Cœur₂) = 11/50
• P(Cœur₁ ∩ Cœur₂ ∩ Cœur₃) = 1/4 × 12/51 × 11/50 = 11/850

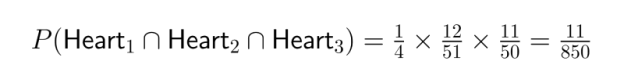
La règle de dérivation en chaîne s'avère particulièrement utile en science des données lors de la modélisation de séquences d'événements ou du traitement de processus à plusieurs étapes.

Exemples illustrant la probabilité conjointe

Afin de consolider notre compréhension de la probabilité conjointe, examinons quelques exemples classiques et explorons des applications pratiques qui démontrent comment ces concepts fonctionnent dans divers contextes.

Exemples classiques

Lancers de dés

Veuillez imaginer lancer deux dés à six faces. Quelle est la probabilité d'obtenir un 4 avec le premier dé et un 6 avec le second dé ?

Étant donné que le résultat du premier lancer de dé n'influence pas le second, il s'agit d'événements indépendants :

• P(Premier dé = 4) = 1/6
• P(Deuxième dé = 6) = 1/6
• P(Premier dé = 4 ∩ Deuxième dé = 6) = 1/6 × 1/6 = 1/36

Cela nous indique qu'il y a environ 2,78 % de chances que cette combinaison spécifique se produise.

Tirage de cartes

Calculons la probabilité de tirer une carte rouge suivie d'un as dans un jeu standard de 52 cartes sans remplacement.

Étant donné que nous procédons à un tirage sans remplacement, ces événements sont dépendants :

• P(carton rouge lors du premier tirage) = 26/52 = 1/2
• P(As au deuxième tirage | Carte rouge au premier tirage) = 3/51 si la première carte était un as rouge, ou 4/51 si la première carte n'était pas un as.

Pour gérer cela correctement, nous devons envisager les deux scénarios :

• P(Rouge non-As puis As) = P(Rouge non-As) × P(As | Rouge non-As) = 24/52 × 4/51 = 24/663
• P(As rouge puis un autre As) = P(As rouge) × P(As | As rouge) = 2/52 × 3/51 = 1/442

Par conséquent, la probabilité conjointe totale est la suivante : P(Carte rouge ∩ As au deuxième tirage) = 24/663 + 1/442 = (24×2 + 3)/1326 = 51/1326 = 1/26

La probabilité est d'environ 3,85 %.

Billes dans un sac

Considérons un sac contenant 5 billes bleues et 3 billes vertes. Calculons la probabilité de tirer deux billes bleues dans deux scénarios différents.

Avec remplacement :

• P(Bleu au premier tirage) = 5/8
• P(Bleu au deuxième tirage) = 5/8 (inchangé car la première bille est remplacée)
• P(Bleu ∩ Bleu) = 5/8 × 5/8 = 25/64 ≈ 39,06 %

Sans remplacement :

• P(Bleu au premier tirage) = 5/8
• P(Bleu au deuxième tirage | Bleu au premier tirage) = 4/7
• P(Bleu ∩ Bleu) = 5/8 × 4/7 = 20/56 = 5/14 ≈ 35,71 %

Cette comparaison met en évidence comment la dépendance créée par le fait de ne pas remplacer les billes réduit la probabilité conjointe.

Applications concrètes

Diagnostic médical

La probabilité conjointe est essentielle dans les contextes médicaux pour l'évaluation de symptômes multiples ou de résultats d'examens. Considérons un scénario diagnostique dans lequel les médecins doivent évaluer des patients présentant les symptômes A et B pour une affection spécifique.

Sur la base des données historiques :

• P(Symptôme A) = 0,30 (30 % de la population présente le symptôme A)
• P(Symptôme B) = 0,25 (25 % de la population présente le symptôme B)
• P(Symptôme A ∩ Symptôme B) = 0,12 (12 % présentent les deux symptômes)

Cette probabilité conjointe aide les médecins à évaluer la probabilité de différentes affections. Il convient de noter que P(A ∩ B) n'est pas égal à P(A) × P(B) = 0,30 × 0,25 = 0,075, ce qui indique que ces symptômes ne sont pas indépendants : le fait de savoir qu'un patient présente un symptôme augmente la probabilité qu'il présente l'autre.

Modélisation des risques financiers

Les analystes financiers doivent fréquemment évaluer la probabilité conjointe de plusieurs conditions de marché se produisant simultanément. Considérons un analyste qui évalue le risque d'une baisse du marché boursier et d'une hausse des taux d'intérêt au cours du prochain trimestre.

Si leurs modèles suggèrent :

• P(Baisse du marché boursier) = 0,35
• P(Hausse des taux d'intérêt) = 0,60
• P(Baisse du marché boursier | Hausse des taux d'intérêt) = 0,45

Le calcul de la probabilité conjointe serait le suivant : P(Baisse du marché boursier ∩ Hausse des taux d'intérêt) = 0,60 × 0,45 = 0,27

Cette probabilité de 27 % permet de quantifier le risque du portefeuille et oriente les stratégies de couverture afin de se prémunir contre ce scénario.

Ces exemples démontrent comment la probabilité conjointe constitue un outil puissant pour quantifier l'incertitude dans divers domaines, qu'il s'agisse d'analyser des jeux de hasard simples ou de prendre des décisions complexes en médecine et en finance.

Probabilité conjointe et probabilité conditionnelle

Les probabilités conjointes et conditionnelles sont des concepts étroitement liés qui nous permettent d'analyser des scénarios complexes impliquant plusieurs événements. Comprendre leur relation fournit des outils puissants pour le raisonnement probabiliste.

La relation fondamentale

La relation entre la probabilité conjointe et la probabilité conditionnelle est exprimée par la formule suivante :

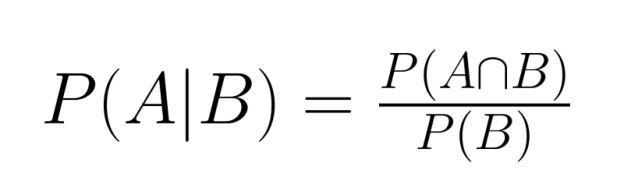
En réorganisant cette équation, nous pouvons exprimer la probabilité conjointe en termes de probabilité conditionnelle :

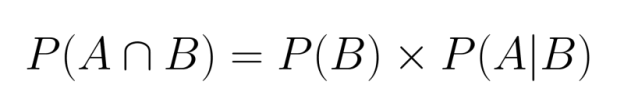
Cette relation démontre que nous pouvons calculer la probabilité conjointe si nous connaissons la probabilité marginale d'un événement et la probabilité conditionnelle de l'autre événement étant donné le premier.

De la même manière, nous pourrions également écrire :

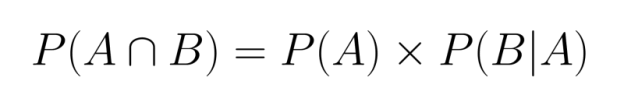
Les deux formulations sont valides et équivalentes, démontrant la nature symétrique de la probabilité conjointe.

Pertinence par rapport au théorème de Bayes

La relation entre la probabilité conjointe et la probabilité conditionnelle est au cœur du théorème de Bayes, un outil fondamental dans l'inférence probabiliste :

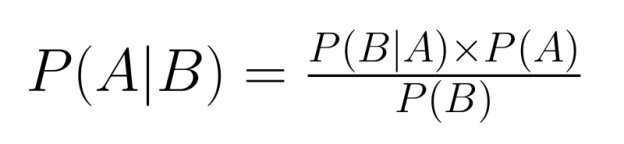
Le théorème de Bayes nous permet de « renverser » les probabilités conditionnelles : si nous connaissons P(B|A), nous pouvons calculer P(A|B). Cela s'avère extrêmement utile lorsque nous disposons d'informations sur une relation conditionnelle, mais que nous devons raisonner sur la relation inverse.

Par exemple, les tests médicaux fournissent souvent des informations sur P(test positif|maladie), mais les médecins doivent déterminer P(maladie|test positif). Le théorème de Bayes comble cette lacune en intégrant la probabilité conjointe :

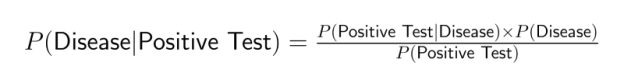
Applications en science des données

La probabilité conjointe constitue la base de nombreuses techniques et applications en science des données. Comprendre comment plusieurs événements interagissent aide les scientifiques des données à élaborer des modèles plus précis et à faire de meilleures prévisions dans divers domaines.

Modélisation prédictive

La probabilité conjointe est fondamentale pour de nombreux algorithmes de classification, en particulier les classificateurs naïfs bayésiens. Ces modèles d'apprentissage automatique populaires calculent la probabilité de différents résultats en fonction de la présence de multiples caractéristiques.

L'approche naïve de Bayes applique le théorème de Bayes avec une hypothèse « naïve » selon laquelle les caractéristiques sont conditionnellement indépendantes. Cela simplifie les calculs de probabilité conjointe :

Malgré cette hypothèse simplificatrice, les classificateurs naïfs de Bayes fonctionnent remarquablement bien pour :

• Classification de texte et filtrage anti-spam
• Analyse des sentiments
• Diagnostic médical
• Segmentation de la clientèle

Cette approche est efficace sur le plan informatique et donne souvent des résultats étonnamment bons, même lorsque l'hypothèse d'indépendance n'est pas strictement vérifiée.

Évaluation des risques

La probabilité conjointe joue un rôle crucial dans les systèmes de détection des fraudes, où plusieurs facteurs de risque doivent être évalués ensemble. Les algorithmes modernes de détection des fraudes analysent les combinaisons de comportements suspects afin d'identifier les transactions potentiellement frauduleuses.

Considérons un système de paiement en ligne qui surveille divers signaux :

• Montant de la transaction
• Situation géographique
• Heure de la transaction
• Informations sur l'appareil
• Modèles de comportement des utilisateurs

Bien que chaque signal pris isolément ne soit pas nécessairement révélateur d'une fraude, certaines combinaisons spécifiques (leur occurrence conjointe) peuvent considérablement accroître les soupçons. Par exemple, une transaction importante effectuée à partir d'un nouvel appareil, dans un pays étranger, à un moment inhabituel, représente un événement conjoint présentant un risque potentiel élevé de fraude.

Cette évaluation conjointe des probabilités permet une notation des risques plus sophistiquée que l'évaluation isolée de chaque facteur, réduisant ainsi à la fois les faux positifs et les faux négatifs.

Apprentissage automatique

Les concepts de probabilité conjointe sont au cœur de nombreux modèles avancés d'apprentissage automatique, notamment :

Réseaux bayésiens: Ces modèles graphiques représentent les variables et leurs relations probabilistes. Ils permettent de raisonner sur des distributions de probabilités conjointes complexes en les décomposant en probabilités conditionnelles plus simples. Les réseaux bayésiens sont largement utilisés dans :

• Systèmes de diagnostic médical
• Analyse génétique
• Systèmes d'aide à la décision
• Modélisation de causalité

Modèles de Markov cachés (HMM): Ces modèles séquentiels utilisent des probabilités conjointes pour modéliser des systèmes dont l'état sous-jacent est caché mais qui produisent des résultats observables. Les applications comprennent :

• Reconnaissance vocale
• Traitement du langage naturel
• Analyse des séquences biologiques
• Modélisation des séries chronologiques financières

Modèles graphiques probabilistes: Ces modèles englobent une catégorie plus large de modèles qui utilisent des structures graphiques pour coder des distributions de probabilités conjointes complexes. Ce sont des outils indispensables pour :

• Reconnaissance d'image
• Systèmes de recommandation
• Détection d'anomalies
• Apprentissage par renforcement

Grâce à ces applications, la probabilité conjointe permet aux scientifiques des données de créer des modèles qui capturent les interdépendances complexes des données du monde réel, ce qui conduit à des prévisions plus précises et à une meilleure prise de décision en situation d'incertitude.

Comment les gens peuvent mal interpréter la probabilité conjointe

Malgré son utilité, la probabilité conjointe est souvent mal comprise ou mal appliquée. Examinons quelques idées fausses courantes et comment les éviter.

Confusion entre probabilité conjointe et probabilité conditionnelle

L'une des erreurs les plus fréquentes consiste à confondre P(A∩B) et P(A|B). Bien qu'ils soient liés, ils représentent des concepts différents :

• La probabilité conjointe P(A∩B) répond : Quelle est la probabilité que A et B se produisent tous les deux ?
• La probabilité conditionnelle P(A|B) répond aux questions suivantes : Étant donné que B s'est produit, quelle est la probabilité que A se produise ?

Par exemple, la probabilité qu'une personne soit à la fois diabétique et âgée de plus de 65 ans (probabilité conjointe) diffère de la probabilité qu'une personne soit diabétique étant donné qu'elle est âgée de plus de 65 ans (probabilité conditionnelle).

Cette distinction est importante dans de nombreux contextes analytiques. Par exemple, lorsqu'un data scientist indique que « 5 % des utilisateurs ont cliqué sur une publicité et effectué un achat », cette probabilité conjointe est très différente de « 40 % des utilisateurs qui ont cliqué sur une publicité ont effectué un achat », qui est une probabilité conditionnelle.

Supposition erronée d'indépendance

Une autre erreur courante consiste à supposer automatiquement que P(A∩B) = P(A) × P(B) sans vérifier que les événements sont réellement indépendants. Cette hypothèse peut entraîner des erreurs importantes lorsque les événements sont réellement dépendants.

Par exemple, dans le cadre d'une analyse de marché, supposer que l'achat du produit A et celui du produit B sont indépendants l'un de l'autre peut conduire à une planification incorrecte des stocks si ces produits sont complémentaires (comme les imprimantes et l'encre) ou substituables (comme différentes marques d'un même article).

Il est essentiel de vérifier l'indépendance : si P(A∩B) ≠ P(A) × P(B), les événements sont dépendants et des calculs de probabilité conjointe plus minutieux sont nécessaires.

Ignorer les probabilités marginales

Lorsqu'ils travaillent avec des probabilités conjointes, les analystes se concentrent parfois exclusivement sur l'intersection, en négligeant la fréquence globale des événements individuels. Cela peut conduire à des conclusions trompeuses sur la solidité des relations.

Par exemple, constater que 90 % des clients ayant acheté les produits A et B ont également acheté le produit C peut sembler remarquable. Cependant, si 89 % de tous les clients achètent le produit C quoi qu'il arrive, la relation apparente est beaucoup plus faible qu'elle ne semblait l'être initialement.

Veuillez toujours comparer les probabilités conjointes aux probabilités marginales pertinentes afin d'éviter de surestimer les relations entre les événements. Le rapport de levée, c'est-à-dire le rapport entre la probabilité conjointe et le produit des probabilités marginales, offre une mesure plus précise de l'association :

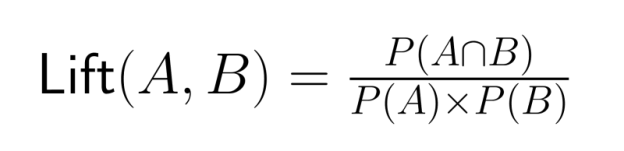
Une valeur de lift supérieure à 1 indique que les événements se produisent ensemble plus souvent que ce à quoi on pourrait s'attendre s'ils étaient indépendants.

Comprendre ces écueils courants aide les scientifiques des données à appliquer correctement la probabilité conjointe et à tirer des conclusions pertinentes de l'analyse probabiliste.

Sujets avancés et considérations supplémentaires

Au fur et à mesure que les scientifiques des données progressent dans leur carrière, ils rencontreront des applications plus sophistiquées de la probabilité conjointe. Explorons quelques concepts avancés qui s'appuient sur les bases que nous avons établies.

Probabilité conjointe dans les espaces à haute dimension

Lorsqu'ils traitent des problèmes liés à l'apprentissage automatique moderne, les scientifiques des données travaillent souvent avec des dizaines, voire des centaines de variables simultanément. Dans ces espaces à haute dimension, le calcul et la représentation des probabilités conjointes deviennent complexes.

Le nombre de paramètres nécessaires pour spécifier une distribution conjointe augmente de manière exponentielle avec le nombre de variables, un phénomène connu sous le nom de « malédiction de la dimensionnalité ». Par exemple, une distribution conjointe de 10 variables binaires nécessite 2¹⁰ - 1 = 1 023 paramètres pour être complètement spécifiée.

Pour gérer cette complexité, les scientifiques des données utilisent des techniques telles que :

• Réduction de la dimensionnalité
• Sélection des variables
• Hypothèses d'indépendance conditionnelle
• Représentations factorisées (telles que les réseaux bayésiens)

Ces approches facilitent les calculs de probabilité conjointe à haute dimension pour des applications pratiques dans des domaines tels que la vision par ordinateur, la génomique et le traitement du langage naturel.

Distributions de probabilité conjointes

Nos exemples précédents concernaient principalement des événements discrets, mais la probabilité conjointe s'étend naturellement aux variables continues par le biais des distributions de probabilité conjointes.

Pour les variables discrètes, nous utilisons les fonctions de masse de probabilité conjointes (PMF), qui spécifient la probabilité que chaque combinaison de variables aléatoires prenne des valeurs spécifiques :

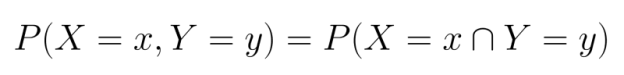
Pour les variables continues, nous utilisons des fonctions de densité de probabilité conjointes (PDF). Contrairement aux PMF, les PDF ne fournissent pas directement des probabilités, mais doivent être intégrées sur des régions afin de déterminer la probabilité que les variables se situent dans ces régions :

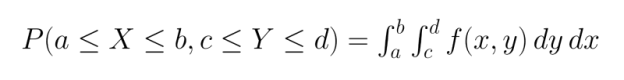
Les distributions conjointes courantes comprennent :

• Distribution normale multivariée
• Distribution t multivariée
• Distribution de Dirichlet
• Distribution multinomiale

La compréhension de ces distributions permet une modélisation plus sophistiquée des relations entre variables continues dans des domaines tels que l'économie, la bio-informatique et les sciences environnementales.

Outils pratiques pour le calcul de la probabilité conjointe

Plusieurs outils logiciels et langages de programmation proposent des fonctions et des bibliothèques permettant de travailler avec des probabilités conjointes :

Python:

• NumPy et SciPy fournissent des fonctions pour les distributions de probabilités multivariées.
• Pandas fournit des outils performants pour les calculs empiriques de probabilités conjointes.
• Les bibliothèques telles que PyMC3 et PyStan implémentent la modélisation bayésienne avec des distributions conjointes.

R:

• Base R comprend de nombreuses fonctions de distribution multivariées.
• Des paquets tels que « copula » permettent de modéliser des structures de dépendance complexes.
• « bnlearn » prend en charge l'analyse des réseaux bayésiens.

SQL:

• Les clauses GROUP BY avec les fonctions COUNT permettent de calculer des probabilités conjointes empiriques.
• Les fonctions de fenêtre permettent une analyse probabiliste plus complexe.
• Les bases de données modernes prennent en charge des fonctions statistiques pour les calculs de probabilité.

Ces outils permettent d'appliquer de manière pratique les concepts de probabilité conjointe à de grands ensembles de données, ce qui permet aux scientifiques des données de construire des modèles probabilistes sophistiqués pour des problèmes complexes.

Pour approfondir votre compréhension de la probabilité conjointe et de ses applications dans l'analyse bayésienne, DataCamp propose plusieurs excellents cours :

• Principes fondamentaux de l'analyse bayésienne des données dans R - Découvrez comment appliquer les méthodes bayésiennes à des problèmes courants d'analyse des données.
• Modélisation bayésienne avec RJAGS - Maîtrisez les techniques pratiques de modélisation bayésienne à l'aide du framework JAGS dans R.
• Analyse bayésienne des données en Python - Acquérir les compétencesnécessaires pour mettre en œuvre des approches bayésiennes dans l'analyse des données à l'aide de Python.

Ces cours vous aideront à approfondir les concepts abordés dans cet article et à appliquer les techniques de probabilité conjointe pour résoudre des problèmes concrets liés à la science des données.

Conclusion

Comme nous l'avons observé tout au long de cet article, la probabilité conjointe est un concept statistique fondamental qui trouve de nombreuses applications dans divers domaines de la science des données. Les ressources de DataCamp, telles que celles partagées dans les plus de 40 ressources Python Statistics for Data Science, constituent d'excellents moyens de renforcer vos connaissances. Cette collection complète comprend des recommandations spécifiques pour l'apprentissage de la théorie des probabilités, de la pensée bayésienne et d'autres concepts statistiques qui s'appuient sur la probabilité conjointe.

Pour ceux qui se préparent à des postes dans le domaine de la science des données, notre guide « Top 35 des questions et réponses d'entretien sur les statistiques » propose des exercices pratiques utiles sur les questions de probabilité conjointe ainsi que d'autres concepts statistiques importants.  Je pense également que notre cours « Probability Puzzles in R » (Casse-têtes probabilistes en R) constitue uneoption intéressante.