Probabilidade conjunta: Teoria, exemplos e aplicações da ciência de dados

Quando um analista meteorológico prevê uma tempestade forte, ele não está só prevendo chuva forte ou ventos fortes separadamente – ele está avaliando a chance de que as duas condições climáticas aconteçam juntas. Esse cenário mostrauma probabilidade conjunta – a chance de dois eventos acontecerem ao mesmo tempo.

Neste artigo, vamos ver como funciona a probabilidade conjunta, dar uma olhada nas fórmulas para eventos dependentes e independentes, resolver exemplos práticos e ver como esse conceito é usado em ciência de dados e machine learning. Pra ter uma referência prática sobre definições e regras básicas de probabilidade, dá uma olhada no guia de referência rápida de regras de probabilidade do DataCamp. Introdução às Regras de Probabilidade. 

O que é probabilidade conjunta?

A probabilidade conjunta mostra a chance de dois (ou mais) eventos acontecerem ao mesmo tempo. Matematicamente, a gente chama isso de P(A∩B), que é lido como “a probabilidade de A intersecção B” ou simplesmente “a probabilidade de A e B”.

Pra entender a probabilidade conjunta, primeiro a gente precisa entender um pouco do contexto:

• Espaço amostral: O conjunto de todos os resultados possíveis em um experimento.
• : Um subconjunto de resultados do espaço amostral.
• Probabilidade marginal: A chance de um único evento acontecer, sem se importar com outros eventos.
• Probabilidade condicional: A chance de algo acontecer depois que outra coisa já rolou.

A probabilidade conjunta é bem diferente entre eventos independentes e dependentes:

• Eventos independentes: Eventos em que a ocorrência de um não afeta a probabilidade do outro. Por exemplo, jogar duas moedas — o resultado do primeiro lançamento não influencia o segundo.
• Eventos dependentes: Eventos em que a ocorrência de um afeta a probabilidade do outro. Por exemplo, comprar cartas sem reposição — tirar uma carta muda a composição do baralho restante.

A gente pode visualizar a probabilidade conjunta usando um diagrama de Venn, onde a área que se sobrepõe representa a interseção dos eventos — os cenários em que ambos os eventos acontecem ao mesmo tempo:

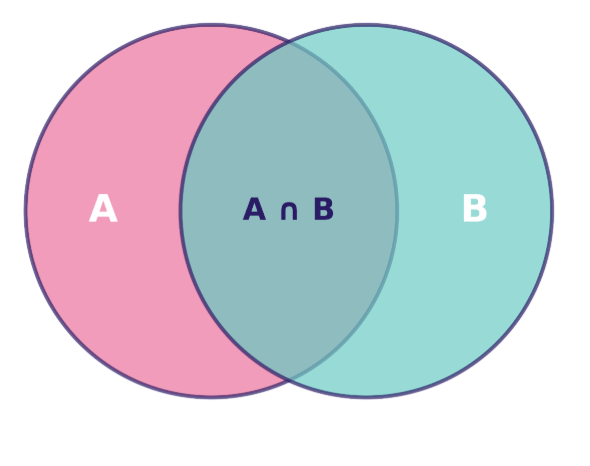
Diagrama de Venn mostrando a relação entre os conjuntos A e B, com sua interseção A ∩ B destacada. Imagem do autor.

A área dessa região sobreposta, em relação ao espaço amostral total, dá a gente P(A∩B) — a probabilidade conjunta que a gente quer calcular.

A Fórmula da Probabilidade Conjunta e suas Principais Propriedades

Entender como calcular a probabilidade conjunta requer abordagens diferentes, dependendo se os eventos são independentes ou dependentes. Vamos dar uma olhada nos dois cenários e ver as regras que regem esses cálculos.

Probabilidade conjunta para eventos independentes

Quando dois eventos são independentes, calcular a probabilidade conjunta deles fica bem simples. Como nenhum dos eventos influencia o outro, podemos simplesmente multiplicar suas probabilidades individuais:

P(A∩B) = P(A) × P(B)

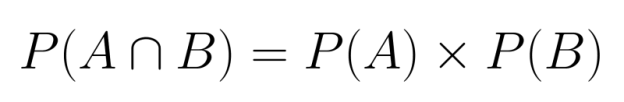
Essa regra de multiplicação vale porque independência quer dizer que saber que um evento rolou não dá nenhuma informação sobre a chance do outro evento acontecer.

Exemplo: Pense em jogar duas moedas justas. A chance de sair cara na primeira moeda é de 1/2, e a chance de sair cara na segunda moeda também é de 1/2. Como esses eventos são independentes (o primeiro lançamento não afeta o segundo), a chance de sair cara nas duas moedas é:

Isso quer dizer que tem 25% de chance de dar duas caras seguidas.

Probabilidade conjunta para eventos dependentes

Quando os eventos são dependentes, a gente precisa levar em conta como o primeiro evento afeta a probabilidade do segundo. Isso exige usar a probabilidade condicional no nosso cálculo:

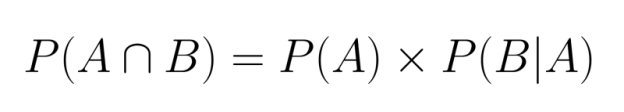
Aqui, P(B|A) representa a probabilidade do evento B acontecer, já que o evento A já aconteceu.

Exemplo: Imagina tirar duas cartas de um baralho normal sem recolocar as cartas no baralho. Qual é a chance de tirar dois ases?

• A chance de tirar um ás na primeira jogada é P(Ás₁) = 4/52 = 1/13
• Depois de tirar um ás, só sobram 3 áses num baralho de 51 cartas, então P(Ás₂|Ás₁) = 3/51 = 1/17
• Então:

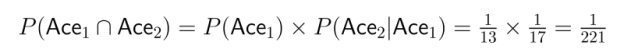
Isso mostra como a dependência afeta bastante o cálculo da probabilidade conjunta.

Regra da multiplicação e regra da cadeia

Os cálculos acima mostram a regra da multiplicação da probabilidade. Essa regra vale para mais de dois eventos, o que nos permite calcular probabilidades conjuntas para vários eventos usando uma cadeia de probabilidades condicionais:

Isso é conhecido como regra da cadeia, que oferece uma maneira sistemática de dividir probabilidades conjuntas complexas em partes mais fáceis de lidar.

Exemplo: Pense na chance de tirar três copas seguidas de um baralho normal sem recolocar as cartas:

• P(Coração₁) = 13/52 = 1/4
• P(Coração₂|Coração₁) = 12/51
• P(Coração₃|Coração₁ ∩ Coração₂) = 11/50
• P(Coração₁ ∩ Coração₂ ∩ Coração₃) = 1/4 × 12/51 × 11/50 = 11/850

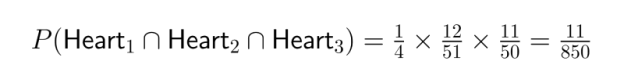
A regra da cadeia é super útil na ciência de dados quando a gente está modelando sequências de eventos ou trabalhando com processos de várias etapas.

Exemplos para ilustrar a probabilidade conjunta

Para entender melhor a probabilidade conjunta, vamos ver alguns exemplos clássicos e explorar aplicações práticas que mostram como esses conceitos funcionam em vários contextos.

Exemplos clássicos

Lançamentos de dados

Imagina jogar dois dados de seis lados. Qual é a chance de tirar um 4 no primeiro dado e um 6 no segundo dado?

Como o resultado do primeiro dado não afeta o segundo, esses eventos são independentes:

• P(Primeiro dado = 4) = 1/6
• P(Segundo dado = 6) = 1/6
• P(Primeiro dado = 4 ∩ Segundo dado = 6) = 1/6 × 1/6 = 1/36

Isso mostra que tem mais ou menos 2,78% de chance dessa combinação específica acontecer.

Sorteio de cartões

Vamos calcular a probabilidade de tirar um cartão vermelho seguido de um Ás de um baralho padrão de 52 cartas sem reposição.

Como estamos tirando sem reposição, esses eventos são dependentes:

• P(Cartão vermelho no primeiro sorteio) = 26/52 = 1/2
• P(Ás na segunda carta | Cartão vermelho na primeira carta) = 3/51 se a primeira carta fosse um Ás vermelho, ou 4/51 se a primeira carta não fosse um Ás.

Para lidar com isso da maneira certa, precisamos pensar nos dois cenários:

• P(Vermelho não Ás e depois Ás) = P(Vermelho não Ás) × P(Ás | Vermelho não Ás) = 24/52 × 4/51 = 24/663
• P(Ás vermelho e depois outro Ás) = P(Ás vermelho) × P(Ás | Ás vermelho) = 2/52 × 3/51 = 1/442

Então, a probabilidade conjunta total é: P(Cartão vermelho ∩ Ás na segunda jogada) = 24/663 + 1/442 = (24×2 + 3)/1326 = 51/1326 = 1/26

A probabilidade é de aproximadamente 3,85%.

Bolas de gude em um saco

Pensa numa sacola com 5 bolinhas azuis e 3 bolinhas verdes. Vamos calcular a probabilidade de tirar duas bolinhas azuis em dois cenários diferentes.

Com substituição:

• P(Azul na primeira jogada) = 5/8
• P(Azul na segunda jogada) = 5/8 (não muda porque a primeira bola é recolocada)
• P(Azul ∩ Azul) = 5/8 × 5/8 = 25/64 ≈ 39,06%

Sem substituição:

• P(Azul na primeira jogada) = 5/8
• P(Azul no segundo sorteio | Azul no primeiro sorteio) = 4/7
• P(Azul ∩ Azul) = 5/8 × 4/7 = 20/56 = 5/14 ≈ 35,71%

Essa comparação mostra como a dependência criada por não trocar as bolinhas de gude diminui a probabilidade conjunta.

Aplicações no mundo real

Diagnóstico médico

A probabilidade conjunta é super importante em contextos médicos quando a gente está avaliando vários sintomas ou resultados de exames. Pense em um cenário de diagnóstico em que os médicos precisam avaliar pacientes com sintomas A e B para uma condição específica.

Com base em dados históricos:

• P(Sintoma A) = 0,30 (30% da galera tem o sintoma A)
• P(Sintoma B) = 0,25 (25% da galera tem o sintoma B)
• P(Sintoma A ∩ Sintoma B) = 0,12 (12% apresentam ambos os sintomas)

Essa probabilidade conjunta ajuda os médicos a avaliar a chance de diferentes condições. Vale a pena notar que P(A ∩ B) não é igual a P(A) × P(B) = 0,30 × 0,25 = 0,075, o que mostra que esses sintomas não são independentes — saber que um paciente tem um sintoma aumenta a chance de ele ter o outro.

Modelagem de risco financeiro

Os analistas de investimentos muitas vezes precisam avaliar a probabilidade conjunta de várias condições de mercado acontecerem ao mesmo tempo. Pense em um analista avaliando o risco tanto de uma queda no mercado de ações quanto de aumento nas taxas de juros no próximo trimestre.

Se os modelos deles sugerirem:

• P(Queda do mercado de ações) = 0,35
• P(Aumento das taxas de juros) = 0,60
• P(Queda do mercado de ações | Aumento das taxas de juros) = 0,45

O cálculo da probabilidade conjunta seria: P(Queda do mercado de ações ∩ Aumento das taxas de juros) = 0,60 × 0,45 = 0,27

Essa probabilidade de 27% ajuda a quantificar o risco do portfólio e orienta as estratégias de hedge para proteção contra esse cenário.

Esses exemplos mostram como a probabilidade conjunta é uma ferramenta poderosa pra quantificar a incerteza em várias áreas, seja analisando jogos de azar simples ou tomando decisões complexas na medicina e nas finanças.

Probabilidade conjunta e probabilidade condicional

Probabilidades conjuntas e condicionais são conceitos bem ligados que nos ajudam a analisar cenários complexos com vários eventos. Entender a relação entre eles dá umas ferramentas bem legais para o raciocínio probabilístico.

A relação fundamental

A relação entre probabilidade conjunta e condicional é expressa pela fórmula:

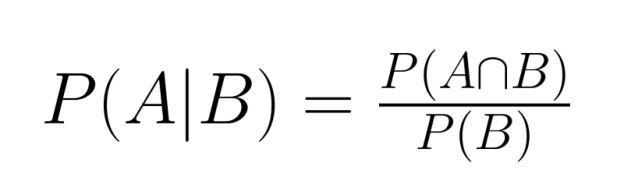
Reorganizando essa equação, podemos expressar a probabilidade conjunta em termos de probabilidade condicional:

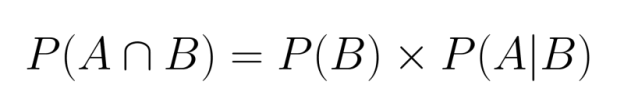
Essa relação mostra que podemos calcular a probabilidade conjunta se soubermos a probabilidade marginal de um evento e a probabilidade condicional do outro, dado o primeiro.

Da mesma forma, também poderíamos escrever:

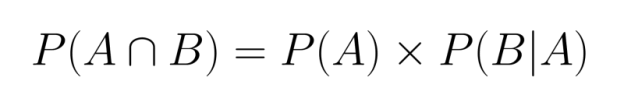
Ambas as formulações são válidas e equivalentes, mostrando a natureza simétrica da probabilidade conjunta.

Relevância para o Teorema de Bayes

A relação entre probabilidade conjunta e condicional é essencial para o Teorema de Bayes, uma ferramenta fundamental na inferência probabilística:

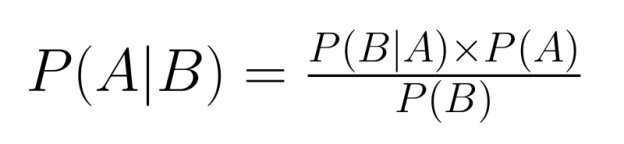
O Teorema de Bayes permite “reverter” as probabilidades condicionais — se a gente sabe P(B|A), dá pra calcular P(A|B). Isso é super útil quando a gente tem informações sobre uma relação condicional, mas precisa pensar sobre a relação inversa.

Por exemplo, os exames médicos geralmente fornecem informações sobre P(Teste Positivo|Doença), mas os médicos precisam determinar P(Doença|Teste Positivo). O Teorema de Bayes preenche essa lacuna ao incluir a probabilidade conjunta:

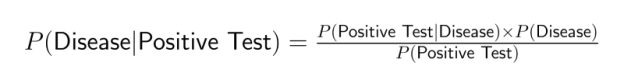
Aplicações em Ciência de Dados

A probabilidade conjunta é a base de várias técnicas e aplicações da ciência de dados. Entender como vários eventos interagem ajuda os cientistas de dados a criar modelos mais precisos e fazer previsões melhores em vários campos.

Modelagem preditiva

A probabilidade conjunta é super importante para muitos algoritmos de classificação, principalmente para os classificadores Naive Bayes. Esses modelos populares de machine learning calculam a probabilidade de diferentes resultados com base na presença de várias características.

A abordagem Naive Bayes usa o Teorema de Bayes com uma suposição “ingênua” de que as características são condicionalmente independentes. Isso simplifica os cálculos de probabilidade conjunta:

Apesar dessa suposição simplista, os classificadores Naive Bayes funcionam super bem para:

• Classificação de texto e filtragem de spam
• Análise de sentimentos
• Diagnóstico médico
• Segmentação de clientes

Essa abordagem é eficiente em termos computacionais e, muitas vezes, tem um desempenho surpreendentemente bom, mesmo quando a suposição de independência não se aplica estritamente.

Avaliação de riscos

A probabilidade conjunta é super importante nos sistemas de detecção de fraudes, onde vários fatores de risco precisam ser avaliados juntos. Os algoritmos modernos de detecção de fraudes analisam combinações de comportamentos suspeitos para identificar transações potencialmente fraudulentas.

Pense num sistema de pagamento online que fica de olho em vários sinais:

• Valor da transação
• Localização geográfica
• Hora da transação
• Informações sobre o dispositivo
• Padrões de comportamento do usuário

Embora cada sinal isoladamente possa não indicar fraude, combinações específicas (sua ocorrência conjunta) podem aumentar significativamente a suspeita. Por exemplo, uma transação grande, feita de um aparelho novo, em outro país, num horário estranho, é um evento que pode ter uma chance alta de ser uma fraude.

Essa avaliação conjunta de probabilidade permite uma pontuação de risco mais sofisticada do que avaliar cada fator isoladamente, reduzindo tanto os falsos positivos quanto os falsos negativos.

machine learning

Os conceitos de probabilidade conjunta são essenciais para muitos modelos avançados de machine learning, incluindo:

Redes Bayesianas: Esses modelos gráficos mostram as variáveis e suas relações probabilísticas. Elas permitem raciocinar sobre distribuições de probabilidade conjunta complexas, dividindo-as em probabilidades condicionais mais simples. As redes bayesianas são muito usadas em:

• Sistemas de diagnóstico médico
• Análise genética
• Sistemas de apoio à decisão
• Modelagem de causalidade

Modelos de Markov ocultos (HMMs): Esses modelos sequenciais usam probabilidades conjuntas para modelar sistemas em que o estado subjacente é oculto, mas produz resultados observáveis. As aplicações incluem:

• Reconhecimento de voz
• Processamento de linguagem natural
• Análise de sequências biológicas
• Modelagem de séries temporais financeiras

Modelos gráficos probabilísticos: Isso inclui uma classe mais ampla de modelos que usam estruturas gráficas para codificar distribuições de probabilidade conjunta complexas. São ferramentas essenciais para:

• Reconhecimento de imagens
• Sistemas de recomendação
• Detecção de anomalias
• Aprendizado por reforço

Com essas aplicações, a probabilidade conjunta permite que os cientistas de dados criem modelos que capturam as complexas interdependências dos dados do mundo real, levando a previsões mais precisas e melhores tomadas de decisão em situações de incerteza.

Como as pessoas podem interpretar mal a probabilidade conjunta

Apesar de ser útil, a probabilidade conjunta é muitas vezes mal interpretada ou mal aplicada. Vamos dar uma olhada em alguns equívocos comuns e como evitá-los.

Confundindo probabilidade conjunta com probabilidade condicional

Um dos erros mais comuns é confundir P(A ∩ B) com P(A|B). Embora estejam relacionados, eles representam conceitos diferentes:

• Probabilidade conjunta P(A∩B) responde: “Qual é a chance de A e B acontecerem juntos?”
• A probabilidade condicional P(A|B) responde: “Dado que B ocorreu, qual é a probabilidade de A ocorrer?”

Por exemplo, a chance de alguém ter diabetes e ter mais de 65 anos (conjunta) é diferente da chance de alguém ter diabetes se tiver mais de 65 anos (condicional).

Essa diferença é importante em vários contextos analíticos. Por exemplo, quando um cientista de dados diz que “5% dos usuários clicaram em um anúncio e fizeram uma compra”, essa probabilidade conjunta é bem diferente de “40% dos usuários que clicaram em um anúncio fizeram uma compra”, que é uma probabilidade condicional.

Supondo incorretamente a independência

Outro erro comum é achar automaticamente que P(A∩B) = P(A) × P(B) sem checar se os eventos são mesmo independentes. Essa suposição pode levar a erros significativos quando os eventos são realmente dependentes.

Por exemplo, na análise de mercado, achar que a compra do produto A e do produto B não tem nada a ver pode levar a um planejamento de estoque errado se esses produtos forem complementares (como impressoras e tinta) ou substitutos (como marcas diferentes do mesmo item).

Testar a independência é super importante — se P(A∩B) ≠ P(A) × P(B), os eventos são dependentes e é preciso fazer cálculos mais cuidadosos de probabilidade conjunta.

Ignorando probabilidades marginais

Quando trabalham com probabilidades conjuntas, os analistas às vezes se concentram só na interseção, sem ligar para a frequência geral dos eventos individuais. Isso pode levar a conclusões erradas sobre a força dos relacionamentos.

Por exemplo, descobrir que 90% dos clientes que compraram os produtos A e B também compraram o produto C pode parecer incrível. Mas, se 89% de todos os clientes compram o produto C de qualquer jeito, a relação aparente é bem mais fraca do que parecia no começo.

Sempre compare as probabilidades conjuntas com as probabilidades marginais relevantes para não exagerar as relações entre os eventos. A razão de elevação — a relação entre a probabilidade conjunta e o produto das probabilidades marginais — oferece uma medida mais precisa da associação:

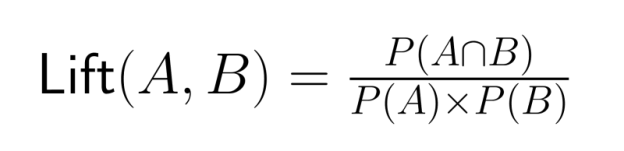
Um valor de elevação maior que 1 mostra que os eventos acontecem juntos com mais frequência do que seria esperado se fossem independentes.

Entender essas armadilhas comuns ajuda os cientistas de dados a aplicar a probabilidade conjunta corretamente e tirar conclusões significativas da análise probabilística.

Tópicos avançados e considerações adicionais

À medida que os cientistas de dados avançam em suas carreiras, eles vão encontrar aplicações mais sofisticadas de probabilidade conjunta. Vamos ver alguns conceitos mais avançados que se baseiam no que já aprendemos.

Probabilidade conjunta em espaços de alta dimensão

Quando lidam com problemas modernos de machine learning, os cientistas de dados geralmente trabalham com dezenas ou até centenas de variáveis ao mesmo tempo. Nesses espaços de alta dimensão, calcular e representar probabilidades conjuntas vira um desafio.

O número de parâmetros necessários para especificar uma distribuição conjunta cresce exponencialmente com o número de variáveis — um fenômeno conhecido como “maldição da dimensionalidade”. Por exemplo, uma distribuição conjunta de 10 variáveis binárias precisa de 2¹⁰ - 1 = 1.023 parâmetros para ser especificada completamente.

Para lidar com essa complexidade, os cientistas de dados usam técnicas como:

• Redução da dimensionalidade
• Seleção de variáveis
• Suposições de independência condicional
• Representações fatorizadas (como redes bayesianas)

Essas abordagens tornam os cálculos de probabilidade conjunta de alta dimensão mais fáceis de lidar para aplicações práticas em áreas como visão computacional, genômica e processamento de linguagem natural.

Distribuições de probabilidade conjunta

Nossos exemplos até agora envolveram principalmente eventos discretos, mas a probabilidade conjunta se estende naturalmente às variáveis contínuas por meio de distribuições de probabilidade conjunta.

Para variáveis discretas, a gente trabalha com funções de massa de probabilidade conjunta (PMFs), que especificam a probabilidade de cada combinação de variáveis aleatórias assumir valores específicos:

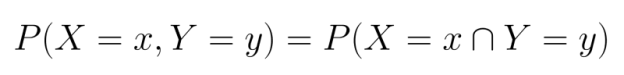
Para variáveis contínuas, usamos funções de densidade de probabilidade conjunta (PDFs). Ao contrário das PMFs, as PDFs não fornecem probabilidades diretamente, mas devem ser integradas em regiões para encontrar a probabilidade de que as variáveis se enquadrem nessas regiões:

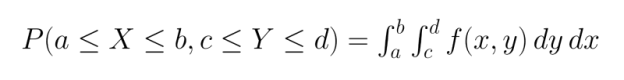
As distribuições conjuntas comuns incluem:

• Distribuição normal multivariada
• Distribuição t multivariada
• Distribuição de Dirichlet
• Distribuição multinomial

Entender essas distribuições permite uma modelagem mais sofisticada das relações entre variáveis contínuas em áreas como economia, bioinformática e ciências ambientais.

Ferramentas práticas para calcular a probabilidade conjunta

Várias ferramentas de software e linguagens de programação oferecem funções e bibliotecas para trabalhar com probabilidades conjuntas:

Python:

• NumPy e SciPy oferecem funções para distribuições de probabilidade multivariadas.
• O Pandas oferece ferramentas poderosas para cálculos empíricos de probabilidade conjunta.
• Bibliotecas como PyMC3 e PyStan fazem modelagem bayesiana com distribuições conjuntas.

R:

• O R básico tem várias funções de distribuição multivariada.
• Pacotes como o “copula” permitem modelar estruturas de dependência complexas.
• O 'bnlearn' dá suporte à análise de redes bayesianas.

SQL:

• As cláusulas GROUP BY com funções COUNT podem calcular probabilidades conjuntas empíricas.
• As funções de janela permitem análises probabilísticas mais complexas.
• Os bancos de dados modernos têm funções estatísticas para calcular probabilidades.

Essas ferramentas tornam prático aplicar conceitos de probabilidade conjunta a grandes conjuntos de dados, permitindo que os cientistas de dados criem modelos probabilísticos sofisticados para problemas complexos.

Pra entender melhor a probabilidade conjunta e como ela funciona na análise bayesiana, o DataCamp tem vários cursos bem legais:

• Fundamentos da análise de dados bayesiana em R - Aprenda a usar métodos bayesianos em problemas comuns de análise de dados
• Modelagem bayesiana com RJAGS - Domine técnicas práticas de modelagem bayesiana usando a estrutura JAGS no R
• Análise de dados bayesiana em Python - Aprendaa usar abordagens bayesianas para analisar dados com Python.

Esses cursos vão te ajudar a aprofundar os conceitos abordados neste artigo e aplicar técnicas de probabilidade conjunta para resolver problemas reais da ciência de dados.

Conclusão

Como vimos ao longo deste artigo, a probabilidade conjunta é um conceito estatístico fundamental com aplicações abrangentes em vários campos da ciência de dados. Os recursos do DataCamp, como os compartilhados nos mais de 40 recursos de estatística Python para ciência de dados, são ótimos pra ajudar você a entender melhor o assunto. Essa coleção completa traz recomendações específicas para aprender teoria da probabilidade, pensamento bayesiano e outros conceitos estatísticos que se baseiam na probabilidade conjunta.

Pra quem tá se preparando pra cargos na área de ciência de dados, nosso guia com as 35 principais perguntas e respostas de estatística oferece uma prática valiosa com questões de probabilidade conjunta, além de outros conceitos estatísticos importantes.  Também acho que nosso curso Probability Puzzles in R é umaopção divertida.