Gemeinsame Wahrscheinlichkeit: Theorie, Beispiele und Anwendungen in der Datenwissenschaft

Wenn ein Wetteranalyst einen heftigen Sturm vorhersagt, sagt er nicht nur starkes Regen oder starken Wind voraus – er schätzt auch, wie wahrscheinlich es ist, dass beide Wetterbedingungen zusammen auftreten . Dieses Beispiel zeigt, wie die Wahrscheinlichkeit, dass zwei Sachen gleichzeitig passieren, funktioniert – das ist die „ “-Wahrscheinlichkeit.

In diesem Artikel schauen wir uns an, wie die gemeinsame Wahrscheinlichkeit funktioniert, sehen uns Formeln für abhängige und unabhängige Ereignisse an, gehen praktische Beispiele durch und schauen, wie dieses Konzept in der Datenwissenschaft und im maschinellen Lernen angewendet wird. Für eine praktische Übersicht über grundlegende Wahrscheinlichkeitsdefinitionen und -regeln schau dir den Spickzettel „Einführung in Wahrscheinlichkeitsregeln“ von DataCamp an. Einführung in die Regeln der Wahrscheinlichkeit von DataCamp. 

Was ist die gemeinsame Wahrscheinlichkeit?

Die gemeinsame Wahrscheinlichkeit zeigt an, wie wahrscheinlich es ist, dass zwei (oder mehr) Ereignisse gleichzeitig passieren. Mathematisch schreiben wir das als P(A∩B), was man als „die Wahrscheinlichkeit von A Schnittmenge B“ oder einfach „die Wahrscheinlichkeit von A und B“ liest.

Um die gemeinsame Wahrscheinlichkeit zu verstehen, müssen wir erst mal den Kontext klären:

• Stichprobenraum: Die Gesamtheit aller möglichen Ergebnisse eines Experiments.
• Veranstaltungs-: Eine Untergruppe von Ergebnissen aus dem Ereignisraum.
• Marginalwahrscheinlichkeit: Die Wahrscheinlichkeit, dass ein einzelnes Ereignis passiert, egal was sonst noch so los ist.
• Bedingte Wahrscheinlichkeit: Die Wahrscheinlichkeit, dass ein Ereignis passiert, wenn schon ein anderes passiert ist.

Die gemeinsame Wahrscheinlichkeit ist bei unabhängigen und abhängigen Ereignissen echt unterschiedlich:

• Unabhängige Veranstaltungen: Ereignisse, bei denen das Auftreten des einen keinen Einfluss auf die Wahrscheinlichkeit des anderen hat. Nimm zum Beispiel das Werfen von zwei Münzen – das Ergebnis des ersten Wurfs hat keinen Einfluss auf den zweiten.
• Abhängige Ereignisse: Ereignisse, bei denen das Auftreten des einen die Wahrscheinlichkeit des anderen beeinflusst. Zum Beispiel, wenn du Karten ziehst, ohne sie zu ersetzen – wenn du eine Karte weglegst, ändert sich die Zusammensetzung des restlichen Stapels.

Wir können die gemeinsame Wahrscheinlichkeit mit einem Venn-Diagramm zeigen, wo der überlappende Bereich die Schnittmenge der Ereignisse darstellt – also die Fälle, in denen beide Ereignisse gleichzeitig passieren:

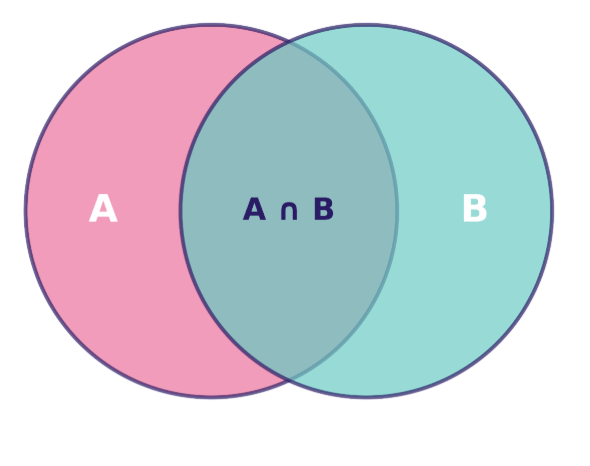
Venn-Diagramm, das die Beziehung zwischen den Mengen A und B zeigt, wobei ihre Schnittmenge A ∩ B hervorgehoben ist. Bild vom Autor.

Die Fläche dieses überlappenden Bereichs im Verhältnis zum gesamten Stichprobenraum ergibt P(A∩B) – die gemeinsame Wahrscheinlichkeit, die wir berechnen wollen.

Die Formel für die gemeinsame Wahrscheinlichkeit und ihre wichtigsten Eigenschaften

Um zu verstehen, wie man die gemeinsame Wahrscheinlichkeit berechnet, braucht man verschiedene Ansätze, je nachdem, ob die Ereignisse unabhängig oder abhängig sind. Schauen wir uns beide Fälle an und sehen wir uns die Regeln an, die für diese Berechnungen gelten.

Gemeinsame Wahrscheinlichkeit für unabhängige Ereignisse

Wenn zwei Ereignisse unabhängig voneinander sind, ist es einfach, ihre gemeinsame Wahrscheinlichkeit zu berechnen. Da keines der beiden Ereignisse das andere beeinflusst, können wir einfach ihre einzelnen Wahrscheinlichkeiten multiplizieren:

P(A∩B) = P(A) × P(B)

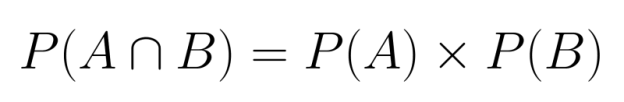
Diese Multiplikationsregel gilt, weil Unabhängigkeit bedeutet, dass die Kenntnis über das Eintreten eines Ereignisses keine Infos über die Wahrscheinlichkeit des anderen Ereignisses liefert.

Beispiel-: Stell dir vor, du würfelst mit zwei fairen Münzen. Die Wahrscheinlichkeit, beim ersten Münzwurf Kopf zu bekommen, ist 1/2, und die Wahrscheinlichkeit, beim zweiten Münzwurf Kopf zu bekommen, ist auch 1/2. Da diese Ereignisse unabhängig voneinander sind (der erste Wurf hat keinen Einfluss auf den zweiten), ist die Wahrscheinlichkeit, dass beide Münzen Kopf zeigen:

Das heißt, es gibt eine 25-prozentige Chance, dass du zweimal hintereinander Kopf wirfst.

Gemeinsame Wahrscheinlichkeit für abhängige Ereignisse

Wenn Ereignisse voneinander abhängen, müssen wir berücksichtigen, wie das erste Ereignis die Wahrscheinlichkeit des zweiten beeinflusst. Dafür müssen wir die bedingte Wahrscheinlichkeit in unsere Berechnung einbeziehen:

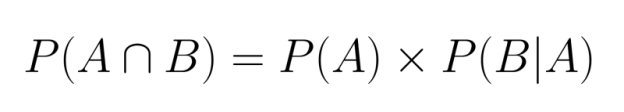
Hier steht P(B|A) für die Wahrscheinlichkeit, dass Ereignis B eintritt, wenn Ereignis A schon passiert ist.

Beispiel-: Stell dir vor, du ziehst zwei Karten aus einem normalen Kartenspiel, ohne sie zurückzulegen. Wie hoch ist die Wahrscheinlichkeit, zwei Asse zu ziehen?

• Die Wahrscheinlichkeit, beim ersten Ziehen ein Ass zu ziehen, ist P(Ass₁) = 4/52 = 1/13.
• Nachdem ein Ass gezogen wurde, sind in einem Kartenspiel mit 51 Karten nur noch 3 Asse übrig, also ist P(Ass₂|Ass₁) = 3/51 = 1/17.
• Also:

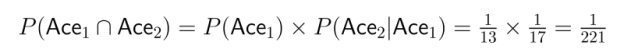
Das zeigt, wie sehr Abhängigkeiten die Berechnung der gemeinsamen Wahrscheinlichkeit beeinflussen.

Multiplikationsregel und Kettenregel

Die obigen Berechnungen zeigen, wie die Multiplikationsregel der Wahrscheinlichkeit funktioniert. Diese Regel gilt für mehr als zwei Ereignisse, sodass wir die gemeinsamen Wahrscheinlichkeiten für mehrere Ereignisse mit einer Kette von bedingten Wahrscheinlichkeiten berechnen können:

Das nennt man die Kettenregel, die eine systematische Methode bietet, um komplizierte gemeinsame Wahrscheinlichkeiten in überschaubare Teile zu zerlegen.

Beispiel-: Überleg mal, wie hoch die Wahrscheinlichkeit ist, dass du aus einem normalen Kartenspiel ohne Zurücklegen drei Herz-Karten hintereinander ziehst:

• P(Herz₁) = 13/52 = 1/4
• P(Heart₂|Heart₁) = 12/51
• P(Heart₃|Heart₁ ∩ Heart₂) = 11/50
• P(Heart₁ ∩ Heart₂ ∩ Heart₃) = 1/4 × 12/51 × 11/50 = 11/850

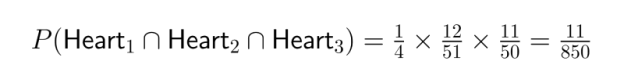
Die Kettenregel ist in der Datenwissenschaft besonders nützlich, wenn man Abfolgen von Ereignissen modelliert oder mit mehrstufigen Prozessen arbeitet.

Beispiele zur Veranschaulichung der gemeinsamen Wahrscheinlichkeit

Um unser Verständnis der gemeinsamen Wahrscheinlichkeit zu vertiefen, schauen wir uns ein paar klassische Beispiele an und sehen uns praktische Anwendungen an, die zeigen, wie diese Konzepte in verschiedenen Situationen funktionieren.

Klassische Beispiele

Würfelwürfe

Stell dir vor, du würfelst mit zwei sechsseitigen Würfeln. Wie hoch ist die Wahrscheinlichkeit, dass du mit dem ersten Würfel eine 4 und mit dem zweiten Würfel eine 6 würfelst?

Da das Ergebnis des ersten Würfels keinen Einfluss auf den zweiten Würfel hat, sind das unabhängige Ereignisse:

• P(Erster Würfel = 4) = 1/6
• P(Zweiter Würfel = 6) = 1/6
• P(Erster Würfel = 4 ∩ Zweiter Würfel = 6) = 1/6 × 1/6 = 1/36

Das heißt, dass die Wahrscheinlichkeit, dass genau diese Kombination auftritt, bei ungefähr 2,78 % liegt.

Kartenziehen

Lass uns mal die Wahrscheinlichkeit berechnen, dass man aus einem normalen Kartenspiel mit 52 Karten ohne Zurücklegen erst eine rote Karte und dann ein Ass zieht.

Da wir ohne Zurücklegen ziehen, hängen diese Ereignisse voneinander ab:

• P(Rote Karte beim ersten Ziehen) = 26/52 = 1/2
• P(Ass beim zweiten Ziehen | Rote Karte beim ersten Ziehen) = 3/51, wenn die erste Karte ein rotes Ass war, oder 4/51, wenn die erste Karte kein Ass war.

Um das richtig zu machen, müssen wir beide Möglichkeiten durchdenken:

• P(Rot ohne Ass, dann Ass) = P(Rot ohne Ass) × P(Ass | Rot ohne Ass) = 24/52 × 4/51 = 24/663
• P(rotes Ass und dann noch ein Ass) = P(rotes Ass) × P(Ass | rotes Ass) = 2/52 × 3/51 = 1/442

Also ist die Gesamtwahrscheinlichkeit: P(Rote Karte ∩ Ass beim zweiten Ziehen) = 24/663 + 1/442 = (24×2 + 3)/1326 = 51/1326 = 1/26

Die Wahrscheinlichkeit liegt bei ungefähr 3,85 %.

Kugeln in einer Tüte

Stell dir einen Beutel vor, der 5 blaue Murmeln und 3 grüne Murmeln enthält. Berechnen wir mal die Wahrscheinlichkeit, dass man in zwei verschiedenen Szenarien zwei blaue Murmeln zieht.

Mit Ersatz:

• P(Blau beim ersten Ziehen) = 5/8
• P(Blau beim zweiten Zug) = 5/8 (bleibt gleich, weil die erste Murmel zurückgelegt wird)
• P(Blau ∩ Blau) = 5/8 × 5/8 = 25/64 ≈ 39,06 %

Ohne Ersatz:

• P(Blau beim ersten Ziehen) = 5/8
• P(Blau beim zweiten Ziehen | Blau beim ersten Ziehen) = 4/7
• P(Blau ∩ Blau) = 5/8 × 4/7 = 20/56 = 5/14 ≈ 35,71 %

Dieser Vergleich zeigt, wie die Abhängigkeit, die entsteht, wenn man die Murmeln nicht ersetzt, die gemeinsame Wahrscheinlichkeit verringert.

Praktische Anwendungen

Medizinische Diagnose

Die gemeinsame Wahrscheinlichkeit ist in der Medizin echt wichtig, wenn man mehrere Symptome oder Testergebnisse anschaut. Stell dir ein Diagnoseszenario vor, in dem Ärzte Patienten mit den Symptomen A und B auf eine bestimmte Erkrankung untersuchen müssen.

Basierend auf historischen Daten:

• P(Symptom A) = 0,30 (30 % der Leute haben Symptom A)
• P(Symptom B) = 0,25 (25 % der Leute haben Symptom B)
• P(Symptom A ∩ Symptom B) = 0,12 (12 % zeigen beide Symptome)

Diese gemeinsame Wahrscheinlichkeit hilft Ärzten dabei, die Wahrscheinlichkeit verschiedener Erkrankungen einzuschätzen. Es ist wichtig zu wissen, dass P(A ∩ B) nicht gleich P(A) × P(B) = 0,30 × 0,25 = 0,075 ist, was bedeutet, dass diese Symptome nicht unabhängig voneinander sind – wenn man weiß, dass ein Patient ein Symptom hat, ist die Wahrscheinlichkeit höher, dass er auch das andere hat.

Modellierung finanzieller Risiken

Investmentanalysten müssen oft die Wahrscheinlichkeit bewerten, dass mehrere Marktbedingungen gleichzeitig auftreten. Stell dir vor, ein Analyst schätzt das Risiko sowohl eines Börsenrückgangs als auch steigender Zinsen im nächsten Quartal ein.

Wenn ihre Modelle zeigen:

• P(Börsenrückgang) = 0,35
• P(Steigende Zinsen) = 0,60
• P(Börsenrückgang | Steigende Zinsen) = 0,45

Die gemeinsame Wahrscheinlichkeitsberechnung würde so aussehen: P(Börsenrückgang ∩ steigende Zinsen) = 0,60 × 0,45 = 0,27

Diese Wahrscheinlichkeit von 27 % hilft dabei, das Portfoliorisiko zu quantifizieren und Absicherungsstrategien zum Schutz vor diesem Szenario zu entwickeln.

Diese Beispiele zeigen, wie die gemeinsame Wahrscheinlichkeit ein super Tool ist, um Unsicherheiten in verschiedenen Bereichen zu messen, egal ob man einfache Glücksspiele analysiert oder komplexe Entscheidungen in der Medizin oder im Finanzwesen trifft.

Gemeinsame Wahrscheinlichkeit und bedingte Wahrscheinlichkeit

Gemeinsame und bedingte Wahrscheinlichkeiten sind eng miteinander verknüpfte Konzepte, mit denen wir komplexe Szenarien mit mehreren Ereignissen analysieren können. Wenn man ihre Beziehung versteht, hat man echt starke Werkzeuge für das probabilistische Denken.

Die grundlegende Beziehung

Die Beziehung zwischen gemeinsamer und bedingter Wahrscheinlichkeit wird durch die Formel ausgedrückt:

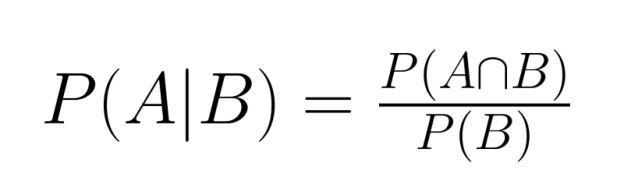
Wenn wir diese Gleichung umstellen, können wir die gemeinsame Wahrscheinlichkeit als bedingte Wahrscheinlichkeit ausdrücken:

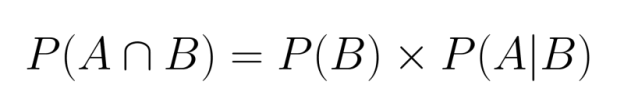
Diese Beziehung zeigt, dass wir die gemeinsame Wahrscheinlichkeit berechnen können, wenn wir die Randwahrscheinlichkeit eines Ereignisses und die bedingte Wahrscheinlichkeit des anderen Ereignisses kennen, wenn das erste gegeben ist.

Genauso könnten wir auch schreiben:

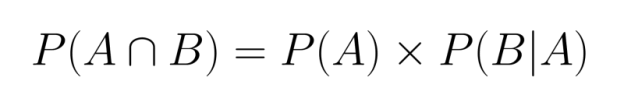
Beide Formulierungen sind richtig und gleichwertig, was zeigt, dass die gemeinsame Wahrscheinlichkeit symmetrisch ist.

Bezug zum Bayes-Theorem

Die Beziehung zwischen gemeinsamer und bedingter Wahrscheinlichkeit ist zentral für den Satz von Bayes, ein grundlegendes Werkzeug in der Wahrscheinlichkeitsinferenz:

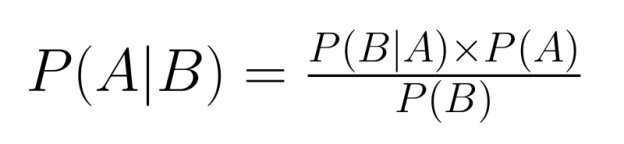
Mit dem Bayes-Theorem können wir bedingte Wahrscheinlichkeiten „umkehren“ – wenn wir P(B|A) kennen, können wir P(A|B) berechnen. Das ist echt super, wenn wir Infos über eine bedingte Beziehung haben, aber über die umgekehrte Beziehung nachdenken müssen.

Medizinische Tests liefern zum Beispiel oft Infos über P(Positiver Test|Krankheit), aber Ärzte müssen P(Krankheit|Positiver Test) herausfinden. Das Bayes'sche Theorem füllt diese Lücke, indem es die gemeinsame Wahrscheinlichkeit mit einbezieht:

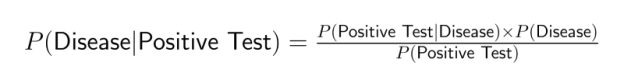
Anwendungen in der Datenwissenschaft

Die gemeinsame Wahrscheinlichkeit ist die Basis für viele Techniken und Anwendungen in der Datenwissenschaft. Wenn man versteht, wie verschiedene Ereignisse zusammenwirken, können Datenwissenschaftler genauere Modelle erstellen und bessere Vorhersagen in verschiedenen Bereichen treffen.

Vorhersagemodelle

Die gemeinsame Wahrscheinlichkeit ist für viele Klassifizierungsalgorithmen wichtig, vor allem für naive Bayes-Klassifikatoren. Diese beliebten Modelle für maschinelles Lernen berechnen die Wahrscheinlichkeit verschiedener Ergebnisse, basierend auf mehreren Merkmalen.

Der Naive-Bayes-Ansatz nutzt das Bayes-Theorem mit der „naiven” Annahme, dass Merkmale bedingt unabhängig sind. Das macht die Berechnung der gemeinsamen Wahrscheinlichkeit einfacher:

Trotz dieser vereinfachenden Annahme funktionieren naive Bayes-Klassifikatoren echt gut für:

• Textklassifizierung und Spamfilterung
• Stimmungsanalyse
• Medizinische Diagnose
• Kundensegmentierung

Dieser Ansatz ist rechnerisch effizient und funktioniert oft überraschend gut, auch wenn die Unabhängigkeitsannahme nicht strikt gilt.

Risikobewertung

Die gemeinsame Wahrscheinlichkeit ist echt wichtig bei Betrugserkennungssystemen, wo mehrere Risikofaktoren zusammen bewertet werden müssen. Moderne Algorithmen zur Betrugserkennung schauen sich Kombinationen von verdächtigen Verhaltensweisen an, um möglicherweise betrügerische Transaktionen zu erkennen.

Stell dir ein Online-Zahlungssystem vor, das verschiedene Signale überwacht:

• Transaktionsbetrag
• Geografische Lage
• Zeitpunkt der Transaktion
• Geräteinfos
• Verhaltensmuster der Nutzer

Auch wenn jedes Signal für sich genommen vielleicht nicht auf Betrug hindeutet, können bestimmte Kombinationen (wenn sie zusammen auftreten) den Verdacht deutlich verstärken. Zum Beispiel ist eine große Transaktion von einem neuen Gerät aus, in einem fremden Land und zu einer ungewöhnlichen Zeit ein gemeinsames Ereignis, bei dem die Wahrscheinlichkeit von Betrug ziemlich hoch sein kann.

Diese gemeinsame Wahrscheinlichkeitsbewertung macht eine genauere Risikobewertung möglich, als wenn man jeden Faktor einzeln anschaut, und reduziert sowohl falsche positive als auch falsche negative Ergebnisse.

Maschinelles Lernen

Gemeinsame Wahrscheinlichkeitskonzepte sind echt wichtig für viele fortgeschrittene Modelle des maschinellen Lernens, wie zum Beispiel:

Bayesian Networks: Diese grafischen Modelle zeigen Variablen und ihre Wahrscheinlichkeitsbeziehungen. Sie machen es möglich, komplexe gemeinsame Wahrscheinlichkeitsverteilungen zu verstehen, indem sie in einfachere bedingte Wahrscheinlichkeiten zerlegt werden. Bayesianische Netzwerke werden häufig eingesetzt in:

• Medizinische Diagnosesysteme
• Genetische Analyse
• Entscheidungsunterstützungssysteme
• Kausalitätsmodellierung

Hidden Markov Models (HMMs): Diese sequenziellen Modelle nutzen gemeinsame Wahrscheinlichkeiten, um Systeme zu modellieren, bei denen der zugrunde liegende Zustand nicht sichtbar ist, aber beobachtbare Ergebnisse erzeugt. Anwendungen sind zum Beispiel:

• Spracherkennung
• Natürliche Sprachverarbeitung
• Biologische Sequenzanalyse
• Modellierung von Finanzzeitreihen

Probabilistische grafische Modelle: Die umfassen eine breitere Gruppe von Modellen, die Graphstrukturen nutzen, um komplexe gemeinsame Wahrscheinlichkeitsverteilungen zu kodieren. Sie sind wichtige Werkzeuge für:

• Bilderkennung
• Empfehlungssysteme
• Anomalieerkennung
• Verstärkendes Lernen

Mit diesen Anwendungen können Datenwissenschaftler dank gemeinsamer Wahrscheinlichkeit Modelle entwickeln, die die komplexen Zusammenhänge in echten Daten erfassen. Das führt zu genaueren Vorhersagen und besseren Entscheidungen, auch wenn man sich nicht ganz sicher ist.

Wie Leute die gemeinsame Wahrscheinlichkeit falsch verstehen können

Obwohl sie echt nützlich ist, wird die gemeinsame Wahrscheinlichkeit oft falsch verstanden oder falsch angewendet. Schauen wir uns mal ein paar häufige Irrtümer an und wie man sie vermeiden kann.

Verwechslung von gemeinsamer Wahrscheinlichkeit und bedingter Wahrscheinlichkeit

Einer der häufigsten Fehler ist, P(A∩B) mit P(A|B) zu verwechseln. Obwohl sie miteinander zusammenhängen, sind es unterschiedliche Konzepte:

• Die gemeinsame Wahrscheinlichkeit P(A∩B) ist: Wie hoch ist die Wahrscheinlichkeit, dass sowohl A als auch B passieren?
• Die bedingte Wahrscheinlichkeit P(A|B) gibt dir die Antwort: „Wenn B passiert ist, wie hoch ist die Chance, dass A passiert?“

Zum Beispiel ist die Wahrscheinlichkeit, dass jemand sowohl Diabetes hat als auch über 65 ist (kombiniert), anders als die Wahrscheinlichkeit, dass jemand Diabetes hat, wenn er über 65 ist (bedingt).

Diese Unterscheidung ist in vielen analytischen Situationen wichtig. Wenn zum Beispiel ein Datenwissenschaftler sagt, dass „5 % der Nutzer sowohl auf eine Anzeige geklickt als auch was gekauft haben“, ist diese gemeinsame Wahrscheinlichkeit ganz anders als „40 % der Nutzer, die auf eine Anzeige geklickt haben, haben was gekauft“, was eine bedingte Wahrscheinlichkeit ist.

Falsche Annahme der Unabhängigkeit

Ein weiterer häufiger Fehler ist, einfach anzunehmen, dass P(A∩B) = P(A) × P(B) ist, ohne zu checken, ob die Ereignisse wirklich unabhängig voneinander sind. Diese Annahme kann zu erheblichen Fehlern führen, wenn Ereignisse tatsächlich voneinander abhängig sind.

Bei der Marktanalyse kann die Annahme, dass der Kauf von Produkt A und Produkt B unabhängig voneinander ist, zu einer falschen Bestandsplanung führen, wenn diese Produkte sich ergänzen (wie Drucker und Tinte) oder austauschbar sind (wie verschiedene Marken desselben Artikels).

Es ist echt wichtig, die Unabhängigkeit zu checken – wenn P(A∩B) ≠ P(A) × P(B) ist, hängen die Ereignisse zusammen, und man muss die gemeinsamen Wahrscheinlichkeiten genauer berechnen.

Geringe Wahrscheinlichkeiten ignorieren

Bei der Arbeit mit gemeinsamen Wahrscheinlichkeiten konzentrieren sich Analysten manchmal nur auf die Schnittmenge und lassen die Gesamtfrequenz einzelner Ereignisse außer Acht. Das kann zu falschen Schlüssen über die Stärke von Beziehungen führen.

Zum Beispiel könnte es beeindruckend klingen, wenn man herausfindet, dass 90 % der Leute, die die Produkte A und B gekauft haben, auch Produkt C gekauft haben. Wenn aber 89 % aller Kunden Produkt C sowieso kaufen, ist der Zusammenhang viel schwächer, als es zuerst aussieht.

Vergleiche immer die gemeinsamen Wahrscheinlichkeiten mit den relevanten Randwahrscheinlichkeiten, um zu vermeiden, dass du die Beziehungen zwischen Ereignissen überbewertest. Die Lift-Quote – das Verhältnis der gemeinsamen Wahrscheinlichkeit zum Produkt der Randwahrscheinlichkeiten – ist ein genaueres Maß für den Zusammenhang:

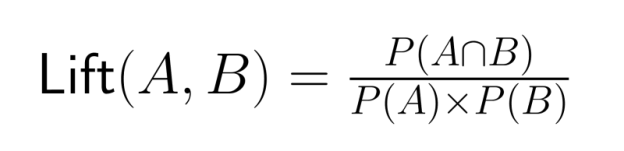
Ein Lift-Wert größer als 1 zeigt, dass Ereignisse öfter zusammen auftreten, als man erwarten würde, wenn sie unabhängig voneinander wären.

Wenn man diese häufigen Fallstricke versteht, können Datenwissenschaftler die gemeinsame Wahrscheinlichkeit richtig anwenden und aus der Wahrscheinlichkeitsanalyse sinnvolle Erkenntnisse gewinnen.

Fortgeschrittene Themen und weitere Überlegungen

Im Laufe ihrer Karriere werden Datenwissenschaftler auf immer komplexere Anwendungen der gemeinsamen Wahrscheinlichkeit stoßen. Schauen wir uns ein paar fortgeschrittene Konzepte an, die auf dem aufbauen, was wir schon gelernt haben.

Gemeinsame Wahrscheinlichkeit in hochdimensionalen Räumen

Bei der Lösung moderner Probleme im Bereich des maschinellen Lernens arbeiten Datenwissenschaftler oft mit Dutzenden oder sogar Hunderten von Variablen gleichzeitig. In diesen hochdimensionalen Räumen wird es schwierig, gemeinsame Wahrscheinlichkeiten zu berechnen und darzustellen.

Die Anzahl der Parameter, die man braucht, um eine gemeinsame Verteilung zu beschreiben, steigt mit der Anzahl der Variablen total schnell an – ein Phänomen, das man als „Fluch der Dimensionalität” bezeichnet. Zum Beispiel braucht man für eine gemeinsame Verteilung von 10 binären Variablen 2¹⁰ - 1 = 1.023 Parameter, um sie komplett zu beschreiben.

Um mit dieser Komplexität klarzukommen, nutzen Datenwissenschaftler Techniken wie:

• Dimensionsreduktion
• Variablenauswahl
• Annahmen zur bedingten Unabhängigkeit
• Faktorisierte Darstellungen (wie Bayes'sche Netzwerke)

Diese Ansätze machen hochdimensionale gemeinsame Wahrscheinlichkeitsberechnungen für praktische Anwendungen in Bereichen wie Computer Vision, Genomik und natürliche Sprachverarbeitung machbar.

Gemeinsame Wahrscheinlichkeitsverteilungen

Unsere Beispiele bisher haben sich hauptsächlich auf diskrete Ereignisse bezogen, aber die gemeinsame Wahrscheinlichkeit lässt sich ganz natürlich durch gemeinsame Wahrscheinlichkeitsverteilungen auf kontinuierliche Variablen ausweiten.

Bei diskreten Variablen arbeiten wir mit gemeinsamen Wahrscheinlichkeitsverteilungen (PMFs), die die Wahrscheinlichkeit angeben, mit der jede Kombination von Zufallsvariablen bestimmte Werte annimmt:

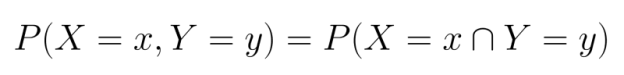
Für kontinuierliche Variablen nehmen wir gemeinsame Wahrscheinlichkeitsdichtefunktionen (PDFs). Im Gegensatz zu PMFs geben PDFs keine direkten Wahrscheinlichkeiten an, sondern müssen über Regionen integriert werden, um die Wahrscheinlichkeit zu ermitteln, dass die Variablen in diese Regionen fallen:

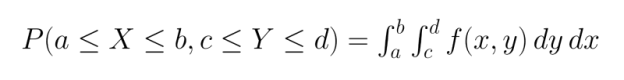
Zu den gängigen gemeinsamen Verteilungen gehören:

• Multivariate Normalverteilung
• Multivariate t-Verteilung
• Dirichlet-Verteilung
• Multinomiale Verteilung

Wenn man diese Verteilungen versteht, kann man die Beziehungen zwischen kontinuierlichen Variablen in Bereichen wie Wirtschaft, Bioinformatik und Umweltwissenschaften besser modellieren.

Praktische Tools zum Berechnen der gemeinsamen Wahrscheinlichkeit

Ein paar Software-Tools und Programmiersprachen haben Funktionen und Bibliotheken, um mit gemeinsamen Wahrscheinlichkeiten zu arbeiten:

Python:

• NumPy und SciPy haben Funktionen für mehrdimensionale Wahrscheinlichkeitsverteilungen.
• Pandas hat echt coole Tools für empirische Berechnungen der gemeinsamen Wahrscheinlichkeit.
• Bibliotheken wie PyMC3 und PyStan machen Bayes'sche Modellierung mit gemeinsamen Verteilungen.

R:

• Base R hat viele Funktionen für multivariate Verteilungen.
• Pakete wie „copula” machen es möglich, komplexe Abhängigkeitsstrukturen zu modellieren.
• „bnlearn“ hilft bei der Analyse von Bayes'schen Netzwerken.

SQL:

• GROUP BY-Klauseln mit COUNT-Funktionen können empirische gemeinsame Wahrscheinlichkeiten berechnen.
• Fensterfunktionen machen komplexere Wahrscheinlichkeitsanalysen möglich.
• Moderne Datenbanken haben statistische Funktionen für Wahrscheinlichkeitsberechnungen.

Mit diesen Tools kann man gemeinsame Wahrscheinlichkeitskonzepte ganz praktisch auf große Datensätze anwenden, sodass Datenwissenschaftler ausgefeilte Wahrscheinlichkeitsmodelle für knifflige Probleme erstellen können.

Um dein Verständnis von gemeinsamer Wahrscheinlichkeit und ihren Anwendungen in der Bayes'schen Analyse zu vertiefen, bietet DataCamp mehrere super Kurse an:

• Grundlagen der Bayes'schen Datenanalyse in R – Lerne, wie du Bayes'sche Methoden auf gängige Probleme der Datenanalyse anwendest.
• Bayesianische Modellierung mit RJAGS – Lerne praktische bayesianische Modellierungstechniken mit dem JAGS-Framework in R
• Bayesianische Datenanalyse in Python – Lerne, wie dumit Python bayesianische Ansätze für die Datenanalyse anwendest.

Diese Kurse helfen dir dabei, die in diesem Artikel behandelten Konzepte zu vertiefen und Techniken der gemeinsamen Wahrscheinlichkeit anzuwenden, um reale Probleme aus dem Bereich Data Science zu lösen.

Fazit

Wie wir in diesem Artikel gesehen haben, ist die gemeinsame Wahrscheinlichkeit ein grundlegendes statistisches Konzept mit weitreichenden Anwendungen in vielen Bereichen der Datenwissenschaft. Die Ressourcen von DataCamp, wie die in den über 40 Python-Statistiken für Datenwissenschaftsressourcen, sind super, um dein Verständnis zu verbessern. Diese umfassende Sammlung enthält konkrete Tipps zum Lernen von Wahrscheinlichkeitstheorie, Bayes'schem Denken und anderen statistischen Konzepten, die auf gemeinsamer Wahrscheinlichkeit basieren.

Für alle, die sich auf Jobs im Bereich Data Science vorbereiten, bietet unser Leitfaden „Die 35 wichtigsten Fragen und Antworten zum Thema Statistik” wertvolle Übungsmöglichkeiten mit Fragen zur gemeinsamen Wahrscheinlichkeit und anderen wichtigen statistischen Konzepten.  Ich finde auch, dass unser Kurs „Probability Puzzles in R” eine cooleOption ist.