programa
Imagina que intentas encontrar el punto más bajo de las colinas con los ojos vendados. Como estás limitado por tu tacto, sólo puedes sentir el suelo inmediatamente a tu alrededor para determinar qué camino es hacia abajo. Esto es esencialmente lo que hacen los algoritmos de aprendizaje automático cuando intentan encontrar la mejor solución a un problema.
Enmarcan el problema en una función matemática cuyas entradas y salidas representan una superficie accidentada. Encontrar el mínimo de esta función significa que has llegado a la mejor solución del problema. Uno de los algoritmos más populares para realizar este proceso se llama Descenso Gradiente Estocástico (SGD).
En este tutorial, aprenderás todo lo que debes saber sobre el algoritmo, incluidas algunas intuiciones iniciales sin las matemáticas, los detalles matemáticos y cómo implementarlo en Python.
¿Qué es el Descenso Gradiente Estocástico? La respuesta breve
El Descenso Gradiente Estocástico (SGD) es una técnica de optimización utilizada en el aprendizaje automático para minimizar los errores en los modelos predictivos. A diferencia del descenso de gradiente normal, que utiliza todo el conjunto de datos para calcular el gradiente y actualizar los parámetros del modelo, el SGD actualiza los parámetros utilizando sólo un punto de datos cada vez. Esto lo hace más rápido y eficaz para grandes conjuntos de datos, aunque puede ser más ruidoso y menos estable. El SGD ayuda a encontrar los valores óptimos de los parámetros del modelo para mejorar la precisión de las predicciones.
¿Qué es la optimización en el aprendizaje automático?
Lo primero que tenemos que entender enseguida es que el descenso estocástico del gradiente (SGD) no es un algoritmo de aprendizaje automático. Se trata más bien de una técnica de optimización que puede aplicarse a los algoritmos de ML.
Entonces, ¿qué es la optimización? Para entenderlo, vayamos ascendiendo desde la fase de planteamiento del problema del aprendizaje automático.
Supongamos que intentamos predecir los precios de los diamantes basándonos en su valor en quilates (un quilate son 0,2 gramos). Se trata de un problema de regresión, ya que el modelo produce valores numéricos.
Para resolver el problema, tenemos a nuestra disposición una amplia gama de algoritmos, pero vamos a elegir Regresión lineal simpleque tiene la sencilla fórmula de f(x) = mx + b donde:
bes el precio base del diamantemes el aumento del precio por quilatexes el valor en quilates del diamantef(x)es el precio previsto del diamante
Esta ecuación lineal representa nuestro modelo. Nuestro objetivo es encontrar los mejores valores para m y b que hagan que nuestras predicciones sean lo más precisas posible en todos los diamantes de nuestro conjunto de datos.
Si tuviéramos otra característica en nuestro conjunto de datos, como el volumen del diamante, nuestra fórmula cambiaría a f(x1, x2) = m1*x1 + m2*x2 + bdonde
bes el precio base del diamantem1es el aumento del precio por quilatem2es el incremento del precio por unidad de volumenx1es el valor en quilates del diamantex2es el volumen del diamantef(x)es el precio previsto del diamante
Ahora, tendríamos que encontrar los valores óptimos para m1, m2y b.
En general, todos los modelos de aprendizaje automático tienen ecuaciones como las anteriores con uno o más parámetros. Así, la definición de optimización en este contexto pasa a ser: "Dado este modelo y este conjunto de datos, encuentra los valores óptimos para los parámetros de la ecuación".
Hay muchos algoritmos de optimización que pueden realizar esta tarea, como el Descenso Gradiente Estocástico , en el que se centra nuestro tutorial. Pero para comprender plenamente cómo funciona la SGD, repasemos algunas ideas fundamentales que la sustentan.
El concepto de error en el aprendizaje automático
Para entender el SGD, necesitamos aprender el algoritmo de descenso de gradiente regular (GD), que comparte muchas de las ideas fundamentales de su versión estocástica. El descenso de gradiente simple parte del concepto de error en el aprendizaje automático.
¿Qué es un error o una pérdida?
Los algoritmos de ML suelen adivinar cuál es la respuesta correcta a un problema. A esta respuesta la llamamospredicción y no siempre es exacta. Así que introducimos un nuevo término llamado "error" o "pérdida" que representa la diferencia entre la respuesta real y la predicción del modelo. Nuestro objetivo es construir un modelo que minimice este error.
Si nuestro modelo f(x) adivina 10.000 $ por un diamante que en realidad cuesta 12.000 $, el error es de 2.000 $. Deberíamos ajustar nuestro modelo para disminuir este error. Pero las predicciones del modelo deben ser buenas para cualquier diamante, no sólo para uno. Por tanto, necesitamos una forma de combinar el error de todos los diamantes de nuestro conjunto de datos. Aquí es donde entran en juego las funciones de coste.
Una función de coste combina todos los errores individuales en un número que representa el rendimiento global de nuestro modelo. Un menor coste global significa que las predicciones de nuestro modelo son mejores.
Funciones de coste en el aprendizaje automático
Las funciones de coste cambian según el tipo de problema que estemos resolviendo.
En los problemas de regresión, el modelo predice valores numéricos como cuánto cuesta un diamante o cuánto tiempo se tarda en nadar una vuelta. En clasificaciónel modelo predice la categoría a la que pertenece algo. Por ejemplo, ¿una seta es comestible o no, o el objeto de la imagen es un gato, un perro o un caballo?
Hay otros tipos de problemas, pero lo importante es que cada uno requiere funciones de costes diferentes. En este tutorial, nos centraremos en Error cuadrático medio (MSE), que se utiliza a menudo en regresión.
La diferencia entre los valores reales (verdad sobre el terreno) y las predicciones del modelo se denomina error o pérdida. En consecuencia, una función que combina todos estos errores o pérdidas se denomina función deerror , función de pérdidao función decoste. Diferentes fuentes pueden utilizar estos términos indistintamente; este tutorial utilizará a partir de ahora el términofunción de pérdida .
Error cuadrático medio
En los problemas de regresión, es habitual ver el siguiente gráfico que compara los valores reales (verdad básica) con las predicciones del modelo.
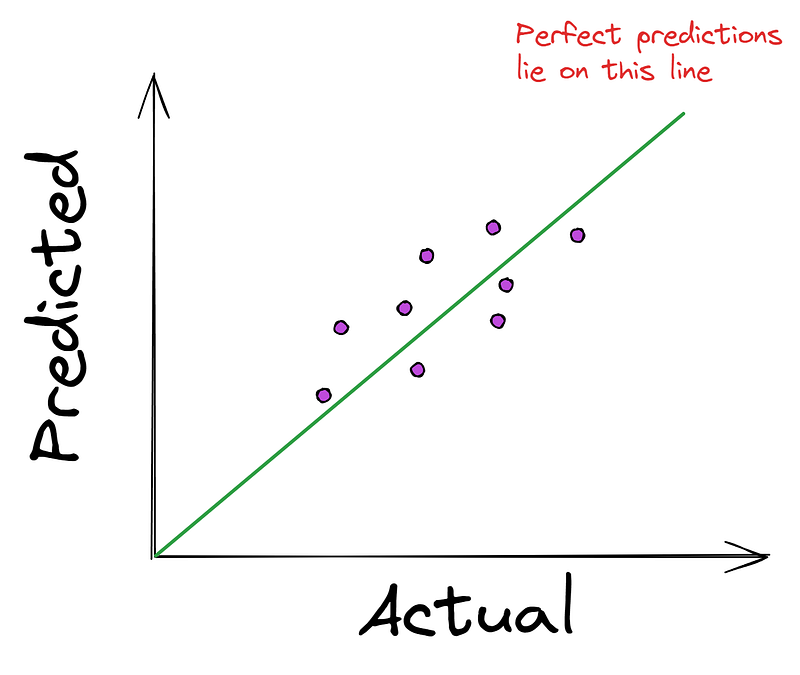
Cuanto más se acerquen los puntos a la línea recta, mejores serán las predicciones del modelo. Por eso, la mayoría de los algoritmos de regresión intentan minimizar la distancia media de los puntos a la línea perfecta. Y como hemos dicho antes, la minimización se produce utilizando una función de coste como el Error Cuadrático Medio (ECM).
El MSE toma los valores reales y predichos como entradas y produce la distancia media al cuadrado a la línea perfecta.
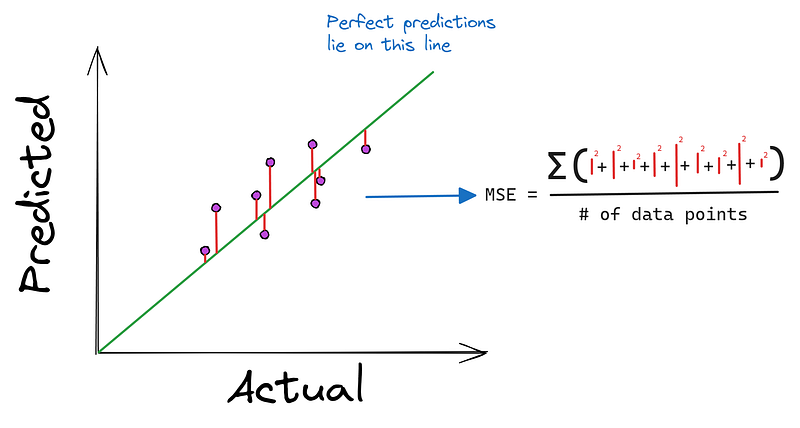
Quizá te preguntes: "¿Por qué elevar al cuadrado las diferencias en lugar de tomar su valor absoluto?". La primera razón es que es muy fácil hallar la derivada de una función cuadrada. Además, elevar al cuadrado las diferencias enfatiza los errores más grandes, penalizando al modelo por sus peores predicciones.
Por eso se prefiere el MSE a otras funciones alternativas, como el Error Absoluto Medio (MAE), que a primera vista parecen más sencillas, pero son más difíciles de diferenciar.
El Gradiente
La siguiente pieza del puzzle del descenso de gradiente es el propio gradiente. Volvamos a nuestra analogía de "colina abajo" para entenderlo mejor.
Gradiente como el camino más empinado
Estábamos en lo alto de la colina con los ojos vendados y queríamos llegar abajo lo antes posible. Si vertiéramos agua a nuestros pies, ¿hacia dónde fluiría? Fluiría cuesta abajo en la dirección del descenso más pronunciado.
Esto es exactamente lo que nos dice el gradiente, pero en sentido contrario. La pendiente apunta hacia arriba, en la dirección de la subida más pronunciada. Cuando intentamos minimizar el error, simplemente vamos en la dirección opuesta al gradiente para encontrar el camino más rápido hacia abajo.
Matemáticamente, el gradiente nos dice cómo cambian las salidas de una función cuando cambiamos sus entradas. Más concretamente, nos indica la dirección en la que la función aumenta más rápidamente.
En el contexto del aprendizaje automático, donde intentamos minimizar el error utilizando una función de pérdida, el gradiente se convierte en nuestra guía para encontrar el camino más rápido para reducir ese error.
El gradiente se representa como un vector, uno por cada parámetro de entrada de nuestra función. Cada número de este vector nos dice cuánto cambiaría la función si hiciéramos un pequeño ajuste en el parámetro correspondiente.
Cómo hallar el gradiente de una función
Entonces, ¿cómo hallar el gradiente de una función?
Para funciones de una sola variable como f(x) = x ** 2el gradiente es la derivada de la función, que se da como un vector con un elemento - . [2x].
Para funciones multivariables como f(x1, x2) = x1 ** 3 - x2 ** 2, el gradiente contiene las derivadas parciales de la función respecto a cada entrada. Así, para la segunda función, el vector gradiente es [3x1 ** 2, 2*x2].
Volviendo al MSE, que tiene la siguiente fórmula:
MSE = (1/n) * Σ(y - f(x))² donde:
f(x)esmx + bmy b son variables de funciónxes el valor en quilates de los diamantesnes el número de puntos de datosyes el precio real de los diamantes
Por tanto, su gradiente son las derivadas parciales de MSE con respecto a m y b:
∂/∂m (MSE) = (-2/n) * Σ(x * (y - (mx + b)))
∂/∂b (MSE) = (-2/n) * Σ(y - (mx + b))
The gradient = [∂/∂m (MSE), ∂/∂b (MSE)]No te preocupes demasiado por estas fórmulas. La idea clave es que nos dicen cómo cambia el error cuadrático medio si cambiamos m o b un poquito.
Descenso Gradiente: Dando pasos hacia la solución
Velocidad de aprendizaje: controlando el tamaño de nuestro paso
Ahora, tenemos todo lo que necesitamos para ejecutar el descenso por pendiente o, en otras palabras, llegar al fondo de la colina de la forma más eficiente posible. Pero, ¿nos lanzamos en esa dirección o damos pequeños pasos? Eso lo determina el gradiente, ¿no? El tamaño del gradiente nos indica cuánto bajamos en cada paso.
Pero supongamos que la pendiente es tan grande que, en lugar de llegar abajo, salimos disparados y acabamos en la cima de otra colina en un solo paso. Sorprendentemente, esto ocurre mucho en el descenso por gradiente, por lo que introducimos un parámetro llamado tamaño del paso, que controla los efectos del gradiente.
Antes de dar un paso, simplemente multiplicamos el gradiente por el tamaño del paso, lo que reduce su magnitud. Por ejemplo, si nuestro gradiente nos dice que demos un paso de 3,56 cuesta abajo, un tamaño de paso de 0,1 convierte la distancia en 0,356.
Tardaremos más en llegar al fondo, pero ahora no corremos el riesgo de saltárnoslo del todo.
El tamaño del paso suele llamarse tasa de aprendizaje en aprendizaje automático y suele tomar valores entre 0,001 y 0,3.
Veamos la versión matemática de este proceso.
Dar pequeños pasos matemáticamente
En primer lugar, damos m y b a los parámetros de nuestro modelo valores aleatorios:
m = 0.215 # Generated randomly
b = 0.059Con ellas, calculamos el MSE inicial en todo el conjunto de datos:
MSE = (1/n) * Σ(y - (0.215 * x + 0.059))² = ...Ahora, para reducir este error, necesitamos dar un pequeño paso en la dirección opuesta al gradiente, o dicho de otro modo, necesitamos actualizar m y b utilizando el gradiente y la tasa de aprendizaje:
m_new = 0.215 - alpha * (∂/∂m (MSE))
b_new = 0.059 - alpha * (∂/∂b (MSE))La mayoría de los recursos eligen alpha o α (la letra griega) para denotar el ritmo de aprendizaje.
Cuando tengamos nuevos valores para m y bcalculamos de nuevo el MSE:
MSE_new = (1/n) * Σ(y - (m_new * x + b_new))²Ahora, calculamos de nuevo el gradiente y continuamos así hasta que alcancemos una condición de parada.
Aprende cómo la velocidad de aprendizaje afecta visualmente al entrenamiento consultando este artículo sobre el descenso de gradiente.
Saber cuándo parar
Como tenemos los ojos vendados, no podemos ver realmente cuándo hemos tocado fondo, sobre todo cuando damos pequeños pasos.
Por tanto, necesitamos algunas condiciones para detener nuestro descenso. Normalmente, se utilizan estas reglas:
- Alcanzar un número predeterminado de pasos (pasos máximos o iteraciones)
- El cambio en el MSE se vuelve muy pequeño después de cada paso (por debajo de un umbral predefinido)
- La pendiente se vuelve muy cercana a cero (lo que indica que estamos en la base de la colina o cerca de ella)
- El MSE empieza a aumentar en lugar de disminuir
Estas reglas las estableces tú, el ingeniero ML, cuando realizas el descenso de gradiente. Las implementaciones del algoritmo en Python suelen tener argumentos para establecer estas reglas y veremos algunos de ellos más adelante.
Ventajas y retos del descenso por gradiente
Ventajas:
- Es un algoritmo sencillo e intuitivo
- Funciona bien para una amplia gama de problemas
- Es computacionalmente eficiente para problemas con muchos parámetros
Desafíos:
- Puede ser lento para conjuntos de datos muy grandes
- Puede atascarse en mínimos locales para problemas no convexos
- Elegir el ritmo de aprendizaje adecuado puede ser complicado
En la siguiente sección, veremos cómo el Descenso Gradiente Estocástico aborda algunos de estos retos, sobre todo para grandes conjuntos de datos.
Descenso Gradiente Estocástico
Una vez que te has familiarizado con el descenso de gradiente normal, el SGD es muy fácil de entender.
El problema del descenso de gradiente regular
Aunque el descenso de gradiente es uno de los algoritmos de optimización más elegantes que existen, tiene una desventaja significativa cuando se trata de grandes conjuntos de datos. Recuerda que en cada paso, calculamos el gradiente utilizando todos los puntos de datos de nuestro conjunto de datos:
∂/∂m (MSE) = (-2/n) * Σ(x * (y - (mx + b)))
∂/∂b (MSE) = (-2/n) * Σ(y - (mx + b))Aquí, x y y son matrices que contienen todos los valores en quilates y precios reales de los diamantes. Esto significa que estaríamos utilizando la información de cada diamante para actualizar los parámetros en cada paso.
Como puedes imaginar, esto se vuelve costoso computacionalmente y lleva mucho tiempo cuando tenemos millones de puntos de datos. En la era de los grandes datos, esta limitación puede hacer que el descenso de gradiente regular sea poco práctico para muchos problemas de aprendizaje automático del mundo real.
El enfoque estocástico: introducir la aleatoriedad
"Estocástico" significa "determinado aleatoriamente", y eso es exactamente lo que hace el SGD: introduce la aleatoriedad en nuestro proceso de optimización.
En lugar de utilizar todos los puntos de datos para calcular el gradiente, el SGD selecciona aleatoriamente un punto de datos en cada paso. Utiliza este único punto para calcular una estimación del gradiente y actualizar los parámetros.
Como el SGD sólo mira un punto de datos cada vez, puede hacer actualizaciones más frecuentes de los parámetros. Esto le permite atravesar la superficie de error (la colina) más rápidamente, sobre todo en el caso de grandes conjuntos de datos.
Sin embargo, esta velocidad tiene un coste. Como estamos utilizando un único punto de datos para estimar el gradiente de todo el conjunto de datos, nuestras estimaciones son mucho más ruidosas. Esto significa que nuestra trayectoria por la superficie de error es menos suave y más errática.
Las matemáticas que hay detrás del Descenso Gradiente Estocástico
Para realizar el SGD, primero definimos una función estocástica de costes.
En lugar de calcular el Error Cuadrático Medio de todos los puntos de datos, ahora observamos el error cuadrático de un único punto elegido al azar:
Cost = (y - f(x))²Donde y es el precio real del diamante elegido al azar, y f(x) = mx + b es nuestro precio previsto para ese diamante.
A continuación, calculamos el gradiente estocástico de esta función de coste con respecto a nuestros parámetros m y b:
∂/∂m (Cost) = -2x(y - (mx + b))
∂/∂b (Cost) = -2(y - (mx + b))
The stochastic gradient = [∂/∂m (Cost), ∂/∂b (Cost)]Utilizando este gradiente estocástico, actualizamos nuestros parámetros de la misma manera que el descenso por gradiente normal:
m_new = m_old - learning_rate * ∂/∂m (Cost)
b_new = b_old - learning_rate * ∂/∂b (Cost)La idea clave en SGD es que cada paso implica un único punto de datos elegido al azar. Las reglas para saber cuándo detener el descenso son las mismas que las del descenso por gradiente normal.
Variaciones del SGD y cuándo utilizarlas
En la práctica, rara vez se utiliza el SGD vainilla, en el que los parámetros se actualizan para cada ejemplo de entrenamiento. La razón es que las actualizaciones del algoritmo tienen una varianza demasiado alta, lo que puede hacer que la función de pérdida fluctúe, dificultando la convergencia al mínimo exacto.
El descenso de gradiente regular es potente y proporciona resultados más estables, pero como hemos dicho antes, utiliza todos los puntos de datos en cada paso, lo que lo hace poco práctico para los conjuntos de datos actuales.
Para lograr el equilibrio entre estabilidad y velocidad, se utiliza con frecuencia eldescenso de gradiente por mini lotes, sobre todo en redes neuronales. En la DG mini-lote, en lugar de utilizar una única muestra aleatoria, se utiliza un lote de muestras al realizar las actualizaciones de los parámetros. Los tamaños de lote habituales son 16, 32, 64, etc.
Así, si utilizas un tamaño de lote de 1, entonces tienes SGD. Si el tamaño del lote es igual al tamaño del conjunto de datos, tienes un descenso por gradiente normal. Cualquier tamaño de lote distinto de esos valores te da un descenso por gradiente en mini lotes.
Aquí tienes una tabla que resume sus diferencias y cuándo utilizar cada una:
| Tipo | Frecuencia de actualización | Eficiencia computacional | Requisitos de memoria | Estabilidad de la convergencia | Mejor caso práctico |
| Descenso Gradiente (DG) | Todo el conjunto de datos por actualización | El más lento debido al uso del conjunto de datos completo | Requiere todo el conjunto de datos en memoria | Más estable, pero más lento | Conjuntos de datos pequeños en los que la estabilidad es crucial |
| Descenso Gradiente Estocástico (SGD) | Un ejemplo por actualización | El más rápido, procesa un ejemplo cada vez | Requiere poca memoria | Alta varianza, puede fluctuar | Grandes conjuntos de datos que necesitan actualizaciones rápidas |
| Mini-lote de descenso gradiente | Lote de ejemplos por actualización | Equilibra eficiencia y velocidad, más eficiente que GD, más lento que SGD | Requiere memoria para un lote | Más estable que la SGD, menos estable que la GD | Grandes conjuntos de datos que necesitan un equilibrio entre estabilidad y eficacia |
Épocas en los Algoritmos de Descenso Gradiente
Un concepto importante en cualquier tipo de algoritmo de optimización es una época. Se refiere a una pasada completa por todo el conjunto de datos de entrenamiento.
En una época, el algoritmo procesa cada muestra del conjunto de datos de entrenamiento exactamente una vez. Para cada muestra (o mini lote de muestras), el modelo hace predicciones, calcula la pérdida y actualiza los pesos según el gradiente de la pérdida. Una época marca un ciclo de mejora del modelo. Después de cada época, puedes observar cómo ha cambiado el rendimiento del modelo.
El entrenamiento suele implicar varias épocas (se recomiendan al menos 10). El número de épocas es un hiperparámetro que puedes ajustar. A menudo, los datos se barajan antes de cada época para evitar que el modelo aprenda el orden de los ejemplos de entrenamiento.
En nuestra analogía de la exploración de colinas con los ojos vendados, una época es una exploración completa de todo el paisaje. Durante cada época, tú:
- Toma muestras del terreno en muchos lugares (ejemplos de formación de procesos)
- Da pequeños pasos cuesta abajo basándote en la pendiente local (actualiza los parámetros del modelo)
Después de cada exploración completa, vuelves a empezar desde tu nueva posición. Múltiples épocas dan al modelo repetidas oportunidades de explorar el paisaje de pérdidas, mejorando sus posibilidades de encontrar un buen mínimo.
Sin embargo, las épocas múltiples no garantizan encontrar el mínimo global, y todo el proceso puede verse influido por factores como el punto de partida o la complejidad del paisaje de pérdidas.
SGD en acción: Un ejemplo de recorrido
En esta sección, implementaremos SGD con soporte para tamaño de lote (mini-Lote SGD) utilizando sólo Numpy.
En primer lugar, vamos a importar las bibliotecas necesarias:
import seaborn as sns
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
np.random.seed(42)Utilizaremos 10.000 puntos de datos del conjunto de datos Diamantes disponible en Seaborn. Sólo tomaremos como objetivo la característica quilates y la columna precio:
# Load the data
dataset_size = 10_000
diamonds = sns.load_dataset('diamonds')
# Extract the target and the feature
xy = diamonds[['carat', 'price']].values
np.random.shuffle(xy) # Shuffle the data
xy = xy[:dataset_size]
xy.shape
(10000, 2)Ahora, dividamos los datos en conjuntos de entrenamiento y de prueba, fijando el tamaño del entrenamiento en el 80% del total.
# Split the data
np.random.shuffle(xy)
train_size = int(0.8 * dataset_size)
train_xy, test_xy = xy[:train_size], xy[train_size:]
train_xy.shape
(8000, 2)A continuación, vamos a definir nuestra función modelo:
def model(m, x, b):
"""Simple linear model"""
return m * x + bEstamos haciendo una regresión lineal simple con sólo dos variables independientes m y b.
También debemos definir nuestra función de pérdida MSE:
def loss(y_true, y_pred):
"""Mean squared error"""
return np.mean((y_true - y_pred) ** 2)Ahora definimos una función llamada stochastic_gradient_descent que toma seis argumentos:
xyyrepresentan la característica única y el objetivo en nuestro problemaepochsindica cuántas veces queremos realizar el descenso (más sobre esto más adelante)learning_ratees el tamaño del pasobatch_sizepara controlar la frecuencia con la que actualizamos los parámetrosstopping_thresholdfija el valor mínimo que debe disminuir la pérdida en cada paso
def stochastic_gradient_descent(
x, y, epochs=100, learning_rate=0.01, batch_size=32, stopping_threshold=1e-6
):
"""
SGD with support for mini-batches.
"""Para empezar, inicializamos los parámetros que queremos optimizar con valores aleatorios y fijamos la pérdida en infinito:
# Initialize the model parameters randomly
m = np.random.randn()
b = np.random.randn()
n = len(x) # The number of data points
previous_loss = np.infA continuación, iniciamos un bucle for utilizando el parámetroepochs. Dentro del bucle, barajamos los datos para que los cálculos sean más robustos:
for i in range(epochs):
# Shuffle the data
indices = np.random.permutation(n)
x = x[indices]
y = y[indices]A continuación, se inicia el cálculo del gradiente real dentro de otro bucle for bucle.
for j in range(0, n, batch_size):
x_batch = x[j:j + batch_size]
y_batch = y[j:j + batch_size]Extraemos el lote de x y y y calculamos los gradientes:
# Compute the gradients
y_pred = model(m, x_batch, b)
m_gradient = -2 * np.mean(x_batch * (y_batch - y_pred))
b_gradient = -2 * np.mean(y_batch - y_pred)Utilizamos la función model que creamos anteriormente para hacer una predicción con los valores actuales de m y b. A continuación, hallamos las derivadas parciales que forman el gradiente utilizando la fórmula que hemos indicado en el apartado anterior.
Utilizando las derivadas parciales y la tasa de aprendizaje, actualizamos los parámetros:
# Update the model parameters
m -= learning_rate * m_gradient
b -= learning_rate * b_gradientAquí está el código completo hasta ahora:
def stochastic_gradient_descent(
x, y, epochs=100, learning_rate=0.01, batch_size=32, stopping_threshold=1e-6
):
"""
SGD with support for mini-batches.
"""
# Initialize the model parameters randomly
m = np.random.randn()
b = np.random.randn()
n = len(x)
previous_loss = np.inf
for i in range(epochs):
# Shuffle the data
indices = np.random.permutation(n)
x = x[indices]
y = y[indices]
for j in range(0, n, batch_size):
x_batch = x[j:j + batch_size]
y_batch = y[j:j + batch_size]
# Compute the gradients
y_pred = model(m, x_batch, b)
m_gradient = -2 * np.mean(x_batch * (y_batch - y_pred))
b_gradient = -2 * np.mean(y_batch - y_pred)
# Update the model parameters
m -= learning_rate * m_gradient
b -= learning_rate * b_gradientContinuando la función fuera del bucle interno, calculamos la pérdida de la época:
# Compute the loss
y_pred = model(m, x, b)
current_loss = loss(y, y_pred)Si el current_loss es menor que stopping_threshold detenemos todo el proceso:
if previous_loss - current_loss < stopping_threshold:
break
previous_loss = current_lossEn caso contrario, fijamos previous_loss en current_loss. Al final, devolvemos los parámetros optimizados m y b:
return m, bHe pegado todo el código en este gist de GitHub para que puedas verlo en su totalidad.

Comprobemos lo bien que funcionan los parámetros encontrados ejecutando el modelo en el conjunto de pruebas:
# Find the optimal parameters
m, b = stochastic_gradient_descent(train_xy[:, 0], train_xy[:, 1])
# Make predictions
y_preds = model(m, test_xy[:, 0], b)
# Compute and print the loss
mean_squared_error = loss(test_xy[:, 1], y_preds)
mean_squared_error ** 0.5
1595.3955619759456La raíz cuadrada del MSE es de unos 1.600 $, lo que significa que nuestro modelo se equivoca por término medio en 1.600 $. Para mejorar el error, podemos aumentar el número de épocas o utilizar un conjunto de datos mayor.
Utilización de los DGS en problemas del mundo real
La aplicación del SGD en la última sección es tosca e ineficaz. Simplemente sirve para solidificar la intuición que hemos construido en secciones anteriores con un recorrido de codificación.
En la práctica, casi nunca reimplementas SGD manualmente, sino que utilizas versiones ya disponibles en marcos de trabajo populares.
Por ejemplo, Scikit-learn proporciona SGDRegressor y SGDClassifier estimadores para entrenar varios algoritmos de ML como
- Regresión lineal
- Regresión logística
- Regresión Ridge
- SVMs
con SGD como algoritmo de optimización.
from sklearn.linear_model import SGDRegressor, SGDClassifier
# SGD for Linear Regression with 1000 epochs
regressor = SGDRegressor(loss='squared_loss', max_iter=1000)En PyTorch, está disponible como clase SGD dentro del módulo optim módulo:
import torch.optim as optim
optimizer = optim.SGD(model.parameters(), lr=0.01)Para aprender a entrenar modelos y optimizarlos en PyTorch, consulta el curso Introducción a PyTorch de DataCamp.
En Keras, SGD está disponible con el mismo nombre:
from tensorflow.keras.optimizers import SGD
optimizer = SGD(learning_rate=0.01)Para aprender a entrenar modelos y optimizarlos en TensorFlow, consulta el curso Introducción a TensorFlow de DataCamp.
Trucos y consejos prácticos para utilizar SGD
Hay muchas buenas prácticas y consejos para utilizar SGD o algoritmos similares. A continuación, expondremos algunas de ellas:
1. Mezcla tus datos
- Aleatorizar el orden de los ejemplos de entrenamiento antes de cada época
- Evita los ciclos en la optimización, garantiza lotes diversos
2. Utiliza minilotes
- Equilibrio entre el SGD puro y el descenso de gradiente por lotes
- Tamaños de lote habituales: 32 a 256
3. Normaliza las entradas
- Escala las características a media cero y varianza unitaria
- Garantiza una contribución igual de las características, una convergencia más rápida
4. Elige un ritmo de aprendizaje adecuado
- Empieza por poco (por ejemplo, 0,1, 0,01, 0,001)
- Ajustar en función de los resultados
5. Aplicar programas de ritmo de aprendizaje
- Utiliza el decaimiento de la tasa de aprendizaje con el tiempo
- Opciones: decaimiento escalonado, decaimiento exponencial, decaimiento 1/t
6. Utiliza el impulso
- Añadir el término impulso a las actualizaciones
- Acelera la SGD, amortigua las oscilaciones
7. Considera los métodos de ritmo de aprendizaje adaptativo
- Prueba con Adam, RMSprop o Adagrad
- Ajusta automáticamente las tasas de aprendizaje por parámetro
8. Aplicar recorte de degradado
- Útil para explotar gradientes (por ejemplo, en RNNs)
- Recorta las normas de gradiente al valor máximo
9. Supervisar el rendimiento de la validación
- Comprueba regularmente el rendimiento del conjunto de validación
- Poner en marcha la parada anticipada si es necesario
10. Utiliza la regularización
- Aplicar regularización L1/L2 o abandono
- Evita el sobreajuste, especialmente en modelos grandes
Conclusión
Hoy hemos aprendido uno de los algoritmos de optimización clave en el aprendizaje automático: el Descenso Gradiente Estocástico.
En primer lugar, hemos construido la intuición y sus ideas fundamentales considerando un algoritmo regular de descenso de gradiente. Hemos utilizado mucho la analogía de la ladera en la que intentamos encontrar el fondo con los ojos vendados.
Hemos aprendido que la SGD y la DG normal se diferencian por la cantidad de puntos de datos utilizados al realizar las actualizaciones de los parámetros. Para consolidar nuestra intuición y concretar los detalles matemáticos, hemos implementado SGD en Numpy.
Recuerda que el SGD es sólo una parte de todo el proceso de formación en ML. Para saber más sobre su papel, consulta los siguientes recursos:
Preguntas frecuentes sobre el descenso gradiente estocástico
¿Cuáles son las principales diferencias entre el Descenso Gradiente Estocástico (SGD) y el Descenso Gradiente Mini-Lotes?
El SGD actualiza los parámetros utilizando un punto de datos cada vez, lo que da lugar a actualizaciones más frecuentes pero con mayor varianza. El Descenso Gradiente en Mini-Lotes utiliza un pequeño lote de puntos de datos, equilibrando la frecuencia de actualización y la estabilidad, y suele ser más eficaz para conjuntos de datos más grandes.
¿Cómo elegir la tasa de aprendizaje adecuada para SGD?
Elegir la tasa de aprendizaje adecuada implica experimentar y afinar. Es habitual empezar con un valor pequeño, como 0,01 o 0,001, y ajustarlo en función del rendimiento del modelo. Utilizar programas de velocidad de aprendizaje o métodos de velocidad de aprendizaje adaptativa, como Adam o RMSprop, también puede ayudar a encontrar una velocidad de aprendizaje óptima.
¿Cuáles son los problemas habituales que se plantean al utilizar SGD y cómo pueden mitigarse?
Los problemas más comunes son la alta varianza en las actualizaciones y la dificultad de convergencia. Se pueden mitigar utilizando minilotes, impulso, programas de velocidad de aprendizaje y técnicas como el recorte de gradiente.
¿Puede utilizarse el Descenso Gradiente Estocástico para todos los tipos de problemas de aprendizaje automático?
Aunque el SGD es versátil y puede utilizarse para muchos tipos de problemas, es especialmente adecuado para escenarios a gran escala. Sin embargo, puede no ser ideal para problemas que requieran una gran precisión, debido a sus actualizaciones ruidosas.
¿Cuáles son algunas bibliotecas o marcos populares que implementan SGD para el aprendizaje automático en Python?
Las bibliotecas más populares son Scikit-learn (SGDRegressor, SGDClassifier), TensorFlow (optimizador SGD) y PyTorch (optim.SGD). Estas bibliotecas ofrecen implementaciones eficientes y fáciles de usar del SGD.

