Programa
Imagine que você está tentando encontrar o ponto mais baixo entre as colinas com os olhos vendados. Como você está limitado pelo seu tato, só pode sentir o chão imediatamente ao seu redor para determinar o caminho para baixo. Isso é essencialmente o que os algoritmos de machine learning fazem quando estão tentando encontrar a melhor solução para um problema.
Eles enquadram o problema em uma função matemática cujas entradas e saídas representam uma superfície montanhosa. Encontrar o mínimo dessa função significa que você alcançou a melhor solução para o problema. Um dos algoritmos mais populares para realizar esse processo é o chamado Stochastic Gradient Descent (SGD).
Neste tutorial, você aprenderá tudo o que deve saber sobre o algoritmo, incluindo alguma intuição inicial sem a matemática, os detalhes matemáticos e como implementá-lo em Python.
O que é o Stochastic Gradient Descent? A resposta curta
O Stochastic Gradient Descent (SGD) é uma técnica de otimização usada no machine learning para minimizar erros em modelos preditivos. Diferentemente da descida de gradiente regular, que usa todo o conjunto de dados para calcular o gradiente e atualizar os parâmetros do modelo, o SGD atualiza os parâmetros usando apenas um ponto de dados por vez. Isso o torna mais rápido e mais eficiente para grandes conjuntos de dados, embora possa ser mais ruidoso e menos estável. O SGD ajuda a encontrar os valores ideais dos parâmetros do modelo para melhorar a precisão das previsões.
O que é otimização no machine learning?
A primeira coisa que você precisa entender de imediato é que o gradiente descendente estocástico (SGD) não é um algoritmo de machine learning. Em vez disso, é apenas uma técnica de otimização que pode ser aplicada aos algoritmos de ML.
Então, o que é otimização? Para que você entenda isso, vamos começar pelo estágio de declaração do problema do machine learning.
Digamos que estejamos tentando prever os preços dos diamantes com base no valor do quilate (um quilate equivale a 0,2 gramas). Esse é um problema de regressão, pois o modelo produz valores numéricos.
Para resolver o problema, temos uma grande variedade de algoritmos à nossa disposição, mas vamos escolher Regressão linear simplesque tem a fórmula simples de f(x) = mx + b onde:
bé o preço base do diamantemé o aumento de preço por quilatexé o valor em quilates do diamantef(x)é o preço previsto do diamante
Essa equação linear representa nosso modelo. Nosso objetivo é encontrar os melhores valores para m e b que tornarão nossas previsões tão precisas quanto possível em todos os diamantes do nosso conjunto de dados.
Se tivéssemos outro recurso em nosso conjunto de dados, como o volume do diamante, nossa fórmula mudaria para f(x1, x2) = m1*x1 + m2*x2 + b, onde:
bé o preço base do diamantem1é o aumento de preço por quilatem2é o aumento de preço por unidade de volumex1é o valor em quilates do diamantex2é o volume do diamantef(x)é o preço previsto do diamante
Agora, precisaríamos encontrar os valores ideais para m1, m2, e b.
Em geral, todos os modelos de machine learning têm equações como as acima, com um ou mais parâmetros. Assim, a definição de otimização nesse contexto passa a ser: "Considerando esse modelo e esse conjunto de dados, encontre os valores ideais para os parâmetros da equação."
Há muitos algoritmos de otimização que podem realizar essa tarefa, como o Stochastic Gradient Descent , que é o foco do nosso tutorial. Mas para que você entenda completamente como o SGD funciona, vamos rever algumas ideias fundamentais por trás dele.
O conceito de erro no machine learning
Para entender o SGD, precisamos aprender o algoritmo regular de descida de gradiente (GD), que compartilha muitas das ideias fundamentais por trás de sua versão estocástica. A descida de gradiente simples começa com o conceito de erro no machine learning.
O que é um erro ou perda?
Os algoritmos de ML geralmente adivinham qual é a resposta correta para um problema. Chamamos essa resposta de prediction e ela nem sempre é precisa. Assim, introduzimos um novo termo chamado "erro" ou "perda" que representa a diferença entre a resposta real e a previsão do modelo. Nosso objetivo é criar um modelo que minimize esse erro.
Se o nosso modelo f(x) adivinhar US$ 10.000 para um diamante que na verdade custa US$ 12.000, o erro será de US$ 2.000. Devemos ajustar nosso modelo para diminuir esse erro. Mas as previsões do modelo devem ser boas para qualquer diamante, não apenas para um único. Portanto, precisamos de uma maneira de combinar o erro de todos os diamantes em nosso conjunto de dados. É aqui que entram as funções de custo.
Uma função de custo combina todos os erros individuais em um número que representa o desempenho geral do nosso modelo. Um custo geral menor significa que as previsões do nosso modelo são melhores.
Funções de custo em machine learning
As funções de custo mudam de acordo com o tipo de problema que estamos resolvendo.
Em problemas de regressão, o modelo prevê valores numéricos, como quanto custa um diamante ou quanto tempo você leva para nadar uma volta. Em classificaçãoo modelo prevê a categoria à qual algo pertence. Por exemplo, um cogumelo é comestível ou não, ou o objeto na imagem é um gato, um cachorro ou um cavalo?
Há outros tipos de problemas, mas o ponto importante é que cada um deles exige funções de custo diferentes. Neste tutorial, vamos nos concentrar em Erro médio quadrático (MSE), que é frequentemente usado em regressão.
A diferença entre os valores reais (verdade terrestre) e as previsões do modelo é chamada de erro ou perda. Consequentemente, uma função que combina todos esses erros ou perdas é chamada defunção de erro , função de perdaou função decusto. Fontes diferentes podem usar esses termos de forma intercambiável; neste tutorial, você usará o termofunção de perda a partir de agora.
Erro médio quadrático
Em problemas de regressão, é comum você ver o gráfico a seguir, que plota os valores reais (verdade terrestre) em relação às previsões do modelo.
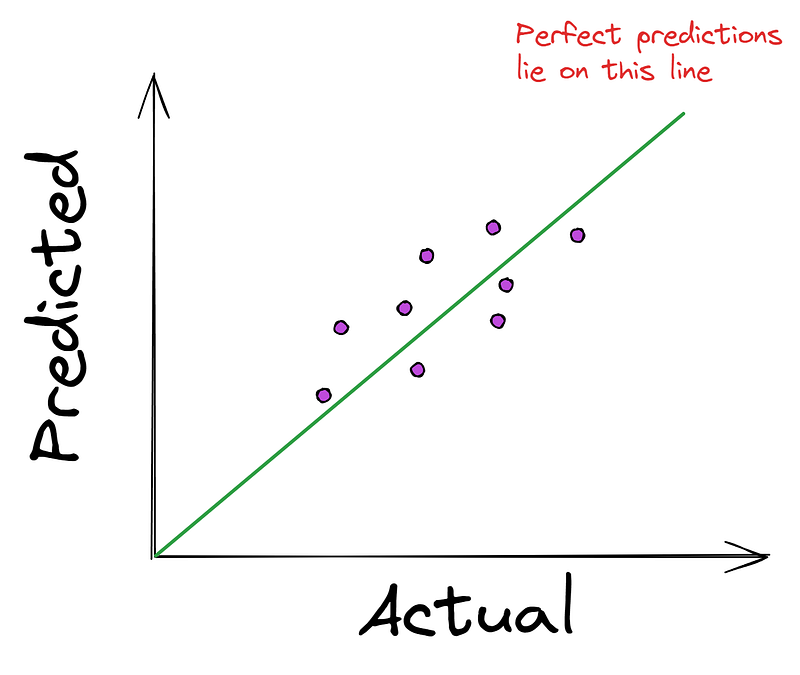
Quanto mais próximos os pontos estiverem da linha reta, melhores serão as previsões do modelo. Portanto, a maioria dos algoritmos de regressão tenta minimizar a distância média dos pontos até a linha perfeita. E, como mencionamos anteriormente, a minimização ocorre usando uma função de custo como o erro quadrático médio (MSE).
O MSE usa os valores reais e previstos como entradas e produz a distância média ao quadrado da linha perfeita.
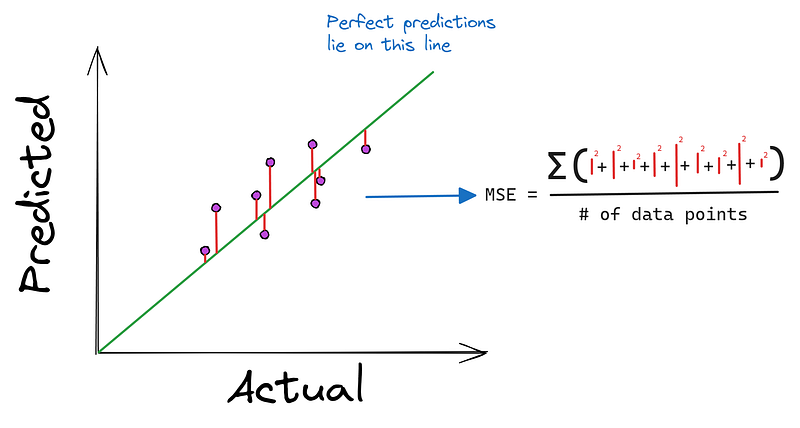
Você pode estar se perguntando: "Por que elevar as diferenças ao quadrado em vez de tomar seu valor absoluto?". O primeiro motivo é que é muito fácil encontrar a derivada de uma função quadrada. Além disso, elevar as diferenças ao quadrado enfatiza erros maiores, penalizando o modelo por suas piores previsões.
É por isso que o MSE é preferido a outras funções alternativas, como o erro absoluto médio (MAE), que, aparentemente, parece mais simples, mas é mais difícil de diferenciar.
O Gradiente
A próxima peça do quebra-cabeça da descida de gradiente é o próprio gradiente. Vamos voltar à nossa analogia "descendo a colina" para entender melhor.
Gradiente como o caminho mais íngreme
Estávamos no topo da colina com os olhos vendados e queríamos chegar à base o mais rápido possível. Se derramássemos água em nossos pés, para que lado ela fluiria? Ele fluiria para baixo na direção da descida mais íngreme.
Isso é exatamente o que o gradiente nos diz, mas na direção oposta. O gradiente aponta para cima, na direção da subida mais íngreme. Quando estamos tentando minimizar o erro, simplesmente vamos na direção oposta do gradiente para encontrar o caminho mais rápido para baixo.
Matematicamente, o gradiente nos informa como os resultados de uma função mudam à medida que alteramos suas entradas. Mais especificamente, ele nos indica a direção em que a função aumenta mais rapidamente.
No contexto do machine learning, em que estamos tentando minimizar o erro usando uma função de perda, o gradiente se torna nosso guia para encontrar o caminho mais rápido para reduzir esse erro.
O gradiente é representado como um vetor - um para cada parâmetro de entrada da nossa função. Cada número nesse vetor nos informa o quanto a função mudaria se fizéssemos um pequeno ajuste no parâmetro correspondente.
Como encontrar o gradiente de uma função
Então, como você encontra o gradiente de uma função?
Para funções de variável única, como f(x) = x ** 2o gradiente é a derivada da função, que é dada como um vetor com um elemento - [2x].
Para funções multivariáveis, como f(x1, x2) = x1 ** 3 - x2 ** 2, o gradiente contém as derivadas parciais da função em relação a cada entrada. Portanto, para a segunda função, o vetor de gradiente é [3x1 ** 2, 2*x2].
Voltando ao MSE, que tem a seguinte fórmula:
MSE = (1/n) * Σ(y - f(x))² onde:
f(x)émx + bme b são variáveis de funçãoxé o valor em quilates dos diamantesné o número de pontos de dadosyé o preço real dos diamantes
Portanto, seu gradiente é a derivada parcial de MSE com relação a m e b:
∂/∂m (MSE) = (-2/n) * Σ(x * (y - (mx + b)))
∂/∂b (MSE) = (-2/n) * Σ(y - (mx + b))
The gradient = [∂/∂m (MSE), ∂/∂b (MSE)]Não se preocupe muito com essas fórmulas. A ideia principal é que eles nos informam como o erro quadrático médio muda se alterarmos m ou b um pouquinho.
Descida de gradiente: Dando passos em direção à solução
Taxa de aprendizado: controle do tamanho da etapa
Agora, temos tudo o que precisamos para executar a descida do gradiente ou, em outras palavras, chegar ao fundo da colina da forma mais eficiente possível. Mas será que vamos pular nessa direção ou dar pequenos passos? Bem, isso é determinado pelo gradiente, não é? O tamanho do gradiente nos informa o quanto descemos em cada etapa.
Mas suponha que o gradiente seja tão grande que, em vez de chegarmos ao fundo, saltamos e acabamos no topo de outra colina em um único passo. Surpreendentemente, isso acontece muito na descida do gradiente, por isso introduzimos um parâmetro chamado tamanho da etapa, que controla os efeitos do gradiente.
Antes de dar um passo, simplesmente multiplicamos o gradiente pelo tamanho do passo, o que reduz sua magnitude. Por exemplo, se o nosso gradiente nos diz para dar um passo de 3,56 para baixo, um tamanho de passo de 0,1 transforma a distância em 0,356.
Levará mais tempo para chegarmos ao fundo, mas agora não corremos o risco de ignorá-lo completamente.
O tamanho da etapa é geralmente chamado de taxa de aprendizado no machine learning e, normalmente, assume valores entre 0,001 e 0,3.
Então, vamos ver a versão matemática desse processo.
Dar pequenos passos matematicamente
Primeiro, fornecemos m e b os parâmetros do nosso modelo, valores aleatórios:
m = 0.215 # Generated randomly
b = 0.059Com isso, calculamos o MSE inicial em todo o conjunto de dados:
MSE = (1/n) * Σ(y - (0.215 * x + 0.059))² = ...Agora, para reduzir esse erro, precisamos dar um pequeno passo na direção oposta do gradiente ou, em outras palavras, precisamos atualizar m e b usando o gradiente e a taxa de aprendizado:
m_new = 0.215 - alpha * (∂/∂m (MSE))
b_new = 0.059 - alpha * (∂/∂b (MSE))A maioria dos recursos escolhe alpha ou α (a letra grega) para indicar a taxa de aprendizado.
Depois que tivermos novos valores para m e bcalculamos novamente o MSE:
MSE_new = (1/n) * Σ(y - (m_new * x + b_new))²Agora, calculamos o gradiente novamente e continuamos dessa forma até atingirmos uma condição de parada.
Para saber como a taxa de aprendizado afeta o treinamento visualmente, confira este artigo sobre descida de gradiente.
Saber quando parar
Como estamos com os olhos vendados, não podemos realmente ver quando chegamos ao fundo do poço, especialmente quando damos pequenos passos.
Portanto, precisamos de algumas condições para interromper nossa descida. Normalmente, essas regras são usadas:
- Atingir um número predeterminado de etapas (máximo de etapas ou iterações)
- A alteração no MSE torna-se muito pequena após cada etapa (abaixo de um limite predefinido)
- O gradiente fica muito próximo de zero (indicando que estamos na base da colina ou perto dela)
- O MSE começa a aumentar em vez de diminuir
Essas regras são definidas por você, o engenheiro de ML, quando estiver executando a descida de gradiente. As implementações do algoritmo em Python geralmente têm argumentos para definir essas regras, e veremos alguns deles mais tarde.
Vantagens e desafios da descida de gradiente
Vantagens:
- É um algoritmo simples e intuitivo
- Ele funciona bem em uma ampla gama de problemas
- É computacionalmente eficiente para problemas com muitos parâmetros
Desafios:
- Ele pode ser lento para conjuntos de dados muito grandes
- Ele pode ficar preso em mínimos locais para problemas não convexos
- A escolha da taxa de aprendizado correta pode ser complicada
Na próxima seção, veremos como o Stochastic Gradient Descent aborda alguns desses desafios, principalmente para grandes conjuntos de dados.
Descida de gradiente estocástica
Depois que você entender a descida de gradiente regular, o SGD se tornará muito fácil de entender.
O problema com a descida de gradiente regular
Embora o gradiente descendente seja um dos algoritmos de otimização mais elegantes que existem, ele tem uma desvantagem significativa ao lidar com grandes conjuntos de dados. Lembre-se de que, em cada etapa, calculamos o gradiente usando todos os pontos de dados em nosso conjunto de dados:
∂/∂m (MSE) = (-2/n) * Σ(x * (y - (mx + b)))
∂/∂b (MSE) = (-2/n) * Σ(y - (mx + b))Aqui, x e y são matrizes que contêm todos os valores em quilates e os preços reais dos diamantes. Isso significa que estaríamos usando as informações de cada diamante para atualizar os parâmetros em cada etapa.
Como você pode imaginar, isso se torna computacionalmente caro e demorado quando temos milhões de pontos de dados. Na era do big data, essa limitação pode tornar a descida de gradiente regular impraticável para muitos problemas de machine learning do mundo real.
A abordagem estocástica: introduzindo a aleatoriedade
"Estocástico" significa "determinado aleatoriamente", e é exatamente isso que o SGD faz: ele introduz a aleatoriedade em nosso processo de otimização.
Em vez de usar todos os pontos de dados para calcular o gradiente, o SGD seleciona aleatoriamente um ponto de dados em cada etapa. Ele usa esse único ponto para calcular uma estimativa do gradiente e atualizar os parâmetros.
Como o SGD analisa apenas um ponto de dados por vez, ele pode fazer atualizações mais frequentes nos parâmetros. Isso permite que você percorra a superfície de erro (a colina) mais rapidamente, especialmente em grandes conjuntos de dados.
No entanto, essa velocidade tem um custo. Como estamos usando um único ponto de dados para estimar o gradiente de todo o conjunto de dados, nossas estimativas são muito mais ruidosas. Isso significa que nosso caminho na superfície de erro é menos suave e mais irregular.
A matemática por trás do Stochastic Gradient Descent
Para realizar o SGD, primeiro definimos uma função de custo estocástica.
Em vez de calcular o erro quadrático médio de todos os pontos de dados, agora analisamos o erro quadrático de um único ponto escolhido aleatoriamente:
Cost = (y - f(x))²Onde y é o preço real do diamante escolhido aleatoriamente, e f(x) = mx + b é o nosso preço previsto para esse diamante.
Em seguida, calculamos o gradiente estocástico dessa função de custo em relação aos nossos parâmetros m e b:
∂/∂m (Cost) = -2x(y - (mx + b))
∂/∂b (Cost) = -2(y - (mx + b))
The stochastic gradient = [∂/∂m (Cost), ∂/∂b (Cost)]Usando esse gradiente estocástico, atualizamos nossos parâmetros da mesma forma que a descida de gradiente regular:
m_new = m_old - learning_rate * ∂/∂m (Cost)
b_new = b_old - learning_rate * ∂/∂b (Cost)A ideia principal do SGD é que cada etapa envolve um único ponto de dados escolhido aleatoriamente. As regras de quando interromper a descida permanecem as mesmas da descida de gradiente regular.
Variações de SGD e quando usá-las
Na prática, o vanilla SGD, em que os parâmetros são atualizados para cada exemplo de treinamento, raramente é usado. O motivo é que as atualizações do algoritmo têm uma variação muito alta, o que pode fazer com que a função de perda flutue, dificultando a convergência para o mínimo exato.
A descida de gradiente regular é poderosa e fornece resultados mais estáveis, mas, como mencionamos anteriormente, ela usa todos os pontos de dados em cada etapa, o que a torna impraticável para os conjuntos de dados atuais.
Para atingir o equilíbrio entre estabilidade e velocidade, ogradiente de descida em mini-lotes é usado com frequência, especialmente em redes neurais. No GD em mini-lote, em vez de usar uma única amostra aleatória, umlote de amostras é usado ao fazer atualizações de parâmetros. Os tamanhos comuns de lotes incluem 16, 32, 64 e assim por diante.
Portanto, se você usar um tamanho de lote de 1, terá SGD. Se o tamanho do lote for igual ao tamanho do conjunto de dados, você terá uma descida gradiente regular. Qualquer tamanho de lote diferente desses valores dá a você uma descida de gradiente em mini-lote.
Aqui está uma tabela que resume suas diferenças e quando você deve usar cada uma delas:
| Tipo | Frequência de atualização | Eficiência computacional | Requisitos de memória | Estabilidade da convergência | Melhor caso de uso |
| Descida de gradiente (GD) | Todo o conjunto de dados por atualização | Mais lento devido ao uso do conjunto de dados completo | Requer todo o conjunto de dados na memória | Mais estável, mas mais lento | Conjuntos de dados pequenos em que a estabilidade é crucial |
| Descida de Gradiente Estocástico (SGD) | Um exemplo por atualização | O mais rápido, processa um exemplo por vez | Baixa necessidade de memória | Alta variação, pode flutuar | Grandes conjuntos de dados que precisam de atualizações rápidas |
| Descida de gradiente em minibatelada | Lote de exemplos por atualização | Equilibra eficiência e velocidade, mais eficiente que o GD, mais lento que o SGD | Requer memória para um lote | Mais estável que o SGD, menos estável que o GD | Grandes conjuntos de dados que precisam de um equilíbrio entre estabilidade e eficiência |
Épocas em algoritmos de gradiente descendente
Um conceito importante em qualquer tipo de algoritmo de otimização é uma época. Refere-se a uma passagem completa por todo o conjunto de dados de treinamento.
Em uma época, o algoritmo processa cada amostra do conjunto de dados de treinamento exatamente uma vez. Para cada amostra (ou mini-lote de amostras), o modelo faz previsões, calcula a perda e atualiza os pesos de acordo com o gradiente da perda. Uma época marca um ciclo de aprimoramento do modelo. Após cada época, você pode observar normalmente como o desempenho do modelo mudou.
O treinamento geralmente envolve várias épocas (recomenda-se pelo menos 10). O número de épocas é um hiperparâmetro que você pode ajustar. Muitas vezes, os dados são embaralhados antes de cada época para evitar que o modelo aprenda a ordem dos exemplos de treinamento.
Em nossa analogia de exploração de colinas com os olhos vendados, uma época é uma exploração completa de todo o cenário. Durante cada época, você:
- Faça amostragem do solo em vários locais (exemplos de treinamento de processos)
- Dê pequenos passos para baixo com base na inclinação local (atualize os parâmetros do modelo)
Após cada exploração completa, você recomeça a partir de sua nova posição. Várias épocas dão ao modelo oportunidades repetidas de explorar o cenário de perdas, aumentando suas chances de encontrar um bom mínimo.
No entanto, várias épocas não garantem que você encontre o mínimo global, e todo o processo pode ser influenciado por fatores como o ponto de partida ou a complexidade do cenário de perdas.
SGD em ação: Um exemplo de passo a passo
Nesta seção, implementaremos o SGD com suporte para o tamanho do lote (GD em mini-lote) usando apenas o Numpy.
Primeiro, vamos importar as bibliotecas necessárias:
import seaborn as sns
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
np.random.seed(42)Usaremos 10.000 pontos de dados do conjunto de dados Diamonds disponível no Seaborn. Consideraremos apenas o recurso de quilates e a coluna de preço como alvo:
# Load the data
dataset_size = 10_000
diamonds = sns.load_dataset('diamonds')
# Extract the target and the feature
xy = diamonds[['carat', 'price']].values
np.random.shuffle(xy) # Shuffle the data
xy = xy[:dataset_size]
xy.shape
(10000, 2)Agora, vamos dividir os dados em conjuntos de treinamento e teste, definindo o tamanho do treinamento como 80% do total.
# Split the data
np.random.shuffle(xy)
train_size = int(0.8 * dataset_size)
train_xy, test_xy = xy[:train_size], xy[train_size:]
train_xy.shape
(8000, 2)Em seguida, vamos definir nossa função de modelo:
def model(m, x, b):
"""Simple linear model"""
return m * x + bEstamos fazendo uma regressão linear simples com apenas duas variáveis independentes m e b.
Também devemos definir nossa função de perda MSE:
def loss(y_true, y_pred):
"""Mean squared error"""
return np.mean((y_true - y_pred) ** 2)Agora, definimos uma função chamada stochastic_gradient_descent que recebe seis argumentos:
xeyrepresentam o recurso único e o alvo em nosso problemaepochsindica quantas vezes queremos executar a descida (mais sobre isso mais tarde)learning_rateé o tamanho da etapabatch_sizepara controlar a frequência com que fazemos atualizações de parâmetrosstopping_thresholddefine o valor mínimo que a perda deve diminuir em cada etapa
def stochastic_gradient_descent(
x, y, epochs=100, learning_rate=0.01, batch_size=32, stopping_threshold=1e-6
):
"""
SGD with support for mini-batches.
"""Para começar, inicializamos os parâmetros que queremos otimizar com valores aleatórios e definimos a perda como infinita:
# Initialize the model parameters randomly
m = np.random.randn()
b = np.random.randn()
n = len(x) # The number of data points
previous_loss = np.infEm seguida, iniciamos um loop for usando o parâmetroepochs. Dentro do loop, embaralhamos os dados para tornar os cálculos mais robustos:
for i in range(epochs):
# Shuffle the data
indices = np.random.permutation(n)
x = x[indices]
y = y[indices]Em seguida, o cálculo real do gradiente começa em outro for loop.
for j in range(0, n, batch_size):
x_batch = x[j:j + batch_size]
y_batch = y[j:j + batch_size]Extraímos o lote de x e y e calculamos os gradientes:
# Compute the gradients
y_pred = model(m, x_batch, b)
m_gradient = -2 * np.mean(x_batch * (y_batch - y_pred))
b_gradient = -2 * np.mean(y_batch - y_pred)Usamos a função model que criamos acima para fazer uma previsão com os valores atuais de m e b. Em seguida, encontramos as derivadas parciais que compõem o gradiente usando a fórmula que indicamos na seção anterior.
Usando as derivadas parciais e a taxa de aprendizado, atualizamos os parâmetros:
# Update the model parameters
m -= learning_rate * m_gradient
b -= learning_rate * b_gradientAqui está o código completo até o momento:
def stochastic_gradient_descent(
x, y, epochs=100, learning_rate=0.01, batch_size=32, stopping_threshold=1e-6
):
"""
SGD with support for mini-batches.
"""
# Initialize the model parameters randomly
m = np.random.randn()
b = np.random.randn()
n = len(x)
previous_loss = np.inf
for i in range(epochs):
# Shuffle the data
indices = np.random.permutation(n)
x = x[indices]
y = y[indices]
for j in range(0, n, batch_size):
x_batch = x[j:j + batch_size]
y_batch = y[j:j + batch_size]
# Compute the gradients
y_pred = model(m, x_batch, b)
m_gradient = -2 * np.mean(x_batch * (y_batch - y_pred))
b_gradient = -2 * np.mean(y_batch - y_pred)
# Update the model parameters
m -= learning_rate * m_gradient
b -= learning_rate * b_gradientContinuando a função fora do loop interno, calculamos a perda para a época:
# Compute the loss
y_pred = model(m, x, b)
current_loss = loss(y, y_pred)Se o current_loss for menor que o stopping_threshold interromperemos todo o processo:
if previous_loss - current_loss < stopping_threshold:
break
previous_loss = current_lossCaso contrário, defin imosprevious_loss como current_loss. No final, retornamos os parâmetros otimizados m e b:
return m, bColei o código inteiro em neste gist do GitHub para que você possa ver o quadro completo.

Vamos testar se os parâmetros encontrados funcionam bem executando o modelo no conjunto de teste:
# Find the optimal parameters
m, b = stochastic_gradient_descent(train_xy[:, 0], train_xy[:, 1])
# Make predictions
y_preds = model(m, test_xy[:, 0], b)
# Compute and print the loss
mean_squared_error = loss(test_xy[:, 1], y_preds)
mean_squared_error ** 0.5
1595.3955619759456A raiz quadrada do MSE é de cerca de US$ 1.600, o que significa que nosso modelo está errado em US$ 1.600, em média. Para melhorar o erro, podemos aumentar o número de épocas ou usar um conjunto de dados maior.
Uso do SGD em problemas do mundo real
A implementação do SGD na última seção é rudimentar e ineficiente. Ele serve apenas para solidificar a intuição que construímos nas seções anteriores com um passo a passo de codificação.
Na prática, você quase nunca reimplementa o SGD manualmente, mas usa versões já disponíveis em estruturas populares.
Por exemplo, o Scikit-learn fornece SGDRegressor e SGDClassifier para treinar vários algoritmos de ML, como:
- Regressão linear
- Regressão logística
- Regressão Ridge
- SVMs
com o SGD como algoritmo de otimização.
from sklearn.linear_model import SGDRegressor, SGDClassifier
# SGD for Linear Regression with 1000 epochs
regressor = SGDRegressor(loss='squared_loss', max_iter=1000)No PyTorch, ele está disponível como a classe SGD dentro do módulo optim módulo:
import torch.optim as optim
optimizer = optim.SGD(model.parameters(), lr=0.01)Para aprender a treinar modelos e otimizá-los no PyTorch, consulte o curso Introdução ao PyTorch da DataCamp.
No Keras, o SGD está disponível com o mesmo nome:
from tensorflow.keras.optimizers import SGD
optimizer = SGD(learning_rate=0.01)Para aprender a treinar modelos e otimizá-los no TensorFlow, consulte o curso Introdução ao TensorFlow da DataCamp.
Dicas e truques práticos ao usar SGD
Há muitas práticas recomendadas e dicas para usar o SGD ou algoritmos semelhantes. A seguir, descreveremos algumas delas:
1. Embaralhe seus dados
- Randomizar a ordem dos exemplos de treinamento antes de cada época
- Evita ciclos na otimização e garante lotes diversificados
2. Use mini-lotes
- Equilíbrio entre SGD puro e descida de gradiente em lote
- Tamanhos comuns de lotes: 32 a 256
3. Normalizar entradas
- Dimensione os recursos para média zero e variância unitária
- Garante a contribuição igualitária de recursos, convergência mais rápida
4. Escolha a taxa de aprendizado adequada
- Comece pequeno (por exemplo, 0,1, 0,01, 0,001)
- Ajustar com base no desempenho
5. Implementar cronogramas de taxa de aprendizado
- Usar o decaimento da taxa de aprendizado ao longo do tempo
- Opções: decaimento em etapas, decaimento exponencial, decaimento 1/t
6. Use o impulso
- Adicionar o termo momentum às atualizações
- Acelera o SGD, amortece as oscilações
7. Considere os métodos de taxa de aprendizado adaptável
- Experimente o Adam, o RMSprop ou o Adagrad
- Ajusta automaticamente as taxas de aprendizagem por parâmetro
8. Aplicar recorte de gradiente
- Útil para a explosão de gradientes (por exemplo, em RNNs)
- Cortar normas de gradiente para o valor máximo
9. Monitorar o desempenho da validação
- Verificar regularmente o desempenho do conjunto de validação
- Implemente a interrupção antecipada, se necessário
10. Use a regularização
- Aplique a regularização L1/L2 ou o abandono
- Evita o ajuste excessivo, especialmente em modelos grandes
Conclusão
Hoje, aprendemos um dos principais algoritmos de otimização em machine learning: o Stochastic Gradient Descent.
Primeiro, desenvolvemos a intuição e suas ideias fundamentais ao considerar um algoritmo de descida de gradiente regular. Usamos muito a analogia de uma encosta em que estamos tentando encontrar o fundo com os olhos vendados.
Aprendemos que o SGD e o GD regular diferem na quantidade de pontos de dados usados para fazer atualizações de parâmetros. Para solidificar nossa intuição e detalhar os detalhes matemáticos, implementamos o SGD no Numpy.
Lembre-se de que o SGD é apenas parte de todo o processo de treinamento de ML. Para saber mais sobre sua função, confira os recursos a seguir:
Perguntas frequentes sobre a descida de gradiente estocástico
Quais são as principais diferenças entre o Stochastic Gradient Descent (SGD) e o Mini-Batch Gradient Descent?
O SGD atualiza os parâmetros usando um ponto de dados de cada vez, o que resulta em atualizações mais frequentes, mas com maior variação. O Mini-Batch Gradient Descent usa um pequeno lote de pontos de dados, equilibrando a frequência de atualização e a estabilidade, e geralmente é mais eficiente para conjuntos de dados maiores.
Como você escolhe a taxa de aprendizagem correta para SGD?
A escolha da taxa de aprendizado correta envolve experimentação e ajuste. É comum você começar com um valor pequeno, como 0,01 ou 0,001, e ajustá-lo com base no desempenho do modelo. O uso de programações de taxa de aprendizagem ou de métodos de taxa de aprendizagem adaptável, como Adam ou RMSprop, também pode ajudar a encontrar uma taxa de aprendizagem ideal.
Quais são os problemas comuns enfrentados ao usar o SGD e como eles podem ser atenuados?
Os problemas comuns incluem alta variação nas atualizações e dificuldade de convergência. Isso pode ser atenuado com o uso de minilotes, momentum, programações de taxa de aprendizado e técnicas como o recorte de gradiente.
O Stochastic Gradient Descent pode ser usado para todos os tipos de problemas de machine learning?
Embora o SGD seja versátil e possa ser usado para muitos tipos de problemas, ele é particularmente adequado para cenários de grande escala. No entanto, ele pode não ser ideal para problemas que exigem alta precisão devido a suas atualizações com ruído.
Quais são algumas bibliotecas ou estruturas populares que implementam SGD para machine learning em Python?
As bibliotecas populares incluem Scikit-learn (SGDRegressor, SGDClassifier), TensorFlow (otimizador SGD) e PyTorch (optim.SGD). Essas bibliotecas oferecem implementações eficientes e fáceis de usar do SGD.

