Cours
La préparation rigoureuse de vos données est essentielle, à la fois pour la performance des modèles et pour l’interprétation des résultats. C’est précisément là qu’interviennent la normalisation et la standardisation : deux techniques fondamentales de mise à l’échelle des caractéristiques, utilisées soit pour améliorer les performances, soit pour faciliter l’analyse des résultats.
Dans cet article, je vais vous présenter ces notions et mettre en lumière leurs différences pratiques. À la fin, vous saurez quand utiliser la normalisation et quand privilégier la standardisation dans vos flux de prétraitement des données. En vous familiarisant avec ces deux approches, vous augmenterez la performance de vos modèles, interpréterez mieux vos résultats et éviterez les erreurs fréquentes liées à des données non mises à l’échelle. Ces différences, parfois subtiles, sont pourtant déterminantes dans le domaine de l’apprentissage automatique. Si vous souhaitez sérieusement devenir expert, inscrivez-vous dès aujourd’hui à notre cursus Scientifique en apprentissage automatique en Python.
Devenez un scientifique ML
Comprendre la mise à l'échelle des caractéristiques
La normalisation et la standardisation appartiennent toutes deux à la catégorie de la mise à l’échelle des caractéristiques (feature scaling). La mise à l’échelle constitue une étape essentielle dans la préparation des données pour les modèles d’apprentissage automatique. Elle consiste à transformer les valeurs des variables d’un jeu de données afin de les ramener à une échelle comparable, garantissant ainsi que chaque caractéristique contribue de manière équitable au processus d’apprentissage du modèle.
La mise à l’échelle est particulièrement importante lorsque les caractéristiques se situent sur des échelles très différentes — par exemple, une variable comprise entre 1 et 10 et une autre entre 1 000 et 10 000. Dans ce cas, les modèles ont tendance à privilégier les valeurs les plus grandes, ce qui introduit des biais dans les prédictions. Cela peut nuire à la performance globale et ralentir la convergence lors de l’entraînement.
La mise à l’échelle permet de résoudre ce problème en ajustant l’amplitude des données sans en déformer les différences relatives. Parmi les différentes méthodes disponibles, la normalisation et la standardisation sont les plus couramment utilisées. Ces deux techniques aident les modèles d’apprentissage automatique à fonctionner de façon optimale, en équilibrant l’impact des variables, en réduisant l’influence des valeurs aberrantes et, dans certains cas, en améliorant la vitesse de convergence.
Qu'est-ce que la normalisation ?
La normalisation est une notion large, et il existe différentes façons de normaliser les données. De manière générale, la normalisation désigne le processus qui consiste à ajuster des valeurs mesurées sur des échelles différentes pour les ramener à une échelle commune. Parfois, il est préférable d’illustrer par un exemple. Pour chaque type de normalisation ci-dessous, nous considérerons un modèle permettant de comprendre la relation entre le prix d’une maison et sa taille.
Types de normalisation
Examinons quelques-uns des principaux types. N'oubliez pas qu'il ne s'agit pas d'une liste exhaustive :
Normalisation min-max
Avec la normalisation min-max, nous pourrions réévaluer la taille des maisons pour qu'elle se situe dans une fourchette de 0 à 1. Cela signifie que la plus petite taille de maison sera représentée par 0, et la plus grande taille de maison par 1.
Normalisation logarithmique
La normalisation logarithmique est une autre technique de normalisation. En utilisant la normalisation logarithmique, nous appliquons une transformation logarithmique aux prix des logements. Cette technique permet de réduire l'impact des prix les plus élevés, en particulier s'il existe des différences significatives entre eux.
Échelle décimale
L'échelle décimale est une autre technique de normalisation. Pour cet exemple, nous pourrions ajuster la taille des maisons en déplaçant la virgule pour rendre les valeurs plus petites. Cela signifie que la taille des maisons est ramenée à une échelle plus raisonnable tout en conservant leurs différences relatives.
Normalisation de la moyenne (centrage sur la moyenne)
La normalisation de la moyenne, dans ce contexte, consisterait à ajuster les prix des maisons en soustrayant le prix moyen du prix de chaque maison. Ce processus centre les prix à zéro, montrant comment la taille de chaque maison se compare à la moyenne. Ce faisant, nous pouvons analyser quelles tailles de maisons sont plus grandes ou plus petites que la moyenne, ce qui facilite l'interprétation de leurs prix relatifs.
Quand faut-il normaliser les données ?
Comme vous l'avez peut-être déduit des exemples ci-dessus, la normalisation est particulièrement utile lorsque la distribution des données est inconnue ou ne suit pas une distribution gaussienne. Les prix de l'immobilier sont un bon exemple, car certaines maisons sont très, très chères, et les modèles ne traitent pas toujours bien les valeurs aberrantes.
L'objectif de la normalisation est donc de créer un meilleur modèle. Nous pourrions normaliser la variable dépendante afin que les erreurs soient réparties plus uniformément, ou bien nous pourrions normaliser les variables d'entrée afin de nous assurer que les caractéristiques à grande échelle ne dominent pas celles à plus petite échelle.
La normalisation est la plus efficace dans les scénarios suivants :
- Distribution inconnue ou non gaussienne: Lorsque la distribution des données n'est pas connue ou ne suit pas un modèle normal (gaussien). Par exemple, dans le cas d'une régression linéaire, nous pouvons vouloir normaliser la variable dépendante pour qu'elle ressemble davantage à une courbe en cloche, ce qui nous permet d'avoir une meilleure confiance dans nos estimations.
- Algorithmes basés sur la distance: La normalisation est nécessaire lors de l'utilisation d'algorithmes d'apprentissage automatique qui s'appuient sur les distances entre les points de données, tels que les k-voisins les plus proches (k-NN), afin d'éviter que les caractéristiques à grande échelle ne dominent les calculs de distance.
Qu'est-ce que la standardisation ?
Alors que la normalisation met les caractéristiques à l'échelle d'un intervalle spécifique, la standardisation, également appelée mise à l'échelle du score z, transforme les données de manière à ce qu'elles aient une moyenne de 0 et un écart type de 1. Ce processus ajuste les valeurs des caractéristiques en soustrayant la moyenne et en divisant par l'écart type. Vous avez peut-être entendu parler de "centrer et mettre à l'échelle" les données. La standardisation renvoie à la même chose : d'abord le centrage, puis la mise à l'échelle.
La formule de la standardisation est la suivante :
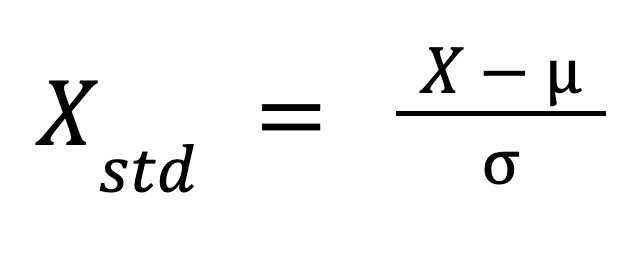
Où ?
- X est la valeur originale,
- mu est la moyenne de la caractéristique, et
- sigma est l'écart-type de la caractéristique.
Cette formule redimensionne les données de manière à ce que leur distribution ait une moyenne de 0 et un écart-type de 1.
Quand devez-vous standardiser des données ?
La standardisation est la plus appropriée dans les cas suivants :
- Algorithmes basés sur le gradient: La machine à vecteurs de support (SVM) nécessite des données standardisées pour une performance optimale. Bien que les modèles tels que la régression linéaire et la régression logistique ne supposent pas de standardisation, ils peuvent tout de même en bénéficier, en particulier lorsque les caractéristiques varient considérablement en termes d'ampleur, ce qui permet de garantir des contributions équilibrées de chaque caractéristique et d'améliorer l'optimisation.
- Réduction de la dimensionnalité: La standardisation se fait par des techniques de réduction de la dimensionnalité telles que l'ACP, car l'ACP identifie la direction dans laquelle la variance des données est maximisée. La normalisation de la moyenne seule n'est pas suffisante car l'ACP prend en compte à la fois la moyenne et la variance, et des échelles de caractéristiques différentes fausseraient l'analyse.
Normalisation vs. Standardisation : Principales différences
Il est parfois difficile de faire la distinction entre normalisation et standardisation. D'une part, la normalisation est parfois utilisée comme un terme plus général, alors que la standardisation a un sens un peu plus spécifique ou spécifiquement technique. En outre, les analystes et les scientifiques des données qui sont familiarisés avec les termes peuvent encore avoir du mal à distinguer les cas d'utilisation.
Bien qu'il s'agisse dans les deux cas de techniques de mise à l'échelle des caractéristiques, elles diffèrent dans leurs approches et leurs applications. Il est essentiel de comprendre ces différences pour choisir la bonne technique pour votre modèle d'apprentissage automatique.
Méthodes de remise à l'échelle
La normalisation redéfinit les valeurs des caractéristiques dans une fourchette prédéfinie, souvent comprise entre 0 et 1, ce qui est particulièrement utile pour les modèles dans lesquels l'échelle des caractéristiques varie considérablement. En revanche, la standardisation centre les données autour de la moyenne (0) et les échelonne en fonction de l'écart-type (1).
Sensibilité aux valeurs aberrantes
Les différentes techniques de normalisation n'ont pas toutes la même efficacité dans le traitement des valeurs aberrantes. La normalisation de la moyenne peut permettre de corriger les valeurs aberrantes dans certains scénarios, mais d'autres techniques peuvent ne pas être aussi efficaces. En général, les techniques de normalisation ne traitent pas le problème des valeurs aberrantes aussi efficacement que la standardisation, car cette dernière s'appuie explicitement sur la moyenne et l'écart-type.
Cas d'utilisation
La normalisation est largement utilisée dans les algorithmes basés sur la distance, tels que les k-voisins les plus proches (k-NN), où les caractéristiques doivent être à la même échelle pour garantir la précision des calculs de distance. La standardisation, en revanche, est essentielle pour les algorithmes basés sur le gradient tels que les machines à vecteurs de support (SVM) et est fréquemment appliquée dans les techniques de réduction de la dimensionnalité telles que l'ACP, où le maintien de la variance correcte des caractéristiques est important.
Tableau récapitulatif des différences
Examinons toutes ces différences essentielles dans un tableau récapitulatif afin de faciliter la comparaison entre normalisation et standardisation :
| Catégorie | Normalisation | Standardisation |
|---|---|---|
| Méthode de remise à l'échelle | Met les données à l'échelle d'une plage (généralement de 0 à 1) sur la base des valeurs minimales et maximales. | Centre les données autour de la moyenne (0) et les échelonne en fonction de l'écart-type (1). |
| Sensibilité aux valeurs aberrantes | La normalisation peut aider à corriger les valeurs aberrantes si elle est utilisée correctement, en fonction de la technique. | La standardisation est une approche plus cohérente pour résoudre les problèmes de valeurs aberrantes. |
| Algorithmes courants | Souvent appliqué dans des algorithmes tels que k-NN et les réseaux neuronaux qui exigent que les données soient à une échelle cohérente. | Convient le mieux aux algorithmes qui exigent que les caractéristiques aient une échelle commune, tels que la régression logistique, le SVM et l'ACP. |
Visualiser les différences
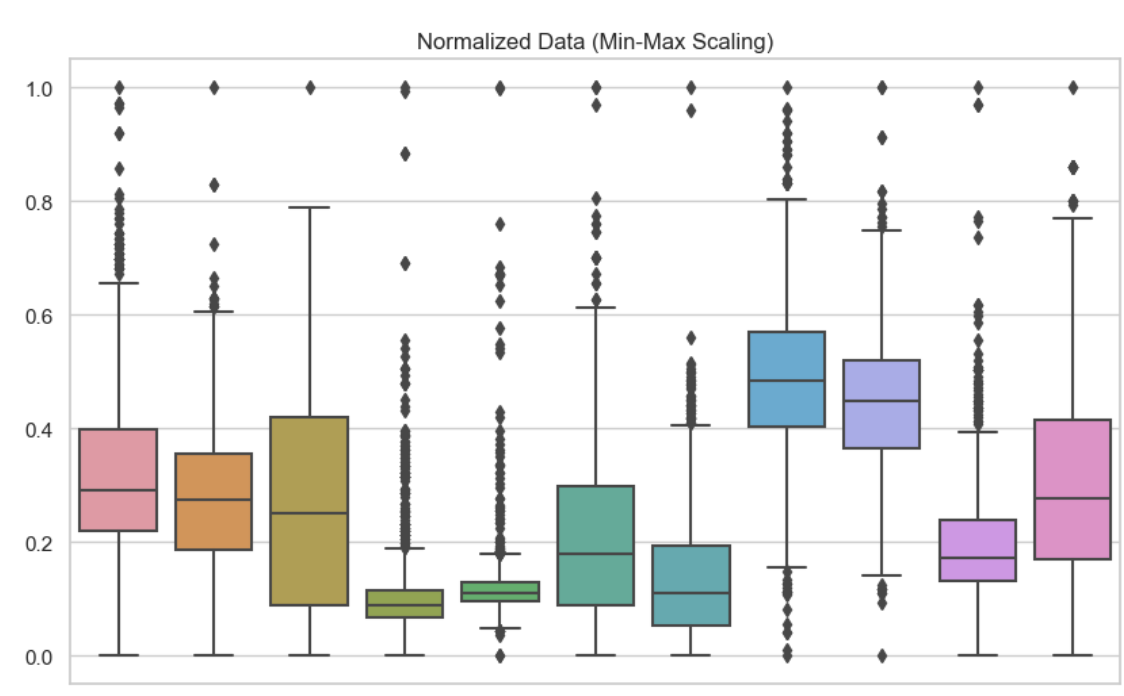
Pour comprendre les différences entre la normalisation et la standardisation, il est utile de voir leurs effets visuellement et en termes de performance du modèle. J'ai inclus ici des diagrammes en boîte pour illustrer ces différentes techniques de mise à l'échelle des caractéristiques. Ici, j'ai utilisé la normalisation min-max pour chacune des variables de mon ensemble de données. Nous pouvons constater qu'aucune valeur n'est inférieure à 0 ou supérieure à 1.
Données normalisées. Image par l'auteur
Dans ce deuxième visuel, j'ai utilisé la standardisation pour chacune des variables. On constate que les données sont centrées sur zéro.
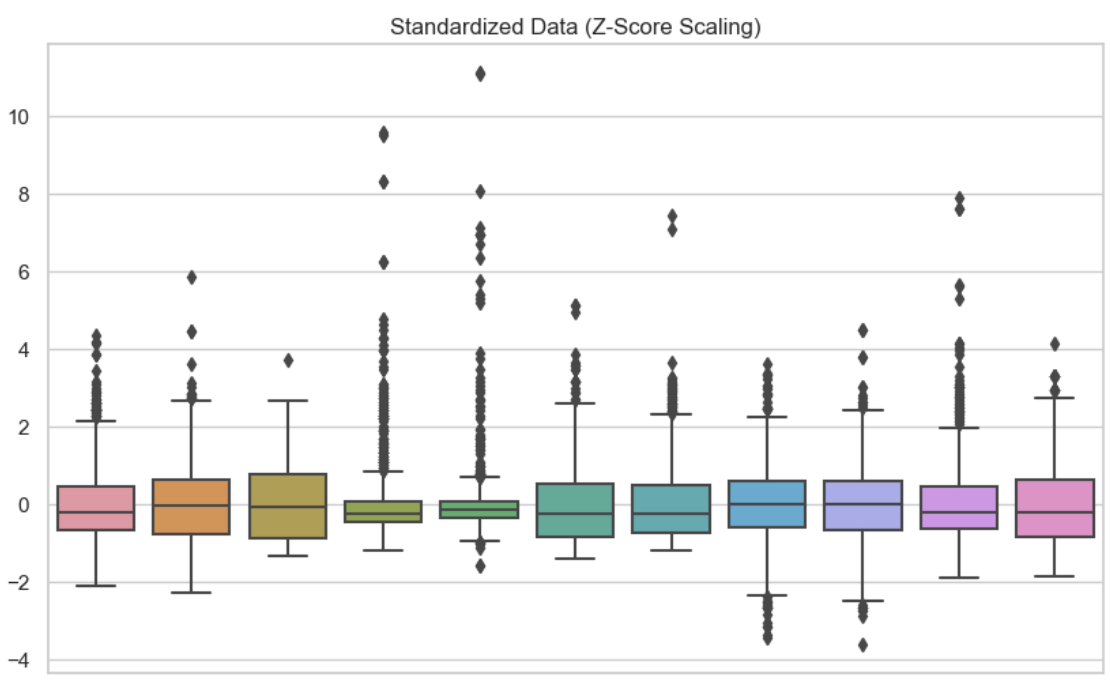 Données standardisées. Image par l'auteur
Données standardisées. Image par l'auteur
Avantages et inconvénients
Les avantages sont notamment l'amélioration de la performance du modèle et l'équilibre des contributions des caractéristiques. Cependant, la normalisation peut limiter l'interprétabilité en raison de l'échelle fixe, tandis que la standardisation peut également rendre l'interprétation plus difficile car les valeurs ne reflètent plus leurs unités d'origine. Il y a toujours un compromis entre la complexité et la précision du modèle.
Normalisation et standardisation dans la régression linéaire
Examinons comment la normalisation (dans ce cas, la normalisation de la moyenne) et la standardisation peuvent modifier l'interprétation d'un modèle de régression linéaire simple. Le R-carré ou le R-carré ajusté serait le même pour chaque modèle, de sorte que l'échelonnement des caractéristiques ne concerne ici que l'interprétation de notre modèle.
| Transformation appliquée | Variable indépendante (taille du logement) | Variable dépendante (prix des logements) | Interprétation |
|---|---|---|---|
| Normalisation de la moyenne | Moyenne Normalisée | Original | Vous prévoyez le prix initial du logement pour chaque changement de taille du logement par rapport à la moyenne. |
| Standardisation | Standardisé | Original | Vous prévoyez le prix initial de l'habitation pour chaque variation d'un écart-type de la taille de l'habitation. |
| Normalisation de la moyenne | Original | Moyenne Normalisée | Vous prévoyez le prix du logement par rapport à la moyenne pour chaque augmentation d'une unité de la taille initiale du logement. |
| Standardisation | Original | Standardisé | Vous prévoyez le prix standardisé de l'habitation pour chaque augmentation d'une unité de la taille de l'habitation d'origine. |
| Normalisation de la moyenne (les deux variables) | Moyenne Normalisée | Moyenne Normalisée | Vous prédisez le prix du logement par rapport à la moyenne pour chaque changement de taille du logement par rapport à la moyenne. |
| Standardisation (les deux variables) | Standardisé | Standardisé | Vous prévoyez le prix standardisé d'un logement pour chaque variation d'un écart-type de la taille du logement. |
Autre point important, dans une régression linéaire, si vous standardisez les variables indépendantes et dépendantes, le r-carré restera le même. En effet, le r-carré mesure la proportion de la variance de y qui est expliquée par x, et cette proportion reste la même, que les variables soient standardisées ou non. Cependant, la standardisation de la variable dépendante modifiera l'EQM, car l'EQM est mesurée dans les mêmes unités que la variable dépendante. Puisque y est maintenant normalisé, le RMSE sera plus faible après la standardisation. Plus précisément, elle reflète l'erreur en termes d'écart-type de la variable standardisée, et non en termes d'unités d'origine. Si la régression vous intéresse particulièrement, suivez notre cours Introduction à la régression avec statsmodels en Python pour devenir un expert.
Conclusion
La mise à l'échelle des caractéristiques, qui comprend la normalisation et la standardisation, est un élément essentiel du prétraitement des données dans l'apprentissage automatique. La compréhension des contextes appropriés pour l'application de chaque technique peut améliorer de manière significative la performance et la précision de vos modèles.
Si vous cherchez à développer et à approfondir votre compréhension de la mise à l'échelle des fonctionnalités et de son rôle dans l'apprentissage automatique, nous avons plusieurs excellentes ressources à DataCamp qui peuvent vous aider à démarrer. Vous pouvez consulter notre article sur la normalisation dans l'apprentissage automatique pour les concepts fondamentaux, ou envisager notre cours sur l 'apprentissage automatique de bout en bout, qui couvre des applications réelles.
Devenez un scientifique ML
Professionnel expérimenté des données et écrivain passionné par l'autonomisation des experts en herbe dans le domaine des données.