Règle de Cramer : Une méthode directe pour résoudre des systèmes linéaires

La règle de Cramer fournit une formule directe pour résoudre des systèmes d'équations linéaires à l'aide de déterminants. Bien que les méthodes de calcul modernes soient souvent plus performantes que la règle de Cramer pour résoudre des systèmes complexes, la compréhension de cette technique nous aide à appréhender la relation entre les systèmes linéaires, les déterminants et la théorie des matrices en algèbre linéaire. 

Cet article présente la règle de Cramer, sa formule, ses fondements mathématiques et son interprétation géométrique. Nous illustrons également son application à travers de multiples exemples, ses limites, ses alternatives et les cas où elle est la plus efficace dans le domaine de la science des données.

Qu'est-ce que la règle de Cramer ?

La règle de Cramer stipule que chaque variable du système peut être trouvée en divisant deux déterminants : le déterminant d'une matrice de coefficients modifiée par le déterminant de la matrice de coefficients d'origine.

Cette matrice modifiée est créée en remplaçant une colonne de coefficients par les constantes figurant à droite des équations.

Pour comprendre les conditions du théorème, considérons un système d'équations linéaires représenté sous forme matricielle comme Ax = b, où :

• A est la matrice des coefficients.
• x est le vecteur des inconnues
• b est le vecteur des constantes

La règle de Cramer ne s'applique que lorsque A est carré (même nombre d'équations que d'inconnues) et a un déterminant non nul, garantissant ainsi l'existence d'une solution unique.

Fondements mathématiques et formules

Pour un système n×n général, la règle de Cramer stipule que la i-ième composante du vecteur solution est :

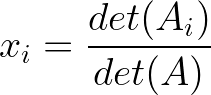
Formule de la règle de Cramer. (Image et toutes les images ci-dessous par l'auteur)

Où :

• _xi est la i-ième variable que nous cherchons à résoudre.
• det(_Ai) est le déterminant de la matrice A dont la i-ème colonne est remplacée par le vecteur b.
• det(A) est le déterminant de la matrice des coefficients d'origine.

Pour mieux comprendre, prenons l'exemple d'un système 2×2 :

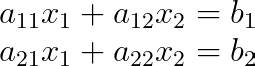
La matrice des coefficients A et le vecteur constant b sont les suivants :

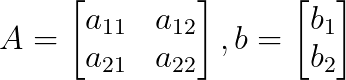
Selon la règle de Cramer :

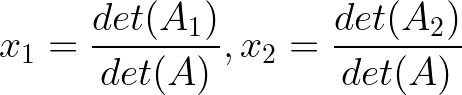
Où A₁ est A avec la première colonne remplacée par b :

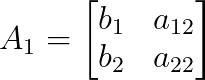
Et A₂ est A avec la deuxième colonne remplacée par b :

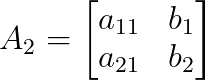
Le déterminant d'une matrice 2×2 se calcule comme suit :

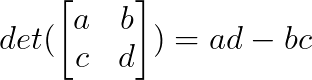
Une fois que nous avons compris le modèle de la solution ci-dessus, nous pouvons l'appliquer directement à tout système compatible sans résoudre d'équations simultanées. Nous étendrons également cette règle à un système 3x3 dans l'un des exemples suivants.

Interprétation géométrique de la règle de Cramer

En plus d'être une formule directe pour résoudre des systèmes linéaires, la règle de Cramer possède également une interprétation géométrique riche.

Aires de parallélogrammes en 2D

Considérez les colonnes de la matrice A comme des vecteurs dans le plan. Ces vecteurs forment un parallélogramme, et le déterminant de A représente l'aire signée de ce parallélogramme.

Lorsque nous remplaçons une colonne par le vecteur b, nous créons un nouveau parallélogramme. Le déterminant de cette nouvelle matrice, det⁡(Ai), représente la surface de la forme modifiée où l'un des vecteurs de direction d'origine a été remplacé par b.

Ainsi :

Chaque variable xi indique la proportion de b qui se trouve dans la direction du vecteur colonne i de A, mise à l'échelle par rapport à la surface totale couverte par les colonnes de A.

Volumes de parallélépipèdes en 3D

La même logique s'applique à la 3D. Ici, le déterminant de A représente le volume du parallélépipède formé par les trois vecteurs colonnes de A.

• En remplaçant une colonne par b, nous obtenons un nouveau parallélépipède.
• Le rapport det⁡(_Ai)/det⁡(A) donne la contribution volumique relative de cette colonne à la forme globale.

En 2D comme en 3D, la règle de Cramer mesure la quantité de b qui « remplit » le volume défini par les colonnes de A.

Guide étape par étape pour appliquer la règle de Cramer

Examinons deux exemples pour illustrer comment la règle de Cramer s'applique à des systèmes de différentes tailles.

Résolution d'un système 2x2

Considérons le système de deux équations linéaires suivant :

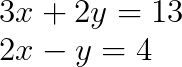
Étape 1 : Identifiez la matrice des coefficients et le vecteur constant.

Nous pouvons écrire le système sous la forme d'une matrice de coefficients A et d'un vecteur constant b comme suit :

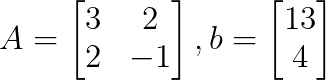
Étape 2 : Calculez le déterminant de la matrice des coefficients.

Le déterminant de A sera :

det(A) = (3)(-1) - (2)(2)
det(A) = -3 - 4
det(A) = -7

Puisque det(A) = -7 ≠ 0, le système possède une solution unique, et nous pouvons appliquer la règle de Cramer.

Étape 3 : Créer des matrices modifiées et calculer leurs déterminants

Pour x, remplacez la première colonne de A par b :

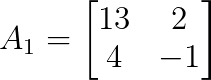
Calculons maintenant le déterminant de A₁ :

det(A₁) = (13)(-1) - (2)(4)
det(A₁) = -13 - 8
det(A₁) = -21

Pour y, remplacez la deuxième colonne de A par b :

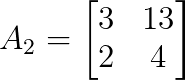
Calculons maintenant le déterminant de A₂ :

det(A₂) = (3)(4) - (13)(2)
det(A₂) = 12 - 26
det(A₂) = -14

Étape 4 : Appliquez les formules de la règle de Cramer.

Nous pouvons calculer les valeurs à l'aide de la formule suivante :

x = det(A₁) / det(A) = -21 / -7 = 3
y = det(A₂) / det(A) = -14 / -7 = 2

Enfin, nous pouvons vérifier les résultats en substituant les valeurs dans l'équation :

• Première équation : 3(3) + 2(2) = 9 + 4 = 13 
• Deuxième équation : 2(3) — 1(2) = 6–2 = 4 

Nous avons ainsi résolu le système linéaire 2x2 à l'aide de la règle de Cramer.

Résolution d'un système 3x3

Passons maintenant à un système 3x3 plus complexe :

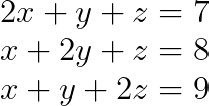
Nous allons répéter les mêmes étapes ci-dessus pour cet exemple.

Étape 1 : Identifiez la matrice des coefficients et le vecteur constant.

À partir du système linéaire, nous pouvons écrire la matrice des coefficients A et le vecteur constant b comme suit :

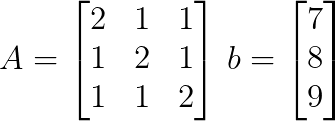
Étape 2 : Calculez le déterminant de la matrice des coefficients.

En utilisant l'expansion le long de la première ligne :

det(A) =       2|2  1| - 1 |1  1| + 1 |1  2|
        		 |1  2|     |1  2|       |1  1|

Calcul de chaque déterminant 2×2 :

|2  1| = (2)(2) - (1)(1) = 4 - 1 = 3
|1  2|

|1  1| = (1)(2) - (1)(1) = 2 - 1 = 1
|1  2|

|1  2| = (1)(1) - (2)(1) = 1 - 2 = -1
|1  1|

Par conséquent, le déterminant de A est :

det(A) = 2(3) - 1(1) + 1(-1)
det(A) = 6 - 1 - 1
det(A) = 4

Puisque det(A) = 4 ≠ 0, le système a une solution unique, et nous pouvons appliquer la règle de Cramer.

Étape 3 : Créer des matrices modifiées et calculer leurs déterminants

Pour x, remplacez la première colonne de A par b :

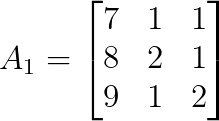
Nous pouvons développer la première ligne :

det(A₁) = 7|2  1| - 1|8  1| + 1|8  2|
   	        |1  2|     |9  2|      |9  1|

Calcul du déterminant de A₁ :

det(A₁) = 7(3) - 1(16 - 9) + 1(8 - 18)
det(A₁) = 21 - 1(7) + 1(-10)
det(A₁) = 21 - 7 - 10
det(A₁) = 4

Pour y, remplacez la deuxième colonne de A par b :

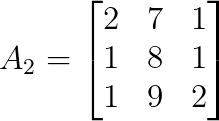
Nous pouvons calculer le déterminant de A₂ comme suit :

det(A₂) = 2|8  1| - 7|1  1| + 1|1  8|
                     |9  2|     |1  2|    |1  9|

det(A₂) = 2(16 - 9) - 7(2 - 1) + 1(9 - 8)
det(A₂) = 2(7) - 7(1) + 1(1)
det(A₂) = 14 - 7 + 1
det(A₂) = 8

Pour z, remplacez la troisième colonne de A par b :

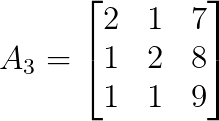
Nous pouvons calculer le déterminant de A₃ comme suit :

det(A₃) = 2|2  8| - 1|1  8| + 7|1  2|
                     |1  9|      |1  9|       |1  1|

det(A₃) = 2(18 - 8) - 1(9 - 8) + 7(1 - 2)
det(A₃) = 2(10) - 1(1) + 7(-1)
det(A₃) = 20 - 1 - 7
det(A₃) = 12

Étape 4 : Appliquez les formules de la règle de Cramer.

Étant donné que nous avons calculé toutes les valeurs nécessaires, nous pouvons calculer les valeurs de x, y et z directement à l'aide de la formule suivante :

x = det(A₁) / det(A) = 4 / 4 = 1
y = det(A₂) / det(A) = 8 / 4 = 2
z = det(A₃) / det(A) = 12 / 4 = 3

Enfin, nous pouvons vérifier les résultats en substituant les valeurs dans l'équation :

• Première équation : 2(1) + 1(2) + 1(3) = 2 + 2 + 3 = 7 
• Deuxième équation : 1(1) + 2(2) + 1(3) = 1 + 4 + 3 = 8 
• Troisième équation : 1(1) + 1(2) + 2(3) = 1 + 2 + 6 = 9 

Veuillez noter que le processus reste cohérent : nous remplaçons les colonnes par le vecteur constant et calculons les déterminants. Le cas 3×3 nécessite davantage de calculs, mais la méthode sous-jacente est identique à celle du cas 2×2.

Limites, alternatives et cas d'utilisation de la règle de Cramer

Comme tous les algorithmes, la règle de Cramer comporte également quelques limites. Comprenons-les :

Complexité informatique

Pour un système n×n, la règle de Cramer nécessite le calcul de (n+1) déterminants. Étant donné que le calcul d'un déterminant à l'aide de l'expansion des cofacteurs présente une complexité de O(n!), la complexité globale devient prohibitive pour les grands systèmes. 

Même avec des algorithmes déterminants plus efficaces, cette méthode reste peu pratique au-delà des petits systèmes.

Problèmes de stabilité numérique

La règle de Cramer peut souffrir d'instabilité numérique lorsque les déterminants sont proches de zéro. 

De petites erreurs d'arrondi dans le calcul de det(A) peuvent entraîner des erreurs importantes dans la solution lors de la division par une valeur proche de zéro. Cela rend la méthode peu fiable pour les systèmes mal conditionnés, qui sont courants dans les données réelles.

Alternatives à la règle de Cramer

En raison de la complexité informatique initiale, nous avons souvent recours à l'une des alternatives suivantes :

• L'élimination gaussienne avecpivotement partiel transforme le système en une forme échelonnée avec une complexité O(n³), ce qui le rend beaucoup plus efficace que la règle de Cramer pour les systèmes supérieurs à 3×3.
• Décomposition LU factorise la matrice des coefficients en matrices triangulaires inférieures et supérieures, ce qui permet de résoudre efficacement plusieurs systèmes ayant la même matrice de coefficients.
• La décomposition QR offreune meilleure stabilité numérique pour les systèmes mal conditionnés en décomposant la matrice en composantes orthogonales et triangulaires supérieures.

Quand utiliser la règle de Cramer ?

Malgré ces limites, la règle de Cramer est utile dans des contextes spécifiques tels que :

• Analyse théorique et démonstrations en algèbre linéaire
• Calcul symbolique nécessitant des solutions algébriques exactes
• Systèmes de petite taille (2×2 ou 3×3) où les formules explicites sont gérables.
• Cadres éducatifs pour la compréhension du lien entre les déterminants et les systèmes linéaires
• Obtenir des solutions fermées dans le cadre d'un travail analytique

Il convient toutefois de noter que, dans la pratique de la science des données, la règle de Cramer sert davantage d'outil conceptuel et théorique pour comprendre les systèmes linéaires que de méthode de calcul.

Conclusion

La règle de Cramer est une approche directe et basée sur une formule permettant de résoudre des systèmes d'équations linéaires à l'aide de déterminants. Nous avons examiné comment cette méthode calcule la valeur de chaque variable, étudié des exemples 2×2 et 3×3, et acquis une compréhension de son interprétation géométrique. Enfin, nous avons également découvert les limites, les alternatives et les cas d'utilisation de la règle de Cramer.

Pour approfondir vos connaissances sur les systèmes linéaires et leurs solutions, nous vous invitons à explorer notre cours Algèbre linéaire pour la science des données, où vous découvrirez plusieurs techniques d'algèbre linéaire telles que la règle de Cramer.