Cramers Regel: Eine direkte Methode zum Lösen linearer Gleichungssysteme

Die Cramer-Regel gibt eine direkte Formel, um lineare Gleichungssysteme mit Determinanten zu lösen. Auch wenn moderne Rechenmethoden oft besser funktionieren als die Cramersche Regel, um große Systeme zu lösen, hilft uns das Verständnis dieser Technik, die Beziehung zwischen linearen Systemen, Determinanten und der Matrixtheorie in der linearen Algebra zu verstehen. 

Dieser Artikel erklärt die Cramer-Formel, wie sie funktioniert, was dahintersteckt und wie man sie in der Geometrie versteht. Außerdem zeigen wir anhand von mehreren Beispielen, wie man das Ganze anwendet, wo die Grenzen sind, welche Alternativen es gibt und wann es in der Datenwissenschaft am besten funktioniert.

Was ist die Cramer-Regel?

Nach der Cramer-Regel kann man jede Variable im System durch Teilen von zwei Determinanten finden: die Determinante einer modifizierten Koeffizientenmatrix durch die Determinante der ursprünglichen Koeffizientenmatrix.

Diese geänderte Matrix entsteht, indem eine Spalte mit Koeffizienten durch die Konstanten auf der rechten Seite der Gleichungen ersetzt wird.

Um die Bedingungen des Satzes zu verstehen, schau dir ein System linearer Gleichungen an, das in Matrixform als Ax = b dargestellt ist, wobei:

• A ist die Koeffizientenmatrix.
• x ist der Vektor der Unbekannten
• b ist der Vektor der Konstanten

Die Cramer-Regel gilt nur, wenn A quadratisch ist (gleiche Anzahl von Gleichungen wie Unbekannte) und einen Determinantenwert ungleich Null hat, wodurch eine eindeutige Lösung gewährleistet ist.

Mathematische Grundlagen und Formeln

Für ein allgemeines n×n-System besagt die Cramer-Regel, dass die i-te Komponente des Lösungsvektors wie folgt lautet:

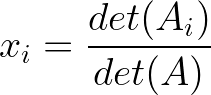
Cramers Regelformel. (Bild und alle Bilder unten vom Autor)

Wo:

• _xi ist die i-te Variable, die wir lösen wollen.
• det(_Ai) ist die Determinante der Matrix A, bei der die i-te Spalte durch den Vektor b ersetzt wurde.
• det(A) ist die Determinante der ursprünglichen Koeffizientenmatrix.

Um das besser zu verstehen, schauen wir uns mal ein 2×2-System an:

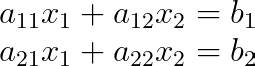
Die Koeffizientenmatrix A und der konstante Vektor b sind:

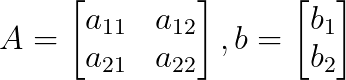
Nach Cramers Regel:

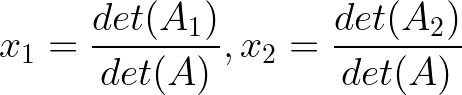
Wobei A₁ A ist, bei dem die erste Spalte durch b ersetzt wurde:

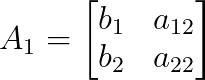
Und A₂ ist A, wo die zweite Spalte durch b ersetzt wurde:

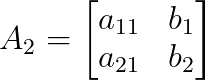
Der Determinante einer 2×2-Matrix wird wie folgt berechnet:

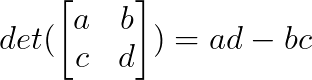
Sobald wir das Muster der obigen Lösung verstanden haben, können wir es direkt auf jedes kompatible System anwenden, ohne gleichzeitige Gleichungen lösen zu müssen. Wir werden die Regel später in einem der Beispiele auch auf ein 3x3-System ausweiten.

Geometrische Interpretation der Cramer-Regel

Die Cramer-Regel ist nicht nur eine direkte Formel zum Lösen linearer Gleichungssysteme, sondern hat auch eine interessante geometrische Bedeutung.

Flächen von Parallelogrammen in 2D

Stell dir die Spalten der Matrix A wie Vektoren in der Ebene vor. Diese Vektoren bilden ein Parallelogramm, und die Determinante von A ist die Fläche des Parallelogramms mit Vorzeichen.

Wenn wir eine Spalte durch den Vektor b ersetzen, entsteht ein neues Parallelogramm. Der Determinante dieser neuen Matrix, det⁡(Ai), entspricht die Fläche der veränderten Form, in der einer der ursprünglichen Richtungsvektoren durch b ersetzt wurde.

Also:

Jede Variable xi sagt uns, wie viel von b in Richtung des i-ten Spaltenvektors von A liegt, skaliert durch die Gesamtfläche, die von den Spalten von A aufgespannt wird.

Volumen von Parallelepipeden in 3D

Das Gleiche gilt auch für 3D. Hier steht die Determinante von A für das Volumen des Parallelepipeds, das durch die drei Spaltenvektoren von A gebildet wird.

• Wenn wir eine Säule durch b ersetzen, kriegen wir ein neues Parallelepiped.
• Das Verhältnis det⁡(_Ai)/det⁡(A) gibt den relativen Volumenanteil dieser Säule an der Gesamtform an.

Sowohl in 2D als auch in 3D misst die Cramer-Regel, wie viel b das Volumen „ausfüllt“, das durch die Spalten von A definiert ist.

Schritt-für-Schritt-Anleitung zur Anwendung der Cramer-Regel

Schauen wir uns zwei Beispiele an, um zu zeigen, wie Cramers Regel bei Systemen unterschiedlicher Größe funktioniert.

Lösen eines 2x2-Systems

Schau dir mal dieses System aus zwei linearen Gleichungen an:

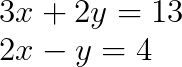
Schritt 1: Identifiziere die Koeffizientenmatrix und den konstanten Vektor.

Wir können das System als Koeffizientenmatrix A und einen konstanten Vektor b wie folgt schreiben:

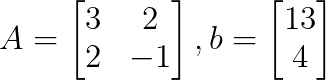
Schritt 2: Berechne die Determinante der Koeffizientenmatrix.

Der Determinante von A ist:

det(A) = (3)(-1) - (2)(2)
det(A) = -3 - 4
det(A) = -7

Da det(A) = -7 ≠ 0 ist, hat das System eine eindeutige Lösung, und wir können die Cramer-Regel anwenden.

Schritt 3: Erstelle geänderte Matrizen und rechne ihre Determinanten aus.

Für x ersetze die erste Spalte von A durch b:

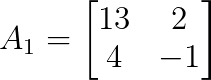
Berechnen wir jetzt die Determinante von A₁:

det(A₁) = (13)(-1) - (2)(4)
det(A₁) = -13 - 8
det(A₁) = -21

Für y ersetze die zweite Spalte von A durch b:

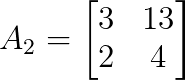
Berechnen wir jetzt die Determinante von A₂:

det(A₂) = (3)(4) - (13)(2)
det(A₂) = 12 - 26
det(A₂) = -14

Schritt 4: Wende die Formeln der Cramer-Regel an.

Wir können die Werte mit der folgenden Formel berechnen:

x = det(A₁) / det(A) = -21 / -7 = 3
y = det(A₂) / det(A) = -14 / -7 = 2

Zum Schluss können wir die Ergebnisse überprüfen, indem wir die Werte wieder in die Gleichung einsetzen:

• Erste Gleichung: 3(3) + 2(2) = 9 + 4 = 13 
• Zweite Gleichung: 2(3) — 1(2) = 6–2 = 4 

So haben wir das lineare 2x2-System mit der Cramer-Regel gelöst.

Lösen eines 3x3-Systems

Jetzt schauen wir uns mal ein komplexeres 3x3-System an:

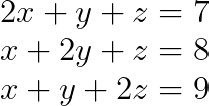
Wir machen die gleichen Schritte wie oben für dieses Beispiel.

Schritt 1: Identifiziere die Koeffizientenmatrix und den konstanten Vektor.

Aus dem linearen System können wir die Koeffizientenmatrix A und den konstanten Vektor b wie folgt schreiben:

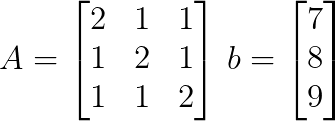
Schritt 2: Berechne die Determinante der Koeffizientenmatrix.

Mit der Erweiterung entlang der ersten Zeile:

det(A) =       2|2  1| - 1 |1  1| + 1 |1  2|
        		 |1  2|     |1  2|       |1  1|

Berechnung jeder 2×2-Determinante:

|2  1| = (2)(2) - (1)(1) = 4 - 1 = 3
|1  2|

|1  1| = (1)(2) - (1)(1) = 2 - 1 = 1
|1  2|

|1  2| = (1)(1) - (2)(1) = 1 - 2 = -1
|1  1|

Deshalb ist der Determinante von A:

det(A) = 2(3) - 1(1) + 1(-1)
det(A) = 6 - 1 - 1
det(A) = 4

Da det(A) = 4 ≠ 0 ist, hat das System eine eindeutige Lösung, und wir können die Cramer-Regel anwenden.

Schritt 3: Erstelle geänderte Matrizen und rechne ihre Determinanten aus.

Für x ersetze die erste Spalte von A durch b:

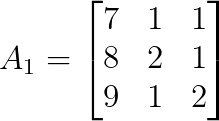
Wir können entlang der ersten Zeile erweitern:

det(A₁) = 7|2  1| - 1|8  1| + 1|8  2|
   	        |1  2|     |9  2|      |9  1|

Berechne die Determinante von A₁:

det(A₁) = 7(3) - 1(16 - 9) + 1(8 - 18)
det(A₁) = 21 - 1(7) + 1(-10)
det(A₁) = 21 - 7 - 10
det(A₁) = 4

Für y ersetze die zweite Spalte von A durch b:

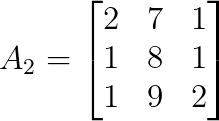
Wir können die Determinante von A₂ wie folgt berechnen:

det(A₂) = 2|8  1| - 7|1  1| + 1|1  8|
                     |9  2|     |1  2|    |1  9|

det(A₂) = 2(16 - 9) - 7(2 - 1) + 1(9 - 8)
det(A₂) = 2(7) - 7(1) + 1(1)
det(A₂) = 14 - 7 + 1
det(A₂) = 8

Für z ersetze die dritte Spalte von A durch b:

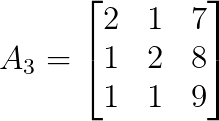
Wir können die Determinante von A₃ wie folgt berechnen:

det(A₃) = 2|2  8| - 1|1  8| + 7|1  2|
                     |1  9|      |1  9|       |1  1|

det(A₃) = 2(18 - 8) - 1(9 - 8) + 7(1 - 2)
det(A₃) = 2(10) - 1(1) + 7(-1)
det(A₃) = 20 - 1 - 7
det(A₃) = 12

Schritt 4: Wende die Formeln der Cramer-Regel an.

Da wir alle notwendigen Werte berechnet haben, können wir die Werte von x, y und z direkt mit der Formel berechnen:

x = det(A₁) / det(A) = 4 / 4 = 1
y = det(A₂) / det(A) = 8 / 4 = 2
z = det(A₃) / det(A) = 12 / 4 = 3

Zum Schluss können wir die Ergebnisse überprüfen, indem wir die Werte wieder in die Gleichung einsetzen:

• Erste Gleichung: 2(1) + 1(2) + 1(3) = 2 + 2 + 3 = 7 
• Zweite Gleichung: 1(1) + 2(2) + 1(3) = 1 + 4 + 3 = 8 
• Dritte Gleichung: 1(1) + 1(2) + 2(3) = 1 + 2 + 6 = 9 

Schau dir an, wie der Prozess immer gleich bleibt: Wir ersetzen Spalten durch den konstanten Vektor und berechnen Determinanten. Der 3×3-Fall braucht mehr Rechenaufwand, aber die Methode ist die gleiche wie beim 2×2-Fall.

Einschränkungen, Alternativen und wann man die Cramer-Regel anwendet

Wie alle Algorithmen hat auch die Cramer-Regel ein paar Einschränkungen. Lass uns das mal verstehen:

Rechenaufwand

Für ein n×n-System musst du nach der Cramerschen Regel (n+1) Determinanten berechnen. Da die Berechnung einer Determinante mit Hilfe der Cofaktor-Entwicklung eine Komplexität von O(n!) hat, wird die Gesamtkomplexität für große Systeme echt schwierig. 

Selbst mit effizienteren Determinantenalgorithmen bleibt die Methode für Systeme, die größer als kleine Systeme sind, nicht praktikabel.

Probleme mit der numerischen Stabilität

Die Cramer-Regel kann numerisch instabil sein, wenn die Determinanten fast null sind. 

Kleine Rundungsfehler bei der Berechnung von det(A) können zu großen Fehlern in der Lösung führen, wenn durch einen Wert nahe Null geteilt wird. Das macht die Methode für schlecht konditionierte Systeme, die in echten Daten oft vorkommen, nicht so zuverlässig.

Alternativen zur Cramer-Regel

Wegen der primären Begrenzung der Rechenkomplexität greifen wir oft auf eine der folgenden Alternativen zurück:

• Die Gaußsche Eliminationsmethode mitpartieller Pivotisierung verwandelt das System in eine Zeilenstufenform mit einer Komplexität von O(n³) und ist damit für Systeme, die größer als 3×3 sind, wesentlich effizienter als die Cramersche Regel.
• LU-Zerlegung zerlegt die Koeffizientenmatrix in untere und obere Dreiecksmatrizen, was eine effiziente Lösung mehrerer Systeme mit derselben Koeffizientenmatrix ermöglicht.
• Die QR-Zerlegung sorgtfür eine bessere numerische Stabilität bei schlecht konditionierten Systemen, indem sie die Matrix in orthogonale und obere dreieckige Komponenten zerlegt.

Wann man die Cramer-Regel anwendet

Trotz dieser Einschränkungen ist die Cramer-Regel in bestimmten Situationen echt nützlich, zum Beispiel:

• Theoretische Analyse und Beweise in der linearen Algebra
• Symbolische Berechnung, wo genaue algebraische Lösungen gebraucht werden
• Kleine Systeme (2×2 oder 3×3), bei denen die Formeln ganz einfach sind
• Bildungsumgebungen zum Verständnis des Zusammenhangs zwischen Determinanten und linearen Systemen
• Ableitung geschlossener Lösungen in analytischen Arbeiten

Allerdings sollte man wissen, dass Cramers Regel in der Datenwissenschaft eher ein konzeptionelles und theoretisches Werkzeug zum Verständnis linearer Systeme ist als eine Berechnungsmethode.

Fazit

Die Cramer-Regel ist eine direkte und formelbasierte Methode, um lineare Gleichungssysteme mithilfe von Determinanten zu lösen. Wir haben uns angesehen, wie diese Methode den Wert jeder Variablen berechnet, haben 2×2- und 3×3-Beispiele durchgearbeitet und ein Verständnis für die geometrische Interpretation gewonnen. Zum Schluss haben wir auch noch die Einschränkungen, Alternativen und Anwendungsfälle der Cramer-Regel kennengelernt.

Wenn du mehr über lineare Systeme und ihre Lösungen erfahren willst, schau dir unseren Kurs „Lineare Algebra für Data Science“ an. Dort lernst du verschiedene Techniken der linearen Algebra kennen, zum Beispiel die Cramer-Regel.