Regla de Cramer: Un método directo para resolver sistemas lineales

La regla de Cramer proporciona una fórmula directa para resolver sistemas de ecuaciones lineales utilizando determinantes. Aunque los métodos computacionales modernos suelen funcionar mejor que la regla de Cramer para resolver sistemas grandes, comprender esta técnica nos ayuda a entender la relación entre los sistemas lineales, los determinantes y la teoría de matrices en álgebra lineal. 

Este artículo presenta la regla de Cramer, la fórmula, sus fundamentos matemáticos y la interpretación geométrica. También demostramos su aplicación a través de múltiples ejemplos, sus limitaciones, alternativas y cuándo es más eficaz en contextos de ciencia de datos.

¿Qué es la regla de Cramer?

La regla de Cramer establece que cada variable del sistema puede encontrarse dividiendo dos determinantes: el determinante de una matriz de coeficientes modificada por el determinante de la matriz de coeficientes original.

Esta matriz modificada se crea sustituyendo una columna de coeficientes por las constantes del lado derecho de las ecuaciones.

Para comprender las condiciones del teorema, considera un sistema de ecuaciones lineales representadas en forma matricial como Ax = b, donde:

• A es la matriz de coeficientes.
• x es el vector de incógnitas
• b es el vector de constantes

La regla de Cramer solo se aplica cuando A es cuadrada (el mismo número de ecuaciones que incógnitas) y tiene un determinante distinto de cero, lo que garantiza que existe una solución única.

Fundamentos matemáticos y fórmulas

Para un sistema n×n general, la regla de Cramer establece que el componente i-ésimo del vector solución es:

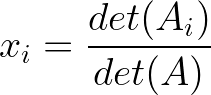
Fórmula de la regla de Cramer. (Imagen y todas las imágenes a continuación del autor)

Dónde:

• _xi es la variable i-ésima que estamos resolviendo.
• det(_Ai) es el determinante de la matriz A con su columna i-ésima sustituida por el vector b.
• det(A) es el determinante de la matriz de coeficientes original.

Para entenderlo mejor, consideremos un sistema 2×2:

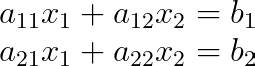
La matriz de coeficientes A y el vector constante b son:

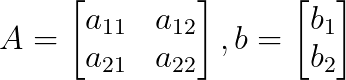
Según la regla de Cramer:

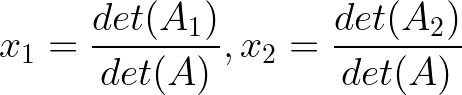
Donde A₁ es A con la primera columna sustituida por b:

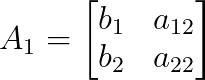
Y A₂ es A con la segunda columna sustituida por b:

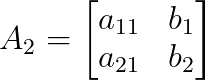
El determinante de una matriz 2×2 se calcula como:

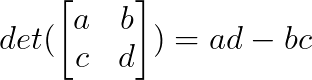
Una vez que entendemos el patrón de la solución anterior, podemos aplicarlo directamente a cualquier sistema compatible sin resolver ecuaciones simultáneas. También ampliaremos la regla a un sistema 3x3 en uno de los ejemplos posteriores.

Interpretación geométrica de la regla de Cramer

Además de ser una fórmula directa para resolver sistemas lineales, la regla de Cramer también tiene una rica interpretación geométrica.

Áreas de paralelogramos en 2D

Piensa en las columnas de la matriz A como vectores en el plano. Estos vectores forman un paralelogramo, y el determinante de A representa el área con signo de ese paralelogramo.

Cuando sustituimos una columna por el vector b, creamos un nuevo paralelogramo. El determinante de esta nueva matriz, det⁡(Ai), representa el área de la forma modificada donde uno de los vectores de dirección originales ha sido sustituido por b.

Por lo tanto:

Cada variable xi nos dice cuánto de b se encuentra en la dirección del vector columna i-ésimo de A, escalado por el área total abarcada por las columnas de A.

Volúmenes de paralelepípedos en 3D

La misma lógica se aplica al 3D. Aquí, el determinante de A representa el volumen del paralelepípedo formado por los tres vectores columna de A.

• Al sustituir una columna por b obtenemos un nuevo paralelepípedo.
• La relación det⁡(_Ai)/det⁡(A) proporciona la contribución relativa del volumen de esa columna a la forma general.

Tanto en 2D como en 3D, la regla de Cramer mide cuánto «llena» b el volumen definido por las columnas de A.

Guía paso a paso para aplicar la regla de Cramer

Veamos dos ejemplos para demostrar cómo se aplica la regla de Cramer a sistemas de diferentes tamaños.

Resolución de un sistema 2x2

Considera este sistema de dos ecuaciones lineales:

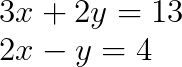
Paso 1: Identifica la matriz de coeficientes y el vector constante.

Podemos escribir el sistema como una matriz de coeficientes A y un vector constante b, como se muestra a continuación:

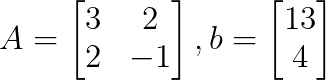
Paso 2: Calcula el determinante de la matriz de coeficientes.

El determinante de A será:

det(A) = (3)(-1) - (2)(2)
det(A) = -3 - 4
det(A) = -7

Dado que det(A) = -7 ≠ 0, el sistema tiene una solución única y podemos aplicar la regla de Cramer.

Paso 3: Crea matrices modificadas y calcula sus determinantes.

Para x, sustituye la primera columna de A por b:

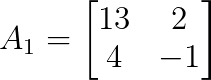
Ahora calculemos el determinante de A₁:

det(A₁) = (13)(-1) - (2)(4)
det(A₁) = -13 - 8
det(A₁) = -21

Para y, sustituye la segunda columna de A por b:

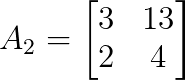
Ahora calculemos el determinante de A₂:

det(A₂) = (3)(4) - (13)(2)
det(A₂) = 12 - 26
det(A₂) = -14

Paso 4: Aplica las fórmulas de la regla de Cramer.

Podemos calcular los valores mediante la fórmula:

x = det(A₁) / det(A) = -21 / -7 = 3
y = det(A₂) / det(A) = -14 / -7 = 2

Por último, podemos verificar los resultados sustituyendo los valores en la ecuación:

• Primera ecuación: 3(3) + 2(2) = 9 + 4 = 13 
• Segunda ecuación: 2(3) — 1(2) = 6–2 = 4 

De este modo, hemos resuelto el sistema lineal 2x2 utilizando la regla de Cramer.

Resolución de un sistema 3x3

Ahora ampliemos a un sistema más complejo de 3x3:

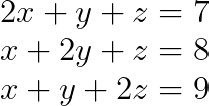
Repetiremos los mismos pasos anteriores para este ejemplo.

Paso 1: Identifica la matriz de coeficientes y el vector constante.

A partir del sistema lineal, podemos escribir la matriz de coeficientes A y el vector constante b como:

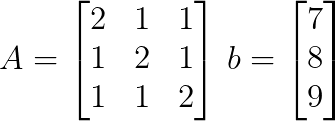
Paso 2: Calcula el determinante de la matriz de coeficientes.

Usando la expansión a lo largo de la primera fila:

det(A) =       2|2  1| - 1 |1  1| + 1 |1  2|
        		 |1  2|     |1  2|       |1  1|

Cálculo de cada determinante 2×2:

|2  1| = (2)(2) - (1)(1) = 4 - 1 = 3
|1  2|

|1  1| = (1)(2) - (1)(1) = 2 - 1 = 1
|1  2|

|1  2| = (1)(1) - (2)(1) = 1 - 2 = -1
|1  1|

Por lo tanto, el determinante de A es:

det(A) = 2(3) - 1(1) + 1(-1)
det(A) = 6 - 1 - 1
det(A) = 4

Dado que det(A) = 4 ≠ 0, el sistema tiene una solución única y podemos aplicar la regla de Cramer.

Paso 3: Crea matrices modificadas y calcula sus determinantes.

Para x, sustituye la primera columna de A por b:

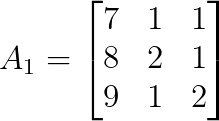
Podemos expandir a lo largo de la primera fila:

det(A₁) = 7|2  1| - 1|8  1| + 1|8  2|
   	        |1  2|     |9  2|      |9  1|

Cálculo del determinante de A₁:

det(A₁) = 7(3) - 1(16 - 9) + 1(8 - 18)
det(A₁) = 21 - 1(7) + 1(-10)
det(A₁) = 21 - 7 - 10
det(A₁) = 4

Para y, sustituye la segunda columna de A por b:

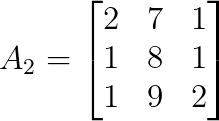
Podemos calcular el determinante de A₂ de la siguiente manera:

det(A₂) = 2|8  1| - 7|1  1| + 1|1  8|
                     |9  2|     |1  2|    |1  9|

det(A₂) = 2(16 - 9) - 7(2 - 1) + 1(9 - 8)
det(A₂) = 2(7) - 7(1) + 1(1)
det(A₂) = 14 - 7 + 1
det(A₂) = 8

Para z, sustituye la tercera columna de A por b:

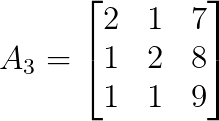
Podemos calcular el determinante de A₃ de la siguiente manera:

det(A₃) = 2|2  8| - 1|1  8| + 7|1  2|
                     |1  9|      |1  9|       |1  1|

det(A₃) = 2(18 - 8) - 1(9 - 8) + 7(1 - 2)
det(A₃) = 2(10) - 1(1) + 7(-1)
det(A₃) = 20 - 1 - 7
det(A₃) = 12

Paso 4: Aplica las fórmulas de la regla de Cramer.

Ya que hemos calculado todos los valores necesarios, podemos calcular los valores de x, y y z directamente mediante la fórmula:

x = det(A₁) / det(A) = 4 / 4 = 1
y = det(A₂) / det(A) = 8 / 4 = 2
z = det(A₃) / det(A) = 12 / 4 = 3

Por último, podemos verificar los resultados sustituyendo los valores en la ecuación:

• Primera ecuación: 2(1) + 1(2) + 1(3) = 2 + 2 + 3 = 7 
• Segunda ecuación: 1(1) + 2(2) + 1(3) = 1 + 4 + 3 = 8 
• Tercera ecuación: 1(1) + 1(2) + 2(3) = 1 + 2 + 6 = 9 

Observa cómo el proceso sigue siendo coherente: sustituimos las columnas por el vector constante y calculamos los determinantes. El caso 3×3 requiere más cálculos, pero el método subyacente es idéntico al del caso 2×2.

Limitaciones, alternativas y cuándo utilizar la regla de Cramer

Como todos los algoritmos, la regla de Cramer también tiene algunas limitaciones. Entendámoslos:

Complejidad computacional

Para un sistema n×n, la regla de Cramer requiere calcular (n+1) determinantes. Dado que calcular un determinante utilizando la expansión de cofactores tiene una complejidad de O(n!), la complejidad global se vuelve prohibitiva para sistemas grandes. 

Incluso con algoritmos determinantes más eficientes, el método sigue siendo poco práctico más allá de los sistemas pequeños.

Problemas de estabilidad numérica

La regla de Cramer puede sufrir inestabilidad numérica cuando los determinantes son cercanos a cero. 

Pequeños errores de redondeo en el cálculo de det(A) pueden dar lugar a grandes errores en la solución al dividir por un valor cercano a cero. Esto hace que el método no sea fiable para sistemas en mal estado, que son habituales en los datos del mundo real.

Alternativas a la regla de Cramer

Debido a la limitación de la complejidad computacional primaria, a menudo recurrimos a una de las siguientes alternativas:

• La eliminación gaussiana conpivote parcial transforma el sistema a forma escalonada con complejidad O(n³), lo que lo hace mucho más eficiente que la regla de Cramer para sistemas mayores que 3×3.
• Descomposición LU factoriza la matriz de coeficientes en matrices triangulares inferiores y superiores, lo que da como resultado una solución eficiente de múltiples sistemas con la misma matriz de coeficientes.
• La descomposición QR proporcionauna mayor estabilidad numérica para sistemas mal condicionados al descomponer la matriz en componentes ortogonales y triangulares superiores.

Cuándo utilizar la regla de Cramer

A pesar de estas limitaciones, la regla de Cramer es valiosa en contextos específicos, tales como:

• Análisis teórico y demostraciones en álgebra lineal
• Cálculo simbólico en el que se necesitan soluciones algebraicas exactas.
• Sistemas pequeños (2×2 o 3×3) en los que las fórmulas explícitas son manejables.
• Entornos educativos para comprender la conexión entre los determinantes y los sistemas lineales
• Derivación de soluciones cerradas en trabajos analíticos

Sin embargo, cabe señalar que, en la práctica de la ciencia de datos, la regla de Cramer sirve más como herramienta conceptual y teórica para comprender los sistemas lineales que como método computacional.

Conclusión

La regla de Cramer es un método directo y basado en fórmulas para resolver sistemas de ecuaciones lineales mediante determinantes. Exploramos cómo este método calcula el valor de cada variable, trabajamos con ejemplos de 2×2 y 3×3, y comprendimos su interpretación geométrica. Por último, también aprendimos las limitaciones, las alternativas y cuándo utilizar la regla de Cramer.

Para profundizar en tu comprensión de los sistemas lineales y sus soluciones, te recomendamos que explores nuestro curso Álgebra lineal para la ciencia de datos, donde aprenderás varias técnicas de álgebra lineal, como la regla de Cramer.