Regra de Cramer: Um método direto para resolver sistemas lineares

A regra de Cramer dá uma fórmula direta pra resolver sistemas de equações lineares usando determinantes. Embora os métodos computacionais modernos geralmente funcionem melhor do que a regra de Cramer para resolver sistemas grandes, entender essa técnica ajuda a entender a relação entre sistemas lineares, determinantes e teoria das matrizes na álgebra linear. 

Este artigo apresenta a regra de Cramer, a fórmula, os fundamentos matemáticos e a interpretação geométrica. Também mostramos como usar isso com vários exemplos, as limitações, alternativas e quando é mais eficaz em ciência de dados.

O que é a Regra de Cramer?

A regra de Cramer diz que cada variável no sistema pode ser encontrada dividindo dois determinantes: o determinante de uma matriz de coeficientes modificada pelo determinante da matriz de coeficientes original.

Essa matriz modificada é criada substituindo uma coluna de coeficientes pelas constantes do lado direito das equações.

Para entender as condições do teorema, pense num sistema de equações lineares representado na forma de matriz como Ax = b, onde:

• A é a matriz de coeficientes
• x é o vetor das incógnitas
• b é o vetor de constantes

A regra de Cramer só vale quando A é quadrado (tem o mesmo número de equações que incógnitas) e tem um determinante diferente de zero, garantindo que existe uma solução única.

Fundamentos matemáticos e fórmulas

Para um sistema n×n geral, a regra de Cramer diz que o i-ésimo componente do vetor solução é:

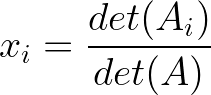
Fórmula da regra de Cramer. (Imagem e todas as imagens abaixo pelo autor)

Onde:

• _xi é a i-ésima variável que estamos resolvendo
• det(_Ai) é o determinante da matriz A com a sua coluna i substituída pelo vetor b.
• det(A) é o determinante da matriz de coeficientes original

Para entender melhor, vamos pensar num sistema 2×2:

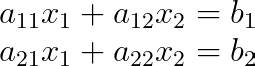
A matriz de coeficientes A e o vetor constante b são:

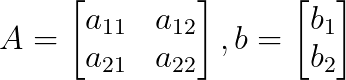
De acordo com a regra de Cramer:

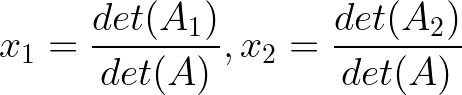
Onde A₁ é A com a primeira coluna substituída por b:

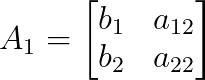
E A₂ é A com a segunda coluna substituída por b:

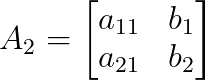
O determinante de uma matriz 2×2 é calculado assim:

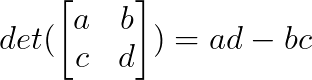
Depois de entender o padrão da solução acima, podemos aplicá-lo diretamente a qualquer sistema compatível sem precisar resolver equações simultâneas. Também vamos estender a regra para um sistema 3x3 em um dos exemplos mais adiante.

Interpretação geométrica da regra de Cramer

Além de ser uma fórmula direta para resolver sistemas lineares, a Regra de Cramer também tem uma interpretação geométrica bem interessante.

Áreas de paralelogramos em 2D

Pensa nas colunas da matriz A como vetores no plano. Esses vetores formam um paralelogramo, e o determinante de A representa a área assinada desse paralelogramo.

Quando a gente substitui uma coluna pelo vetor b, a gente cria um novo paralelogramo. O determinante dessa nova matriz, det⁡(Ai), mostra a área da forma modificada onde um dos vetores de direção originais foi substituído por b.

Então:

Cada variável xi nos diz quanto de b está na direção do i-ésimo vetor coluna de A, escalonado pela área total abrangida pelas colunas de A.

Volumes de paralelepípedos em 3D

A mesma lógica vale para o 3D. Aqui, o determinante de A representa o volume do paralelepípedo formado pelos três vetores coluna de A.

• Substituindo uma coluna por b, a gente consegue um novo paralelepípedo.
• A relação det⁡(_Ai)/det⁡(A) mostra a contribuição relativa do volume dessa coluna para a forma geral.

Tanto em 2D quanto em 3D, a Regra de Cramer mede o quanto b “preenche” o volume definido pelas colunas de A.

Guia passo a passo para aplicar a regra de Cramer

Vamos ver dois exemplos pra mostrar como a regra de Cramer funciona em sistemas de tamanhos diferentes.

Resolvendo um sistema 2x2

Pensa nesse sistema de duas equações lineares:

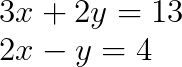
Passo 1: Identifique a matriz de coeficientes e o vetor constante

Podemos escrever o sistema como uma matriz de coeficientes A e um vetor constante b, como mostrado abaixo:

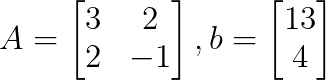
Passo 2: Calcule o determinante da matriz de coeficientes

O determinante de A vai ser:

det(A) = (3)(-1) - (2)(2)
det(A) = -3 - 4
det(A) = -7

Como det(A) = -7 ≠ 0, o sistema tem uma solução única e podemos usar a regra de Cramer.

Passo 3: Crie matrizes modificadas e calcule seus determinantes

Para x, troca a primeira coluna de A por b:

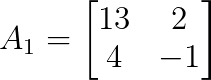
Agora vamos calcular o determinante de A₁:

det(A₁) = (13)(-1) - (2)(4)
det(A₁) = -13 - 8
det(A₁) = -21

Para y, troca a segunda coluna de A por b:

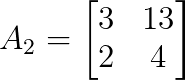
Agora vamos calcular o determinante de A₂:

det(A₂) = (3)(4) - (13)(2)
det(A₂) = 12 - 26
det(A₂) = -14

Passo 4: Aplique as fórmulas da regra de Cramer

A gente pode calcular os valores com a fórmula:

x = det(A₁) / det(A) = -21 / -7 = 3
y = det(A₂) / det(A) = -14 / -7 = 2

Por fim, podemos conferir os resultados colocando os valores de volta na equação:

• Primeira equação: 3(3) + 2(2) = 9 + 4 = 13 
• Segunda equação: 2(3) — 1(2) = 6–2 = 4 

Então, resolvemos o sistema linear 2x2 usando a regra de Cramer.

Resolvendo um sistema 3x3

Agora vamos passar para um sistema 3x3 mais complexo:

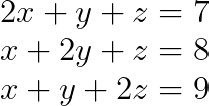
Vamos repetir os mesmos passos acima para este exemplo.

Passo 1: Identifique a matriz de coeficientes e o vetor constante

A partir do sistema linear, podemos escrever a matriz de coeficientes A e o vetor constante b como:

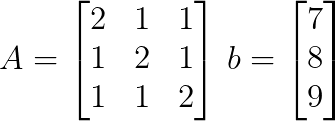
Passo 2: Calcule o determinante da matriz de coeficientes

Usando a expansão ao longo da primeira linha:

det(A) =       2|2  1| - 1 |1  1| + 1 |1  2|
        		 |1  2|     |1  2|       |1  1|

Calculando cada determinante 2×2:

|2  1| = (2)(2) - (1)(1) = 4 - 1 = 3
|1  2|

|1  1| = (1)(2) - (1)(1) = 2 - 1 = 1
|1  2|

|1  2| = (1)(1) - (2)(1) = 1 - 2 = -1
|1  1|

Então, o determinante de A é:

det(A) = 2(3) - 1(1) + 1(-1)
det(A) = 6 - 1 - 1
det(A) = 4

Como det(A) = 4 ≠ 0, o sistema tem uma solução única e podemos usar a regra de Cramer.

Passo 3: Crie matrizes modificadas e calcule seus determinantes

Para x, troca a primeira coluna de A por b:

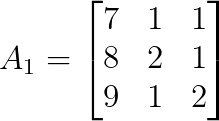
A gente pode expandir ao longo da primeira linha:

det(A₁) = 7|2  1| - 1|8  1| + 1|8  2|
   	        |1  2|     |9  2|      |9  1|

Calculando o determinante de A₁:

det(A₁) = 7(3) - 1(16 - 9) + 1(8 - 18)
det(A₁) = 21 - 1(7) + 1(-10)
det(A₁) = 21 - 7 - 10
det(A₁) = 4

Para y, troca a segunda coluna de A por b:

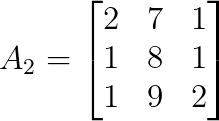
Podemos calcular o determinante de A₂ assim:

det(A₂) = 2|8  1| - 7|1  1| + 1|1  8|
                     |9  2|     |1  2|    |1  9|

det(A₂) = 2(16 - 9) - 7(2 - 1) + 1(9 - 8)
det(A₂) = 2(7) - 7(1) + 1(1)
det(A₂) = 14 - 7 + 1
det(A₂) = 8

Para z, troca a terceira coluna de A por b:

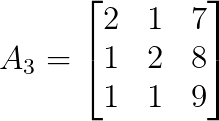
A gente pode calcular o determinante de A₃ assim:

det(A₃) = 2|2  8| - 1|1  8| + 7|1  2|
                     |1  9|      |1  9|       |1  1|

det(A₃) = 2(18 - 8) - 1(9 - 8) + 7(1 - 2)
det(A₃) = 2(10) - 1(1) + 7(-1)
det(A₃) = 20 - 1 - 7
det(A₃) = 12

Passo 4: Aplique as fórmulas da regra de Cramer

Como já calculamos todos os valores necessários, podemos calcular os valores de x, y e z direto pela fórmula:

x = det(A₁) / det(A) = 4 / 4 = 1
y = det(A₂) / det(A) = 8 / 4 = 2
z = det(A₃) / det(A) = 12 / 4 = 3

Por fim, podemos conferir os resultados colocando os valores de volta na equação:

• Primeira equação: 2(1) + 1(2) + 1(3) = 2 + 2 + 3 = 7 
• Segunda equação: 1(1) + 2(2) + 1(3) = 1 + 4 + 3 = 8 
• Terceira equação: 1(1) + 1(2) + 2(3) = 1 + 2 + 6 = 9 

Observe como o processo permanece consistente: substituímos as colunas pelo vetor constante e calculamos os determinantes. O caso 3×3 precisa de mais cálculos, mas o método é o mesmo do caso 2×2.

Limitações, alternativas e quando usar a regra de Cramer

Como todos os algoritmos, a regra de Cramer também tem algumas limitações. Vamos entender como funcionam:

Complexidade computacional

Para um sistema n×n, a regra de Cramer precisa calcular (n+1) determinantes. Como calcular um determinante usando expansão de cofator tem uma complexidade de O(n!), a complexidade geral fica muito alta para sistemas grandes. 

Mesmo com algoritmos determinantes mais eficientes, o método continua impraticável para sistemas maiores que pequenos.

Problemas de estabilidade numérica

A regra de Cramer pode ter instabilidade numérica quando os determinantes estão perto de zero. 

Pequenos erros de arredondamento no cálculo de det(A) podem levar a grandes erros na solução ao dividir por um valor próximo de zero. Isso faz com que o método não seja confiável para sistemas mal condicionados, que são comuns em dados do mundo real.

Alternativas à Regra de Cramer

Por causa da complexidade computacional, a gente costuma usar uma das seguintes alternativas:

• A eliminação gaussiana compivô parcial transforma o sistema para a forma escalonada com complexidade O(n³), tornando-o muito mais eficiente do que a regra de Cramer para sistemas maiores que 3×3.
• Decomposição LU fatora a matriz de coeficientes em matrizes triangulares inferiores e superiores, resultando em uma solução eficiente de múltiplos sistemas com a mesma matriz de coeficientes.
• A decomposição QR dáuma estabilidade numérica melhor para sistemas mal condicionados, dividindo a matriz em componentes ortogonais e triangulares superiores.

Quando usar a regra de Cramer

Apesar dessas limitações, a regra de Cramer é útil em contextos específicos, como:

• Análise teórica e provas em álgebra linear
• Cálculo simbólico onde são necessárias soluções algébricas exatas
• Sistemas pequenos (2×2 ou 3×3) onde as fórmulas explícitas são fáceis de lidar.
• Ambientes educacionais para entender a conexão entre determinantes e sistemas lineares
• Derivando soluções de forma fechada em trabalhos analíticos

Mas, vale lembrar que, na prática da ciência de dados, a regra de Cramer é mais uma ferramenta conceitual e teórica pra entender sistemas lineares do que um método computacional.

Conclusão

A regra de Cramer é uma maneira direta e baseada em fórmulas pra resolver sistemas de equações lineares usando determinantes. A gente viu como esse método calcula o valor de cada variável, deu uma olhada em exemplos 2×2 e 3×3 e entendeu a interpretação geométrica dele. Por fim, também vimos as limitações, alternativas e quando usar a regra de Cramer.

Para entender melhor os sistemas lineares e suas soluções, dá uma olhada no nosso curso Álgebra Linear para Ciência de Dados, onde você vai aprender várias técnicas de álgebra linear, como a regra de Cramer.