Cramer's Rule: A Direct Method for Solving Linear Systems

Cramer’s rule provides a direct formula for solving systems of linear equations using determinants. While modern computational methods often perform better than Cramer’s rule for solving large systems, understanding this technique helps us comprehend the relationship between linear systems, determinants, and matrix theory in linear algebra. 

This article introduces Cramer’s rule, the formula, its mathematical foundations, and the geometric interpretation. We also demonstrate its application through multiple examples, its limitations, alternatives, and when it’s most effective in data science contexts.

What Is Cramer’s Rule?

Cramer’s rule states that each variable in the system can be found by dividing two determinants: the determinant of a modified coefficient matrix by the determinant of the original coefficient matrix.

This modified matrix is created by replacing one column of coefficients with the constants from the right-hand side of the equations.

To understand the conditions of the theorem, consider a system of linear equations represented in matrix form as Ax = b, where:

• A is the coefficient matrix
• x is the vector of unknowns
• b is the vector of constants

Cramer’s rule only applies when A is square (same number of equations as unknowns) and has a non-zero determinant, ensuring a unique solution exists.

Mathematical Foundations and Formulas

For a general n×n system, Cramer’s rule states that the i-th component of the solution vector is:

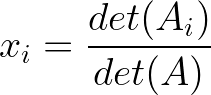
Cramer’s rule formula. (Image and all images below by the Author)

Where:

• x_i is the i-th variable we’re solving for
• det(A_i) is the determinant of matrix A with its i-th column replaced by vector b
• det(A) is the determinant of the original coefficient matrix

To understand this better, let’s consider a 2×2 system:

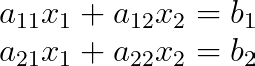
The coefficient matrix A and constant vector b are:

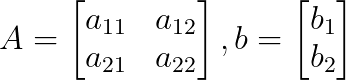
According to Cramer’s rule:

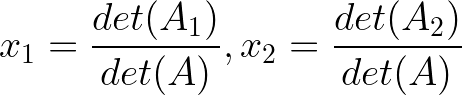
Where A₁ is A with the first column replaced by b:

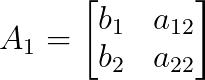
And A₂ is A with the second column replaced by b:

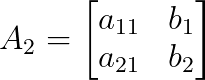
The determinant of a 2×2 matrix is calculated as:

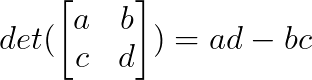
Once we understand the pattern of the solution above, we can apply it to any compatible system directly without solving simultaneous equations. We will also extend the rule to a 3x3 system in one of the examples later.

Geometric Interpretation of Cramer’s Rule

In addition to being a direct formula for solving linear systems, Cramer’s Rule also has a rich geometric interpretation.

Areas of parallelograms in 2D

Think of the columns of matrix A as vectors in the plane. These vectors form a parallelogram, and the determinant of A represents the signed area of that parallelogram.

When we replace one column with the vector b, we create a new parallelogram. The determinant of this new matrix, det⁡(Ai), represents the area of the modified shape where one of the original direction vectors has been substituted by b.

Thus:

Each variable xi​ tells us how much of b lies in the direction of the ith column vector of A, scaled by the overall area spanned by A’s columns.

Volumes of parallelepipeds in 3D

The same logic extends to 3D. Here, the determinant of A represents the volume of the parallelepiped formed by the three column vectors of A.

• Replacing one column with b gives us a new parallelepiped.
• The ratio det⁡(A_i)/det⁡(A) gives the relative volume contribution of that column to the overall shape.

In both 2D and 3D, Cramer’s Rule measures how much b “fills” the volume defined by A’s columns.

Step-by-Step Guide to Applying Cramer’s Rule

Let’s work through two examples to demonstrate how Cramer’s rule applies to systems of different sizes.

Solving a 2x2 system

Consider this system of two linear equations:

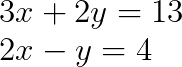
Step 1: Identify the coefficient matrix and constant vector

We can write the system as a coefficient matrix A and a constant vector b as below:

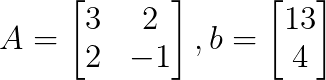
Step 2: Calculate the determinant of the coefficient matrix

The determinant of A will be:

det(A) = (3)(-1) - (2)(2)
det(A) = -3 - 4
det(A) = -7

Since det(A) = -7 ≠ 0, the system has a unique solution, and we can apply Cramer’s rule.

Step 3: Create modified matrices and calculate their determinants

For x, replace the first column of A with b:

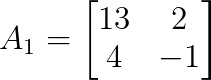
Now let’s calculate the determinant of A₁:

det(A₁) = (13)(-1) - (2)(4)
det(A₁) = -13 - 8
det(A₁) = -21

For y, replace the second column of A with b:

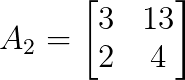
Now let’s calculate the determinant of A₂:

det(A₂) = (3)(4) - (13)(2)
det(A₂) = 12 - 26
det(A₂) = -14

Step 4: Apply Cramer’s rule formulas

We can calculate the values through the formula:

x = det(A₁) / det(A) = -21 / -7 = 3
y = det(A₂) / det(A) = -14 / -7 = 2

Finally, we can verify the results by substituting the values back into the equation:

• First equation: 3(3) + 2(2) = 9 + 4 = 13 
• Second equation: 2(3) — 1(2) = 6–2 = 4 

Thus, we have solved the 2x2 linear system using Cramer’s rule.

Solving a 3x3 system

Now let’s extend to a more complex 3x3 system:

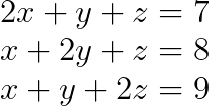
We’ll be repeating the same steps above for this example.

Step 1: Identify the coefficient matrix and constant vector

From the linear system, we can write the coefficient matrix A and constant vector b as:

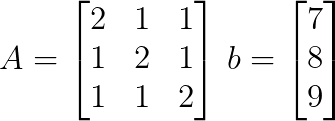
Step 2: Calculate the determinant of the coefficient matrix

Using the expansion along the first row:

det(A) =       2|2  1| - 1 |1  1| + 1 |1  2|
        		 |1  2|     |1  2|       |1  1|

Calculating each 2×2 determinant:

|2  1| = (2)(2) - (1)(1) = 4 - 1 = 3
|1  2|

|1  1| = (1)(2) - (1)(1) = 2 - 1 = 1
|1  2|

|1  2| = (1)(1) - (2)(1) = 1 - 2 = -1
|1  1|

Therefore, the determinant of A is:

det(A) = 2(3) - 1(1) + 1(-1)
det(A) = 6 - 1 - 1
det(A) = 4

Since det(A) = 4 ≠ 0, the system has a unique solution, and we can apply Cramer’s rule.

Step 3: Create modified matrices and calculate their determinants

For x, replace the first column of A with b:

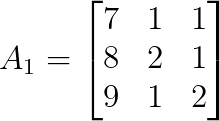
We can expand along the first row:

det(A₁) = 7|2  1| - 1|8  1| + 1|8  2|
   	        |1  2|     |9  2|      |9  1|

Calculating the determinant of A₁:

det(A₁) = 7(3) - 1(16 - 9) + 1(8 - 18)
det(A₁) = 21 - 1(7) + 1(-10)
det(A₁) = 21 - 7 - 10
det(A₁) = 4

For y, replace the second column of A with b:

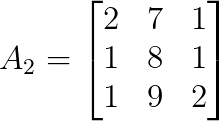
We can calculate the determinant of A₂ as below:

det(A₂) = 2|8  1| - 7|1  1| + 1|1  8|
                     |9  2|     |1  2|    |1  9|

det(A₂) = 2(16 - 9) - 7(2 - 1) + 1(9 - 8)
det(A₂) = 2(7) - 7(1) + 1(1)
det(A₂) = 14 - 7 + 1
det(A₂) = 8

For z, replace the third column of A with b:

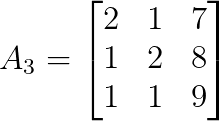
We can calculate the determinant of A₃ as below:

det(A₃) = 2|2  8| - 1|1  8| + 7|1  2|
                     |1  9|      |1  9|       |1  1|

det(A₃) = 2(18 - 8) - 1(9 - 8) + 7(1 - 2)
det(A₃) = 2(10) - 1(1) + 7(-1)
det(A₃) = 20 - 1 - 7
det(A₃) = 12

Step 4: Apply Cramer’s rule formulas

Since we have calculated all the necessary values, we can calculate the values of x, y, and z directly through the formula:

x = det(A₁) / det(A) = 4 / 4 = 1
y = det(A₂) / det(A) = 8 / 4 = 2
z = det(A₃) / det(A) = 12 / 4 = 3

Finally, we can verify the results by substituting the values back into the equation:

• First equation: 2(1) + 1(2) + 1(3) = 2 + 2 + 3 = 7 
• Second equation: 1(1) + 2(2) + 1(3) = 1 + 4 + 3 = 8 
• Third equation: 1(1) + 1(2) + 2(3) = 1 + 2 + 6 = 9 

Notice how the process remains consistent: we replace columns with the constant vector and calculate determinants. The 3×3 case requires more computation, but the underlying method is identical to the 2×2 case.

Limitations, Alternatives, and When to Use Cramer’s Rule

Like all algorithms, Cramer’s rule also comes with a few limitations. Let’s understand them:

Computational complexity

For an n×n system, Cramer’s rule requires computing (n+1) determinants. Since calculating a determinant using cofactor expansion has a complexity of O(n!), the overall complexity becomes prohibitive for large systems. 

Even with more efficient determinant algorithms, the method remains impractical beyond small systems.

Numerical stability issues

Cramer’s rule can suffer from numerical instability when determinants are close to zero. 

Small rounding errors in computing det(A) can lead to large errors in the solution when dividing by a near-zero value. This makes the method unreliable for ill-conditioned systems, which are common in real-world data.

Alternatives to Cramer’s Rule

Due to the primary computational complexity limitation, we often resort to one of the following alternatives:

• Gaussian elimination with partial pivoting transforms the system to row echelon form with O(n³) complexity, making it vastly more efficient than Cramer’s rule for systems larger than 3×3.
• LU decomposition factors the coefficient matrix into lower and upper triangular matrices, resulting in an efficient solution of multiple systems with the same coefficient matrix.
• QR decomposition provides better numerical stability for ill-conditioned systems by decomposing the matrix into orthogonal and upper triangular components.

When to use Cramer’s rule

Despite these limitations, Cramer’s rule is valuable in specific contexts such as:

• Theoretical analysis and proofs in linear algebra
• Symbolic computation where exact algebraic solutions are needed
• Small systems (2×2 or 3×3) where the explicit formulas are manageable
• Educational settings for understanding the connection between determinants and linear systems
• Deriving closed-form solutions in analytical work

However, it’s worth noting that, in data science practice, Cramer’s rule serves more as a conceptual and theoretical tool for understanding linear systems than as a computational method.

Conclusion

Cramer’s rule is a direct and formula-based approach to solving systems of linear equations through determinants. We explored how this method calculates the value of each variable, worked through 2×2 and 3×3 examples, and gained an understanding of its geometric interpretation. Finally, we also learned about the limitations, alternatives, and when to use Cramer’s rule.

To deepen your understanding of linear systems and their solutions, consider exploring our Linear Algebra for Data Science course, where you’ll learn about several linear algebra techniques like Cramer’s rule.