Cours
La courbe de demande est l'un des outils les plus intéressants et les plus utiles pour comprendre le comportement des consommateurs et les stratégies de tarification. Il est généralement utilisé pour analyser la relation entre le prix d'un bien ou d'un service et la quantité vendue, bien que dans d'autres contextes il puisse être utilisé pour analyser la dynamique du marché ou prévoir les résultats en matière de revenus.
Dans cet article, nous allons tout apprendre sur la courbe de demande. Nous examinerons à la fois les caractéristiques qui les définissent et les termes qui s'y rapportent. Plus tard, je prendrai également le temps de montrer comment la courbe de demande peut être étendue pour trouver le prix optimal qui maximise le profit - un peu d'algèbre appliquée utile pour créer une technique d'optimisation élémentaire que j'ai trouvée utile dans mon propre travail.
En suivant ces méthodes, je vous garantis que vous serez en mesure non seulement de prendre des décisions sur les stratégies de tarification, mais aussi d'articuler clairement les méthodes de manière à fournir un cadre pour les projets futurs. Même si j'utiliserai R et SQL dans cet article, sachez que vous pouvez utiliser ces mêmes méthodes avec d'autres outils majeurs qui existent, comme Excel, Python, Tableau et Power BI. Enfin, pour devenir un véritable expert en matière de tarification, je vous recommande vivement notre cours Forecasting Product Demand in R.
Qu'est-ce qu'une courbe de demande ?
La courbe de demande est un concept fondamental de la stratégie de fixation des prix et de l'économie en général. Il s'agit d'un moyen visuel convaincant de représenter la relation entre le prix d'un bien ou d'un service et la quantité demandée par les consommateurs. Les principaux éléments d'une courbe de demande sont le prix sur un axe et la quantité demandée sur l'autre. En voici un exemple :
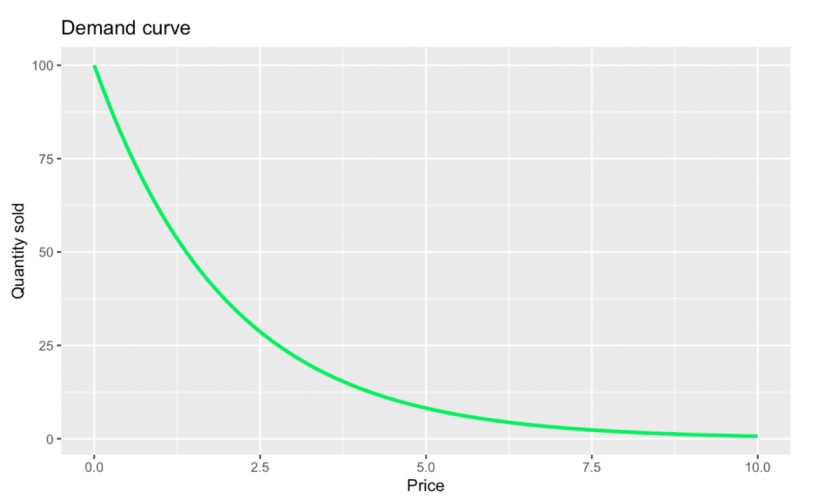
Une forme de base de la courbe de demande. Image par l'auteur.
Composantes d'une courbe de demande
Dans le graphique ci-dessus, vous remarquerez une chose qui est quelque peu évidente à première vue : le prix et la quantité vendue ont une relation inverse. Plus formellement, nous pourrions dire que la courbe de demande est très liée à ce que l'on appelle la loi de la demande, qui stipule que, toutes choses étant égales par ailleurs, lorsque le prix d'un produit diminue, la quantité demandée augmente. On parle parfois d'une relation entre le prix et la quantité, ce qui signifie que le prix d'un produit influe directement sur la quantité que les consommateurs sont prêts à acheter.
Toutefois, ce graphique contient également un élément un peu moins évident, à savoir que la quantité vendue chute plus rapidement lorsque le prix est bas et s'aplanit lorsque le prix est élevé. La courbure est liée à d'autres concepts, tels que l'élasticité changeante et l'utilité marginale décroissante, que j'aborderai dans la section suivante.
Élasticité de la demande par rapport au prix
L'un des concepts clés qui ressort de la relation inverse entre le prix et la quantité demandée est l'élasticité de la demande par rapport au prix, qui mesure la sensibilité de la quantité demandée à un changement de prix. Formellement, l'élasticité est souvent calculée comme suit :
![]()
On dit d'un produit qu'il est demande si une variation relativement faible du prix entraîne une variation importante de la quantité demandée. Les appareils électroniques haut de gamme ou les sacs à main griffés peuvent connaître une forte baisse de la demande si leur prix augmente ne serait-ce qu'un peu, car les consommateurs peuvent trouver des produits de substitution.
Un produit est inélastique La demande d'un produit est inélastique si des variations importantes du prix entraînent des variations relativement faibles de la quantité demandée. Les produits de première nécessité tels que l'essence ou les médicaments en sont des exemples classiques. Même si le prix augmente, les consommateurs sont toujours contraints d'acheter pratiquement la même quantité parce qu'il n'y a pas d'alternative.
Types de courbes de demande
Bien que j'aie montré un exemple de courbe de demande, sachez qu'elle peut prendre de nombreuses formes différentes en fonction des caractéristiques sous-jacentes du marché, du produit et des préférences des consommateurs. Bien qu'elle soit toujours descendante, cette relation ne doit pas nécessairement suivre une forme mathématique unique .
Courbes de demande linéaires
Les courbes de demande linéaires se caractérisent par un taux de variation constant entre le prix et la quantité. Ces cas sont courants dans les scénarios de marché simples. Elles sont représentées par une ligne droite.
Courbes de demande non linéaires
Comme nous l'avons vu, les courbes de demande ne sont pas toujours tracées comme des lignes parfaitement droites parce que la relation entre le prix et la quantité n'est pas toujours bien représentée par une simple fonction linéaire univoque. Il y a plusieurs raisons à cela, que j'ai commencé à évoquer plus haut :
- Changement d'élasticité: L'élasticité de la demande, c'est-à-dire la sensibilité de la demande à un changement de prix, varie souvent en différents points de la courbe. Par exemple, lorsque les prix sont très élevés, les acheteurs peuvent réagir fortement à la moindre baisse de prix.
- Utilité marginale décroissante: Dans de nombreux modèles économiques, chaque unité supplémentaire d'un bien apporte au consommateur un peu moins d'utilité que la précédente. Par conséquent, les consommateurs peuvent être disposés à acheter beaucoup plus si les prix passent d'un niveau élevé à un niveau modéré, mais une fois que vous avez atteint une certaine fourchette, une nouvelle baisse des prix n'entraîne pas une augmentation aussi importante de la quantité désirée ou vendue.
Dans la pratique, les courbes de demande non linéaires peuvent être plus réalistes parce qu'elles décrivent mieux un taux de changement variable. Après tout, les données du monde réel sont désordonnées et le comportement des consommateurs est complexe. Cela dit, il existe souvent des moyens de linéariser une courbe non linéaire, comme je le montrerai plus loin.
Courbe de demande individuelle et courbe de demande du marché
Nous pouvons également comparer les différences de demande au niveau du consommateur et du marché. Une courbe de demande individuelle représente la relation entre le prix d'un produit et la quantité demandée par un seul consommateur. Il reflète les préférences personnelles et la volonté de payer.
Une courbe de demande de marché combine la demande de tous les consommateurs d'un marché. Elle regroupe les courbes de demande individuelles, montrant la quantité totale demandée à chaque point de prix. En raison de leur construction, les courbes de demande de marché sont utilisées par les entreprises pour évaluer le potentiel du marché.
Courbe de demande et courbe d'offre
Si vous étudiez les courbes de demande, vous avez peut-être également entendu parler de ce que l'on appelle une courbe d' offre. En fait, la courbe d'offre et la courbe de demande sont les deux faces d'une même pièce. Alors que la courbe de demande indique la quantité d'un produit que les consommateurs sont prêts à acheter à différents prix, la courbe d'offre représente la quantité que les producteurs sont prêts à vendre à ces mêmes prix.
Si vous tracez une courbe de demande et une courbe d'offre sur le même graphique, vous verrez qu'elles se croisent. L'intersection de ces courbes, appelée point d'équilibre, est censée déterminer le prix et la quantité du marché. Ainsi, lorsque la demande est supérieure à l'offre, les prix ont tendance à augmenter, ce qui incite les producteurs à produire davantage. Mais lorsque l'offre dépasse la demande, les prix baissent, ce qui incite à acheter davantage.
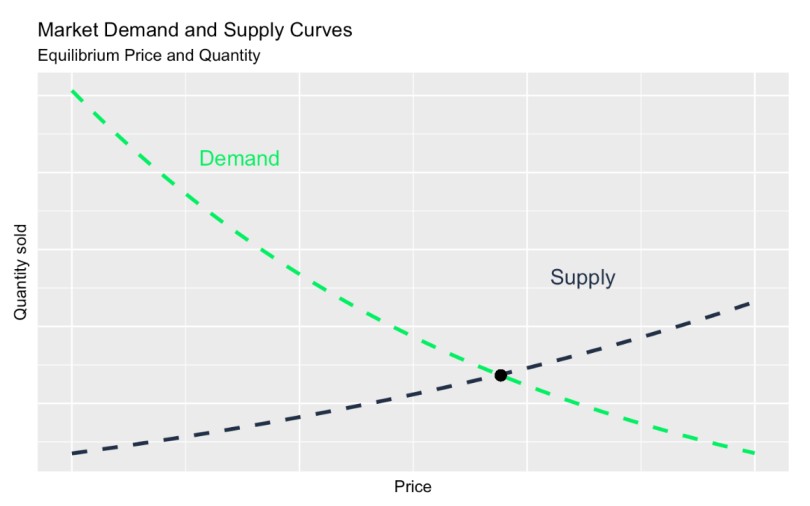
Courbe de demande et courbe d'offre. Image par l'auteur.
Utiliser une courbe de demande en science des données
Il existe de nombreuses façons d'utiliser les courbes de demande pour prendre des décisions commerciales. Je vais vous présenter une façon spécifique de rendre les courbes de demande utiles : Nous utiliserons nos données pour créer une courbe de demande et un modèle de demande en utilisant une technique de régression quadratique. Je vous montrerai comment vous pouvez utiliser cette technique à la fois dans R et SQL, où elle peut être utilisée dans des tableaux de bord interactifs Power BI ou Tableau.
Avant de continuer, je tiens à dire que, si vous lisez ceci et pensez que vous pourriez vouloir faire monter en compétence toute une équipe en même temps, comme une équipe de département d'analystes commerciaux ou de data scientists, DataCamp for Business est là pour vous aider. Nous aiderons votre équipe à développer des compétences et des techniques utiles dans le contexte spécifique de votre entreprise. De nombreux projets d'analyse de données lourdes nécessitent plusieurs contributeurs - alors contactez notre équipe DataCamp pour en savoir plus.
Faites progresser les compétences de votre équipe en matière de science des données
Exploitez tout le potentiel de la science des données avec DataCamp for Business. Accédez à des cours complets, des projets et des rapports centralisés pour des équipes de 2 personnes ou plus.

Utilisation d'une courbe de demande pour analyser les prix en R
Créons et analysons une courbe de demande à l'aide de R. Pour simuler un ensemble de données, j'ai créé une courbe de type décroissance exponentielle avec du bruit dispersé autour d'elle. L'idée est que chaque point de données représente une semaine de ventes pour un concessionnaire automobile, au cours de laquelle le concessionnaire propose différentes offres spéciales et essaie différents niveaux de prix pour le même type de voiture afin d'augmenter les ventes.
# Load necessary library
library(tidyverse)
# Define parameters for the exponential decay
a <- 100 # Initial value
b <- 0.5 # Decay rate
# Define a realistic price range
price <- seq(10000, 40000, length.out = 200) # Price from $10,000 to $40,000
# Calculate the exponential decay
y <- a * exp(-b * (price / 10000)) # Adjust decay rate to match price scaling
# Add mixed noise (additive + slight proportional)
set.seed(42) # For reproducibility
additive_noise <- rnorm(length(y), mean = 0, sd = 1) # Constant additive noise
proportional_noise <- rnorm(length(y), mean = 0, sd = 0.05 * y) # Small proportional noise
y_noisy <- y + additive_noise + proportional_noise
# Ensure no negative values (optional, as sales can't be negative)
y_noisy[y_noisy < 0] <- 0.01
# Combine price and noisy y into a data frame
demand_curve_data <- data.frame(
price = price,
quantity_sold = y_noisy
)
# Clean and prepare the data
demand_curve_data <- demand_curve_data %>%
mutate(quantity_sold = round(quantity_sold, 0)) %>%
filter(quantity_sold != 0)
# Plot the noisy exponential decay
ggplot(demand_curve_data, aes(x = price, y = quantity_sold)) +
geom_point(color = '#203147', alpha = 0.6) +
geom_line(
aes(y = a * exp(-b * (price / 10000))),
color = '#01ef63',
size = 1.2,
linetype = "dashed"
) +
labs(
title = "Cars Sold",
subtitle = "Demand Curve (Cars Sold)",
x = "Price ($)",
y = "Quantity Sold"
) +
scale_x_continuous(labels = scales::dollar_format()) # Format x-axis as dollars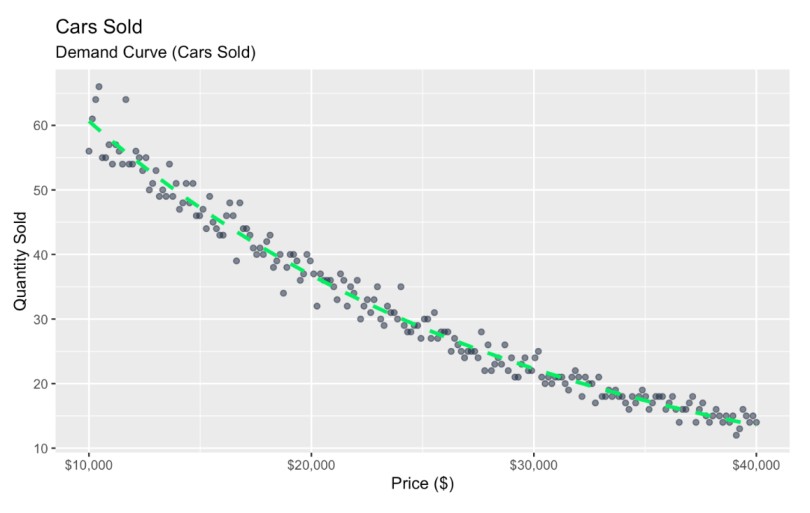 Courbe Courbe de demande avec bruit. Image par l'auteur
Courbe Courbe de demande avec bruit. Image par l'auteur
Ici, j'ai représenté sur un graphique la relation entre le prix et la quantité vendue, et j'ai utilisé des points du nuage de points pour représenter la variation naturelle, qui peut être due à de nombreuses raisons différentes.
À la lecture de ce graphique, on constate qu'à mesure que le prix augmente, les ventes diminuent, et que cette relation est plus sensible dans certaines gammes de prix que dans d'autres. Mais, en fonction de l'utilisation que vous faites des données, cet aperçu général peut ne pas être suffisant pour informer une décision commerciale pratique. D'après mon expérience, les patrons veulent souvent voir un aperçu normatif qui apporte une réponse concrète à une question commerciale plus urgente. L'une de ces questions est la suivante : Quel est le prix de la voiture qui maximise réellement le revenu global ?
Nous pourrions commencer par essayer de faire quelques suppositions en regardant simplement le graphique.
- Sur la partie inférieure, nous voyons, en suivant la ligne verte, que la quantité vendue est de 60 lorsque la valeur x du prix est de 10 000 $. Cela se traduirait par une recette totale de 600 000 dollars sur le site .
- En haut de l'échellenous voyons la ligne verte atteindre environ 10, où les valeurs x sont de 40 000 $, ce qui équivaut à $400,000 de revenus.
- Au milieu du site, la ligne verte atteint 30 et le prix est de 25 000 $. Cela équivaut à 750 000 dollars.
Vous commencez peut-être à avoir l'impression que le prix qui maximise le revenu global se situe quelque part au milieu. D'un point de vue conceptuel, c'est logique : Nous nous attendons à ce que des prix très bas génèrent un volume élevé de ventes mais des revenus relativement faibles, tandis que des prix très élevés génèreraient beaucoup moins de ventes et toujours des revenus relativement faibles. Mais quelque part au milieu, il doit y avoir un prix optimal qui maximise les revenus.
Maintenant, au lieu de regarder le graphique à la loupe, apprenons une meilleure façon, plus efficace et plus solide, de maximiser le revenu global. Nous pouvons déterminer le prix optimal en résolvant un problème d'optimisation rudimentaire. Nous créons d'abord un modèle linéaire, puis nous plions ce modèle en parabole et nous trouvons le point le plus élevé.
La première étape consiste à linéariser la relation. Comme j'ai construit tout cela avec une fonction de décroissance exponentielle, je sais que cela sera bien linéarisé en prenant le logarithme de la quantité vendue. Pour simplifier, ignorons toute hétéroscédasticité.
# Create a linearized version of the data
demand_curve_data$log_quantity_sold <- log(demand_curve_data$quantity_sold)
# Plot the linearized relationship
ggplot(demand_curve_data, aes(x = price, y = log_quantity_sold)) +
geom_point(color = '#203147', alpha = 0.6) +
geom_smooth(method = "lm", color = '#01ef63', se = FALSE) +
labs(
title = "Cars Sold",
subtitle = "Demand Curve (Log Quantity Sold)",
x = "Price ($)",
y = "Log of Quantity Sold"
) +
scale_x_continuous(labels = scales::dollar_format()) # Format x-axis as dollars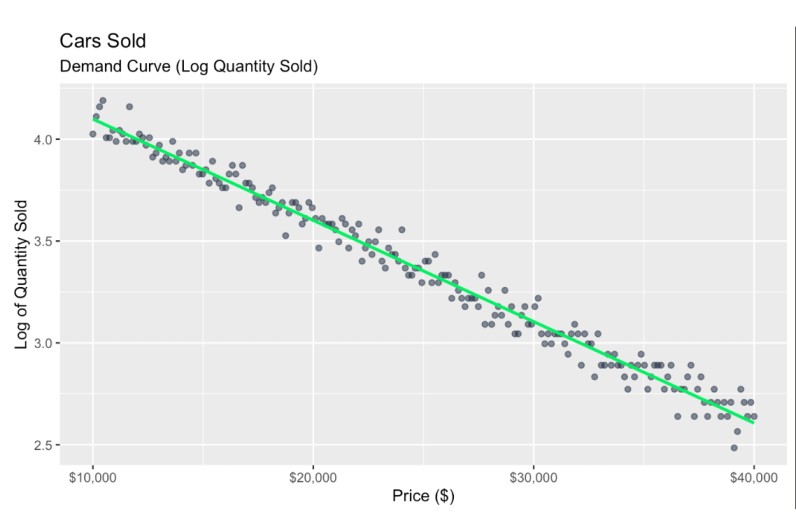
Courbe de demande transformée. Image par l'auteur
Nous pouvons maintenant créer une nouvelle variable appelée revenue qui est définie comme price multiplié par log_quantity_sold. Notons que nous créons un objet modèle linéaire à l'aide de la fonction lm() car nous voulons avoir accès aux nombres associés aux coefficients du modèle.
Pour l'étape suivante, nous insérons l'équation de notre modèle linéaire dans notre formule. Si nous n'avions pas eu de transformateur de bois :
-
Cela signifie que notre équation :
revenue = price * quantity_soldpeut maintenant être écrite commerevenue = price * (b0 + b1 * price). -
Ensuite, nous distribuons les termes. Tout comme nous répartissons les termes dans x(1-x) pour obtenir x-x2, nous réécrivons notre équation sous la forme suivante :
revenue = b0 * Price + b1 * price2.
Remarquez maintenant que nous aurions revenue défini par une équation qui a price comme terme au carré. Il s'agit là de la partie essentielle car, en représentant graphiquement price sous la forme d'un terme au carré, nous avons créé une fonction de maximisation.
Cependant, comme nous disposons d'une transformation logarithmique, nous devons effectuer une rétro-transformation exponentielle du modèle log-linéaire.
-
Cela signifie que notre équation :
revenue = price * log_quantity_soldva maintenant s'écrirerevenue = price * eb0 + b1 * price. -
Nous pouvons maintenant factoriser cette équation sous une nouvelle forme, si nous le souhaitons :
revenue=price * eb0 * eb1⋅price. Mais cette équation particulière ne se distribue pas de la même manière qu'une équation linéaire ou polynomiale, car la fonction exponentielle ne permet pas de séparer ou de distribuer les termes comme les termes algébriques plus standard, ci-dessus.
Quoi qu'il en soit, poursuivons :
# Fit a linear model to the log-transformed quantity sold
model <- lm(log_quantity_sold ~ price, data = demand_curve_data)
# Create a revenue model based on the linear model coefficients
revenue_model_data <- demand_curve_data %>%
mutate(
revenue_model = price * exp(coef(model)[1] + coef(model)[2] * price) # Modeled revenue
)
# Plot the revenue model
ggplot(revenue_model_data, aes(x = price, y = revenue_model)) +
geom_point(color = '#203147', alpha = 0.6) + # Actual revenue points
geom_line(color = '#01ef63', size = 1.2) + # Revenue model line
labs(
title = "Car Sales",
subtitle = "Revenue Model",
x = "Price ($)",
y = "Revenue ($)"
) +
scale_y_continuous(labels = scales::dollar_format()) + # Format y-axis as dollars
theme_minimal() + # Apply a minimal theme for aesthetics
theme(
text = element_text(family = "Arial", size = 12),
plot.title = element_text(face = "bold", size = 16),
plot.subtitle = element_text(size = 14)
)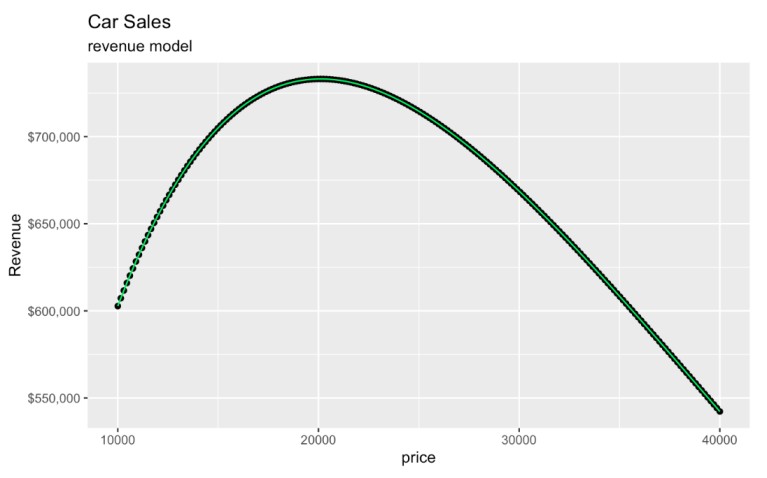
Modèle de revenus créé à partir d'une courbe de demande. Image par l'auteur.
Il est intéressant de noter que, même si le modèle original utilisait log_quantity_soldle graphique que nous avons créé est entièrement sur les échelles originales de price et revenue. La transformation logarithmique n'affecte que le modèle sous-jacent, et notre rétro-transformation impliquant e a ramené notre graphique à l'échelle d'origine pour qu'il reste facile à interpréter.
Trouver l'endroit où la dérivée est égale à zéro
Notre dernier point clé est le suivant : L'endroit au sommet de la parabole, où la dérivée est égale à zéro, sera le prix théorique qui maximisera les recettes.
Nous pouvons nous rappeler que nous trouvons la dérivée d'une équation telle que 3x² + 2x en multipliant avec les exposants pour obtenir 6x + 2. Le même raisonnement s'applique, mais rappelez-vous que dans cet exemple, nous devons d'abord rétro-transformer nos valeurs logarithmiques avant de former la fonction de revenu. En revenant à l'échelle d'origine avant de trouver le revenu maximum, nous savons que nous trouvons le prix qui maximise le revenu réel, et non une métrique transformée. Il s'agit donc de lafonction de revenu à différencier : revenue = price * e(b0 + b1 * price).
Travaillons ensemble. Ici, je prends les coefficients du modèle linéaire. Je définis ensuite une fonction de revenu. Enfin, je calcule le prix optimal et j'apprends à connaître la recette totale attendue associée.
# Model coefficients
b0 <- 4.596 # Intercept
b1 <- -4.974e-05 # Slope for price
# Define the revenue function
revenue <- function(P, b0, b1) {
P * exp(b0 + b1 * P)
}
# Calculate the optimal price (analytical solution from dR/dP = 0) - shortcut code here
(optimal_price <- -1 / b1)
# Calculate maximum revenue
(max_revenue <- revenue(optimal_price, b0, b1))[1] 20104.54
[1] 732853.5Vous avez peut-être remarqué que j'avais une ligne de code pour le prix optimal qui n'était pas bien expliquée dans le contexte. Je me réfère à cette partie du code : (optimal_price <- -1 / b1). Permettez-moi de vous montrer comment j'ai découvert que le prix optimal est égal à -1 moins la pente.
Tout d'abord, nous devons nous rappeler ce que l'on appelle la règle du produit en calcul, qui stipule que, si la fonction de x "f de x" est égale à u(x) multiplié par v(x), alors la dérivée, que nous pouvons écrire f'(x), est égale à la dérivée de la première chose multipliée par la section de la chose, puis ajoutée à la première chose multipliée par la dérivée de la deuxième chose.
# the product rule in calculus
f(x) = u(x) * v(x)
f'(x) = u'(x) * v(x) + u(x) * v'(x)Voici à nouveau notre équation, ainsi que la dérivée :
# our equation:
revenue = price * e^(b0 + b1 * price)
# the derivative of our equation
derivative = 1 * e^(b0 + b1 * price) + price * b1 * e^(b0 + b1 * price)Je sais que la dérivée du prix ici est 1 parce que c'est la chose dont nous trouvons la dérivée. "Dans quelle mesure le prix varie-t-il lorsque le prix change ? Il s'agit d'une relation individuelle.
D'autre part, la dérivée de e(b0 + b1 * prix) n'est pas nette comme l'est une fonction simple, comme 2x2, par exemple, qui a pour dérivée 4x.
Dans l'expression qui nous intéresse ici, l'exposant est un polynôme. L'astuce consiste à examiner attentivement tous les termes : Pour commencer,
-
b0n'est qu'une valeur unique, la dérivée est donc nulle. -
priceest égal à 1, comme nous l'avons déjà vu. -
b1est le facteur d'échelle, nous plaçons donc ce nombre devant, puis, comme le veut la règle, nous laissons l'exposant du polynôme inchangé.
La dérivée de e(b0 + b1 * price) est donc b1 * e(b0 + b1 * price). C'est ce qu'on appelle la règle de la chaîne, comme je vais le montrer ici :
# the chain rule in calculus
f(x) = x^g(x)
f'(x) = g'(x) * x^g(x)La dernière chose à faire est de procéder à l'affacturage.
L'algèbre nous dit qu'il s'agit de la même chose :
A + B * A = A(1+B)Et lorsque je regarde de près le produit dérivé avec lequel je travaille, je me rends compte qu'il y a une partie A et une partie B :
Le "A" est e(b0 + b1 * price) et le "B" est price * b1. Je peux donc tenir compte de ce qui suit
e^(b0 + b1 * price) + price * b1 * e^(b0 + b1 * price)à cela :
e^(b0 + b1 * price)(1 + price * b1)Enfin, je dois fixer cette dérivée à zéro pour trouver l'endroit où la pente cesse de monter et commence à descendre, c'est-à-dire le sommet de la parabole.
e^(b0 + b1 * price)(1 + price * b1) = 0Pour finir, je sais que lorsque A * B est égal à zéro, A ou B (ou les deux) doivent être égaux à zéro. Mais convenient, je sais que e(b0 + b1 * price) ne peut jamais être égal à zéro car il s'agit d'un exposant. S'il était positif, le nombre serait grand ; si l'exposant était évalué à 0, le résultat serait 1 ; si l'exposant était négatif, le résultat serait une petite fraction. Je peux donc en écarter la moitié lorsque je résous la question du zéro.
Il ne me reste plus qu'à déplacer les choses et à résoudre price.
(1 + b1 * price) = 0
b1 * price = -1
price = - 1 / b1C'est ainsi que j'ai trouvé -1 / b1 à insérer dans notre fonction personnalisée du code R.
Pour reprendre là où nous nous sommes arrêtés, nous pouvons représenter graphiquement le prix optimal et voir les recettes qui y sont associées.
Le prix optimal est de 20 104,54 $, ce qui permet d'escompter un revenu total de 732 853,50 $, plus ou moins. Je dis "plus ou moins" parce que, si vous vérifiez les calculs, nous supposons que 36,45 voitures ont été vendues, mais nous ne pouvons pas vendre la moitié d'une voiture.
ggplot(revenue_model_data, aes(x = price, y = revenue_model)) +
geom_point() + geom_line(color = '#01ef63') +
ggtitle("Car Sales") + labs(subtitle = "revenue model") +
ylab("Revenue") +
scale_y_continuous(labels = scales::dollar_format()) +
geom_vline(xintercept = optimal_price, linetype = "dashed", color = '#203147') +
geom_point(aes(x = optimal_price, y = max_revenue), color = '#203147', size = 3) 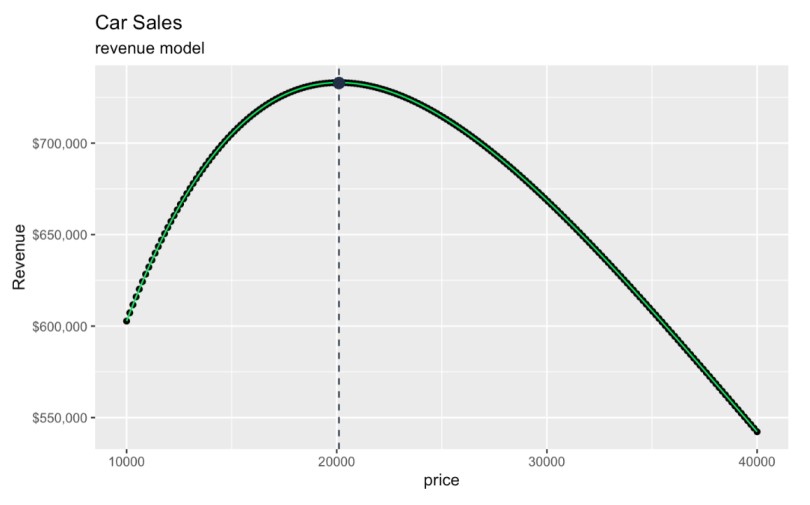 Trouver le prix qui maximise le revenu. Image par l'auteur.
Trouver le prix qui maximise le revenu. Image par l'auteur.
Dans un autre flux de travail, nous pourrions même étendre ces idées pour considérer le profit au lieu du revenu. Je ne vais pas tout expliquer ici, mais sachez que nous pouvons considérer profit = revenue - cost, où cost est considéré comme quantity * unit cost. Si le coût unitaire est constant et que la quantité peut être remplacée par une expression telle que 1 - price, nous obtenons à nouveau une parabole inversée.
Si vous souhaitez en savoir plus sur l'utilisation du calcul et des dérivés dans l'apprentissage automatique, essayez notre cours Introduction à l'apprentissage profond avec PyTorch qui explore en détail la descente de gradient dans le contexte de l'ajustement des hyperparamètres. Le contexte est différent, mais vous pouvez appliquer un raisonnement similaire. L'optimisation, sous ses différentes formes, comme vous le voyez, est une compétence clé de la science des données, et la pratique aide.
Courbe de demande vs. Courbe de Laffer
Si vous avez étudié l'économie, vous reconnaîtrez peut-être cette parabole comme étant similaire à la courbe de Laffer, un concept quelque peu controversé qui illustre l'influence des taux d'imposition sur les recettes fiscales de l'État.
Bien que je considère la courbe de Laffer et cette transformation de la courbe de demande comme des problèmes de type "maximisation vs. taux", la courbe de Laffer est spécifique à la fiscalité : l'axe des x représente le taux d'imposition (0 % à 100 %) et l'axe des y représente le total des recettes fiscales perçues. D'un point de vue conceptuel, la courbe de Laffer est également une forme en U inversé car, à l'extrémité supérieure, nous considérerions que, si le taux d'imposition était trop élevé, il ne produirait aucune recette parce que les particuliers ou les entreprises ne seraient pas incités à s'engager dans des activités imposables. Les économistes peuvent ne pas être d'accord sur la partie "incitative".

La courbe de Laffer dans Ferris Bueller's Day Off. Source : YouTube
Utilisation d'une courbe de demande pour analyser les prix dans SQL
Maintenant que l'idée a été exposée, je souhaite partager avec vous un script SQL qui effectuera le même travail. Cette fonction effectue une régression sur quantity_sold par rapport à price. Il vous permettra ensuite de trouver le prix optimal pour maximiser les recettes sur la base des coefficients de régression, et de déterminer les recettes maximales correspondantes.
Je pense que le script suivant sera particulièrement utile lors de la création de tableaux de bord dynamiques dans Power BI ou Tableau, car vous aurez des mises à jour de données en temps réel sans avoir besoin de mettre quoi que ce soit hors ligne.
Vous verrez également que j'ai utilisé une approche manuelle pour trouver les coefficients de régression à l'aide des fonctions agrégées de SQL, car la plupart des dialectes SQL ne disposent pas de fonctions de régression spécialisées que vous pouvez utiliser. Vous serez peut-être surpris d'apprendre que la régression linéaire simple fonctionne bien en SQL car les coefficients du modèle pour la régression linéaire simple peuvent être exprimés en termes de corrélation, d'écart type et de valeurs moyennes entre x et y.
-- SQL script to perform linear regression on log(quantity_sold) vs price,
-- calculate the optimal price to maximize revenue, and determine the maximum revenue.
WITH regression_data AS (
SELECT
COUNT(*) AS N,
SUM(price) AS sum_x,
SUM(LOG(quantity_sold)) AS sum_y,
SUM(price * LOG(quantity_sold)) AS sum_xy,
SUM(price * price) AS sum_x2,
SUM(LOG(quantity_sold) * LOG(quantity_sold)) AS sum_y2
FROM sales_data
),
regression_coefficients AS (
SELECT
N,
sum_x,
sum_y,
sum_xy,
sum_x2,
sum_y2,
(N * sum_xy - sum_x * sum_y) / (N * sum_x2 - sum_x * sum_x) AS slope,
(sum_y - ((N * sum_xy - sum_x * sum_y) / (N * sum_x2 - sum_x * sum_x)) * sum_x) / N AS intercept
FROM regression_data
),
optimal_price AS (
SELECT
slope,
intercept,
(-1 / slope) AS optimal_P
FROM regression_coefficients
),
max_revenue AS (
SELECT
optimal_P,
slope,
intercept,
optimal_P * EXP(intercept + slope * optimal_P) AS max_R
FROM optimal_price
)
SELECT
optimal_P AS Optimal_Price,
max_R AS Maximum_Revenue
FROM max_revenue;Optimal_Price | Maximum_Revenue
------------- | ----------------
20104.32 | 402082.58Veuillez noter que le script SQL fourni peut nécessiter des ajustements en fonction du dialecte SQL utilisé, car la syntaxe peut varier. En outre, à des fins de dépannage, je m'assurerais que votre tableau de données de vente contient des valeurs valides et positives pour price et quantity_sold, car des valeurs négatives ou nulles peuvent entraîner des erreurs.
De plus, si vous souhaitez incorporer une transformation logarithmique, comme nous l'avons fait dans la section R, vous pouvez le faire, mais, selon votre dialecte, la fonction du logarithme naturel peut être nommée différemment, soit LN ou LOG. Enfin, je dirais que, pour améliorer vos compétences en SQL en tant qu'analyste, vous devriez explorer le cursus de carrière Associate Data Analyst in SQL, afin de développer un ensemble complet d'outils.
Exceptions à la courbe de la demande
Il existe des exceptions notables où le comportement du consommateur peut défier le modèle standard de la courbe de demande :
Produits Giffen
Les biens de Giffen sont un type rare de biens inférieurs pour lesquels la loi de la demande ne s'applique pas. Lorsque le prix d'un bien de Giffen augmente, les consommateurs peuvent paradoxalement en acheter davantage plutôt que moins. En effet, ce bien représente une part tellement importante du budget du consommateur que lorsque son prix augmente, le consommateur ne peut plus se permettre d'acheter des produits de substitution plus souhaitables et est contraint d'acheter encore plus de biens de Giffen. Un exemple historique classique (bien que discuté) est l'augmentation du prix du pain au cours du 19e siècle dans certaines régions (l'Angleterre, par exemple), où les gens ont fini par consommer plus de pain parce qu'ils ne pouvaient pas s'offrir d'autres aliments plus chers.
Les biens de Veblen
Les produits Veblen sont des produits de luxe ou des symboles de statut - tels que les sacs à main de créateurs, les vins fins ou les montres haut de gamme - dont la demande augmente en même temps que le prix. Une partie de leur attrait provient de la perception qu'un prix élevé est le signe d'une exclusivité ou d'un statut social plus élevé, ce qui rend le bien plus désirable au fur et à mesure qu'il devient plus cher. Vous pouvez considérer cela comme de la "consommation ostentatoire".
Autres cas particuliers
- Effets de groupe ou de réseau: Certains biens prennent de la valeur pour chaque consommateur à mesure qu'ils sont utilisés par un plus grand nombre de personnes (par exemple, les plateformes de médias sociaux, certains écosystèmes logiciels). La demande peut augmenter non seulement en raison du prix, mais aussi de la popularité croissante du bien ou de la taille du réseau.
- Effet snob: Certains consommateurs achètent des biens précisément parce que peu d'autres personnes les possèdent. Dans ces cas, des prix plus bas pourraient faire paraître le produit "moins exclusif", ce qui en diminuerait l'attrait.
- Actifs spéculatifs ou d'investissement: Pour des actifs comme certaines crypto-monnaies ou matières premières, si le marché pense que les prix vont continuer à augmenter, la demande peut bondir en réponse à la hausse des prix, plutôt que de chuter.
Dans tous ces exemples, la relation habituelle entre le prix et la quantité s'inverse ou devient plus complexe en raison de facteurs psychologiques, culturels ou situationnels qui annulent l'hypothèse classique selon laquelle les consommateurs veulent simplement "plus à des prix plus bas".
Courbe de demande Termes courants
Nous avons examiné quelques termes différents dans cet article. Créons un tableau pour vous aider à y voir plus clair.
| Concept | Description |
|---|---|
| Courbe de demande | Représentation graphique montrant la relation entre le prix d'un bien et la quantité demandée par les consommateurs. |
| Loi de la demande | Elle affirme que, toutes choses étant égales par ailleurs, lorsque le prix d'un produit diminue, la quantité demandée augmente. |
| Relation prix-quantité | Indique que le prix d'un produit influence directement la quantité que les consommateurs sont prêts à acheter. |
| Élasticité | Mesure la sensibilité de la quantité demandée à un changement de prix. |
| Utilité marginale décroissante | Se réfère à la diminution de la satisfaction ou de l'utilité résultant de la consommation d'unités supplémentaires d'un produit. |
Réflexions finales
Nous avons couvert beaucoup de terrain : Nous avons tout pratiqué, des courbes et modèles de demande aux transformations logarithmiques et exponentielles, en passant par les techniques de régression quadratique et l'optimisation.
Continuez à apprendre l'analyse commerciale avec DataCamp. Envisagez de vous inscrire à des cours tels que ceux que j'ai mentionnés précédemment : Forecasting Product Demand in R et Data-Driven Decision Making for Business, qui vous apprendront tous deux à utiliser les données pour améliorer vos décisions dans le domaine des affaires et de la finance. Rien ne remplace les compétences techniques et la connaissance des bonnes techniques.
En outre, continuez à pratiquer les éléments essentiels de la science des données. En plus des cours de base sur la régression(Introduction à la régression avec statsmodels en Python et Introduction à la régression en R) apprenez la modélisation non linéaire avec les modèles additifs généralisés (GAM) en R ou les bases de la statistique en Python. Je vous recommande également d'entreprendre notre cursus complet de scientifique en apprentissage automatique en Python. Choisissez le domaine dans lequel vous êtes le plus faible, afin d'apprendre le plus.

Je suis rédacteur et éditeur dans le domaine de la science des données. Je suis particulièrement intéressé par l'algèbre linéaire, les statistiques, R, etc. Je joue également beaucoup aux échecs !