Curso
La curva de demanda es una de las herramientas más interesantes y útiles para comprender el comportamiento de los consumidores y las estrategias de fijación de precios. Suele utilizarse para analizar la relación entre el precio de un bien o servicio y la cantidad vendida, aunque en otros contextos puede emplearse para analizar la dinámica del mercado o prever los resultados de los ingresos.
En este artículo aprenderemos todo sobre la curva de demanda. Exploraremos tanto las características definitorias como los términos relacionados. Más adelante, también encontraré tiempo para mostrar cómo se puede ampliar la curva de demanda para encontrar el precio óptimo que maximiza el beneficio: un poco útil de álgebra aplicada para crear una técnica de optimización elemental que me resultó útil en mi propio trabajo.
Siguiendo estos métodos, te garantizo que no sólo serás capaz de tomar decisiones sobre estrategias de fijación de precios, sino que también serás capaz de articular claramente los métodos de forma que sirvan de marco para futuros proyectos. Aunque en este artículo utilizaré R y SQL, debes saber que puedes utilizar estos mismos métodos con otras herramientas importantes, como Excel, Python, Tableau y Power BI. Por último, quiero decir que, para convertirte realmente en un experto en fijación de precios, te recomiendo encarecidamente nuestro curso Previsión de la demanda de productos en R.
¿Qué es una curva de demanda?
Una curva de demanda es un concepto fundamental de la estrategia de precios y de la economía en general. Es una forma visual convincente de representar la relación entre el precio de un bien o servicio y la cantidad demandada por los consumidores. Los principales componentes de una curva de demanda incluyen el precio en un eje y la cantidad demandada en el otro. He aquí un ejemplo:
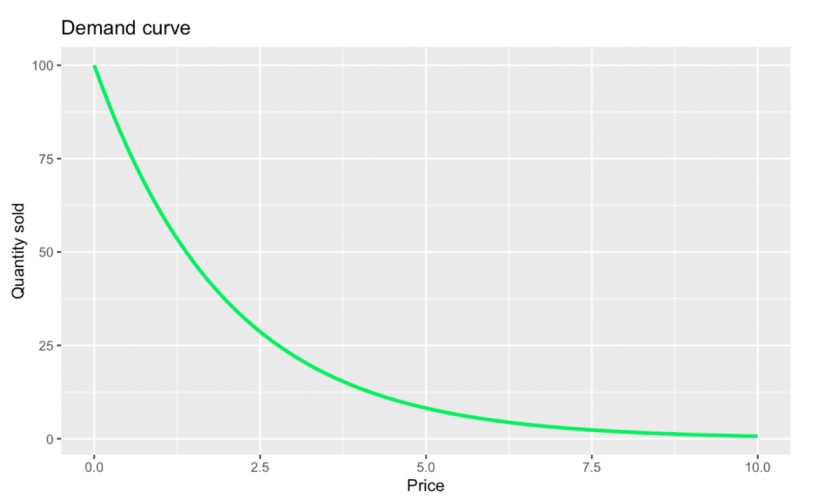
Una forma básica de curva de demanda. Imagen del autor.
Componentes de una curva de demanda
En el gráfico anterior, observarás algo que resulta algo obvio a primera vista: que el precio y la cantidad vendida tienen una relación inversa. Más formalmente, podríamos decir que la curva de demanda está muy relacionada con lo que se conoce como ley de la demanda, que afirma que, en igualdad de condiciones, a medida que disminuye el precio de un producto, aumenta la cantidad demandada. A veces, esta misma idea se denomina relación precio-cantidad, lo que significa que el precio de un producto influye directamente en la cantidad que los consumidores están dispuestos a comprar.
Sin embargo, este gráfico concreto también contiene algo un poco menos obvio, y es que la cantidad vendida cae más precipitadamente cuando el precio es bajo y se aplana cuando el precio es alto. La curvatura aquí se relaciona con otros conceptos, como la elasticidad cambiante y la utilidad marginal decreciente, que trataré en la siguiente sección.
Elasticidad-precio de la demanda
Un concepto clave que se desprende de la relación inversa entre precio y cantidad demandada es la elasticidad-precio de la demanda, que mide lo sensible que es la cantidad demandada a un cambio de precio. Formalmente, la elasticidad suele calcularse como:
![]()
Se dice que un producto tiene elástico si un cambio relativamente pequeño en el precio provoca un gran cambio en la cantidad demandada. Los productos electrónicos de gama alta o los bolsos de diseño pueden sufrir una fuerte caída de la demanda si sus precios suben aunque sea un poco, porque los consumidores pueden encontrar sustitutos.
Un producto tiene inelástico si grandes cambios en el precio provocan cambios relativamente pequeños en la cantidad demandada. Necesidades como la gasolina o los medicamentos son ejemplos clásicos. Aunque suba el precio, los consumidores siguen viéndose obligados a comprar casi la misma cantidad porque no hay alternativas.
Tipos de curvas de demanda
Aunque he mostrado un ejemplo de curva de demanda, debes saber que puede adoptar muchas formas distintas en función de las características subyacentes del mercado, el producto y las preferencias del consumidor. Aunque siempre tiene una pendiente descendente, esta relación no tiene por qué seguir una única forma matemática.
Curvas de demanda lineales
Las curvas de demanda lineales presentan una tasa de variación constante entre el precio y la cantidad. Serían habituales en escenarios de mercado sencillos. Se representan mediante una línea recta.
Curvas de demanda no lineales
Como hemos visto, las curvas de demanda no siempre se dibujan como líneas perfectamente rectas, porque la relación entre precio y cantidad no siempre está bien representada por una simple función lineal uno a uno. Hay varias razones, que he empezado a mencionar antes:
- Cambio de elasticidad: La elasticidad de la demanda, es decir, lo sensible que es la demanda a un cambio de precio, suele variar en distintos puntos de la curva. Por ejemplo, cuando los precios son muy altos, los compradores pueden reaccionar con fuerza incluso a una ligera bajada de precios.
- Utilidad marginal decreciente: En muchos modelos económicos, cada unidad adicional de un bien proporciona al consumidor un poco menos de utilidad que la anterior. Como resultado, los consumidores pueden estar dispuestos a comprar mucho más si los precios bajan de niveles altos a moderados, pero una vez que se alcanza un determinado rango, bajar más el precio no provoca el mismo gran aumento de la cantidad deseada o vendida.
En la práctica, las curvas de demanda no lineales pueden ser más realistas porque representan mejor una tasa de cambio variable. Al fin y al cabo, los datos del mundo real son confusos, y el comportamiento del consumidor es complejo. Dicho esto, a menudo hay formas de linealizar una curva no lineal, como mostraré más adelante.
Curva de demanda individual frente a curva de demanda del mercado
También podemos comparar las diferencias en la demanda a nivel de consumidor y de mercado. Una curva de demanda individual representa la relación entre el precio de un producto y la cantidad demandada por un único consumidor. Refleja las preferencias personales y la disposición a pagar.
Una curva de demanda de mercado combina la demanda de todos los consumidores de un mercado. Agrega curvas de demanda individuales, mostrando la cantidad total demandada en cada punto de precio. Por la forma en que están construidas, las empresas utilizan las curvas de demanda de mercado para calibrar el potencial de mercado.
Curva de demanda vs. curva de oferta
Si estás estudiando las curvas de demanda, es posible que también hayas oído hablar de lo que se llama curva de oferta. Esencialmente, una curva de oferta y una curva de demanda son dos caras de la misma moneda. Mientras que la curva de demanda muestra qué cantidad de un producto están dispuestos a comprar los consumidores a distintos precios, la curva de oferta representa qué cantidad están dispuestos a vender los productores a esos mismos precios.
Ahora bien, si trazas una curva de demanda y una curva de oferta en el mismo gráfico, verás un lugar donde se cruzan. Se cree que la intersección de estas curvas, conocida como punto de equilibrio, determina el precio y la cantidad del mercado. Así pues, cuando la demanda supera a la oferta, los precios tienden a subir, lo que incentiva a los productores a producir más. Pero cuando la oferta supera a la demanda, los precios bajan, lo que anima a comprar más.
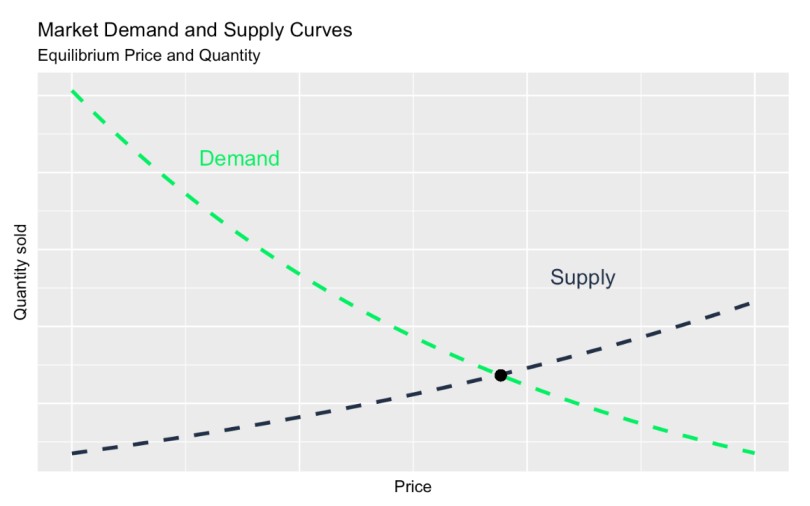
Curva de demanda frente a curva de oferta. Imagen del autor.
Utilizar una curva de demanda en la ciencia de datos
Hay muchas formas distintas de utilizar las curvas de demanda para tomar decisiones empresariales. Aquí voy a explicarte una forma concreta de hacer útiles las curvas de demanda: Utilizaremos nuestros datos para crear una curva de demanda y un modelo de demanda utilizando una técnica de regresión cuadrática. Mostraré cómo puedes utilizar esta técnica tanto en R como en SQL, donde se puede utilizar en cuadros de mando interactivos de Power BI o Tableau.
Antes de continuar, quiero decir que, si estás leyendo esto y crees que podrías querer mejorar las competencias de todo un equipo a la vez, como un equipo de departamento de analistas empresariales o científicos de datos, DataCamp for Business está aquí para ayudarte. Ayudaremos a tu equipo a desarrollar habilidades y técnicas que sean útiles en el contexto específico de tu empresa. Muchos proyectos de análisis de datos pesados requieren múltiples colaboradores, así que ponte en contacto con nuestro equipo de DataCamp para saber más.
Mejora las habilidades de tu equipo en Ciencia de Datos
Libera todo el potencial de la ciencia de datos con DataCamp para empresas. Accede a cursos completos, proyectos e informes centralizados para equipos de 2 o más personas.

Utilizar una curva de demanda para analizar los precios en R
Vamos a crear y analizar una curva de demanda utilizando R. Para simular un conjunto de datos, he creado una curva de tipo decaimiento exponencial con ruido disperso a su alrededor. La idea es que cada punto de datos representa una semana de ventas de un concesionario de coches, en la que el concesionario ofrece diferentes ofertas especiales y prueba diferentes niveles de precios para el mismo tipo de coche, en un intento de aumentar las ventas.
# Load necessary library
library(tidyverse)
# Define parameters for the exponential decay
a <- 100 # Initial value
b <- 0.5 # Decay rate
# Define a realistic price range
price <- seq(10000, 40000, length.out = 200) # Price from $10,000 to $40,000
# Calculate the exponential decay
y <- a * exp(-b * (price / 10000)) # Adjust decay rate to match price scaling
# Add mixed noise (additive + slight proportional)
set.seed(42) # For reproducibility
additive_noise <- rnorm(length(y), mean = 0, sd = 1) # Constant additive noise
proportional_noise <- rnorm(length(y), mean = 0, sd = 0.05 * y) # Small proportional noise
y_noisy <- y + additive_noise + proportional_noise
# Ensure no negative values (optional, as sales can't be negative)
y_noisy[y_noisy < 0] <- 0.01
# Combine price and noisy y into a data frame
demand_curve_data <- data.frame(
price = price,
quantity_sold = y_noisy
)
# Clean and prepare the data
demand_curve_data <- demand_curve_data %>%
mutate(quantity_sold = round(quantity_sold, 0)) %>%
filter(quantity_sold != 0)
# Plot the noisy exponential decay
ggplot(demand_curve_data, aes(x = price, y = quantity_sold)) +
geom_point(color = '#203147', alpha = 0.6) +
geom_line(
aes(y = a * exp(-b * (price / 10000))),
color = '#01ef63',
size = 1.2,
linetype = "dashed"
) +
labs(
title = "Cars Sold",
subtitle = "Demand Curve (Cars Sold)",
x = "Price ($)",
y = "Quantity Sold"
) +
scale_x_continuous(labels = scales::dollar_format()) # Format x-axis as dollars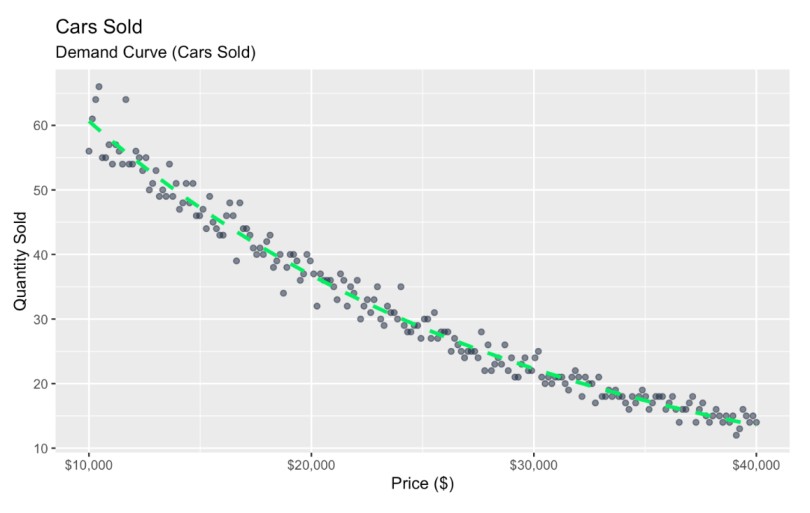 de demanda con ruidoCurva de demanda con ruido. Imagen del autor
de demanda con ruidoCurva de demanda con ruido. Imagen del autor
Aquí he representado gráficamente una relación entre el precio y la cantidad vendida, y he utilizado puntos de dispersión para representar la variación natural, que podría deberse a muchas razones diferentes.
Leyendo este gráfico, vemos que a medida que aumenta el precio, disminuyen las ventas, y esta relación es más sensible en unos rangos de precios que en otros. Pero, dependiendo de lo que hagas con los datos, esta visión general puede no ser suficiente para tomar una decisión empresarial práctica. Según mi experiencia, los jefes suelen querer ver una visión normativa que ofrezca una respuesta concreta a una cuestión empresarial más apremiante. Una de estas preguntas es: ¿Cuál es el precio del coche que realmente maximiza los ingresos totales?
Podríamos empezar intentando hacer algunas conjeturas con sólo mirar el gráfico.
- En el extremo inferior, vemos, siguiendo la línea verde, que la cantidad vendida es 60 cuando el valor x del precio es 10.000 $. Esto se traduciría en 600.000 $ de ingresos totales .
- En el extremo superiorvemos que la línea verde llega a 10 más o menos, donde los valores x son 40.000 $, lo que equivale a $400,000 de ingresos.
- Justo en el centro, vemos que la línea verde llega a 30, donde el precio es de 25.000 $. Esto equivale a 750.000 $.
Puede que ahora estés empezando a tener la sensación de que el precio que maximiza los ingresos totales está en algún punto intermedio. Conceptualmente, esto tiene sentido: Esperamos que los precios superbajos produzcan un gran volumen de ventas pero unos ingresos relativamente pequeños, mientras que los precios superaltos producirían muchas menos ventas y también unos ingresos relativamente pequeños. Pero en algún punto intermedio debe haber un precio óptimo que maximice los ingresos.
Ahora, en lugar de mirar el gráfico a ojo, aprendamos una forma mejor, más eficaz y sólida de maximizar los ingresos totales. Podemos averiguar el precio óptimo resolviendo un problema rudimentario de optimización. Primero creamos un modelo lineal, luego doblamos ese modelo en una parábola y encontramos el punto más alto.
Nuestro primer paso aquí es linealizar la relación. Como he construido todo esto con una función de decaimiento exponencial, sé que se linealizará bien tomando el logaritmo de la cantidad vendida. Para simplificar, ignoremos cualquier heteroscedasticidad.
# Create a linearized version of the data
demand_curve_data$log_quantity_sold <- log(demand_curve_data$quantity_sold)
# Plot the linearized relationship
ggplot(demand_curve_data, aes(x = price, y = log_quantity_sold)) +
geom_point(color = '#203147', alpha = 0.6) +
geom_smooth(method = "lm", color = '#01ef63', se = FALSE) +
labs(
title = "Cars Sold",
subtitle = "Demand Curve (Log Quantity Sold)",
x = "Price ($)",
y = "Log of Quantity Sold"
) +
scale_x_continuous(labels = scales::dollar_format()) # Format x-axis as dollars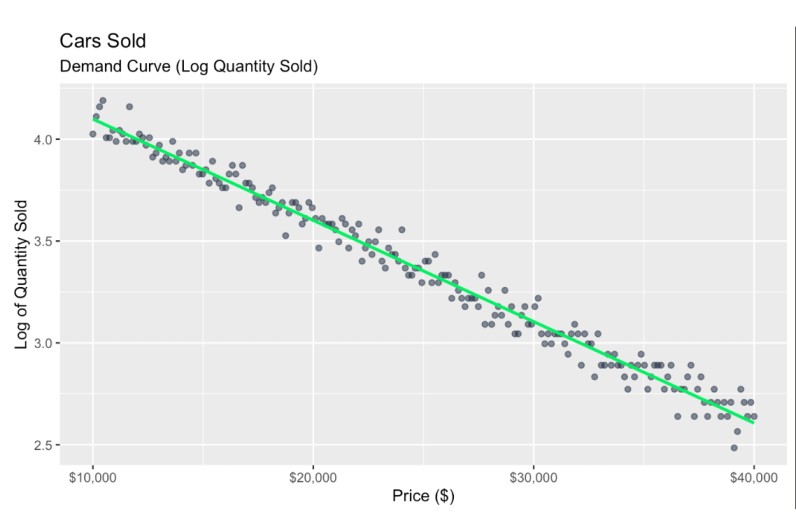
Curva de demanda transformada. Imagen del autor
Ahora, podemos crear una nueva variable llamada revenue que se define como price veces la log_quantity_sold. Como nota, creamos un objeto modelo lineal utilizando la función lm() porque queremos acceder a los números asociados a los coeficientes del modelo.
Para nuestro siguiente paso, insertamos la ecuación de nuestro modelo lineal en nuestra fórmula. Si no hubiéramos tenido transformación logarítmica:
-
Esto significaría que nuestra ecuación:
revenue = price * quantity_soldpuede escribirse ahora comorevenue = price * (b0 + b1 * price). -
Después, distribuiríamos los términos. Igual que distribuiríamos los términos en x(1-x) para hacer x-x2, reescribiríamos nuestra ecuación como,
revenue = b0 * Price + b1 * price2.
Observa ahora que tendríamos revenue definido por una ecuación que tiene price como término al cuadrado. Esta es realmente la parte clave porque, al graficar price como un término al cuadrado, hemos creado ahora una función maximizadora.
Sin embargo, como tenemos una transformación logarítmica, tenemos que hacer una retrotransformación exponencial del modelo logarítmico-lineal.
-
Esto significa que nuestra ecuación:
revenue = price * log_quantity_soldse va a escribir ahora comorevenue = price * eb0 + b1 * price. -
Ahora podemos factorizar esta ecuación en una nueva forma, si lo preferimos:
revenue=price * eb0 * eb1⋅price. Pero esta ecuación en concreto no se distribuye del mismo modo que una ecuación lineal o polinómica, porque la función exponencial no permite separar ni distribuir los términos como los términos algebraicos más estándar, más arriba.
En cualquier caso, continuemos:
# Fit a linear model to the log-transformed quantity sold
model <- lm(log_quantity_sold ~ price, data = demand_curve_data)
# Create a revenue model based on the linear model coefficients
revenue_model_data <- demand_curve_data %>%
mutate(
revenue_model = price * exp(coef(model)[1] + coef(model)[2] * price) # Modeled revenue
)
# Plot the revenue model
ggplot(revenue_model_data, aes(x = price, y = revenue_model)) +
geom_point(color = '#203147', alpha = 0.6) + # Actual revenue points
geom_line(color = '#01ef63', size = 1.2) + # Revenue model line
labs(
title = "Car Sales",
subtitle = "Revenue Model",
x = "Price ($)",
y = "Revenue ($)"
) +
scale_y_continuous(labels = scales::dollar_format()) + # Format y-axis as dollars
theme_minimal() + # Apply a minimal theme for aesthetics
theme(
text = element_text(family = "Arial", size = 12),
plot.title = element_text(face = "bold", size = 16),
plot.subtitle = element_text(size = 14)
)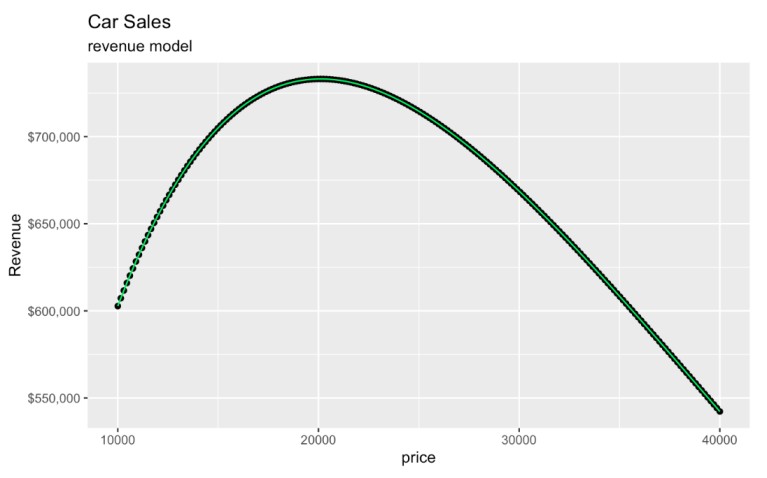
Modelo de ingresos creado a partir de una curva de demanda. Imagen del autor.
Curiosamente, aunque el modelo original utilizaba log_quantity_soldel gráfico que hemos creado está totalmente en las escalas originales de price y revenue. La transformación logarítmica sólo afecta al modelo subyacente, y nuestra retrotransformación con e pone nuestro gráfico en la escala original para que siga siendo fácil de interpretar.
Encontrar el punto en que la derivada es igual a cero
Ahora, nuestro último punto clave es éste: El lugar en la parte superior de la parábola, donde la derivada es igual a cero, va a ser el precio teórico que maximiza los ingresos.
Podemos recordar que hallamos la derivada de una ecuación como 3x² + 2x multiplicando por los exponentes para obtener 6x + 2. Este mismo razonamiento es aplicable, pero, de nuevo, recuerda que, en este ejemplo, primero tenemos que retrotransformar nuestros valores registrados antes de formar la función de ingresos. Al volver a la escala original antes de encontrar el máximo de ingresos, sabemos que estamos encontrando el precio que maximiza los ingresos reales, no alguna métrica transformada. Así que esta es la función de ingresos correcta para diferenciar: revenue = price * e(b0 + b1 * price).
Vamos a solucionarlo. Aquí tomo los coeficientes del modelo lineal. A continuación, defino una función de ingresos. Por último, calculo el precio óptimo y conozco los ingresos totales esperados asociados.
# Model coefficients
b0 <- 4.596 # Intercept
b1 <- -4.974e-05 # Slope for price
# Define the revenue function
revenue <- function(P, b0, b1) {
P * exp(b0 + b1 * P)
}
# Calculate the optimal price (analytical solution from dR/dP = 0) - shortcut code here
(optimal_price <- -1 / b1)
# Calculate maximum revenue
(max_revenue <- revenue(optimal_price, b0, b1))[1] 20104.54
[1] 732853.5Te habrás dado cuenta de que tenía una línea de código para el precio óptimo que no estaba bien explicada en el contexto. Me refiero a esta parte del código: (optimal_price <- -1 / b1). Permíteme que te muestre cómo lo he averiguado, que el precio óptimo es -1 menos la pendiente.
En primer lugar, tenemos que recordar lo que se llama la regla del producto en cálculo, que establece que, si la función de x "f de x" es igual a u(x) por v(x), entonces la derivada, que podemos escribir como f'(x), es igual a la derivada de la primera cosa multiplicada por la de la sección, luego sumada a la primera cosa por estas derivada de la segunda cosa.
# the product rule in calculus
f(x) = u(x) * v(x)
f'(x) = u'(x) * v(x) + u(x) * v'(x)Aquí está de nuevo nuestra ecuación, junto con la derivada:
# our equation:
revenue = price * e^(b0 + b1 * price)
# the derivative of our equation
derivative = 1 * e^(b0 + b1 * price) + price * b1 * e^(b0 + b1 * price)Sé que la derivada del precio aquí es 1 porque es de lo que estamos hallando la derivada. "¿Cuánto cambia el precio cuando cambia el precio?" Es una relación de uno a uno.
Por otro lado, la derivada de e(b0 + b1 * precio) no es nítida como lo es una función simple, como 2x2, por ejemplo, que tiene como derivada 4x.
En la expresión con la que trabajamos aquí, el exponente es un polinomio. El truco está en fijarse bien en todos los términos: Para empezar,
-
b0es un único valor, por lo que la derivada es cero -
pricees 1, como ya hemos manejado. -
b1es el factor de escala, así que ponemos ese número delante, y luego, según la regla, dejamos igual el exponente del polinomio.
Por tanto, la derivada de e(b0 + b1 * price) es b1 * e(b0 + b1 * price). Esto se conoce como la regla de la cadena, como mostraré aquí:
# the chain rule in calculus
f(x) = x^g(x)
f'(x) = g'(x) * x^g(x)Lo último es hacer un poco de factoring.
El álgebra nos dice que son iguales:
A + B * A = A(1+B)Y cuando miro de cerca el derivado con el que trabajo, me doy cuenta de que hay una parte A y una parte B:
La "A" es e(b0 + b1 * price) y la "B" es price * b1. Así puedo factorizar esto
e^(b0 + b1 * price) + price * b1 * e^(b0 + b1 * price)a esto:
e^(b0 + b1 * price)(1 + price * b1)Por último, tengo que poner esta derivada a cero para encontrar el lugar donde la pendiente deja de subir y empieza a bajar, que es el vértice de la parábola.
e^(b0 + b1 * price)(1 + price * b1) = 0Como truco final, sé que, cuando A * B es igual a cero, A o B (o ambos) tienen que ser iguales a cero. Pero convenientemente, sé que e(b0 + b1 * price) nunca puede ser igual a cero porque es un exponente. Si fuera positivo, el número sería grande; si el exponente se evaluara en 0, el resultado sería 1; si el exponente fuera negativo, el resultado sería una fracción pequeña. Así puedo descartar la mitad al resolver para cero.
Lo único que tengo que hacer ahora es mover las cosas de sitio y resolver para price.
(1 + b1 * price) = 0
b1 * price = -1
price = - 1 / b1Así es como encontré -1 / b1 para ponerlo en nuestra función personalizada de código R.
Ahora, para continuar donde lo dejamos, podemos representar gráficamente el precio óptimo y ver sus ingresos asociados.
El precio óptimo es de 20.104,54 $, lo que arroja unos ingresos totales esperados de 732.853,50 $, más o menos. Digo "más o menos" porque, si compruebas las matemáticas, partimos de la base de 36,45 coches vendidos, pero no podemos vender medio coche.
ggplot(revenue_model_data, aes(x = price, y = revenue_model)) +
geom_point() + geom_line(color = '#01ef63') +
ggtitle("Car Sales") + labs(subtitle = "revenue model") +
ylab("Revenue") +
scale_y_continuous(labels = scales::dollar_format()) +
geom_vline(xintercept = optimal_price, linetype = "dashed", color = '#203147') +
geom_point(aes(x = optimal_price, y = max_revenue), color = '#203147', size = 3) 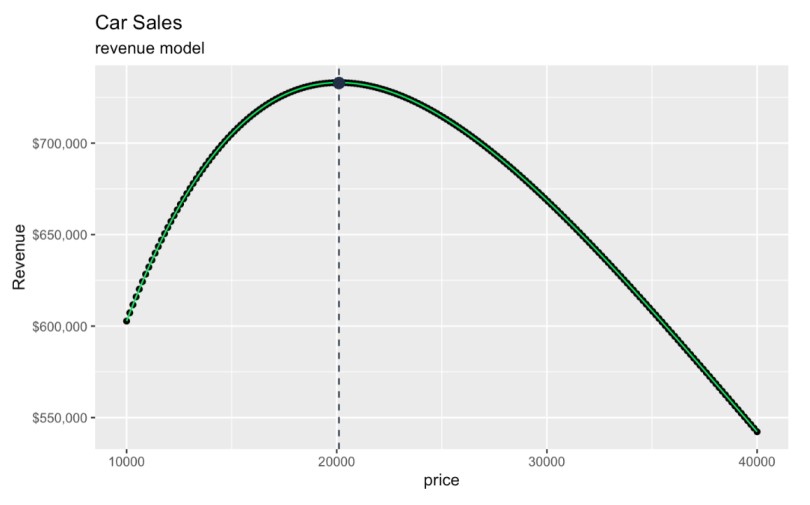 el precio que maximiza los ingresosEncontrar el precio que maximiza los ingresos. Imagen del autor.
el precio que maximiza los ingresosEncontrar el precio que maximiza los ingresos. Imagen del autor.
En otro flujo de trabajo, podríamos incluso ampliar estas ideas para considerar los beneficios en lugar de los ingresos. No voy a elaborarlo todo aquí, pero para ello, debes saber que podríamos considerar profit = revenue - cost, donde cost se considera quantity * unit cost. Si el coste unitario es constante y la cantidad puede sustituirse por una expresión como 1 - price, volvemos a obtener una parábola invertida.
Si te interesa saber más sobre la función del cálculo y las derivadas en el aprendizaje automático, prueba nuestro curso Introducción al Aprendizaje Profundo con PyTorch, que explora en detalle el descenso de gradiente en el contexto del ajuste de hiperparámetros. El contexto es diferente, pero puedes aplicar algunas ideas similares. La optimización, en sus diferentes formas, como estás viendo, es una habilidad clave en la ciencia de datos, y la práctica ayuda.
Curva de demanda vs. Curva de Laffer
Si has estudiado economía, puede que reconozcas esta parábola como algo parecido a la curva de Laffer, que es un concepto algo controvertido que ilustra cómo influyen los tipos impositivos en los ingresos fiscales del gobierno.
Aunque yo consideraría que tanto la curva de Laffer como esta transformación en la curva de demanda son problemas del tipo "maximizar frente a tasa", la curva de Laffer es específica de la fiscalidad: el eje x representaría la tasa impositiva (0% a 100%), y el eje y sería el total de ingresos fiscales recaudados. Conceptualmente, la curva de Laffer también tiene forma de U inversa porque, en el extremo superior, consideraríamos que, si el tipo impositivo fuera demasiado alto, no produciría ingresos porque no habría incentivos para que los particulares o las empresas realizaran actividades imponibles. Los economistas pueden discrepar en la parte del "incentivo".

La curva de Laffer en Ferris Bueller's Day Off. Fuente: YouTube
Utilizar una curva de demanda para analizar los precios en SQL
Ahora que hemos repasado la idea, quiero compartir también un script SQL que hará el mismo trabajo. Esta función realizará una regresión de quantity_sold frente a price. A continuación, te permitirá encontrar el precio óptimo para maximizar los ingresos basándote en los coeficientes de regresión, y determinar los ingresos máximos correspondientes.
Creo que el siguiente script será especialmente útil cuando crees cuadros de mando dinámicos en Power BI o Tableau, porque tendrás actualizaciones de datos en tiempo real sin necesidad de desconectar nada.
Verás también que utilicé un método manual para hallar los coeficientes de regresión utilizando funciones agregadas de SQL, ya que la mayoría de los dialectos de SQL no tienen funciones de regresión especializadas que puedas utilizar. Quizá te sorprenda saber que la regresión lineal simple funciona bien en SQL, porque los coeficientes del modelo de regresión lineal simple pueden expresarse en términos de correlación, desviación típica y valores medios entre x e y.
-- SQL script to perform linear regression on log(quantity_sold) vs price,
-- calculate the optimal price to maximize revenue, and determine the maximum revenue.
WITH regression_data AS (
SELECT
COUNT(*) AS N,
SUM(price) AS sum_x,
SUM(LOG(quantity_sold)) AS sum_y,
SUM(price * LOG(quantity_sold)) AS sum_xy,
SUM(price * price) AS sum_x2,
SUM(LOG(quantity_sold) * LOG(quantity_sold)) AS sum_y2
FROM sales_data
),
regression_coefficients AS (
SELECT
N,
sum_x,
sum_y,
sum_xy,
sum_x2,
sum_y2,
(N * sum_xy - sum_x * sum_y) / (N * sum_x2 - sum_x * sum_x) AS slope,
(sum_y - ((N * sum_xy - sum_x * sum_y) / (N * sum_x2 - sum_x * sum_x)) * sum_x) / N AS intercept
FROM regression_data
),
optimal_price AS (
SELECT
slope,
intercept,
(-1 / slope) AS optimal_P
FROM regression_coefficients
),
max_revenue AS (
SELECT
optimal_P,
slope,
intercept,
optimal_P * EXP(intercept + slope * optimal_P) AS max_R
FROM optimal_price
)
SELECT
optimal_P AS Optimal_Price,
max_R AS Maximum_Revenue
FROM max_revenue;Optimal_Price | Maximum_Revenue
------------- | ----------------
20104.32 | 402082.58Ten en cuenta que el script SQL proporcionado puede necesitar ajustes dependiendo del dialecto SQL utilizado, ya que la sintaxis puede variar. Además, a efectos de resolución de problemas, yo me aseguraría de que tu tabla de datos de ventas contiene valores válidos y positivos tanto para price como para quantity_sold, ya que los valores negativos o cero pueden dar lugar a errores.
Además, si quisieras incorporar una transformación logarítmica, como hicimos en la sección de R, podrías hacerlo, pero, dependiendo de tu dialecto, la función logaritmo natural podría denominarse de otra forma, LN o LOG. Por último, yo diría que, para mejorar tu competencia en SQL como analista, deberías explorar la trayectoria profesional de Analista de Datos Asociado en SQL, para que desarrolles un conjunto completo de herramientas.
Excepciones a la curva de la demanda
Hay excepciones notables en las que el comportamiento del consumidor puede desafiar el patrón estándar de la curva de demanda:
Bienes Giffen
Los bienes Giffen son un tipo raro de bien inferior para el que no se cumple la ley de la demanda. Cuando sube el precio de un bien Giffen, paradójicamente los consumidores pueden comprar más en vez de menos. Esto ocurre porque el bien constituye una parte tan importante del presupuesto del consumidor que, cuando sube su precio, éste ya no puede permitirse sustitutos más deseables y se ve obligado a comprar aún más del bien Giffen. Un ejemplo histórico clásico (aunque discutido) es la subida del precio del pan durante el siglo XIX en algunos lugares (Inglaterra, quizá), donde la gente acabó consumiendo más pan porque no podía permitirse otros alimentos más caros.
Bienes Veblen
Los bienes Veblen son productos de lujo o símbolos de estatus -como los bolsos de diseño, los vinos finos o los relojes de alta gama- cuya demanda aumenta a medida que sube el precio. Parte de su atractivo procede de la percepción de que un precio más elevado indica exclusividad o un estatus social más alto, lo que hace que el bien sea más deseable a medida que se encarece. Podrías pensar en esto como "consumo conspicuo".
Otros casos especiales
- Bandwagon o efectos de red: Algunos bienes adquieren más valor para cada consumidor a medida que más personas los utilizan (por ejemplo, las plataformas de medios sociales, determinados ecosistemas de software). La demanda puede aumentar no sólo por el precio, sino por la creciente popularidad del bien o el tamaño de la red.
- Efecto esnob: Algunos consumidores compran bienes precisamente porque pocas personas los tienen. En estos casos, unos precios más bajos podrían hacer que el bien pareciera "menos exclusivo", disminuyendo su atractivo.
- Activos especulativos o de inversión: En el caso de activos como ciertas criptomonedas o materias primas, si el mercado cree que los precios seguirán subiendo, la demanda puede saltar en respuesta a las subidas de precios, en lugar de caer.
En todos estos ejemplos, la relación habitual precio-cantidad se invierte o se hace más compleja debido a factores psicológicos, culturales o situacionales que anulan la suposición clásica de que los consumidores simplemente quieren "más a precios más bajos".
Curva de demanda Términos comunes
En este artículo hemos considerado algunos términos diferentes. Vamos a crear una tabla para ayudar a mantener todo esto claro.
| Concepto | Descripción |
|---|---|
| Curva de demanda | Representación gráfica que muestra la relación entre el precio de un bien y la cantidad demandada por los consumidores. |
| Ley de la demanda | Afirma que, en igualdad de condiciones, a medida que disminuye el precio de un producto, aumenta la cantidad demandada. |
| Relación precio-cantidad | Indica que el precio de un producto influye directamente en la cantidad que los consumidores están dispuestos a comprar. |
| Elasticidad | Mide la sensibilidad de la cantidad demandada a una variación del precio. |
| Utilidad marginal decreciente | Se refiere a la disminución de la satisfacción o utilidad por consumir unidades adicionales de un producto. |
Reflexiones finales
Cubrimos mucho terreno: Practicamos desde curvas de demanda y modelos de demanda, hasta transformadas logarítmicas y exponenciales, pasando por técnicas de regresión cuadrática y optimización.
Sigue aprendiendo análisis empresarial con DataCamp. Considera la posibilidad de matricularte en cursos como los que he mencionado antes: Previsión de la Demanda de Productos en R y Toma de Decisiones Basada en Datos para Empresas, que te enseñarán a utilizar los datos para mejorar tus decisiones en los negocios y las finanzas. No hay sustituto para tener ciertas habilidades técnicas y conocer las técnicas adecuadas.
Además, sigue practicando las cosas fundamentales de la ciencia de datos. Además de los cursos básicos de regresión(Introducción a la regresión con statsmodels en Python e Introducción a la regresión en R) aprende Modelización no lineal con modelos aditivos generalizados (GAM) en R o Fundamentos de estadística en Python. También recomiendo emprender nuestra carrera completa de Científico de Aprendizaje Automático en Python. Elige aquello en lo que seas más débil, así aprenderás más.

