Curso
A curva de demanda é uma das ferramentas mais interessantes e úteis para entender o comportamento do consumidor e as estratégias de preços. É comumente usado para analisar a relação entre o preço de um bem ou serviço e a quantidade vendida, embora em outros contextos possa ser usado para analisar a dinâmica do mercado ou prever resultados de receita.
Neste artigo, você aprenderá tudo sobre a curva de demanda. Exploraremos as características definidoras e os termos relacionados. Mais adiante, também terei tempo para mostrar como a curva de demanda pode ser estendida para encontrar o preço ideal que maximiza o lucro - uma parte útil da álgebra aplicada para criar uma técnica de otimização elementar que achei útil em meu próprio trabalho.
Seguindo esses métodos, garanto que você poderá não apenas tomar decisões sobre estratégias de preços, mas também será capaz de articular claramente os métodos de forma a fornecer a estrutura para projetos futuros. Embora eu vá usar R e SQL neste artigo, saiba que você pode usar esses mesmos métodos com outras ferramentas importantes, como Excel, Python, Tableau e Power BI. Por fim, gostaria de dizer que, para você realmente se tornar um especialista em preços, recomendo enfaticamente nosso curso Forecasting Product Demand in R.
O que é uma curva de demanda?
A curva de demanda é um conceito fundamental na estratégia de preços e na economia em geral. É uma forma visual atraente de representar a relação entre o preço de um bem ou serviço e a quantidade demandada pelos consumidores. Os principais componentes de uma curva de demanda incluem o preço em um eixo e a quantidade demandada no outro. Aqui está um exemplo:
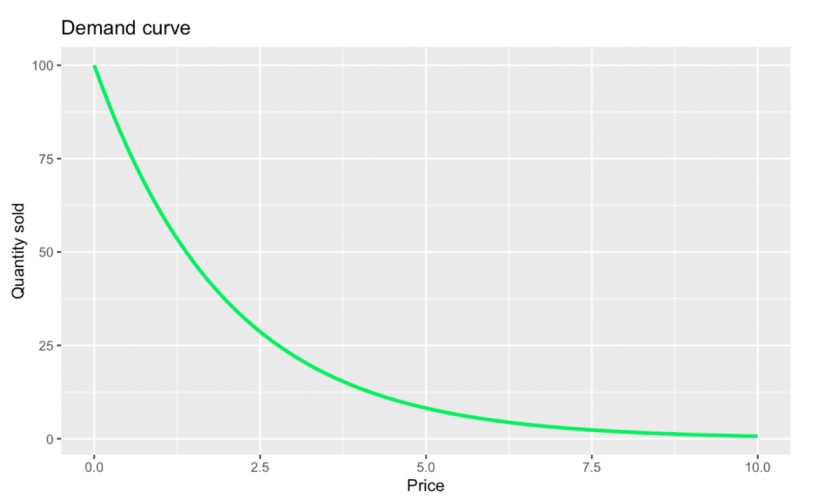
Um formato básico de curva de demanda. Imagem do autor.
Componentes de uma curva de demanda
No gráfico acima, você notará algo que é um tanto óbvio à primeira vista: que o preço e a quantidade vendida têm uma relação inversa. De maneira mais formal, poderíamos dizer que a curva de demanda está muito relacionada ao que é conhecido como a lei da demanda, que afirma que, se todo o resto for igual, à medida que o preço de um produto diminui, a quantidade demandada aumenta. Às vezes, essa mesma ideia é chamada de relação entre preço e quantidade, o que significa que o preço de um produto influencia diretamente a quantidade que os consumidores estão dispostos a comprar.
No entanto, esse gráfico específico também contém algo um pouco menos óbvio, que é o fato de a quantidade vendida cair mais acentuadamente quando o preço é baixo e se estabilizar quando o preço é alto. A curvatura aqui está relacionada a outros conceitos, como a mudança de elasticidade e a diminuição da utilidade marginal, que abordarei na próxima seção.
Elasticidade de preço da demanda
Um conceito importante que emerge da relação inversa entre preço e quantidade demandada é a elasticidade-preço da demanda, que mede a sensibilidade da quantidade demandada a uma mudança no preço. Formalmente, a elasticidade é geralmente calculada como:
![]()
Diz-se que um produto tem elástica se uma mudança relativamente pequena no preço levar a uma grande mudança na quantidade demandada. Eletrônicos de alta qualidade ou bolsas de grife podem sofrer uma queda acentuada na demanda se seus preços subirem um pouco, porque os consumidores podem encontrar substitutos.
Um produto tem inelástica se grandes mudanças no preço levarem a mudanças relativamente pequenas na quantidade demandada. Necessidades como gasolina ou remédios são exemplos clássicos. Mesmo que o preço suba, os consumidores ainda são obrigados a comprar quase a mesma quantidade porque não há alternativas.
Tipos de curvas de demanda
Embora eu tenha mostrado um exemplo de curva de demanda, saiba que ela pode assumir muitas formas diferentes, dependendo das características subjacentes do mercado, do produto e das preferências do consumidor. Embora seja sempre inclinada para baixo, essa relação não precisa seguir uma única forma matemática.
Curvas de demanda lineares
As curvas de demanda lineares apresentam uma taxa de variação constante entre preço e quantidade. Isso seria comum em cenários simples de mercado. Eles são representados por uma linha reta.
Curvas de demanda não lineares
Como vimos, as curvas de demanda nem sempre são desenhadas como linhas perfeitamente retas porque a relação entre preço e quantidade nem sempre é bem representada por uma função linear simples de um para um. Há vários motivos para isso, que comecei a mencionar anteriormente:
- Mudança de elasticidade: A elasticidade da demanda, ou seja, o grau de sensibilidade da demanda a uma mudança no preço, geralmente varia em diferentes pontos da curva. Por exemplo, quando os preços estão muito altos, os compradores podem reagir fortemente até mesmo a uma pequena queda de preço.
- Diminuição da utilidade marginal: Em muitos modelos econômicos, cada unidade adicional de um bem proporciona ao consumidor um pouco menos de utilidade do que a anterior. Como resultado, os consumidores podem estar dispostos a comprar muito mais se os preços caírem de níveis altos para níveis moderados, mas quando você atinge uma determinada faixa, reduzir ainda mais o preço não provoca o mesmo grande aumento na quantidade desejada ou vendida.
Na prática, as curvas de demanda não lineares podem ser mais realistas porque são melhores para representar uma taxa de mudança variável. Afinal de contas, os dados do mundo real são confusos e o comportamento do consumidor é complexo. Dito isso, muitas vezes há maneiras de linearizar uma curva não linear, como mostrarei mais adiante.
Curva de demanda individual vs. curva de demanda de mercado
Também podemos comparar as diferenças na demanda no nível do consumidor e do mercado. Uma curva de demanda individual representa a relação entre o preço de um produto e a quantidade demandada por um único consumidor. Ele reflete as preferências pessoais e a disposição de pagar.
Uma curva de demanda de mercado combina a demanda de todos os consumidores em um mercado. Ele agrega curvas de demanda individuais, mostrando a quantidade total demandada em cada ponto de preço. Devido à forma como são construídas, as curvas de demanda do mercado são usadas pelas empresas para avaliar o potencial do mercado.
Curva de demanda vs. curva de oferta
Se você estiver estudando curvas de demanda, talvez também tenha ouvido falar do que é chamado de curva de oferta. Essencialmente, uma curva de oferta e uma curva de demanda são dois lados da mesma moeda. Enquanto a curva de demanda mostra a quantidade de um produto que os consumidores estão dispostos a comprar a preços diferentes, a curva de oferta representa a quantidade que os produtores estão dispostos a vender a esses mesmos preços.
Agora, se você traçar uma curva de demanda e uma curva de oferta no mesmo gráfico, verá um local onde elas se cruzam. Acredita-se que a interseção dessas curvas, conhecida como ponto de equilíbrio, determine o preço e a quantidade de mercado. Portanto, quando a demanda supera a oferta, os preços tendem a subir, o que incentiva os produtores a produzir mais. Mas quando a oferta excede a demanda, os preços caem, o que incentiva mais compras.
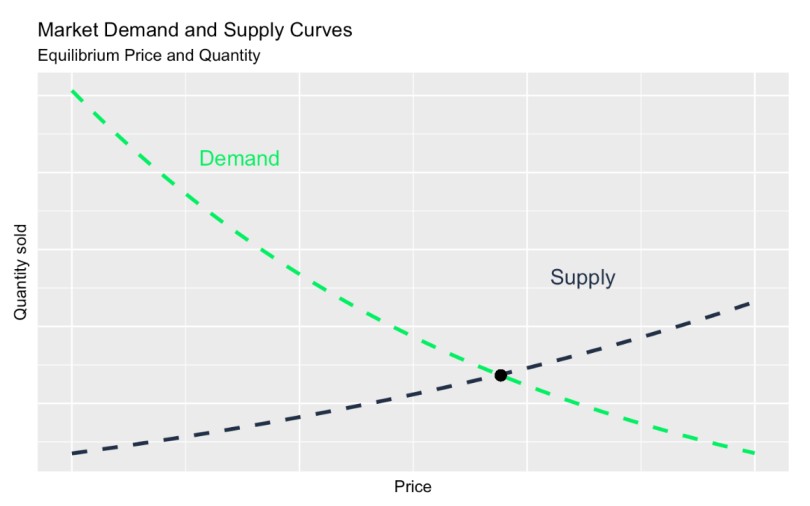
Curva de demanda vs. curva de oferta. Imagem do autor.
Uso de uma curva de demanda na ciência de dados
Há muitas maneiras diferentes de usar as curvas de demanda para tomar decisões de negócios. Aqui, vou mostrar a você uma maneira específica de tornar as curvas de demanda úteis: Usaremos nossos dados para criar uma curva de demanda e um modelo de demanda usando uma técnica de regressão quadrática. Mostrarei como você pode usar essa técnica tanto no R quanto no SQL, onde ela pode ser usada em painéis interativos do Power BI ou do Tableau.
Antes de continuar, quero dizer que, se você está lendo isto e acha que pode querer aprimorar as habilidades de uma equipe inteira de uma só vez, como uma equipe de departamento de analistas de negócios ou cientistas de dados, o DataCamp for Business está aqui para ajudar. Ajudaremos a sua equipe a desenvolver habilidades e técnicas que sejam úteis no seu contexto comercial específico. Muitos projetos de análise de dados pesados exigem vários colaboradores, portanto, entre em contato com a equipe do DataCamp para saber mais.
Aprimore as habilidades de ciência de dados da sua equipe
Descubra todo o potencial da ciência de dados com o DataCamp for Business. Acesse cursos abrangentes, projetos e relatórios centralizados para equipes de 2 ou mais pessoas.

Usando uma curva de demanda para analisar os preços em R
Vamos criar e analisar uma curva de demanda usando o R. Para simular um conjunto de dados, criei uma curva do tipo decaimento exponencial com ruído disperso em torno dela. A ideia aqui é que cada ponto de dados represente uma semana de vendas para uma concessionária de automóveis, na qual a concessionária oferece diferentes promoções e experimenta diferentes níveis de preços para o mesmo tipo de carro, em uma tentativa de aumentar as vendas.
# Load necessary library
library(tidyverse)
# Define parameters for the exponential decay
a <- 100 # Initial value
b <- 0.5 # Decay rate
# Define a realistic price range
price <- seq(10000, 40000, length.out = 200) # Price from $10,000 to $40,000
# Calculate the exponential decay
y <- a * exp(-b * (price / 10000)) # Adjust decay rate to match price scaling
# Add mixed noise (additive + slight proportional)
set.seed(42) # For reproducibility
additive_noise <- rnorm(length(y), mean = 0, sd = 1) # Constant additive noise
proportional_noise <- rnorm(length(y), mean = 0, sd = 0.05 * y) # Small proportional noise
y_noisy <- y + additive_noise + proportional_noise
# Ensure no negative values (optional, as sales can't be negative)
y_noisy[y_noisy < 0] <- 0.01
# Combine price and noisy y into a data frame
demand_curve_data <- data.frame(
price = price,
quantity_sold = y_noisy
)
# Clean and prepare the data
demand_curve_data <- demand_curve_data %>%
mutate(quantity_sold = round(quantity_sold, 0)) %>%
filter(quantity_sold != 0)
# Plot the noisy exponential decay
ggplot(demand_curve_data, aes(x = price, y = quantity_sold)) +
geom_point(color = '#203147', alpha = 0.6) +
geom_line(
aes(y = a * exp(-b * (price / 10000))),
color = '#01ef63',
size = 1.2,
linetype = "dashed"
) +
labs(
title = "Cars Sold",
subtitle = "Demand Curve (Cars Sold)",
x = "Price ($)",
y = "Quantity Sold"
) +
scale_x_continuous(labels = scales::dollar_format()) # Format x-axis as dollars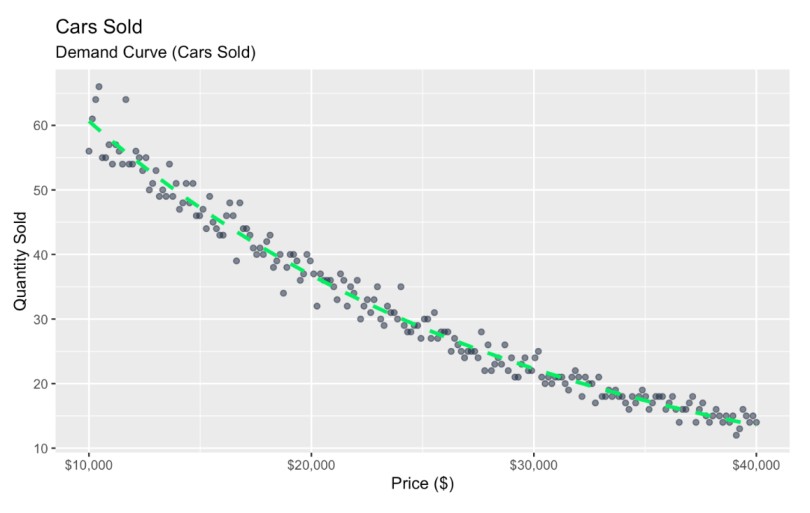 Curva de demanda com ruído. Imagem do autor
Curva de demanda com ruído. Imagem do autor
Aqui, fiz um gráfico da relação entre preço e quantidade vendida e usei pontos de dispersão para representar a variação natural, que pode ser causada por vários motivos diferentes.
Lendo esse gráfico, vemos que, à medida que o preço aumenta, as vendas diminuem, e essa relação é mais sensível em algumas faixas de preço do que em outras. Mas, dependendo do que você estiver fazendo com os dados, esse insight geral pode não ser suficiente para informar uma decisão prática de negócios. Em minha experiência, os chefes geralmente querem ver um insight normativo que forneça uma resposta concreta a uma questão comercial mais urgente. Uma dessas perguntas é: Qual é o preço do carro que realmente maximiza a receita geral?
Poderíamos começar tentando fazer algumas suposições apenas observando o gráfico.
- Na extremidade inferior, vemos, seguindo a linha verde, que a quantidade vendida é 60, onde o valor x do preço é US$ 10.000. Isso se traduziria em US$ 600.000 em receita total .
- Na extremidade altavemos a linha verde atingir 10 ou mais, onde os valores de x são US$ 40.000, o que equivale a $400,000 em receita.
- Bem no meio, vemos a linha verde atingir 30, onde o preço é de US$ 25.000. Isso equivale a US$ 750.000.
Você deve estar começando a ter a sensação de que o preço que maximiza a receita geral está em algum lugar no meio. Conceitualmente, isso faz sentido: Esperamos que os preços superbaixos gerem um grande volume de vendas, mas uma receita relativamente pequena, enquanto os preços superaltos gerariam um número muito menor de vendas e uma receita ainda relativamente pequena. Mas, em algum ponto intermediário, deve haver um preço ideal que maximize a receita.
Agora, em vez de olhar para o gráfico, vamos aprender uma maneira melhor, mais eficiente e sólida de maximizar a receita geral. Podemos descobrir o preço ideal resolvendo um problema rudimentar de otimização. Primeiro criamos um modelo linear, depois dobramos esse modelo em uma parábola e encontramos o ponto mais alto.
Nossa primeira etapa aqui é linearizar a relação. Como construí tudo isso com uma função de decaimento exponencial, sei que ela será bem linearizada ao tomar o logaritmo da quantidade vendida. Para simplificar, vamos ignorar qualquer heterocedasticidade.
# Create a linearized version of the data
demand_curve_data$log_quantity_sold <- log(demand_curve_data$quantity_sold)
# Plot the linearized relationship
ggplot(demand_curve_data, aes(x = price, y = log_quantity_sold)) +
geom_point(color = '#203147', alpha = 0.6) +
geom_smooth(method = "lm", color = '#01ef63', se = FALSE) +
labs(
title = "Cars Sold",
subtitle = "Demand Curve (Log Quantity Sold)",
x = "Price ($)",
y = "Log of Quantity Sold"
) +
scale_x_continuous(labels = scales::dollar_format()) # Format x-axis as dollars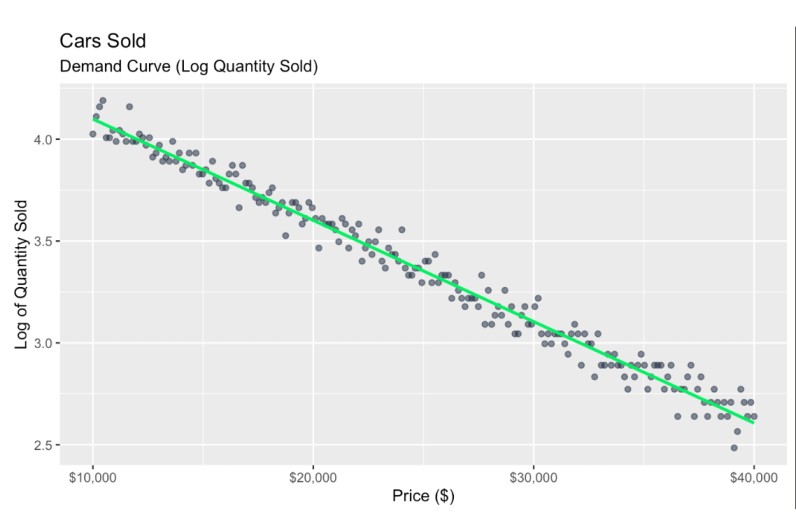
Curva de demanda transformada. Imagem do autor
Agora, podemos criar uma nova variável chamada revenue, que é definida como price vezes log_quantity_sold. Como observação, criamos um objeto de modelo linear usando a função lm() porque queremos acessar os números associados aos coeficientes do modelo.
Na próxima etapa, inserimos a equação do modelo linear em nossa fórmula. Se não tivéssemos tido uma transformação de toras:
-
Isso significa que nossa equação:
revenue = price * quantity_soldagora pode ser escrita comorevenue = price * (b0 + b1 * price). -
Depois, distribuiríamos os termos. Assim como distribuiríamos os termos em x(1-x) para formar x-x2, reescreveríamos nossa equação como
revenue = b0 * Price + b1 * price2.
Observe agora que teríamos revenue definido por uma equação que tem price como um termo ao quadrado. Essa é realmente a parte mais importante porque, ao representar graficamente price como um termo ao quadrado, criamos uma função de maximização.
No entanto, como temos uma transformação logarítmica, temos que fazer uma retrotransformação exponencial do modelo log-linear.
-
Isso significa que nossa equação:
revenue = price * log_quantity_soldagora será escrita comorevenue = price * eb0 + b1 * price. -
Agora podemos fatorar essa equação em uma nova forma, se preferirmos:
revenue=price * eb0 * eb1⋅price. Mas essa equação em particular não se distribui da mesma forma que uma equação linear ou polinomial porque a função exponencial não permite que os termos sejam separados ou distribuídos como os termos algébricos mais comuns, acima.
De qualquer forma, vamos continuar:
# Fit a linear model to the log-transformed quantity sold
model <- lm(log_quantity_sold ~ price, data = demand_curve_data)
# Create a revenue model based on the linear model coefficients
revenue_model_data <- demand_curve_data %>%
mutate(
revenue_model = price * exp(coef(model)[1] + coef(model)[2] * price) # Modeled revenue
)
# Plot the revenue model
ggplot(revenue_model_data, aes(x = price, y = revenue_model)) +
geom_point(color = '#203147', alpha = 0.6) + # Actual revenue points
geom_line(color = '#01ef63', size = 1.2) + # Revenue model line
labs(
title = "Car Sales",
subtitle = "Revenue Model",
x = "Price ($)",
y = "Revenue ($)"
) +
scale_y_continuous(labels = scales::dollar_format()) + # Format y-axis as dollars
theme_minimal() + # Apply a minimal theme for aesthetics
theme(
text = element_text(family = "Arial", size = 12),
plot.title = element_text(face = "bold", size = 16),
plot.subtitle = element_text(size = 14)
)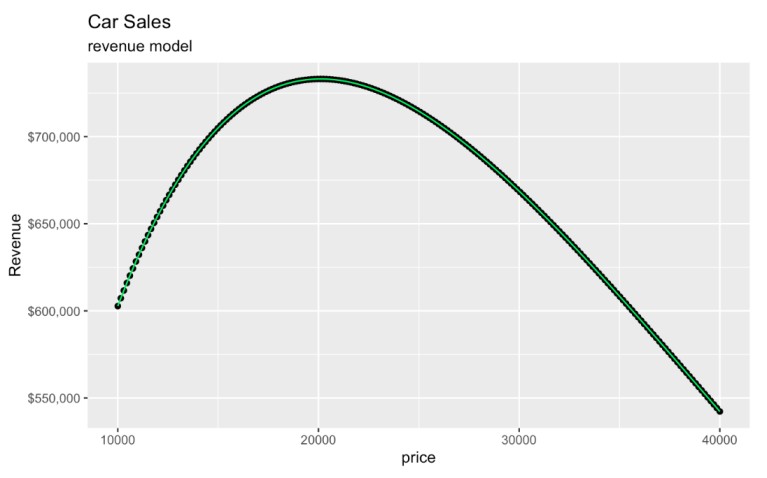
Modelo de receita criado a partir de uma curva de demanda. Imagem do autor.
É interessante notar que, embora o modelo original tenha usado log_quantity_soldo gráfico que criamos está inteiramente nas escalas originais de price e revenue. A transformação logarítmica afeta apenas o modelo subjacente, e nossa transformação reversa envolvendo e coloca nosso gráfico na escala original para que ainda seja fácil de interpretar.
Encontrar onde a derivada é igual a zero
Agora, nosso último ponto-chave é o seguinte: O local no topo da parábola, onde a derivada é igual a zero, será o preço teórico que maximiza a receita.
Talvez você se lembre de que encontramos a derivada de uma equação como 3x² + 2x multiplicando-a pelos expoentes para obter 6x + 2. Esse mesmo raciocínio se aplica, mas, novamente, lembre-se de que, neste exemplo, primeiro precisamos transformar nossos valores registrados antes de formar a função de receita. Ao traduzir de volta para a escala original antes de encontrar a receita máxima, sabemos que estamos encontrando o preço que maximiza a receita real, e não alguma métrica transformada. Portanto, essa é a função de receita correta para você diferenciar: revenue = price * e(b0 + b1 * price).
Vamos resolver isso. Aqui, utilizo os coeficientes do modelo linear. Em seguida, defino uma função de receita. Por fim, calculo o preço ideal e aprendo sobre a receita total esperada associada.
# Model coefficients
b0 <- 4.596 # Intercept
b1 <- -4.974e-05 # Slope for price
# Define the revenue function
revenue <- function(P, b0, b1) {
P * exp(b0 + b1 * P)
}
# Calculate the optimal price (analytical solution from dR/dP = 0) - shortcut code here
(optimal_price <- -1 / b1)
# Calculate maximum revenue
(max_revenue <- revenue(optimal_price, b0, b1))[1] 20104.54
[1] 732853.5Você deve ter notado que eu tinha uma linha de código para o preço ideal que não foi bem explicada no contexto. Estou me referindo a esta parte do código: (optimal_price <- -1 / b1). Deixe-me mostrar a você como descobri isso, que o preço ideal é -1 menos a inclinação.
Primeiro, temos que nos lembrar do que é chamado de regra do produto no cálculo, que afirma que, se a função de x "f de x" for igual a u(x) vezes v(x), então a derivada, que podemos escrever como f'(x), é igual à derivada da primeira coisa multiplicada pela coisa da seção, depois adicionada à primeira coisa vezes essa derivada da segunda coisa.
# the product rule in calculus
f(x) = u(x) * v(x)
f'(x) = u'(x) * v(x) + u(x) * v'(x)Aqui está nossa equação novamente, junto com a derivada:
# our equation:
revenue = price * e^(b0 + b1 * price)
# the derivative of our equation
derivative = 1 * e^(b0 + b1 * price) + price * b1 * e^(b0 + b1 * price)Eu sei que a derivada do preço aqui é 1, porque é a coisa da qual estamos encontrando a derivada. "Quanto o preço muda conforme o preço muda?" Bem, é um relacionamento individual.
Por outro lado, a derivada de e(b0 + b1 * preço) não é simples como uma função simples é simples, como 2x2, por exemplo, que tem como derivada 4x.
Na expressão com a qual estamos trabalhando aqui, o expoente é um polinômio. O truque aqui é examinar atentamente todos os termos: Para começar,
-
b0é apenas um valor único, portanto, a derivada é zero -
priceé 1, como já tratamos. -
b1é o fator de escala, portanto, colocamos esse número na frente e, em seguida, conforme a regra, deixamos o expoente polinomial igual.
Portanto, a derivada de e(b0 + b1 * price) é b1 * e(b0 + b1 * price). Isso é conhecido como a regra da cadeia, como mostrarei aqui:
# the chain rule in calculus
f(x) = x^g(x)
f'(x) = g'(x) * x^g(x)A última coisa é fazer um cálculo.
A álgebra nos diz que eles são os mesmos:
A + B * A = A(1+B)E quando olho atentamente para o derivado com o qual estou trabalhando, percebo que há uma parte A e uma parte B:
O "A" é e(b0 + b1 * price) e o "B" é price * b1. Então, posso considerar isso
e^(b0 + b1 * price) + price * b1 * e^(b0 + b1 * price)para isso:
e^(b0 + b1 * price)(1 + price * b1)Por fim, tenho que definir essa derivada como zero para encontrar o local onde a inclinação para de subir e começa a descer, que é o topo da parábola.
e^(b0 + b1 * price)(1 + price * b1) = 0Como um truque final, sei que, quando A * B é igual a zero, A ou B (ou ambos) devem ser iguais a zero. Mas convenientemente, sei que e(b0 + b1 * price) nunca pode ser igual a zero porque é um expoente. Se fosse positivo, o número seria grande; se o expoente fosse avaliado como 0, o resultado seria 1; se o expoente fosse negativo, o resultado seria uma fração pequena. Assim, posso descartar a metade ao resolver para zero.
A única coisa que preciso fazer agora é mover as coisas e resolver para price.
(1 + b1 * price) = 0
b1 * price = -1
price = - 1 / b1Foi assim que encontrei -1 / b1 para colocar em nossa função personalizada do código R.
Agora, para continuar de onde paramos, podemos fazer um gráfico do preço ideal e ver a receita associada a ele.
O preço ideal é de US$ 20.104,54, o que resulta em uma receita total esperada de US$ 732.853,50, mais ou menos. Estou dizendo "mais ou menos" porque, se você verificar a matemática, estamos assumindo que 36,45 carros foram vendidos, mas não podemos vender metade de um carro.
ggplot(revenue_model_data, aes(x = price, y = revenue_model)) +
geom_point() + geom_line(color = '#01ef63') +
ggtitle("Car Sales") + labs(subtitle = "revenue model") +
ylab("Revenue") +
scale_y_continuous(labels = scales::dollar_format()) +
geom_vline(xintercept = optimal_price, linetype = "dashed", color = '#203147') +
geom_point(aes(x = optimal_price, y = max_revenue), color = '#203147', size = 3) 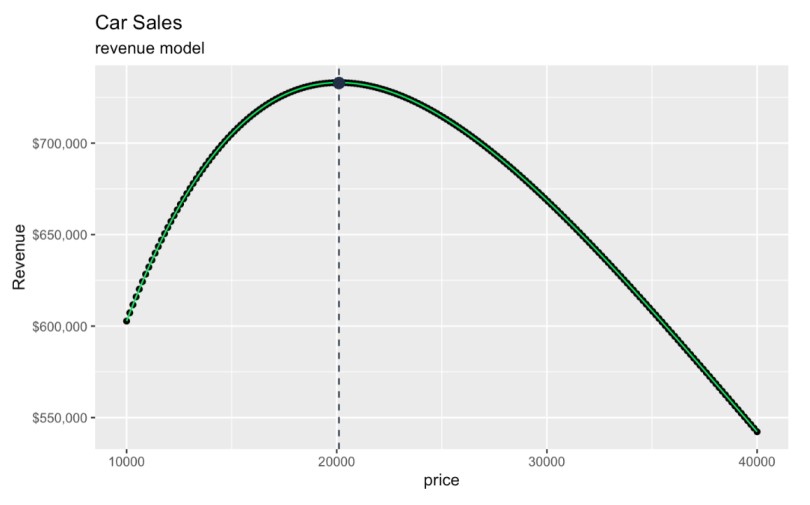 Como encontrar o a receitaComo encontrar o preço que maximiza a receita. Imagem do autor.
Como encontrar o a receitaComo encontrar o preço que maximiza a receita. Imagem do autor.
Em outro fluxo de trabalho, poderíamos até mesmo estender essas ideias para considerar o lucro em vez da receita. Não vou explicar tudo aqui, mas, para isso, você deve saber que podemos considerar profit = revenue - cost, onde cost é considerado como quantity * unit cost. Se o custo unitário for constante e a quantidade puder ser substituída por uma expressão como 1 - price, então teremos novamente uma parábola invertida.
Se você estiver interessado em saber mais sobre como o cálculo e as derivadas aparecem no machine learning, experimente nosso curso Introdução ao Deep Learning com PyTorch, que explora a descida de gradiente em detalhes no contexto do ajuste de hiperparâmetros. O contexto é diferente, mas você pode aplicar um raciocínio semelhante. A otimização, em suas diferentes formas, como você está vendo, é uma habilidade fundamental na ciência de dados, e a prática ajuda.
Curva de demanda vs. Curva de Laffer
Se você estudou economia, talvez reconheça essa parábola como algo semelhante à curva de Laffer, que é um conceito um tanto controverso que ilustra como as alíquotas de impostos influenciam a receita tributária do governo.
Embora eu considere que tanto a curva de Laffer quanto essa transformação na curva de demanda sejam problemas do tipo "maximizar vs. taxa", a curva de Laffer é específica para tributação: o eixo x representaria a taxa de imposto (0% a 100%) e o eixo y seria a receita tributária total arrecadada. Conceitualmente, a curva de Laffer também tem a forma de um U invertido porque, na extremidade alta, consideraríamos que, se a alíquota de imposto fosse muito alta, ela não geraria receita porque não haveria incentivo para que indivíduos ou empresas se envolvessem em atividades tributáveis. Os economistas podem discordar dessa parte do "incentivo".

A curva de Laffer em Ferris Bueller's Day Off. Fonte: YouTube
Usando uma curva de demanda para analisar preços no SQL
Agora que você já entendeu a ideia, quero compartilhar também um script SQL que fará o mesmo trabalho. Essa função executará uma regressão em quantity_sold versus price. Em seguida, ele permitirá que você encontre o preço ideal para maximizar a receita com base nos coeficientes de regressão e determine a receita máxima correspondente.
Acho que o script a seguir será particularmente útil ao criar painéis dinâmicos no Power BI ou no Tableau, pois você terá atualizações de dados em tempo real sem a necessidade de colocar nada off-line.
Você verá também que usei uma abordagem manual para encontrar os coeficientes de regressão usando funções agregadas do SQL, já que a maioria dos dialetos do SQL não tem funções de regressão especializadas que você possa usar. Talvez você se surpreenda ao saber que a regressão linear simples funciona bem no SQL porque os coeficientes do modelo para regressão linear simples podem ser expressos em termos de correlação, desvio padrão e valores médios entre x e y.
-- SQL script to perform linear regression on log(quantity_sold) vs price,
-- calculate the optimal price to maximize revenue, and determine the maximum revenue.
WITH regression_data AS (
SELECT
COUNT(*) AS N,
SUM(price) AS sum_x,
SUM(LOG(quantity_sold)) AS sum_y,
SUM(price * LOG(quantity_sold)) AS sum_xy,
SUM(price * price) AS sum_x2,
SUM(LOG(quantity_sold) * LOG(quantity_sold)) AS sum_y2
FROM sales_data
),
regression_coefficients AS (
SELECT
N,
sum_x,
sum_y,
sum_xy,
sum_x2,
sum_y2,
(N * sum_xy - sum_x * sum_y) / (N * sum_x2 - sum_x * sum_x) AS slope,
(sum_y - ((N * sum_xy - sum_x * sum_y) / (N * sum_x2 - sum_x * sum_x)) * sum_x) / N AS intercept
FROM regression_data
),
optimal_price AS (
SELECT
slope,
intercept,
(-1 / slope) AS optimal_P
FROM regression_coefficients
),
max_revenue AS (
SELECT
optimal_P,
slope,
intercept,
optimal_P * EXP(intercept + slope * optimal_P) AS max_R
FROM optimal_price
)
SELECT
optimal_P AS Optimal_Price,
max_R AS Maximum_Revenue
FROM max_revenue;Optimal_Price | Maximum_Revenue
------------- | ----------------
20104.32 | 402082.58Saiba que o script SQL fornecido pode precisar de ajustes, dependendo do dialeto SQL usado, pois a sintaxe pode variar. Além disso, para fins de solução de problemas, eu me certificaria de que a tabela de dados de vendas contenha valores válidos e positivos para price e quantity_sold, pois valores negativos ou zero podem levar a erros.
Além disso, se você quiser incorporar uma transformação de log, como fizemos na seção R, poderá fazer isso, mas, dependendo do seu dialeto, a função de logaritmo natural poderá ter um nome diferente, LN ou LOG. Por fim, eu diria que, para aprimorar sua proficiência em SQL como analista, você deve explorar o programa de carreira Associate Data Analyst in SQL, para desenvolver um conjunto completo de ferramentas.
Exceções à curva de demanda
Há exceções notáveis em que o comportamento do consumidor pode desafiar o padrão da curva de demanda:
Produtos Giffen
Os produtos Giffen são um tipo raro de produto inferior para o qual a lei da demanda não se aplica. Quando o preço de um bem de Giffen aumenta, os consumidores podem, paradoxalmente, comprar mais em vez de menos. Isso ocorre porque o bem representa uma parte tão grande do orçamento do consumidor que, quando seu preço sobe, ele não pode mais comprar substitutos mais desejáveis e é forçado a comprar ainda mais do bem de Giffen. Um exemplo histórico clássico (embora debatido) é o aumento do preço do pão durante o século XIX em alguns lugares (Inglaterra, talvez), onde as pessoas acabaram consumindo mais pão porque não podiam comprar outros alimentos mais caros.
Mercadorias Veblen
Os produtos Veblen são produtos de luxo ou símbolos de status - como bolsas de grife, vinhos finos ou relógios de alta qualidade - cuja demanda aumenta com o aumento do preço. Parte de seu apelo vem da percepção de que um preço mais alto indica exclusividade ou status social mais elevado, tornando o bem mais desejável à medida que se torna mais caro. Você pode pensar nisso como "consumo conspícuo".
Outros casos especiais
- Bandwagon ou efeitos de rede: Alguns produtos se tornam mais valiosos para cada consumidor à medida que mais pessoas os utilizam (por exemplo, plataformas de mídia social, determinados ecossistemas de software). A demanda pode aumentar não apenas por causa do preço, mas também por causa da crescente popularidade do produto ou do tamanho da rede.
- Efeito esnobe: Alguns consumidores compram produtos exatamente porque poucas pessoas os têm. Nesses casos, preços mais baixos podem fazer com que o produto pareça "menos exclusivo", diminuindo o apelo.
- Ativos especulativos ou de investimento: Para ativos como determinadas criptomoedas ou commodities, se o mercado acreditar que os preços continuarão subindo, a demanda pode aumentar em resposta aos aumentos de preços, em vez de cair.
Em todos esses exemplos, a relação usual entre preço e quantidade se inverte ou se torna mais complexa devido a fatores psicológicos, culturais ou situacionais que substituem a suposição clássica de que os consumidores simplesmente querem "mais por preços mais baixos".
Curva de demanda Termos comuns
Consideramos alguns termos diferentes neste artigo. Vamos criar uma tabela para ajudar você a manter tudo isso em ordem.
| Conceito | Descrição |
|---|---|
| Curva de demanda | Uma representação gráfica que mostra a relação entre o preço de um bem e a quantidade demandada pelos consumidores. |
| Lei da demanda | Afirma que, se todo o resto for igual, à medida que o preço de um produto diminui, a quantidade demandada aumenta. |
| Relação entre preço e quantidade | Indica que o preço de um produto influencia diretamente a quantidade que os consumidores estão dispostos a comprar. |
| Elasticidade | Mede a sensibilidade da quantidade demandada a uma mudança no preço. |
| Diminuição da utilidade marginal | Refere-se à diminuição da satisfação ou da utilidade do consumo de unidades adicionais de um produto. |
Considerações finais
Cobrimos uma grande quantidade de terreno: Praticamos tudo, desde curvas de demanda e modelos de demanda, até transformações logarítmicas e exponenciais, técnicas de regressão quadrática e otimização.
Continue aprendendo análise de negócios com a DataCamp. Considere a possibilidade de se inscrever em cursos como os que mencionei anteriormente: Forecasting Product Demand in R e Data-Driven Decision Making for Business, ambos ensinarão a você como usar dados para aprimorar suas decisões em negócios e finanças. Não há nada que substitua o fato de você ter algumas habilidades técnicas e conhecer as técnicas corretas.
Além disso, continue praticando os principais aspectos da ciência de dados. Além dos cursos básicos de regressão(Introdução à Regressão com statsmodels em Python e Introdução à Regressão em R), você aprenderá Modelagem Não Linear com Modelos Aditivos Generalizados (GAMs) em R ou Fundamentos de Estatística em Python. Também recomendo que você faça o nosso programa de carreira completo de Cientista de Machine Learning em Python. Escolha aquilo em que você é mais fraco, para aprender mais.



