Kurs
Die Nachfragekurve ist eines der interessantesten und nützlichsten Instrumente zum Verständnis von Verbraucherverhalten und Preisstrategien. Sie wird in der Regel zur Analyse des Verhältnisses zwischen dem Preis einer Ware oder Dienstleistung und der verkauften Menge verwendet, kann aber auch in anderen Zusammenhängen zur Analyse der Marktdynamik oder zur Vorhersage von Umsatzergebnissen genutzt werden.
In diesem Artikel werden wir alles über die Nachfragekurve erfahren. Wir werden sowohl die definierenden Merkmale als auch die verwandten Begriffe untersuchen. Später werde ich auch zeigen, wie die Nachfragekurve erweitert werden kann, um den optimalen Preis zu finden, der den Gewinn maximiert - ein nützliches Stück angewandter Algebra, um eine elementare Optimierungstechnik zu entwickeln, die ich bei meiner eigenen Arbeit als nützlich empfunden habe.
Wenn du diese Methoden befolgst, garantiere ich dir, dass du nicht nur in der Lage sein wirst, Entscheidungen über Preisstrategien zu treffen, sondern dass du auch in der Lage sein wirst, die Methoden so klar zu formulieren, dass sie den Rahmen für zukünftige Projekte bilden. Auch wenn ich in diesem Artikel R und SQL verwende, kannst du die gleichen Methoden auch mit anderen wichtigen Tools wie Excel, Python, Tableau und Power BI anwenden. Abschließend möchte ich noch sagen, dass ich, um wirklich ein Preisexperte zu werden, unseren Kurs " Prognose der Produktnachfrage in R" sehr empfehle.
Was ist eine Nachfragekurve?
Eine Nachfragekurve ist ein grundlegendes Konzept in der Preisstrategie und in der Wirtschaft im Allgemeinen. Es ist eine überzeugende visuelle Methode, um das Verhältnis zwischen dem Preis einer Ware oder Dienstleistung und der von den Verbrauchern nachgefragten Menge darzustellen. Zu den wichtigsten Komponenten einer Nachfragekurve gehören der Preis auf der einen und die nachgefragte Menge auf der anderen Achse. Hier ist ein Beispiel:
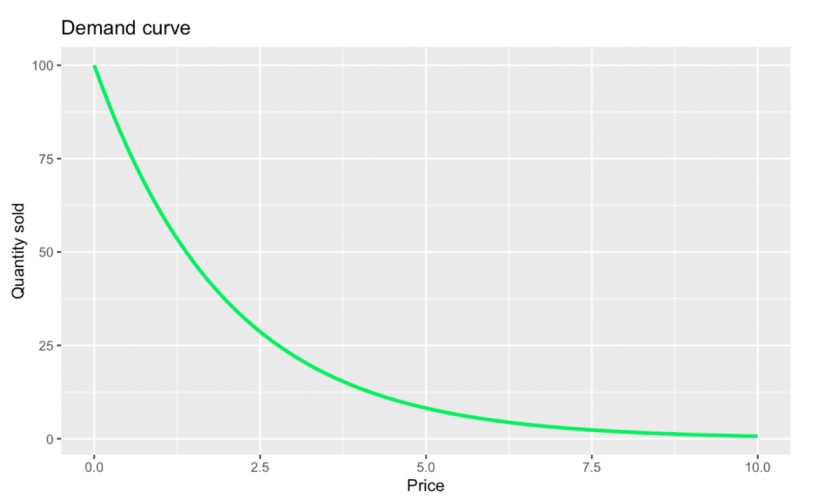
Eine grundlegende Form der Nachfragekurve. Bild vom Autor.
Bestandteile einer Nachfragekurve
In der obigen Grafik wird dir etwas auffallen, das auf den ersten Blick offensichtlich ist: dass Preis und verkaufte Menge in einem umgekehrten Verhältnis zueinander stehen. Formaler ausgedrückt könnte man sagen, dass die Nachfragekurve viel mit dem sogenannten Gesetz der Nachfrage zu tun hat, das besagt, dass bei sonst gleichen Bedingungen die nachgefragte Menge steigt, wenn der Preis für ein Produkt sinkt. Manchmal wird diese Idee auch als Preis-Mengen-Beziehung bezeichnet, was bedeutet, dass der Preis eines Produkts einen direkten Einfluss darauf hat, wie viel die Verbraucher zu kaufen bereit sind.
Dieses Diagramm zeigt aber auch etwas weniger Offensichtliches: Die verkaufte Menge sinkt stärker, wenn der Preis niedrig ist, und flacht ab, wenn der Preis hoch ist. Die Krümmung hängt mit anderen Konzepten zusammen, wie z. B. der veränderlichen Elastizität und dem abnehmenden Grenznutzen, die ich im nächsten Abschnitt behandeln werde.
Preiselastizität der Nachfrage
Ein Schlüsselkonzept, das sich aus dem umgekehrten Verhältnis zwischen Preis und nachgefragter Menge ergibt, ist die Preiselastizität der Nachfrage, die angibt, wie empfindlich die nachgefragte Menge auf eine Preisänderung reagiert. Formal wird die Elastizität oft wie folgt berechnet:
![]()
Ein Produkt hat angeblich elastische wenn eine relativ kleine Preisänderung zu einer großen Änderung der nachgefragten Menge führt. Hochwertige Elektronik oder Designer-Handtaschen könnten einen starken Nachfragerückgang erleben, wenn ihre Preise auch nur ein bisschen steigen, weil die Verbraucherinnen und Verbraucher Ersatz finden können.
Ein Produkt hat unelastische Ein Produkt hat eine unelastische Nachfrage, wenn große Preisänderungen zu relativ kleinen Änderungen in der nachgefragten Menge führen. Notwendige Dinge wie Benzin oder Medikamente sind klassische Beispiele. Selbst wenn der Preis steigt, sind die Verbraucher gezwungen, fast die gleiche Menge zu kaufen, weil es keine Alternativen gibt.
Arten von Nachfragekurven
Obwohl ich ein Beispiel für eine Nachfragekurve gezeigt habe, solltest du wissen, dass sie viele verschiedene Formen annehmen kann, je nach den zugrundeliegenden Merkmalen des Marktes, des Produkts und der Verbraucherpräferenzen. Sie ist zwar immer abfallend, aber diese Beziehung muss nicht einer bestimmten mathematischen Form folgen.
Lineare Nachfragekurven
Lineare Nachfragekurven weisen eine konstante Änderungsrate zwischen Preis und Menge auf. Diese würden in einfachen Marktszenarien üblich sein. Sie werden durch eine gerade Linie dargestellt.
Nicht-lineare Nachfragekurven
Wie wir gesehen haben, werden Nachfragekurven nicht immer als perfekte Geraden gezeichnet, weil das Verhältnis zwischen Preis und Menge nicht immer durch eine einfache eins-zu-eins lineare Funktion gut dargestellt wird. Dafür gibt es mehrere Gründe, die ich vorhin schon erwähnt habe:
- Veränderte Elastizität: Die Nachfrageelastizität, d. h. wie empfindlich die Nachfrage auf eine Preisänderung reagiert, variiert oft an verschiedenen Punkten der Kurve. Wenn die Preise zum Beispiel sehr hoch sind, können die Käufer schon auf einen leichten Preisrückgang stark reagieren.
- Abnehmender Grenznutzen: In vielen Wirtschaftsmodellen bringt jede zusätzliche Einheit eines Gutes dem Verbraucher ein bisschen weniger Nutzen als die vorherige. Daher sind die Verbraucher vielleicht bereit, viel mehr zu kaufen, wenn die Preise von einem hohen auf ein moderates Niveau sinken, aber sobald man eine bestimmte Spanne erreicht hat, führt eine weitere Preissenkung nicht mehr zu einem großen Anstieg der gewünschten oder verkauften Menge.
In der Praxis können nichtlineare Nachfragekurven realistischer sein, weil sie eine variable Veränderungsrate besser abbilden können. Schließlich sind reale Daten chaotisch und das Verbraucherverhalten ist komplex. Allerdings gibt es oft Möglichkeiten, eine nicht lineare Kurve zu linearisieren, wie ich später zeigen werde.
Individuelle Nachfragekurve vs. Marktnachfragekurve
Wir können auch Unterschiede in der Nachfrage auf der Ebene der Verbraucher und des Marktes vergleichen. Eine individuelle Nachfragekurve stellt die Beziehung zwischen dem Preis eines Produkts und der von einem einzelnen Verbraucher nachgefragten Menge dar. Sie spiegelt die persönlichen Vorlieben und die Zahlungsbereitschaft wider.
Eine Marktnachfragekurve fasst die Nachfrage aller Verbraucher auf einem Markt zusammen. Sie fasst die einzelnen Nachfragekurven zusammen und zeigt die gesamte nachgefragte Menge zu jedem Preispunkt. Aufgrund ihres Aufbaus werden Marktnachfragekurven von Unternehmen genutzt, um das Marktpotenzial abzuschätzen.
Nachfragekurve vs. Angebotskurve
Wenn du dich mit Nachfragekurven beschäftigst, hast du vielleicht auch schon von einer sogenannten Angebotskurve gehört. Im Grunde genommen sind eine Angebots- und eine Nachfragekurve zwei Seiten derselben Medaille. Während die Nachfragekurve zeigt, wie viel eines Produkts die Verbraucher zu verschiedenen Preisen zu kaufen bereit sind, stellt die Angebotskurve dar, wie viel die Produzenten zu denselben Preisen zu verkaufen bereit sind.
Wenn du nun eine Nachfrage- und eine Angebotskurve in dasselbe Diagramm einträgst, siehst du eine Stelle, an der sie sich kreuzen. Der Schnittpunkt dieser Kurven, der sogenannte Gleichgewichtspunkt, soll den Marktpreis und die Menge bestimmen. Wenn die Nachfrage das Angebot übersteigt, steigen die Preise, was für die Produzenten einen Anreiz darstellt, mehr zu produzieren. Aber wenn das Angebot die Nachfrage übersteigt, sinken die Preise, was zu mehr Käufen anregt.
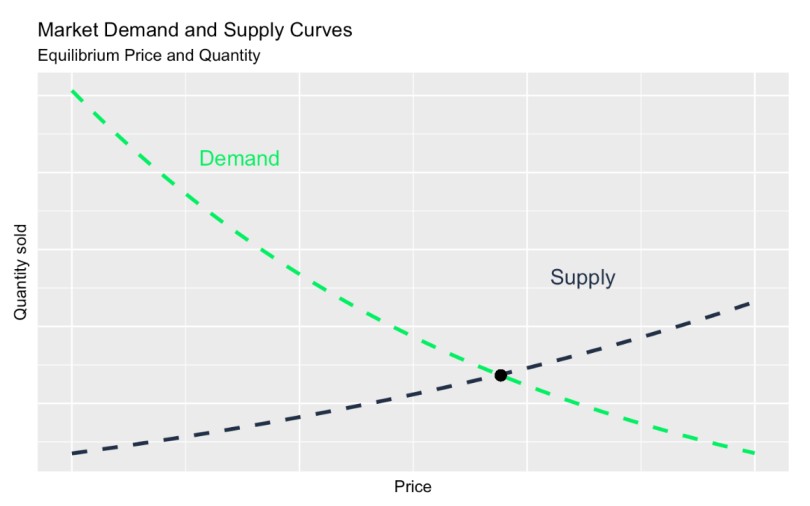
Nachfragekurve vs. Angebotskurve. Bild vom Autor.
Verwendung einer Bedarfskurve in der Datenwissenschaft
Es gibt viele verschiedene Möglichkeiten, die Nachfragekurven für Geschäftsentscheidungen zu nutzen. Hier werde ich dir eine konkrete Möglichkeit zeigen, wie wir Nachfragekurven nützlich machen können: Wir werden unsere Daten nutzen, um sowohl eine Nachfragekurve als auch ein Nachfragemodell mit Hilfe einer quadratischen Regressionstechnik zu erstellen. Ich zeige dir, wie du diese Technik sowohl in R als auch in SQL einsetzen kannst, um sie in interaktiven Power BI- oder Tableau-Dashboards zu nutzen.
Bevor ich fortfahre, möchte ich sagen, dass, wenn du dies liest und denkst, dass du vielleicht ein ganzes Team auf einmal weiterbilden willst, z.B. ein Team aus einer Abteilung von Business-Analysten oder Data Scientists, dann ist DataCamp for Business genau das Richtige für dich. Wir helfen deinem Team, Fähigkeiten und Techniken zu entwickeln, die in deinem spezifischen Geschäftskontext hilfreich sind. Bei vielen umfangreichen Datenanalyseprojekten sind mehrere Mitarbeiter/innen erforderlich - melde dich bei unserem DataCamp-Team, um mehr zu erfahren.
Fördere die Data Science-Fähigkeiten deines Teams
Entdecke das volle Potenzial von Data Science mit dem DataCamp for Business. Erhalte Zugang zu umfassenden Kursen, Projekten und zentralisierten Berichten für Teams von 2 oder mehr Personen.

Die Verwendung einer Nachfragekurve zur Analyse der Preise in R
Um einen Datensatz zu simulieren, habe ich eine exponentiell abfallende Kurve mit gestreutem Rauschen um sie herum erstellt. Die Idee dahinter ist, dass jeder Datenpunkt eine Verkaufswoche eines Autohauses darstellt, in der das Autohaus verschiedene Sonderangebote anbietet und verschiedene Preisniveaus für denselben Fahrzeugtyp ausprobiert, um den Umsatz zu steigern.
# Load necessary library
library(tidyverse)
# Define parameters for the exponential decay
a <- 100 # Initial value
b <- 0.5 # Decay rate
# Define a realistic price range
price <- seq(10000, 40000, length.out = 200) # Price from $10,000 to $40,000
# Calculate the exponential decay
y <- a * exp(-b * (price / 10000)) # Adjust decay rate to match price scaling
# Add mixed noise (additive + slight proportional)
set.seed(42) # For reproducibility
additive_noise <- rnorm(length(y), mean = 0, sd = 1) # Constant additive noise
proportional_noise <- rnorm(length(y), mean = 0, sd = 0.05 * y) # Small proportional noise
y_noisy <- y + additive_noise + proportional_noise
# Ensure no negative values (optional, as sales can't be negative)
y_noisy[y_noisy < 0] <- 0.01
# Combine price and noisy y into a data frame
demand_curve_data <- data.frame(
price = price,
quantity_sold = y_noisy
)
# Clean and prepare the data
demand_curve_data <- demand_curve_data %>%
mutate(quantity_sold = round(quantity_sold, 0)) %>%
filter(quantity_sold != 0)
# Plot the noisy exponential decay
ggplot(demand_curve_data, aes(x = price, y = quantity_sold)) +
geom_point(color = '#203147', alpha = 0.6) +
geom_line(
aes(y = a * exp(-b * (price / 10000))),
color = '#01ef63',
size = 1.2,
linetype = "dashed"
) +
labs(
title = "Cars Sold",
subtitle = "Demand Curve (Cars Sold)",
x = "Price ($)",
y = "Quantity Sold"
) +
scale_x_continuous(labels = scales::dollar_format()) # Format x-axis as dollars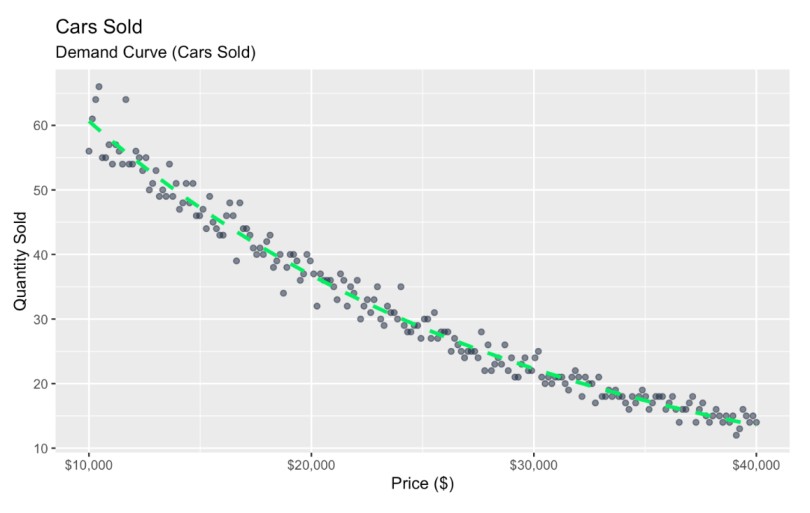 Nachfragekurve mit Lärm. Bild vom Autor
Nachfragekurve mit Lärm. Bild vom Autor
Hier habe ich die Beziehung zwischen Preis und verkaufter Menge grafisch dargestellt und die Punkte im Streudiagramm verwendet, um die natürlichen Schwankungen darzustellen, die viele verschiedene Ursachen haben können.
Aus dieser Grafik geht hervor, dass die Verkäufe mit steigendem Preis sinken, wobei diese Beziehung in einigen Preisklassen stärker ausgeprägt ist als in anderen. Aber je nachdem, was du mit den Daten machst, reichen diese allgemeinen Erkenntnisse vielleicht nicht aus, um eine praktische Geschäftsentscheidung zu treffen. Meiner Erfahrung nach wollen Chefs oft eine normative Erkenntnis sehen, die eine konkrete Antwort auf eine dringende Geschäftsfrage liefert. Eine solche Frage ist: Welches ist der Autopreis, der den Gesamtertrag maximiert?
Wir könnten zunächst versuchen, einige Vermutungen anzustellen, indem wir uns das Diagramm ansehen.
- Auf der unteren Seite sehen wir anhand der grünen Linie, dass die verkaufte Menge 60 beträgt, wobei der x-Wert für den Preis 10.000 $ ist. Dies würde 600.000 $ an Gesamteinnahmen bedeuten.
- Am oberen Endesehen wir, dass die grüne Linie bei 10 oder so liegt, wo die x-Werte 40.000 $ betragen, was $400,000 an Einnahmen.
- Genau in der Mitte sehen wir, dass die grüne Linie die 30 erreicht, wo der Preis 25.000 $ beträgt. Das entspricht 750.000 $.
Vielleicht bekommst du jetzt langsam das Gefühl, dass der Preis, der den Gesamtertrag maximiert, irgendwo in der Mitte liegt. Vom Konzept her ist das sinnvoll: Wir gehen davon aus, dass super niedrige Preise zu hohen Verkaufszahlen, aber relativ geringen Einnahmen führen, während super hohe Preise zu viel weniger Verkäufen und ebenfalls relativ geringen Einnahmen führen würden. Aber irgendwo in der Mitte muss es einen optimalen Preis geben, der die Einnahmen maximiert.
Anstatt das Diagramm mit den Augen zu betrachten, sollten wir einen besseren, effizienteren und solideren Weg finden, um den Gesamtumsatz zu maximieren. Wir können den optimalen Preis herausfinden, indem wir ein rudimentäres Optimierungsproblem lösen. Wir erstellen zunächst ein lineares Modell, biegen dieses Modell dann zu einer Parabel und finden den höchsten Punkt.
Unser erster Schritt besteht darin, die Beziehung zu linearisieren. Da ich all dies mit einer exponentiellen Abklingfunktion konstruiert habe, weiß ich, dass es sich gut linearisieren lässt, indem ich den Logarithmus der verkauften Menge nehme. Der Einfachheit halber ignorieren wir jegliche Heteroskedastizität.
# Create a linearized version of the data
demand_curve_data$log_quantity_sold <- log(demand_curve_data$quantity_sold)
# Plot the linearized relationship
ggplot(demand_curve_data, aes(x = price, y = log_quantity_sold)) +
geom_point(color = '#203147', alpha = 0.6) +
geom_smooth(method = "lm", color = '#01ef63', se = FALSE) +
labs(
title = "Cars Sold",
subtitle = "Demand Curve (Log Quantity Sold)",
x = "Price ($)",
y = "Log of Quantity Sold"
) +
scale_x_continuous(labels = scales::dollar_format()) # Format x-axis as dollars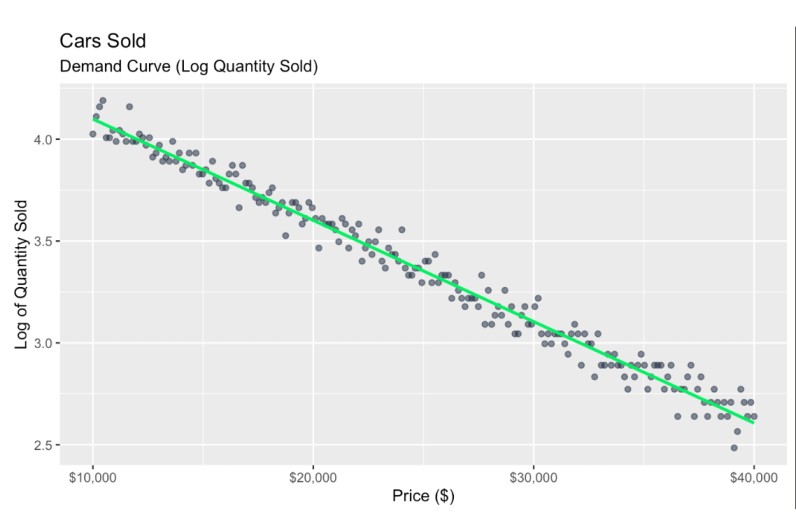
Umgeformte Nachfragekurve. Bild vom Autor
Jetzt können wir eine neue Variable namens revenue erstellen, die als price mal log_quantity_sold definiert ist. Wir erstellen ein lineares Modellobjekt mit der Funktion lm(), weil wir Zugriff auf die Zahlen haben wollen, die mit den Modellkoeffizienten verbunden sind.
Im nächsten Schritt setzen wir unsere lineare Modellgleichung in unsere Formel ein. Wenn wir keine Log-Transformation gehabt hätten:
-
Das würde bedeuten, dass unsere Gleichung:
revenue = price * quantity_soldnun alsrevenue = price * (b0 + b1 * price)geschrieben werden kann. -
Dann würden wir die Begriffe verteilen. Genauso wie wir die Terme in x(1-x) verteilen würden, um x-x2 zu erhalten, würden wir unsere Gleichung umschreiben:
revenue = b0 * Price + b1 * price2.
Beachte, dass revenue durch eine Gleichung definiert ist, die price als quadratischen Term enthält. Das ist der entscheidende Teil, denn indem wir price als quadratischen Term grafisch darstellen, haben wir jetzt eine maximierende Funktion erstellt.
Da wir jedoch eine Log-Transformation haben, müssen wir eine exponentielle Rücktransformation des log-linearen Modells durchführen.
-
Das bedeutet, dass unsere Gleichung:
revenue = price * log_quantity_soldjetzt alsrevenue = price * eb0 + b1 * pricegeschrieben wird. -
Wir können diese Gleichung nun in eine neue Form bringen, wenn wir wollen:
revenue=price * eb0 * eb1⋅price. Aber diese spezielle Gleichung verteilt sich nicht auf die gleiche Weise wie eine lineare oder polynomiale Gleichung, weil die Exponentialfunktion es nicht erlaubt, Terme zu trennen oder zu verteilen wie die normalen algebraischen Terme, siehe oben.
Lass uns auf jeden Fall weitermachen:
# Fit a linear model to the log-transformed quantity sold
model <- lm(log_quantity_sold ~ price, data = demand_curve_data)
# Create a revenue model based on the linear model coefficients
revenue_model_data <- demand_curve_data %>%
mutate(
revenue_model = price * exp(coef(model)[1] + coef(model)[2] * price) # Modeled revenue
)
# Plot the revenue model
ggplot(revenue_model_data, aes(x = price, y = revenue_model)) +
geom_point(color = '#203147', alpha = 0.6) + # Actual revenue points
geom_line(color = '#01ef63', size = 1.2) + # Revenue model line
labs(
title = "Car Sales",
subtitle = "Revenue Model",
x = "Price ($)",
y = "Revenue ($)"
) +
scale_y_continuous(labels = scales::dollar_format()) + # Format y-axis as dollars
theme_minimal() + # Apply a minimal theme for aesthetics
theme(
text = element_text(family = "Arial", size = 12),
plot.title = element_text(face = "bold", size = 16),
plot.subtitle = element_text(size = 14)
)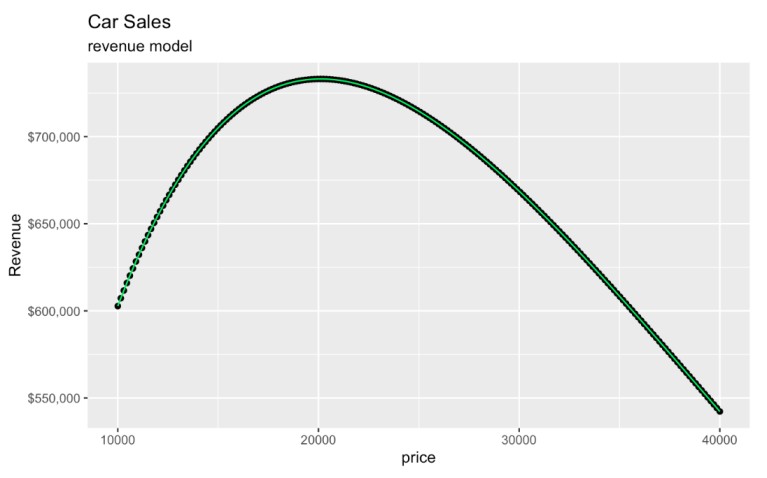
Einkommensmodell, das aus einer Nachfragekurve erstellt wird. Bild vom Autor.
Interessanterweise, auch wenn das ursprüngliche Modell log_quantity_soldverwendet hat, ist die von uns erstellte Grafik vollständig auf den ursprünglichen Skalen von price und revenue. Die Log-Transformation wirkt sich nur auf das zugrundeliegende Modell aus, und unsere Rücktransformation mit e bringt unser Diagramm auf die ursprüngliche Skala, sodass es immer noch leicht zu interpretieren ist.
Herausfinden, wo die Ableitung gleich Null ist
Unser letzter wichtiger Punkt ist dieser: Die Stelle an der Spitze der Parabel, an der die Ableitung gleich Null ist, ist der theoretische Preis, der die Einnahmen maximiert.
Wir erinnern uns vielleicht daran, dass wir die Ableitung einer Gleichung wie 3x² + 2x finden, indem wir mit den Exponenten multiplizieren, um 6x + 2 zu erhalten. Die gleiche Argumentation gilt auch hier, aber denk daran, dass wir in diesem Beispiel zuerst unsere protokollierten Werte zurücktransformieren müssen, bevor wir die Umsatzfunktion bilden können. Indem wir vor der Ermittlung des Umsatzmaximums auf die ursprüngliche Skala zurückrechnen, wissen wir, dass wir den Preis finden, der den tatsächlichen Umsatz maximiert, und nicht irgendeine transformierte Metrik. Dies ist also die richtige Einnahmefunktion, die es zu unterscheiden gilt: revenue = price * e(b0 + b1 * price).
Lass es uns ausarbeiten. Hier nehme ich die Koeffizienten des linearen Modells. Dann definiere ich eine Ertragsfunktion. Schließlich berechne ich den optimalen Preis und erfahre den damit verbundenen erwarteten Gesamtertrag.
# Model coefficients
b0 <- 4.596 # Intercept
b1 <- -4.974e-05 # Slope for price
# Define the revenue function
revenue <- function(P, b0, b1) {
P * exp(b0 + b1 * P)
}
# Calculate the optimal price (analytical solution from dR/dP = 0) - shortcut code here
(optimal_price <- -1 / b1)
# Calculate maximum revenue
(max_revenue <- revenue(optimal_price, b0, b1))[1] 20104.54
[1] 732853.5Du hast vielleicht bemerkt, dass ich eine Codezeile für den optimalen Preis hatte, die im Kontext nicht gut erklärt wurde. Ich beziehe mich auf diesen Teil des Codes: (optimal_price <- -1 / b1). Ich möchte dir kurz zeigen, wie ich herausgefunden habe, dass der optimale Preis -1 minus die Steigung ist.
Zunächst müssen wir uns an die so genannte Produktregel in der Infinitesimalrechnung erinnern, die besagt, dass, wenn die Funktion von x "f von x" gleich u(x) mal v(x) ist, dann ist die Ableitung, die wir als f'(x) schreiben können, gleich der Ableitung der ersten Sache multipliziert mit der Abschnittssache, dann addiert mit der ersten Sache mal dieser Ableitung der zweiten Sache.
# the product rule in calculus
f(x) = u(x) * v(x)
f'(x) = u'(x) * v(x) + u(x) * v'(x)Hier ist unsere Gleichung noch einmal, zusammen mit der Ableitung:
# our equation:
revenue = price * e^(b0 + b1 * price)
# the derivative of our equation
derivative = 1 * e^(b0 + b1 * price) + price * b1 * e^(b0 + b1 * price)Ich weiß, dass die Ableitung des Preises hier 1 ist, denn das ist das, wovon wir die Ableitung finden. "Wie stark ändert sich der Preis, wenn sich die Preise ändern?" Nun, es ist eine Eins-zu-Eins-Beziehung.
Auf der anderen Seite ist die Ableitung von e(b0 + b1 * Preis) nicht so ordentlich, wie eine einfache Funktion ordentlich ist, wie zum Beispiel 2x2, deren Ableitung 4x ist.
In dem Ausdruck, mit dem wir hier arbeiten, ist der Exponent ein Polynom. Der Trick dabei ist, dass du dir alle Begriffe genau ansiehst: Für den Anfang,
-
b0ist nur ein einziger Wert, also ist die Ableitung dort null -
priceist 1, wie wir bereits behandelt haben. -
b1ist der Skalierungsfaktor, also stellen wir diese Zahl voran und lassen den Polynomexponenten gemäß der Regel gleich.
Die Ableitung von e(b0 + b1 * price) ist also b1 * e(b0 + b1 * price). Das ist die sogenannte Kettenregel, wie ich hier zeigen werde:
# the chain rule in calculus
f(x) = x^g(x)
f'(x) = g'(x) * x^g(x)Als Letztes musst du noch ein paar Faktoren berücksichtigen.
Die Algebra sagt uns, dass sie gleich sind:
A + B * A = A(1+B)Und wenn ich mir das Derivat, mit dem ich arbeite, genau ansehe, wird mir klar, dass es einen A- und einen B-Teil gibt:
Das "A" ist e(b0 + b1 * price) und das "B" ist price * b1. Ich kann also Folgendes berücksichtigen
e^(b0 + b1 * price) + price * b1 * e^(b0 + b1 * price)dazu:
e^(b0 + b1 * price)(1 + price * b1)Schließlich muss ich diese Ableitung auf Null setzen, um den Ort zu finden, an dem die Steigung aufhört, nach oben zu gehen, und beginnt, nach unten zu gehen, das ist der Scheitelpunkt der Parabel.
e^(b0 + b1 * price)(1 + price * b1) = 0Als letzten Trick weiß ich, dass, wenn A * B gleich Null ist, entweder A oder B (oder beide) gleich Null sein müssen. Aber convenienterweise weiß ich, dass e(b0 + b1 * price) niemals gleich Null sein kann, weil es ein Exponent ist. Wäre er positiv, wäre die Zahl groß; wäre der Exponent gleich 0, wäre das Ergebnis 1; wäre der Exponent negativ, wäre das Ergebnis ein kleiner Bruch. Ich kann also die Hälfte verwerfen, wenn ich nach Null löse.
Das Einzige, was ich jetzt tun muss, ist, die Dinge zu verschieben und für price zu lösen.
(1 + b1 * price) = 0
b1 * price = -1
price = - 1 / b1So habe ich -1 / b1 gefunden, um die Funktion in unseren R-Code einzubauen.
Um dort weiterzumachen, wo wir aufgehört haben, können wir den optimalen Preis grafisch darstellen und die damit verbundenen Einnahmen sehen.
Der optimale Preis liegt bei 20.104,54 $, was zu erwarteten Gesamteinnahmen in Höhe von 732.853,50 $ führt, mehr oder weniger. Ich sage "mehr oder weniger", denn wenn du nachrechnest, gehen wir von 36,45 verkauften Autos aus, aber wir können kein halbes Auto verkaufen.
ggplot(revenue_model_data, aes(x = price, y = revenue_model)) +
geom_point() + geom_line(color = '#01ef63') +
ggtitle("Car Sales") + labs(subtitle = "revenue model") +
ylab("Revenue") +
scale_y_continuous(labels = scales::dollar_format()) +
geom_vline(xintercept = optimal_price, linetype = "dashed", color = '#203147') +
geom_point(aes(x = optimal_price, y = max_revenue), color = '#203147', size = 3) 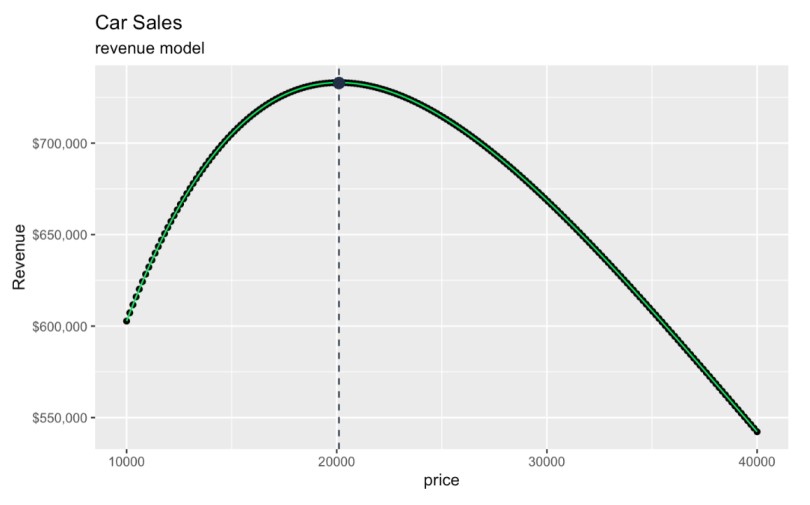 Den Preis finden, der den Umsatz maximiert. Bild vom Autor.
Den Preis finden, der den Umsatz maximiert. Bild vom Autor.
In einem anderen Arbeitsablauf könnten wir diese Ideen sogar erweitern, um den Gewinn statt der Einnahmen zu berücksichtigen. Ich werde hier nicht alles ausarbeiten, aber um das zu tun, musst du wissen, dass wir profit = revenue - cost in Betracht ziehen können, wobei cost als quantity * unit cost betrachtet wird. Wenn die Stückkosten konstant sind und die Menge durch einen Ausdruck wie 1 - price ersetzt werden kann, erhalten wir wieder eine auf dem Kopf stehende Parabel.
Wenn du mehr darüber erfahren möchtest, wie Kalküle und Ableitungen im maschinellen Lernen eingesetzt werden, solltest du unseren Kurs Einführung in das Deep Learning mit PyTorch besuchen, in dem der Gradientenabstieg im Zusammenhang mit der Abstimmung von Hyperparametern ausführlich behandelt wird. Der Kontext ist ein anderer, aber du kannst einige ähnliche Überlegungen anstellen. Wie du siehst, ist die Optimierung in ihren verschiedenen Formen eine Schlüsselqualifikation in der Datenwissenschaft, und Übung hilft.
Nachfragekurve vs. Laffer-Kurve
Wenn du Wirtschaftswissenschaften studiert hast, kennst du diese Parabel vielleicht als etwas Ähnliches wie die Laffer-Kurve, ein etwas umstrittenes Konzept, das veranschaulicht, wie Steuersätze das Steueraufkommen der Regierung beeinflussen.
Während ich sowohl die Laffer-Kurve als auch diese Transformation der Nachfragekurve als Probleme des Typs "Maximierung vs. Steuersatz" betrachten würde, ist die Laffer-Kurve spezifisch für die Besteuerung: Die x-Achse stellt den Steuersatz (0 % bis 100 %) dar, und die y-Achse ist das gesamte Steueraufkommen. Konzeptionell ist die Laffer-Kurve auch eine umgekehrte U-Form, denn am oberen Ende würden wir davon ausgehen, dass ein zu hoher Steuersatz keine Einnahmen bringen würde, weil es keinen Anreiz für Einzelpersonen oder Unternehmen gäbe, steuerpflichtige Aktivitäten zu unternehmen. Wirtschaftswissenschaftler sind sich vielleicht nicht einig, was den "Anreiz" angeht.

Die Laffer-Kurve in Ferris Bueller's Day Off. Quelle: YouTube
Verwendung einer Nachfragekurve zur Analyse von Preisen in SQL
Jetzt, wo wir die Idee durchgegangen sind, möchte ich auch ein SQL-Skript vorstellen, das die gleiche Arbeit erledigt. Mit dieser Funktion wird eine Regression von quantity_sold gegen price durchgeführt. Dann kannst du auf der Grundlage der Regressionskoeffizienten den optimalen Preis zur Maximierung des Umsatzes finden und den entsprechenden maximalen Umsatz ermitteln.
Ich denke, dass das folgende Skript besonders nützlich ist, wenn du dynamische Dashboards in Power BI oder Tableau erstellst, weil du dann Daten in Echtzeit aktualisieren kannst, ohne dass du etwas offline nehmen musst.
Du wirst auch sehen, dass ich die Regressionskoeffizienten mithilfe von SQL-Aggregatfunktionen manuell ermittelt habe, da die meisten SQL-Dialekte keine speziellen Regressionsfunktionen haben, die du verwenden kannst. Es mag dich überraschen, dass die einfache lineare Regression in SQL gut funktioniert, weil die Modellkoeffizienten für die einfache lineare Regression als Korrelation, Standardabweichung und Mittelwert zwischen x und y ausgedrückt werden können.
-- SQL script to perform linear regression on log(quantity_sold) vs price,
-- calculate the optimal price to maximize revenue, and determine the maximum revenue.
WITH regression_data AS (
SELECT
COUNT(*) AS N,
SUM(price) AS sum_x,
SUM(LOG(quantity_sold)) AS sum_y,
SUM(price * LOG(quantity_sold)) AS sum_xy,
SUM(price * price) AS sum_x2,
SUM(LOG(quantity_sold) * LOG(quantity_sold)) AS sum_y2
FROM sales_data
),
regression_coefficients AS (
SELECT
N,
sum_x,
sum_y,
sum_xy,
sum_x2,
sum_y2,
(N * sum_xy - sum_x * sum_y) / (N * sum_x2 - sum_x * sum_x) AS slope,
(sum_y - ((N * sum_xy - sum_x * sum_y) / (N * sum_x2 - sum_x * sum_x)) * sum_x) / N AS intercept
FROM regression_data
),
optimal_price AS (
SELECT
slope,
intercept,
(-1 / slope) AS optimal_P
FROM regression_coefficients
),
max_revenue AS (
SELECT
optimal_P,
slope,
intercept,
optimal_P * EXP(intercept + slope * optimal_P) AS max_R
FROM optimal_price
)
SELECT
optimal_P AS Optimal_Price,
max_R AS Maximum_Revenue
FROM max_revenue;Optimal_Price | Maximum_Revenue
------------- | ----------------
20104.32 | 402082.58Bitte beachte, dass das bereitgestellte SQL-Skript je nach verwendetem SQL-Dialekt möglicherweise angepasst werden muss, da die Syntax variieren kann. Zur Fehlersuche würde ich außerdem sicherstellen, dass deine Tabelle mit den Verkaufsdaten sowohl für price als auch für quantity_sold gültige und positive Werte enthält, da negative oder Nullwerte zu Fehlern führen können.
Wenn du eine Logarithmus-Transformation einbauen willst, wie wir es im R-Abschnitt getan haben, kannst du das auch tun, aber je nach deinem Dialekt könnte die Funktion des natürlichen Logarithmus anders heißen, entweder LN oder LOG. Um deine SQL-Kenntnisse als Analyst zu verbessern, solltest du den Lernpfad zum Associate Data Analyst in SQL erkunden, damit du ein komplettes Instrumentarium entwickeln kannst.
Ausnahmen von der Nachfragekurve
Es gibt bemerkenswerte Ausnahmen, bei denen das Verbraucherverhalten dem Standardmuster der Nachfragekurve widersprechen kann:
Giffener Waren
Giffen-Güter sind eine seltene Art von minderwertigen Gütern, für die das Gesetz der Nachfrage nicht gilt. Wenn der Preis eines Giffengutes steigt, können die Verbraucher paradoxerweise eher mehr als weniger davon kaufen. Dies geschieht, weil das Gut einen so großen Teil des Budgets eines Verbrauchers ausmacht, dass er sich bei einer Preiserhöhung keine begehrenswerteren Ersatzprodukte mehr leisten kann und gezwungen ist, noch mehr von dem Giffen-Gut zu kaufen. Ein klassisches (wenn auch umstrittenes) historisches Beispiel ist der Anstieg der Brotpreise im 19. Jahrhundert in einigen Ländern (z. B. England), wo die Menschen schließlich mehr Brot konsumierten, weil sie sich andere, teurere Lebensmittel nicht leisten konnten.
Veblen-Güter
Veblen-Güter sind Luxusgüter oder Produkte mit Statussymbolen - wie Designer-Handtaschen, edle Weine oder hochwertige Uhren -, deren Nachfrage mit steigendem Preis zunimmt. Ein Teil ihrer Anziehungskraft rührt von der Vorstellung her, dass ein höherer Preis Exklusivität oder einen höheren sozialen Status signalisiert, wodurch die Ware umso begehrenswerter wird, je teurer sie ist. Du könntest dies als "auffälligen Konsum" bezeichnen.
Andere Sonderfälle
- Bandwagon oder Netzwerkeffekte: Manche Güter werden für jeden Verbraucher wertvoller, je mehr Menschen sie nutzen (z. B. Social-Media-Plattformen, bestimmte Software-Ökosysteme). Die Nachfrage kann nicht nur wegen des Preises steigen, sondern auch wegen der wachsenden Beliebtheit des Gutes oder der Größe des Netzes.
- Snob-Effekt: Manche Verbraucher kaufen Waren, weil nur wenige andere Menschen sie haben. In diesen Fällen könnten niedrigere Preise das Gut "weniger exklusiv" erscheinen lassen, was die Attraktivität verringert.
- Spekulations- oder Anlagevermögen: Wenn der Markt davon ausgeht, dass die Preise für bestimmte Kryptowährungen oder Rohstoffe weiter steigen werden, kann die Nachfrage als Reaktion auf den Preisanstieg ansteigen, anstatt zu fallen.
In all diesen Beispielen kehrt sich das übliche Preis-Mengen-Verhältnis um oder wird aufgrund psychologischer, kultureller oder situativer Faktoren komplexer, die die klassische Annahme, dass Verbraucher einfach "mehr zu niedrigeren Preisen" wollen, außer Kraft setzen.
Nachfragekurve Allgemeine Begriffe
Wir haben uns in diesem Artikel mit ein paar verschiedenen Begriffen beschäftigt. Damit das alles übersichtlich bleibt, wollen wir eine Tabelle erstellen.
| Konzept | Beschreibung |
|---|---|
| Nachfragekurve | Eine grafische Darstellung, die das Verhältnis zwischen dem Preis eines Gutes und der von den Verbrauchern nachgefragten Menge zeigt. |
| Gesetz der Nachfrage | Er besagt, dass bei sonst gleichen Bedingungen die nachgefragte Menge steigt, wenn der Preis eines Produkts sinkt. |
| Preis-Mengen-Verhältnis | Zeigt an, dass der Preis eines Produkts die Menge, die die Verbraucher zu kaufen bereit sind, direkt beeinflusst. |
| Elastizität | Misst, wie empfindlich die nachgefragte Menge auf eine Preisänderung reagiert. |
| Abnehmender Grenznutzen | Bezieht sich auf die Abnahme der Zufriedenheit oder des Nutzens durch den Konsum zusätzlicher Einheiten eines Produkts. |
Schlussgedanken
Wir haben viel erlebt: Wir haben alles geübt, von Nachfragekurven und Nachfragemodellen über Logarithmus- und Exponentialtransformationen bis hin zu quadratischen Regressionstechniken und Optimierung.
Lerne mit dem DataCamp die Geschäftsanalyse weiter. Ziehe in Erwägung, Kurse wie die oben genannten zu besuchen: Forecasting Product Demand in R und Data-Driven Decision Making for Business, in denen du lernst, wie du Daten nutzen kannst, um deine Entscheidungen in Wirtschaft und Finanzen zu verbessern. Es gibt keinen Ersatz für technische Fähigkeiten und das Wissen um die richtigen Techniken.
Übe auch weiterhin die grundlegenden Dinge der Datenwissenschaft. Zusätzlich zu den Kernkursen zur Regression(Einführung in die Regression mit statsmodels in Python und Einführung in die Regression in R) lernst du Nichtlineare Modellierung mit verallgemeinerten additiven Modellen (GAMs) in R oder Grundlagen der Statistik in Python. Ich empfehle dir auch unseren Lernpfad für Machine Learning Scientist in Python. Wähle die Sache, in der du am schwächsten bist, damit du am meisten lernst.

