Coefficient de détermination : Ce que nous indique le coefficient R au carré

Imaginez que vous essayez de prédire la note d'un examen en fonction du nombre d'heures d'étude. Maintenant, dans quelle mesure vos prédictions correspondent-elles aux résultats réels ? C'est ce qu'indique le coefficient de détermination, également appelé^R² (R au carré).

Il nous indique dans quelle mesure le changement d'une variable (par exemple, les résultats d'un examen) peut s'expliquer par les changements d'une autre variable (par exemple, le nombre d'heures d'étude). De cette manière, vous pouvez évaluer dans quelle mesure votre modèle correspond aux données.

Dans cet article, nous vous aiderons à comprendre ce que signifie^R², pourquoi il est important, et comment le calculer et l'interpréter, même si vous êtes novice en statistiques. 

Qu'est-ce que le coefficient de détermination ?

Le coefficient de détermination, généralement noté^R² (R au carré), est un nombre qui indique dans quelle mesure un modèle de régression explique les données. Il indique dans quelle mesure le changement dans le résultat (variable dépendante) peut être expliqué par les éléments que nous utilisons pour le prédire (variable(s) indépendante(s)). 

Supposons que vous souhaitiez estimer le poids d'une personne à partir de sa taille. Si^R² est proche de 1, votre prédiction est très précise. La plupart des différences de poids peuvent être attribuées à des différences de taille. Si^R² est proche de 0, votre prédiction est essentiellement une supposition, car dans ce cas, la taille n'explique pas une grande partie de la variation de poids.

Nous nous attendons à des valeurs^R² comprises entre 0 et 1 :

• 0 signifie que le modèle n'explique aucune variabilité dans les données.

• 1 signifie que le modèle explique toute la variabilité.

• Des valeurs proches de l'1 e indiquent un meilleur ajustement, ce qui signifie que votre modèle capture davantage la tendance des données.

Régression linéaire simple

Lorsque vous travaillez avec une seule variable indépendante, le modèle est appelé régression linéaire simple. Dans ce cas,^R² présente une relation claire avec le coefficient de corrélation de Pearson (r): R^² = r^²

Cela signifie que s'il existe une forte corrélation positive ou négative entre votre prédicteur et le résultat,^R² sera élevé.

Remarque : Dans les modèles comportant plusieurs prédicteurs (appelés régression multiple),^R² indique toujours la part de variance expliquée, mais il ne s'agit plus seulement^{de r²}, car vous combinez désormais les effets de plusieurs variables.

Le coefficient de détermination peut-il être négatif ?

^R² varie généralement entre 0 et 1. Cependant, il arrive parfois que le coefficient R^² soit négatif^. Cela peut se produire si :

• Votre modèle ne comprend pas d'interception (une valeur constante de départ).
• Vous utilisez un type de modèle inadapté aux données.

Un^R² négatif signifie que votre modèle est moins performant que la moyenne. En d'autres termes, cela correspond si peu aux données que cela peut induire en erreur.

Comment calculer le coefficient de détermination

Il existe deux méthodes courantes pour calculer^R²:

1. Utilisation de la somme des carrés
2. Utilisation du coefficient de corrélation (r)

Examinons les deux cas.

Utilisation de la somme des carrés

La formule la plus courante pour^R² est la suivante :

Ici, la somme des carrés résiduels (la partie inexpliquée) mesure l'écart entre les valeurs réelles et les valeurs prédites par votre modèle. C'est l'erreur que votre modèle commet.

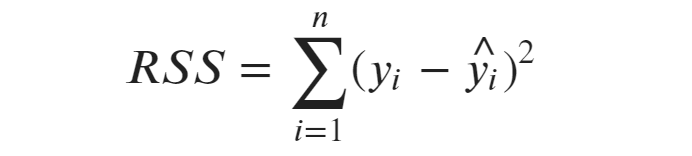
La somme totale des carrés correspond à la variation totale des données observées. Il nous indique l'écart entre les valeurs réelles et la moyenne de la variable dépendante.

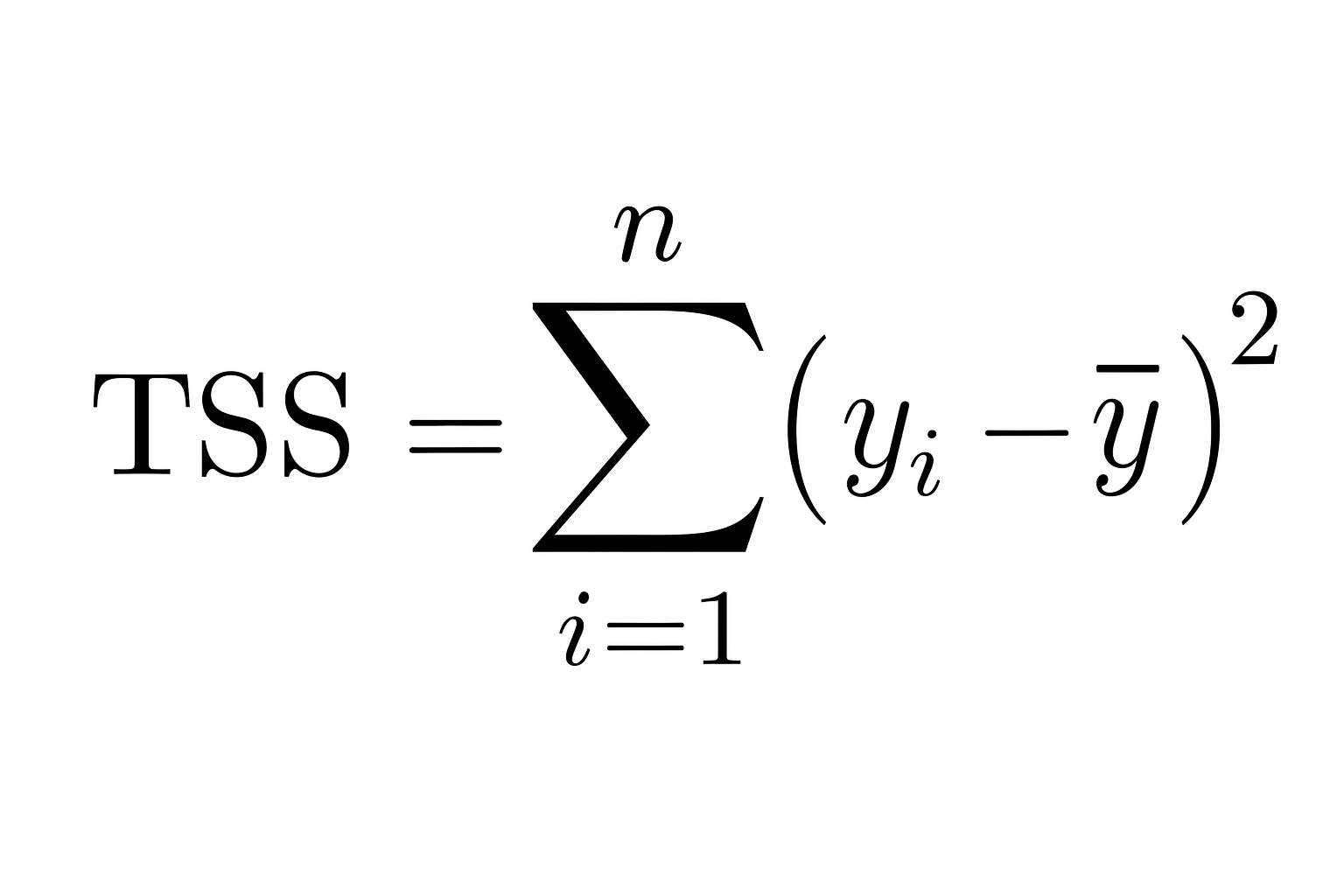
Ainsi, plus la somme des carrés résiduels est faible par rapport à la somme des carrés totale, plus votre modèle correspond aux données et plus^R² se rapproche de 1.

Comprenons cela à l'aide d'un exemple : 

Supposons que vous disposiez d'un petit ensemble de données contenant les valeurs suivantes :

Tout d'abord, calculez la moyenne des valeurs réelles :

• y = (10+12+14)/3 = 12

Calculez ensuite la somme des carrés totaux (la distance entre les valeurs réelles et la moyenne) :

• somme des carrés totale = (10 − 12)² + (12 − 12)² + (14 − 12)² = 4 + 0 + 4 = 8

Ensuite, calculez la somme des carrés résiduels (écart entre les valeurs réelles et les valeurs prédites) :

• somme des carrés résiduels = (10 − 12)² + (12 − 11)² + (14 − 13)² = 4 + 1 + 1 = 6

Ajoutez maintenant ceci à la formule :

• ^R² = 1 − ( somme des carrés résiduels / somme totale des carrés) = 1 − (6/8) = 1 − 0,75 = 0,25

Ainsi,^R² = 0,25, ce qui signifie que le modèle explique 25 % de la variation des données.

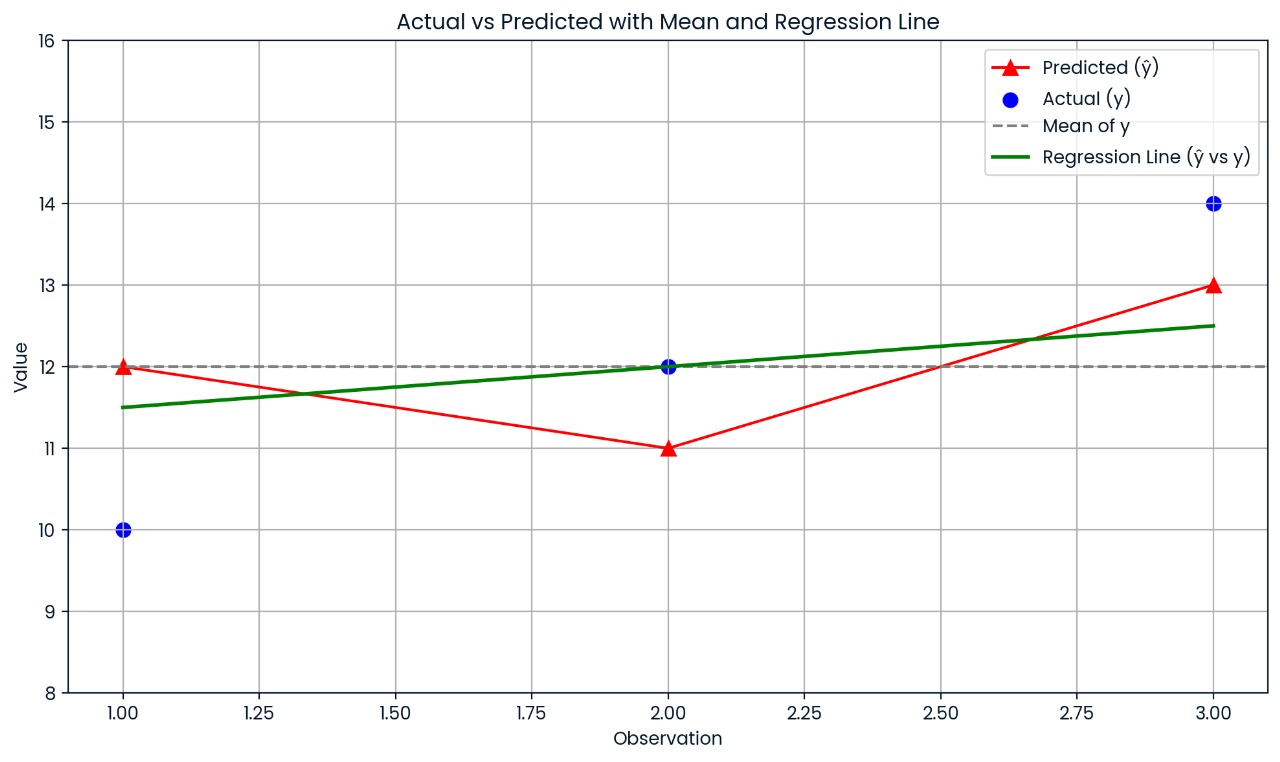
Ce graphique montre l'écart entre chaque valeur réelle et sa valeur prévue. Les prévisions du modèle sont assez imprécises, ce qui explique pourquoi le R² n'est que de 0,25 ; seulement 25 % de la variation est expliquée.

Utilisation du coefficient de corrélation

Si vous utilisez une régression linéaire simple (une seule variable indépendante), veuillez utiliser la formule suivante :

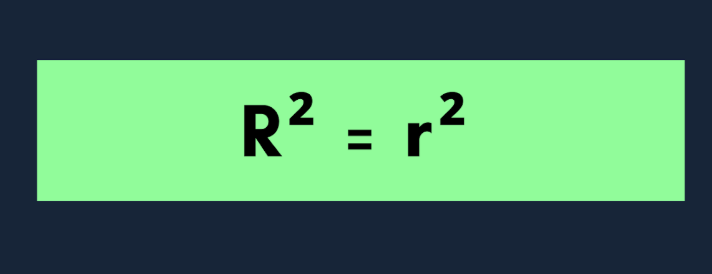
Ici, r est le coefficient de corrélation de Pearson entre les valeurs réelles et les valeurs prévues. Ce raccourci ne fonctionne que lorsqu'il n'y a qu'un seul prédicteur.

Supposons que la corrélation entre X et Y soit : r = −0,8

Même si la corrélation est négative (ce qui signifie que les variables évoluent dans des directions opposées),^R² est positif : ^R² = (−0,8)^² = 0,64

Ainsi, 64 % de la variation du résultat peut toujours être expliquée par le prédicteur, même si la relation est négative. C'est pourquoi^R² est toujours positif ou nul ; il représente la quantité de variation expliquée, et non la direction.

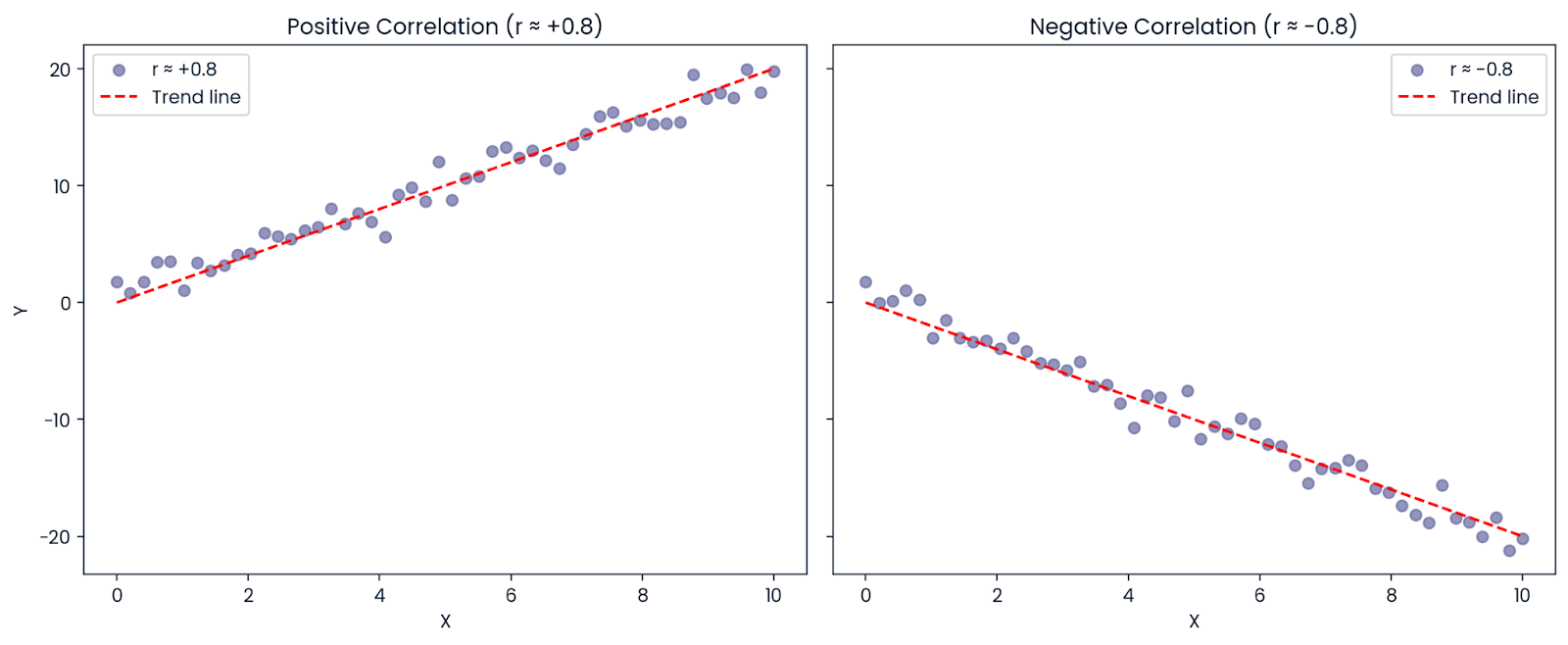
Corrélation positive et négative. Image par l'auteur.

Comment interpréter le coefficient de détermination

Le coefficient de détermination nous indique dans quelle mesure la variation du résultat (variable dépendante) est expliquée par notre modèle. En termes simples, c'est comme demander : « Dans quelle mesure les changements que j'essaie de prédire peuvent-ils être expliqués par les données que j'utilise ? »

Supposons que vous construisiez un modèle pour prédire les notes d'examen des étudiants en fonction du nombre d'heures qu'ils consacrent à leurs études. Si votre modèle vous donne : ^R² = 0,90

Cela signifie que 90 % des différences dans les résultats aux examens peuvent s'expliquer par des différences dans le temps consacré à l'étude. Les 10 % restants proviennent d'autres facteurs que votre modèle n'a pas pris en compte, tels que le sommeil, les aptitudes naturelles, les connaissances préalables ou la difficulté du test.

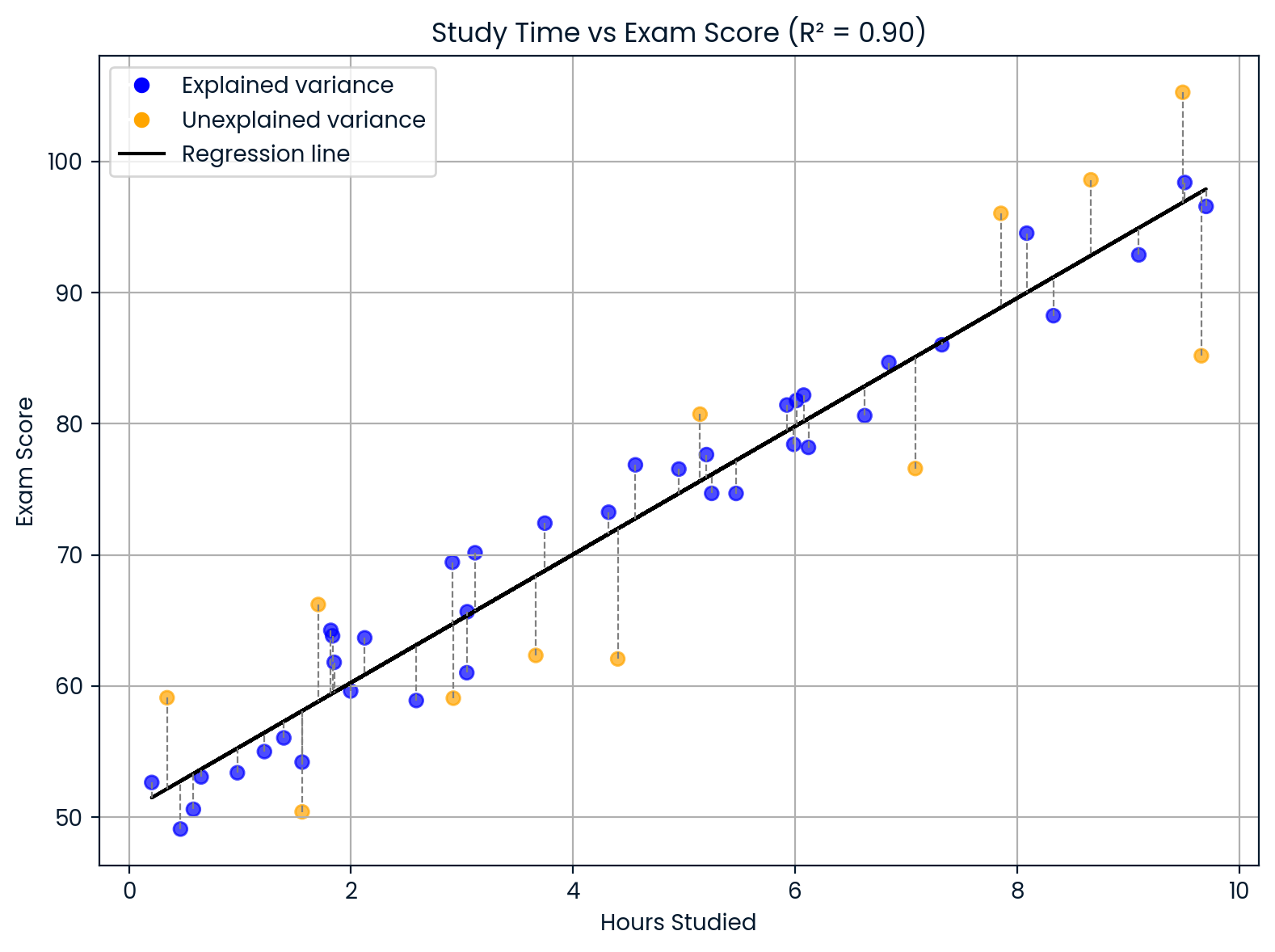
Interprétation du coefficient de détermination. Image par l'auteur.

Ce graphique montre l'influence du temps consacré à l'étude sur les résultats aux examens. 

• La ligne noire représente les prévisions du modèle. 
• Les points bleus représentent les scores obtenus par le modèle en fonction du temps d'étude. 
• Les points orange représentent les scores qui ne correspondent pas, probablement en raison d'autres facteurs tels que le sommeil, la difficulté du test ou les connaissances préalables de l'élève. Étant donné que^R² = 0,90, la plupart des scores suivent le modèle, mais pas tous.

Directives de Cohen

Jacob Cohen a élaboré un guide très utilisé pour nous aider à comprendre la signification des différentes valeurs^R² lors de l'interprétation de la force d'une relation.

Voici les repères approximatifs de Cohen pour^R²:

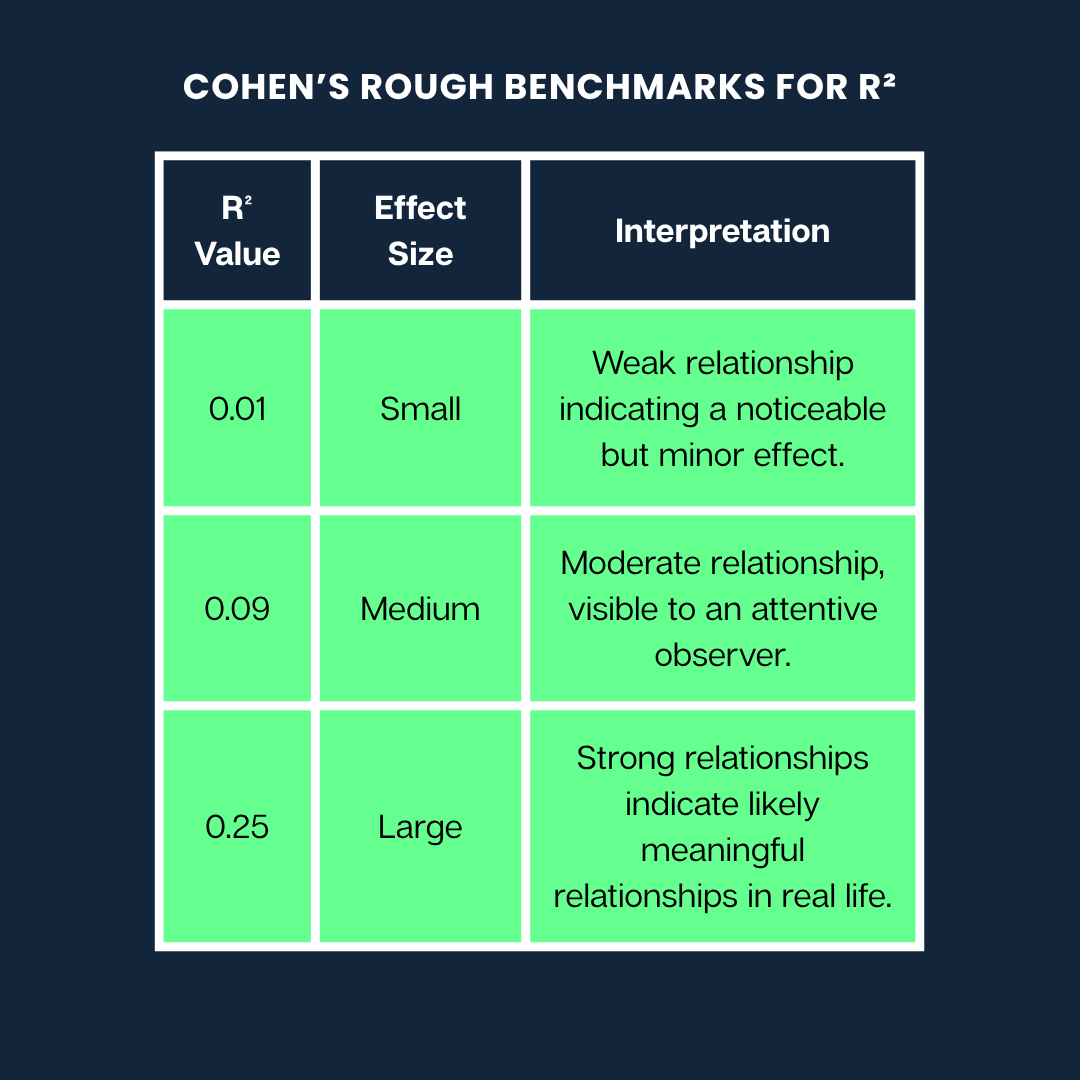
Les repères approximatifs de Cohen. Image par l'auteur

Remarque: Il s'agit de directives générales. Ce qui est considéré comme un effet « important » ou « faible » peut varier considérablement selon votre domaine (par exemple, la psychologie ou l'ingénierie) et le contexte de la recherche.

Limites et idées fausses courantes

Bien que^R² soit utile, il est important de comprendre ce qu'il peut et ne peut pas vous indiquer. Voici quelques malentendus et limites courants à prendre en compte :

Mythe n° 1 : Un coefficient de détermination élevé indique un modèle plus performant.

On pourrait penser qu'un^R² plus élevé signifie toujours un meilleur modèle, mais ce n'est pas nécessairement le cas. ^{Le R²} augmente toujours ou reste identique lorsque vous ajoutez des variables à un modèle, même si ces variables sont totalement non pertinentes. 

Pourquoi ? 

En effet, le modèle offre davantage de flexibilité pour s'adapter aux données d'entraînement, même s'il ne s'agit que d'ajuster un bruit aléatoire. Cela peut entraîner un surajustement, c'est-à-dire que votre modèle semble très performant sur les données utilisées pour son apprentissage, mais qu'il fonctionne mal sur de nouvelles données.

Conseil : U =R² ajusté lors de la comparaison de modèles comportant différents nombres de prédicteurs. Il pénalise la complexité inutile et peut aider à détecter le surajustement. 

Mythe n° 2 : Un coefficient de détermination élevé signifie des prédictions précises sur de nouvelles données ou des relations de causalité.

^R² mesure uniquement la capacité du modèle à décrire les données dont vous disposez déjà. Il ne vous indique pas :

• Si le modèle permet de faire de bonnes prédictions sur de nouvelles données
• Si une variable en entraîne une autre

Un^R² élevé peut même être obtenu par hasard si vous utilisez de nombreux prédicteurs. Il est donc important de toujours examiner d'autres mesures d'évaluation des modèles (telles que RMSE ou MAE pour la qualité des prédictions) et de garder à l'esprit que corrélation n'implique pas causalité.

Mythe n° 3 : Un R-carré faible indique que le modèle est inapproprié.

Parfois, dans des systèmes complexes (tels que la prédiction du comportement humain ou des marchés financiers), un faible^R² est prévisible.

Par exemple, si vous modélisez quelque chose qui est influencé par de nombreux facteurs imprévisibles ou non mesurables, votre modèle peut tout de même être utile, même avec un^R² faible^. Il peut mettre en évidence une tendance significative ou fournir des informations utiles, même s'il n'explique pas une grande partie de la variance.

Dans le domaine de la recherche médicale ou psychologique, il est courant d'observer des valeurs^R² faibles, car les résultats dépendent de nombreuses variables qui interagissent entre elles.

Autres variantes : R-carré partiel et généralisations

Si^R² aide à comprendre comment le modèle s'intègre dans la régression linéaire, il existe d'autres variantes et généralisations qui facilitent différents contextes de modélisation.

R-carré ajusté

À l'instar du^R² standard,^{le R²} ajusté nous indique dans quelle mesure la variation de la variable dépendante est expliquée par le modèle. Cependant, il va plus loin en pénalisant la complexité inutile. En d'autres termes, cela vous dissuade de surcharger votre modèle avec des prédicteurs supplémentaires qui ne sont pas utiles.

Sa formule est la suivante :

Adjusted R² = 1 - [ (1 - R²) × (n - 1) / (n - p - 1) ]

Ici :

• n est le nombre d'observations (points de données)

• p est le nombre de prédicteurs (variables indépendantes)

La formule ajuste^R² à la baisse si une nouvelle variable n'améliore pas le modèle. Cette pénalité s'alourdit à mesure que vous ajoutez des prédicteurs.

Par exemple, si vous ajoutez une nouvelle variable qui améliore la précision de votre modèle,^{le R²} ajusté augmentera. Cependant, si cette variable ne change pratiquement rien ou n'apporte qu'une aide fortuite,^{le R²} ajusté diminuera, vous alertant d'un éventuel surajustement.

Cela rend^{le R²} ajusté utile pour comparer des modèles.

Supposons que vous souhaitiez choisir entre un modèle plus simple avec trois prédicteurs et un modèle plus complexe avec six prédicteurs. Même si le modèle complexe présente un^R² légèrement supérieur, le^R² ajusté peut être inférieur, ce qui indique que la complexité supplémentaire n'en vaut pas la peine.

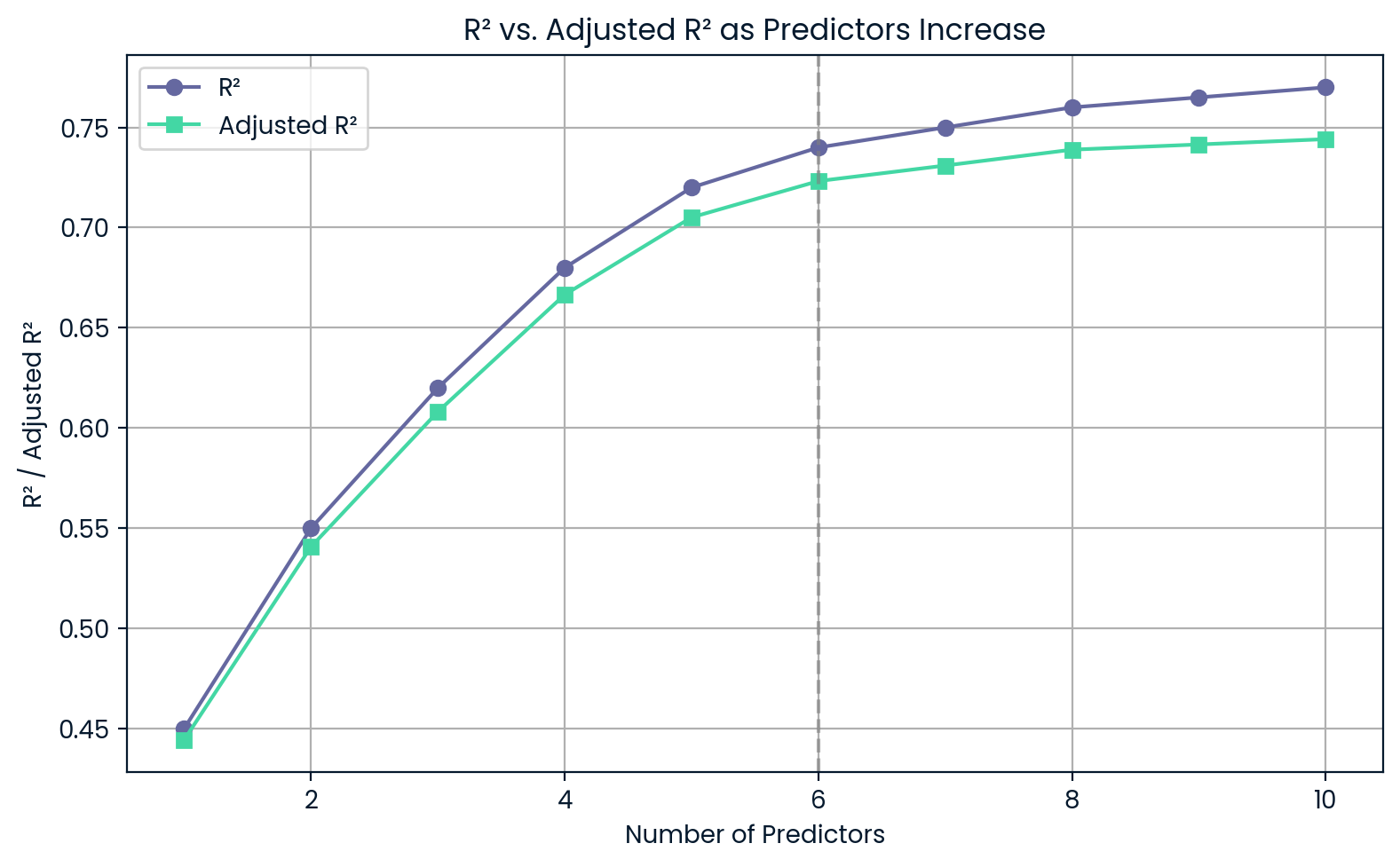
R² par rapport à R² ajusté à mesure que les prédicteurs augmentent. Image par l'auteur.

Ce graphique montre qu'à mesure que vous ajoutez des prédicteurs,^R² continue d'augmenter, même si ces prédicteurs ne sont pas très utiles. D'autre part,^{le R²} ajusté diminue si vous en ajoutez trop, ce qui vous avertit d'un surajustement.

Coefficient de détermination partielle

^{Le R²} partiel (ou coefficient de détermination partielle) nous indique la part de variance supplémentaire de la variable dépendante qui peut être expliquée par l'ajout d'un prédicteur spécifique à un modèle qui en comprend déjà d'autres.

Pour calculer^{le R²} partiel, nous comparons deux modèles :

• Le modèle réduit, qui exclut le prédicteur en question.
• Le modèle complet, qui inclut tous les prédicteurs

La formule du^R² partiel repose sur la réduction de la somme des carrés des erreurs (SSE) lorsque la nouvelle variable est ajoutée. Une forme courante est la suivante :

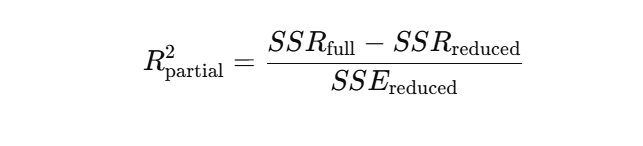
Ou en termes de sommes des carrés de régression :

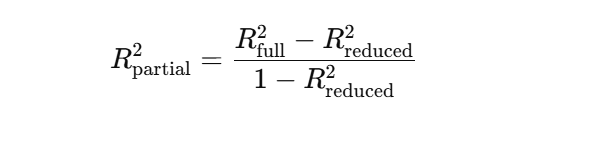
Supposons que vous construisiez un modèle pour prédire les ventes d'un produit. 

Vous avez déjà « prix du produit » et « saison » dans le modèle. Maintenant, vous souhaitez déterminer si l'ajout des « dépenses marketing » améliore les prévisions. Le R² partiel vous indique dans quelle mesure la variance des ventes s'explique par l'inclusion des « dépenses marketing ».

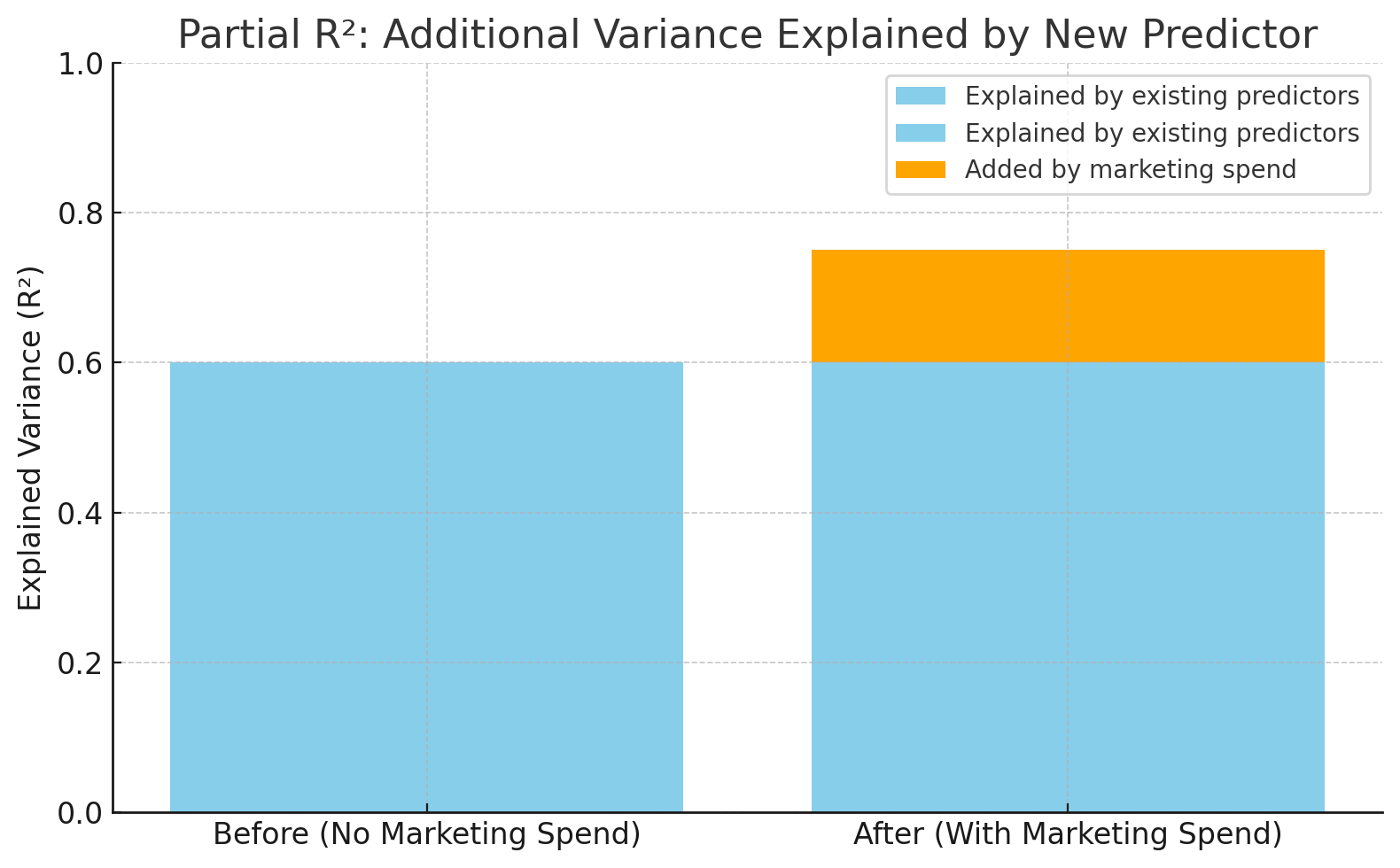
^{Le R²} est passé de 0,60 à 0,75 après l'ajout des dépenses marketing. Image par l'auteur.

Ce graphique montre à quel point le modèle gagne en précision lorsque les « dépenses marketing » sont ajoutées. ^R² passe de 0,60 à 0,75, ce qui signifie que la nouvelle variable explique 15 % de plus de la variation des ventes — c'est le R² partiel^.

Coefficient de détermination dans la régression logistique

Dans la régression logistique, la variable de résultat est catégorielle, telle que oui/non, réussite/échec, de sorte que^{le R²} traditionnel ne s'applique pas. Nous utilisons plutôt des mesures^pseudo-R², qui ont un objectif similaire : estimer dans quelle mesure le modèle explique la variation des résultats.

Deux valeurs^pseudo-R² courantes sont :

• Cox et Snell^R²: Les estimations expliquent la variance, mais leur valeur maximale est inférieure à 1, même pour un modèle parfait.
• Nagelkerke^R²: Une version corrigée du^{coefficient R²} de Cox & Snell qui s'étend jusqu'à 1, ce qui facilite son interprétation comme le coefficient^R² traditionnel^.

Supposons que vous modélisiez la probabilité qu'un client clique sur une publicité (oui/non). Étant donné que le résultat est binaire, il n'est pas possible d'utiliser le R² habituel^. Cependant, les valeurs^pseudo-R² telles que Nagelkerke permettent de comparer des modèles logistiques et d'évaluer leur pouvoir prédictif, même si elles ne sont pas directement équivalentes à^R² dans la régression linéaire.

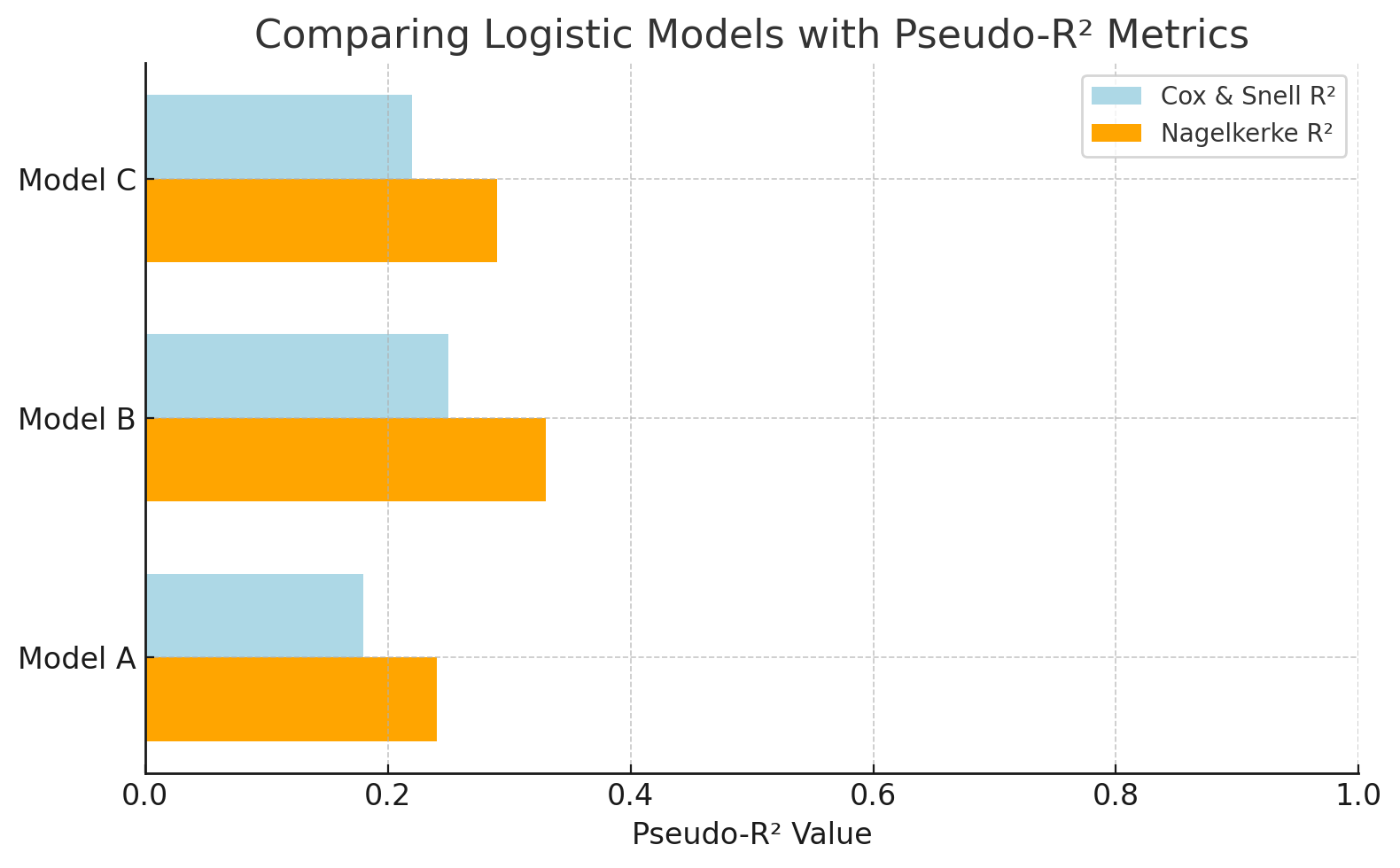
Comparez les modèles logistiques à l'aide de mesures^pseudo-R ². Image par l'auteur.

Ce graphique compare des modèles de régression logistique à l'aide de valeurs^pseudo-R ². ^{Le R²} de Nagelkerke offre une échelle plus interprétable que celle de Cox et Snell. Cela facilite l'évaluation de la capacité de chaque modèle à expliquer le résultat (par exemple, prédire les clics sur une publicité).

Coefficient de détermination par rapport à d'autres mesures d'ajustement du modèle

Bien que^R² soit utile pour comprendre la part de variation expliquée, il ne mesure pas l'écart entre vos prédictions et la réalité. C'est là que les mesures basées sur les erreurs telles que RMSE, MAE et MAPE s'avèrent utiles.

Voici une brève comparaison :

Applications pratiques dans divers domaines

Examinons maintenant quelques-uns des innombrables cas où le coefficient de détermination a été utilisé. 

Économie : Explication des fluctuations du PIB

En économie,^R² est utilisé pour expliquer les variations d'indicateurs généraux tels que le produit intérieur brut (PIB). Par exemple, un modèle peut inclure des variables telles que les taux d'intérêt, les dépenses de consommation et les balances commerciales pour prévoir le PIB.

Si un tel modèle renvoie un^R² de 0.83, cela signifie que 83 % de la variation du PIB peut être expliquée par ces facteurs économiques. Cela aide les économistes à comprendre dans quelle mesure les fluctuations du PIB peuvent être attribuées à des facteurs connus.

Une étude de l'a utilisé des données de l'enquête sur la santé et la nutrition des adultes (NHANES) menée aux s du PIB en tant que variable indépendante pour prédire l'indice S&P 500 et a obtenu un^R² de 0.83. Cela a démontré une relation étroite entre l'activité économique et les tendances boursières.

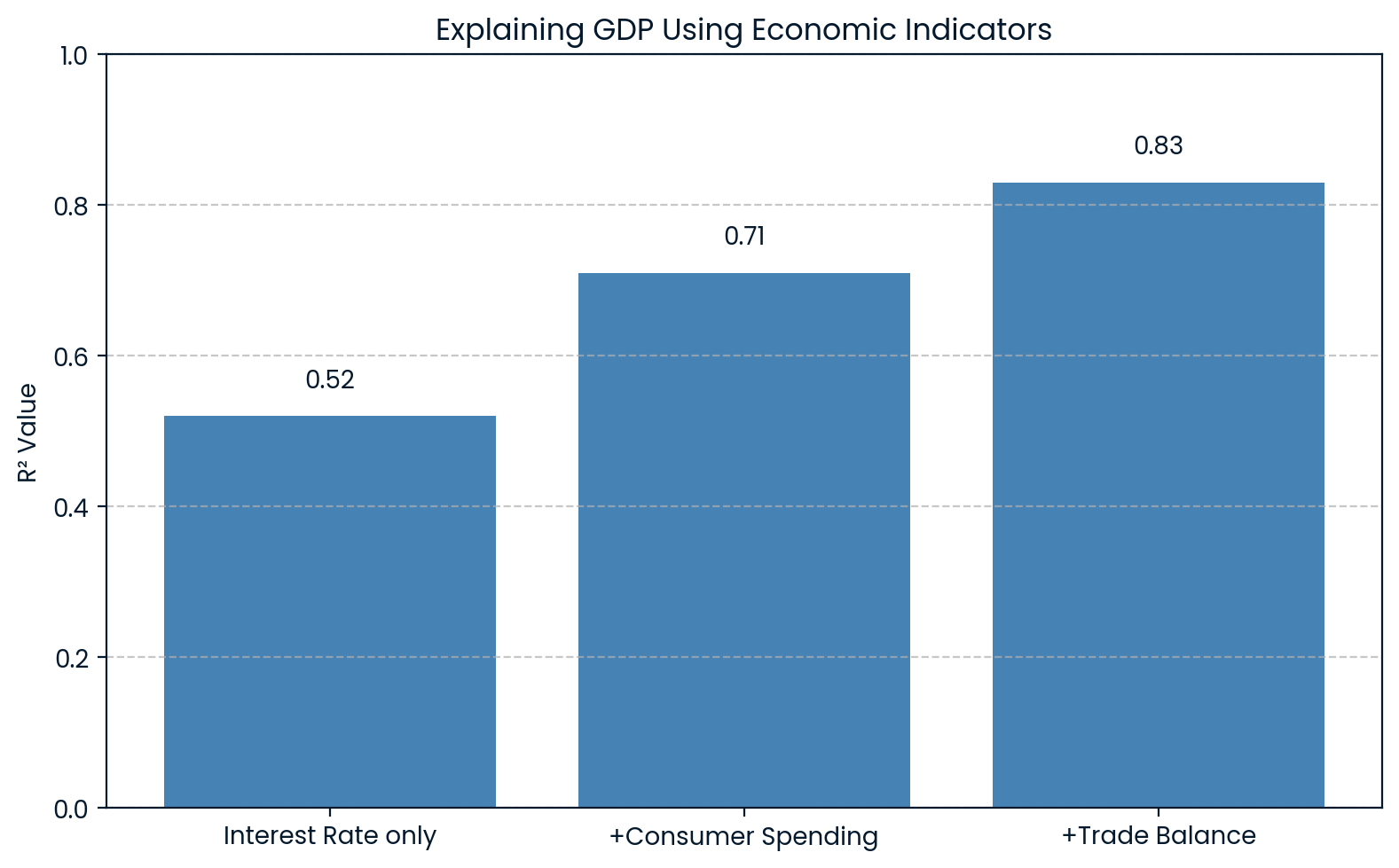
^R² expliquant l'économie du PIB. Image par l'auteur.

Le graphique montre que plus on ajoute d'indicateurs économiques au modèle, plus le^R² augmente, passant de 0.52 à 0.83 avec les trois variables. Cela montre clairement que chaque facteur ajouté permet de mieux expliquer les fluctuations du PIB.

Finances : Évolution du cours de l'action par rapport à l'indice boursier

En finance,^R² est utilisé pour mesurer dans quelle mesure les rendements d'une action s'expliquent par les mouvements globaux du marché. Pour ce faire, on calcule la régression des rendements d'une action par rapport à un indice boursier tel que le S&P 500.

0.82Par exemple, si vous effectuez une régression des rendements d'Apple (AAPL) par rapport à l'indice S&P 500 et obtenez^R² = 0,85, cela signifie que 85 % des fluctuations des rendements d'Apple s'expliquent par l'évolution du marché dans son ensemble.

• Un^R² élevé suggère que le titre est étroitement lié au marché.
• Un faible^R² implique que le titre est plus indépendant.

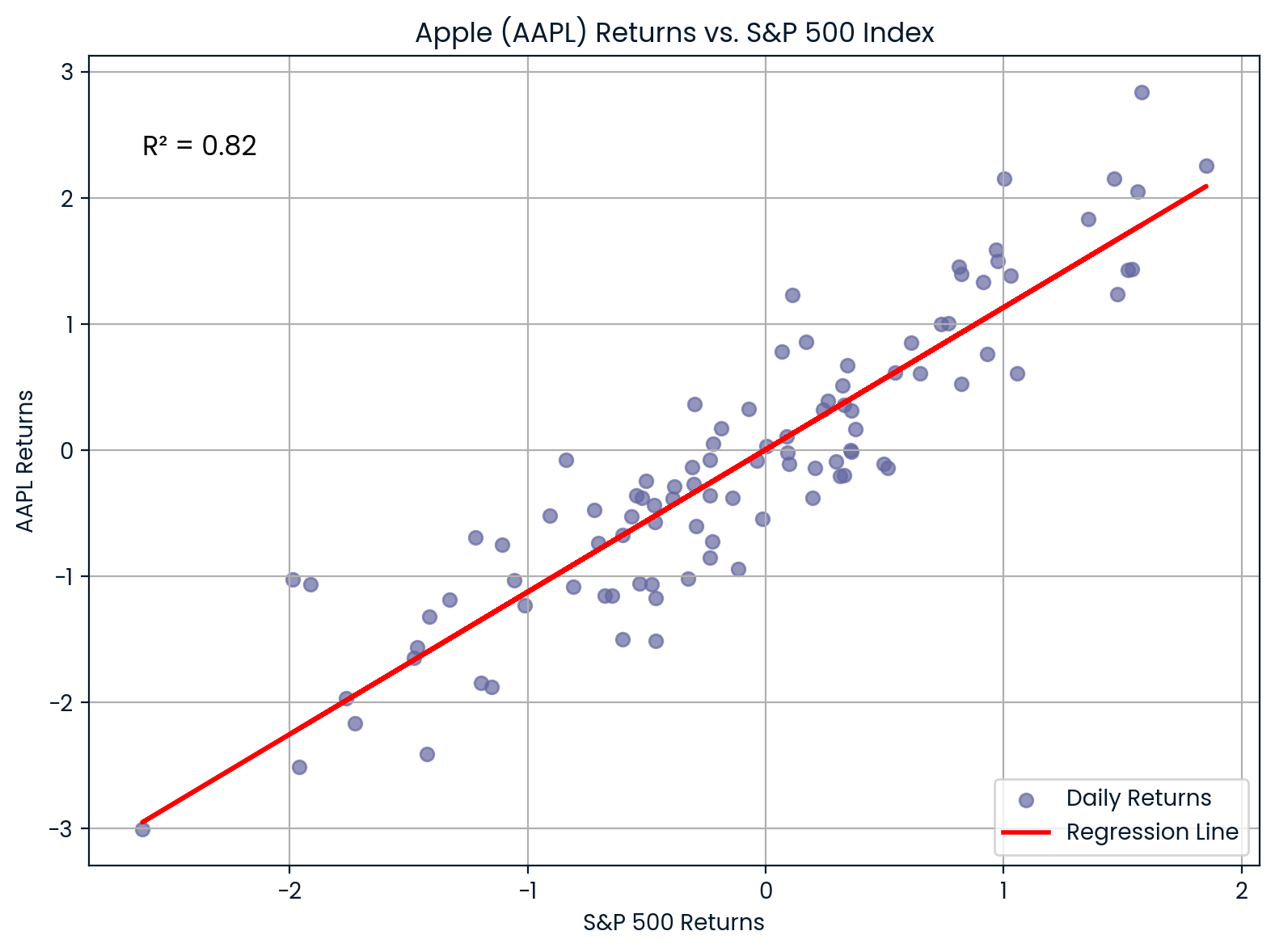
Corrélation entre l'AAPL et le S&P 500. Image par l'auteur.

Le graphique illustre la forte corrélation entre Apple (AAPL) et l'indice S&P 500. 0.82Avec un^R² de 0,988, la plupart des fluctuations du cours de l'action Apple suivent de près les tendances du marché, ce qui témoigne d'une forte sensibilité au marché.

Marketing : Dépenses publicitaires et conversions

En marketing,^R² indique dans quelle mesure les dépenses publicitaires expliquent les taux de conversion des clients.

Supposons que vous travaillez dans une entreprise de commerce électronique et que vous souhaitez savoir si l'augmentation des dépenses publicitaires mensuelles améliore les taux de conversion. Vous effectuez une régression linéaire et obtenez^R² = 0,98. Cela signifie que 98 % de la variation du taux de conversion s'explique par vos dépenses publicitaires, ce qui suggère une relation très forte.

Ces informations aident les spécialistes du marketing à :

• Prévisions des résultats de conversion
• Justifier les budgets publicitaires
• Prévoir le retour sur investissement (ROI)

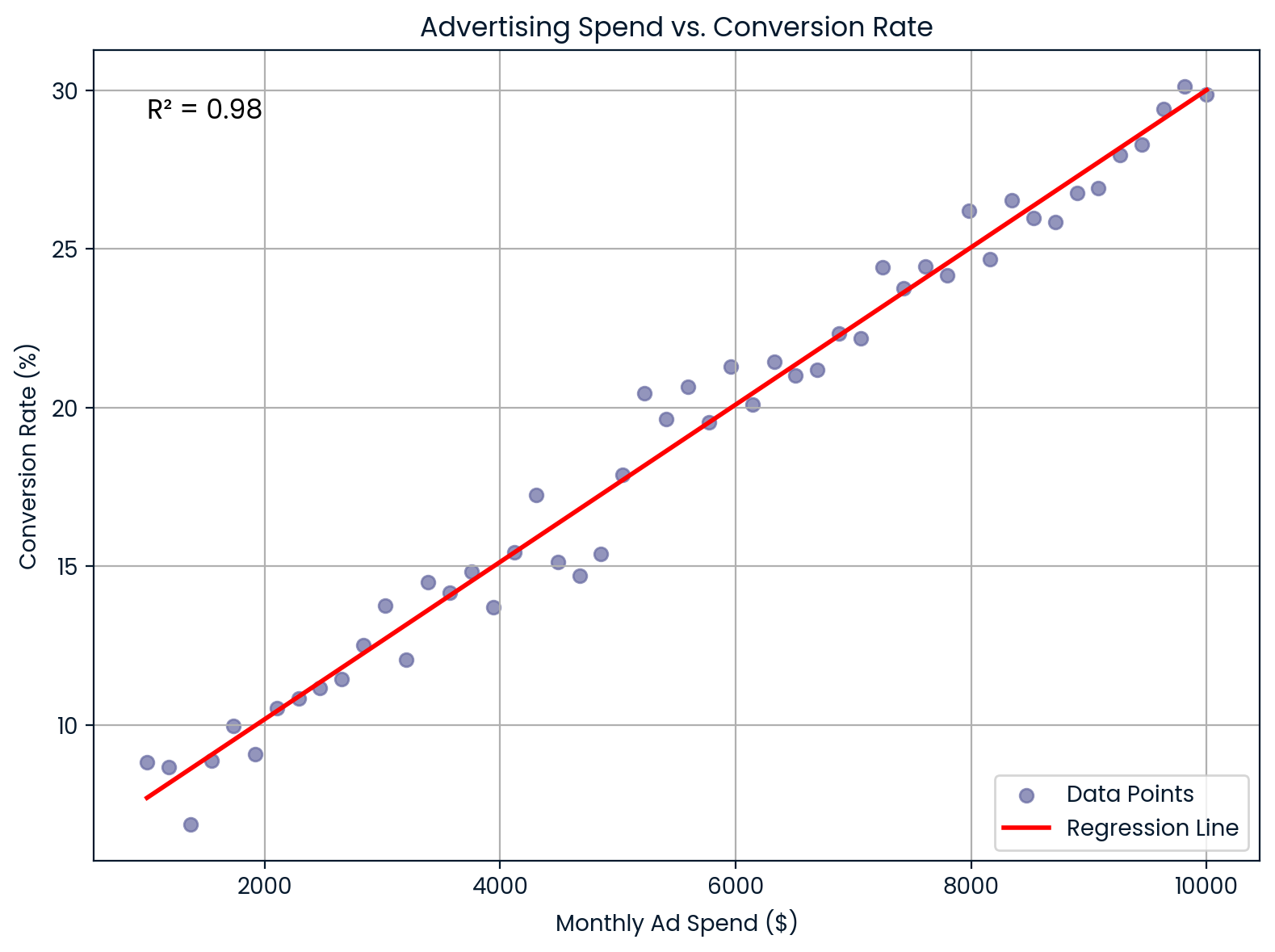
Dépenses publicitaires mensuelles par rapport au taux de conversion. Image par l'auteur.

Ce graphique illustre une relation linéaire presque parfaite entre les dépenses publicitaires mensuelles et le taux de conversion. Il offre une forte valeur prédictive pour le retour sur investissement et la planification budgétaire.

Apprentissage automatique : Modèles de régression de notation

En apprentissage automatique,^R² est utilisé comme mesure de performance pour les tâches de régression. Les bibliothèques telles que scikit-learn proposent la fonction r2_score() pour effectuer ce calcul.

Il vous indique dans quelle mesure votre modèle explique la variabilité des données :

• 1 U^{n R²} proche de 0,90 indique une bonne adéquation et une faible erreur.

• 0 U^{n R²} proche de 0,50000000000000000000

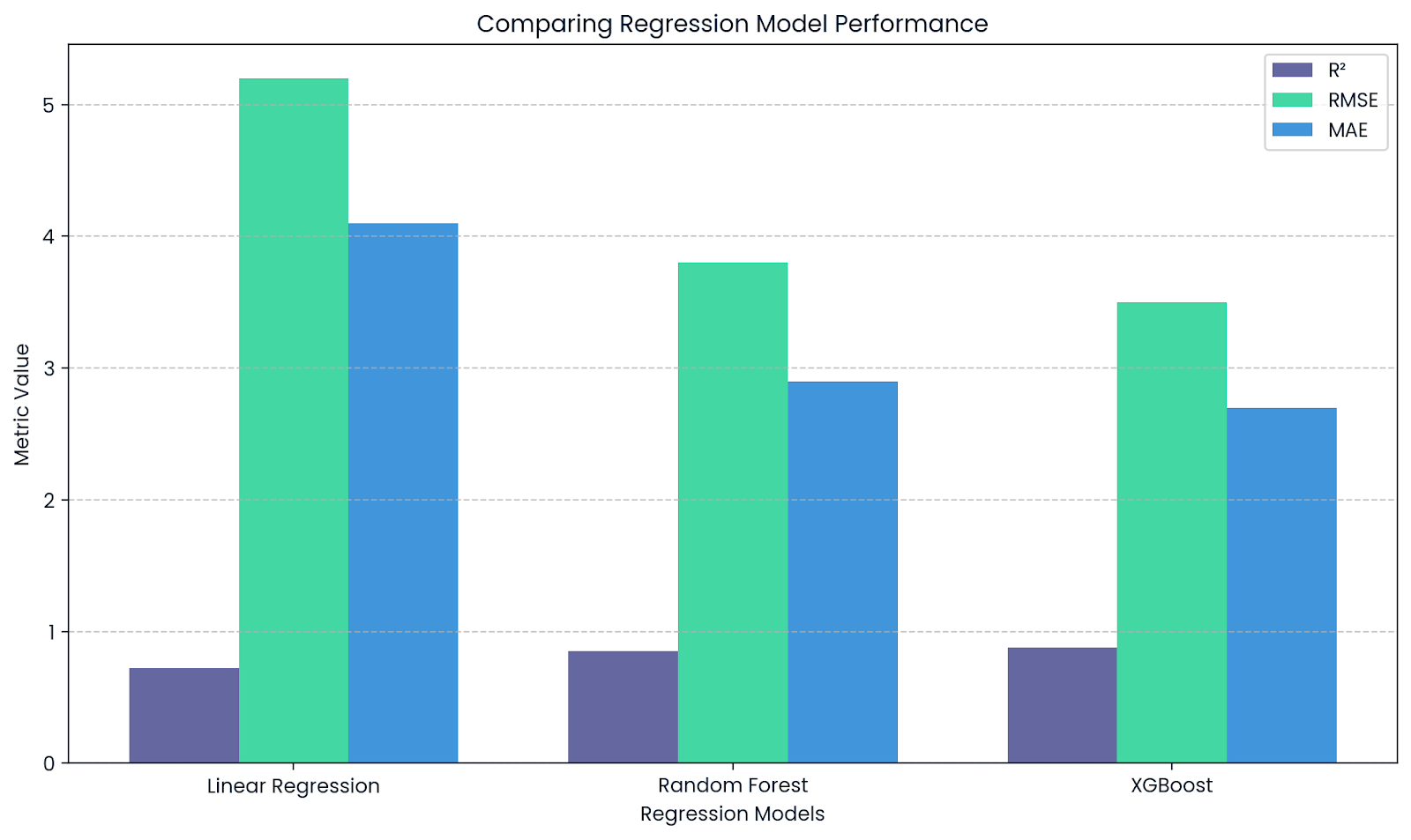
^R² complète RMSE et MAE. Image par l'auteur.

Ce graphique montre comment le R² complète d'autres mesures telles que le RMSE et le MAE lors de l'évaluation des modèles de régression. Alors que^R² indique le pouvoir explicatif, RMSE et MAE fournissent des informations sur l'ampleur réelle des erreurs de prédiction.

Rapport sur le coefficient de détermination dans la recherche

Si vous incluez^R² dans un article de recherche ou un projet, il y a quelques règles de mise en forme à respecter :

• Veuillez mettre^R² en italique et, oui, il doit s'agir d'un R majuscule, et non minuscule. 
• N'utilisez pas de zéro devant la virgule décimale. Ainsi, au lieu d'écrire^R² = 0,73, écrivez^R² = 0,73. À moins que vous n'ayez vraiment besoin de plus de détails, arrondissez à deux décimales.

Si vous utilisez^R² dans le cadre d'une analyse de régression ou d'une ANOVA et que vous vérifiez la significativité de votre modèle, veuillez inclure quelques éléments supplémentaires : la statistique F, les degrés de liberté et la valeur p. Ils indiquent au lecteur dans quelle mesure nous pouvons être certains que votre modèle explique quelque chose de significatif.

Ainsi, lorsque vous communiquez vos résultats, cela peut ressembler à ceci :

Le modèle explique une part importante de la variance des ventes,^R² = 0,73, F(2, 97) = 25,42, p < 0,001.

Toutefois, si vous ne procédez pas à un test d'hypothèse, par exemple si vous effectuez une analyse exploratoire ou évaluez les performances d'un modèle à l'aide d'une validation croisée, vous pouvez tout à fait indiquer la valeur R² seule.

Le coefficient de détermination dans Python, R et Excel

Voyons comment calculer^R² de trois manières différentes : Python, R et Excel à travers un mini-projet dans lequel nous prédisons les notes des étudiants en fonction de leur temps d'étude.

Nous utiliserons l'ensemble de données suivant pour les trois exemples :

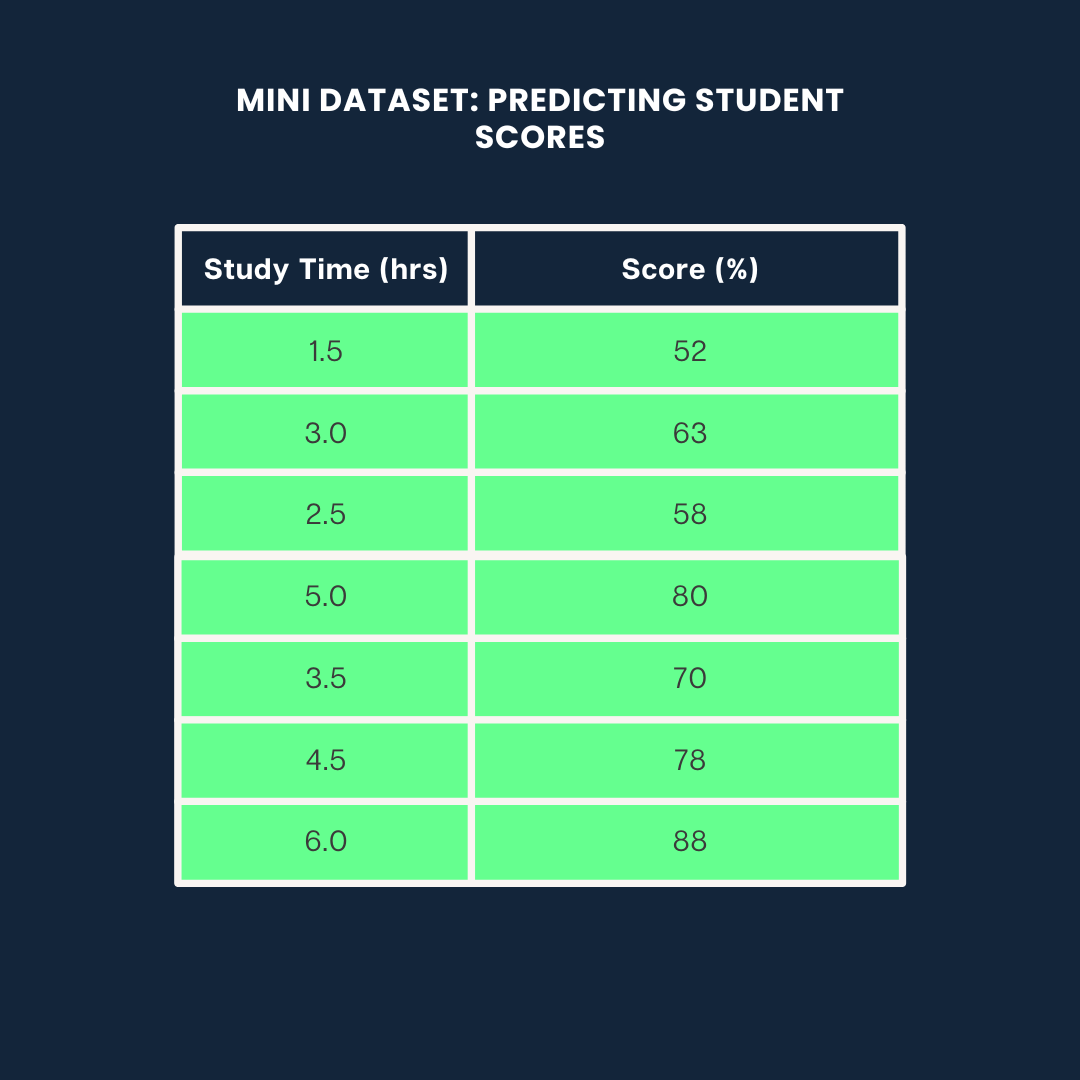
Exemple d'ensemble de données. Image par l'auteur

Coefficient de détermination en Python

Voici comment calculer^R² en Python à l'aide d'scikit-learn:

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

# Data
study_time = np.array([1.5, 3.0, 2.5, 5.0, 3.5, 4.5, 6.0]).reshape(-1, 1)
scores = np.array([52, 63, 58, 80, 70, 78, 88])

# Model
model = LinearRegression()
model.fit(study_time, scores)
predicted_scores = model.predict(study_time)

# R² score
r2 = r2_score(scores, predicted_scores)
print(f"R² = {r2:.2f}")

0.99

Cela signifie que 99 % de la variance des scores s'explique par le temps consacré à l'étude.

Si vous souhaitez en savoir plus sur les modèles de régression et statistiques, veuillez consulter notre guide Introduction à la régression avec statsmodels en Python. 

Coefficient de détermination dans R

Dans R, vous pouvez calculer R² en quelques lignes à l'aide de la fonction lm():

# Data
study_time <- c(1.5, 3.0, 2.5, 5.0, 3.5, 4.5, 6.0)
scores <- c(52, 63, 58, 80, 70, 78, 88)

# Linear model
model <- lm(scores ~ study_time)

# R-squared
summary(model)$r.squared

0.9884718

Environ 98 % de la variance des scores s'explique par le temps consacré à l'étude. Si vous souhaitez en savoir plus sur la régression dans R, veuillez consulter notre cours Introduction à la régression dans R.

Coefficient de détermination dans Excel

Dans Excel, vous pouvez calculer R² à l'aide de la fonction intégrée « RSQ() ». En supposant que :

• Le temps d'étude est indiqué dans les cellules. A2:A8

• Les scores sont dans les cellules. B2:B8

La syntaxe est la suivante :

RSQ(known_y's,known_x's)

J'ai utilisé la formule suivante :

=RSQ(B2:B8,A2:A8)

Cela indique à Excel de calculer la valeur^R² entre la variable dépendante (les scores) et la variable indépendante (le temps d'étude).

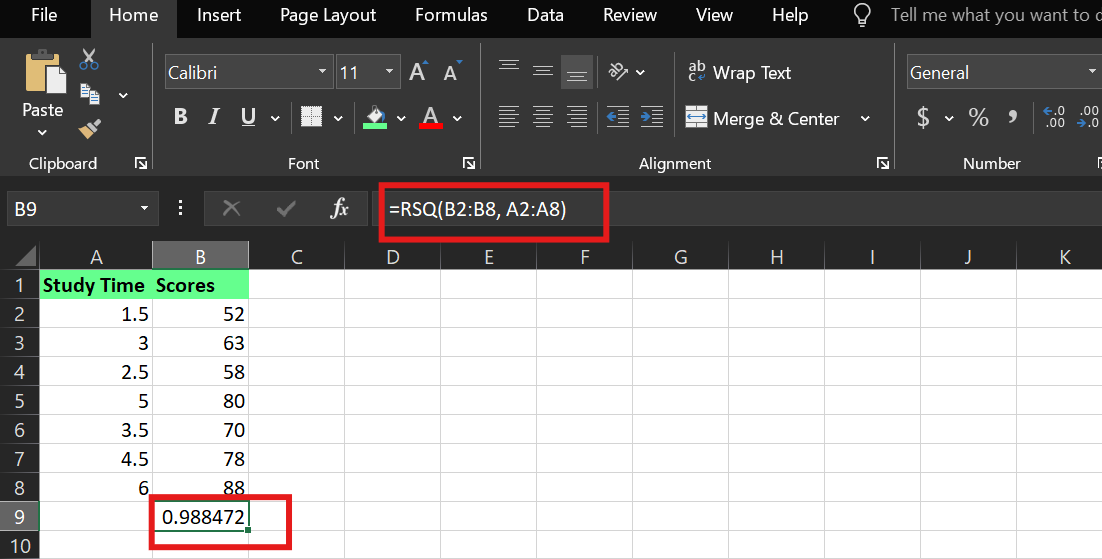
Exemple de^R² dans Excel. Image par l'auteur.  

Points à retenir

Que vous prédisiez les notes d'étudiants, les rendements boursiers ou le comportement des clients, le coefficient de détermination vous indique dans quelle mesure votre modèle comprend réellement le résultat. 

Un coefficient de détermination élevé peut sembler impressionnant, mais ne vous laissez pas tromper en pensant que le modèle est parfait ou qu'il prouve un lien de cause à effet. Un faible coefficient de détermination n'est pas nécessairement synonyme d'échec ; il peut simplement indiquer que votre système est complexe ou que vos variables sont incomplètes.

Ainsi, si vous créez ou analysez des modèles, posez-vous les questions suivantes :

• Qu'est-ce que j'explique bien ?
• Qu'est-ce qui m'échappe ?
• Et mon modèle est-il utile, et pas seulement précis ?

Commencez par adopter cet état d'esprit, et vous utiliserez le coefficient de détermination comme un outil pour prendre de meilleures décisions.