Distribution géométrique : Guide complet pour modéliser les premiers événements réussis

Combien d'entretiens d'embauche devrez-vous passer avant de décrocher le poste de vos rêves ? Combien de tentatives sont nécessaires avant qu'une campagne marketing génère sa première vente ? La distribution géométrique répond à ces questions relatives au « temps d'attente » en modélisant le nombre d'essais nécessaires jusqu'à ce que le premier succès se produise.

Ce guide présente les fondements mathématiques de la distribution géométrique, ses propriétés distinctives et ses applications pratiques qui la rendent utile pour les personnes travaillant avec des scénarios d'essais séquentiels. Pour rafraîchir vos connaissances sur les distributions de probabilité, nous vous recommandons de suivre notre cours Introduction aux statistiques. 

Qu'est-ce que la distribution géométrique ?

La distribution géométrique est une distribution de probabilité discrète qui modélise le nombre d'essais de Bernoulli indépendants nécessaires pour obtenir le premier succès. Chaque essai a la même probabilité de réussite, et les essais sont indépendants les uns des autres.

Cette distribution se présente sous deux formes courantes : l'une qui compte le nombre total d'essais jusqu'au premier succès (y compris le succès), et l'autre qui ne compte que le nombre d'échecs avant le premier succès. Les deux formes sont largement utilisées en fonction du contexte d'application spécifique. Tout au long de ce guide, nous utiliserons la première forme, en comptant le nombre total d'essais jusqu'au premier succès, où X peut prendre les valeurs 1, 2, 3, etc.

Comprendre la distribution géométrique

Examinons la structure mathématique et les caractéristiques qui définissent cette distribution.

Définition fondamentale et structure de probabilité

La distribution géométrique requiert trois conditions essentielles : des essais indépendants, une probabilité de réussite identique pour tous les essais et une probabilité fixe p où 0 < p ≤ 1. La notation standard utilise p pour la probabilité de réussite et q = 1-p pour la probabilité d'échec.

La fonction de masse de probabilité (PMF) pour le nombre d'essais X jusqu'au premier succès est la suivante : 

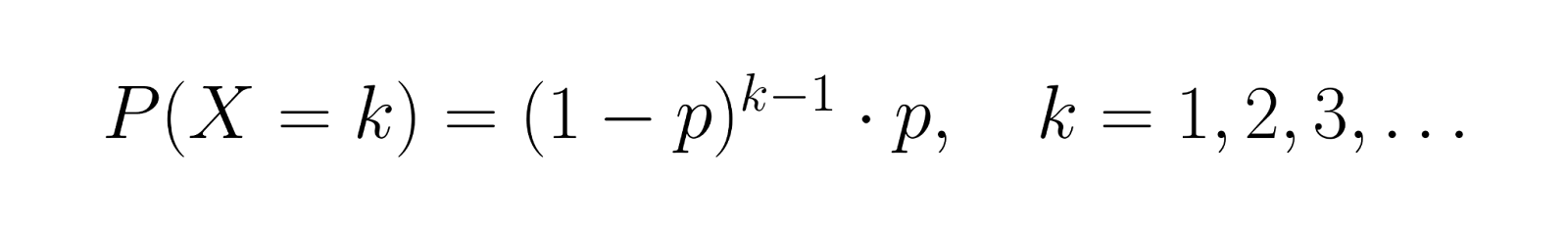
Cette formule calcule la probabilité de rencontrer exactement k-1 échecs suivis d'un succès. Par exemple, si p = 0,3, la probabilité de réussite au troisième essai est P(X = 3) = (0,7)² × 0,3 = 0,147.

Probabilités cumulées et fonction de distribution

La fonction de distribution cumulative (CDF) nous donne :

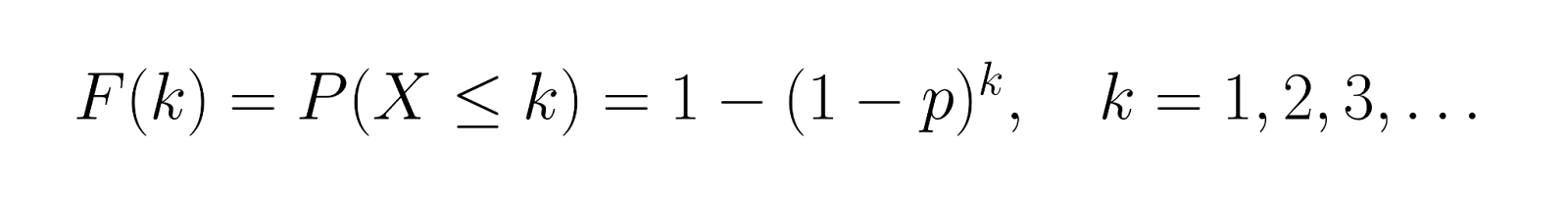
Cela représente la probabilité d'obtenir un résultat positif après k essais. En reprenant notre exemple où p = 0,3, calculons la CDF pour les premières valeurs :

• F(1) = P(X ≤ 1) = 1 - (0,7)¹ = 0,3
• F(2) = P(X ≤ 2) = 1 - (0,7)² = 1 - 0,49 = 0,51
• F(3) = P(X ≤ 3) = 1 - (0,7)³ = 1 - 0,343 = 0,657

Cela indique qu'il y a 30 % de chances de réussite lors du premier essai, 51 % de chances de réussite lors des deux premiers essais et 65,7 % de chances de réussite lors des trois premiers essais.

Représentation graphique de la distribution géométrique

Les modèles visuels de la distribution géométrique fournissent des informations clés sur les scénarios de « temps d'attente ». Ces graphiques illustrent comment la probabilité se concentre dans les premiers essais et diminue de manière exponentielle, rendant la distribution utile pour modéliser des situations où le succès est plus probable à court terme qu'à long terme.

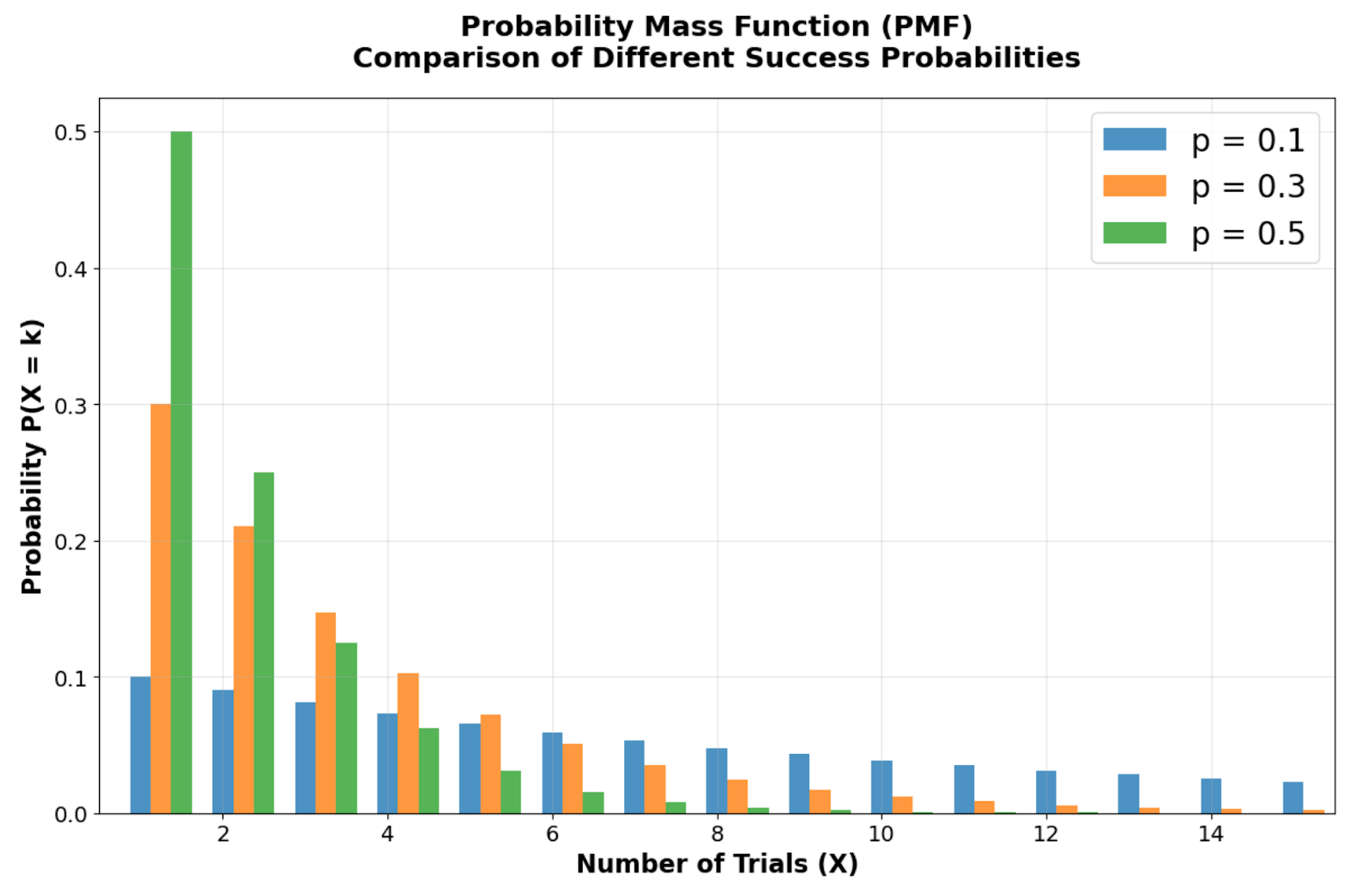
Comparaison des fonctions de masse de probabilité illustrant comment différentes probabilités de réussite (p = 0,1, 0,3, 0,5) affectent la forme de la distribution. Image par l'auteur

En examinant la comparaison des fonctions de masse de probabilité entre différentes probabilités de réussite, vous pouvez observer la forme asymétrique caractéristique de la distribution géométrique, avec son mode toujours situé à X = 1 (premier essai). Veuillez noter que les barres de probabilité commencent au niveau le plus élevé lors du premier essai et diminuent de manière géométrique à chaque essai suivant. À mesure que la probabilité de réussite p diminue, la distribution devient plus étalée, reflétant des temps d'attente plus longs. Par exemple, avec p = 0,1, il n'y a que 10 % de chances de réussite immédiate, ce qui crée une queue droite plus prononcée par rapport à p = 0,5.

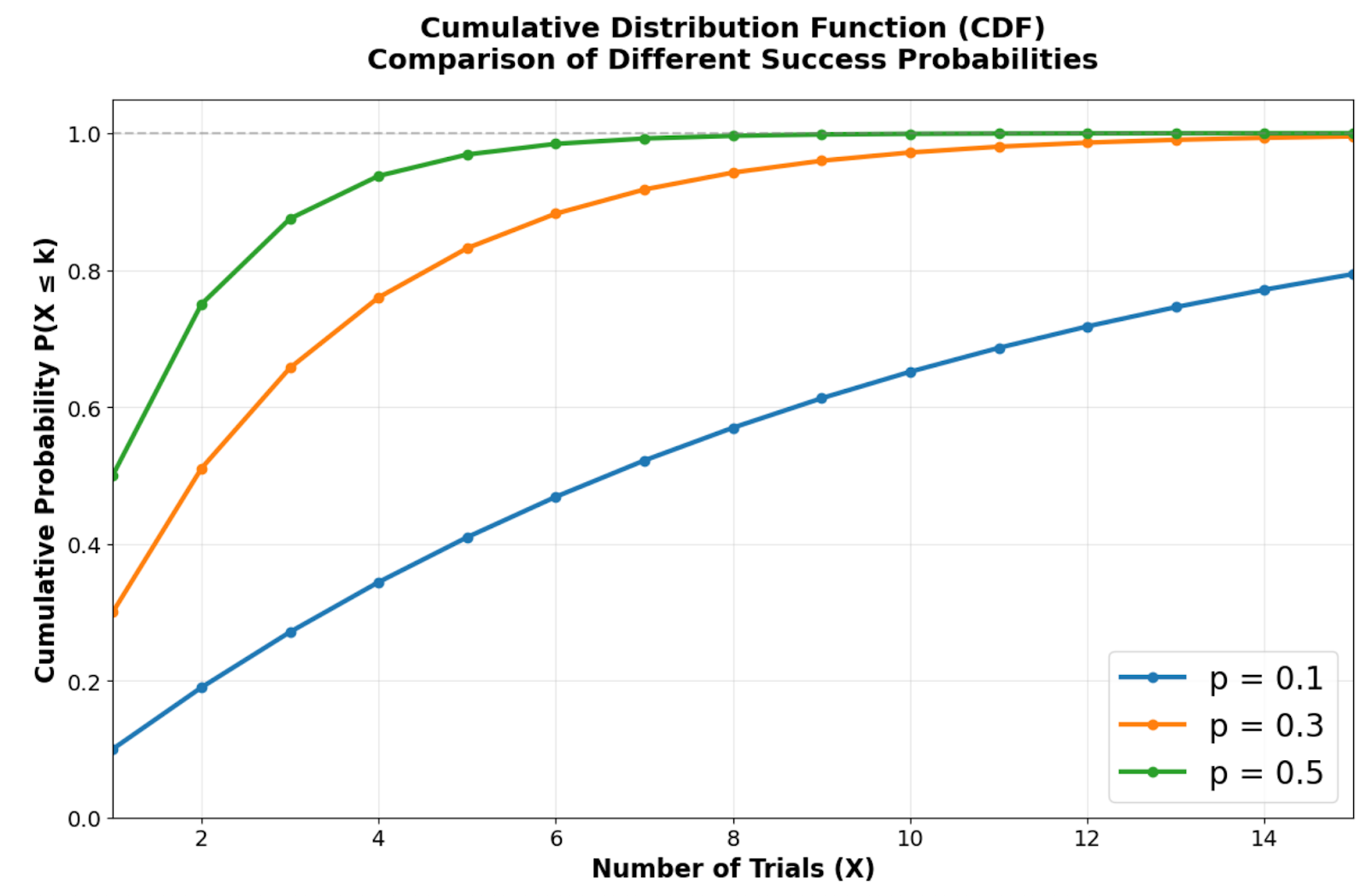
Fonction de distribution cumulative illustrant la rapidité avec laquelle différentes probabilités de succès se rapprochent de la certitude. Image par l'auteur. 

La fonction de distribution cumulative montre à quelle vitesse la distribution géométrique tend vers la certitude. Des probabilités de réussite plus élevées créent des courbes plus abruptes qui atteignent des probabilités cumulées élevées en seulement quelques essais. Par exemple, avec p = 0,5, il y a environ 75 % de chances de réussite lors des deux premiers essais, tandis que p = 0,1 nécessite un nombre d'essais nettement plus important pour atteindre le même niveau de certitude.

Comparaison côte à côte mettant en évidence le modèle de décroissance exponentielle dans PMF et l'approche rapide vers la certitude dans CDF. Image par l'auteur. 

Ce modèle de décroissance exponentielle explique pourquoi la distribution géométrique fonctionne bien pour modéliser des scénarios où le succès rapide est plus probable que des périodes d'attente prolongées. L'ascension rapide de la CDF vers 1 explique pourquoi cette distribution est efficace pour modéliser des processus où les temps d'attente sont courts, ce qui la rend utile pour le contrôle qualité, l'analyse de conversion des clients et les scénarios de test de fiabilité.

Créer vos propres visualisations de distributions géométriques

Vous pouvez recréer ces visualisations et explorer différentes valeurs de paramètres à l'aide des bibliothèques scipy et matplotlib de Python. Voici comment générer les informations visuelles clés qui mettent en évidence les caractéristiques les plus importantes de la distribution géométrique :

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Create side-by-side plots for PMF and CDF
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
fig.suptitle('Geometric Distribution: Key Visual Insights', fontsize=24, fontweight='bold')

# Simple PMF showing exponential decay (using p = 0.3)
x_simple = np.arange(1, 11)
pmf_simple = stats.geom.pmf(x_simple, 0.3)

ax1.bar(x_simple, pmf_simple, alpha=0.8, color='steelblue', edgecolor='black', linewidth=1)
ax1.set_title('PMF: Exponential Decay Pattern', fontsize=18, fontweight='bold', pad=15)
ax1.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax1.set_ylabel('Probability', fontsize=14, fontweight='bold')
ax1.grid(True, alpha=0.3)
ax1.tick_params(axis='both', which='major', labelsize=14)

# Simple CDF showing approach to 1
cdf_simple = stats.geom.cdf(x_simple, 0.3)

ax2.plot(x_simple, cdf_simple, 'o-', linewidth=4, markersize=8, color='darkgreen')
ax2.set_title('CDF: Rapid Approach to Certainty', fontsize=18, fontweight='bold', pad=15)
ax2.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax2.set_ylabel('Cumulative Probability', fontsize=14, fontweight='bold')
ax2.grid(True, alpha=0.3)
ax2.set_ylim(0, 1.05)
ax2.tick_params(axis='both', which='major', labelsize=14)

plt.tight_layout()
plt.show()	

Ce code crée une visualisation ciblée qui met en évidence les deux caractéristiques visuelles les plus importantes de la distribution géométrique. Le panneau de gauche montre comment les probabilités diminuent de manière exponentielle à partir du premier essai, tandis que le panneau de droite illustre l'accumulation rapide de la masse de probabilité dans la CDF.

Veuillez modifier la probabilité de réussite de 0,3 à différentes valeurs telles que 0,1 ou 0,7 pour observer comment la forme de la distribution évolue. Des probabilités plus faibles génèrent des courbes PMF plus plates et des CDF qui augmentent plus lentement, tandis que des probabilités plus élevées entraînent des baisses plus marquées et une approche plus rapide de la certitude.

Propriété sans mémoire de la distribution géométrique

La distribution géométrique présente une caractéristique unique qui la distingue de la plupart des autres distributions discrètes.

La propriété sans mémoire

La propriété sans mémoire stipule que P(X > s + t | X > s) = P(X > t) pour toute valeur entière positive de s et t. Cela signifie que la probabilité de devoir procéder à des essais supplémentaires ne dépend pas du nombre d'essais infructueux déjà effectués.

Mathématiquement, cette propriété apparaît parce que P(X > k) = (1-p)^k, ce qui simplifie le calcul de la probabilité conditionnelle. Concrètement, si vous avez déjà passé cinq entretiens d'embauche infructueux, la distribution de probabilité pour les entretiens futurs reste identique à celle du début : les échecs passés n'influencent pas les probabilités futures.

Relation avec les essais et expériences de Bernoulli

Chaque essai dans une expérience géométrique représente un essai de Bernoulli indépendant avec une probabilité de réussite constante p. La distribution géométrique modélise la séquence de ces essais jusqu'à la première réussite, ce qui en fait l'analogue discret des problèmes de « temps d'attente ».

Cette relation explique pourquoi la distribution géométrique apparaît fréquemment dans le contrôle qualité, où chaque élément testé représente un essai de Bernoulli et où nous souhaitons détecter le premier élément défectueux. L'hypothèse d'indépendance garantit que la détection d'éléments défectueux lors des premiers tests ne modifie pas la probabilité de détecter des défauts lors des tests suivants.

Contraste avec les analogues continus

L a distribution exponentielle sert de distribution à t, la contrepartie continue de la distribution géométrique, toutes deux partageant la propriété sans mémoire. Alors que la distribution géométrique modélise des temps d'attente discrets (nombre d'essais), la distribution exponentielle modélise des temps d'attente continus (temps jusqu'à un événement).

Ces deux distributions trouvent des applications dans l'analyse de fiabilité et la théorie des files d'attente. Par exemple, la distribution géométrique peut modéliser le nombre de requêtes serveur jusqu'à la première défaillance, tandis que la distribution exponentielle modélise le temps jusqu'à la prochaine défaillance du serveur.

Propriétés mathématiques et calculs

Maintenant que nous avons posé les concepts fondamentaux et défini les propriétés uniques, explorons les outils mathématiques qui permettent d'effectuer des calculs de probabilité précis et de prendre des décisions éclairées. Ces formules et relations s'avéreront essentielles lors de l'application de la distribution géométrique à des problèmes concrets.

Moyenne, variance et écart type

La valeur attendue (moyenne) de la distribution géométrique est la suivante : 

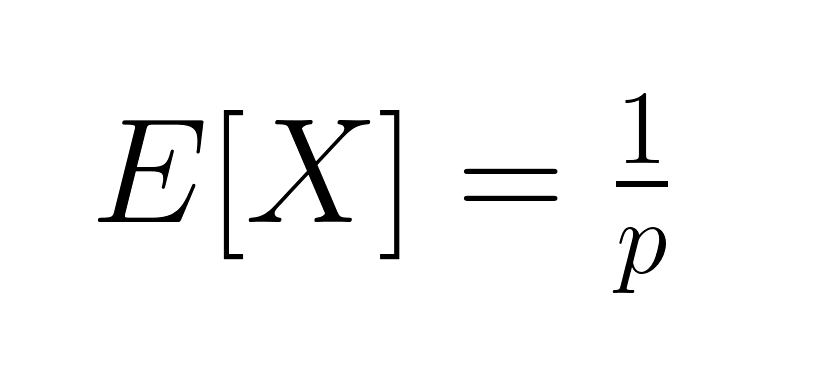
Ceci représente le nombre moyen d'essais nécessaires pour obtenir un résultat positif. La variance est égale à :

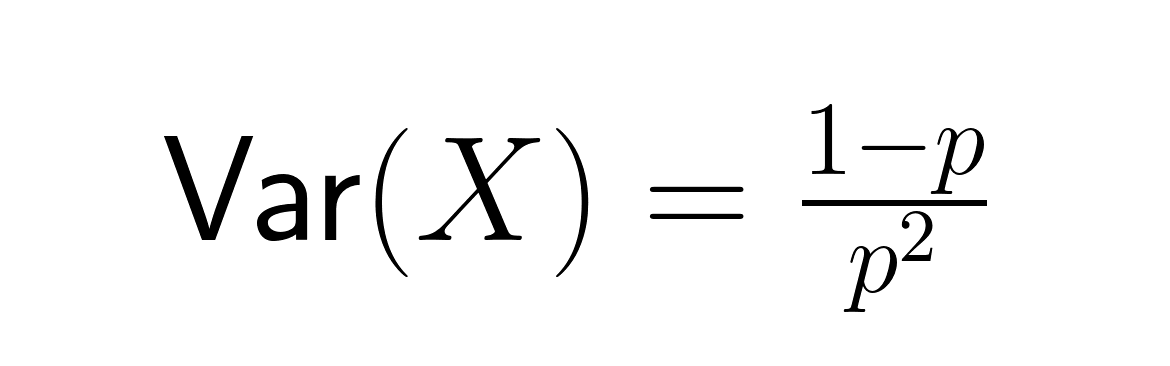
L'écart type est :

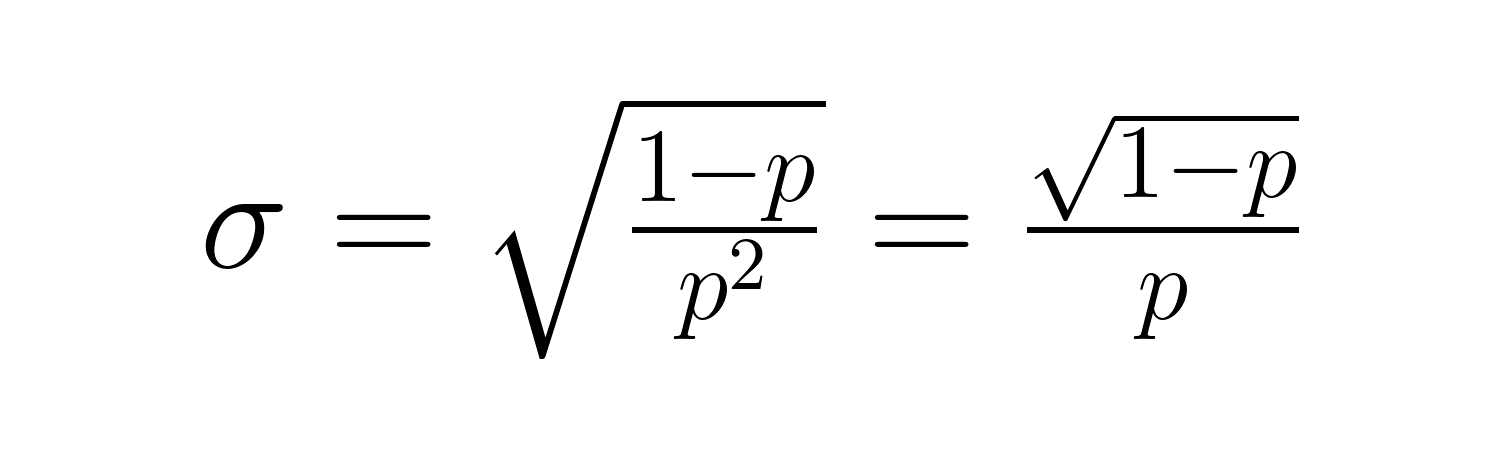
Ces formules révèlent des relations importantes : lorsque p diminue, le temps d'attente prévu et la variabilité augmentent considérablement. Par exemple, avec p = 0,2, le nombre d'essais attendu est de 5, mais avec p = 0,05, il passe à 20 essais. La variance augmente encore plus considérablement, passant de 20 à 380.

Moments et fonctions génératrices

Pour une analyse plus approfondie, la fonction génératrice des moments (MGF) pour la distribution géométrique est la suivante :

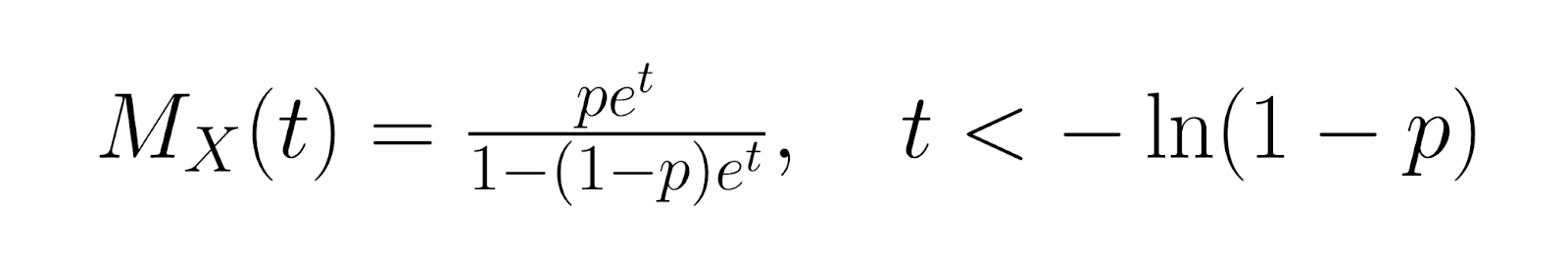La fonction génératrice de probabilités (PGF) est la suivante :

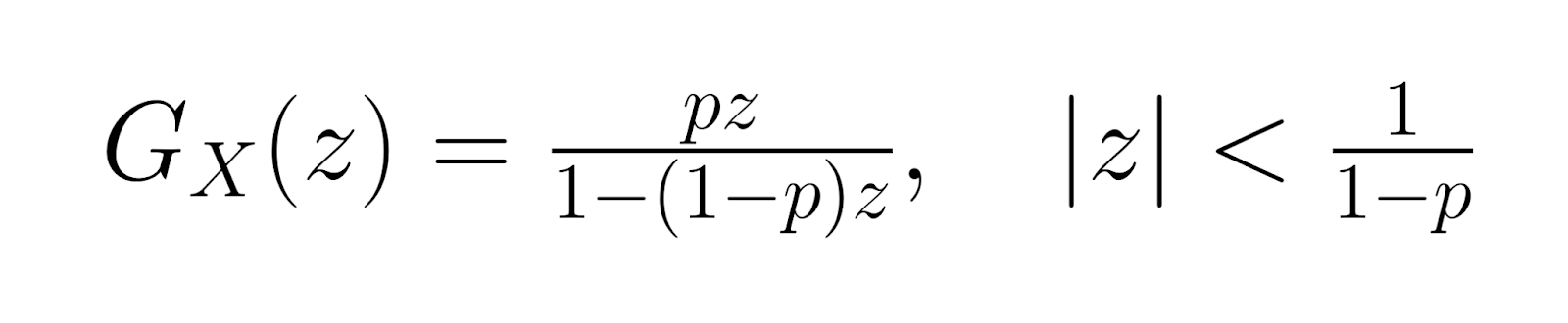
Ces fonctions génératrices facilitent les analyses statistiques avancées et offrent des méthodes alternatives pour dériver les propriétés de distribution. Les moments d'ordre supérieur peuvent être calculés à l'aide des dérivées de ces fonctions, ce qui permet une caractérisation complète de la forme et du comportement de la distribution.

Entropie et mesures de l'information (niveau avancé)

En entrant dans un domaine plus spécialisé, l'entropie de la distribution géométrique est égale à :

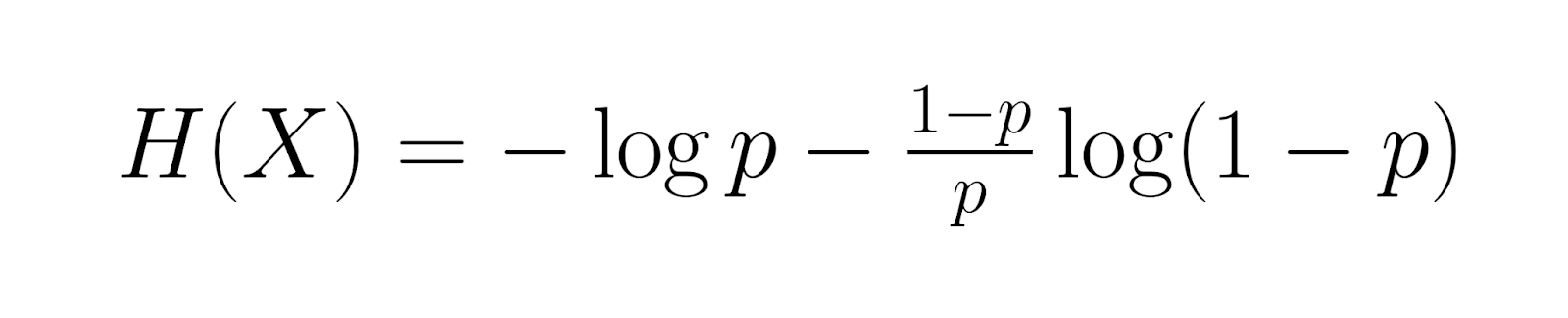
Cette mesure évalue le contenu informatif moyen. Information de Fisher, donnée par :

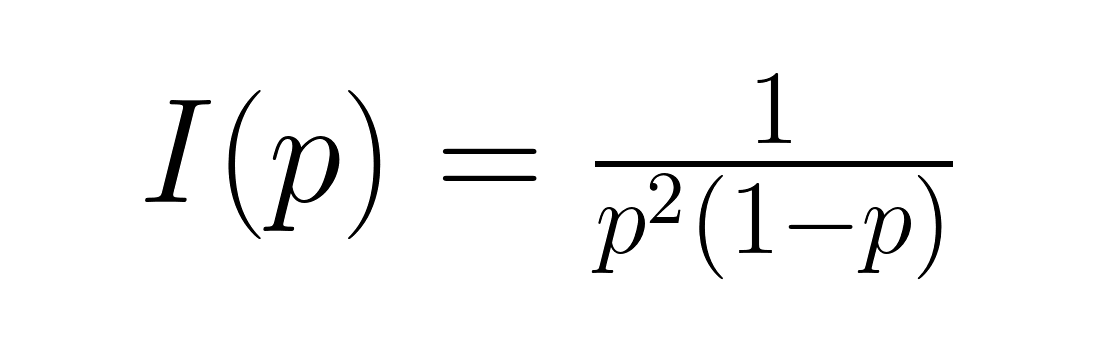
Ceci quantifie la quantité d'informations sur le paramètre p contenues dans les données. Ces mesures s'avèrent précieuses dans les applications de la théorie de l'information et la conception optimale d'expériences, où la compréhension du contenu informatif aide à déterminer la taille appropriée des échantillons et les procédures d'estimation.

Méthodes d'estimation des paramètres

L'estimation de la probabilité de réussite p à partir des données observées nécessite de comprendre différentes approches statistiques et leurs compromis.

Estimation du maximum de vraisemblance (EMV)

L'approche d'estimation du maximum de vraisemblance consiste à déterminer la probabilité de succès qui rend vos données observées les plus susceptibles de s'être produites. Pour calculer cette estimation, divisez le nombre total d'événements réussis par la somme de tous les essais effectués au cours de vos observations. Cet estimateur fournit des résultats non biaisés et fonctionne efficacement avec des échantillons de grande taille.

Voici comment cela fonctionne en pratique : si vous constatez un succès après respectivement 3, 7, 2 et 8 essais, vous calculerez la MLE en prenant vos 4 observations et en les divisant par le total des 20 essais (3+7+2+8), ce qui vous donnera une probabilité de succès estimée à 0,2 ou 20 %. L'approche MLE maximise la probabilité d'observer les données réelles que vous avez collectées, ce qui en fait la méthode la plus efficace sur le plan statistique dans des conditions standard.

Méthode des moments

Comme approche alternative, la méthode de l'estimateur des moments fonctionne en définissant la moyenne de votre échantillon comme étant égale à la moyenne théorique de la distribution géométrique. Étant donné que la moyenne théorique est égale à un divisé par la probabilité de réussite, vous pouvez estimer la probabilité de réussite en divisant votre moyenne échantillonnée par un. Bien que cette méthode soit plus simple à calculer que la MLE, elle peut s'avérer moins efficace sur le plan statistique et produire parfois des estimations qui se situent en dehors de la plage de probabilité valide comprise entre zéro et un.

Les deux méthodes produisent des résultats similaires lorsque l'on travaille avec des échantillons de grande taille, mais la MLE offre généralement de meilleures propriétés statistiques. Le choix entre les différentes méthodes dépend souvent des contraintes informatiques et des exigences spécifiques de votre analyse.

Estimation bayésienne

Lorsque vous disposez d'informations préalables sur la probabilité de réussite, l'estimation bayésienne vous permet d'intégrer ces connaissances à travers une distribution de probabilité a priori. La distribution bêta est couramment utilisée comme distribution a priori, car elle fonctionne bien mathématiquement avec les données de distribution géométrique. L'approche bayésienne combine vos croyances antérieures avec les données observées afin de produire des estimations actualisées des paramètres grâce à ce que l'on appelle la distribution a posteriori.

La relation mathématique crée une distribution bêta mise à jour qui intègre à la fois vos connaissances préalables et vos nouvelles observations. Cette approche est particulièrement efficace lorsque vous disposez de données limitées ou lorsque vous souhaitez intégrer des connaissances spécialisées sur le processus modélisé. Par exemple, si votre expérience dans le secteur vous a appris que les taux de réussite se situent généralement dans une certaine fourchette, vous pouvez intégrer cette connaissance pour améliorer vos estimations, même avec des échantillons de petite taille.

Applications de la distribution géométrique

La distribution géométrique est largement utilisée dans divers secteurs et contextes analytiques où la modélisation des premiers événements de réussite fournit des informations utiles.

Ingénierie de fiabilité et contrôle qualité

Les processus de fabrication utilisent souvent la distribution géométrique pour modéliser la détection des défauts et l'analyse des défaillances des composants. Les inspecteurs chargés du contrôle qualité peuvent estimer le nombre d'articles à inspecter avant de trouver une unité défectueuse, ce qui contribue à optimiser les procédures d'inspection et l'allocation des ressources.

Par exemple, si les données historiques indiquent un taux de défaut de 2 %, la distribution géométrique prévoit qu'il faudra inspecter en moyenne 50 articles avant de trouver le premier défaut. Ces informations permettent de déterminer la taille des lots et la fréquence des inspections afin de maintenir les normes de qualité tout en minimisant les coûts.

Acquisition de clients et gestion du réseau

Les équipes marketing utilisent la distribution géométrique pour modéliser les processus de conversion des clients, en estimant le nombre de contacts ou de publicités nécessaires avant de conclure une vente. Cette analyse sert de base aux décisions relatives à l'allocation budgétaire et à la stratégie de campagne.

Dans le domaine des télécommunications, les ingénieurs réseau utilisent la distribution géométrique pour modéliser les taux de réussite de la transmission de paquets et optimiser les mécanismes de réessai. Comprendre le nombre prévu de tentatives de transmission permet de concevoir des protocoles efficaces et d'améliorer les performances globales du réseau.

Jeux, analyse sportive et autres exemples concrets

Les analystes sportifs utilisent la distribution géométrique pour modéliser les événements liés au score, tels que le nombre de tentatives nécessaires à un joueur de basket-ball pour marquer son premier tir à trois points dans un match. Cette analyse contribue à la prise de décisions stratégiques et à l'évaluation des performances.

Les applications de jeux incluent la modélisation du nombre de tentatives nécessaires pour réaliser des événements rares ou terminer des niveaux difficiles. Les plateformes en ligne utilisent ces informations pour équilibrer la difficulté du jeu et maintenir l'engagement des joueurs grâce à des systèmes de récompenses adaptés.

Exemples de problèmes résolus et questions d'entraînement

Considérons un scénario dans lequel une campagne marketing a un taux de conversion de 15 %. Pour déterminer la probabilité d'obtenir la première conversion lors du 5e contact : P(X = 5) = (0,85)⁴ × 0,15 = 0,0783, soit environ 7,83 %.

À titre d'exercice, veuillez calculer la probabilité qu'un inspecteur du contrôle qualité trouve le premier article défectueux au cours des 10 premières inspections, étant donné un taux de défaut de 8 %. Utilisez la formule CDF : P(X ≤ 10) = 1 - (0,92)¹⁰ = 0,5656, soit environ 56,56 %.

Limites et hypothèses

Pour comprendre quand la distribution géométrique s'applique de manière appropriée, il est nécessaire de reconnaître ses hypothèses sous-jacentes et ses limites potentielles.

La distribution géométrique suppose des essais indépendants avec une probabilité de réussite constante, ce qui n'est pas toujours le cas dans de nombreux scénarios réels. Par exemple, le comportement des clients montre souvent une certaine dépendance : les interactions précédentes peuvent influencer les probabilités de conversion futures. De même, les systèmes mécaniques peuvent subir une usure qui modifie les taux de défaillance au fil du temps.

Le non-respect de ces hypothèses peut entraîner des prévisions inexacteset des décisions inappropriées. Les professionnels des données doivent valider les hypothèses d'indépendance à l'aide de tests statistiques et envisager d'autres modèles lorsque des dépendances sont détectées. Les alternatives courantes comprennent la distribution binomiale négative pourles données surdispersées ou les modèles de chaînes de Markov pour les essais dépendants.

Conclusion

La compréhension de la distribution géométrique va au-delà des connaissances théoriques : elle vous permet de prendre des décisions éclairées en matière d'allocation des ressources, d'optimisation des processus et d'évaluation des risques. Que vous conceviez des procédures de contrôle qualité ou optimisiez des campagnes marketing, cette distribution offre des informations quantitatives qui permettent d'obtenir de meilleurs résultats.

Pour poursuivre votre apprentissage, explorez notre cours Distributions de probabilités multivariées dans R afin de comprendre comment la distribution géométrique est liée à d'autres modèles de probabilité, ou approfondissez vos connaissances en techniques d'estimation grâce à notre cours Modèles linéaires généralisés dans R pour des applications de modélisation avancées.