Distribución geométrica: Guía completa para modelar los primeros eventos exitosos

¿Cuántas entrevistas de trabajo podrías necesitar antes de conseguir el puesto de tus sueños? ¿Cuántos intentos se necesitan para que una campaña de marketing genere su primera venta? La distribución geométrica responde a estas preguntas sobre el «tiempo de espera» modelando el número de intentos necesarios hasta que se produce el primer éxito.

Esta guía abarca los fundamentos matemáticos de la distribución geométrica, sus propiedades distintivas y sus aplicaciones prácticas, que la hacen muy útil para quienes trabajan con escenarios de ensayos secuenciales. Para refrescar tus conocimientos sobre distribuciones de probabilidad, te recomendamos que realices nuestro curso Introducción a la estadística. 

¿Qué es la distribución geométrica?

La distribución geométrica es una distribución de probabilidad discreta que modela el número de ensayos independientes de Bernoulli necesarios para lograr el primer éxito. Cada ensayo tiene la misma probabilidad de éxito, y los ensayos son independientes entre sí.

Esta distribución se presenta en dos formas comunes: una que cuenta el número total de intentos hasta el primer éxito (incluido el éxito) y otra que cuenta solo el número de fallos antes del primer éxito. Ambas formas se utilizan ampliamente dependiendo del contexto específico de la aplicación. A lo largo de esta guía, utilizaremos la primera forma, contando el número total de intentos hasta el primer éxito, donde X puede tomar los valores 1, 2, 3, y así sucesivamente.

Comprender la distribución geométrica

Examinemos la estructura matemática y las características que definen esta distribución.

Definición fundamental y estructura de probabilidad

La distribución geométrica requiere tres condiciones clave: ensayos independientes, probabilidad idéntica de éxito en todos los ensayos y una probabilidad fija p donde 0 < p ≤ 1. La notación estándar utiliza p para la probabilidad de éxito y q = 1-p para la probabilidad de fracaso.

La función de masa de probabilidad (PMF) para el número de intentos X hasta el primer éxito es: 

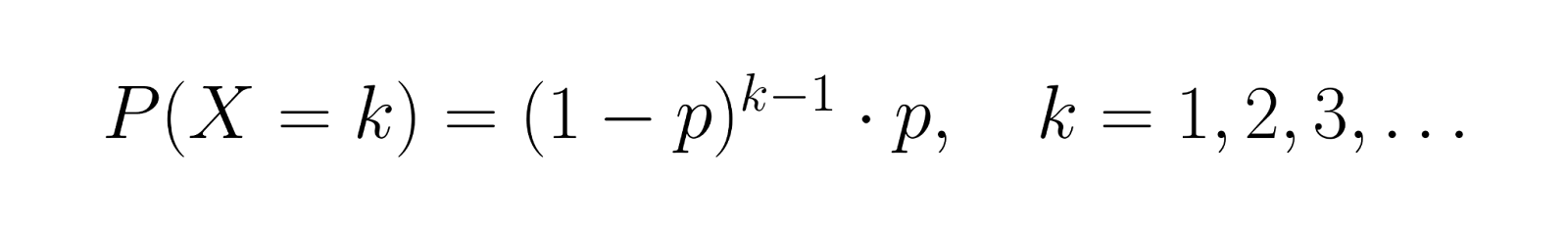
Esta fórmula calcula la probabilidad de experimentar exactamente k-1 fallos seguidos de un éxito. Por ejemplo, si p = 0,3, la probabilidad de éxito en el tercer intento es P(X = 3) = (0,7)² × 0,3 = 0,147.

Probabilidades acumulativas y función de distribución

La función de distribución acumulativa (CDF) nos da:

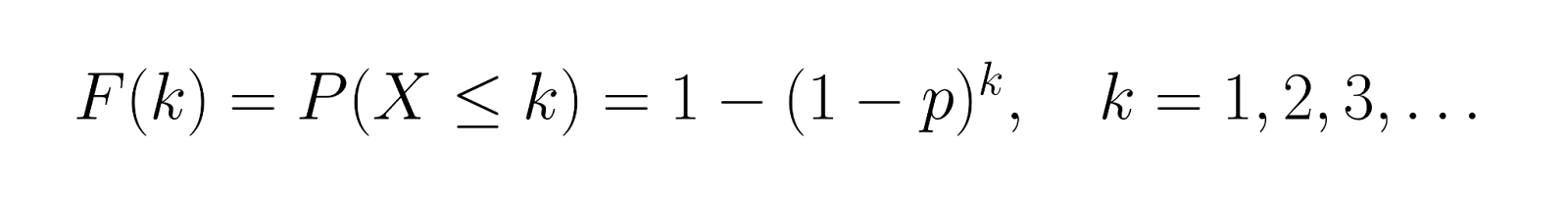
Esto representa la probabilidad de alcanzar el éxito en k intentos. Utilizando nuestro ejemplo donde p = 0,3, calculemos la CDF para los primeros valores:

• F(1) = P(X ≤ 1) = 1 - (0.7)¹ = 0.3
• F(2) = P(X ≤ 2) = 1 - (0.7)² = 1 - 0.49 = 0.51
• F(3) = P(X ≤ 3) = 1 - (0,7)³ = 1 - 0,343 = 0,657

Esto muestra que hay un 30 % de posibilidades de éxito en el primer intento, un 51 % de posibilidades de éxito en los dos primeros intentos y un 65,7 % de posibilidades de éxito en los tres primeros intentos.

Representación gráfica de la distribución geométrica

Los patrones visuales de la distribución geométrica muestran información clave sobre los escenarios de «tiempo de espera». Estos gráficos muestran cómo la probabilidad se concentra en los primeros ensayos y disminuye exponencialmente, lo que hace que la distribución sea útil para modelar situaciones en las que es más probable que el éxito se produzca antes que después.

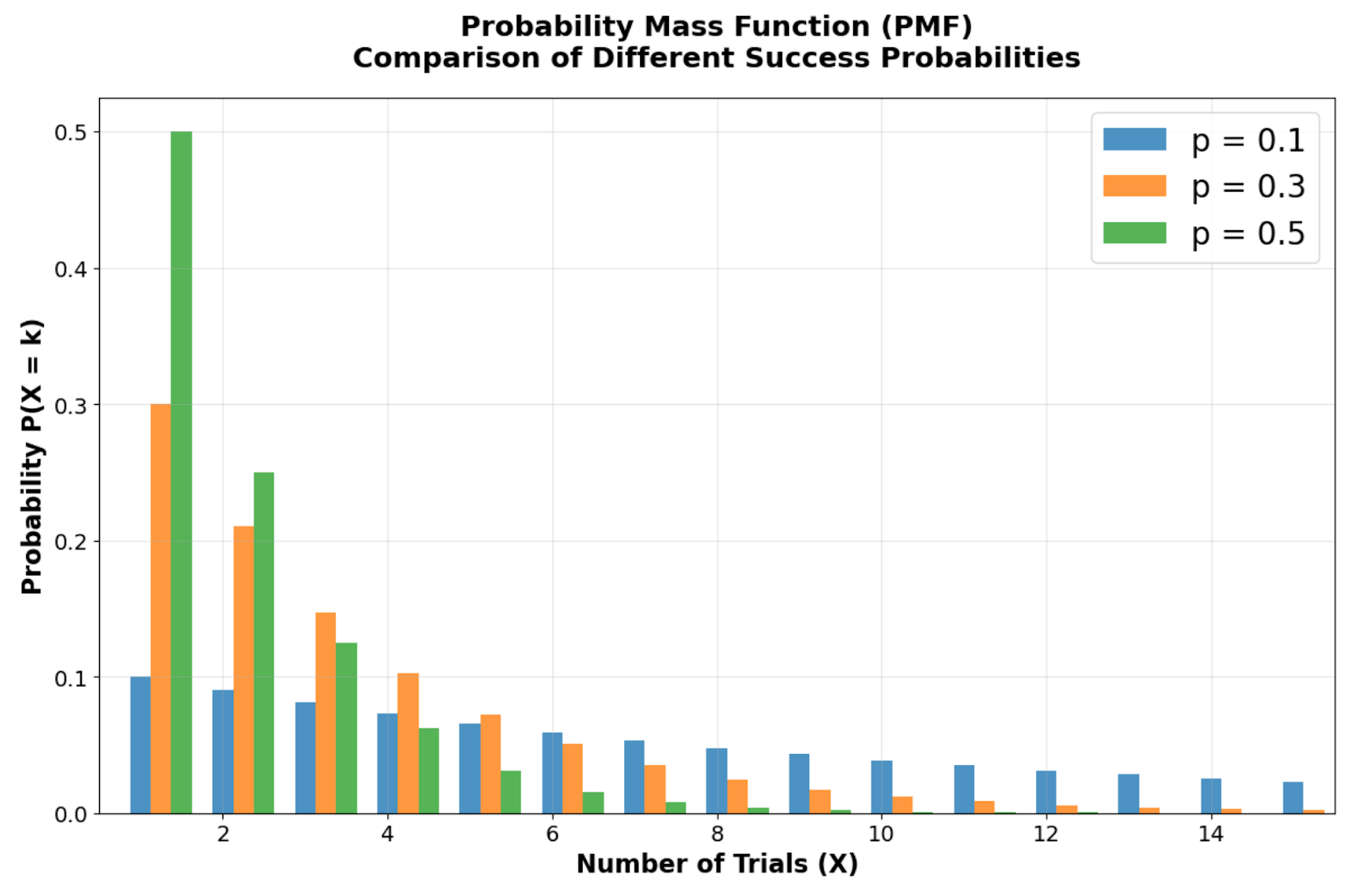
Comparación de la función de masa de probabilidad que muestra cómo diferentes probabilidades de éxito (p = 0,1, 0,3, 0,5) afectan a la forma de la distribución. Imagen del autor

Al observar la comparación de la función de masa de probabilidad entre diferentes probabilidades de éxito, se puede ver la forma distintiva asimétrica a la derecha de la distribución geométrica, con su moda siempre en X = 1 (el primer intento). Observa cómo las barras de probabilidad comienzan más altas en el primer intento y disminuyen geométricamente en cada intento posterior. A medida que disminuye la probabilidad de éxito p, la distribución se vuelve más dispersa, lo que refleja tiempos de espera más largos. Por ejemplo, con p = 0,1, solo hay un 10 % de posibilidades de éxito inmediato, lo que crea una cola derecha más pronunciada en comparación con p = 0,5.

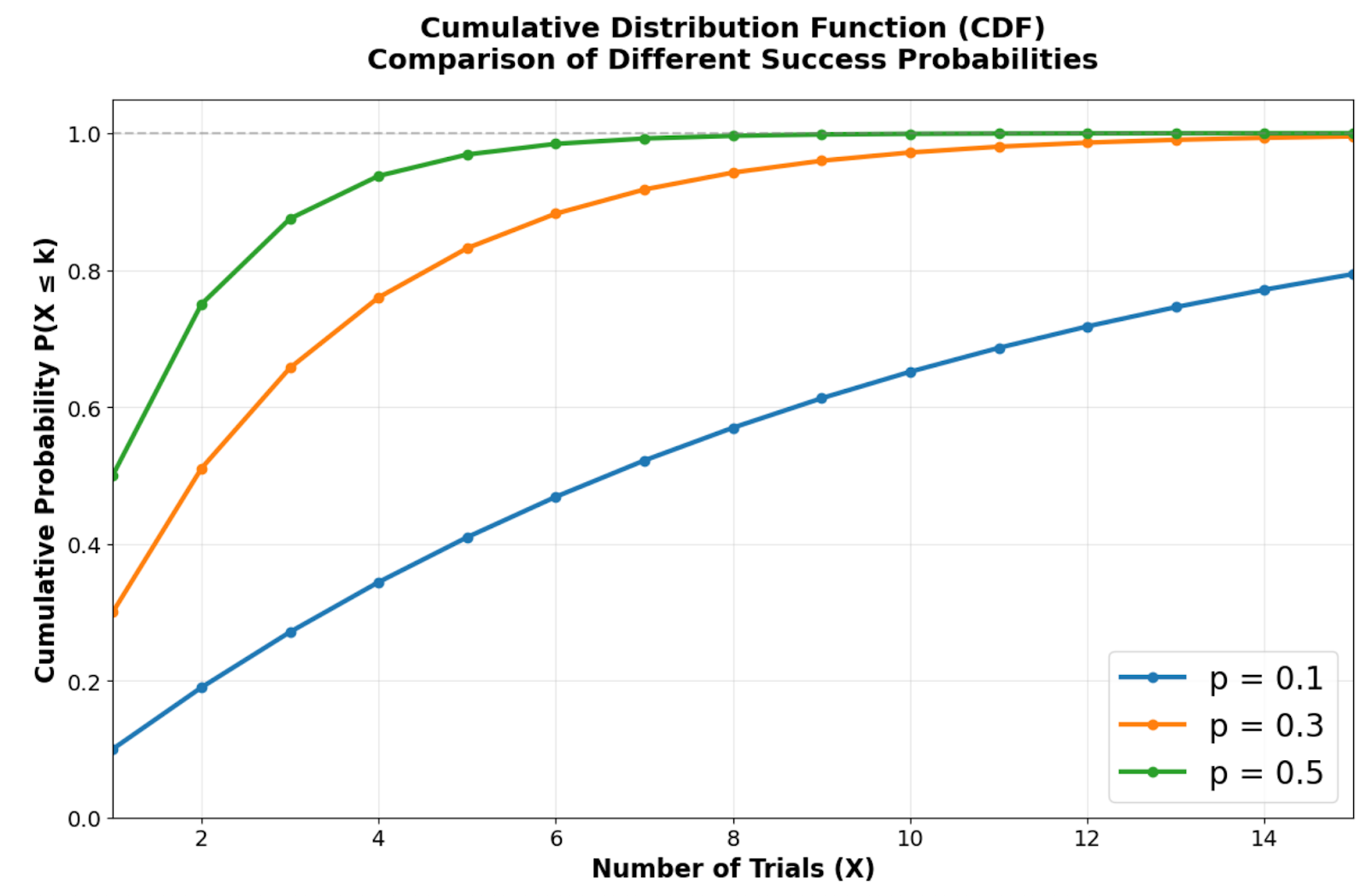
Función de distribución acumulativa que muestra la rapidez con la que las diferentes probabilidades de éxito se acercan a la certeza. Imagen del autor. 

La función de distribución acumulativa muestra la rapidez con la que la distribución geométrica se aproxima a la certeza. Las probabilidades de éxito más altas crean curvas más pronunciadas que alcanzan probabilidades acumulativas elevadas en solo unos pocos intentos. Por ejemplo, con p = 0,5, hay aproximadamente un 75 % de probabilidades de éxito en los dos primeros intentos, mientras que con p = 0,1 se necesitan muchos más intentos para alcanzar el mismo nivel de certeza.

Comparación lado a lado que destaca el patrón de decaimiento exponencial en PMF y la rápida aproximación a la certeza en CDF. Imagen del autor. 

Este patrón de decaimiento exponencial explica por qué la distribución geométrica funciona bien para modelar escenarios en los que es más probable que se produzca un éxito temprano que períodos de espera prolongados. El rápido ascenso de la CDF hacia 1 demuestra por qué esta distribución es eficaz para modelar procesos en los que los tiempos de espera son cortos, lo que la hace valiosa para el control de calidad, el análisis de conversión de clientes y los escenarios de pruebas de fiabilidad.

Creación de tus propias visualizaciones de distribución geométrica

Puedes recrear estas visualizaciones y explorar diferentes valores de parámetros utilizando las bibliotecas scipy y matplotlib de Python. A continuación, te mostramos cómo generar las ideas visuales clave que resaltan las características más importantes de la distribución geométrica:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Create side-by-side plots for PMF and CDF
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
fig.suptitle('Geometric Distribution: Key Visual Insights', fontsize=24, fontweight='bold')

# Simple PMF showing exponential decay (using p = 0.3)
x_simple = np.arange(1, 11)
pmf_simple = stats.geom.pmf(x_simple, 0.3)

ax1.bar(x_simple, pmf_simple, alpha=0.8, color='steelblue', edgecolor='black', linewidth=1)
ax1.set_title('PMF: Exponential Decay Pattern', fontsize=18, fontweight='bold', pad=15)
ax1.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax1.set_ylabel('Probability', fontsize=14, fontweight='bold')
ax1.grid(True, alpha=0.3)
ax1.tick_params(axis='both', which='major', labelsize=14)

# Simple CDF showing approach to 1
cdf_simple = stats.geom.cdf(x_simple, 0.3)

ax2.plot(x_simple, cdf_simple, 'o-', linewidth=4, markersize=8, color='darkgreen')
ax2.set_title('CDF: Rapid Approach to Certainty', fontsize=18, fontweight='bold', pad=15)
ax2.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax2.set_ylabel('Cumulative Probability', fontsize=14, fontweight='bold')
ax2.grid(True, alpha=0.3)
ax2.set_ylim(0, 1.05)
ax2.tick_params(axis='both', which='major', labelsize=14)

plt.tight_layout()
plt.show()	

Este código crea una visualización enfocada que enfatiza las dos características visuales más importantes de la distribución geométrica. El panel izquierdo muestra cómo las probabilidades disminuyen exponencialmente desde el primer ensayo, mientras que el panel derecho muestra la rápida acumulación de masa de probabilidad en la CDF.

Intenta cambiar la probabilidad de éxito de 0,3 a otros valores, como 0,1 o 0,7, para ver cómo cambia la forma de la distribución. Las probabilidades más bajas crean curvas PMF más planas y CDF de crecimiento más lento, mientras que las probabilidades más altas crean descensos más pronunciados y se acercan más rápidamente a la certeza.

Propiedad sin memoria de la distribución geométrica

La distribución geométrica tiene una característica única que la diferencia de la mayoría de las demás distribuciones discretas.

La propiedad sin memoria

La propiedad sin memoria establece que P(X > s + t | X > s) = P(X > t) para cualquier número entero positivo s y t. Esto significa que la probabilidad de necesitar ensayos adicionales no depende del número de ensayos fallidos que ya se hayan realizado.

Matemáticamente, esta propiedad surge porque P(X > k) = (1-p)^k, lo que simplifica el cálculo de la probabilidad condicional. En términos prácticos, si ya has tenido cinco entrevistas de trabajo sin éxito, la distribución de probabilidad para futuras entrevistas sigue siendo idéntica a la que tenías cuando empezaste: los fracasos del pasado no influyen en las probabilidades futuras.

Relación con los ensayos y experimentos de Bernoulli

Cada ensayo en un experimento geométrico representa un ensayo de Bernoulli independiente con una probabilidad de éxito constante p. La distribución geométrica modela la secuencia de estos ensayos hasta el primer éxito, lo que la convierte en el análogo discreto de los problemas de «tiempo de espera».

Esta relación explica por qué la distribución geométrica aparece con frecuencia en el control de calidad, donde cada elemento probado representa una prueba de Bernoulli y nos interesa detectar el primer elemento defectuoso. La suposición de independencia garantiza que encontrar elementos defectuosos en pruebas tempranas no cambia la probabilidad de encontrar defectos en pruebas posteriores.

Contraste con análogos continuos

La distribución exponencial sirve como tla contrapartida continua de la distribución geométrica, ambas comparten la propiedad sin memoria. Mientras que la distribución geométrica modela tiempos de espera discretos (número de intentos), la distribución exponencial modela tiempos de espera continuos (tiempo hasta que se produce un evento).

Ambas distribuciones encuentran aplicaciones en el análisis de fiabilidad y la teoría de colas. Por ejemplo, la distribución geométrica podría modelar el número de solicitudes al servidor hasta el primer fallo, mientras que la distribución exponencial modela el tiempo hasta que se produce el siguiente fallo del servidor.

Propiedades matemáticas y cálculos

Una vez establecidos los conceptos fundamentales y las propiedades únicas, exploremos las herramientas matemáticas que permiten realizar cálculos probabilísticos precisos y tomar decisiones informadas. Estas fórmulas y relaciones resultarán esenciales a la hora de aplicar la distribución geométrica a problemas del mundo real.

Media, varianza y desviación estándar

El valor esperado (media) de la distribución geométrica es: 

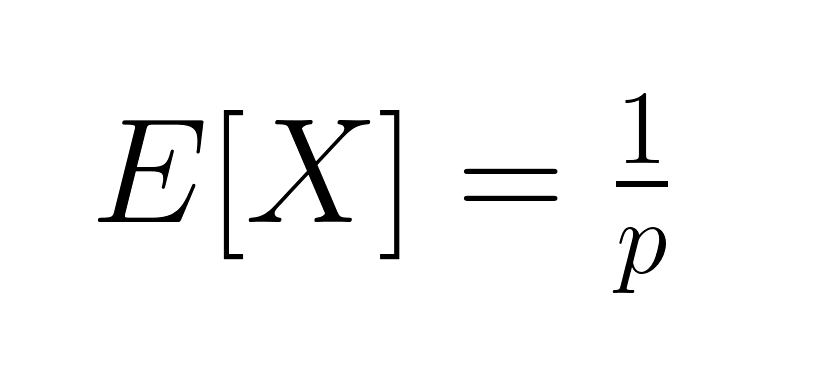
Esto representa el número medio de intentos necesarios para alcanzar el éxito. La varianza es igual a:

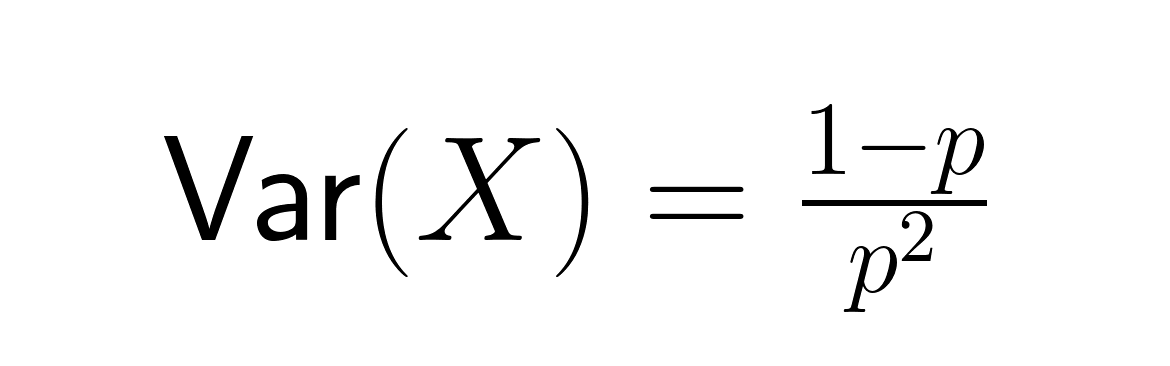
La desviación estándar es:

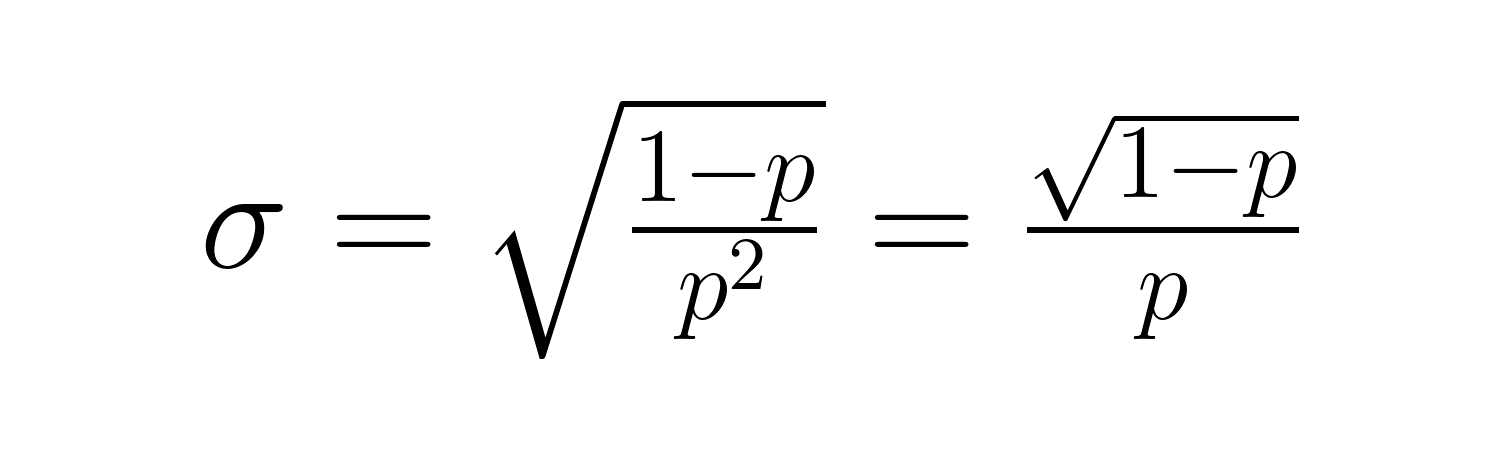
Estas fórmulas revelan relaciones importantes: a medida que p disminuye, tanto el tiempo de espera esperado como la variabilidad aumentan significativamente. Por ejemplo, con p = 0,2, el número esperado de ensayos es 5, pero con p = 0,05, salta a 20 ensayos. La variación aumenta aún más drásticamente, pasando de 20 a 380.

Momentos y funciones generadoras

Para un análisis más avanzado, la función generadora de momentos (MGF) para la distribución geométrica es:

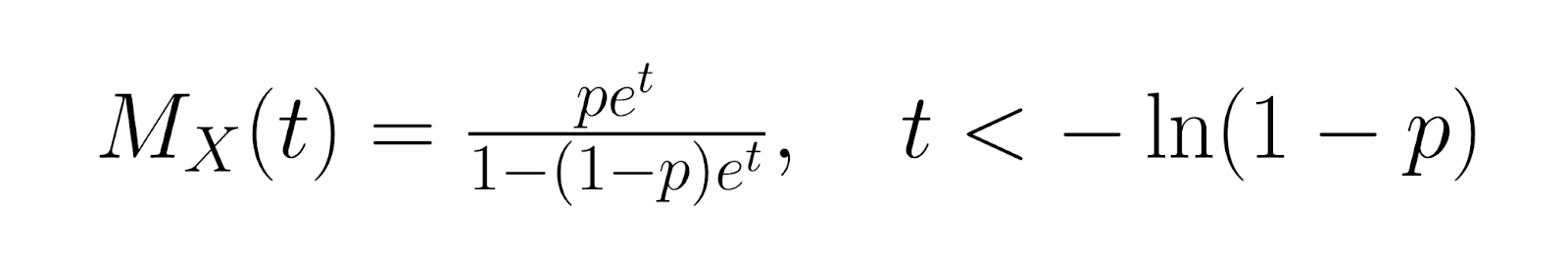La función generadora de probabilidades (PGF) es:

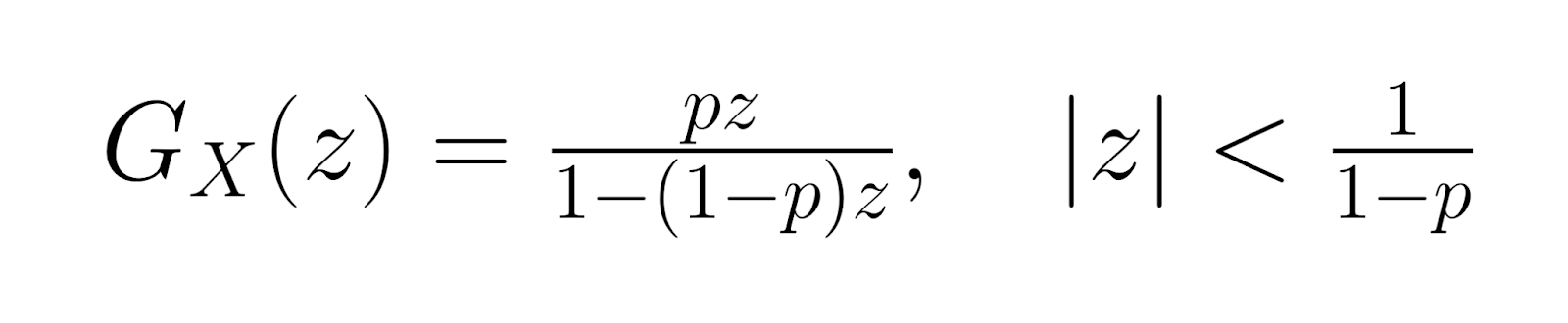
Estas funciones generadoras ayudan en el análisis estadístico avanzado y proporcionan métodos alternativos para derivar propiedades de distribución. Los momentos de orden superior se pueden calcular utilizando derivadas de estas funciones, lo que permite una caracterización completa de la forma y el comportamiento de la distribución.

Entropía y medidas de información (avanzado)

Entrando en un terreno más especializado, la entropía de la distribución geométrica es igual a:

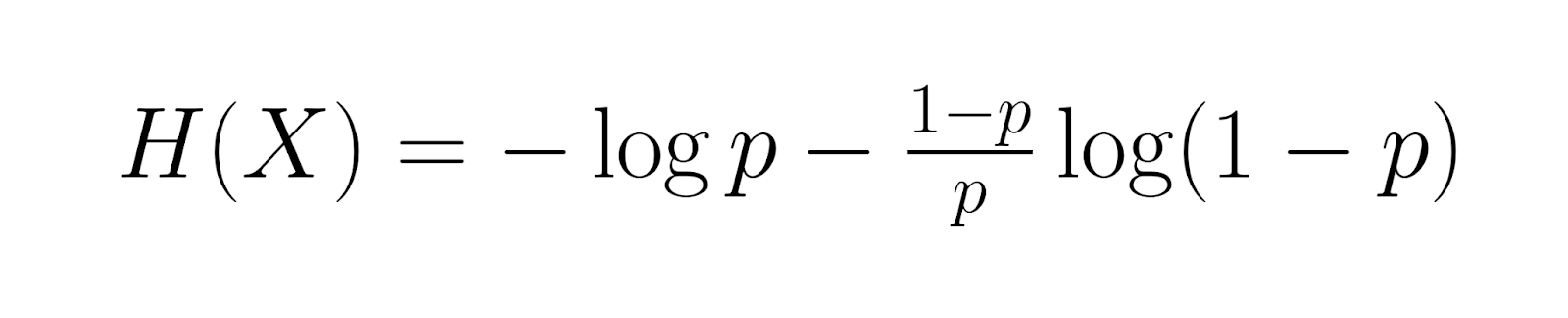
Mide el contenido medio de información. Información de Fisher, dada por:

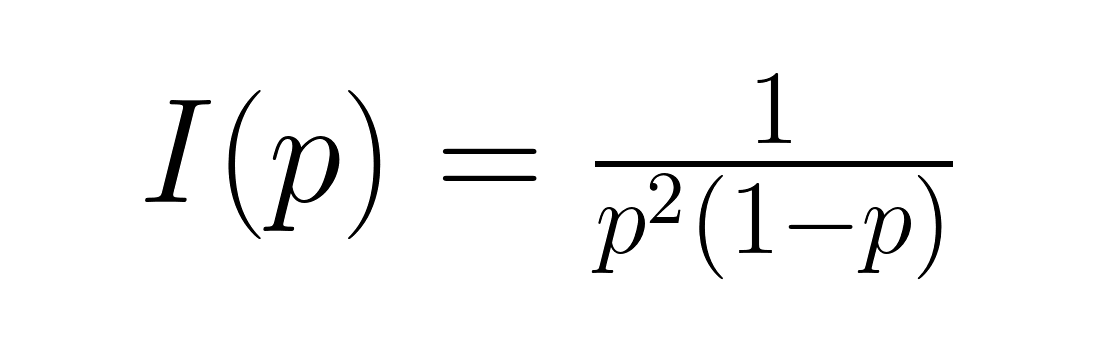
Esto cuantifica la cantidad de información sobre el parámetro p contenida en los datos. Estas medidas resultan valiosas en aplicaciones de teoría de la información y diseño experimental óptimo, donde comprender el contenido de la información ayuda a determinar los tamaños de muestra y los procedimientos de estimación adecuados.

Métodos de estimación de parámetros

Estimar la probabilidad de éxito p a partir de los datos observados requiere comprender diferentes enfoques estadísticos y sus ventajas e inconvenientes.

Estimación de máxima verosimilitud (MLE)

El enfoque de estimación de máxima verosimilitud funciona buscando la probabilidad de éxito que hace que los datos observados sean los más probables. Para calcular esta estimación, divides el número total de eventos exitosos por la suma de todos los intentos en tus observaciones. Este estimador proporciona resultados imparciales y funciona de manera eficiente cuando se trabaja con muestras de gran tamaño.

Así es como funciona en la práctica: si observas éxito después de 3, 7, 2 y 8 intentos respectivamente, calcularías el MLE tomando tus 4 observaciones y dividiéndolas por el total de 20 intentos (3+7+2+8), lo que te daría una probabilidad de éxito estimada de 0,2 o 20 %. El enfoque MLE maximiza la probabilidad de observar los datos reales que has recopilado, lo que lo convierte en el método más eficiente desde el punto de vista estadístico en condiciones estándar.

Método de los momentos

Como enfoque alternativo, el estimador del método de los momentos funciona estableciendo el promedio de la muestra igual al promedio teórico de la distribución geométrica. Dado que la media teórica es igual a uno dividido por la probabilidad de éxito, puedes estimar la probabilidad de éxito dividiendo uno entre la media de la muestra. Aunque este método ofrece una mayor simplicidad computacional en comparación con el MLE, puede ser menos eficiente desde el punto de vista estadístico y, en ocasiones, puede producir estimaciones que se encuentran fuera del rango de probabilidad válido de cero a uno.

Ambos métodos producen resultados similares cuando se trabaja con muestras grandes, pero el MLE suele ofrecer propiedades estadísticas superiores. La elección entre los distintos métodos suele depender de las limitaciones computacionales y los requisitos específicos de tu análisis.

estimación bayesiana

Cuando se dispone de información previa sobre la probabilidad de éxito, la estimación bayesiana permite incorporar este conocimiento a través de una distribución de probabilidad a priori. La distribución beta suele servir como distribución a priori porque funciona bien matemáticamente con datos de distribución geométrica. El enfoque bayesiano combina tus creencias previas con los datos observados para producir estimaciones actualizadas de los parámetros a través de lo que se denomina distribución a posteriori.

La relación matemática crea una distribución beta actualizada que incorpora tanto tus conocimientos previos como las nuevas observaciones. Este enfoque funciona especialmente bien cuando se dispone de datos limitados o cuando se desea incorporar conocimientos especializados sobre el proceso que se está modelando. Por ejemplo, si sabes por experiencia en el sector que las tasas de éxito suelen situarse dentro de un determinado rango, puedes incorporar este conocimiento para mejorar tus estimaciones incluso con muestras de tamaño reducido.

Aplicaciones de la distribución geométrica

La distribución geométrica se utiliza ampliamente en diversos sectores y contextos analíticos en los que la modelización de los primeros eventos exitosos proporciona información valiosa.

Ingeniería de fiabilidad y control de calidad

Los procesos de fabricación suelen utilizar la distribución geométrica para modelar la detección de defectos y el análisis de fallos de componentes. Los inspectores de control de calidad pueden estimar el número previsto de artículos que deben inspeccionar antes de encontrar una unidad defectuosa, lo que ayuda a optimizar los procedimientos de inspección y la asignación de recursos.

Por ejemplo, si los datos históricos muestran una tasa de defectos del 2 %, la distribución geométrica predice una media de 50 artículos inspeccionados antes de encontrar el primer defecto. Esta información ayuda a determinar los tamaños de lote y las frecuencias de inspección adecuados para mantener los estándares de calidad y minimizar los costes.

Adquisición de clientes y gestión de redes

Los equipos de marketing aplican la distribución geométrica para modelar los procesos de conversión de clientes, estimando cuántos contactos o anuncios son necesarios antes de lograr una venta. Este análisis sirve de base para las decisiones sobre la asignación presupuestaria y la estrategia de campaña.

En telecomunicaciones, los ingenieros de redes utilizan la distribución geométrica para modelar las tasas de éxito de la transmisión de paquetes y optimizar los mecanismos de reintento. Comprender el número esperado de intentos de transmisión ayuda a diseñar protocolos eficientes y a mejorar el rendimiento general de la red.

Juegos, análisis deportivo y ejemplos adicionales del mundo real.

Los analistas deportivos utilizan la distribución geométrica para modelar eventos puntuables, como el número de intentos necesarios para que un jugador de baloncesto enceste su primer triple en un partido. Este análisis contribuye a la toma de decisiones estratégicas y a la evaluación del rendimiento.

Las aplicaciones de juegos incluyen la modelización del número de intentos necesarios para lograr eventos poco frecuentes o completar niveles difíciles. Las plataformas en línea utilizan esta información para equilibrar la dificultad del juego y mantener el interés de los jugadores mediante estructuras de recompensas adecuadas.

Ejemplos resueltos y preguntas de práctica

Considera un escenario en el que una campaña de marketing tiene una tasa de conversión del 15 %. Para hallar la probabilidad de obtener la primera conversión en el quinto contacto: P(X = 5) = (0,85)⁴ × 0,15 = 0,0783 o aproximadamente el 7,83 %.

Para practicar, calcula la probabilidad de que un inspector de control de calidad encuentre el primer artículo defectuoso en las primeras 10 inspecciones, dada una tasa de defectos del 8 %. Utiliza la fórmula CDF: P(X ≤ 10) = 1 - (0,92)¹⁰ = 0,5656 o aproximadamente el 56,56 %.

Limitaciones y supuestos

Para comprender cuándo se aplica adecuadamente la distribución geométrica, es necesario reconocer sus supuestos subyacentes y sus posibles limitaciones.

La distribución geométrica asume ensayos independientes con una probabilidad de éxito constante, lo que puede no darse en muchos escenarios reales. Por ejemplo, el comportamiento de los clientes suele mostrar dependencia: las interacciones anteriores pueden influir en las probabilidades de conversión futuras. Del mismo modo, los sistemas mecánicos pueden sufrir un desgaste que modifique las tasas de fallo con el tiempo.

Las violaciones de estas suposiciones pueden dar lugar a predicciones inexactasy a una toma de decisiones deficiente. Los profesionales de datos deben validar las hipótesis de independencia mediante pruebas estadísticas y considerar modelos alternativos cuando se detecten dependencias. Las alternativas más comunes incluyen la distribución binomial negativa paradatos sobredispersos o los modelos de cadenas de Markov para ensayos dependientes.

Conclusión

Comprender la distribución geométrica va más allá del conocimiento teórico: te permite tomar decisiones informadas sobre la asignación de recursos, la optimización de procesos y la evaluación de riesgos. Tanto si estás diseñando procedimientos de control de calidad como optimizando campañas de marketing, esta distribución ofrece información cuantitativa que te ayudará a obtener mejores resultados.

Para seguir aprendiendo, explora nuestro curso Distribuciones de probabilidad multivariantes en R para comprender cómo se relaciona la distribución geométrica con otros modelos de probabilidad, o profundiza en las técnicas de estimación con nuestro curso Modelos lineales generalizados en R para aplicaciones de modelado avanzadas.