Distribuição geométrica: Um guia completo para modelar os primeiros eventos de sucesso

Quantas entrevistas de emprego você pode precisar antes de conseguir o emprego dos seus sonhos? Quantas tentativas são necessárias para que uma campanha de marketing gere a primeira venda? A distribuição geométrica responde a essas perguntas sobre “tempo de espera” modelando o número de tentativas necessárias até que o primeiro sucesso ocorra.

Este guia fala sobre a base matemática da distribuição geométrica, suas propriedades únicas e aplicações práticas que a tornam útil para quem trabalha com cenários de testes sequenciais. Para refrescar a memória sobre distribuições de probabilidade, considere fazer nosso curso Introdução à Estatística. 

O que é a distribuição geométrica?

A distribuição geométrica é uma distribuição de probabilidade discreta que mostra o número de tentativas independentes de Bernoulli necessárias para conseguir o primeiro sucesso. Cada tentativa tem a mesma chance de dar certo, e as tentativas são independentes umas das outras.

Essa distribuição vem em duas formas comuns: uma que conta o número total de tentativas até o primeiro sucesso (incluindo o sucesso) e outra que conta só o número de falhas antes do primeiro sucesso. Ambas as formas são bem usadas dependendo do contexto específico da aplicação. Ao longo deste guia, vamos usar a primeira forma, contando o número total de tentativas até o primeiro sucesso, onde X pode ter os valores 1, 2, 3 e assim por diante.

Entendendo a Distribuição Geométrica

Vamos ver a estrutura matemática e as características que definem essa distribuição.

Definição básica e estrutura de probabilidade

A distribuição geométrica precisa de três condições principais: tentativas independentes, probabilidade igual de sucesso em todas as tentativas e uma probabilidade fixa p, onde 0 < p ≤ 1. A notação padrão usa p para a probabilidade de sucesso e q = 1-p para a probabilidade de falha.

A função de massa de probabilidade (PMF) para o número de tentativas X até o primeiro sucesso é: 

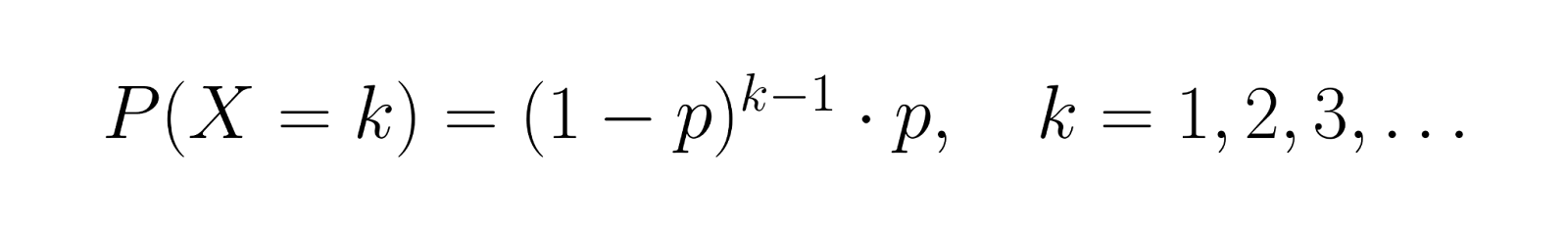
Essa fórmula calcula a chance de ter exatamente k-1 falhas seguidas de um sucesso. Por exemplo, se p = 0,3, a chance de sucesso na terceira tentativa é P(X = 3) = (0,7)² × 0,3 = 0,147.

Probabilidades acumuladas e função de distribuição

A função de distribuição cumulativa (CDF) nos dá:

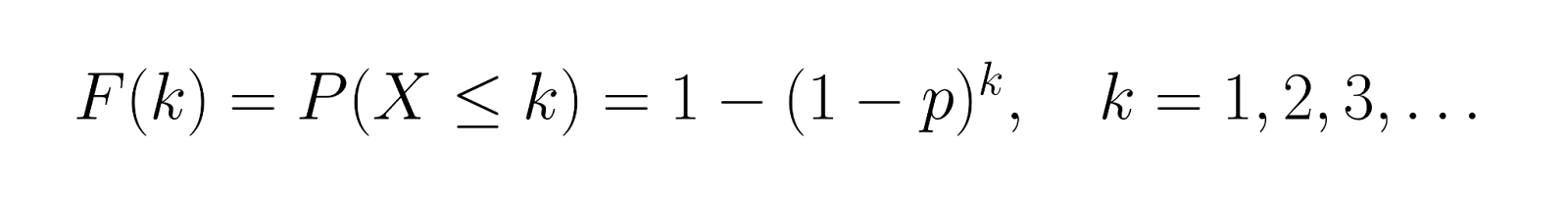
Isso mostra a chance de dar certo em k tentativas. Usando nosso exemplo em que p = 0,3, vamos calcular a CDF para os primeiros valores:

• F(1) = P(X ≤ 1) = 1 - (0,7)¹ = 0,3
• F(2) = P(X ≤ 2) = 1 - (0,7)² = 1 - 0,49 = 0,51
• F(3) = P(X ≤ 3) = 1 - (0,7)³ = 1 - 0,343 = 0,657

Isso mostra que tem 30% de chance de dar certo na primeira tentativa, 51% de chance nas duas primeiras tentativas e 65,7% de chance nas três primeiras tentativas.

Representação gráfica da distribuição geométrica

Os padrões visuais da distribuição geométrica mostram insights importantes sobre cenários de “tempo de espera”. Esses gráficos mostram como a probabilidade se concentra nas primeiras tentativas e diminui exponencialmente, tornando a distribuição útil para modelar situações em que o sucesso é mais provável no início do que no final.

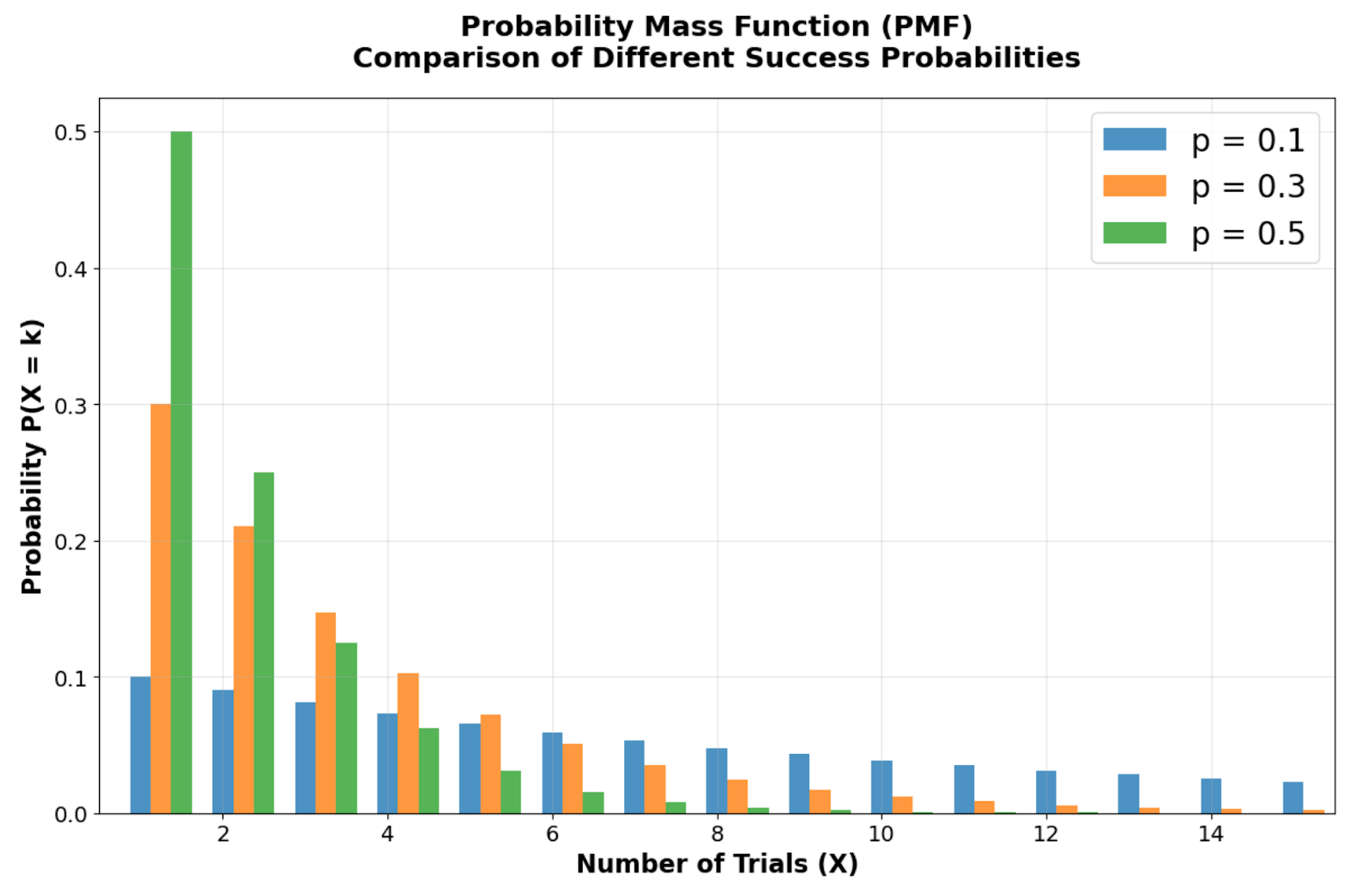
Comparação da Função de Massa de Probabilidade mostrando como diferentes probabilidades de sucesso (p = 0,1, 0,3, 0,5) afetam a forma da distribuição. Imagem do autor

Olhando para a comparação da função de massa de probabilidade entre diferentes probabilidades de sucesso, você pode ver a forma inclinada para a direita característica da distribuição geométrica, com seu modo sempre em X = 1 (a primeira tentativa). Repara como as barras de probabilidade começam mais altas na primeira tentativa e diminuem geometricamente a cada tentativa seguinte. À medida que a probabilidade de sucesso p diminui, a distribuição fica mais espalhada, refletindo tempos de espera mais longos. Por exemplo, com p = 0,1, tem só 10% de chance de sucesso imediato, criando uma cauda direita mais acentuada em comparação com p = 0,5.

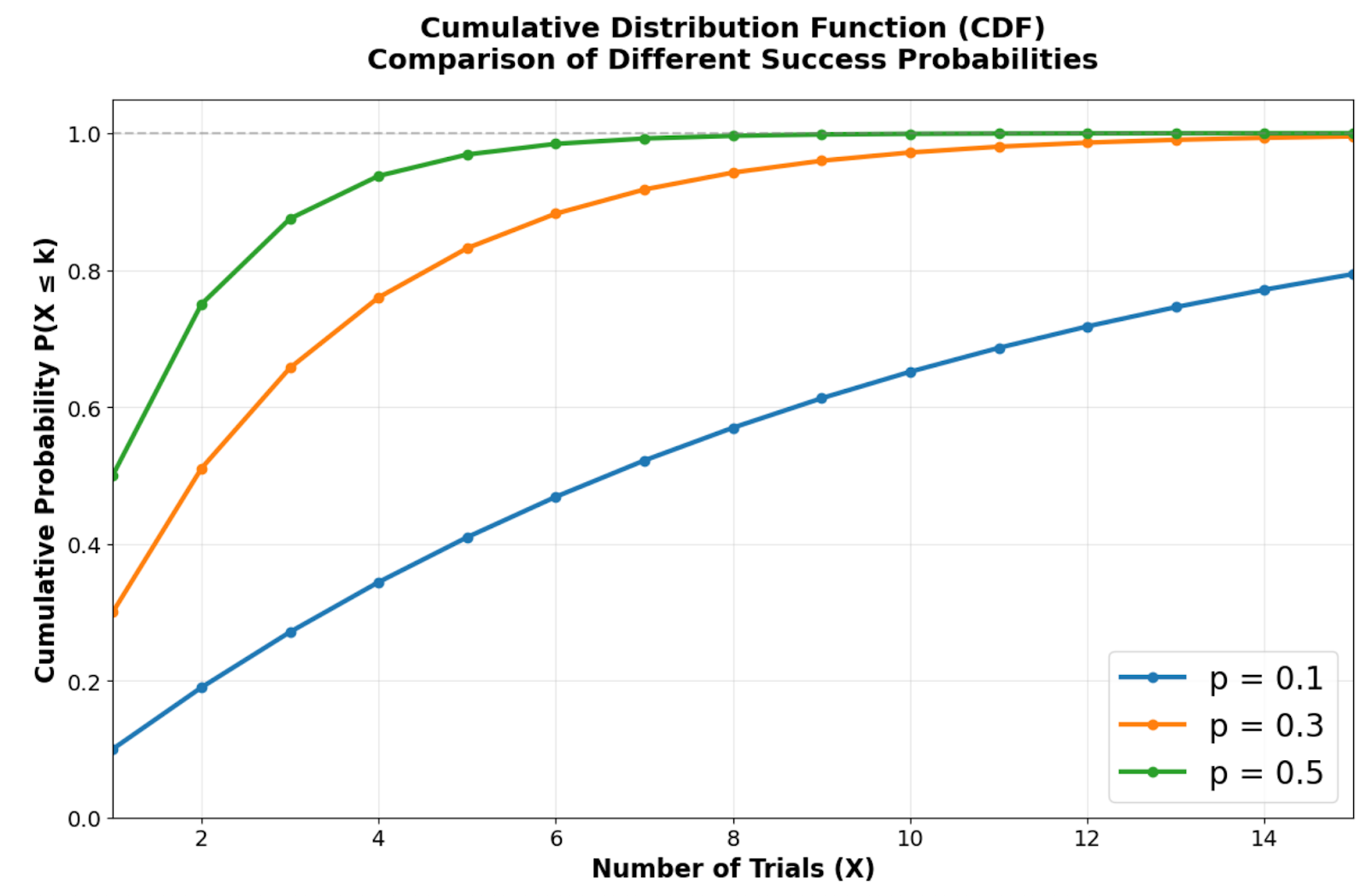
Função de distribuição cumulativa que mostra a rapidez com que diferentes probabilidades de sucesso se aproximam da certeza. Imagem do autor. 

A função de distribuição cumulativa mostra como a distribuição geométrica chega rápido à certeza. Probabilidades de sucesso mais altas criam curvas mais íngremes que atingem probabilidades cumulativas altas em apenas algumas tentativas. Por exemplo, com p = 0,5, tem cerca de 75% de chance de dar certo nas duas primeiras tentativas, enquanto p = 0,1 precisa de muito mais tentativas pra chegar no mesmo nível de certeza.

Comparação lado a lado mostrando o padrão de decaimento exponencial no PMF e a rápida aproximação à certeza no CDF. Imagem do autor. 

Esse padrão de queda exponencial explica por que a distribuição geométrica funciona bem pra modelar cenários em que o sucesso rápido é mais provável do que longos períodos de espera. A rápida ascensão da CDF em direção a 1 mostra por que essa distribuição é boa para modelar processos com tempos de espera curtos, o que a torna útil para controle de qualidade, análise de conversão de clientes e testes de confiabilidade.

Criando suas próprias visualizações de distribuição geométrica

Você pode recriar essas visualizações e explorar diferentes valores de parâmetros usando as bibliotecas scipy e matplotlib do Python. Veja como gerar os principais insights visuais que destacam as características mais importantes da distribuição geométrica:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Create side-by-side plots for PMF and CDF
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
fig.suptitle('Geometric Distribution: Key Visual Insights', fontsize=24, fontweight='bold')

# Simple PMF showing exponential decay (using p = 0.3)
x_simple = np.arange(1, 11)
pmf_simple = stats.geom.pmf(x_simple, 0.3)

ax1.bar(x_simple, pmf_simple, alpha=0.8, color='steelblue', edgecolor='black', linewidth=1)
ax1.set_title('PMF: Exponential Decay Pattern', fontsize=18, fontweight='bold', pad=15)
ax1.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax1.set_ylabel('Probability', fontsize=14, fontweight='bold')
ax1.grid(True, alpha=0.3)
ax1.tick_params(axis='both', which='major', labelsize=14)

# Simple CDF showing approach to 1
cdf_simple = stats.geom.cdf(x_simple, 0.3)

ax2.plot(x_simple, cdf_simple, 'o-', linewidth=4, markersize=8, color='darkgreen')
ax2.set_title('CDF: Rapid Approach to Certainty', fontsize=18, fontweight='bold', pad=15)
ax2.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax2.set_ylabel('Cumulative Probability', fontsize=14, fontweight='bold')
ax2.grid(True, alpha=0.3)
ax2.set_ylim(0, 1.05)
ax2.tick_params(axis='both', which='major', labelsize=14)

plt.tight_layout()
plt.show()	

Esse código cria uma visualização focada que destaca as duas características visuais mais importantes da distribuição geométrica. O painel esquerdo mostra como as probabilidades caem exponencialmente a partir da primeira tentativa, enquanto o painel direito mostra o rápido acúmulo de massa de probabilidade na CDF.

Tenta mudar a probabilidade de sucesso de 0,3 para valores diferentes, como 0,1 ou 0,7, para ver como a forma da distribuição muda. Probabilidades mais baixas criam curvas PMF mais planas e CDFs que sobem mais devagar, enquanto probabilidades mais altas criam quedas mais íngremes e aproximações mais rápidas à certeza.

Propriedade sem memória da distribuição geométrica

A distribuição geométrica tem uma característica única que a diferencia da maioria das outras distribuições discretas.

A propriedade sem memória

A propriedade sem memória diz que P(X > s + t | X > s) = P(X > t) para qualquer número inteiro positivo s e t. Isso quer dizer que a chance de precisar de mais tentativas não depende de quantas tentativas sem sucesso já rolaram.

Matematicamente, essa propriedade surge porque P(X > k) = (1-p)^k, o que torna o cálculo da probabilidade condicional bem simples. Na prática, se você já teve cinco entrevistas de emprego sem sucesso, a chance de conseguir uma entrevista futura continua a mesma de quando você começou — os fracassos do passado não afetam as chances do futuro.

Relação com os testes e experimentos de Bernoulli

Cada tentativa em um experimento geométrico é como uma tentativa independente de Bernoulli com uma chance constante de sucesso p. A distribuição geométrica mostra a sequência dessas tentativas até a primeira que dá certo, sendo o equivalente discreto dos problemas de “tempo de espera”.

Essa relação explica por que a distribuição geométrica aparece bastante no controle de qualidade, onde cada item testado é tipo um teste de Bernoulli e a gente quer achar o primeiro item com defeito. A suposição de independência garante que encontrar itens com defeito nos testes iniciais não muda a chance de encontrar defeitos nos testes seguintes.

Contraste com análogos contínuos

A distribuição exponencial serve como ta contraparte contínua da distribuição geométrica, ambas compartilhando a propriedade sem memória. Enquanto a distribuição geométrica mostra os tempos de espera discretos (número de tentativas), a distribuição exponencial mostra os tempos de espera contínuos (tempo até um evento).

Ambas as distribuições têm aplicações na análise de confiabilidade e na teoria da fila. Por exemplo, a distribuição geométrica pode modelar o número de solicitações do servidor até a primeira falha, enquanto a distribuição exponencial modela o tempo até a próxima falha do servidor.

Propriedades matemáticas e cálculos

Com os conceitos básicos e as propriedades únicas em mãos, vamos ver as ferramentas matemáticas que permitem fazer cálculos precisos de probabilidade e tomar decisões bem informadas. Essas fórmulas e relações vão ser essenciais na hora de aplicar a distribuição geométrica em problemas do mundo real.

Média, variância e desvio padrão

O valor esperado (média) da distribuição geométrica é: 

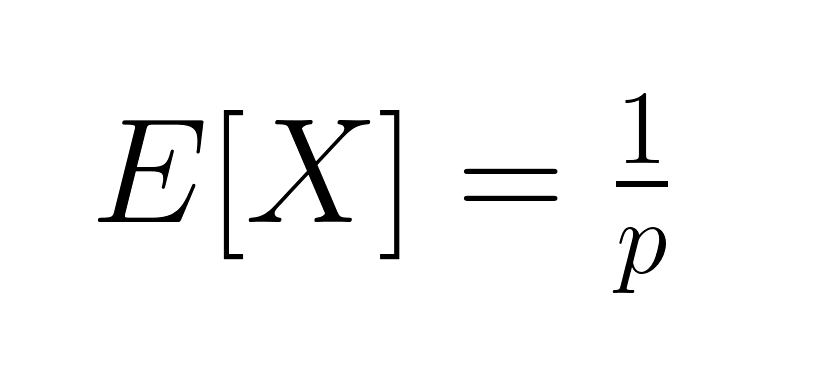
Isso é a média de tentativas que a gente precisa pra conseguir. A variação é igual a:

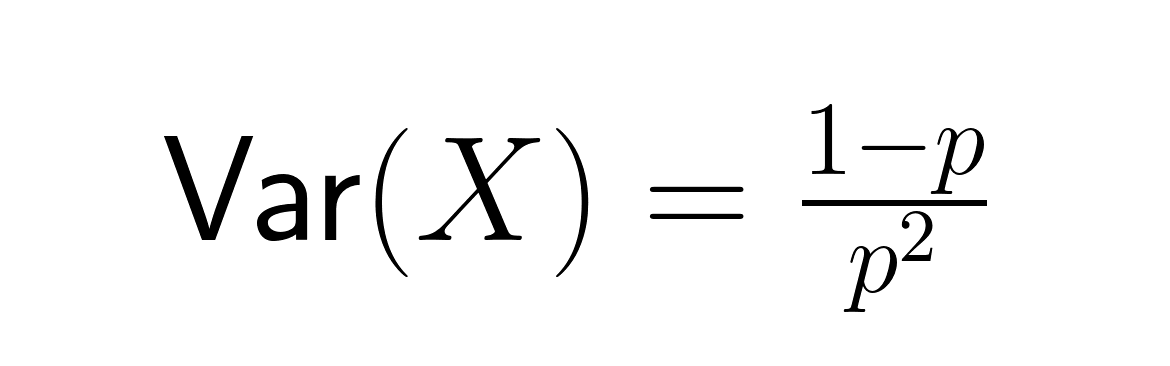
O desvio padrão é:

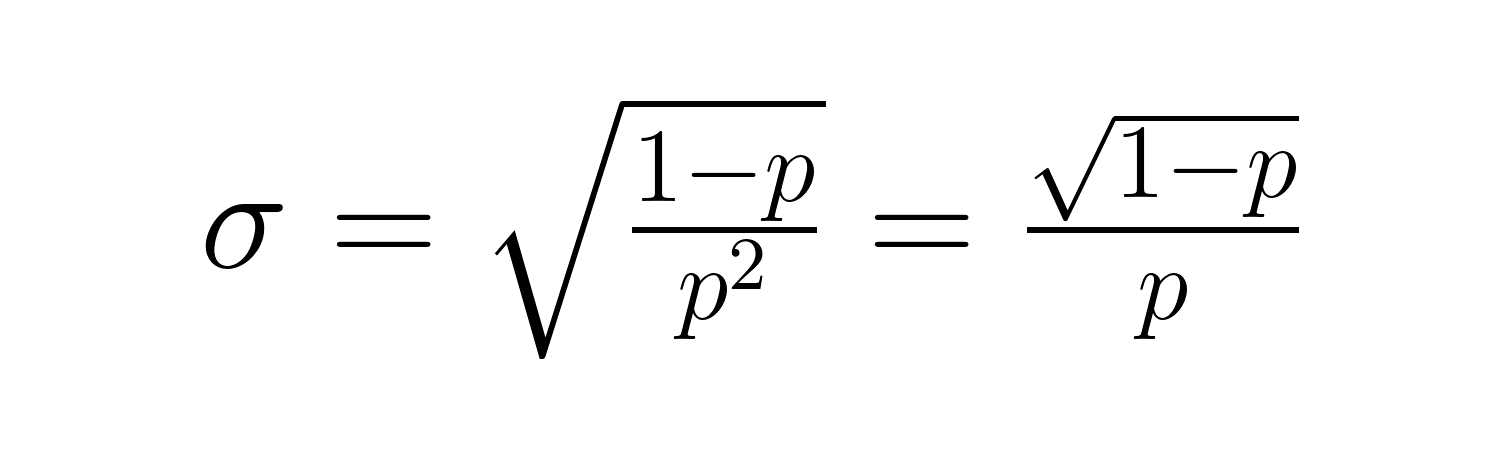
Essas fórmulas mostram relações importantes: quanto menos p, mais o tempo de espera esperado e a variabilidade aumentam bastante. Por exemplo, com p = 0,2, o número esperado de tentativas é 5, mas com p = 0,05, salta para 20 tentativas. A variação aumenta ainda mais, de 20 para 380.

Momentos e funções geradoras

Para uma análise mais avançada, a função geradora de momentos (MGF) para a distribuição geométrica é:

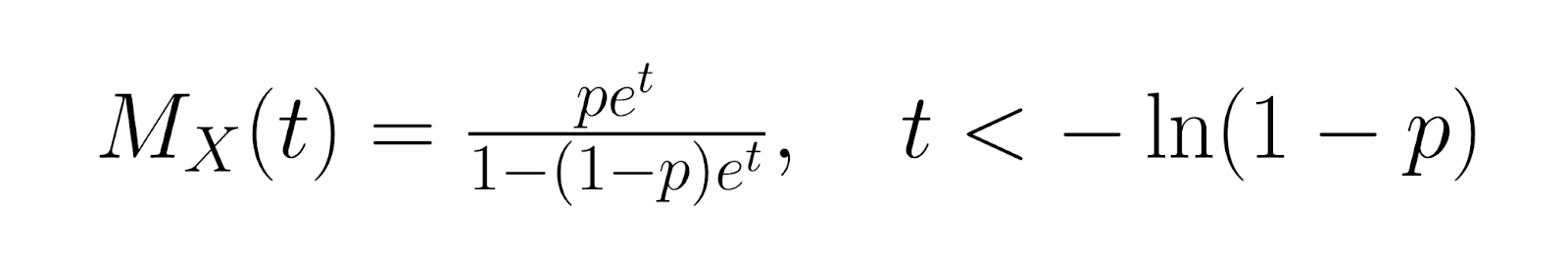A função geradora de probabilidade (PGF) é:

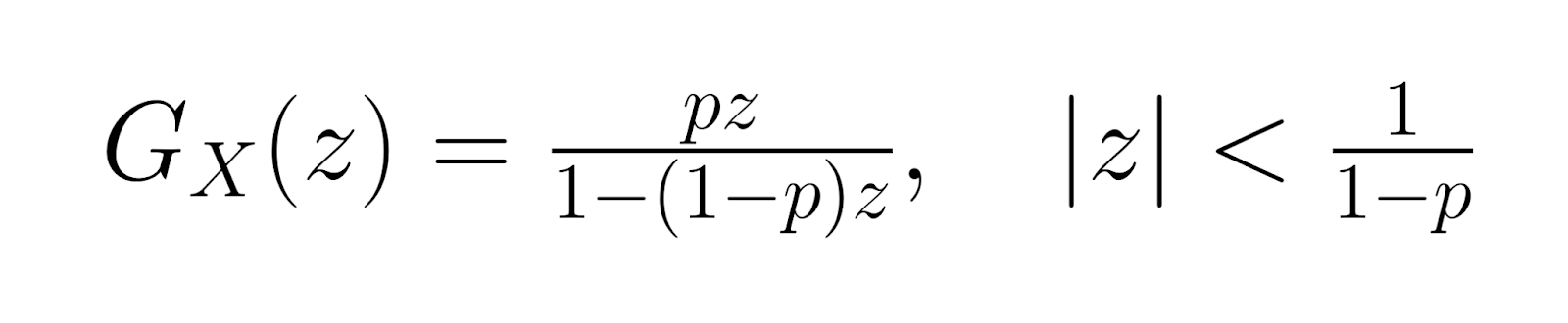
Essas funções geradoras ajudam na análise estatística avançada e oferecem métodos alternativos para derivar propriedades de distribuição. Os momentos de ordem superior podem ser calculados usando derivadas dessas funções, permitindo uma caracterização abrangente da forma e do comportamento da distribuição.

Entropia e medidas de informação (avançado)

Entrando em um território mais especializado, a entropia da distribuição geométrica é igual a:

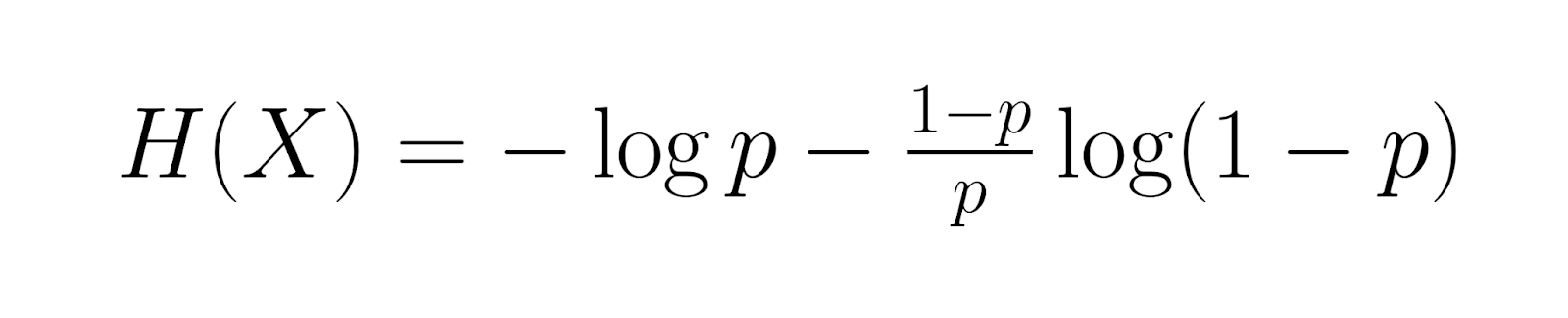
Isso mede o conteúdo médio de informação. Informação de Fisher, dada por:

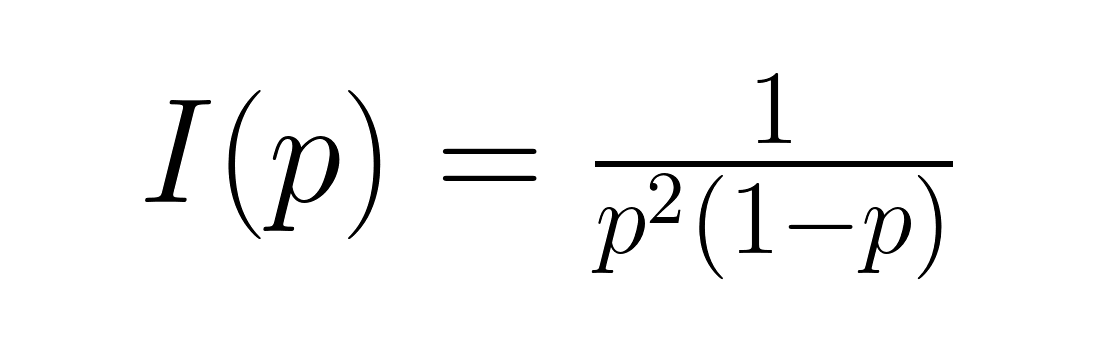
Isso mostra a quantidade de informação sobre o parâmetro p que está nos dados. Essas medidas são super úteis em aplicações de teoria da informação e em projetos experimentais bem otimizados, onde entender o conteúdo da informação ajuda a determinar tamanhos de amostra e procedimentos de estimativa adequados.

Métodos de estimativa de parâmetros

Para estimar a probabilidade de sucesso p a partir dos dados observados, é preciso entender diferentes abordagens estatísticas e suas vantagens e desvantagens.

Estimativa de máxima verossimilhança (MLE)

A abordagem de estimativa de máxima verossimilhança funciona encontrando a probabilidade de sucesso que torna os dados observados mais prováveis de terem ocorrido. Para calcular essa estimativa, você divide o número total de eventos bem-sucedidos pela soma de todas as tentativas em suas observações. Esse estimador dá resultados imparciais e funciona bem quando se trabalha com amostras grandes.

É assim que funciona na prática: se você observar sucesso após 3, 7, 2 e 8 tentativas, respectivamente, você calcularia o MLE pegando suas 4 observações e dividindo pelo total de 20 tentativas (3+7+2+8), o que te daria uma probabilidade de sucesso estimada em 0,2 ou 20%. A abordagem MLE maximiza a probabilidade de observar os dados reais coletados, tornando-a o método estatisticamente mais eficiente em condições padrão.

Método dos momentos

Como uma abordagem alternativa, o estimador do método dos momentos funciona definindo a média da amostra igual à média teórica da distribuição geométrica. Como a média teórica é igual a um dividido pela probabilidade de sucesso, você pode estimar a probabilidade de sucesso dividindo um pela média da sua amostra. Embora esse método seja mais simples de calcular do que o MLE, ele pode ser menos eficiente estatisticamente e, às vezes, pode gerar estimativas que ficam fora da faixa de probabilidade válida de zero a um.

Os dois métodos dão resultados parecidos quando a gente trabalha com amostras grandes, mas o MLE geralmente tem propriedades estatísticas melhores. A escolha entre os métodos geralmente depende das limitações computacionais e dos requisitos específicos da sua análise.

Estimativa bayesiana

Quando você já tem informações sobre a chance de sucesso, a estimativa bayesiana te deixa usar esse conhecimento por meio de uma distribuição de probabilidade prévia. A distribuição Beta costuma ser usada como essa distribuição a priori porque funciona bem matematicamente com dados de distribuição geométrica. A abordagem bayesiana junta suas crenças anteriores com os dados observados para chegar a estimativas atualizadas dos parâmetros através do que chamamos de distribuição posterior.

A relação matemática cria uma distribuição Beta atualizada que junta o que você já sabia com as novas observações. Essa abordagem funciona super bem quando você tem poucos dados ou quer incluir o conhecimento de especialistas sobre o processo que está sendo modelado. Por exemplo, se você sabe por experiência no setor que as taxas de sucesso geralmente ficam dentro de um certo intervalo, pode usar esse conhecimento para melhorar suas estimativas, mesmo com amostras pequenas.

Aplicações da Distribuição Geométrica

A distribuição geométrica é muito usada em vários setores e contextos analíticos, onde modelar os primeiros eventos de sucesso dá uma boa ideia do que vai acontecer.

Engenharia de confiabilidade e controle de qualidade

Os processos de fabricação costumam usar a distribuição geométrica para modelar a detecção de defeitos e a análise de falhas de componentes. Os inspetores de controle de qualidade podem estimar o número esperado de itens a serem inspecionados antes de encontrar uma unidade com defeito, ajudando a otimizar os procedimentos de inspeção e a alocação de recursos.

Por exemplo, se os dados históricos mostram uma taxa de defeitos de 2%, a distribuição geométrica prevê uma média de 50 itens inspecionados antes de encontrar o primeiro defeito. Essas informações ajudam a definir tamanhos de lotes e frequências de inspeção adequados para manter os padrões de qualidade e, ao mesmo tempo, minimizar os custos.

Conquista de clientes e gerenciamento de rede

As equipes de marketing usam a distribuição geométrica pra modelar os processos de conversão de clientes, estimando quantos contatos ou anúncios são necessários antes de fechar uma venda. Essa análise ajuda a decidir como distribuir o orçamento e a estratégia da campanha.

Nas telecomunicações, os engenheiros de rede usam a distribuição geométrica para modelar as taxas de sucesso da transmissão de pacotes e otimizar os mecanismos de repetição. Entender o número esperado de tentativas de transmissão ajuda a criar protocolos eficientes e melhorar o desempenho geral da rede.

Jogos, análise esportiva e mais exemplos reais

Os analistas esportivos usam a distribuição geométrica pra modelar eventos de pontuação, tipo o número de tentativas que um jogador de basquete precisa pra fazer sua primeira cesta de três pontos num jogo. Essa análise ajuda na tomada de decisões estratégicas e na avaliação do desempenho.

Os aplicativos de jogos incluem modelar o número de tentativas necessárias para conseguir eventos raros ou terminar níveis difíceis. As plataformas online usam essas informações para equilibrar a dificuldade do jogo e manter o engajamento dos jogadores por meio de estruturas de recompensa adequadas.

Problemas resolvidos e questões práticas

Imagina que uma campanha de marketing tem uma taxa de conversão de 15%. Para descobrir a chance de conseguir a primeira conversão no quinto contato: P(X = 5) = (0,85)⁴ × 0,15 = 0,0783 ou cerca de 7,83%.

Para praticar, veja a probabilidade de um inspetor de controle de qualidade encontrar o primeiro item com defeito nas primeiras 10 inspeções, considerando uma taxa de defeito de 8%. Use a fórmula CDF: P(X ≤ 10) = 1 - (0,92)¹⁰ = 0,5656 ou aproximadamente 56,56%.

Limitações e suposições

Entender quando a distribuição geométrica se aplica corretamente requer reconhecer suas premissas e possíveis limitações.

A distribuição geométrica assume tentativas independentes com probabilidade de sucesso constante, o que pode não acontecer em muitos cenários reais. Por exemplo, o comportamento do cliente geralmente mostra dependência — interações anteriores podem influenciar as chances de conversão no futuro. Da mesma forma, os sistemas mecânicos podem sofrer desgaste que altera as taxas de falha ao longo do tempo.

Se a gente não seguir essas regras, pode acabar com previsões erradase decisões ruins. Os profissionais de dados devem validar as suposições de independência por meio de testes estatísticos e pensar em modelos alternativos quando perceberem dependências. Algumas alternativas comuns são a distribuição binomial negativa paradados superdispersos ou modelos de cadeia de Markov para testes dependentes.

Conclusão

Entender a distribuição geométrica vai além do conhecimento teórico — ela te ajuda a tomar decisões mais inteligentes sobre como distribuir recursos, otimizar processos e avaliar riscos. Se você está criando procedimentos de controle de qualidade ou otimizando campanhas de marketing, essa distribuição traz insights quantitativos que ajudam a ter resultados melhores.

Para continuar aprendendo, dá uma olhada no nosso curso Distribuições de Probabilidade Multivariadas em R para entender como a distribuição geométrica se relaciona com outros modelos de probabilidade, ou mergulha mais fundo nas técnicas de estimativa com o nosso curso Modelos Lineares Generalizados em R para aplicações avançadas de modelagem.