Geometrische Verteilung: Ein kompletter Leitfaden für die Modellierung erster Erfolgserlebnisse

Wie viele Vorstellungsgespräche musst du wohl führen, bevor du deinen Traumjob bekommst? Wie viele Versuche braucht es, bis eine Marketingkampagne den ersten Verkauf bringt? Die geometrische Verteilung beantwortet diese „Wartezeit”-Fragen, indem sie die Anzahl der Versuche modelliert, die nötig sind, bis der erste Erfolg eintritt.

Dieser Leitfaden erklärt die mathematischen Grundlagen der geometrischen Verteilung, ihre besonderen Eigenschaften und praktische Anwendungen, die sie für Leute, die mit sequenziellen Versuchsszenarien arbeiten, so nützlich machen. Wenn du deine Kenntnisse über Wahrscheinlichkeitsverteilungen auffrischen möchtest, solltest du unseren Kurs „Einführung in die Statistik“ besuchen. 

Was ist die geometrische Verteilung?

Die geometrische Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die die Anzahl der unabhängigen Bernoulli-Versuche modelliert , die nötig sind, um den ersten Erfolg zu erzielen. Jeder Versuch hat die gleiche Chance, dass er klappt, und die Versuche hängen nicht voneinander ab.

Diese Verteilung gibt es in zwei gängigen Formen: Eine zählt die Gesamtzahl der Versuche bis zum ersten Erfolg (einschließlich des Erfolgs) und die andere zählt nur die Anzahl der Fehlversuche vor dem ersten Erfolg. Beide Formen werden je nach Anwendung oft benutzt. In diesem Leitfaden verwenden wir die erste Form und zählen die Gesamtzahl der Versuche bis zum ersten Erfolg, wobei X die Werte 1, 2, 3 usw. annehmen kann.

Die geometrische Verteilung verstehen

Schauen wir uns mal die mathematische Struktur und die Eigenschaften an, die diese Verteilung ausmachen.

Grundlegende Definition und Wahrscheinlichkeitsstruktur

Die geometrische Verteilung braucht drei wichtige Bedingungen: unabhängige Versuche, gleiche Erfolgschancen bei allen Versuchen und eine feste Wahrscheinlichkeit p, wobei 0 < p ≤ 1 ist. In der Standardnotation steht p für die Erfolgswahrscheinlichkeit und q = 1-p für die Misserfolgswahrscheinlichkeit.

Die Wahrscheinlichkeitsverteilungsfunktion (PMF) für die Anzahl der Versuche X bis zum ersten Erfolg ist: 

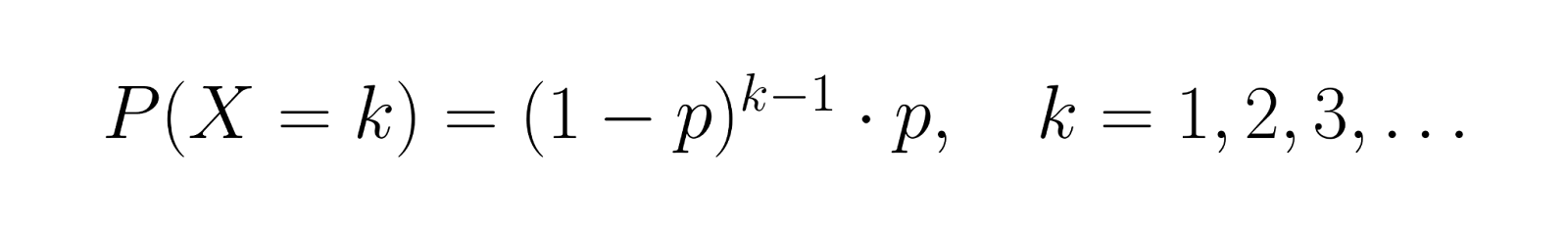
Diese Formel berechnet die Wahrscheinlichkeit, dass genau k-1 Fehler auftreten und dann ein Erfolg kommt. Wenn zum Beispiel p = 0,3 ist, ist die Wahrscheinlichkeit, dass der dritte Versuch klappt, P(X = 3) = (0,7)² × 0,3 = 0,147.

Kumulative Wahrscheinlichkeiten und Verteilungsfunktion

Die kumulative Verteilungsfunktion (CDF) ergibt:

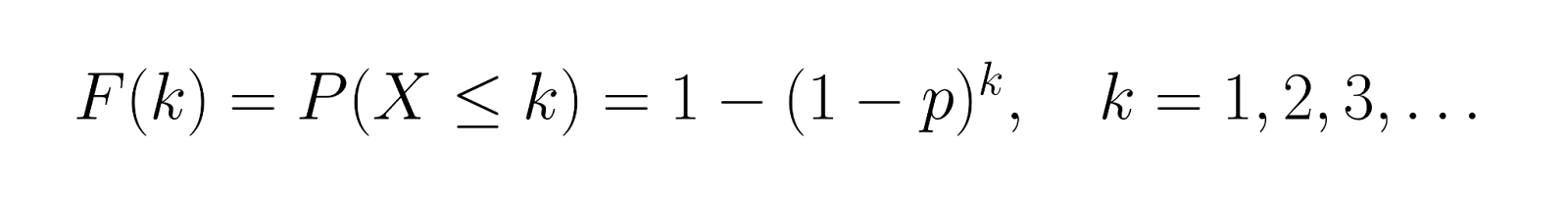
Das ist die Chance, dass du innerhalb von k Versuchen Erfolg hast. Nimm unser Beispiel, wo p = 0,3 ist, und lass uns die CDF für die ersten paar Werte berechnen:

• F(1) = P(X ≤ 1) = 1 - (0,7)¹ = 0,3
• F(2) = P(X ≤ 2) = 1 - (0,7)² = 1 - 0,49 = 0,51
• F(3) = P(X ≤ 3) = 1 - (0,7)³ = 1 - 0,343 = 0,657

Das heißt, beim ersten Versuch gibt's eine 30 %ige Chance, dass es klappt, bei den ersten beiden Versuchen sind es 51 % und bei den ersten drei Versuchen 65,7 %.

Die geometrische Verteilung grafisch darstellen

Die visuellen Muster der geometrischen Verteilung zeigen wichtige Infos zu „Wartezeit”-Szenarien. Diese Diagramme zeigen, wie sich die Wahrscheinlichkeit in frühen Versuchen konzentriert und dann exponentiell abnimmt. Das macht die Verteilung nützlich für die Modellierung von Situationen, in denen der Erfolg eher früher als später wahrscheinlich ist.

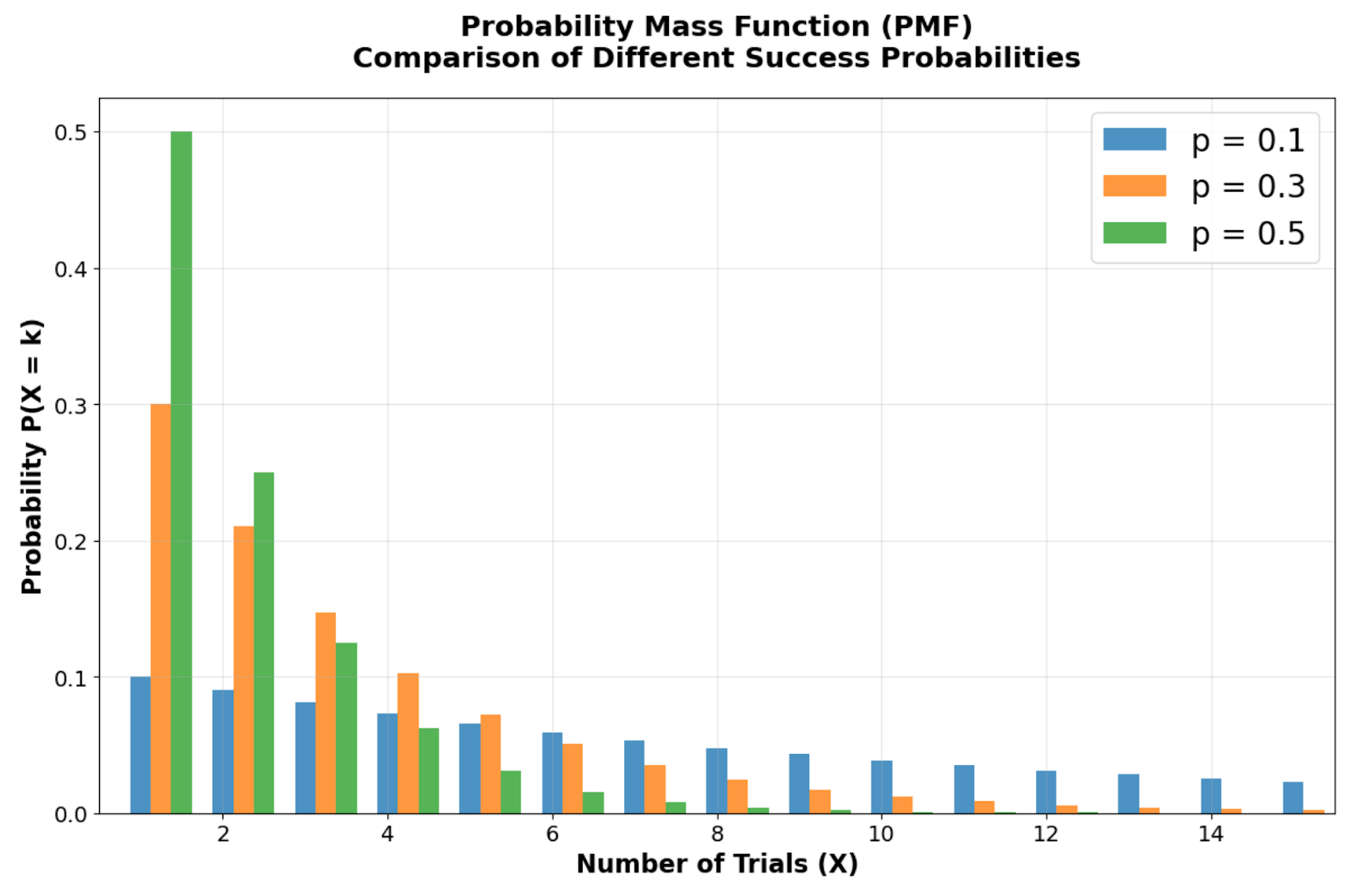
Vergleich der Wahrscheinlichkeitsverteilungsfunktionen, der zeigt, wie unterschiedliche Erfolgswahrscheinlichkeiten (p = 0,1, 0,3, 0,5) die Form der Verteilung beeinflussen. Bild vom Autor

Wenn man sich den Vergleich der Wahrscheinlichkeitsverteilungsfunktionen bei verschiedenen Erfolgswahrscheinlichkeiten ansieht, erkennt man die typische rechtsverzerrte Form der geometrischen Verteilung, deren Modus immer bei X = 1 (dem ersten Versuch) liegt. Schau dir an, wie die Wahrscheinlichkeitsbalken beim ersten Versuch am höchsten sind und bei jedem weiteren Versuch geometrisch abnehmen. Je kleiner die Erfolgswahrscheinlichkeit p wird, desto breiter wird die Verteilung, was längere erwartete Wartezeiten zeigt. Bei p = 0,1 gibt's zum Beispiel nur eine 10-prozentige Chance auf sofortigen Erfolg, was im Vergleich zu p = 0,5 einen ausgeprägteren rechten Rand ergibt.

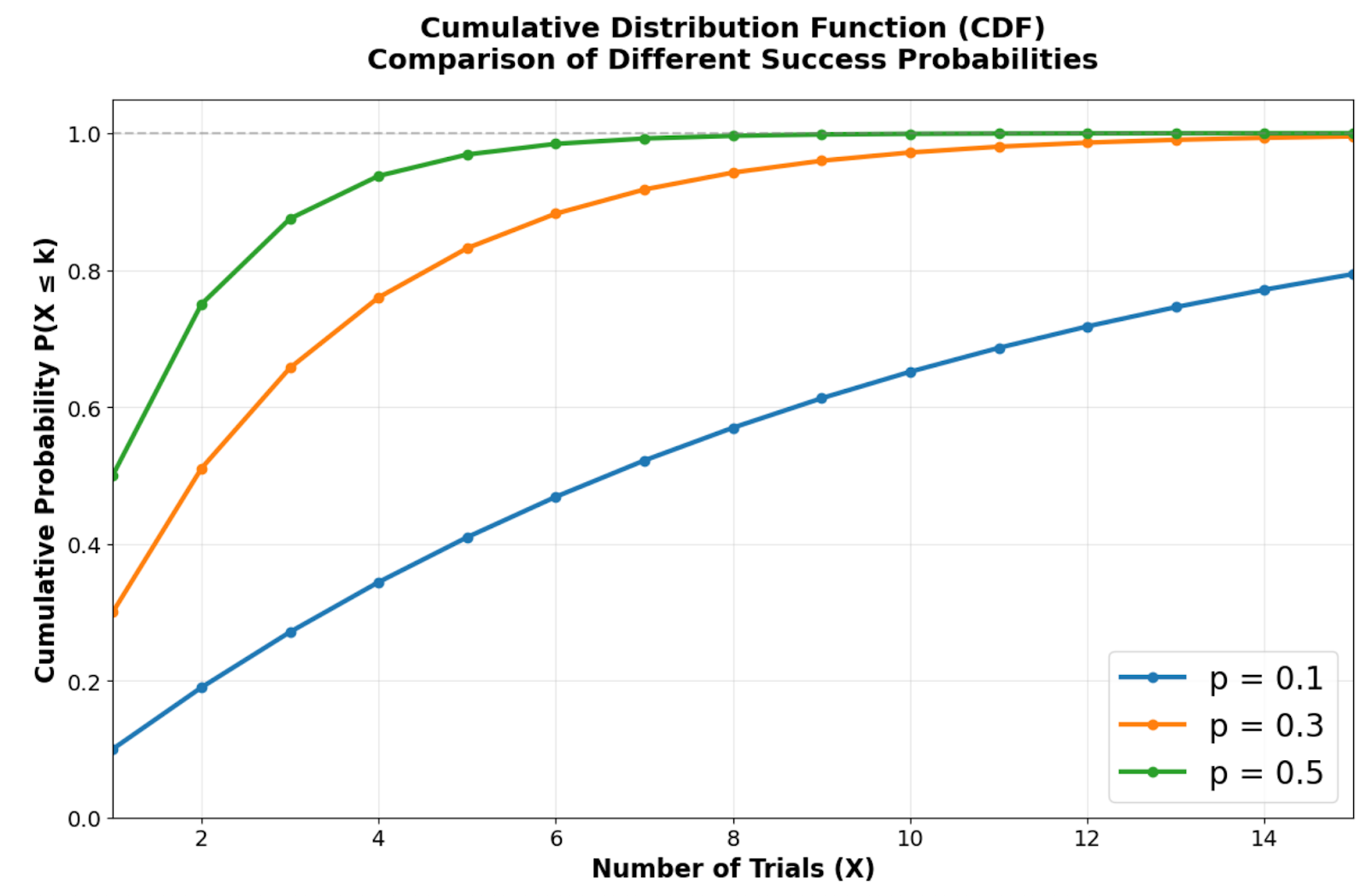
Kumulative Verteilungsfunktion, die zeigt, wie schnell verschiedene Erfolgswahrscheinlichkeiten sich der Gewissheit annähern. Bild vom Autor. 

Die kumulative Verteilungsfunktion zeigt, wie schnell sich die geometrische Verteilung der Gewissheit nähert. Höhere Erfolgschancen sorgen für steilere Kurven, die schon nach wenigen Versuchen hohe kumulative Wahrscheinlichkeiten erreichen. Wenn p = 0,5 ist, gibt's zum Beispiel eine Chance von etwa 75 %, dass es in den ersten beiden Versuchen klappt, während p = 0,1 deutlich mehr Versuche braucht, um die gleiche Sicherheit zu haben.

Ein direkter Vergleich zeigt, wie die PMF exponentiell abnimmt und die CDF schnell näher an den tatsächlichen Wert kommt. Bild vom Autor. 

Dieses exponentielle Abklingmuster erklärt, warum die geometrische Verteilung gut für Szenarien passt, in denen ein früher Erfolg wahrscheinlicher ist als lange Wartezeiten. Der schnelle Anstieg der CDF in Richtung 1 zeigt, warum diese Verteilung gut für die Modellierung von Prozessen mit kurzen Wartezeiten ist. Das macht sie super für die Qualitätskontrolle, die Analyse von Kundenkonversionen und für Zuverlässigkeitstests.

Erstellen eigener Visualisierungen für geometrische Verteilungen

Du kannst diese Visualisierungen nachbauen und verschiedene Parameterwerte mit den Python-Bibliotheken scipy und matplotlib ausprobieren. So bekommst du die wichtigsten visuellen Infos, die die wichtigsten Merkmale der geometrischen Verteilung zeigen:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Create side-by-side plots for PMF and CDF
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
fig.suptitle('Geometric Distribution: Key Visual Insights', fontsize=24, fontweight='bold')

# Simple PMF showing exponential decay (using p = 0.3)
x_simple = np.arange(1, 11)
pmf_simple = stats.geom.pmf(x_simple, 0.3)

ax1.bar(x_simple, pmf_simple, alpha=0.8, color='steelblue', edgecolor='black', linewidth=1)
ax1.set_title('PMF: Exponential Decay Pattern', fontsize=18, fontweight='bold', pad=15)
ax1.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax1.set_ylabel('Probability', fontsize=14, fontweight='bold')
ax1.grid(True, alpha=0.3)
ax1.tick_params(axis='both', which='major', labelsize=14)

# Simple CDF showing approach to 1
cdf_simple = stats.geom.cdf(x_simple, 0.3)

ax2.plot(x_simple, cdf_simple, 'o-', linewidth=4, markersize=8, color='darkgreen')
ax2.set_title('CDF: Rapid Approach to Certainty', fontsize=18, fontweight='bold', pad=15)
ax2.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax2.set_ylabel('Cumulative Probability', fontsize=14, fontweight='bold')
ax2.grid(True, alpha=0.3)
ax2.set_ylim(0, 1.05)
ax2.tick_params(axis='both', which='major', labelsize=14)

plt.tight_layout()
plt.show()	

Dieser Code macht eine Visualisierung, die die beiden wichtigsten optischen Merkmale der geometrischen Verteilung zeigt. Das linke Feld zeigt, wie die Wahrscheinlichkeiten ab dem ersten Versuch exponentiell abnehmen, während das rechte Feld die schnelle Ansammlung der Wahrscheinlichkeitsmasse in der CDF zeigt.

Probier mal, die Erfolgswahrscheinlichkeit von 0,3 auf andere Werte wie 0,1 oder 0,7 zu ändern, um zu sehen, wie sich die Form der Verteilung ändert. Niedrigere Wahrscheinlichkeiten führen zu flacheren PMF-Kurven und langsamer ansteigenden CDFs, während höhere Wahrscheinlichkeiten steilere Abfälle und eine schnellere Annäherung an die Gewissheit bewirken.

Gedächtnislose Eigenschaft der geometrischen Verteilung

Die geometrische Verteilung hat eine coole Eigenschaft, die sie von den meisten anderen diskreten Verteilungen unterscheidet.

Die Eigenschaft, sich nicht zu erinnern

Die Eigenschaft „gedächtnislos“ besagt, dass P(X > s + t | X > s) = P(X > t) für alle positiven ganzen Zahlen s und t gilt. Das heißt, die Wahrscheinlichkeit, dass man noch mehr Versuche braucht, hängt nicht davon ab, wie viele Versuche schon nicht geklappt haben.

Mathematisch ergibt sich diese Eigenschaft, weil P(X > k) = (1-p)^k ist, was die Berechnung der bedingten Wahrscheinlichkeit ganz einfach macht. Praktisch gesehen bleibt die Wahrscheinlichkeit für zukünftige Vorstellungsgespräche dieselbe wie zu Beginn, wenn du schon fünf erfolglose Vorstellungsgespräche hinter dir hast – vergangene Misserfolge beeinflussen die zukünftigen Wahrscheinlichkeiten nicht.

Zusammenhang mit Bernoulli-Versuchen und Experimenten

Jeder Versuch in einem geometrischen Experiment ist wie ein unabhängiger Bernoulli-Versuch mit einer konstanten Erfolgswahrscheinlichkeit p. Die geometrische Verteilung zeigt die Abfolge dieser Versuche bis zum ersten Erfolg und ist damit das diskrete Gegenstück zu „Wartezeitproblemen”.

Diese Beziehung erklärt, warum die geometrische Verteilung häufig in der Qualitätskontrolle auftaucht, wo jeder getestete Artikel ein Bernoulli-Versuch ist und wir daran interessiert sind, den ersten fehlerhaften Artikel zu finden. Die Unabhängigkeitsannahme stellt sicher, dass das Auffinden fehlerhafter Teile in frühen Tests die Wahrscheinlichkeit, dass in späteren Tests Fehler gefunden werden, nicht verändert.

Unterschied zu kontinuierlichen Analogen

Die Exponentialverteilung ist die t-e kontinuierliche Version der geometrischen Verteilung, und beide haben die Eigenschaft, dass sie keine Erinnerung haben. Während die geometrische Verteilung diskrete Wartezeiten (Anzahl der Versuche) beschreibt, geht die exponentielle Verteilung von kontinuierlichen Wartezeiten (Zeit bis zu einem Ereignis) aus.

Beide Verteilungen sind in der Zuverlässigkeitsanalyse und Warteschlangentheorie nützlich. Die geometrische Verteilung könnte zum Beispiel die Anzahl der Serveranfragen bis zum ersten Ausfall zeigen, während die exponentielle Verteilung die Zeit bis zum nächsten Serverausfall angibt.

Mathematische Eigenschaften und Berechnungen

Nachdem wir die grundlegenden Konzepte und einzigartigen Eigenschaften kennengelernt haben, schauen wir uns die mathematischen Werkzeuge an, mit denen wir genaue Wahrscheinlichkeitsberechnungen durchführen und fundierte Entscheidungen treffen können. Diese Formeln und Zusammenhänge sind super wichtig, wenn man die geometrische Verteilung auf echte Probleme anwendet.

Mittelwert, Varianz und Standardabweichung

Der erwartete Wert (Mittelwert) der geometrischen Verteilung ist: 

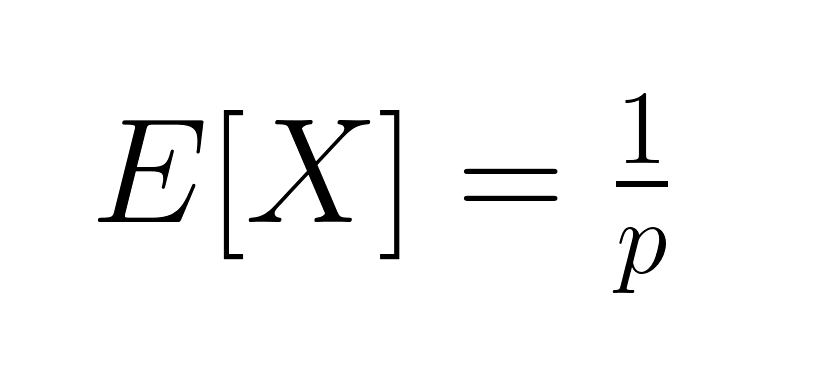
Das ist die durchschnittliche Anzahl der Versuche, die man braucht, um es zu schaffen. Die Varianz ist gleich:

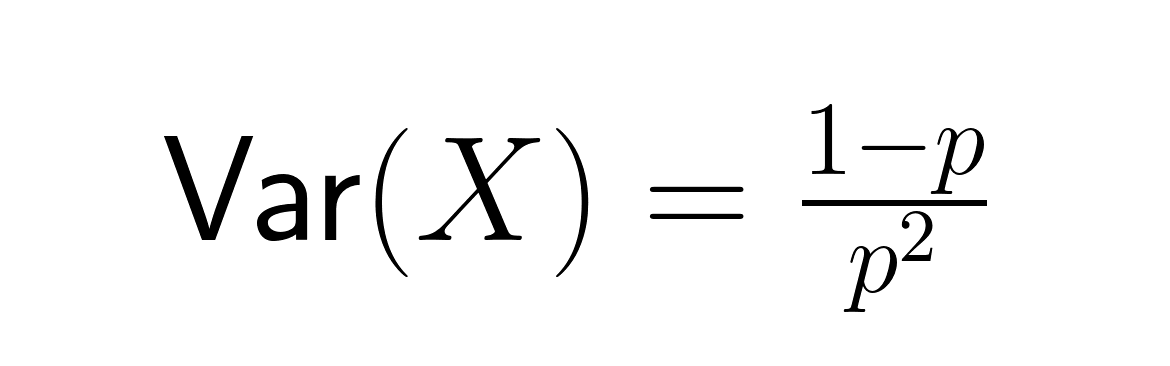
Die Standardabweichung ist:

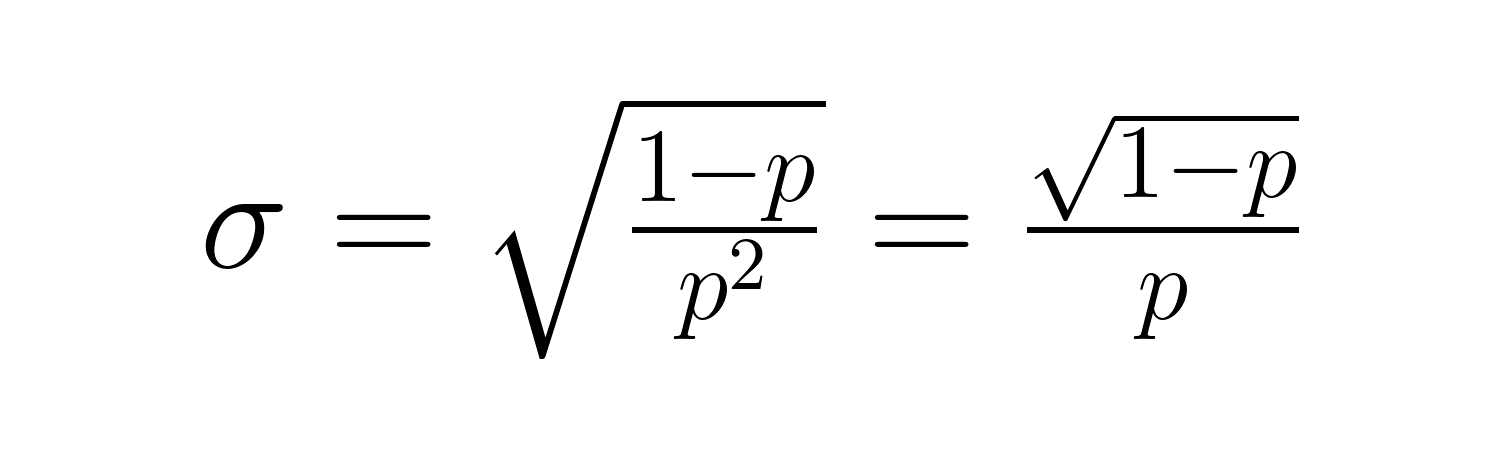
Diese Formeln zeigen wichtige Zusammenhänge: Wenn p kleiner wird, steigen sowohl die erwartete Wartezeit als auch die Schwankungen deutlich an. Wenn zum Beispiel p = 0,2 ist, sind 5 Versuche zu erwarten, aber wenn p = 0,05 ist, springt die Zahl auf 20 Versuche. Die Abweichung wird noch krasser, von 20 auf 380.

Momente und erzeugende Funktionen

Für eine genauere Analyse ist die Momentgenerierende Funktion (MGF) für die geometrische Verteilung:

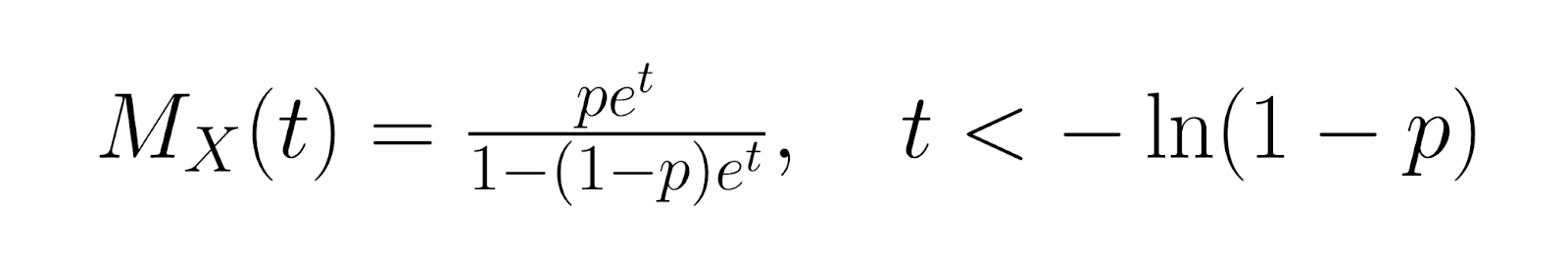Die Wahrscheinlichkeitsfunktion (PGF) ist:

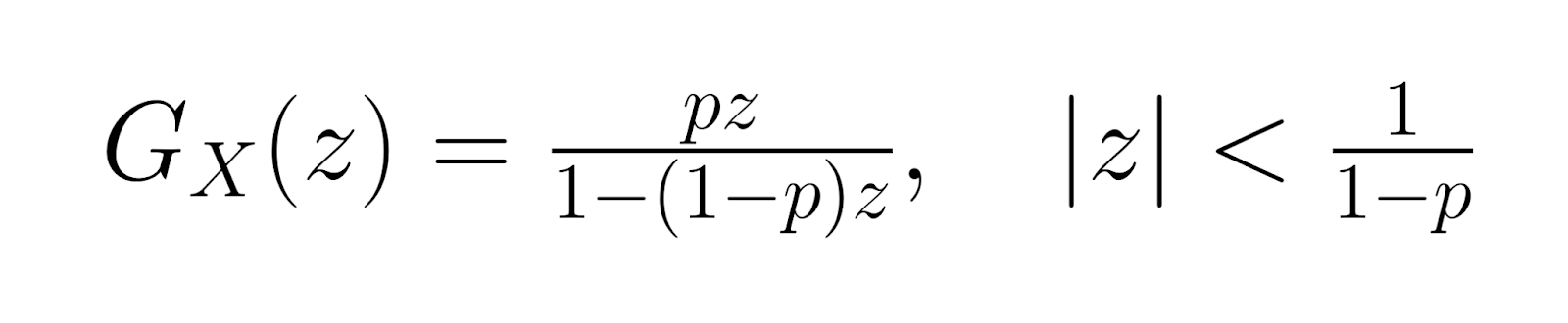
Diese Generierungsfunktionen helfen bei fortgeschrittenen statistischen Analysen und bieten alternative Methoden zur Ableitung von Verteilungseigenschaften. Höhere Momente kann man mit Ableitungen dieser Funktionen berechnen, was eine umfassende Beschreibung der Form und des Verhaltens der Verteilung ermöglicht.

Entropie und Informationsmaße (fortgeschritten)

Wenn wir uns jetzt etwas tiefer ins Thema stürzen, ist die Entropie der geometrischen Verteilung gleich:

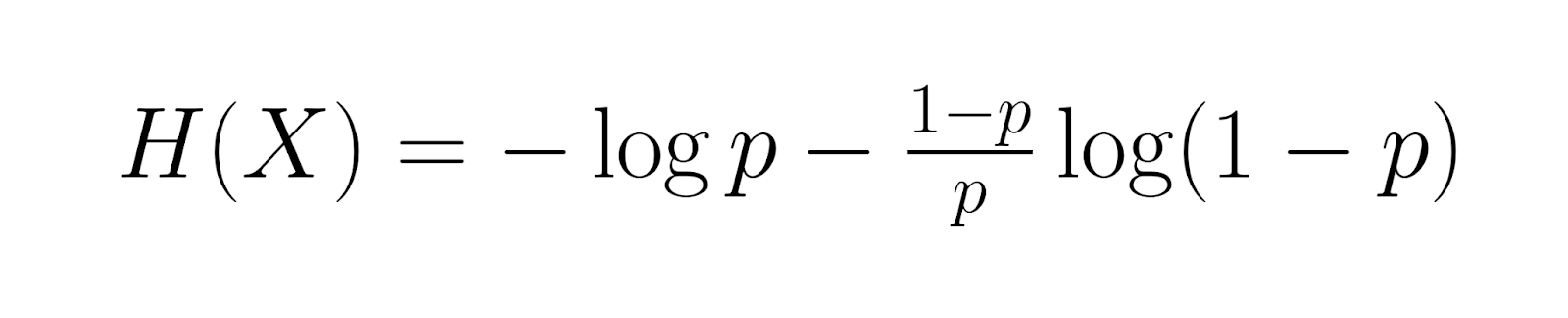
Das misst den durchschnittlichen Informationsgehalt. Fisher-Infos, angegeben durch:

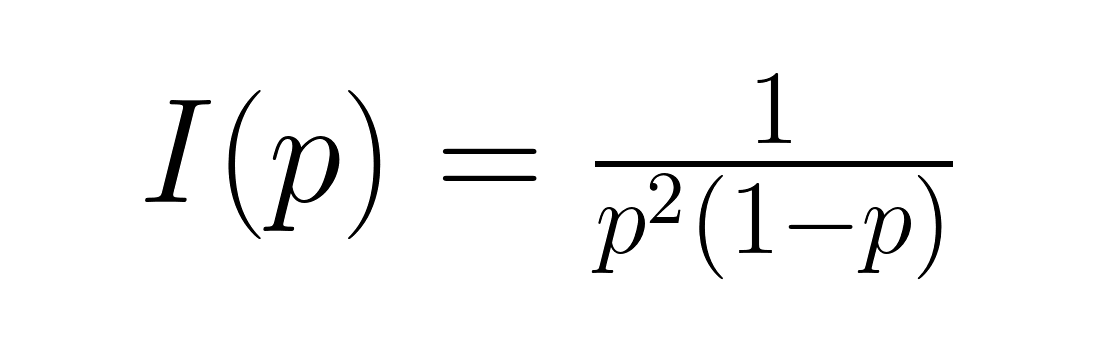
Das sagt dir, wie viele Infos über den Parameter p in den Daten stecken. Diese Maßnahmen sind super nützlich in der Informationstheorie und bei der optimalen Versuchsplanung, wo man den Informationsgehalt verstehen muss, um die richtigen Stichprobengrößen und Schätzverfahren zu bestimmen.

Methoden zur Parameterschätzung

Um die Erfolgswahrscheinlichkeit p aus den Daten zu schätzen, muss man verschiedene statistische Ansätze und ihre Vor- und Nachteile verstehen.

Maximale Wahrscheinlichkeitsschätzung (MLE)

Der Ansatz der Maximum-Likelihood-Schätzung funktioniert so, dass die Erfolgswahrscheinlichkeit ermittelt wird, mit der die beobachteten Daten am ehesten eingetreten sind. Um diesen Schätzwert zu berechnen, teilst du die Gesamtzahl der erfolgreichen Ereignisse durch die Summe aller Versuche in deinen Beobachtungen. Dieser Schätzer liefert unvoreingenommene Ergebnisse und funktioniert gut bei großen Stichproben.

So geht's in der Praxis: Wenn du nach 3, 7, 2 und 8 Versuchen Erfolg hast, berechnest du den MLE, indem du deine 4 Beobachtungen durch die Gesamtzahl der 20 Versuche (3+7+2+8) teilst. Das ergibt eine geschätzte Erfolgswahrscheinlichkeit von 0,2 oder 20 %. Der MLE-Ansatz erhöht die Wahrscheinlichkeit, dass du die tatsächlichen Daten, die du gesammelt hast, auch wirklich siehst, und ist damit unter normalen Bedingungen die statistisch effizienteste Methode.

Momentverfahren

Als Alternative kannst du den Momentenschätzer nehmen, bei dem du den Durchschnitt deiner Stichprobe gleich dem theoretischen Durchschnitt der geometrischen Verteilung machst. Da der theoretische Mittelwert gleich eins geteilt durch die Erfolgswahrscheinlichkeit ist, kannst du die Erfolgswahrscheinlichkeit schätzen, indem du eins geteilt durch deinen Stichprobenmittelwert nimmst. Diese Methode ist zwar im Vergleich zur MLE einfacher zu berechnen, aber statistisch gesehen nicht so zuverlässig und kann manchmal zu Schätzungen führen, die außerhalb des gültigen Wahrscheinlichkeitsbereichs von null bis eins liegen.

Bei großen Stichproben liefern beide Methoden ähnliche Ergebnisse, aber MLE hat im Allgemeinen bessere statistische Eigenschaften. Die Wahl der Methode hängt oft von den Rechenkapazitäten und den speziellen Anforderungen deiner Analyse ab.

Bayesianische Schätzung

Wenn du schon vorher Infos über die Erfolgswahrscheinlichkeit hast, kannst du mit der Bayes'schen Schätzung dieses Wissen über eine vorherige Wahrscheinlichkeitsverteilung einbauen. Die Beta-Verteilung wird oft als Prior verwendet, weil sie mathematisch gut mit geometrischen Verteilungsdaten funktioniert. Der Bayes'sche Ansatz kombiniert deine bisherigen Annahmen mit den beobachteten Daten, um aktualisierte Parameterschätzungen zu erstellen, die als Posteriorverteilung bezeichnet werden.

Die mathematische Beziehung erzeugt eine aktualisierte Beta-Verteilung, die sowohl dein Vorwissen als auch neue Beobachtungen berücksichtigt. Dieser Ansatz eignet sich besonders gut, wenn nur wenige Daten verfügbar sind oder wenn du Expertenwissen über den zu modellierenden Prozess einbeziehen möchtest. Wenn du zum Beispiel aus der Branche weißt, dass die Erfolgsraten normalerweise in einem bestimmten Bereich liegen, kannst du dieses Wissen nutzen, um deine Schätzungen auch bei kleinen Stichproben zu verbessern.

Anwendungen der geometrischen Verteilung

Die geometrische Verteilung wird in vielen Branchen und Analysen oft benutzt, wo die Modellierung von ersten Erfolgsfällen Einblicke gibt.

Zuverlässigkeitstechnik und Qualitätskontrolle

In der Produktion wird oft die geometrische Verteilung benutzt, um Fehler zu erkennen und zu analysieren, wie zum Beispiel, wenn Teile kaputt gehen. Qualitätskontrolleure können ungefähr einschätzen, wie viele Teile sie prüfen müssen, bevor sie einen Fehler finden. Das hilft dabei, die Prüfprozesse und den Ressourceneinsatz zu optimieren.

Wenn zum Beispiel alte Daten eine Fehlerquote von 2 % zeigen, sagt die geometrische Verteilung voraus, dass im Schnitt 50 Teile geprüft werden müssen, bevor der erste Fehler gefunden wird. Diese Infos helfen dabei, die richtigen Chargengrößen und Prüfintervalle zu finden, um die Qualitätsstandards zu halten und gleichzeitig die Kosten niedrig zu halten.

Kundengewinnung und Netzwerkmanagement

Marketingteams nutzen die geometrische Verteilung, um die Kundenkonversionsprozesse zu modellieren und zu schätzen, wie viele Kontakte oder Anzeigen nötig sind, bevor ein Verkauf zustande kommt. Diese Analyse hilft dabei, Entscheidungen über die Budgetverteilung und die Kampagnenstrategie zu treffen.

In der Telekommunikation nutzen Netzwerktechniker die geometrische Verteilung, um die Erfolgsraten bei der Paketübertragung zu modellieren und die Mechanismen für Wiederholungsversuche zu optimieren. Wenn man weiß, wie oft die Daten wahrscheinlich übertragen werden müssen, kann man effizientere Protokolle entwickeln und die Netzwerkleistung insgesamt verbessern.

Spiele, Sportanalysen und weitere Beispiele aus der Praxis

Sportanalysten nutzen die geometrische Verteilung, um Punkte zu modellieren, wie zum Beispiel die Anzahl der Versuche, die ein Basketballspieler braucht, um seinen ersten Dreipunktewurf in einem Spiel zu machen. Diese Analyse hilft bei strategischen Entscheidungen und bei der Bewertung der Leistung.

Gaming-Anwendungen umfassen die Modellierung der Anzahl der Versuche, die nötig sind, um seltene Ereignisse zu erreichen oder schwierige Levels zu meistern. Online-Plattformen nutzen diese Erkenntnisse, um den Schwierigkeitsgrad der Spiele auszugleichen und die Spieler durch passende Belohnungssysteme bei der Stange zu halten.

Gelöste Beispielaufgaben und Übungsfragen

Stell dir mal vor, eine Marketingkampagne hat eine Conversion-Rate von 15 %. So findest du die Wahrscheinlichkeit, dass die erste Conversion beim 5. Kontakt passiert: P(X = 5) = (0,85)⁴ × 0,15 = 0,0783 oder etwa 7,83 %.

Berechne mal, wie hoch die Wahrscheinlichkeit ist, dass ein Qualitätskontrolleur den ersten fehlerhaften Artikel bei den ersten 10 Kontrollen findet, wenn die Fehlerquote bei 8 % liegt. Benutz die CDF-Formel: P(X ≤ 10) = 1 - (0,92)¹⁰ = 0,5656 oder ungefähr 56,56 %.

Einschränkungen und Annahmen

Um zu verstehen, wann die geometrische Verteilung richtig eingesetzt wird, muss man die zugrunde liegenden Annahmen und möglichen Einschränkungen kennen.

Die geometrische Verteilung geht von unabhängigen Versuchen mit gleicher Erfolgswahrscheinlichkeit aus, was in der Realität oft nicht der Fall ist. Zum Beispiel ist das Kundenverhalten oft abhängig von früheren Interaktionen, die die Wahrscheinlichkeit einer zukünftigen Conversion beeinflussen können. Genauso können mechanische Systeme Verschleiß haben, der die Ausfallraten mit der Zeit verändert.

Wenn diese Annahmen nicht stimmen, kann das zu falschen Vorhersagenund schlechten Entscheidungen führen. Datenfachleute sollten die Unabhängigkeitsannahmen durch statistische Tests überprüfen und alternative Modelle in Betracht ziehen, wenn Abhängigkeiten festgestellt werden. Gängige Alternativen sind die negative Binomialverteilung fürüberdisperse Daten oder Markov-Ketten-Modelle für abhängige Versuche.

Fazit

Geometrische Verteilung zu verstehen ist mehr als nur theoretisches Wissen – es hilft dir, kluge Entscheidungen zu treffen, wenn es um die Verteilung von Ressourcen, die Optimierung von Prozessen und die Bewertung von Risiken geht. Egal, ob du Qualitätskontrollverfahren entwickelst oder Marketingkampagnen optimierst – diese Distribution liefert quantitative Einblicke, die zu besseren Ergebnissen führen.

Wenn du weiterlernen willst, schau dir unseren Kurs „Multivariate Wahrscheinlichkeitsverteilungen in R“ an, um zu verstehen, wie die geometrische Verteilung mit anderen Wahrscheinlichkeitsmodellen zusammenhängt, oder vertiefe deine Kenntnisse über Schätzverfahren mit unserem Kurs „Verallgemeinerte lineare Modelle in R“ für fortgeschrittene Modellierungsanwendungen.