Probabilité marginale : Théorie, exemples et applications

Vous analysez le comportement des clients d'une plateforme de commerce électronique, et votre responsable vous demande : Quelle est la probabilité qu'un client quitte l'entreprise, quelle qu'en soit la raison ?

Cette question aborde un sujet plus spécifique que vous ne le pensez. Vous ne vous interrogez pas surle taux de désabonnementpour une catégorie de produits spécifique, ni sur le taux de désabonnement associé à un mode de paiement. Vous vous interrogez sur la probabilité de base d'un événement unique : le départ d'un client, point final.

Il s'agit de la probabilité marginale, qui est à la base de la plupart des calculs de probabilité que vous rencontrerez en science des données.

Qu'est-ce que la probabilité marginale ?

Comme je l'ai mentionné, la probabilité marginale est la probabilité qu'un événement unique se produise, indépendamment des autres variables ou événements. On parle de « marginal » car lorsque l'on présente les probabilités conjointes dans un tableau, ces probabilités d'événements uniques apparaissent dans les marges (les totaux des lignes et des colonnes).

La notation est simple. Pour un événement discret A, nous écrivons P(A). La probabilité marginale découle souvent de la probabilité conjointe. Si B est une variable aléatoire discrète et que vous connaissez la probabilité conjointe que A se produise avec chaque valeur de B, vous pouvez déterminer la probabilité marginale en additionnant : P(A) =_Σb P(A, B=b), où vous effectuez la somme sur toutes les valeurs possibles b que B peut prendre. La probabilité marginale est ce qui subsiste lorsque l'on « additionne » ou « intègre » toutes les autres variables.

Pour bien comprendre ce concept, il est nécessaire de connaître certains termes fondamentaux. L'espace d'échantillonnage est l'ensemble de tous les résultats possibles. Un événement est un sous-ensemble quelconque de l'espace d'échantillonnage. La probabilité conjointe P(A ∩ B) mesure la probabilité que deux événements se produisent simultanément, tandis que la probabilité conditionnelle P(A|B) mesure la probabilité que A se produise ( ) étant donné que B s'est produit.

Je vous recommande de consulter notre fiche de référence « Introduction aux règles de probabilité » pour obtenir des informations rapides sur ces relations. La probabilité marginale occupe une place centrale dans cet écosystème probabiliste. Il s'agit du dénominateur dans les calculs de probabilité conditionnelle et de la base du théorème de Bayes.

Probabilité marginale à partir de tableaux et de distributions

Voyons comment calculer concrètement la probabilité marginale à partir de différentes structures de données. L'approche dépend du type de variables avec lesquelles vous travaillez : discrètes ou continues.

Cas discret (tableaux de contingence)

Lorsqu'on travaille avec des données catégorielles, les probabilités marginales apparaissent naturellement dans les tableaux de contingence. Supposons que vous analysiez le comportement d'achat des clients selon les catégories de produits (électronique, vêtements, livres) et les régions (nord, sud, est, ouest). Chaque cellule contient la probabilité conjointe d'une combinaison catégorie-région. Les totaux des lignes vous indiquent la probabilité marginale pour chaque catégorie de produits (P(Électronique), P(Vêtements), P(Livres)), quelle que soit la région. Les totaux des colonnes indiquent les probabilités marginales pour chaque région.

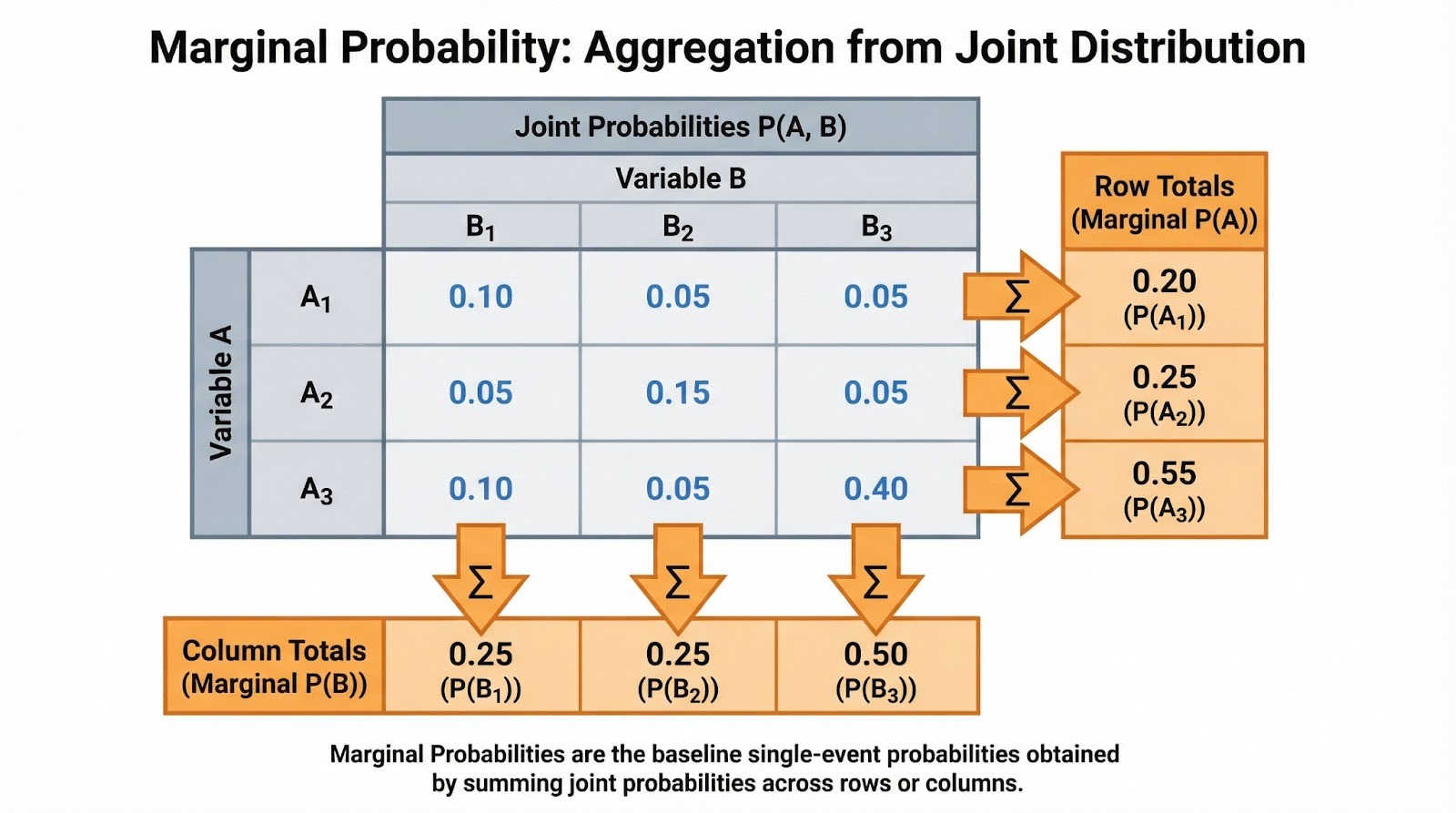
Additionner les probabilités conjointes pour déterminer les probabilités marginales. Image fournie par l'auteur.

Vous rencontrerez souvent ces fréquences sous forme normalisée. Si 500 clients sur 2 000 ont acheté des appareils électroniques, la probabilité marginale P(Appareils électroniques) = 500/2 000 = 0,25. Il s'agit du taux de référence avant de prendre en compte d'autres facteurs. Lorsque vous effectuez une analyse exploratoire des données, je vous recommande de calculer d'abord ces marginales. Ils vous aident à comprendre la structure de base de vos données avant d'approfondir les relations conditionnelles.

Cas continu

Pour les variables aléatoires continues, la probabilité marginale devient une fonction de densité de probabilité marginale (PDF). Si vous disposez de deux variables continues X et Y avec une fonction de densité de probabilité conjointe, la fonction de densité de probabilité marginale de X est obtenue en intégrant toutes les valeurs de Y.

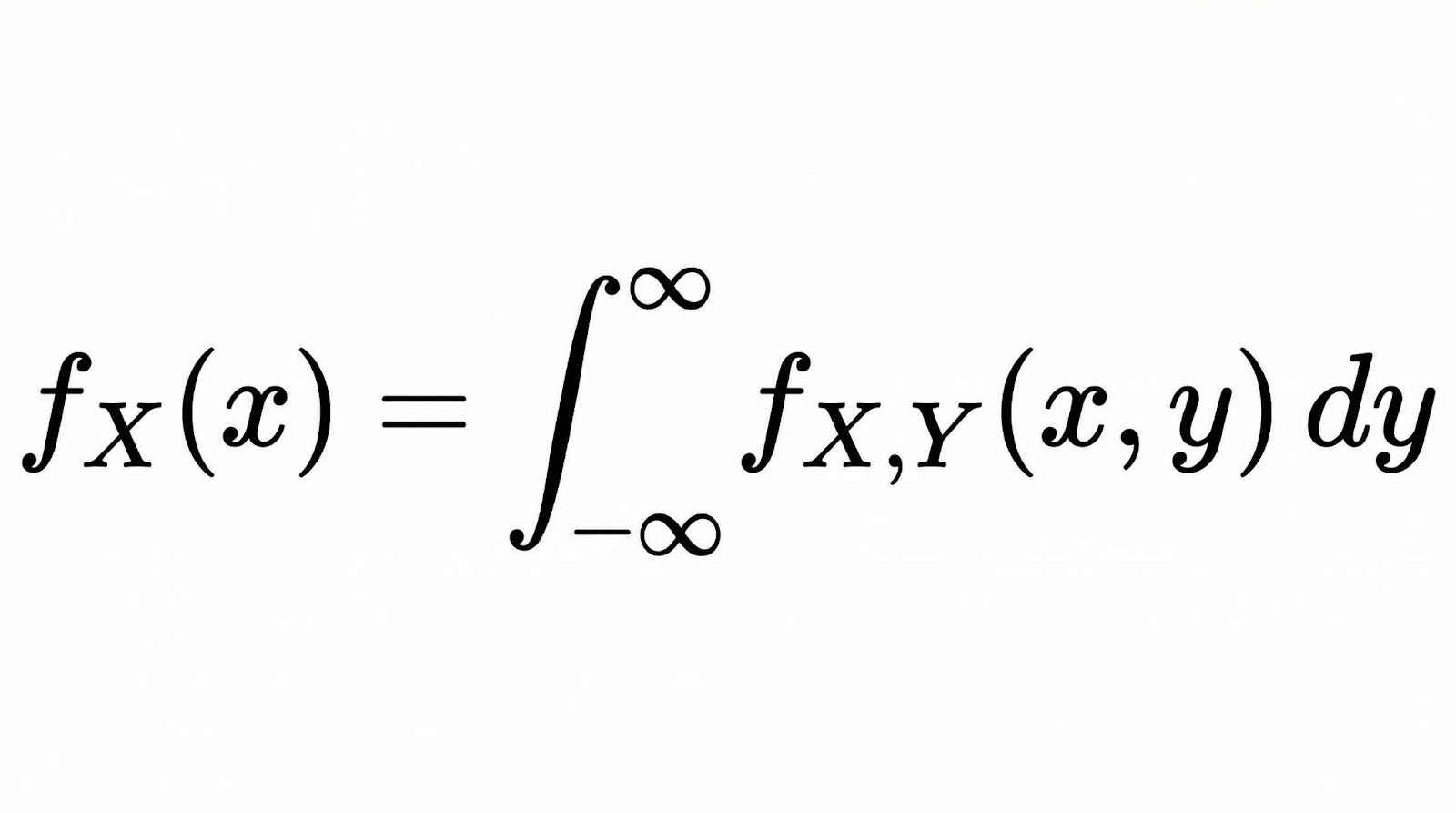
Conceptuellement, l'intégration ici accomplit la même chose que la sommation dans le cas discret. Elle « réduit » la distribution conjointe à une seule dimension en tenant compte de toutes les possibilités de l'autre variable.

Considérez cela comme si vous découpiez une surface 3D (la distribution conjointe) et observiez la zone sous la courbe le long d'un axe. Nos cours sur les principes fondamentaux de l'analyse bayésienne des données dans R aborde ces concepts en profondeur dans le cadre du traitement des distributions continues.

Relation entre la probabilité marginale, conjointe et conditionnelle

Examinons comment la probabilité marginale est liée aux autres types de probabilité que vous utiliserez régulièrement.

Ces trois types de probabilité forment un système cohérent, et la probabilité marginale est souvent le lien qui les unit. De probabilité conjointe, on obtient les marginales en effectuant une somme ou une intégration. À partir des probabilités conjointes et marginales, vous calculez les probabilités conditionnelles à l'aide de la formule P(A|B) = P(A ∩ B) / P(B). Veuillez noter que la probabilité marginale P(B) est le dénominateur. Il normalise la probabilité conjointe pour vous fournir la probabilité conditionnelle.

Cela est important dans la pratique, car lorsque vous interprétez des probabilités conditionnelles, vous avez besoin de la probabilité marginale comme contexte. Une probabilité de 90 % de maladie lorsque les résultats du test sont positifs peut sembler alarmante, mais si la probabilité marginale de maladie n'est que de 1 %, la probabilité réelle après un test positif pourrait être beaucoup plus faible que prévu.

Ceci est visible partout dans l'inférence bayésienne. Une priorité est votre conviction concernant un paramètre avant d'avoir examiné les données. La vraisemblance marginale (également appelée « preuve »), P(Données), est le terme de normalisation dans le théorème de Bayes qui transforme « a priori × vraisemblance » en une probabilité a posteriori appropriée. Notre cours sur l'analyse bayésienne des données en Python explore ces liens à travers des exercices pratiques de modélisation.

Exemples pratiques de probabilité marginale

Examinons à la fois des problèmes de probabilité classiques et des scénarios concrets.

Exemples classiques

Commençons par les dés. Si vous lancez deux dés, quelle est la probabilité que le premier dé affiche un 4, quelle que soit la valeur du second dé ?

L'espace d'échantillonnage comporte 36 résultats également probables. Six d'entre eux affichent un 4 sur le premier dé : (4,1), (4,2), (4,3), (4,4), (4,5), (4,6). Ainsi, P(premier dé = 4) = 6/36 = 1/6. Veuillez noter que nous n'avons imposé aucune condition concernant le deuxième dé. Nous avons simplement compté tous les résultats où le premier dé est un 4.

Voici un autre exemple classique. En tirant une carte d'un jeu standard de 52 cartes, quelle est la probabilité de tirer un cœur, quelle que soit sa valeur ? Il y a 13 cœurs et 52 cartes au total, donc P(Cœur) = 13/52 = 1/4. Cette probabilité marginale est calculée pour toutes les valeurs (de l'as au roi), ce qui vous donne la probabilité inconditionnelle de la couleur.

Exemples concrets

Le dépistage médical constitue une application pratique convaincante. Supposons que vous analysiez la prévalence d'une maladie au sein d'une population. La probabilité marginale P(Maladie) représente le taux de base de la maladie avant la prise en compte des résultats des tests diagnostiques. Si 2 % de la population est atteinte de la maladie, P(maladie) = 0,02. Cette probabilité marginale est essentielle pour interpréter la précision du test. Un test avec une sensibilité de 95 % génère encore de nombreux faux positifs lorsque la maladie est rare.

Dans le domaine du marketing numérique, vous pourriez vous demander : Quelle est la probabilité qu'un utilisateur effectue une conversion, quelle que soit la source du trafic ? Si vous disposez de données sur les conversions provenant de la recherche organique, des publicités payantes, des réseaux sociaux et des e-mails, la probabilité marginale P(Conversion) s'additionne pour toutes les sources. Ce taux de conversion de référence vous aide à évaluer si certaines sources de trafic ont des performances supérieures ou inférieures à la moyenne.

De même, dans le domaine financier, vous pourriez calculer la probabilité marginale d'une baisse du marché, indépendamment des niveaux des taux d'intérêt. Cela vous donne le risque inconditionnel avant de prendre en compte les facteurs macroéconomiques.

Probabilité marginale en science des données et apprentissage automatique

Explorons comment la probabilité marginale apparaît tout au long du processus de science des données.

Analyse exploratoire des données (EDA)

Lorsque vous examinez un ensemble de données pour la première fois, le calcul des probabilités marginales vous aide à comprendre les taux d'événements de référence. Dans un ensemble de données de détection de fraude, P(Fraude) vous indique l'équilibre des classes avant que vous n'examiniez les caractéristiques. Cela permet de déterminer immédiatement si vous êtes confronté à un problème de déséquilibre grave, où la fraude ne concerne que 0,1 % des transactions.

Les distributions marginales pour les caractéristiques individuelles orientent également votre analyse. Si vous élaborez un modèle pour prédire le taux de désabonnement des clients, je vous recommande d'examiner séparément P(Désabonnement), P(Client à forte valeur) et P(Activité récente). Cela vous fournit un contexte avant d'examiner leurs relations communes.

Modélisation prédictive

Les classificateurs naïfs de Bayes s'appuient explicitement sur les probabilités marginales en tant que priors de classe. Lorsqu'on classe un document comme spam ou non spam, P(Spam) correspond à votre conviction préalable avant d'avoir vu les mots contenus dans le document. L'algorithme met ensuite à jour cette probabilité marginale en fonction des probabilités conditionnelles des caractéristiques.

Les distributions marginales des caractéristiques sont également importantes dans l'ingénierie des caractéristiques et le diagnostic des modèles. Si la distribution marginale d'une caractéristique est fortement asymétrique, vous pouvez appliquer des transformations telles que la mise à l'échelle logarithmique ou la transformation de Box-Cox afin de la rendre plus symétrique. 

Les changements entre les ensembles de données sont tout aussi importants. Par exemple, si votre ensemble d'entraînement a P(Classe A)=0,9 mais que votre ensemble de test a P(Classe A)=0,5, vos probabilités prédites et vos mesures de performance peuvent considérablement varier, et vous pourriez avoir besoin d'un seuil de décision différent. Cela se produit parce que le modèle a été formé avec un taux de base, mais qu'il est évalué avec un autre.

Vérifier les distributions marginales avant l'entraînement vous permet de détecter ces problèmes à un stade précoce et de déterminer si vous avez besoin d'un rééchantillonnage, de différents indicateurs d'évaluation, d'un recalibrage ou de modèles distincts pour différents segments de données.

Risque et prise de décision

Les calculs de valeur attendue nécessitent des probabilités marginales. Si vous envisagez de lancer un produit, vous avez besoin de P(Succès) comme probabilité marginale de succès dans toutes les conditions de marché possibles. Multipliez ce résultat par le gain en cas de réussite, ajoutez-le à P(échec) multiplié par le coût de l'échec, et vous obtiendrez votre valeur attendue.

Modélisation probabiliste

Dans les réseaux bayésiens et les modèles graphiques, les nœuds représentent des variables associées à des distributions de probabilité conditionnelles. Les distributions marginales sont obtenues par inférence en propageant les probabilités à travers la structure du réseau ou en observant les preuves et en actualisant les croyances. Les méthodes d'échantillonnage telles que la méthode de Markov Chain Monte Carlo permettent d'approximer ces marginales lorsque le calcul exact devient difficile. Notre cours sur la modélisation bayésienne avec RJAGS présente ces méthodes en pratique.

Ce que les gens comprennent mal à propos de la probabilité marginale

Voici les erreurs qui peuvent dérouter même les praticiens expérimentés.

Confusion entre probabilité marginale et probabilité conditionnelle

Il s'agit probablement de l'erreur la plus courante, et elle est étonnamment facile à commettre. Veuillez imaginer que vous effectuez un test médical avec une sensibilité de 95 % et une spécificité de 90 %. Votre test est positif. La plupart des personnes pensent immédiatement : Le test détecte 95 % des cas, donc il est probable que je sois atteint de la maladie.

Cependant, ce raisonnement omet une information essentielle : quelle est la prévalence de cette maladie ? Si seulement 1 % des personnes sont atteintes (probabilité marginale), alors lorsque vous testez 10 000 personnes, vous obtiendrez environ 95 vrais positifs, mais 990 faux positifs. Cela signifie que la plupart des résultats positifs sont des alertes non fondées. Votre probabilité réelle après un test positif n'est que d'environ 9 %, et non de 95 %.

La confusion provient du fait que les gens se concentrent sur la sensibilité du test (95 %) et oublient le taux de référence (prévalence de 1 %). La probabilité marginale P(Maladie) = 0,01 et la probabilité conditionnelle P(Maladie | Test positif) = 0,09 sont des quantités complètement différentes, mais notre intuition nous incite à les traiter de la même manière.

Ignorer les marginaux lors de l'interprétation des conditionnels

Même lorsque les individus distinguent correctement les probabilités marginales des probabilités conditionnelles, ils ont tendance à ignorer les probabilités marginales lorsqu'ils interprètent les probabilités conditionnelles. Vous pourriez voir un titre d'actualité : Une étude révèle que 80 % des entrepreneurs qui ont réussi ont démarré leur activité avant l'âge de 30 ans. Cela donne P(A commencé avant 30 ans | Entrepreneur prospère) = 0,8. Cependant, sans connaître la probabilité P(Commencé avant 30 ans) pour tous les entrepreneurs, il est impossible de déterminer si le fait de commencer jeune est réellement un indicateur de réussite.

Cela conduit à une prise de décision inappropriée. Si 90 % des entrepreneurs se lancent avant l'âge de 30 ans, cela signifie que les entrepreneurs qui réussissent ne se lancent pas à un âge particulièrement jeune. Ils suivent simplement le modèle général. La probabilité conditionnelle n'a que peu de sens sans la base marginale de comparaison.

Erreur du taux de base

L'erreur du taux de base survient lorsque les individus accordent une importance excessive aux preuves conditionnelles tout en négligeant les probabilités marginales (taux de base).

Voici un exemple courant en science des données : Vous développez un classificateur binaire sur un ensemble de données déséquilibré. La classe positive (ce que vous essayez de prédire) n'apparaît que dans 5 % de vos données. Vous construisez un modèle et atteignez une précision de 95 %. Cela semble formidable, n'est-ce pas ?

Pas vraiment. Si vous construisiez un modèle « simpliste » qui prédit systématiquement la classe négative, il obtiendrait également une précision de 95 % (car 95 % des données sont négatives). Votre modèle sophistiqué n'est pas vraiment plus performant que de toujours répondre « non ».

L'erreur consiste à examiner le chiffre de 95 % de précision de manière isolée, sans tenir compte du taux de base (5 % de classe positive). Lorsque les classes sont déséquilibrées, la précision devient un indicateur trompeur. Il est nécessaire de vérifier la précision, le rappel ou le score F1 afin de déterminer si votre modèle a effectivement appris quelque chose d'utile.

Comprendre les marges vous aide à choisir les bons indicateurs d'évaluation pour les problèmes déséquilibrés.

Sujets avancés et extensions

Dans les modèles à haute dimension comportant des dizaines ou des centaines de variables, il est souvent impossible de calculer avec exactitude les distributions marginales. Le nombre de combinaisons possibles augmente rapidement, et les sommes ou intégrales requises deviennent difficiles à traiter.

Pour y parvenir, les praticiens utilisent des méthodes d'inférence approximative :

• Les méthodes d'échantillonnage (telles que la méthode de Markov Chain Monte Carlo, MCMC) génèrent de nombreux échantillons à partir de la distribution du modèle. Vous pouvez ensuite estimer les probabilités marginales en examinant la fréquence à laquelle les événements se produisent dans ces échantillons.

• L'inférence variationnelle adopte une approche différente : elle remplace une distribution difficile à calculer par une distribution plus simple et l'optimise pour qu'elle soit aussi proche que possible, ce qui accélère souvent les estimations marginales dans les modèles de grande taille.

Des outils modernes tels que Python ( scipy.stats ) pour les distributions de probabilité, pandas pour les tableaux de contingence, et R ( table() et dplyr ) pour les marginales empiriques facilitent ces calculs. Pour les données stockées dans une base de données, la clause SQL « GROUP BY » calcule efficacement les marginales empiriques à partir de grands ensembles de données.

Conclusion

Avant de pouvoir comprendre la relation entre les variables, évaluer les preuves conditionnelles ou construire des modèles bayésiens, il est nécessaire de saisir la probabilité inconditionnelle des événements individuels. C'est la base qui rend tout le reste interprétable.

Lorsque vous interprétez incorrectement les marges, vous risquez de commettre des erreurs d'analyse : confondre les taux de référence avec les probabilités conditionnelles, tomber dans le piège du taux de base ou élaborer des modèles qui ne surpassent pas les références naïves. Maîtrisez les marges, et vous comprendrez comment la probabilité conditionnelle les affine, comment le théorème de Bayes les actualise à l'aide de preuves, et comment les modèles d'apprentissage automatique tirent des enseignements des modèles qu'elles révèlent.