Probabilidade marginal: Teoria, exemplos e aplicações

Você tá analisando o comportamento dos clientes de uma plataforma de comércio eletrônico, e seu gerente pergunta: Qual é a chance de um cliente cancelar, não importa o motivo?

Essa pergunta aborda algo mais específico do que você imagina. Você não está perguntando sobre a rotatividade em uma categoria específica de produtos, nem sobre a rotatividade combinada com um método de pagamento. Você está perguntando sobre a probabilidade básica de um único evento: perda de clientes, ponto final.

Isso é probabilidade marginal e é fundamental para a maioria dos cálculos de probabilidade que você vai encontrar na ciência de dados.

O que é probabilidade marginal?

Como eu falei, a probabilidade marginal é a chance de um único evento acontecer, sem levar em conta outras variáveis ou eventos. É chamado de “marginal” porque, quando você coloca as probabilidades conjuntas numa tabela, essas probabilidades de eventos únicos aparecem nas margens (os totais das linhas e colunas).

A notação é simples. Para um evento discreto A, escrevemos P(A). A probabilidade marginal geralmente vem da probabilidade conjunta. Se B é uma variável aleatória discreta e você sabe a probabilidade conjunta de A acontecer com cada valor de B, dá pra achar a probabilidade marginal somando: P(A) =_Σb P(A, B=b), onde você soma todos os valores possíveis b que B pode assumir. A probabilidade marginal é o que sobra quando você soma ou integra todas as outras variáveis.

Pra entender esse conceito completamente, você vai precisar de alguns termos básicos. O espaço amostral é o conjunto de todos os resultados possíveis. Um evento é qualquer subconjunto do espaço amostral. A probabilidade conjunta P(A ∩ B) mede a chance de dois eventos acontecerem juntos, enquanto a probabilidade condicional P(A|B) mede a chance de A , já que B aconteceu.

Recomendo dar uma olhada na nossa Folha de Referência Rápida sobre Regras de Probabilidade para uma referência rápida e qobre essas relações. A probabilidade marginal está no centro desse ecossistema de probabilidades. É o denominador nos cálculos de probabilidade condicional e o alicerce do Teorema de Bayes.

Probabilidade marginal a partir de tabelas e distribuições

Vamos ver como você realmente calcula a probabilidade marginal a partir de diferentes estruturas de dados. A abordagem depende se você está trabalhando com variáveis discretas ou contínuas.

Caso discreto (tabelas de contingência)

Quando a gente trabalha com dados categóricos, as probabilidades marginais aparecem naturalmente nas tabelas de contingência. Imagina que você está analisando o comportamento de compra dos clientes em diferentes categorias de produtos (eletrônicos, roupas, livros) e regiões (norte, sul, leste, oeste). Cada célula tem a probabilidade conjunta de uma combinação de categoria-região. Os totais das linhas mostram a probabilidade marginal para cada categoria de produto (P(Eletrônicos), P(Roupas), P(Livros)), não importa a região. Os totais das colunas mostram as probabilidades marginais para cada região.

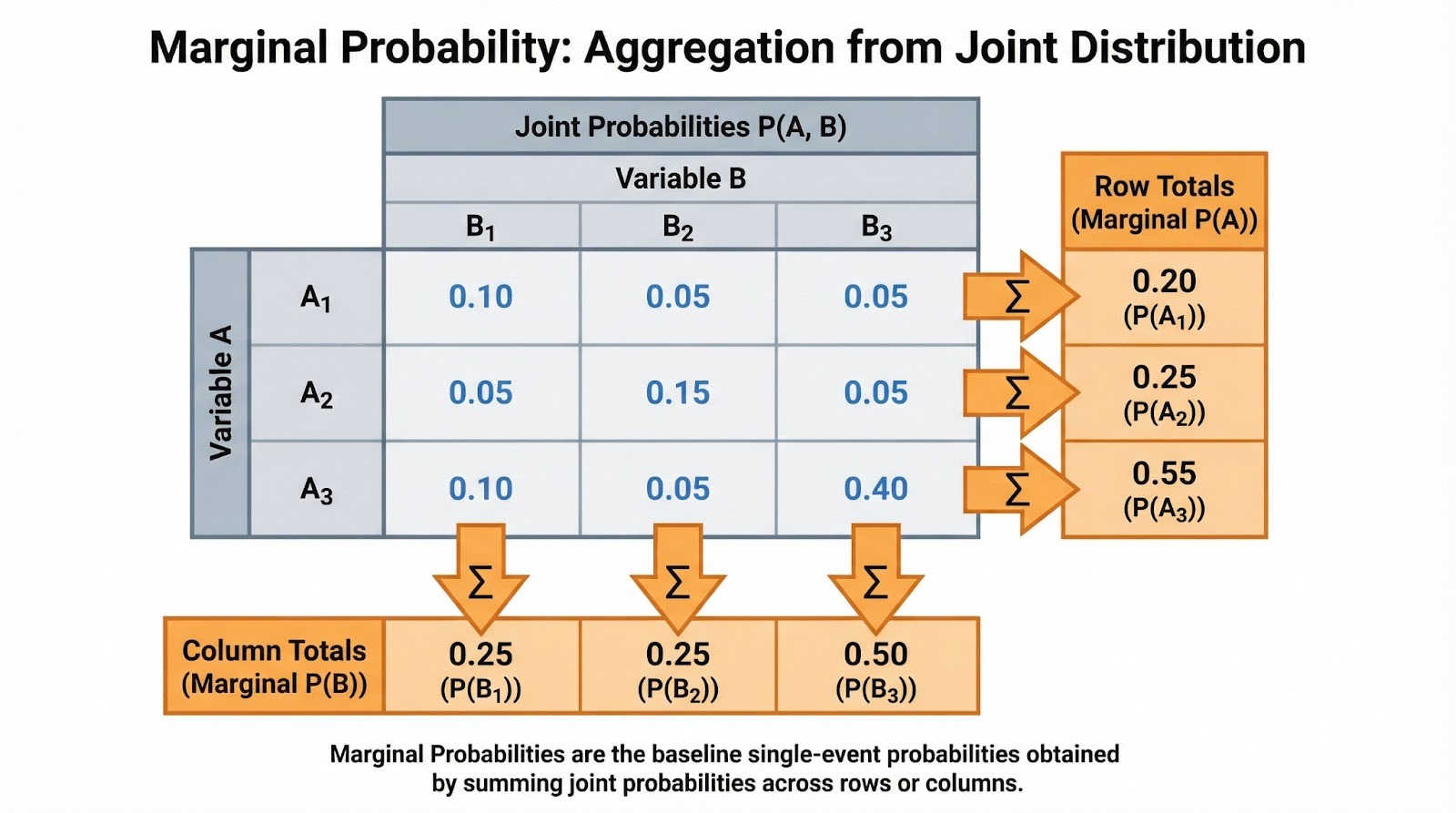
Somando probabilidades conjuntas para encontrar probabilidades marginais. Imagem do autor.

Você vai ver isso com frequência como frequências normalizadas. Se 500 dos 2.000 clientes compraram eletrônicos, a probabilidade marginal P(Eletrônicos) = 500/2.000 = 0,25. Essa é a taxa básica antes de considerar outros fatores. Quando você estiver fazendo uma análise exploratória de dados, eu sugiro calcular primeiro essas marginais. Eles ajudam você a entender a estrutura básica dos seus dados antes de mergulhar nas relações condicionais.

Caso contínuo

Para variáveis aleatórias contínuas, a probabilidade marginal vira uma função de densidade de probabilidade marginal (PDF). Se você tem duas variáveis contínuas X e Y com uma PDF conjunta, a PDF marginal de X é encontrada integrando todos os valores de Y.

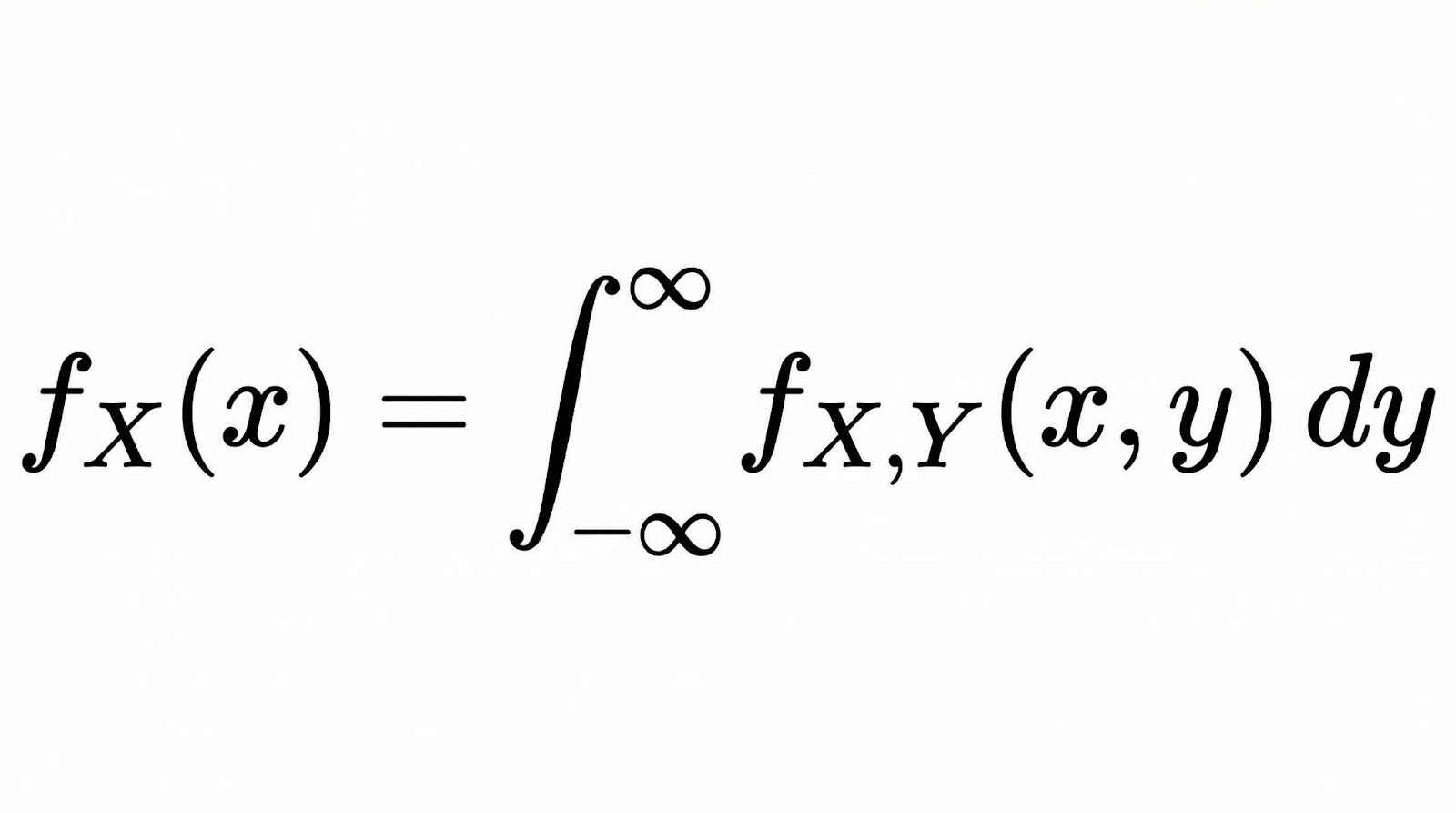
Em termos conceituais, a integração aqui faz a mesma coisa que a soma no caso discreto. Ele “reduz” a distribuição conjunta a uma única dimensão, levando em conta todas as possibilidades da outra variável.

Pense nisso como cortar uma superfície 3D (a distribuição conjunta) e observar a área sob a curva ao longo de um eixo. Nossos Fundamentos da Análise de Dados Bayesiana em R aborda esses conceitos em profundidade ao trabalhar com distribuições contínuas.

Relação entre probabilidade marginal, conjunta e condicional

Vamos ver como a probabilidade marginal se conecta com os outros tipos de probabilidade com os quais você vai trabalhar sempre.

Esses três tipos de probabilidade formam um sistema conectado, e a probabilidade marginal é frequentemente o elemento que os mantém unidos. De probabilidade conjunta, você obtém marginais somando ou integrando. A partir das probabilidades conjuntas e marginais, você calcula as condicionais usando P(A|B) = P(A ∩ B) / P(B). Observe que a probabilidade marginal P(B) é o denominador. Ele normaliza a probabilidade conjunta para te dar a condicional.

Isso é importante na prática porque, quando você está interpretando probabilidades condicionais, você precisa da marginal como contexto. Uma probabilidade de 90% de doença com resultados positivos nos testes parece alarmante, mas se a probabilidade marginal de doença for de apenas 1%, a probabilidade real após um teste positivo pode ser muito menor do que você imagina.

Isso aparece em todo lugar na inferência bayesiana. Uma prioridade é o que você acha sobre um parâmetro antes de ver qualquer dado. A probabilidade marginal (também chamada de evidência), P(Dados), é o termo de normalização no teorema de Bayes que transforma “a priori × probabilidade” em uma probabilidade posterior adequada. Nossa Análise de Dados Bayesiana em Python explora essas conexões por meio de exercícios práticos de modelagem.

Exemplos práticos de probabilidade marginal

Vamos resolver problemas clássicos de probabilidade e cenários do mundo real.

Exemplos clássicos

Vamos começar com os dados. Se você jogar dois dados, qual é a chance do primeiro dado mostrar um 4, não importa o que o segundo dado mostre?

O espaço amostral tem 36 resultados igualmente prováveis. Seis deles têm um 4 no primeiro dado: (4,1), (4,2), (4,3), (4,4), (4,5), (4,6). Então, P(Primeiro dado = 4) = 6/36 = 1/6. Repara que não colocamos nenhuma condição sobre o segundo dado. A gente só contou todos os resultados em que o primeiro dado é 4.

Aqui está outro exemplo clássico. Pegando uma carta de um baralho padrão de 52 cartas, qual é a chance de tirar um coração, sem importar o valor? Tem 13 copas e 52 cartas no total, então P(Copa) = 13/52 = 1/4. Essa probabilidade marginal é somada em todas as classificações (do Ás ao Rei), dando a probabilidade incondicional do naipe.

Exemplos reais

A triagem médica oferece uma aplicação prática super interessante. Imagina que você está analisando a prevalência de uma doença em uma população. A probabilidade marginal P(Doença) mostra a taxa de doença de base antes de pensar nos resultados dos testes diagnósticos. Se 2% da população tem a doença, P(Doença) = 0,02. Essa probabilidade marginal é essencial para entender a precisão do teste. Um teste com 95% de sensibilidade ainda dá muitos falsos positivos quando a doença é rara.

No marketing digital, você pode perguntar: Qual é a chance de um usuário converter, não importa de onde veio o tráfego? Se você tem dados sobre conversões de pesquisa orgânica, anúncios pagos, mídias sociais e e-mail, a probabilidade marginal P(Conversão) soma todas as fontes. Essa taxa de conversão de referência ajuda você a avaliar se fontes de tráfego específicas têm desempenho acima ou abaixo da média.

Da mesma forma, em finanças, você pode calcular a probabilidade marginal de uma queda no mercado, independentemente dos níveis das taxas de juros. Isso dá a você o risco incondicional antes de adicionar fatores macroeconômicos.

Probabilidade marginal em ciência de dados e machine learning

Vamos ver como a probabilidade marginal aparece em todo o fluxo de trabalho da ciência de dados.

Análise exploratória de dados (EDA)

Quando você vê um conjunto de dados pela primeira vez, calcular as probabilidades marginais ajuda a entender as taxas de eventos de referência. Num conjunto de dados de detecção de fraudes, P(Fraude) mostra o equilíbrio das classes antes de você examinar qualquer característica. Isso mostra logo se você está lidando com um problema bem desequilibrado, onde só 0,1% das transações têm fraude.

As distribuições marginais para características individuais também ajudam na sua análise. Se você está criando um modelo para prever a rotatividade de clientes, recomendo examinar P(Rotatividade), P(Cliente de alto valor) e P(Atividade recente) separadamente. Isso dá um contexto antes de você explorar as relações entre eles.

Modelagem preditiva

Os classificadores Naive Bayes dependem explicitamente das probabilidades marginais como priores de classe. Ao classificar um documento como spam ou não spam, P(Spam) é a sua crença prévia antes de ver qualquer palavra no documento. O algoritmo atualiza essa probabilidade marginal com base nas probabilidades condicionais das características.

As distribuições marginais das características também são importantes na engenharia de características e no diagnóstico de modelos. Se a distribuição marginal de uma característica estiver muito distorcida, você pode usar transformações como escala logarítmica ou Box-Cox para deixá-la mais simétrica. 

As mudanças entre conjuntos de dados são igualmente importantes. Por exemplo, se o seu conjunto de treinamento tiver P(Classe A)=0,9, mas o seu conjunto de teste tiver P(Classe A)=0,5, suas probabilidades previstas e métricas de desempenho podem mudar bastante, e você pode precisar de um limite de decisão diferente. Isso rola porque o modelo foi treinado com uma taxa básica, mas tá sendo avaliado com outra.

Verificar as distribuições marginais antes do treinamento ajuda a detectar esses problemas logo no início e decidir se você precisa refazer a amostragem, usar métricas de avaliação diferentes, recalibrar ou usar modelos separados para diferentes segmentos de dados.

Risco e tomada de decisão

Os cálculos do valor esperado precisam de probabilidades marginais. Se você está pensando em lançar um produto, precisa da P(Sucesso) como a probabilidade marginal de sucesso em todas as condições possíveis do mercado. Multiplique isso pelo retorno do sucesso, some ao P(Fracasso) vezes o custo do fracasso e você terá o seu valor esperado.

Modelagem probabilística

Em redes bayesianas e modelos gráficos, os nós representam variáveis com distribuições de probabilidade condicional associadas. As distribuições marginais são obtidas por meio de inferência, propagando probabilidades pela estrutura da rede ou observando evidências e atualizando crenças. Métodos de amostragem como Markov Chain Monte Carlo aproximam essas marginais quando o cálculo exato se torna intratável. Nosso Modelagem Bayesiana com RJAGS mostra esses métodos na prática.

O que as pessoas entendem errado sobre probabilidade marginal

Aqui estão os erros que até os profissionais experientes cometem.

Confundindo probabilidade marginal com condicional

Esse é provavelmente o erro mais comum e, surpreendentemente, é muito fácil de cometer. Imagina que você faz um exame médico com 95% de sensibilidade e 90% de especificidade. Você testou positivo. A maioria das pessoas pensa logo: O teste detecta 95% dos casos, então provavelmente eu tenho a doença.

Mas esse raciocínio deixa de lado uma informação importante: qual é a frequência dessa doença? Se só 1% das pessoas tiverem isso (a probabilidade marginal), então, quando você testar 10.000 pessoas, vai ter cerca de 95 resultados positivos verdadeiros, mas 990 resultados positivos falsos. Isso quer dizer que a maioria dos resultados positivos são alarmes falsos. A probabilidade real depois de dar positivo é só de cerca de 9%, não 95%.

A confusão rola porque as pessoas se concentram na sensibilidade do teste (95%) e esquecem da taxa de referência (prevalência de 1%). A probabilidade marginal P(Doença) = 0,01 e a probabilidade condicional P(Doença | Teste positivo) = 0,09 são coisas completamente diferentes, mas a nossa intuição quer tratá-las da mesma forma.

Ignorando marginais ao interpretar condicionais

Mesmo quando as pessoas distinguem corretamente as probabilidades marginais das condicionais, muitas vezes ignoram as marginais ao interpretar as condicionais. Você pode ver uma manchete de notícias: Um estudo descobriu que 80% dos empreendedores de sucesso começaram antes dos 30 anos. Isso é P(Começou antes dos 30 | Empreendedor de sucesso) = 0,8. Mas sem saber o P(Começou antes dos 30) para todos os empreendedores, não dá pra avaliar se começar jovem realmente é um indicador de sucesso.

Isso leva a decisões erradas. Se 90% de todos os empreendedores começam antes dos 30 anos, então os empreendedores de sucesso não começam jovens em taxas incomuns. Eles estão apenas seguindo o padrão geral. A probabilidade condicional não significa muita coisa sem uma linha de base marginal para comparar.

Falácia da taxa básica

A falácia da taxa básica rola quando as pessoas dão muito peso a evidências condicionais e ignoram as probabilidades marginais (taxas básicas).

Aqui vai um exemplo comum de ciência de dados: Você está criando um classificador binário em um conjunto de dados desequilibrado. A classe positiva (o que você está tentando prever) aparece em apenas 5% dos seus dados. Você cria um modelo e consegue 95% de precisão. Parece ótimo, né?

Na verdade, não. Se você criasse um modelo “burro” que só previsse a classe negativa todas as vezes, ele também teria 95% de precisão (porque 95% dos dados são negativos). Seu modelo sofisticado não está, na verdade, fazendo muito melhor do que sempre adivinhar “não”.

O erro é olhar só para o número de 95% de precisão sem pensar na taxa base (5% de classe positiva). Quando as classes estão desequilibradas, a precisão vira uma métrica enganosa. Você precisa conferir a precisão, a recuperação ou a pontuação F1 pra ver se o seu modelo realmente aprendeu algo útil.

Entender os marginais ajuda você a escolher as métricas de avaliação certas para problemas desequilibrados.

Tópicos avançados e extensões

Em modelos de alta dimensão com dezenas ou centenas de variáveis, muitas vezes é impossível calcular exatamente as distribuições marginais. O número de combinações possíveis cresce rapidamente, e as somas ou integrais necessárias tornam-se intratáveis.

Para lidar com isso, os profissionais usam métodos de inferência aproximada:

• Os métodos de amostragem (como Markov Chain Monte Carlo, MCMC) geram muitas amostras a partir da distribuição do modelo. Você pode então estimar as probabilidades marginais observando a frequência com que os eventos ocorrem nessas amostras.

• A inferência variacional usa uma abordagem diferente: ela troca uma distribuição difícil de calcular por uma mais simples e otimiza-a para ficar o mais próxima possível, tornando as estimativas marginais frequentemente mais rápidas em modelos grandes.

Ferramentas modernas como o Python ( scipy.stats ) para distribuições de probabilidade, o pandas para tabelas de contingência e o R ( table() e dplyr ) para marginais empíricas tornam esses cálculos acessíveis. Para dados armazenados em bancos de dados, a cláusula SQL GROUP BY calcula marginais empíricas de forma eficiente a partir de grandes conjuntos de dados.

Conclusão

Antes de entender a relação entre variáveis, avaliar evidências condicionais ou construir modelos bayesianos, você precisa entender a probabilidade incondicional de eventos individuais. É a linha de base que torna tudo o resto interpretável.

Quando você não entende direito os marginais, fica suscetível a erros analíticos: confundir taxas de referência com probabilidades condicionais, cair na falácia da taxa de referência ou criar modelos que não superam as referências ingênuas. Entenda bem as marginais e você vai ver como a probabilidade condicional as refina, como o Teorema de Bayes as atualiza com evidências e como os modelos de machine learning aprendem com os padrões que elas mostram.