Randwahrscheinlichkeit: Theorie, Beispiele und Anwendungen

Du analysierst das Kundenverhalten für eine E-Commerce-Plattform, und dein Chef fragt dich: Wie hoch ist die Wahrscheinlichkeit, dass ein Kunde weggeht, egal warum?

Diese Frage geht auf etwas Konkreteres ein, als du vielleicht denkst. Du fragst nicht nach derAbwanderungs , wenn es um eine bestimmte Produktkategorie geht, oder nach der Abwanderung in Verbindung mit der Zahlungsmethode „ “. Du fragst nach der Basiswahrscheinlichkeit eines einzelnen Ereignisses: Kundenabwanderung, Punkt.

Das ist die Randwahrscheinlichkeit, und sie ist die Grundlage für die meisten Wahrscheinlichkeitsberechnungen, die du in der Datenwissenschaft sehen wirst.

Was ist marginale Wahrscheinlichkeit?

Wie ich schon gesagt habe, ist die Randwahrscheinlichkeit die Wahrscheinlichkeit, dass ein einzelnes Ereignis eintritt, ohne auf andere Variablen oder Ereignisse zu achten. Es heißt „marginal“, weil diese Wahrscheinlichkeiten für einzelne Ereignisse in den Randbereichen (den Zeilen- und Spaltensummen) einer Tabelle mit den gemeinsamen Wahrscheinlichkeiten auftauchen.

Die Notation ist einfach. Für ein diskretes Ereignis A schreiben wir P(A). Die Randwahrscheinlichkeit ergibt sich oft aus der gemeinsamen Wahrscheinlichkeit. Wenn B eine diskrete Zufallsvariable ist und du die gemeinsame Wahrscheinlichkeit kennst, mit der A bei jedem Wert von B auftritt, kannst du die Randwahrscheinlichkeit durch Summieren ermitteln: P(A) =_Σb P(A, B=b), wobei du alle möglichen Werte b summierst, die B annehmen kann. Die Randwahrscheinlichkeit ist das, was übrig bleibt, wenn man alle anderen Variablen „zusammenfasst“ oder „integriert“.

Um dieses Konzept richtig zu verstehen, brauchst du ein paar grundlegende Begriffe. Der Ereignisraum ist die Menge aller möglichen Ergebnisse. Ein Ereignis ist einfach ein Teilbereich des Ereignisraums. Die gemeinsame Wahrscheinlichkeit P(A ∩ B) zeigt an, wie wahrscheinlich es ist, dass zwei Ereignisse zusammen auftreten, während die bedingte Wahrscheinlichkeit P(A|B) angibt, wie wahrscheinlich es ist, dass A auftritt, wenn B passiert ist.

Ich empfehle dir, dir unser Spickzettel zur Einführung in die Wahrscheinlichkeitsregeln anzuschauen, um einen schnellen Überblick über diese Zusammenhänge zu bekommen. Die Randwahrscheinlichkeit ist das Herzstück dieses Wahrscheinlichkeits-Ökosystems. Es ist der Nenner bei der Berechnung bedingter Wahrscheinlichkeiten und der Baustein für das Bayes-Theorem.

Randwahrscheinlichkeit aus Tabellen und Verteilungen

Schauen wir mal, wie man die Randwahrscheinlichkeit aus verschiedenen Datenstrukturen berechnet. Der Ansatz hängt davon ab, ob du mit diskreten oder kontinuierlichen Variablen arbeitest.

Diskreter Fall (Kontingenz-Tabellen)

Bei der Arbeit mit kategorialen Daten tauchen in Kontingenztabellen ganz natürlich Randwahrscheinlichkeiten auf. Angenommen, du analysierst das Kaufverhalten von Kunden über Produktkategorien (Elektronik, Kleidung, Bücher) und Regionen (Nord, Süd, Ost, West) hinweg. Jede Zelle zeigt die gemeinsame Wahrscheinlichkeit einer Kategorie-Region-Kombination. Die Zeilensummen zeigen dir die Randwahrscheinlichkeit für jede Produktkategorie (P(Elektronik), P(Bekleidung), P(Bücher)), egal in welcher Region. Die Spaltensummen zeigen dir die Randwahrscheinlichkeiten für jede Region.

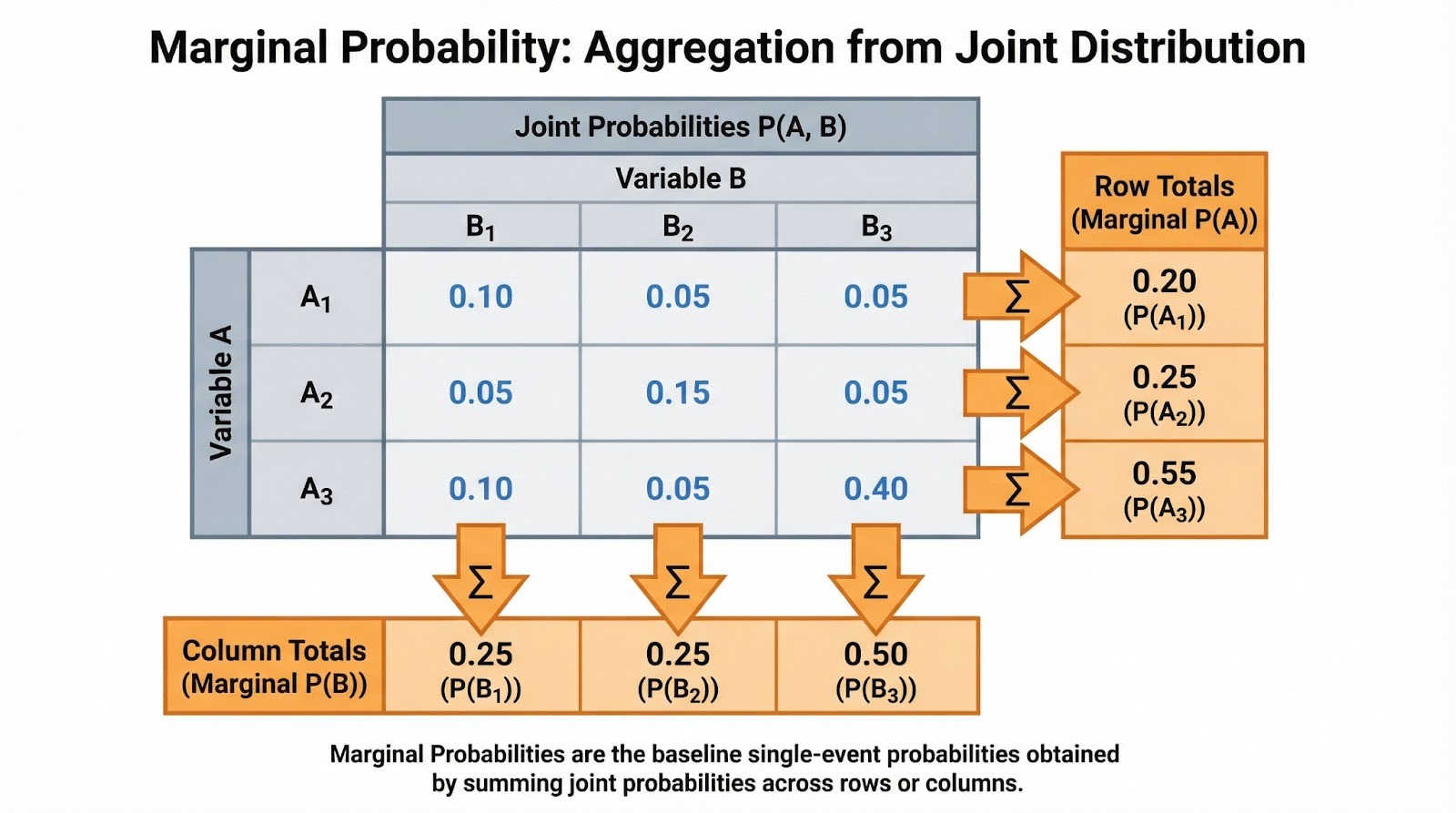
Addier die gemeinsamen Wahrscheinlichkeiten, um die Randwahrscheinlichkeiten zu finden. Bild vom Autor.

Du wirst diese oft als normalisierte Frequenzen sehen. Wenn 500 von 2.000 Kunden Elektronikartikel gekauft haben, ist die Randwahrscheinlichkeit P(Elektronik) = 500/2.000 = 0,25. Das ist der Basiszinssatz, bevor man andere Sachen mit einbezieht. Wenn du eine explorative Datenanalyse machst, würde ich vorschlagen, zuerst diese Randwerte zu berechnen. Sie helfen dir, die grundlegende Struktur deiner Daten zu verstehen, bevor du dich mit bedingten Beziehungen beschäftigst.

Durchgehender Fall

Bei stetigen Zufallsvariablen wird die Randwahrscheinlichkeit zu einer Randwahrscheinlichkeitsdichtefunktion (PDF). Wenn du zwei stetige Variablen X und Y mit einer gemeinsamen Wahrscheinlichkeitsdichtefunktion (PDF) hast, bekommst du die marginale Wahrscheinlichkeitsdichtefunktion von X, indem du über alle Werte von Y integrierst.

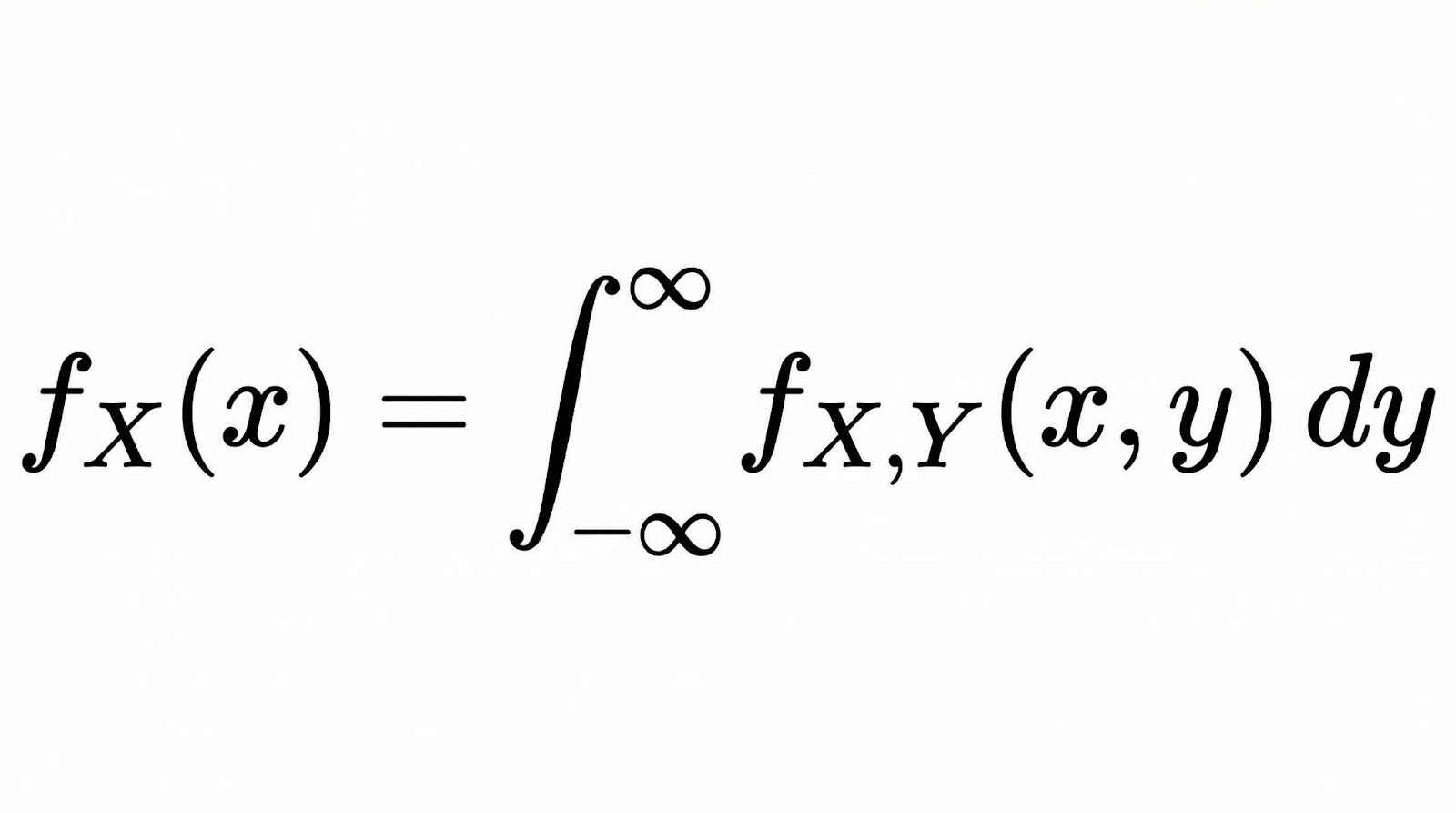
Im Grunde macht die Integration hier dasselbe wie die Summation im diskreten Fall. Es „reduziert“ die gemeinsame Verteilung auf eine einzige Dimension, indem es alle Möglichkeiten der anderen Variablen berücksichtigt.

Stell dir vor, du schneidest durch eine 3D-Oberfläche (die Gelenkverteilung) und schaust dir den Bereich unter der Kurve entlang einer Achse an. Unsere Grundlagen der Bayesschen Datenanalyse in R geht ausführlich auf diese Konzepte ein, wenn es um die Arbeit mit kontinuierlichen Verteilungen geht.

Zusammenhang zwischen Rand-, Gemeinsamer und Bedingter Wahrscheinlichkeit

Schauen wir mal, wie die Randwahrscheinlichkeit mit den anderen Wahrscheinlichkeitstypen zusammenhängt, mit denen du regelmäßig zu tun hast.

Diese drei Arten von Wahrscheinlichkeit bilden ein zusammenhängendes System, und die Randwahrscheinlichkeit ist oft das, was sie zusammenhält. Von gemeinsamen Wahrscheinlichkeitbekommst du Randverteilungen, indem du sie zusammenzählst oder integrierst. Aus den gemeinsamen und marginalen Wahrscheinlichkeiten berechnest du die bedingten Wahrscheinlichkeiten mit P(A|B) = P(A ∩ B) / P(B). Beachte, dass die Randwahrscheinlichkeit P(B) der Nenner ist. Es normalisiert die gemeinsame Wahrscheinlichkeit, um dir die bedingte Wahrscheinlichkeit zu geben.

Das ist in der Praxis wichtig, weil es bei der Interpretation von Bedingte Wahrscheinlichkeiten, brauchst du die Randwahrscheinlichkeit als Kontext. Eine 90-prozentige Wahrscheinlichkeit für eine Krankheit bei positiven Testergebnissen klingt echt beunruhigend, aber wenn die Wahrscheinlichkeit für die Krankheit nur 1 % beträgt, könnte die tatsächliche Wahrscheinlichkeit nach einem positiven Test viel geringer sein, als du denkst.

Das taucht überall in der Bayes'schen Inferenz auf. Eine Priorität ist deine Meinung zu einem Parameter, bevor du irgendwelche Daten siehst. Die marginale Wahrscheinlichkeit (auch als Evidenz bezeichnet), P(Daten), ist der Normalisierungsterm im Bayes-Theorem, der „A-priori-Wahrscheinlichkeit × Wahrscheinlichkeit“ in eine korrekte A-posteriori-Wahrscheinlichkeit umwandelt. Unsere Bayesianische Datenanalyse in Python schaut sich diese Zusammenhänge in praktischen Modellierungsübungen an.

Beispiele für Randwahrscheinlichkeit

Lass uns sowohl klassische Wahrscheinlichkeitsprobleme als auch reale Szenarien durcharbeiten.

Klassische Beispiele

Fangen wir mit Würfeln an. Wenn du zwei Würfel wirfst, wie hoch ist die Wahrscheinlichkeit, dass der erste Würfel eine 4 zeigt, egal was der zweite Würfel anzeigt?

Der Ereignisraum hat 36 gleichwahrscheinliche Ergebnisse. Sechs davon haben eine 4 auf dem ersten Würfel: (4,1), (4,2), (4,3), (4,4), (4,5), (4,6). Also ist P(Erster Würfel = 4) = 6/36 = 1/6. Beachte, dass wir keine Bedingungen für den zweiten Würfel festgelegt haben. Wir haben einfach alle Ergebnisse gezählt, bei denen der erste Würfel eine 4 zeigt.

Hier ist noch ein klassisches Beispiel. Wenn du aus einem normalen Kartenspiel mit 52 Karten ziehst, wie hoch ist die Chance, dass du eine Herzkarte ziehst, egal welcher Wert? Es gibt 13 Herzen und insgesamt 52 Karten, also ist P(Herz) = 13/52 = 1/4. Diese Randwahrscheinlichkeit wird über alle Ränge (Ass bis König) zusammengefasst und ergibt die bedingungslose Wahrscheinlichkeit der Farbe.

Beispiele aus der Praxis

Medizinische Vorsorgeuntersuchungen sind ein echtes Beispiel dafür, wie das in der Praxis funktioniert. Angenommen, du analysierst die Krankheitsprävalenz in einer Population. Die Randwahrscheinlichkeit P(Krankheit) zeigt die Grunderkrankungsrate an, bevor man irgendwelche Diagnosetestergebnisse berücksichtigt. Wenn 2 % der Leute die Krankheit haben, dann ist P(Krankheit) = 0,02. Diese Randwahrscheinlichkeit ist echt wichtig, um die Testgenauigkeit richtig zu verstehen. Ein Test mit einer Sensitivität von 95 % liefert immer noch viele falsche positive Ergebnisse, wenn die Krankheit selten ist.

Im digitalen Marketing könntest du fragen: Wie hoch ist die Wahrscheinlichkeit, dass ein Nutzer konvertiert, egal woher er kommt? Wenn du Daten zu Conversions aus organischer Suche, bezahlten Anzeigen, sozialen Medien und E-Mails hast, addiert sich die marginale Wahrscheinlichkeit P(Conversion) über alle Quellen. Mit dieser Basis-Conversion-Rate kannst du einschätzen, ob bestimmte Traffic-Quellen über oder unter dem Durchschnitt abschneiden.

Ähnlich kannst du in der Finanzwelt die marginale Wahrscheinlichkeit eines Marktrückgangs unabhängig vom Zinsniveau berechnen. Das gibt dir das uneingeschränkte Risiko, bevor du makroökonomische Faktoren mit einbeziehst.

Marginalwahrscheinlichkeit in der Datenwissenschaft und im maschinellen Lernen

Schauen wir mal, wie die Randwahrscheinlichkeit im Datenwissenschafts-Workflow auftaucht.

Explorative Datenanalyse (EDA)

Wenn du zum ersten Mal mit einem Datensatz arbeitest, hilft dir die Berechnung der Randwahrscheinlichkeiten, die Basisereignisraten zu verstehen. In einem Datensatz zur Betrugserkennung gibt dir P(Betrug) Auskunft über die Klassenverteilung, bevor du irgendwelche Merkmale untersuchst. Das zeigt dir sofort, ob du es mit einem echt krassen Ungleichgewicht zu tun hast, bei dem nur 0,1 % der Transaktionen betrügerisch sind.

Randverteilungen für einzelne Merkmale helfen dir auch bei deiner Analyse. Wenn du ein Modell zur Vorhersage der Kundenabwanderung erstellst, würde ich empfehlen, P(Churn), P(High-value customer) und P(Recent activity) separat zu untersuchen. Das gibt dir einen Überblick, bevor du ihre gemeinsamen Beziehungen anschaust.

Vorhersagemodelle

Naive Bayes-Klassifikatoren nutzen explizit Randwahrscheinlichkeiten als Klassenvorverteilungen. Wenn du ein Dokument als Spam oder Nicht-Spam einstufst, ist P(Spam) deine Meinung, bevor du irgendwelche Wörter im Dokument siehst. Der Algorithmus aktualisiert dann diese Randwahrscheinlichkeit anhand der bedingten Merkmalswahrscheinlichkeiten.

Randmerkmalsverteilungen sind auch beim Feature Engineering und bei der Modelldiagnostik wichtig. Wenn die Randverteilung eines Merkmals stark verzerrt ist, kannst du Transformationen wie Log-Skalierung oder Box-Cox anwenden, um sie symmetrischer zu machen. 

Wechsel zwischen Datensätzen sind genauso wichtig. Wenn dein Trainingssatz zum Beispiel P(Klasse A)=0,9 hat, dein Testsatz aber P(Klasse A)=0,5, können sich deine vorhergesagten Wahrscheinlichkeiten und Leistungskennzahlen stark ändern, und du brauchst vielleicht einen anderen Entscheidungsschwellenwert. Das passiert, weil das Modell unter einer bestimmten Basisrate trainiert wurde, aber unter einer anderen bewertet wird.

Wenn du vor dem Training die Randverteilungen checkst, kannst du solche Probleme früh erkennen und entscheiden, ob du ein Resampling, andere Bewertungsmetriken, eine Neukalibrierung oder separate Modelle für verschiedene Datensegmente brauchst.

Risiko und Entscheidungsfindung

Für die Berechnung des erwarteten Werts braucht man Randwahrscheinlichkeiten. Wenn du überlegst, ob du ein Produkt auf den Markt bringen sollst, brauchst du P(Erfolg) als die marginale Erfolgswahrscheinlichkeit unter allen möglichen Marktbedingungen. Multipliziere das mit dem Gewinn bei Erfolg, addiere es zu P(Misserfolg) mal den Kosten des Misserfolgs, und du hast deinen erwarteten Wert.

Wahrscheinlichkeitsmodellierung

In Bayes'schen Netzwerken und grafischen Modellen zeigen Knoten Variablen mit zugehörigen bedingten Wahrscheinlichkeitsverteilungen an. Marginalverteilungen kriegt man durch Inferenz, indem man Wahrscheinlichkeiten durch die Netzwerkstruktur weitergibt oder indem man Beweise beobachtet und Überzeugungen aktualisiert. Sampling-Methoden wie Markov Chain Monte Carlo schätzen diese Randverteilungen, wenn eine exakte Berechnung zu kompliziert wird. Unser Bayesianische Modellierung mit RJAGS zeigt diese Methoden in der Praxis.

Was die Leute bei der Randwahrscheinlichkeit falsch verstehen

Hier sind die Fehler, die selbst erfahrene Leute manchmal machen.

Verwechslung von Randwahrscheinlichkeit und bedingter Wahrscheinlichkeit

Das ist wahrscheinlich der häufigste Fehler, und es ist echt leicht, ihn zu machen. Stell dir vor, du machst einen medizinischen Test mit einer Sensitivität von 95 % und einer Spezifität von 90 %. Dein Test ist positiv. Die meisten Leute denken sofort: Der Test findet 95 % der Fälle, also hab ich die Krankheit wahrscheinlich.

Aber diese Argumentation lässt eine wichtige Info außer Acht: Wie verbreitet ist die Krankheit überhaupt? Wenn nur 1 % der Leute das haben (die Randwahrscheinlichkeit), dann kriegst du bei einem Test von 10.000 Leuten etwa 95 echte positive Ergebnisse, aber 990 falsche positive Ergebnisse. Das heißt, die meisten positiven Ergebnisse sind Fehlalarme. Deine tatsächliche Wahrscheinlichkeit nach einem positiven Test liegt nur bei etwa 9 %, nicht bei 95 %.

Die Verwirrung kommt daher, dass die Leute sich auf die Sensitivität des Tests (95 %) konzentrieren und die Basisrate (1 % Prävalenz) vergessen. Die Randwahrscheinlichkeit P(Krankheit) = 0,01 und die bedingte Wahrscheinlichkeit P(Krankheit | positiver Test) = 0,09 sind total unterschiedliche Größen, aber intuitiv wollen wir sie gleich behandeln.

Marginale bei der Interpretation von Konditionalsätzen ignorieren

Selbst wenn Leute den Unterschied zwischen Rand- und Bedingungswahrscheinlichkeiten richtig verstehen, vergessen sie oft die Randwahrscheinlichkeit, wenn sie Bedingungswahrscheinlichkeiten interpretieren. Du könntest eine Schlagzeile sehen: Eine Studie zeigt, dass 80 % der erfolgreichen Unternehmer vor ihrem 30. Lebensjahr angefangen haben. Das heißt: P(vor dem 30. Lebensjahr angefangen | erfolgreicher Unternehmer) = 0,8. Aber ohne zu wissen, wie hoch P(Start vor 30) bei allen Unternehmern ist, kann man nicht sagen, ob ein früher Start wirklich Erfolg verspricht.

Das führt zu falschen Entscheidungen. Wenn 90 % aller Unternehmer vor ihrem 30. Lebensjahr anfangen, dann fangen erfolgreiche Unternehmer nicht ungewöhnlich oft jung an. Die halten sich einfach an das übliche Muster. Die bedingte Wahrscheinlichkeit sagt ohne die marginale Basis zum Vergleich nicht viel aus.

Basiszinssatz-Irrtum

Der Basisratenirrtum passiert, wenn Leute bedingte Beweise überbewerten und dabei die Randwahrscheinlichkeiten (Basisraten) nicht beachten.

Hier ist ein gängiges Beispiel aus der Datenwissenschaft: Du baust einen binären Klassifikator auf einem unausgewogenen Datensatz auf. Die positive Klasse (das, was du vorhersagen willst) kommt nur in 5 % deiner Daten vor. Du baust ein Modell und erreichst eine Genauigkeit von 95 %. Das klingt doch super, oder?

Nicht wirklich. Wenn du ein „dummes“ Modell bauen würdest, das einfach jedes Mal die negative Klasse vorhersagt, würde es auch eine Genauigkeit von 95 % erreichen (weil 95 % der Daten negativ sind). Dein schickes Modell ist eigentlich nicht viel besser als immer „nein“ zu raten.

Der Fehler ist, dass man die 95 %-Genauigkeit isoliert betrachtet, ohne die Basisrate (5 % positive Klasse) zu berücksichtigen. Wenn die Klassen unausgewogen sind, wird die Genauigkeit zu einer irreführenden Kennzahl. Du musst die Präzision, den Recall oder den F1-Score checken, um zu sehen, ob dein Modell tatsächlich was Nützliches gelernt hat.

Wenn du Marginalwerte verstehst, kannst du die richtigen Bewertungsmetriken für unausgewogene Probleme auswählen.

Fortgeschrittene Themen und Erweiterungen

Bei hochdimensionalen Modellen mit Dutzenden oder Hunderten von Variablen ist es oft unmöglich, Randverteilungen genau zu berechnen. Die Anzahl der möglichen Kombinationen steigt schnell an, und die erforderlichen Summen oder Integrale werden unüberschaubar.

Um das zu regeln, nutzen die Leute da ungefähren Schlussfolgerungsmethoden:

• Sampling-Methoden (wie Markov Chain Monte Carlo, MCMC) machen viele Samples aus der Verteilung des Modells. Du kannst dann die Randwahrscheinlichkeiten schätzen, indem du dir ansiehst, wie oft Ereignisse in diesen Stichproben auftreten.

• Die Variationsinferenz geht anders vor: Sie tauscht eine schwer zu berechnende Verteilung gegen eine einfachere aus und optimiert sie, damit sie so nah wie möglich dran ist. Dadurch sind marginale Schätzungen in großen Modellen oft schneller.

Moderne Tools wie Pythons scipy.stats für Wahrscheinlichkeitsverteilungen, pandas für Kontingenztabellen und Rs table() und dplyr für empirische Randverteilungen machen diese Berechnungen zugänglich. Für Daten, die in einer Datenbank gespeichert sind, berechnet die SQL-Klausel „ GROUP BY “ effizient empirische Randwerte aus großen Datensätzen.

Fazit

Bevor du die Beziehung zwischen Variablen verstehen, bedingte Beweise bewerten oder Bayes'sche Modelle erstellen kannst, musst du die unbedingte Wahrscheinlichkeit einzelner Ereignisse verstehen. Es ist die Basis, die alles andere verständlich macht.

Wenn du Marginalien falsch verstehst, kannst du leicht analytische Fehler machen: Du verwechselst Basisraten mit bedingten Wahrscheinlichkeiten, fällst auf den Basisratenirrtum rein oder entwickelst Modelle, die nicht besser sind als einfache Basiswerte. Wenn du die Randbedingungen richtig verstehst, wirst du auch kapieren, wie die bedingte Wahrscheinlichkeit sie verfeinert, wie das Bayes-Theorem sie mit Beweisen aktualisiert und wie Machine-Learning-Modelle aus den Mustern lernen, die sie aufdecken.