Probabilidad marginal: Teoría, ejemplos y aplicaciones

Estás analizando el comportamiento de los clientes de una plataforma de comercio electrónico y tu jefe te pregunta: ¿Cuál es la probabilidad de que un cliente se vaya, independientemente del motivo?

Esta pregunta aborda algo más específico de lo que podrías pensar. No estás preguntando por la tasa de abandono dada una categoría de producto concreta, ni por la tasa de abandono combinada con un método de pago. Estás preguntando por la probabilidad básica de un único evento: la pérdida de clientes, punto.

Esa es la probabilidad marginal, y es fundamental para la mayoría de los cálculos de probabilidad que encontrarás en la ciencia de datos.

¿Qué es la probabilidad marginal?

Como ya he dicho, la probabilidad marginal es la probabilidad de que ocurra un solo evento, independientemente de otras variables o eventos. Se denomina «marginal» porque, cuando escribes las probabilidades conjuntas en una tabla, estas probabilidades de un solo evento aparecen en los márgenes (los totales de las filas y columnas).

La notación es sencilla. Para un evento discreto A, escribimos P(A). La probabilidad marginal suele derivarse de la probabilidad conjunta. Si B es una variable aleatoria discreta y conoces la probabilidad conjunta de que A ocurra con cada valor de B, puedes hallar la probabilidad marginal sumando: P(A) =_Σb P(A, B=b), donde se suman todos los valores posibles b que puede tomar B. La probabilidad marginal es lo que queda cuando «sumas» o «integras» todas las demás variables.

Para comprender este concepto en su totalidad, necesitarás algunos términos básicos. El espacio muestral es el conjunto de todos los resultados posibles. Un evento es cualquier subconjunto del espacio muestral. La probabilidad conjunta P(A ∩ B) mide la probabilidad de que dos eventos ocurran juntos, mientras que la probabilidad condicional P(A|B) mide la probabilidad de que A ocurra dado que B ha ocurrido.

Recomiendo consultar nuestra hoja de referencia rápida «Introducción a las reglas de probabilidad» para obteneruna referencia rápida y eestas relaciones. La probabilidad marginal ocupa un lugar central en este ecosistema de probabilidades. Es el denominador en los cálculos de probabilidad condicional y la base del teorema de Bayes.

Probabilidad marginal a partir de tablas y distribuciones

Veamos cómo se calcula realmente la probabilidad marginal a partir de diferentes estructuras de datos. El enfoque depende de si trabajas con variables discretas o continuas.

Caso discreto (tablas de contingencia)

Cuando se trabaja con datos categóricos, las probabilidades marginales aparecen de forma natural en las tablas de contingencia. Supongamos que estás analizando el comportamiento de compra de los clientes en diferentes categorías de productos (electrónica, ropa, libros) y regiones (norte, sur, este, oeste). Cada celda contiene la probabilidad conjunta de una combinación de categoría y región. Los totales de las filas te dan la probabilidad marginal para cada categoría de productos (P(Electrónica), P(Ropa), P(Libros)), independientemente de la región. Los totales de las columnas te dan las probabilidades marginales para cada región.

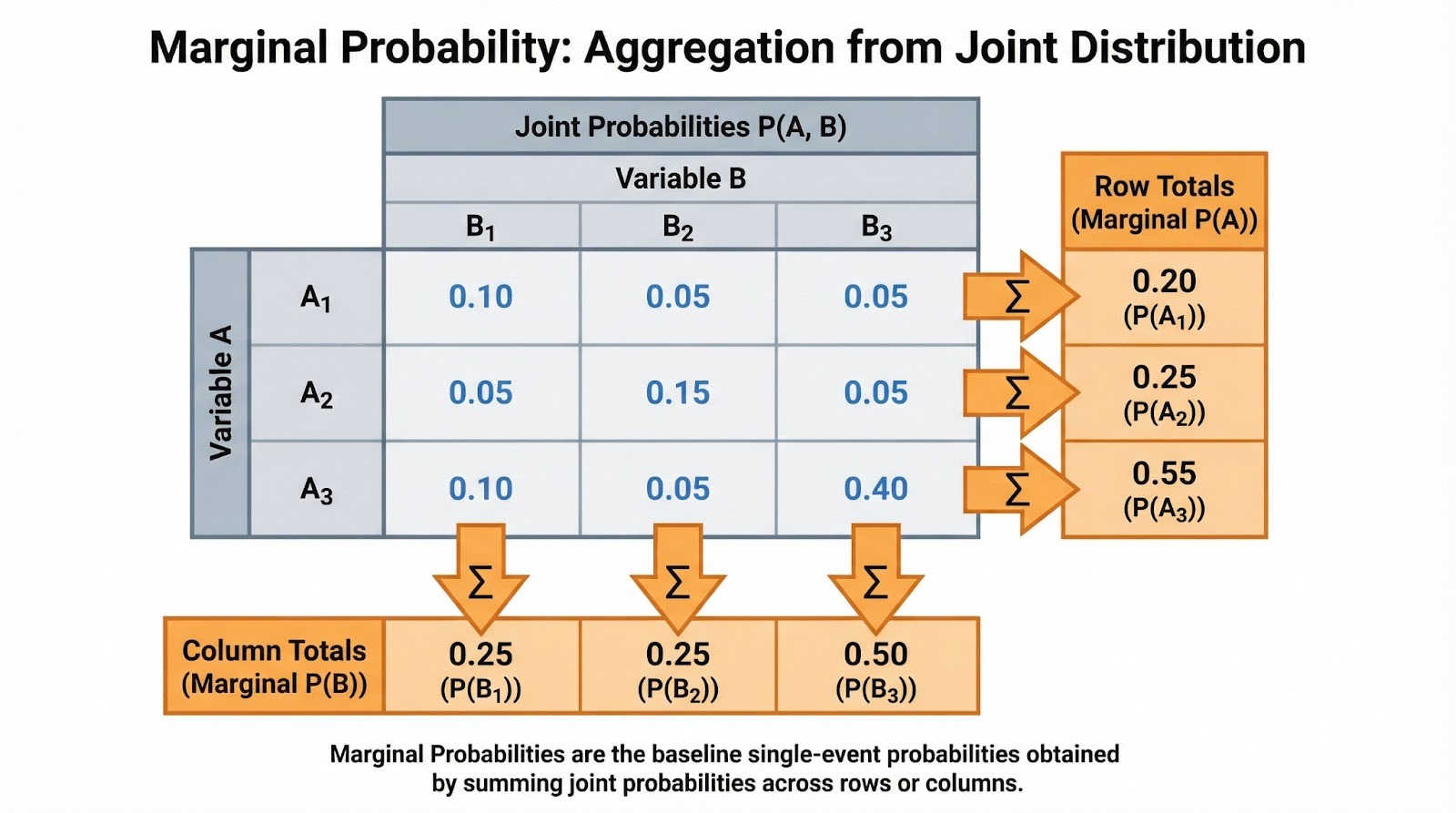
Sumar probabilidades conjuntas para hallar probabilidades marginales. Imagen del autor.

A menudo te encontrarás con ellas como frecuencias normalizadas. Si 500 de 2000 clientes compraron productos electrónicos, la probabilidad marginal P(Electrónica) = 500/2000 = 0,25. Esta es la tasa de referencia antes de tener en cuenta cualquier otro factor. Cuando realices un análisis exploratorio de datos, te sugiero que calcules primero estos marginales. Te ayudan a comprender la estructura básica de tus datos antes de profundizar en las relaciones condicionales.

Caso continuo

Para las variables aleatorias continuas, la probabilidad marginal se convierte en una función de densidad de probabilidad marginal (PDF). Si tienes dos variables continuas X e Y con una PDF conjunta, la PDF marginal de X se calcula integrando todos los valores de Y.

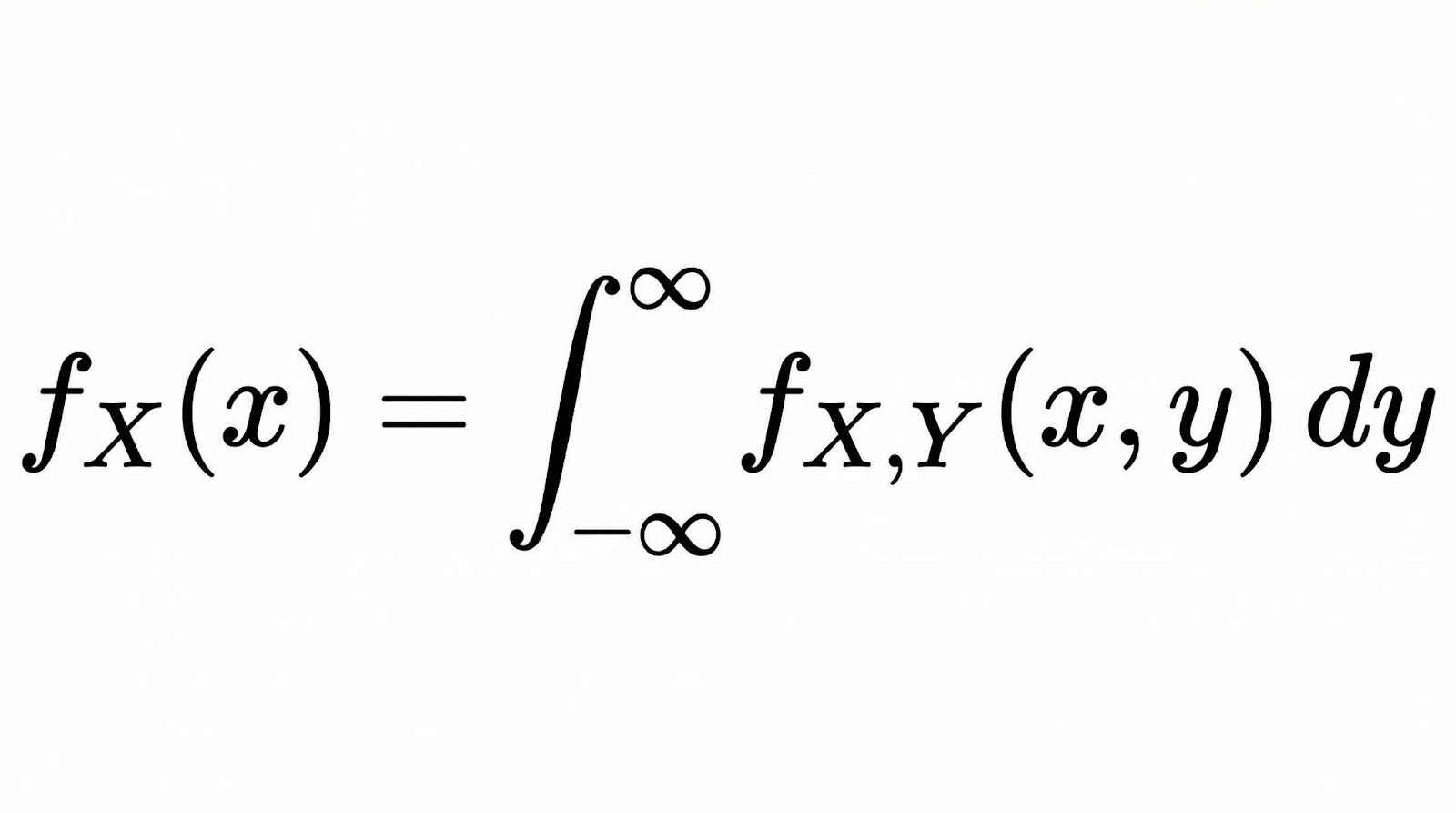
Conceptualmente, la integración aquí hace lo mismo que la suma en el caso discreto. «Colapsa» la distribución conjunta a una sola dimensión al tener en cuenta todas las posibilidades de la otra variable.

Piensa en ello como si cortaras una superficie 3D (la distribución conjunta) y observaras el área bajo la curva a lo largo de un eje. Nuestros Fundamentos del análisis bayesiano de datos en R cubre estos conceptos en profundidad cuando se trabaja con distribuciones continuas.

Relación entre probabilidad marginal, conjunta y condicional

Examinemos cómo la probabilidad marginal se relaciona con los otros tipos de probabilidad con los que trabajarás habitualmente.

Estos tres tipos de probabilidad forman un sistema conectado, y la probabilidad marginal suele ser el nexo que los une. Probabilidad conjunta probabilidad conjunta, se obtienen las marginales sumando o integrando. A partir de las probabilidades conjuntas y marginales, calculas las condicionales utilizando P(A|B) = P(A ∩ B) / P(B). Observa que la probabilidad marginal P(B) es el denominador. Normaliza la probabilidad conjunta para darte la condicional.

Esto es importante en la práctica porque, cuando interpretas probabilidades condicionales, necesitas la marginal como contexto. Una probabilidad del 90 % de padecer la enfermedad tras obtener un resultado positivo en la prueba puede parecer alarmante, pero si la probabilidad marginal de padecerla es solo del 1 %, la probabilidad real tras un resultado positivo podría ser mucho menor de lo que cabría esperar.

Esto aparece en todas partes en la inferencia bayesiana. Una prioridad es tu creencia sobre un parámetro antes de ver ningún dato. La verosimilitud marginal (también llamada evidencia), P(Datos), es el término de normalización en el teorema de Bayes que convierte «a priori × verosimilitud» en una probabilidad a posteriori adecuada. Nuestro Análisis bayesiano de datos en Python explora estas conexiones a través de ejercicios prácticos de modelización.

Ejemplos prácticos de probabilidad marginal

Trabajemos tanto con problemas clásicos de probabilidad como con situaciones reales.

Ejemplos clásicos

Empecemos con los dados. Si lanzas dos dados, ¿cuál es la probabilidad de que el primer dado muestre un 4, independientemente del valor del segundo dado?

El espacio muestral tiene 36 resultados igualmente probables. Seis de ellos tienen un 4 en el primer dado: (4,1), (4,2), (4,3), (4,4), (4,5), (4,6). Por lo tanto, P(Primera tirada = 4) = 6/36 = 1/6. Observa que no hemos puesto ninguna condición sobre el segundo dado. Simplemente contamos todos los resultados en los que el primer dado es un 4.

Aquí tienes otro ejemplo clásico. Si se roba una carta de una baraja estándar de 52 cartas, ¿cuál es la probabilidad de que sea un corazón, independientemente del valor? Hay 13 corazones y 52 cartas en total, por lo que P(Corazón) = 13/52 = 1/4. Esta probabilidad marginal se agrega a todos los rangos (desde el as hasta el rey), lo que te da la probabilidad incondicional del palo.

Ejemplos del mundo real

Las pruebas médicas ofrecen una aplicación práctica muy interesante. Supongamos que estás analizando la prevalencia de una enfermedad en una población. La probabilidad marginal P(Enfermedad) representa la tasa de enfermedad basal antes de considerar los resultados de cualquier prueba diagnóstica. Si el 2 % de la población padece la enfermedad, P(Enfermedad) = 0,02. Esta probabilidad marginal es esencial para interpretar la precisión de la prueba. Una prueba con una sensibilidad del 95 % sigue dando muchos falsos positivos cuando la enfermedad es poco frecuente.

En marketing digital, es posible que te preguntes: ¿Cuál es la probabilidad de que un usuario se convierta, independientemente de la fuente de tráfico? Si tienes datos sobre conversiones procedentes de búsquedas orgánicas, anuncios pagados, redes sociales y correo electrónico, la probabilidad marginal P(Conversión) se suma entre todas las fuentes. Esta tasa de conversión de referencia te ayuda a evaluar si las fuentes de tráfico específicas tienen un rendimiento superior o inferior a la media.

Del mismo modo, en finanzas, tú podrías calcular la probabilidad marginal de una caída del mercado independientemente de los niveles de los tipos de interés. Esto te da el riesgo incondicional antes de incorporar los factores macroeconómicos.

Probabilidad marginal en ciencia de datos y machine learning

Exploremos cómo aparece la probabilidad marginal a lo largo del flujo de trabajo de la ciencia de datos.

Análisis exploratorio de datos (EDA)

Cuando te enfrentas por primera vez a un conjunto de datos, calcular las probabilidades marginales te ayuda a comprender las tasas de eventos de referencia. En un conjunto de datos de detección de fraudes, P(Fraude) indica el equilibrio de clases antes de examinar cualquier característica. Esto revela inmediatamente si se trata de un problema gravemente desequilibrado en el que solo se produce fraude en el 0,1 % de las transacciones.

Las distribuciones marginales de las características individuales también orientan tu análisis. Si estás creando un modelo para predecir la pérdida de clientes, te recomiendo examinar P(Pérdida), P(Cliente de alto valor) y P(Actividad reciente) por separado. Esto proporciona contexto antes de explorar tus relaciones conjuntas.

Modelización predictiva

Los clasificadores bayesianos ingenuos se basan explícitamente en probabilidades marginales como priores de clase. Al clasificar un documento como spam o no spam, P(Spam) es tu creencia previa antes de ver ninguna palabra del documento. A continuación, el algoritmo actualiza esta probabilidad marginal basándose en las probabilidades condicionales de las características.

Las distribuciones marginales de características también son importantes en la ingeniería de características y el diagnóstico de modelos. Si la distribución marginal de una característica está muy sesgada, puedes aplicar transformaciones como el escalado logarítmico o Box-Cox para hacerla más simétrica. 

Los cambios entre conjuntos de datos son igualmente importantes. Por ejemplo, si tu conjunto de entrenamiento tiene P(Clase A)=0,9, pero tu conjunto de prueba tiene P(Clase A)=0,5, tus probabilidades previstas y métricas de rendimiento pueden cambiar mucho, y es posible que necesites un umbral de decisión diferente. Esto ocurre porque el modelo se ha entrenado con una tasa base, pero se evalúa con otra.

Comprobar las distribuciones marginales antes del entrenamiento te ayuda a detectar estos problemas de forma temprana y a decidir si necesitas un nuevo muestreo, métricas de evaluación diferentes, una recalibración o modelos separados para diferentes segmentos de datos.

Riesgo y toma de decisiones

Los cálculos del valor esperado requieren probabilidades marginales. Si estás decidiendo si lanzar un producto, necesitas P(Éxito) como la probabilidad marginal de éxito en todas las condiciones de mercado posibles. Multiplica esto por la recompensa por el éxito, súmalo a P(Fracaso) multiplicado por el coste del fracaso y obtendrás tu valor esperado.

Modelización probabilística

En las redes bayesianas y los modelos gráficos, los nodos representan variables con distribuciones de probabilidad condicional asociadas. Las distribuciones marginales se obtienen mediante inferencia, propagando probabilidades a través de la estructura de la red u observando pruebas y actualizando creencias. Los métodos de muestreo como la cadena de Markov Monte Carlo aproximan estas marginales cuando el cálculo exacto resulta inviable. Nuestro modelización bayesiana con RJAGS muestra estos métodos en la práctica.

Lo que la gente entiende mal sobre la probabilidad marginal

Estos son los errores que cometen incluso los profesionales con experiencia.

Confundir probabilidad marginal con probabilidad condicional

Este es probablemente el error más común, y es sorprendentemente intuitivo cometerlo. Imagina que te haces una prueba médica con una sensibilidad del 95 % y una especificidad del 90 %. Tu resultado es positivo. La mayoría de la gente piensa inmediatamente: La prueba detecta el 95 % de los casos, así que probablemente tengas la enfermedad.

Pero ese razonamiento omite una información fundamental: ¿qué tan común es la enfermedad en primer lugar? Si solo el 1 % de las personas lo padecen (la probabilidad marginal), al realizar la prueba a 10 000 personas, obtendrás unos 95 positivos verdaderos, pero 990 positivos falsos. Esto significa que la mayoría de los resultados positivos son falsas alarmas. La probabilidad real después de dar positivo es solo del 9 %, no del 95 %.

La confusión se debe a que la gente se centra en la sensibilidad de la prueba (95 %) y se olvida de la tasa de referencia (prevalencia del 1 %). La probabilidad marginal P(Enfermedad) = 0,01 y la probabilidad condicional P(Enfermedad | Prueba positiva) = 0,09 son cantidades completamente diferentes, pero nuestra intuición nos lleva a tratarlas como si fueran iguales.

Ignorar los marginales al interpretar los condicionales

Incluso cuando las personas distinguen correctamente entre probabilidades marginales y condicionales, a menudo ignoran las marginales al interpretar las condicionales. Es posible que veas un titular de noticias: Un estudio revela que el 80 % de los empresarios de éxito empezaron antes de los 30 años. Es decir, P(Empezaste antes de los 30 | Eres un emprendedor de éxito) = 0,8. Pero sin conocer el valor de P(Empezó antes de los 30) para todos los emprendedores, no se puede evaluar si empezar joven realmente predice el éxito.

Esto conduce a una toma de decisiones errónea. Si el 90 % de todos los emprendedores comienzan antes de los 30 años, entonces los emprendedores exitosos no comienzan jóvenes en proporciones inusuales. Simplemente están siguiendo el patrón general. La probabilidad condicional no tiene mucho sentido sin una referencia marginal con la que compararla.

Falacia de la tasa básica

La falacia de la tasa base se produce cuando las personas dan demasiada importancia a las pruebas condicionales y pasan por alto las probabilidades marginales (tasas base).

He aquí un ejemplo habitual de ciencia de datos: Estás creando un clasificador binario en un conjunto de datos desequilibrado. La clase positiva (lo que intentas predecir) solo aparece en el 5 % de tus datos. Construyes un modelo y alcanzas una precisión del 95 %. Suena genial, ¿verdad?

En realidad, no. Si creas un modelo «tonto» que solo predice la clase negativa en todas las ocasiones, también obtendrás una precisión del 95 % (porque el 95 % de los datos son negativos). Tu sofisticado modelo no está funcionando mucho mejor que adivinar siempre «no».

El error es fijarse en la cifra de precisión del 95 % de forma aislada, sin tener en cuenta la tasa base (5 % de clase positiva). Cuando las clases están desequilibradas, la precisión se convierte en una métrica engañosa. Debes comprobar la precisión, la recuperación o la puntuación F1 para ver si tu modelo realmente ha aprendido algo útil.

Comprender los marginales te ayuda a elegir las métricas de evaluación adecuadas para problemas desequilibrados.

Temas avanzados y extensiones

En modelos de alta dimensión con docenas o cientos de variables, a menudo resulta imposible calcular con exactitud las distribuciones marginales. El número de combinaciones posibles crece rápidamente y las sumas o integrales requeridas se vuelven imposibles de resolver.

Para manejar esto, los profesionales utilizan métodos de inferencia aproximada:

• Los métodos de muestreo (como Markov Chain Monte Carlo, MCMC) generan muchas muestras a partir de la distribución del modelo. A continuación, puedes estimar las probabilidades marginales observando la frecuencia con la que se producen los eventos en esas muestras.

• La inferencia variacional adopta un enfoque diferente: sustituye una distribución difícil de calcular por otra más sencilla y la optimiza para que sea lo más precisa posible, lo que a menudo agiliza las estimaciones marginales en modelos de gran tamaño.

Herramientas modernas como scipy.stats de Python para distribuciones de probabilidad, pandas para tablas de contingencia y table() y dplyr de R para marginales empíricas hacen que estos cálculos sean accesibles. Para los datos almacenados en bases de datos, la cláusula « GROUP BY » (calcular marginales) de SQL calcula de forma eficiente los marginales empíricos a partir de grandes conjuntos de datos.

Conclusión

Antes de poder comprender la relación entre variables, evaluar pruebas condicionales o construir modelos bayesianos, es necesario comprender la probabilidad incondicional de los eventos individuales. Es la línea de base la que hace que todo lo demás sea interpretable.

Cuando se malinterpretan los marginales, se es vulnerable a cometer errores analíticos: confundir las tasas de referencia con las probabilidades condicionales, caer en la falacia de la tasa base o crear modelos que no superan a las tasas de referencia ingenuas. Si entiendes bien los marginales, comprenderás cómo la probabilidad condicional los refina, cómo el teorema de Bayes los actualiza con pruebas y cómo los modelos de machine learning aprenden de los patrones que revelan.