Entendendo a distribuição de Pareto: Um guia abrangente

Você já organizou uma festa de pizza e percebeu algo interessante? Com certeza. Em minha última reunião, observei que, enquanto a maioria das pessoas pegava uma ou duas fatias, alguns convidados devoravam quase metade das pizzas. Enquanto observava o desenrolar da situação, fiquei impressionado: Eu estava testemunhando um exemplo do mundo real de um dos padrões mais fascinantes da ciência de dados: a distribuição de Pareto.

Adoro esse exemplo porque ele capta perfeitamente o que é a distribuição de Pareto: a observação de que, em muitas situações, um pequeno grupo é responsável por uma grande parte do resultado.

Como cientista de dados, passei a apreciar como essa distribuição nos ajuda a entender e modelar situações em que "os poucos vitais" dominam "os muitos triviais". Pense nisso: 20% dos clientes de uma empresa geralmente geram 80% de sua receita, ou 20% do conteúdo de um site pode gerar 80% de seu tráfego. Esse padrão é tão comum que se tornou conhecido como o princípio de Pareto ou a "regra 80/20", embora as proporções exatas possam variar.

Mas eis o que torna a Distribuição de Pareto realmente especial: ela não é apenas uma observação casual - é uma ferramenta matemática poderosa que nos ajuda a modelar e prever esses padrões desequilibrados nos dados. Independentemente de você estar analisando a desigualdade econômica, otimizando operações comerciais ou estudando fenômenos naturais, a compreensão da Distribuição de Pareto pode fornecer informações valiosas sobre por que as coisas nem sempre são distribuídas uniformemente - e o que isso significa para nossa análise.

A capacidade exclusiva da distribuição de Pareto de destacar desequilíbrios a tornou indispensável em campos que vão da economia às ciências naturais. Se você estiver ansioso para explorar padrões estatísticos semelhantes, considere mergulhar em recursos como Foundations of Probability in Python para obter uma base em conceitos de probabilidade ou Multivariate Probability Distributions in R para expandir seu kit de ferramentas analíticas. Para quem aprende visualmente, a folha de dicas de introdução às regras de probabilidade serve como uma excelente referência rápida para os princípios fundamentais.

O que é a distribuição de Pareto?

Quando o economista italiano Vilfredo Pareto olhou para seu jardim em 1896, notou algo peculiar: 20% de suas vagens de ervilha continham 80% das ervilhas. Essa observação o levou a explorar padrões semelhantes na propriedade de terras, onde descobriu que 80% das terras da Itália pertenciam a 20% de sua população. O que começou como uma observação de jardim se transformou em uma das ferramentas mais versáteis da estatística para entender distribuições desiguais.

Contexto histórico

No final do século XIX, a pesquisa de Vilfredo Pareto foi muito além das vagens de ervilha e da propriedade da terra. Ele analisou os padrões de distribuição de riqueza em diferentes países e períodos de tempo, descobrindo uma relação matemática consistente. Ele descobriu que a minoria rica possuía a maioria dos ativos em todas as sociedades que estudou. Esse padrão apareceu de forma tão consistente que outros pesquisadores começaram a aplicar suas ideias a diferentes campos, da economia às ciências naturais.

A distribuição ganhou destaque quando o consultor de gestão Joseph Juran se deparou com o trabalho de Pareto em 1937. Juran batizou o padrão de "Princípio de Pareto" e o aplicou ao controle de qualidade, mostrando que a maioria dos defeitos de fabricação era decorrente de um pequeno número de causas. Essa aplicação ajudou a transformar o gerenciamento da qualidade industrial e Spark um interesse mais amplo nas ideias de Pareto.

Principais características 

A distribuição de Pareto se destaca de outras distribuições estatísticas por meio de vários recursos exclusivos:

1. Comportamento de lei de potência: Ao contrário da curva de sino (distribuição normal), em que os valores extremos se tornam exponencialmente raros, a distribuição de Pareto segue uma lei de potência. Isso significa que os valores extremos ocorrem com mais frequência do que você poderia esperar.
2. Invariância de escala: Se você aumentar o zoom em qualquer parte de uma distribuição de Pareto, o padrão será semelhante ao todo. Essa propriedade, conhecida como invariância de escala, ajuda a explicar por que a distribuição aparece em contextos tão diversos.
3. O princípio 80/20: Embora os números exatos possam variar (pode ser 90/10 ou 70/30), a ideia central permanece: uma pequena porcentagem de causas cria uma grande porcentagem de efeitos.
4. Cauda pesada: A "cauda" da distribuição (a parte que representa valores maiores) diminui mais lentamente do que as distribuições exponenciais. Essa propriedade matemática explica por que os valores extremos - como os bilionários na distribuição de riqueza - ocorrem com mais frequência do que uma distribuição normal poderia prever.

Essas características tornam a distribuição de Pareto particularmente boa para modelar situações em que os recursos, efeitos ou resultados se concentram em um pequeno subconjunto de uma população.

Formulação matemática da distribuição de Pareto

Vamos decompor a matemática por trás da distribuição de Pareto em partes digeríveis. Embora as fórmulas possam parecer intimidadoras no início, vou orientar você em cada componente, passo a passo.

Fórmula de distribuição de Pareto

A função de densidade de probabilidade (PDF) da distribuição de Pareto tem a seguinte forma:

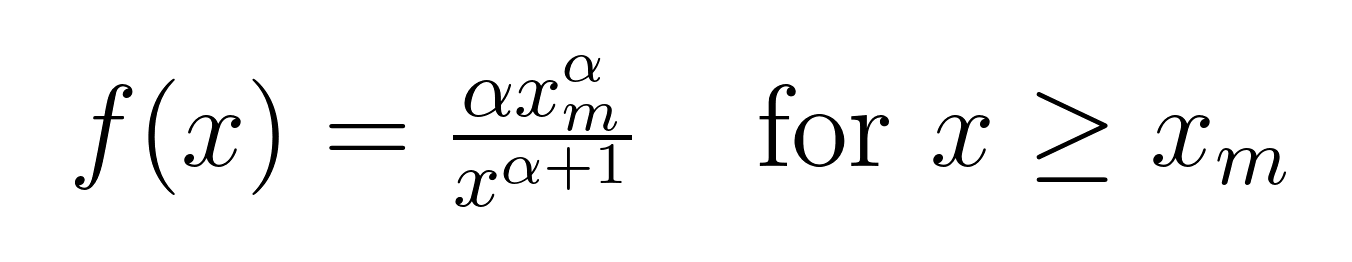
Vamos decodificar o significado de cada símbolo:

• x é nossa variável aleatória (como riqueza, tamanho da cidade ou tráfego do site)
• xₘ é o valor mínimo possível de x (também chamado de parâmetro de escala)
• α (alfa) é o parâmetro de forma que determina a rapidez com que a cauda diminui

A função de distribuição cumulativa (CDF) nos dá a probabilidade de que um valor seja menor ou igual a x:

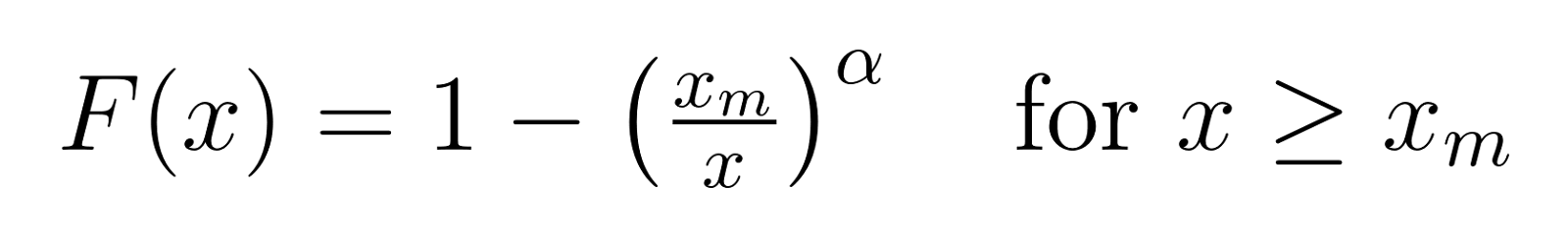
Para tornar essas fórmulas mais concretas, vamos ver o que significam os diferentes valores de α:

Entendendo o princípio de Pareto

A famosa regra 80/20 surge naturalmente da distribuição de Pareto quando α ≈ 1,16.

Na análise de dados, esse princípio nos ajuda:

1. Identificar fatores de alto impacto em nosso conjunto de dados
2. Concentrar os recursos nas variáveis mais influentes
3. Prever onde os valores extremos podem ocorrer
4. Defina expectativas realistas sobre a distribuição de dados

Por exemplo, ao analisar os dados do cliente, podemos descobrir que:

• 20% dos produtos geram 80% das vendas
• 20% das correções de bugs resolvem 80% das reclamações dos clientes
• 20% das campanhas de marketing geram 80% das novas inscrições

Esses insights ajudam as empresas a tomar decisões informadas sobre onde concentrar seus esforços para obter o máximo impacto.

Aplicações da distribuição de Pareto

De políticas econômicas a desastres naturais, a distribuição de Pareto aparece em lugares surpreendentes.

Economia e distribuição de riqueza

Entre no distrito financeiro de qualquer país e você verá a distribuição de Pareto em ação. Bancos e economistas o utilizam para rastrear a concentração de riqueza, modelar as disparidades de renda e analisar políticas fiscais. Por exemplo, quando os economistas estudaram a riqueza global em 2023, eles descobriram que o 1% mais rico dos adultos possuía 44% da riqueza mundial. Essa distribuição ajuda os formuladores de políticas a entender as lacunas de riqueza e a projetar intervenções econômicas. Se você estiver interessado em ideias de distribuição de riqueza, temos tutoriais sobre o coeficiente de Gini e a curva de Lorenz.

Negócios e marketing

Nos negócios, o princípio de Pareto ajuda as empresas a trabalhar de forma mais inteligente, e não mais difícil. Considere um site de comércio eletrônico que analisa os dados de seus clientes:

• Segmentação de clientes: Identificar e reter clientes VIP que geram mais receita
• Gerenciamento de estoque: Concentre-se nos produtos com maior número de vendas e otimize o armazenamento
• Alocação de recursos: Direcionar as equipes de vendas para leads promissores e priorizar os principais recursos

Fenômenos naturais e pesquisa científica

A natureza também segue os padrões de Pareto. Os cientistas usam essa distribuição para estudar:

• Padrões geográficos: Populações urbanas, redes fluviais, tamanhos de incêndios florestais
• Eventos geológicos: Magnitudes de terremotos e tremores secundários
• Sistemas biológicos: Abundância de espécies em ecossistemas

Veja o caso dos terremotos - sua distribuição de magnitude segue um padrão de Pareto, com muitos pequenos tremores e raros terremotos devastadores. Esse entendimento ajuda os sismólogos a desenvolver melhores modelos de previsão e avaliações de risco.

Visualização da distribuição de Pareto

A visualização de dados dá vida às propriedades exclusivas da distribuição de Pareto. Vamos explorar a aparência gráfica dessa distribuição e o que suas formas nos dizem sobre os dados que estamos analisando.

Representação gráfica

A maneira mais comum de visualizar a distribuição de Pareto é por meio de sua função de densidade de probabilidade (PDF). Isso nos mostra como os valores são distribuídos em nosso conjunto de dados.

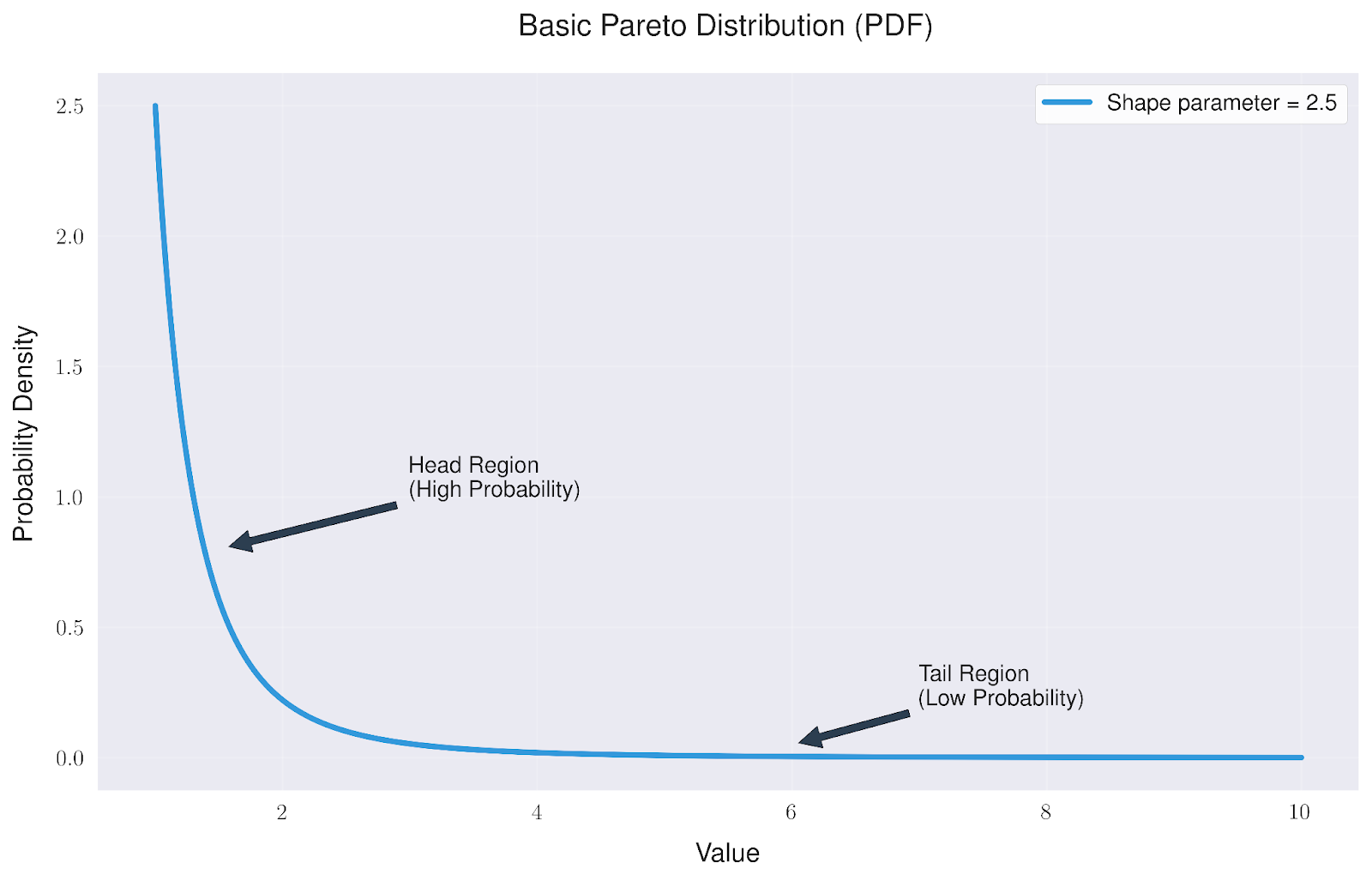
A distribuição básica de Pareto tem uma forma distinta que nos diz duas coisas importantes:

1. A região da "cabeça" mostra uma alta concentração de probabilidade perto do valor mínimo
2. A região da "cauda" se estende muito para a direita, mostrando que, embora os valores extremos sejam raros, eles são mais comuns do que em muitas outras distribuições

O que torna a distribuição de Pareto particularmente interessante é como ela muda com diferentes parâmetros de forma. Esses parâmetros influenciam diretamente o grau de extremo de nossos valores.

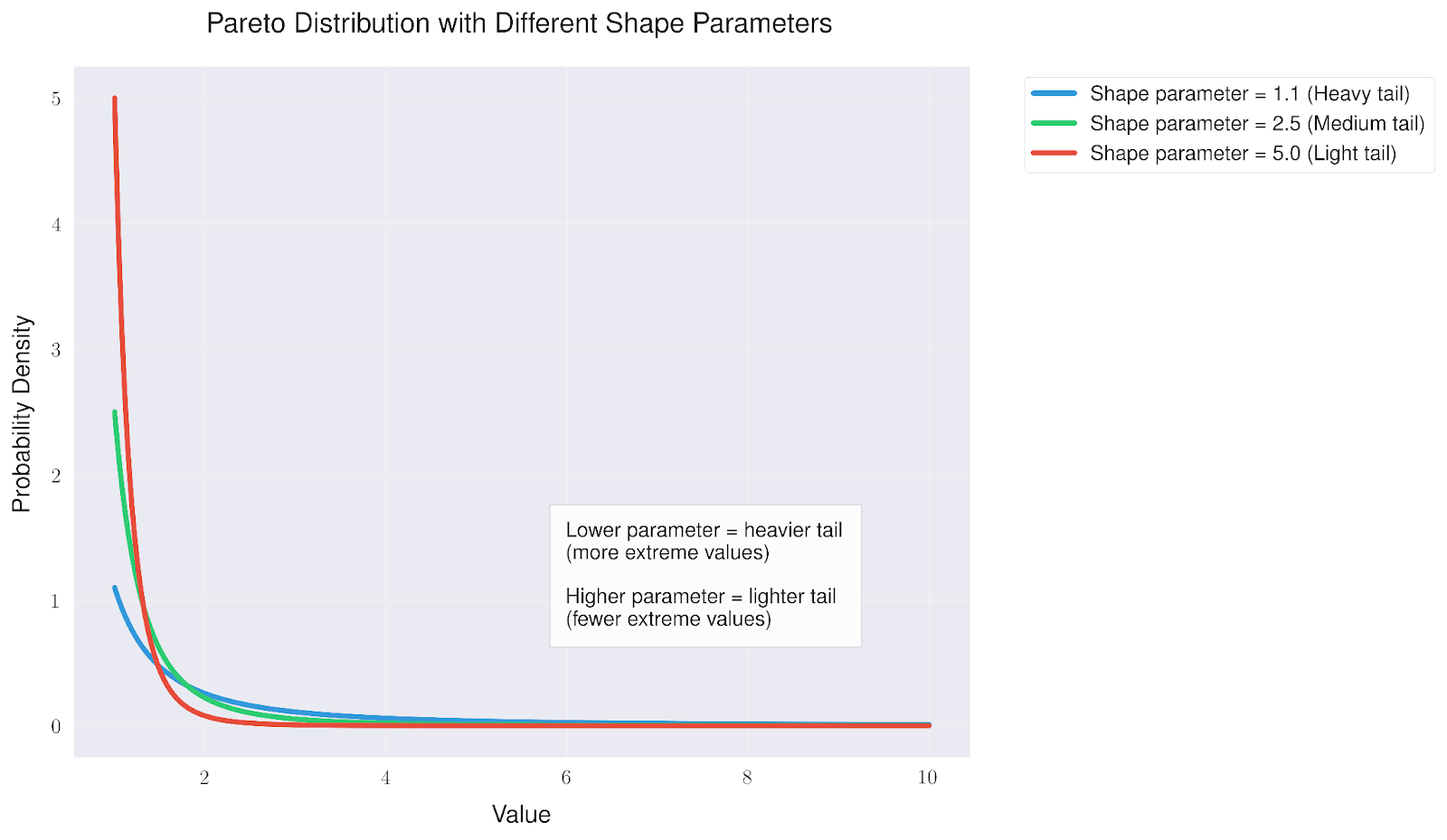
A análise de diferentes parâmetros de forma revela que você pode ter uma visão mais ampla do que a de uma forma:

• Valores mais baixos (como 1,1) criam uma "cauda pesada", onde é mais provável que ocorram valores extremos
• Os valores médios (em torno de 2,5) oferecem um equilíbrio entre eventos comuns e extremos
• Valores mais altos (como 5,0) criam uma "cauda leve" em que os valores extremos se tornam cada vez mais raros

Essa flexibilidade torna a distribuição de Pareto útil para modelar vários fenômenos do mundo real, desde a distribuição de riqueza (geralmente com cauda pesada) até defeitos de fabricação (geralmente com cauda mais leve).

A distribuição de riqueza costuma ter uma cauda pesada, o que implica uma probabilidade não negligenciável de valores extremamente grandes, de modo que eventos raros, mas enormes (como bilionários), têm um grande impacto. Isso faz sentido porque há um efeito de composição, pois as pessoas com dinheiro podem investir. As distribuições de cauda leve (como alguns tipos de defeitos de fabricação) decaem mais rapidamente devido a processos limitados e estáveis, o que significa que os valores extremos são muito menos prováveis, pois os grandes desvios são raros.

Ferramentas para visualização

Para visualizar a distribuição de Pareto, dependemos principalmente de linguagens de programação estatística e software especializado. O Python se destaca como uma escolha popular, oferecendo bibliotecas poderosas como scipy.stats para cálculos, juntamente com matplotlib e seaborn para criar visualizações claras e com qualidade de publicação. O R também se destaca nesse domínio, com suas robustas funções estatísticas integradas e o versátil pacote ggplot2 para plotagem. 

Embora o Excel seja excelente para criar gráficos de Pareto (gráficos de barras que mostram o princípio 80/20), ele não é a melhor ferramenta para visualizar e trabalhar com a distribuição de probabilidade de Pareto em si. Para a análise estatística e a visualização adequadas da distribuição de Pareto, recomendamos que você use as ferramentas de programação mencionadas acima.

Para fortalecer sua compreensão sobre a visualização de distribuições de probabilidade, vários recursos podem servir como pontos de partida valiosos. O tutorial Probability Distributions in Python oferece a você experiência prática com a implementação de várias distribuições, incluindo exemplos detalhados usando as bibliotecas estatísticas do Python. Para os interessados nos aspectos visuais, o artigo Data Visualizations that Capture Distributions (Visualizações de dados que capturam distribuições ) aborda técnicas especificamente projetadas para representar distribuições estatísticas de forma eficaz. Por fim, a Folha de dicas de visualização de dados serve como uma referência rápida para você escolher e criar visualizações adequadas para diferentes tipos de dados de distribuição. Esses recursos juntos fornecem uma boa base para você entender e visualizar a distribuição de Pareto.

Limitações e desafios da distribuição de Pareto

Toda ferramenta estatística tem seus limites, e a distribuição de Pareto não é exceção. Embora seja uma lente poderosa para visualizar determinados tipos de dados, saber quando não usá-la é tão importante quanto saber quando ela se encaixa perfeitamente. Deixe-me compartilhar algumas considerações importantes que aprendi a observar ao trabalhar com essa distribuição.

Premissas e restrições

Pense na distribuição de Pareto como uma lente de câmera especializada - ela funciona de forma brilhante para determinadas fotos, mas pode distorcer outras. Suas premissas básicas funcionam como as especificações técnicas que precisamos respeitar:

Primeiro, há o requisito de valor mínimo. Ao contrário de algumas outras distribuições que podem lidar com qualquer número, a distribuição de Pareto precisa de um ponto de partida claro acima de zero. Isso é como ter uma aposta mínima em um cassino - você não pode jogar com menos do que esse valor. Isso se torna particularmente complicado quando seus dados incluem zeros ou valores negativos, como quando você acompanha cenários de lucros e perdas.

A distribuição também pressupõe que cada evento seja isolado, independente dos outros. Mas a vida real raramente funciona dessa forma. Veja o acúmulo de riqueza, por exemplo: ter dinheiro geralmente facilita a obtenção de mais dinheiro. Essas interconexões podem tornar a distribuição de Pareto menos precisa do que esperamos.

Talvez o mais intrigante seja o fato de que a distribuição pressupõe invariância de escala - a ideia de que as diferenças relativas importam mais do que as absolutas. Embora isso geralmente seja verdade, os cenários do mundo real às vezes quebram essa regra. O impacto de dobrar a riqueza de alguém, por exemplo, é muito diferente em diferentes níveis de riqueza.

Interpretações errôneas e armadilhas comuns

De acordo com minha experiência, há várias armadilhas nas quais até mesmo analistas experientes podem cair ao trabalhar com a distribuição de Pareto. 

O mais comum é a generalização excessiva. O fato de você ver um padrão semelhante a 80/20 não significa automaticamente que você está vendo uma distribuição de Pareto. É como supor que todo pássaro que você vê é uma águia - a forma pode ser semelhante, mas os detalhes são importantes. Sempre teste o ajuste de sua distribuição antes de tirar conclusões.

A estimativa de parâmetros apresenta outro desafio. O parâmetro de forma (α) pode ser particularmente sensível a outliers, especialmente em conjuntos de dados menores. É como tentar medir a altura média de uma população - alguns indivíduos muito altos ou baixos podem distorcer significativamente os resultados se o tamanho da amostra for muito pequeno.

Quando se trata de prever eventos extremos, a cauda pesada da distribuição de Pareto pode ser tanto uma bênção quanto uma maldição. Embora seja excelente para modelar a possibilidade de resultados extremos, às vezes pode sugerir que eles são mais prováveis do que realmente são. Isso é particularmente importante em cenários de avaliação de risco - você não quer superestimar ou subestimar eventos raros.

Por fim, há o que eu chamo de "cegueira do contexto" - ficar tão preso à elegância matemática da distribuição que nos esquecemos de perguntar se ela faz sentido para nossa situação específica. Lembre-se de que o mapa não é o território, e a distribuição de Pareto é apenas um mapa entre muitos.

Em caso de dúvida, considere distribuições alternativas e sempre valide suas suposições com base no conhecimento real do seu domínio. Afinal, as estatísticas devem servir à nossa compreensão da realidade, e não o contrário.

O princípio de Pareto na vida real

O projeto da natureza na dinâmica do ecossistema

Nos ecossistemas naturais, o princípio de Pareto se revela por meio do fascinante conceito de espécies-chave - aqueles poucos organismos que exercem uma influência enorme sobre seu ambiente. Considere como os lobos em Yellowstone afetam tudo, desde as populações de alces até os padrões dos rios, ou como os recifes de corais, que compreendem apenas uma pequena fração do espaço oceânico, sustentam quase um quarto de todas as espécies marinhas. Essa distribuição natural 80/20 aparece em tudo, desde o tamanho das copas das árvores até a distribuição das chuvas nas estações.

A sinfonia da distribuição de riqueza

Pense na distribuição de riqueza como uma apresentação de orquestra, em que alguns instrumentos principais conduzem a melodia principal, enquanto outros fornecem o apoio essencial de fundo. Assim como a primeira seção do violino geralmente lidera a orquestra, uma pequena porcentagem de indivíduos detém a maior parte da riqueza global, criando uma composição econômica complexa. Esse padrão tem implicações profundas para a política econômica, levantando questões sobre como manter tanto o dinamismo que a concentração de riqueza pode impulsionar quanto a harmonia social que exige uma participação mais ampla. Entender esse paralelo musical nos ajuda a apreciar tanto a eficiência quanto os desafios da riqueza concentrada.

A regra da inovação: quando menos gera mais

No campo da inovação, o princípio de Pareto se manifesta na forma como as ideias revolucionárias surgem de um subconjunto surpreendentemente pequeno de tentativas. Empresas como a Apple e o Google descobriram que cerca de 20% de seus produtos geram 80% de sua receita, enquanto na pesquisa científica, uma pequena fração dos artigos obtém a maioria das citações. Esse padrão aparece em todos os setores criativos, desde canções de sucesso em catálogos de música até filmes de grande sucesso em portfólios de estúdios.

Ondulações sociais: o efeito de rede

O princípio de Pareto é aplicado na forma como as informações se espalham pelas redes sociais. Alguns poucos influenciadores selecionados, que representam talvez 20% dos usuários, geralmente geram 80% do envolvimento nas plataformas sociais. Esse mesmo padrão aparece na viralidade do conteúdo, em que uma pequena porcentagem de publicações captura a maioria dos compartilhamentos e interações.

Conclusão

A distribuição de Pareto destaca como as ferramentas estatísticas podem revelar padrões significativos de concentração nos dados. Para que você entenda melhor esses conceitos, oferecemos oportunidades valiosas de aprendizado. Nosso curso Foundations of Probability in R apresenta os princípios básicos, enquanto o Introduction to Portfolio Analysis in R demonstra como essas ideias se aplicam a contextos financeiros. Além disso, nosso tutorial Probabilidade e estatística de pôquer com Python oferece uma maneira única de explorar os conceitos de probabilidade em ação, tornando o aprendizado envolvente e prático. Esses recursos oferecem uma base sólida para que você aplique insights estatísticos em uma série de cenários práticos.