Cartes auto-organisatrices : Un guide intuitif avec des exemples en Python

Mise en place de l'environnement pour SOM

Avant de construire le SOM, nous devons préparer l'environnement avec les paquets nécessaires. 

Installation des bibliothèques Python 

Nous avons besoin de ces paquets : 

• MiniSom est un outil Python basé sur NumPy qui crée et entraîne des SOMs. 
• NumPy est utilisé pour accéder à des fonctions mathématiques telles que la division de tableaux, l'obtention de valeurs uniques, etc. 
• matplotlib est utilisé pour tracer divers graphiques et diagrammes afin de visualiser les données. 
• Le paquet datasets de sklearn est utilisé pour importer des ensembles de données sur lesquels appliquer le SOM.
• Le paquet MinMaxScaler de sklearn normalise l'ensemble des données .

L'extrait de code suivant importe ces paquets : 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

Préparation du jeu de données

Dans ce tutoriel, nous utilisons MiniSom pour construire un SOM et l'entraîner sur l' ensemble de données canoniques IRIS. Ce jeu de donnéesest composé de 3 classes de plantes d'iris. Chaque classe compte 50 instances. Pour préparer les données, nous suivons les étapes suivantes : 

• Importez le jeu de données Iris à partir de sklearn,
• Extrayez les vecteurs de données et les scalaires cibles. 
• Normaliser les vecteurs de données. Dans ce tutoriel, nous utilisons le MinMaxScaler de scikit-learn. 
• Déclarez un ensemble d'étiquettes pour chacune des trois classes de plantes Iris. 

Le code suivant met en œuvre ces étapes : 

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Implémentation de cartes auto-organisatrices (SOM) en Python

Pour mettre en œuvre un SOM en Python, nous définissons et initialisons la grille avant de l'entraîner sur le jeu de données. Nous pouvons ensuite visualiser les neurones entraînés et l'ensemble des données regroupées. 

Définition de la grille SOM

Comme nous l'avons expliqué précédemment, une SOM est une grille de neurones. MiniSom permet de créer des grilles bidimensionnelles. Les dimensions X et Y de la grille correspondent au nombre de neurones sur chaque axe. Pour définir la grille SOM, nous devons également spécifier :

• Les dimensions X et Y de la grille
• Le nombre de variables d'entrée - il s'agit du nombre de lignes de données. 

Déclarez ces paramètres comme des constantes Python :

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

L'exemple de code ci-dessous illustre comment déclarer la grille à l'aide de MiniSom :

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

Les deux premiers paramètres sont le nombre de neurones le long des axes X et Y, et le troisième paramètre est le nombre de variables. 

Nous déclarons d'autres paramètres et hyperparamètres lors de la création de la grille SOM. Nous les expliquerons plus loin dans ce tutoriel. Pour l'instant, déclarez ces paramètres comme indiqué ci-dessous : 

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

Créez un SOM à l'aide de ces paramètres :

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

Initialisation des neurones

La commande ci-dessus crée un SOM avec des poids aléatoires pour tous les neurones. L'initialisation des neurones avec des poids tirés des données (au lieu de nombres aléatoires) peut rendre le processus d'apprentissage plus efficace. 

Lorsque vous utilisez MiniSom pour créer une carte auto-organisatrice (SOM), il y a deux façons d'initialiser les poids des neurones en fonction des données :

• Initialisation aléatoire: Les poids initiaux des neurones sont tirés au hasard à partir des données d'entrée. Pour ce faire, nous appliquons la fonction .random_weights_init() au SOM.
• Initialisation de l'ACP: L'initialisation de l'analyse en composantes principales (ACP) utiliseles composantes principales des données d'entréepour initialiser les poids. Les poids initiaux des neurones couvrent les deux premières composantes principales. Cela permet souvent d'accélérer la convergence. 

Dans ce guide, nous utilisons l'initialisation de l'ACP. Pour appliquer l'initialisation PCA aux poids SOM, utilisez la fonction .pca_weights_init() comme indiqué ci-dessous :

som.pca_weights_init(data)

Formation du SOM

Le processus d'apprentissage met à jour les poids du SOM afin de minimiser la distance entre les neurones et les points de données. 

Nous expliquons ci-dessous le processus de formation itératif :

• Initialisation: Les vecteurs de poids de tous les neurones sont initialisés, généralement avec des valeurs aléatoires. Il est également possible d'initialiser les poids en échantillonnant la distribution des données d'entrée.
• Sélection des entrées: Un vecteur d'entrée est sélectionné (au hasard) dans l'ensemble de données d'apprentissage.
• Identification du BMU: Le neurone dont le vecteur de poids est le plus proche du vecteur d'entrée est identifié comme étant le BMU. 
• Mise à jour sur les quartiers: Le BMU et ses neurones voisins mettent à jour leurs vecteurs de poids. Le taux d'apprentissage et la fonction de voisinage déterminent quels neurones sont mis à jour et dans quelle mesure. Au pas d'itération tétant donné le vecteur d'entrée xle vecteur de poids du neurone i sous la forme de w_ile taux d'apprentissage (t)et la fonction de voisinage h_bi (cette fonction quantifie l'étendue de la mise à jour pour le neurone i compte tenu du neurone BMU b), la formule de mise à jour du poids du neurone i est exprimée comme suit :
• Taux de décroissance du taux d'apprentissage et du rayon de voisinage: Le taux d'apprentissage et le rayon de voisinage diminuent avec le temps. Dans les premières itérations, le processus de formation procède à des ajustements plus importants sur un voisinage plus large. Les itérations ultérieures permettent d'affiner les poids en apportant des modifications moins importantes aux poids des neurones adjacents. Cela permet à la carte de se stabiliser et de converger. 

Pour entraîner le SOM, nous présentons le modèle avec les données d'entrée. Pour ce faire, nous avons le choix entre deux approches : 

• Prélevez des échantillons au hasard dans les données d'entrée. La fonction .train_random() met en œuvre cette technique.
• Parcourez séquentiellement les vecteurs des données d'entrée. Cette opération est réalisée à l'aide de la fonction .train_batch().

Ces fonctions acceptent les données d'entrée et le nombre d'itérations comme paramètres. Dans ce guide, nous utilisons la fonction .train_random() . Déclarez le nombre d'itérations comme une constante et transmettez-le à la fonction d'apprentissage : 

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

Après avoir exécuté le script et terminé la formation, un message indiquant l'erreur de quantification s'affiche :

quantization error: 0.05357240680504421 

L'erreur de quantification indique la quantité d'informations perdues lorsque le SOM quantifie (réduit la dimensionnalité) les données. Une erreur de quantification importante indique une plus grande distance entre les neurones et les points de données. Cela signifie également que le regroupement est moins fiable. 

Visualisation des neurones SOM 

Nous disposons maintenant d'un modèle SOM formé. Pour la visualiser, nous utilisons une carte de distance (également connue sous le nom de U-matrix). La carte de distance affiche les neurones du SOM sous la forme d'une grille de cellules. La couleur de chaque cellule représente sa distance par rapport aux neurones voisins. 

La carte des distances est une grille ayant les mêmes dimensions que le SOM. Chaque cellule de la carte des distances est la somme normalisée des distances (euclidiennes) entre un neurone et ses voisins. 

Accédez au site SOM distance map en utilisant la fonction .distance_map(). Pour générer la matrice U, nous suivons les étapes suivantes :

• Utilisez pyplot pour créer une figure ayant les mêmes dimensions que le SOM. Dans cet exemple, les dimensions sont 8x8. 
• Tracez la carte des distances à l'aide de matplotlib en utilisant la fonction .pcolor(). Dans cet exemple, nous utilisons gist_yarg comme palette de couleurs. 
• Affichez le site colorbar, un index qui associe différentes couleurs à différentes valeurs scalaires. Dans ce cas, les distances étant normalisées, les valeurs de la distance scalaire sont comprises entre 0 et 1. 

Le code ci-dessous met en œuvre ces étapes : 

# create the grid
plt.figure(figsize=(8, 8))
#plot the distance map
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# show the color bar
plt.colorbar()
plt.show()

Dans cet exemple, la matrice U utilise un schéma de couleurs monotone. Il peut être compris à l'aide des lignes directrices suivantes :

• Les tons clairs représentent des neurones proches les uns des autres, et les tons foncés des neurones plus éloignés les uns des autres. 
• Les groupes de teintes plus claires peuvent être interprétés comme des grappes. Les nœuds sombres entre les groupes peuvent être interprétés comme les limites entre les groupes. 

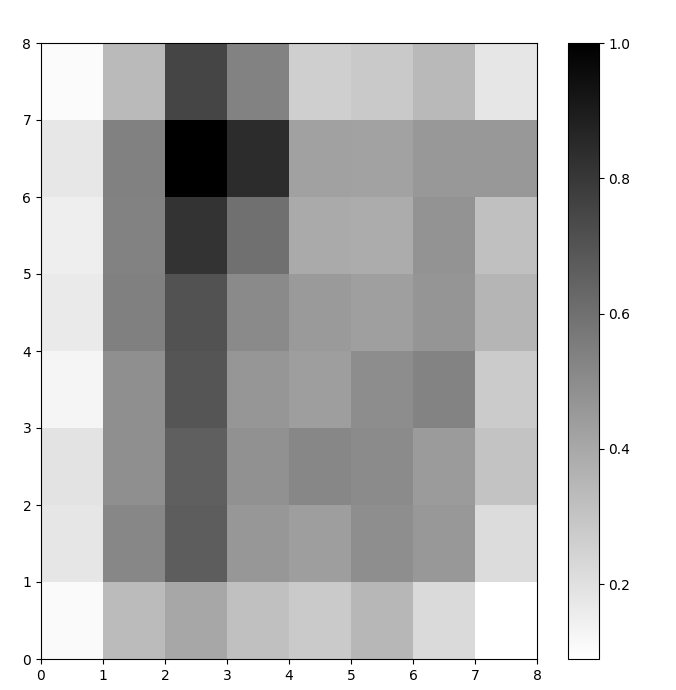
Figure 1 : Matrice U d'une SOM entraînée sur l'ensemble de données Iris (image de l'auteur)

Évaluation des résultats du regroupement SOM

La figure précédente illustre graphiquement les neurones du SOM. Dans cette section, nous montrons comment visualiser la façon dont le SOM a regroupé les données. 

Identifier les grappes

Nous superposons des marqueurs à la matrice U ci-dessus pour indiquer la classe d'Iris que chaque cellule (neurone) représente. Pour ce faire :

• Comme précédemment, créez une figure 8x8 à l'aide de pyplot, tracez la carte des distances et affichez la barre de couleurs.
• Spécifiez un tableau de trois marqueurs matplotlib, un pour chaque classe de plante Iris. 
• Spécifiez un tableau de trois codes de couleur matplotlib, un pour chaque classe de plante Iris .
• Tracez itérativement le neurone gagnant pour chaque point de données :
• Déterminez les (coordonnées du) neurone gagnant pour chaque point de données à l'aide de la fonction .winner(). 
• Représentez la position de chaque neurone gagnant au milieu de chaque cellule de la grille. w[0] et w[1] indiquent les coordonnées X et Y du neurone, respectivement. Une valeur de 0,5 est ajoutée à chaque coordonnée pour la placer au milieu de la cellule. 

Le code ci-dessous montre comment procéder :

# plot the distance map
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# create the markers and colors for each class
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# plot the winning neuron for each data point
for count, datapoint in enumerate(data):
    # get the winner
    w = som.winner(datapoint)  
    # place a marker on the winning position for the sample data point
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

L'image obtenue est présentée ci-dessous : 

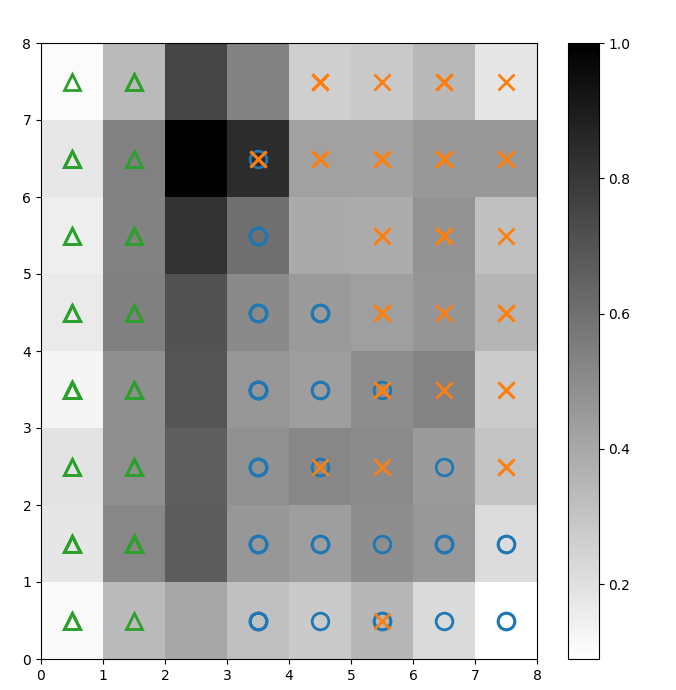
Figure 2 : Matrice U superposée aux marqueurs de classe (image de l'auteur)

D'après la documentation du jeu de données Iris, "une classe est linéairement séparable des deux autres ; ces dernières ne sont pas linéairement séparables les unes des autres". Dans la matrice U ci-dessus, ces trois classes sont représentées par trois marqueurs : le triangle, le cercle et la croix. 

Remarquez qu'il n'y a pas de limite claire entre les cercles bleus et les croix orange. En outre, dans de nombreuses cellules, deux classes sont superposées sur le même neurone. Cela signifie que le neurone est équidistant des deux classes. 

Visualisation du résultat du regroupement

Un SOM est un modèle de regroupement. Les points de données similaires correspondent au même neurone. Les points de données de la même classe sont dirigés vers un groupe de neurones voisins. Nous traçons tous les points de données sur la grille SOM afin de mieux étudier le comportement de regroupement. 

Les étapes suivantes décrivent comment créer ce diagramme de dispersion :

• Obtenez les coordonnées X et Y du neurone gagnant pour chaque point de données. 
• Tracez la carte des distances, comme nous l'avons fait pour la Figure 1.
• Utilisez plt.scatter() pour créer un diagramme de dispersion de tous les neurones gagnants pour chaque point de données. Ajoutez un décalage aléatoire à chaque point pour éviter les chevauchements entre les points de données d'une même cellule.

Nous mettons en œuvre ces étapes dans le code ci-dessous : 

# get the X and Y coordinates of the winning neuron for each data pointw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# plot the distance map
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# make a scatter plot of all the winning neurons for each data point
# add a random offset to each point to avoid overlaps
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

Le graphique suivant montre le diagramme de dispersion de la sortie :

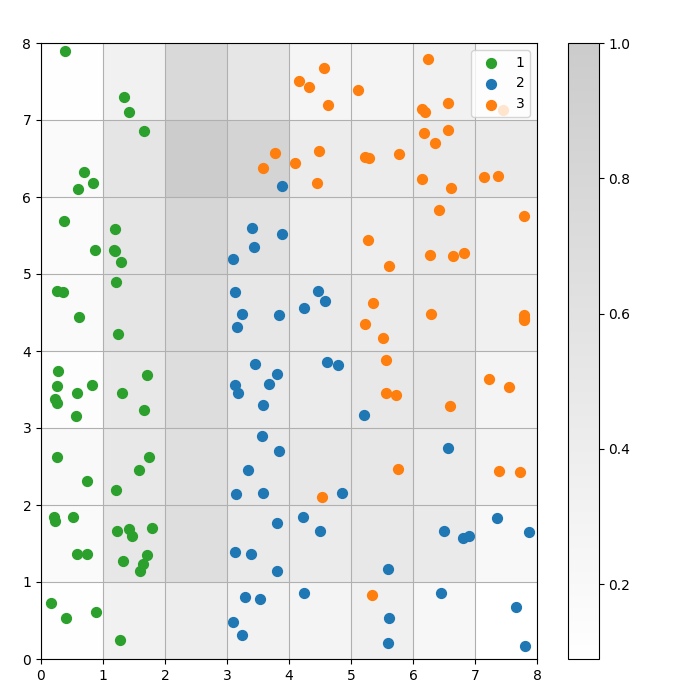Figure 3 : Diagramme de dispersion des points de données dans les cellules (image de l'auteur)

Dans le nuage de points ci-dessus, observez que : 

• Certaines cellules contiennent à la fois des points bleus et des points orange. 
• Les points verts sont clairement séparés du reste des données, mais les points bleus et orange ne le sont pas. 
• Les observations ci-dessus concordent avec le fait qu'un seul des trois groupes de l'ensemble de données Iris est clairement délimité. 
• En Figure 1les nœuds sombres entre les grappes (qui peuvent être interprétés comme les limites entre les grappes) correspondent aux cellules vides dans le diagramme de dispersion.

Vous pouvez accéder au code complet et l'exécuter sur ce cahier DataLab. 

Ajustement du modèle SOM

Les sections précédentes ont montré comment créer et entraîner un modèle SOM et comment étudier les résultats visuellement. Dans cette section, nous expliquons comment ajuster les performances des modèles SOM. 

Hyperparamètres clés à ajuster

Comme pour tout modèle d'apprentissage automatique, les hyperparamètres ont un impact considérable sur les performances du modèle. 

Voici quelques-uns des hyperparamètres importants pour l'apprentissage des SOM :

• La taillede la grille détermine la taille de la carte. Le nombre de neurones dans une carte dont la taille de la grille est AxB est A*B. 
• Le taux d'apprentissage détermine dans quelle mesure les poids sont modifiés à chaque itération. Nous fixons le taux d'apprentissage initial, qui diminue au fil du temps en fonction de la fonction de décroissance. 
• La fonction fonction de décroissance détermine la mesure dans laquelle le taux d'apprentissage est réduit à chaque itération suivante.
• La fonction de voisinage est une fonction mathématique qui spécifie quels neurones doivent être considérés comme les voisins de la BMU.
• L'écart-type spécifie la dispersion de la fonction de voisinage. Par exemple, une fonction de voisinage gaussienne ayant un écart-type élevé aura un voisinage plus large que la même fonction ayant un écart-type plus faible. Nous fixons l'écart-type initial, qui diminue au fil du temps en fonction de la fonction de décroissance sigma. 
• La décroissance sigma permet de contrôler la réduction de l'écart-type à chaque itération suivante.
• Le nombre d'itérations d'apprentissage détermine combien de fois les poids sont mis à jour. À chaque itération de formation, les poids des neurones sont mis à jour une fois. 
• La fonction fonction de distance est une fonction mathématique qui calcule la distance entre les neurones et les points de données.
• La topologie détermine la disposition de la structure de la grille. Les neurones de la grille peuvent être disposés de manière rectangulaire ou hexagonale. 

Dans la section suivante, nous discutons des lignes directrices pour la définition des valeurs de ces hyperparamètres. 

Impact de l'ajustement des hyperparamètres

Les valeurs des hyperparamètres doivent être déterminées en fonction du modèle et de l'ensemble des données. Dans une certaine mesure, la détermination de ces valeurs est un processus d'essais et d'erreurs. Dans cette section, nous donnons des indications pour le réglage de chaque hyperparamètre. À côté de chaque hyperparamètre, nous mentionnons (entre parenthèses) les constantes Python respectives utilisées dans le code d'exemple.

• Taille de la grille (SOM_X_AXIS_NODES et SOM_X_AXIS_NODES) : La taille de la grille dépend de la taille de l'ensemble de données. En règle générale, pour un ensemble de données de taille N, la grille doit contenir environ 5*sqrt(N) neurones. Par exemple, si l'ensemble de données comporte 150 échantillons, la grille doit contenir 5*sqrt(150) = environ 61 neurones. Dans ce tutoriel, l'ensemble de données Iris comporte 150 lignes et nous utilisons une grille de 8x8. 
• Taux d'apprentissage initial (ALPHA) : Un taux plus élevé accélère la convergence, tandis que des taux plus faibles sont utilisés pour des ajustements plus fins après les premières itérations. Le taux d'apprentissage initial doit être suffisamment élevé pour permettre une adaptation rapide, mais pas trop pour ne pas dépasser les valeurs de poids optimales. Dans cet article, le taux d'apprentissage initial est de 0,5. 
• Écart-type initial (SIGMA0) : Il détermine la taille initiale ou l'étendue du quartier. Une valeur plus élevée prend en compte des modèles plus globaux. Dans cet exemple, nous utilisons un écart-type de départ de 1,5. 
• Pour le taux de décroissance (DECAY_FUNC ) et le taux de décroissance sigma (SIGMA_DECAY_FUNC ), nous pouvons choisir parmi trois types de fonctions de décroissance :
• Décroissance inverse: Cette fonction convient si les données présentent des motifs à la fois globaux et locaux. Dans ce cas, nous avons besoin d'une phase plus longue d'apprentissage général avant de nous concentrer sur les modèles locaux. 
• Décroissance linéaire: C'est une bonne chose pour les ensembles de données pour lesquels nous voulons une taille de voisinage stable et uniforme ou une réduction du taux d'apprentissage. C'est utile si les données ne nécessitent pas beaucoup d'ajustements.
• Décroissance asymptotique: Cette fonction est utile si les données sont complexes et à haute dimension. Dans ce cas, il est préférable de consacrer plus de temps à l'exploration globale avant de passer progressivement à des détails plus fins. 
• Fonction de voisinage (NEIGHBORHOOD_FUNC) : Le choix par défaut de la fonction de voisinage est la fonction gaussienne. D'autres fonctions, expliquées ci-dessous, sont également utilisées. 
• Gaussien (par défaut) : Il s'agit d'une courbe en forme de cloche. Le degré de mise à jour d'un neurone diminue progressivement au fur et à mesure que sa distance par rapport au neurone gagnant augmente. Il assure une transition douce et continue et préserve la topologie des données. Il convient à la plupart des usages généraux en raison de son comportement stable et prévisible.
• Bulle: Cette fonction crée un quartier de largeur fixe. Tous les neurones situés dans ce voisinage sont mis à jour de la même manière, et les neurones situés en dehors de ce voisinage ne sont pas mis à jour (pour un point de données donné). Elle est moins coûteuse en termes de calcul et plus facile à mettre en œuvre. Elle est utile pour les cartes plus petites où les limites nettes des quartiers ne compromettent pas l'efficacité du regroupement. 
• Chapeau mexicain: Il comporte une région positive centrale entourée d'une région négative. Les neurones proches du BMU sont mis à jour pour se rapprocher du point de données, et les neurones plus éloignés sont mis à jour pour s'éloigner du point de données. Cette technique permet d'améliorer le contraste et de rendre plus nettes les caractéristiques de la carte. Comme il met l'accent sur des groupes distincts, il est efficace dans les tâches de reconnaissance des formes où une séparation claire des groupes est souhaitée.
• Triangle: Cette fonction définit la taille du voisinage sous la forme d'un triangle, le BMU ayant la plus grande influence. Elle diminue linéairement avec la distance par rapport à la BMU. Il est utilisé pour le regroupement de données avec des transitions graduelles entre les groupes ou les caractéristiques, telles que les images, la parole ou les données de séries temporelles, où les points de données voisins sont censés partager des caractéristiques similaires. 
• Fonction de distance (DISTANCE_FUNC) : Pour mesurer la distance entre les neurones et les points de données, nous avons le choix entre 4 méthodes :
• Distance euclidienne (choix par défaut) : Utile lorsque les données sont continues et que l'on souhaite mesurer la distance en ligne droite. Elle convient à la plupart des tâches générales, en particulier lorsque les points de données sont uniformément répartis et liés dans l'espace.
• Distance cosinusoïdale: Bon choix pour les textes ou les données éparses à haute dimension où l'angle entre les vecteurs est plus important que la magnitude. Il est utile pour comparer la directionnalité des données.
• Distance de Manhattan: Idéal lorsque les points de données se trouvent sur une grille ou un treillis (par exemple, les pâtés de maisons). Elle est moins sensible aux valeurs aberrantes que la distance euclidienne.
• Distance de Chebyshev: Convient aux situations où le mouvement peut se produire dans n'importe quelle direction (par exemple, distances de l'échiquier). Elle est utile pour les espaces discrets où l'on souhaite privilégier la différence d'axe maximale.
• Topologie (TOPOLOGY) : Dans une grille, les neurones peuvent être disposés selon une structure hexagonale ou rectangulaire : 
• Rectangulaire (par défaut) : chaque neurone a 4 voisins immédiats. C'est le bon choix lorsque les données n'ont pas de relation spatiale claire. Elle est également plus simple sur le plan informatique. 
• Hexagonal: chaque neurone a 6 voisins. C'est l'option préférée si les données ont des relations spatiales mieux représentées par une grille hexagonale. C'est le cas pour les distributions de données circulaires ou angulaires.
• Nombre d'itérations de formation (N_ITERATIONS) : En principe, des temps d'apprentissage plus longs permettent de réduire les erreurs et de mieux aligner les poids sur les données d'entrée. Cependant, la performance du modèle augmente asymptotiquement avec le nombre d'itérations. Ainsi, après un certain nombre d'itérations, l'augmentation des performances due aux interactions ultérieures n'est que marginale. Le choix du nombre correct d'itérations demande un peu d'expérimentation. Dans ce tutoriel, nous entraînons le modèle sur 5000 itérations. 

Pour déterminer la bonne configuration des hyperparamètres, nous vous recommandons d'expérimenter différentes options sur un sous-ensemble plus petit des données.

Conclusion

Les cartes auto-organisatrices sont un outil robuste pour l'apprentissage non supervisé. Ils sont utilisés pour le regroupement, la réduction de la dimensionnalité, la détection des anomalies et la visualisation des données. Comme elles préservent les propriétés topologiques des données de haute dimension et les représentent sur une grille de dimension inférieure, les SOM facilitent la visualisation et l'interprétation d'ensembles de données complexes. 

Ce tutoriel a abordé les principes sous-jacents des SOM et a montré comment mettre en œuvre un SOM à l'aide de la bibliothèque MiniSom Python. Il a également montré comment analyser visuellement les résultats et expliqué les hyperparamètres importants utilisés pour former les SOMs et affiner leurs performances.