Mapas auto-organizáveis: Um guia intuitivo com exemplos em Python

Configurando o ambiente para o SOM

Antes de criar o SOM, precisamos preparar o ambiente com os pacotes necessários. 

Instalação de bibliotecas Python 

Precisamos desses pacotes: 

• O MiniSom é uma ferramenta Python baseada no NumPy que cria e treina SOMs. 
• O NumPy é usado para acessar funções matemáticas, como dividir matrizes, obter valores exclusivos, etc. 
• matplotlib é usado para traçar vários gráficos e tabelas para visualizar os dados. 
• O pacote datasets de sklearn é usado para importar conjuntos de dados nos quais você aplicará o SOM .
• O pacote MinMaxScaler de sklearn normaliza o conjunto de dados .

O trecho de código a seguir importa esses pacotes: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

Preparando o conjunto de dados

Neste tutorial, usamos o MiniSom para criar um SOM e, em seguida, treiná-lo no conjunto de dados IRIS canônico. Esse conjunto de dadosconsiste em 3 classes de plantas de íris. Cada classe tem 50 instâncias. Para preparar os dados, seguimos estas etapas: 

• Importe o conjunto de dados do Iris de sklearn,
• Extraia os vetores de dados e os escalares de destino. 
• Normalize os vetores de dados. Neste tutorial, usamos o MinMaxScaler do scikit-learn. 
• Declare um conjunto de rótulos para cada uma das três classes de plantas Iris. 

O código a seguir implementa essas etapas: 

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Implementação de mapas auto-organizáveis (SOM) em Python

Para implementar um SOM em Python, definimos e inicializamos a grade antes de treiná-la no conjunto de dados. Em seguida, podemos visualizar os neurônios treinados e o conjunto de dados agrupados. 

Definição da grade SOM

Conforme explicado anteriormente, um SOM é uma grade de neurônios. Usando o MiniSom, podemos criar grades bidimensionais. As dimensões X e Y da grade são o número de neurônios ao longo de cada eixo. Para definir a grade do SOM, também precisamos especificar:

• As dimensões X e Y da grade
• O número de variáveis de entrada - esse é o número de linhas de dados. 

Declare esses parâmetros como constantes Python:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

O código de exemplo abaixo ilustra como você pode declarar a grade usando o MiniSom:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

Os dois primeiros parâmetros são o número de neurônios ao longo dos eixos X e Y, e o terceiro parâmetro é o número de variáveis. 

Declaramos outros parâmetros e hiperparâmetros ao criar a grade SOM. Explicaremos isso mais adiante no tutorial. Por enquanto, declare esses parâmetros conforme mostrado abaixo: 

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

Crie um SOM usando esses parâmetros:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

Inicialização dos neurônios

O comando acima cria um SOM com pesos aleatórios para todos os neurônios. A inicialização dos neurônios com pesos extraídos dos dados (em vez de números aleatórios) pode tornar o processo de treinamento mais eficiente. 

Ao usar o MiniSom para criar um mapa de auto-organização (SOM), há duas maneiras de inicializar os pesos dos neurônios com base nos dados:

• Inicialização aleatória: Os pesos iniciais dos neurônios são extraídos aleatoriamente dos dados de entrada. Fazemos isso aplicando a função .random_weights_init() ao SOM .
• Inicialização do PCA: A inicialização da análise de componentes principais (PCA) usaos componentes principais dos dados de entradapara inicializar os pesos. Os pesos iniciais dos neurônios abrangem os dois primeiros componentes principais. Isso geralmente leva a uma convergência mais rápida. 

Neste guia, usamos a inicialização do PCA. Para aplicar a inicialização do PCA aos pesos do SOM, use a função .pca_weights_init(), conforme mostrado abaixo:

som.pca_weights_init(data)

Treinamento do SOM

O processo de treinamento atualiza os pesos do SOM para minimizar a distância entre os neurônios e os pontos de dados. 

A seguir, explicamos o processo de treinamento iterativo:

• Inicialização: Os vetores de peso de todos os neurônios são inicializados, normalmente com valores aleatórios. Também é possível inicializar os pesos por amostragem da distribuição de dados de entrada.
• Seleção de entrada: Um vetor de entrada é selecionado (aleatoriamente) do conjunto de dados de treinamento.
• Identificação da BMU: O neurônio com o vetor de peso mais próximo do vetor de entrada é identificado como a BMU. 
• Atualização da vizinhança: A BMU e seus neurônios vizinhos atualizam seus vetores de peso. A taxa de aprendizado e a função de vizinhança decidem quais neurônios são atualizados e em que quantidade. Na etapa de iteração tdado o vetor de entrada xo vetor de peso do neurônio i como w_i, a taxa de aprendizado (t)e a função de vizinhança h_bi (essa função quantifica a extensão da atualização do neurônio i dado o neurônio BMU b), a fórmula de atualização de peso para o neurônio i é expressa como:
• Taxa de decaimento da taxa de aprendizado e raio da vizinhança: Tanto a taxa de aprendizado quanto o raio da vizinhança diminuem com o tempo. Nas iterações anteriores, o processo de treinamento faz ajustes maiores em uma vizinhança maior. As iterações posteriores ajudam a ajustar os pesos, fazendo alterações menores nos pesos dos neurônios adjacentes. Isso permite que o mapa se estabilize e convirja. 

Para treinar o SOM, apresentamos o modelo com os dados de entrada. Você pode escolher uma das duas abordagens para fazer isso: 

• Escolha amostras aleatórias dos dados de entrada. A função .train_random() implementa essa técnica .
• Executar sequencialmente os vetores nos dados de entrada. Isso é feito usando a função .train_batch().

Essas funções aceitam os dados de entrada e o número de iterações como parâmetros. Neste guia, usamos a função .train_random() . Declare o número de iterações como uma constante e passe-o para a função de treinamento: 

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

Após a execução do script e a conclusão do treinamento, é exibida uma mensagem com o erro de quantização:

quantization error: 0.05357240680504421 

O erro de quantização indica a quantidade de informações perdidas quando o SOM quantiza (reduz a dimensionalidade) os dados. Um grande erro de quantização indica uma distância maior entre os neurônios e os pontos de dados. Isso também significa que o agrupamento é menos confiável. 

Visualização dos neurônios do SOM 

Agora temos um modelo SOM treinado. Para visualizá-lo, usamos um mapa de distância (também conhecido como U-matrix). O mapa de distância exibe os neurônios do SOM como uma grade de células. A cor de cada célula representa sua distância dos neurônios vizinhos. 

O mapa de distância é uma grade com as mesmas dimensões do SOM. Cada célula no mapa de distância é a soma normalizada das distâncias (euclidianas) entre um neurônio e seus vizinhos. 

Acesse o site SOM distance map usando a função .distance_map(). Para gerar a matriz U, seguimos estas etapas:

• Use o site pyplot para criar uma figura com as mesmas dimensões do SOM. Neste exemplo, as dimensões são 8x8. 
• Trace o mapa de distância usando o matplotlib com a função .pcolor(). Neste exemplo, usamos gist_yarg como o esquema de cores. 
• Exibir o colorbar, um índice que mapeia cores diferentes para valores escalares diferentes. Nesse caso, como as distâncias são normalizadas, os valores de distância escalar variam de 0 a 1. 

O código abaixo implementa essas etapas: 

# create the grid
plt.figure(figsize=(8, 8))
#plot the distance map
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# show the color bar
plt.colorbar()
plt.show()

Neste exemplo, a matriz U usa um esquema de cores monótono. Você pode entender isso usando estas diretrizes:

• Tons mais claros representam neurônios próximos e tons mais escuros representam neurônios mais distantes dos outros. 
• Grupos de tons mais claros podem ser interpretados como clusters. Os nós escuros entre os clusters podem ser interpretados como os limites entre os clusters. 

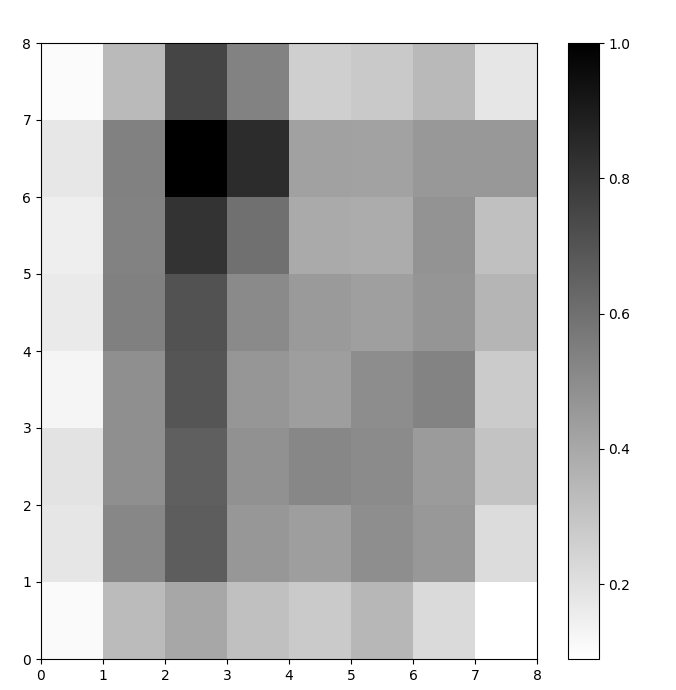
Figura 1: Matriz U do SOM treinado no conjunto de dados Iris (imagem do autor)

Avaliação dos resultados do SOM Clustering

A figura anterior ilustrou graficamente os neurônios do SOM. Nesta seção, mostramos como visualizar como o SOM agrupou os dados. 

Identificação de grupos

Sobrepomos marcadores sobre a matriz U acima para indicar a classe da planta Iris que cada célula (neurônio) representa. Para fazer isso:

• Como antes, crie uma figura 8x8 usando pyplot, trace o mapa de distância e mostre a barra de cores .
• Especifique uma matriz de três marcadores matplotlib, um para cada classe de planta Iris. 
• Especifique uma matriz de três códigos de cores matplotlib, um para cada classe de planta Iris.
• Trace iterativamente o neurônio vencedor para cada ponto de dados:
• Determine o neurônio vencedor (coordenadas do) para cada ponto de dados usando a função .winner(). 
• Trace a posição de cada neurônio vencedor no meio de cada célula da grade. w[0] e w[1] fornecem as coordenadas X e Y do neurônio, respectivamente. Um valor de 0,5 é adicionado a cada coordenada para plotá-la no meio da célula. 

O código abaixo mostra como você pode fazer isso:

# plot the distance map
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# create the markers and colors for each class
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# plot the winning neuron for each data point
for count, datapoint in enumerate(data):
    # get the winner
    w = som.winner(datapoint)  
    # place a marker on the winning position for the sample data point
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

A imagem resultante é mostrada abaixo: 

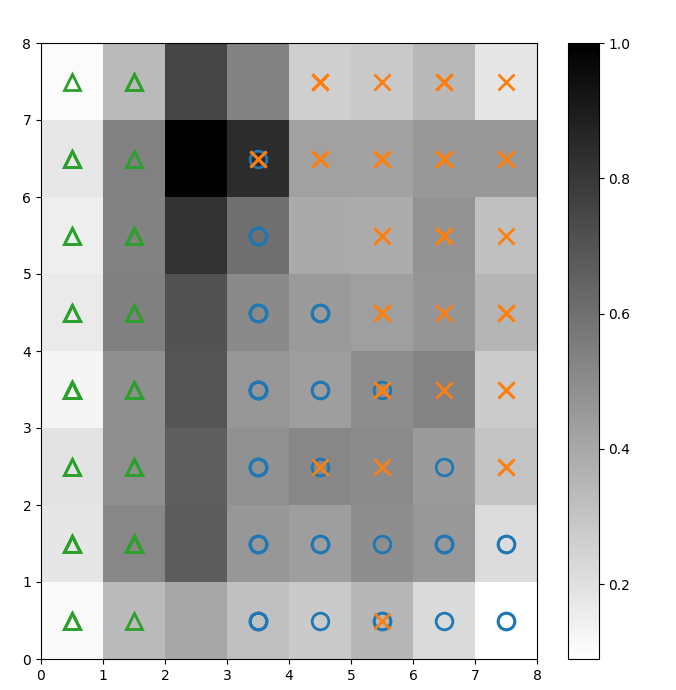
Figura 2: Matriz U sobreposta com marcadores de classe (imagem do autor)

Com base na documentação do conjunto de dados do Iris, "uma classe do é linearmente separável das outras duas; as últimas não são linearmente separáveis umas das outras". Na matriz U acima, essas três classes são representadas por três marcadores: triângulo, círculo e cruz. 

Observe que não há um limite claro entre os círculos azuis e as cruzes laranja. Além disso, duas classes são sobrepostas no mesmo neurônio em muitas células. Isso significa que o neurônio está equidistante de ambas as classes. 

Visualização do resultado do agrupamento

Um SOM é um modelo de agrupamento. Pontos de dados semelhantes são mapeados para o mesmo neurônio. Os pontos de dados da mesma classe são mapeados para um cluster de neurônios vizinhos. Traçamos todos os pontos de dados na grade do SOM para estudar melhor o comportamento de agrupamento. 

As etapas a seguir descrevem como você pode criar esse gráfico de dispersão:

• Obtenha as coordenadas X e Y do neurônio vencedor para cada ponto de dados. 
• Trace o mapa de distância, como fizemos para Figura 1.
• Use o site plt.scatter() para criar um gráfico de dispersão de todos os neurônios vencedores para cada ponto de dados. Adicione um deslocamento aleatório a cada ponto para evitar sobreposições entre pontos de dados na mesma célula.

Implementamos essas etapas no código abaixo: 

# get the X and Y coordinates of the winning neuron for each data pointw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# plot the distance map
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# make a scatter plot of all the winning neurons for each data point
# add a random offset to each point to avoid overlaps
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

O gráfico a seguir mostra o gráfico de dispersão de saída:

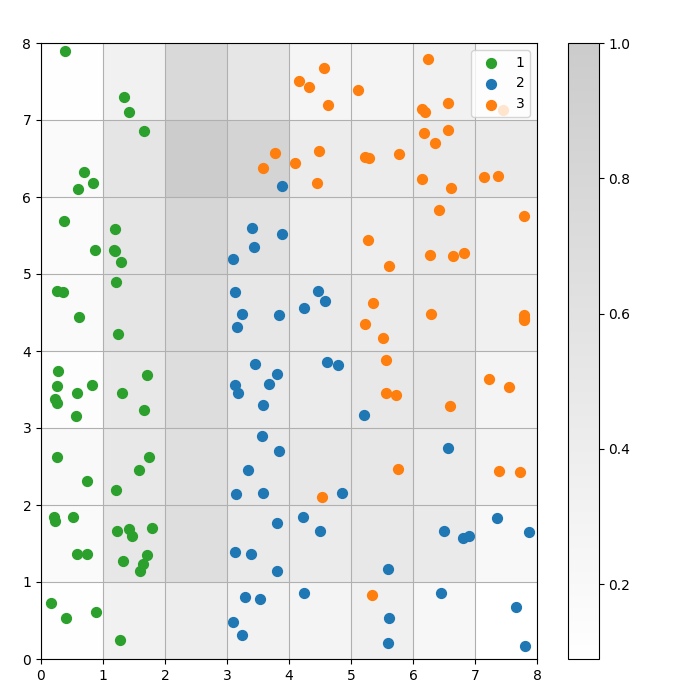Figura 3: Gráfico de dispersão de pontos de dados dentro das células (imagem do autor)

No gráfico de dispersão acima, observe que: 

• Algumas células contêm pontos azuis e laranja. 
• Os pontos verdes estão claramente separados do restante dos dados, mas os pontos azuis e laranja não estão claramente separados. 
• As observações acima se alinham ao fato de que apenas um dos três clusters no conjunto de dados do Iris tem um limite claro. 
• Em Figura 1os nós escuros entre os clusters (que podem ser interpretados como os limites entre os clusters) correspondem a células vazias no gráfico de dispersão.

Você pode acessar e executar o código completo neste notebook do DataLab. 

Ajuste do modelo SOM

As seções anteriores mostraram como criar e treinar um modelo SOM e como estudar os resultados visualmente. Nesta seção, discutiremos como ajustar o desempenho dos modelos SOM. 

Principais hiperparâmetros a serem ajustados

Como em qualquer modelo de aprendizado de máquina, os hiperparâmetros afetam consideravelmente o desempenho do modelo. 

Alguns dos hiperparâmetros importantes no treinamento de SOMs são:

• O tamanho da grade decide o tamanho do mapa. O número de neurônios em um mapa com um tamanho de grade AxB é A*B. 
• A taxa de aprendizado decide o quanto os pesos são alterados em cada iteração. Definimos a taxa de aprendizado inicial e ela diminui com o tempo de acordo com a função de decaimento. 
• A função de decaimento decide até que ponto a taxa de aprendizado é reduzida em cada iteração subsequente.
• A função de vizinhança é uma função matemática que especifica quais neurônios devem ser considerados como vizinhos da BMU.
• O desvio padrão especifica a dispersão da função de vizinhança. Por exemplo, uma função de vizinhança gaussiana com um desvio padrão alto terá uma vizinhança maior do que a mesma função com um desvio padrão menor. Definimos o desvio padrão inicial, que diminui com o tempo de acordo com a função de decaimento sigma. 
• O decaimento de sigma controla o quanto o desvio padrão é reduzido em cada iteração subsequente.
• O número de iterações de treinamento decide quantas vezes os pesos são atualizados. Em cada iteração de treinamento, os pesos dos neurônios são atualizados uma vez. 
• A função função de distância é uma função matemática que calcula a distância entre os neurônios e os pontos de dados.
• A topologia decide o layout da estrutura da grade. Os neurônios na grade podem ser dispostos em um padrão retangular ou hexagonal. 

Na próxima seção, discutiremos as diretrizes para definir os valores desses hiperparâmetros. 

Impacto do ajuste de hiperparâmetros

Os valores dos hiperparâmetros devem ser decididos com base no modelo e no conjunto de dados. Até certo ponto, a determinação desses valores é um processo de tentativa e erro. Nesta seção, fornecemos diretrizes para o ajuste de cada hiperparâmetro. Ao lado de cada hiperparâmetro, mencionamos (entre parênteses) as respectivas constantes Python usadas no código de exemplo.

• Tamanho da grade (SOM_X_AXIS_NODES e SOM_X_AXIS_NODES): O tamanho da grade depende do tamanho do conjunto de dados. A regra geral é que, com um conjunto de dados de tamanho N, a grade deve conter aproximadamente 5*sqrt(N) neurônios. Por exemplo, se o conjunto de dados tiver 150 amostras, a grade deverá conter 5*sqrt(150) = aproximadamente 61 neurônios. Neste tutorial, o conjunto de dados Iris tem 150 linhas e usamos uma grade 8x8. 
• Taxa de aprendizado inicial (ALPHA): Uma taxa mais alta acelera a convergência, enquanto taxas mais baixas são usadas para ajustes mais finos após as primeiras iterações. A taxa de aprendizado inicial deve ser grande o suficiente para permitir uma adaptação rápida, mas não tão grande que ultrapasse os valores ideais de peso. Neste artigo, a taxa de aprendizado inicial é de 0,5. 
• Desvio padrão inicial (SIGMA0): Ele determina o tamanho inicial ou a expansão da vizinhança. Um valor maior considera padrões mais globais. Neste exemplo, usamos um desvio padrão inicial de 1,5. 
• Para a taxa de decaimento (DECAY_FUNC ) e a taxa de decaimento sigma (SIGMA_DECAY_FUNC ), podemos escolher entre um dos três tipos de funções de decaimento :
• Decaimento inverso: Essa função é adequada se os dados tiverem padrões globais e locais. Nesses casos, precisamos de uma fase mais longa de aprendizado amplo antes de nos concentrarmos nos padrões locais. 
• Decaimento linear: Isso é bom para conjuntos de dados em que queremos um tamanho de vizinhança estável e uniforme ou uma redução da taxa de aprendizado. Isso é útil se os dados não precisarem de muito ajuste fino.
• Decaimento assintótico: Essa função é útil se os dados forem complexos e de alta dimensão. Nesses casos, é melhor dedicar mais tempo à exploração global antes de passar gradualmente para os detalhes mais finos. 
• Função de vizinhança (NEIGHBORHOOD_FUNC): A escolha padrão da função de vizinhança é a função Gaussiana. Outras funções, conforme explicado abaixo, também são usadas. 
• Gaussiano (padrão): Essa é uma curva em forma de sino. O grau de atualização de um neurônio diminui suavemente à medida que sua distância do neurônio vencedor aumenta. Ele oferece uma transição suave e contínua e preserva a topologia dos dados. Ele é adequado para a maioria das finalidades gerais devido ao seu comportamento estável e previsível.
• Bubble: Essa função cria uma vizinhança de largura fixa. Todos os neurônios dentro dessa vizinhança são atualizados igualmente, e os neurônios fora dessa vizinhança não são atualizados (para um determinado ponto de dados). Ele é computacionalmente mais barato e mais fácil de implementar. É útil para mapas menores em que os limites nítidos da vizinhança não comprometem o agrupamento eficaz. 
• Chapéu mexicano: Ele tem uma região central positiva cercada por uma região negativa. Os neurônios próximos à BMU são atualizados para se aproximarem do ponto de dados, e os neurônios mais distantes são atualizados para se afastarem do ponto de dados. Essa técnica aprimora o contraste e torna mais nítidas as características do mapa. Como ele enfatiza grupos distintos, é eficaz em tarefas de reconhecimento de padrões em que se deseja uma separação clara dos grupos.
• Triângulo: Essa função define o tamanho da vizinhança como um triângulo, com a BMU tendo a maior influência. Ele diminui linearmente com a distância da BMU. É usado para clusterizar dados com transições graduais entre clusters ou recursos, como dados de imagem, fala ou séries temporais, em que se espera que os pontos de dados vizinhos compartilhem características semelhantes. 
• Função de distância (DISTANCE_FUNC): Para medir a distância entre os neurônios e os pontos de dados, podemos escolher entre quatro métodos:
• Distância euclidiana (opção padrão): Útil quando os dados são contínuos e queremos medir a distância em linha reta. Ele é adequado para a maioria das tarefas gerais, especialmente quando os pontos de dados são distribuídos uniformemente e relacionados espacialmente.
• Distância do cosseno: Boa opção para texto ou dados esparsos de alta dimensão em que o ângulo entre os vetores é mais importante do que a magnitude. É útil para comparar a direcionalidade dos dados.
• Distância de Manhattan: Ideal quando os pontos de dados estão em uma grade ou malha (por exemplo, quarteirões da cidade). Isso é menos sensível a exceções do que a distância euclidiana.
• Distância de Chebyshev: Adequado para situações em que o movimento pode ocorrer em qualquer direção (por exemplo, distâncias de tabuleiro de xadrez). É útil para espaços discretos em que queremos priorizar a diferença máxima entre os eixos.
• Topologia (TOPOLOGY): Em uma grade, os neurônios podem ser dispostos em uma estrutura hexagonal ou retangular: 
• Rectangular (padrão): cada neurônio tem 4 vizinhos imediatos. Essa é a escolha certa quando os dados não têm uma relação espacial clara. Também é computacionalmente mais simples. 
• Hexagonal: cada neurônio tem 6 vizinhos. Essa é a opção preferida se os dados tiverem relações espaciais melhor representadas com uma grade hexagonal. Esse é o caso das distribuições de dados circulares ou angulares.
• Número de iterações de treinamento (N_ITERATIONS): Em princípio, tempos de treinamento mais longos levam a erros menores e a um melhor alinhamento dos pesos com os dados de entrada. No entanto, o desempenho do modelo aumenta assintoticamente com o número de iterações. Assim, após um determinado número de iterações, o aumento de desempenho das interações subsequentes é apenas marginal. Para decidir o número correto de iterações, você precisa fazer algumas experiências. Neste tutorial, treinamos o modelo em 5.000 iterações. 

Para determinar a configuração correta dos hiperparâmetros, recomendamos que você experimente várias opções em um subconjunto menor de dados.

Conclusão

Os mapas auto-organizáveis são uma ferramenta robusta para aprendizado não supervisionado. Eles são usados para agrupamento, redução de dimensionalidade, detecção de anomalias e visualização de dados. Como eles preservam as propriedades topológicas dos dados de alta dimensão e os representam em uma grade de dimensão inferior, os SOMs facilitam a visualização e a interpretação de conjuntos de dados complexos. 

Este tutorial discutiu os princípios subjacentes dos SOMs e mostrou como implementar um SOM usando a biblioteca MiniSom Python. Ele também demonstrou como analisar visualmente os resultados e explicou os hiperparâmetros importantes usados para treinar SOMs e ajustar seu desempenho.