Selbstorganisierende Karten: Ein intuitiver Leitfaden mit Python-Beispielen

Einrichten der Umgebung für SOM

Bevor wir das SOM erstellen, müssen wir die Umgebung mit den notwendigen Paketen vorbereiten. 

Installation der Python-Bibliotheken 

Wir brauchen diese Pakete: 

• MiniSom ist ein NumPy-basiertes Python-Tool, das SOMs erstellt und trainiert. 
• NumPy wird verwendet, um auf mathematische Funktionen zuzugreifen, z. B. um Arrays aufzuteilen, eindeutige Werte zu erhalten usw. 
• matplotlib wird verwendet, um verschiedene Diagramme und Tabellen zur Visualisierung der Daten zu erstellen. 
• Das Paket datasets von sklearn wird verwendet, um Datensätze zu importieren, auf die das SOM angewendet werden soll .
• Das Paket MinMaxScaler von sklearn normalisiert den Datensatz .

Der folgende Codeschnipsel importiert diese Pakete: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

Vorbereiten des Datensatzes

In diesem Lernprogramm verwenden wir MiniSom, um ein SOM zu erstellen und es dann auf dem kanonischen IRIS-Datensatzzu trainieren. Diesesaset besteht aus 3 Klassen von Schwertlilienpflanzen. Jede Klasse hat 50 Instanzen. Um die Daten vorzubereiten, gehen wir folgendermaßen vor: 

• Importiere den Iris-Datensatz von sklearn,
• Extrahiere die Datenvektoren und die Zielskalare. 
• Normalisiere die Datenvektoren. In diesem Lernprogramm verwenden wir den MinMaxScaler von scikit-learn. 
• Erkläre eine Reihe von Etiketten für jede der drei Klassen von Iris-Pflanzen. 

Der folgende Code setzt diese Schritte um: 

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Implementierung von Self-Organizing Maps (SOM) in Python

Um ein SOM in Python zu implementieren, definieren und initialisieren wir das Gitter, bevor wir es mit dem Datensatz trainieren. Wir können dann die trainierten Neuronen und den geclusterten Datensatz visualisieren. 

Festlegen des SOM-Gitters

Wie bereits erklärt, ist ein SOM ein Gitter aus Neuronen. Mit MiniSom können wir 2-dimensionale Raster erstellen. Die X- und Y-Dimensionen des Rasters sind die Anzahl der Neuronen entlang jeder Achse. Um das SOM-Gitter zu definieren, müssen wir auch angeben:

• Die X- und Y-Abmessungen des Rasters
• Die Anzahl der Eingabevariablen - das ist die Anzahl der Datenzeilen. 

Deklariere diese Parameter als Python-Konstanten:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

Der Beispielcode unten zeigt, wie du das Raster mit MiniSom deklarierst:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

Die ersten beiden Parameter sind die Anzahl der Neuronen entlang der X- und Y-Achse und der dritte Parameter ist die Anzahl der Variablen. 

Bei der Erstellung des SOM-Gitters geben wir weitere Parameter und Hyperparameter an. Wir werden diese später im Lernprogramm erklären. Deklariere diese Parameter zunächst wie unten gezeigt: 

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

Erstelle ein SOM mit diesen Parametern:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

Initialisierung der Neuronen

Der obige Befehl erstellt ein SOM mit zufälligen Gewichten für alle Neuronen. Die Initialisierung der Neuronen mit Gewichten aus den Daten (anstelle von Zufallszahlen) kann den Trainingsprozess effizienter machen. 

Wenn du MiniSom verwendest, um eine selbstorganisierende Karte (SOM) zu erstellen, gibt es zwei Möglichkeiten, die Gewichte der Neuronen auf der Grundlage der Daten zu initialisieren:

• Zufällige Initialisierung: Die Anfangsgewichte der Neuronen werden zufällig aus den Eingabedaten gezogen. Wir tun dies, indem wir die Funktion .random_weights_init() auf das SOM anwenden.
• PCA-Initialisierung: Die Initialisierung der Hauptkomponentenanalyse (PCA) verwendetdie Hauptkomponenten dereingangsdaten, um die Gewichte zu initialisieren. Die Anfangsgewichte der Neuronen umfassen die ersten beiden Hauptkomponenten. Das führt oft zu einer schnelleren Konvergenz. 

In diesem Leitfaden verwenden wir die PCA-Initialisierung. Um die PCA-Initialisierung auf die SOM-Gewichte anzuwenden, verwendest du die Funktion .pca_weights_init() wie unten gezeigt:

som.pca_weights_init(data)

Training der SOM

Der Trainingsprozess aktualisiert die SOM-Gewichte, um den Abstand zwischen den Neuronen und den Datenpunkten zu minimieren. 

Im Folgenden erklären wir den iterativen Ausbildungsprozess:

• Initialisierung: Die Gewichtsvektoren aller Neuronen werden initialisiert, normalerweise mit zufälligen Werten. Es ist auch möglich, die Gewichte durch Stichproben aus der Verteilung der Eingangsdaten zu initialisieren.
• Eingangsauswahl: Ein Eingangsvektor wird (zufällig) aus dem Trainingsdatensatz ausgewählt.
• BMU-Kennung: Das Neuron mit dem Gewichtsvektor, der dem Eingangsvektor am nächsten liegt, wird als BMU identifiziert. 
• Update für die Nachbarschaft: Die BMU und ihre benachbarten Neuronen aktualisieren ihre Gewichtsvektoren. Die Lernrate und die Nachbarschaftsfunktion entscheiden, welche Neuronen aktualisiert werden und um wie viel. Bei dem Iterationsschritt twird der Eingangsvektor xder Gewichtsvektor des Neurons i als w_i, die Lernrate (t)und die Nachbarschaftsfunktion h_bi (diese Funktion quantifiziert das Ausmaß der Aktualisierung für das Neuron i angesichts des BMU-Neurons b), die Formel zur Aktualisierung der Gewichte für Neuron i wie folgt ausgedrückt:
• Abklingrate der Lernrate und Nachbarschaftsradius: Sowohl die Lernrate als auch der Nachbarschaftsradius nehmen mit der Zeit ab. In den früheren Iterationen nimmt der Trainingsprozess größere Anpassungen in einer größeren Nachbarschaft vor. Spätere Iterationen helfen bei der Feinabstimmung der Gewichte, indem sie kleinere Änderungen an den Gewichten benachbarter Neuronen vornehmen. So kann sich die Karte stabilisieren und konvergieren. 

Um das SOM zu trainieren, präsentieren wir dem Modell die Eingabedaten. Dazu können wir zwischen zwei Ansätzen wählen: 

• Ziehe Stichproben nach dem Zufallsprinzip aus den Eingabedaten. Die Funktion .train_random() setzt diese Technik um .
• Gehe nacheinander die Vektoren in den Eingabedaten durch. Dies geschieht mit der Funktion .train_batch().

Diese Funktionen akzeptieren die Eingabedaten und die Anzahl der Iterationen als Parameter. In diesem Leitfaden verwenden wir die Funktion .train_random() . Deklariere die Anzahl der Iterationen als Konstante und übergebe sie an die Trainingsfunktion: 

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

Nachdem das Skript ausgeführt und das Training abgeschlossen wurde, wird eine Meldung mit dem Quantisierungsfehler angezeigt:

quantization error: 0.05357240680504421 

Der Quantisierungsfehler gibt an, wie viel Information verloren geht, wenn das SOM die Daten quantisiert (die Dimensionalität reduziert). Ein großer Quantisierungsfehler weist auf einen größeren Abstand zwischen den Neuronen und den Datenpunkten hin. Das bedeutet auch, dass das Clustering weniger zuverlässig ist. 

SOM-Neuronen visualisieren 

Wir haben jetzt ein trainiertes SOM-Modell. Um sie zu visualisieren, verwenden wir eine Distanzkarte (auch bekannt als U-Matrix). Die Distanzkarte zeigt die Neuronen des SOM als Gitter aus Zellen an. Die Farbe jeder Zelle steht für ihren Abstand zu den benachbarten Neuronen. 

Die Distanzkarte ist ein Raster mit denselben Abmessungen wie das SOM. Jede Zelle in der Distanzkarte ist die normalisierte Summe der (euklidischen) Distanzen zwischen einem Neuron und seinen Nachbarn. 

Rufe die Seite SOM distance map über die Funktion .distance_map() auf. Um die U-Matrix zu erstellen, gehen wir folgendermaßen vor:

• Verwende pyplot , um eine Figur mit denselben Abmessungen wie das SOM zu erstellen. In diesem Beispiel sind die Abmessungen 8x8. 
• Zeichne die Entfernungskarte mit matplotlib und der Funktion .pcolor(). In diesem Beispiel verwenden wir gist_yarg als Farbschema. 
• Zeige den colorbar an, einen Index, der verschiedene Farben verschiedenen Skalarwerten zuordnet. Da die Abstände in diesem Fall normalisiert sind, reichen die skalaren Abstandswerte von 0 bis 1. 

Der folgende Code setzt diese Schritte um: 

# create the grid
plt.figure(figsize=(8, 8))
#plot the distance map
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# show the color bar
plt.colorbar()
plt.show()

In diesem Beispiel verwendet die U-Matrix ein monotones Farbschema. Sie kann mit Hilfe dieser Richtlinien verstanden werden:

• Hellere Schattierungen stehen für eng beieinander liegende Neuronen und dunklere Schattierungen für Neuronen, die weiter von anderen entfernt sind. 
• Gruppen von helleren Schattierungen können als Cluster interpretiert werden. Dunkle Knoten zwischen den Clustern können als die Grenzen zwischen den Clustern interpretiert werden. 

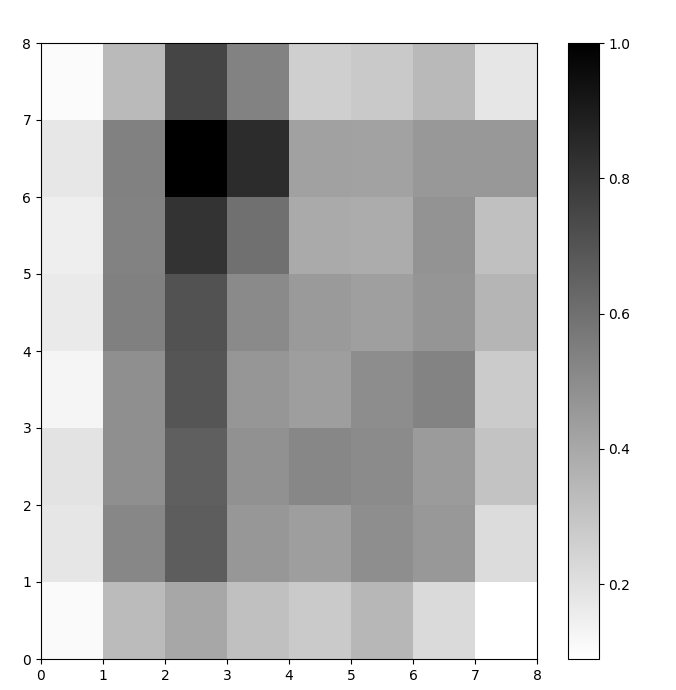
Abbildung 1: U-Matrix von SOM, trainiert mit dem Iris-Datensatz (Bild vom Autor)

Auswertung der SOM-Clustering-Ergebnisse

In der vorherigen Abbildung wurden die Neuronen des SOM grafisch dargestellt. In diesem Abschnitt zeigen wir, wie das SOM die Daten geclustert hat. 

Identifizierung von Clustern

Wir überlagern die obige U-Matrix mit Markierungen, um zu kennzeichnen, welche Klasse der Iris-Pflanze jede Zelle (Neuron) repräsentiert. Um dies zu tun:

• Erstelle wie zuvor mit pyplot eine 8x8 Figur, zeichne die Entfernungskarte und zeige den Farbbalken .
• Gib ein Array mit drei Matplotlib-Markernan, einen für jede Klasse der Iris-Pflanze. 
• Gib ein Array mit drei Matplotlib-Farbcodes an, einen für jede Klasse der Iris-Pflanze.
• Zeichne iterativ das Gewinnerneuron für jeden Datenpunkt auf:
• Bestimme die (Koordinaten des) Gewinnerneurons für jeden Datenpunkt mithilfe der Funktion .winner(). 
• Zeichne die Position jedes Gewinnerneurons in der Mitte jeder Zelle des Rasters ein. w[0] und w[1] geben die X- bzw. Y-Koordinaten des Neurons an. Zu jeder Koordinate wird ein Wert von 0,5 hinzugefügt, damit sie in der Mitte der Zelle liegt. 

Der folgende Code zeigt, wie man das macht:

# plot the distance map
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# create the markers and colors for each class
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# plot the winning neuron for each data point
for count, datapoint in enumerate(data):
    # get the winner
    w = som.winner(datapoint)  
    # place a marker on the winning position for the sample data point
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

Das resultierende Bild ist unten abgebildet: 

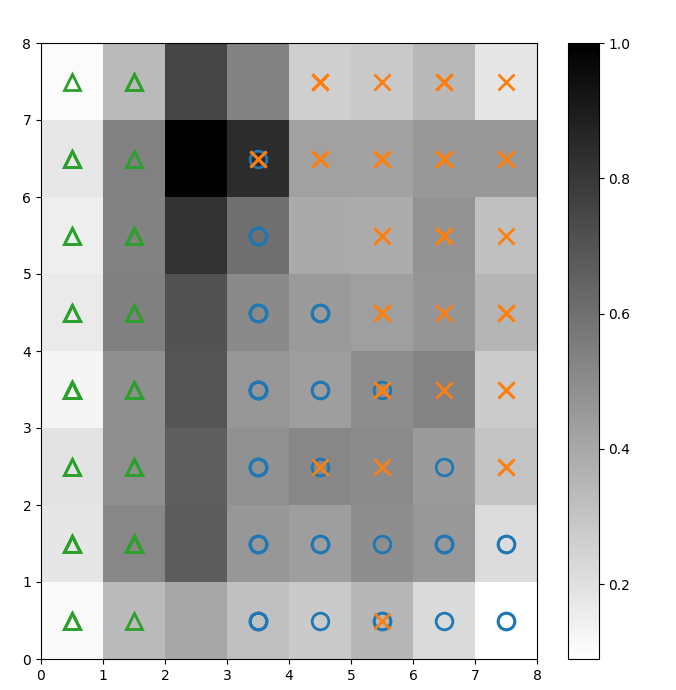
Abbildung 2: U-Matrix überlagert mit Klassenmarkern (Bild vom Autor)

In der Dokumentation des Iris-Datensatzes heißt es: "Eine Klasse ist linear von den anderen beiden trennbar; letztere sind nicht linear voneinander trennbar". In der U-Matrix oben werden diese drei Klassen durch drei Marker dargestellt - Dreieck, Kreis und Kreuz. 

Beachte, dass es keine klare Grenze zwischen den blauen Kreisen und den orangefarbenen Kreuzen gibt. Außerdem überlagern sich in vielen Zellen zwei Klassen auf demselben Neuron. Das bedeutet, dass das Neuron von beiden Klassen gleich weit entfernt ist. 

Visualisierung des Clustering-Ergebnisses

Ein SOM ist ein Clustermodell. Ähnliche Datenpunkte werden demselben Neuron zugeordnet. Datenpunkte der gleichen Klasse werden einem Cluster von benachbarten Neuronen zugeordnet. Wir stellen alle Datenpunkte auf dem SOM-Gitter dar, um das Clustering-Verhalten besser zu untersuchen. 

Die folgenden Schritte beschreiben, wie du dieses Streudiagramm erstellst:

• Erhalte die X- und Y-Koordinaten des Gewinnerneurons für jeden Datenpunkt. 
• Zeichne die Entfernungskarte, wie wir es für Abbildung 1.
• Verwende plt.scatter(), um ein Streudiagramm mit allen gewinnenden Neuronen für jeden Datenpunkt zu erstellen. Füge zu jedem Punkt einen zufälligen Versatz hinzu, um Überschneidungen zwischen Datenpunkten innerhalb derselben Zelle zu vermeiden.

Wir setzen diese Schritte im folgenden Code um: 

# get the X and Y coordinates of the winning neuron for each data pointw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# plot the distance map
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# make a scatter plot of all the winning neurons for each data point
# add a random offset to each point to avoid overlaps
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

Das folgende Diagramm zeigt die Streuung der Ergebnisse:

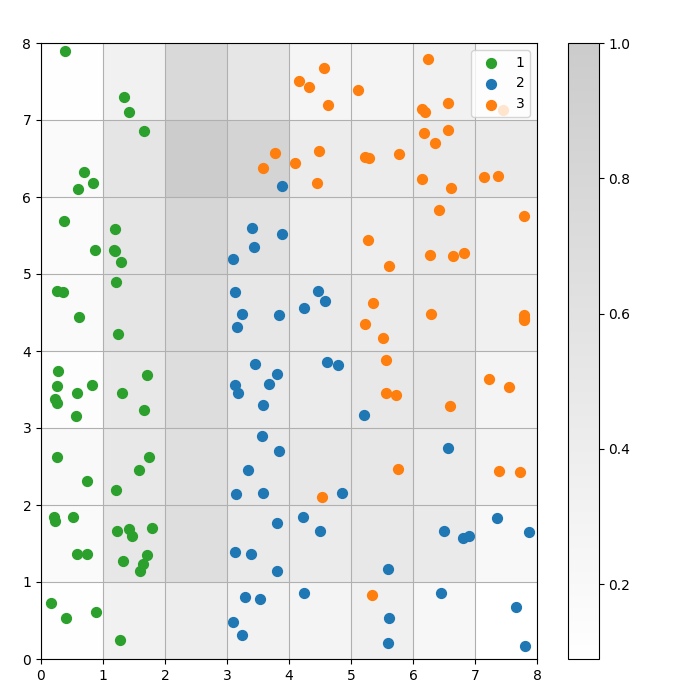Abbildung 3: Streudiagramm von Datenpunkten innerhalb von Zellen (Bild vom Autor)

Im obigen Streudiagramm kannst du sehen, dass: 

• Einige Zellen enthalten sowohl blaue als auch orangefarbene Punkte. 
• Die grünen Punkte sind klar vom Rest der Daten getrennt, aber die blauen und orangefarbenen Punkte sind nicht sauber getrennt. 
• Die obigen Beobachtungen stimmen mit der Tatsache überein, dass nur einer der drei Cluster im Iris-Datensatz eine klare Grenze hat. 
• Unter Abbildung 1stimmen die dunklen Knoten zwischen den Clustern (die als die Grenzen zwischen den Clustern interpretiert werden können) mit den leeren Zellen im Streudiagramm überein.

Du kannst den kompletten Code auf diesem DataLab-Notebook aufrufen und ausführen. 

Abstimmung des SOM-Modells

In den vorherigen Abschnitten wurde gezeigt, wie man ein SOM-Modell erstellt und trainiert und wie man die Ergebnisse visuell untersucht. In diesem Abschnitt erörtern wir, wie die Leistung von SOM-Modellen optimiert werden kann. 

Wichtige Hyperparameter zum Abstimmen

Wie bei jedem maschinellen Lernmodell haben die Hyperparameter einen erheblichen Einfluss auf die Leistung des Modells. 

Einige der Hyperparameter, die beim Training von SOMs wichtig sind, sind:

• Die Rastergröße bestimmt die Größe der Karte. Die Anzahl der Neuronen in einer Karte mit einer Gittergröße von AxB ist A*B. 
• Die Lernrate bestimmt, wie stark die Gewichte in jeder Iteration verändert werden. Wir legen die anfängliche Lernrate fest, die mit der Zeit gemäß der Abklingfunktion abnimmt. 
• Die Abklingfunktion bestimmt, wie stark die Lernrate in jeder nachfolgenden Iteration verringert wird.
• Die Nachbarschaftsfunktion ist eine mathematische Funktion, die angibt, welche Neuronen als Nachbarn der BMU betrachtet werden sollen.
• Die Standardabweichung gibt die Streuung der Nachbarschaftsfunktion an. Zum Beispiel hat eine Gaußsche Nachbarschaftsfunktion mit einer hohen Standardabweichung eine größere Nachbarschaft als die gleiche Funktion mit einer kleineren Standardabweichung. Wir legen die anfängliche Standardabweichung fest, die mit der Zeit gemäß der Sigma-Abklingfunktion abnimmt. 
• Der sigma decay Funktion steuert, wie stark die Standardabweichung in jeder nachfolgenden Iteration verringert wird.
• Die Anzahl der Trainingswiederholungen bestimmt, wie oft die Gewichte aktualisiert werden. In jeder Trainingsiteration werden die Neuronengewichte einmal aktualisiert. 
• Die Abstandsfunktion ist eine mathematische Funktion, die den Abstand zwischen Neuronen und Datenpunkten berechnet.
• Die Topologie bestimmt das Layout der Gitterstruktur. Die Neuronen im Gitter können in einem rechteckigen oder sechseckigen Muster angeordnet sein. 

Im nächsten Abschnitt besprechen wir Richtlinien für die Festlegung der Werte dieser Hyperparameter. 

Auswirkungen der Abstimmung der Hyperparameter

Die Hyperparameterwerte sollten auf der Grundlage des Modells und des Datensatzes festgelegt werden. Bis zu einem gewissen Grad ist die Bestimmung dieser Werte ein Prozess von Versuch und Irrtum. In diesem Abschnitt geben wir Richtlinien für die Abstimmung der einzelnen Hyperparameter an. Neben jedem Hyperparameter stehen (in Klammern) die jeweiligen Python-Konstanten, die im Beispielcode verwendet werden.

• Rastergröße (SOM_X_AXIS_NODES und SOM_X_AXIS_NODES): Die Größe des Rasters hängt von der Größe des Datensatzes ab. Als Faustregel gilt, dass das Raster bei einem Datensatz der Größe N ungefähr 5*sqrt(N) Neuronen enthalten sollte. Wenn der Datensatz zum Beispiel 150 Stichproben hat, sollte das Raster 5*sqrt(150) = ca. 61 Neuronen enthalten. In diesem Lernprogramm hat der Iris-Datensatz 150 Zeilen und wir verwenden ein 8x8-Gitter. 
• Anfängliche Lernrate (ALPHA): Eine höhere Rate beschleunigt die Konvergenz, während niedrigere Raten für feinere Anpassungen nach frühen Iterationen verwendet werden. Die anfängliche Lernrate sollte groß genug sein, um eine schnelle Anpassung zu ermöglichen, aber nicht so groß, dass sie über die optimalen Gewichtswerte hinausgeht. In diesem Artikel ist die anfängliche Lernrate 0,5. 
• Anfängliche Standardabweichung (SIGMA0): Sie bestimmt die anfängliche Größe oder Ausbreitung des Viertels. Ein größerer Wert berücksichtigt mehr globale Muster. In diesem Beispiel gehen wir von einer Standardabweichung von 1,5 aus. 
• Für die Zerfallsrate (DECAY_FUNC ) und die Sigma-Zerfallsrate (SIGMA_DECAY_FUNC ) können wir eine von drei Arten von Zerfallsfunktionen wählen :
• Inverser Zerfall: Diese Funktion ist geeignet, wenn die Daten sowohl globale als auch lokale Muster aufweisen. In solchen Fällen brauchen wir eine längere Phase des breiten Lernens, bevor wir uns auf lokale Muster konzentrieren. 
• Linearer Zerfall: Das ist gut für Datensätze, bei denen wir eine stetige und gleichmäßige Verringerung der Nachbarschaftsgröße oder Lernrate wünschen. Das ist nützlich, wenn die Daten nicht viel Feinschliff brauchen.
• Asymptotischer Zerfall: Diese Funktion ist nützlich, wenn die Daten komplex und hochdimensional sind. In solchen Fällen ist es besser, mehr Zeit auf die globale Erkundung zu verwenden, bevor man schrittweise zu feineren Details übergeht. 
• Nachbarschaftsfunktion (NEIGHBORHOOD_FUNC): Die Standardauswahl für die Nachbarschaftsfunktion ist die Gauß-Funktion. Andere Funktionen, wie unten erklärt, werden ebenfalls verwendet. 
• Gaussian (Standard): Dies ist eine glockenförmige Kurve. Das Ausmaß, in dem ein Neuron aktualisiert wird, nimmt mit zunehmendem Abstand zum Gewinnerneuron gleichmäßig ab. Sie sorgt für einen sanften und kontinuierlichen Übergang und bewahrt die Topologie der Daten. Aufgrund seines stabilen und vorhersehbaren Verhaltens ist es für die meisten allgemeinen Zwecke geeignet.
• Bubble: Diese Funktion erstellt eine Nachbarschaft mit fester Breite. Alle Neuronen innerhalb dieser Nachbarschaft werden gleichermaßen aktualisiert, und Neuronen außerhalb dieser Nachbarschaft werden (für einen bestimmten Datenpunkt) nicht aktualisiert. Sie ist rechnerisch günstiger und einfacher zu implementieren. Sie ist nützlich für kleinere Karten, bei denen scharfe Nachbarschaftsgrenzen eine effektive Clusterbildung nicht gefährden. 
• Mexikanischer Hut: Er hat einen zentralen positiven Bereich, der von einem negativen Bereich umgeben ist. Neuronen, die sich in der Nähe der BMU befinden, werden aktualisiert, um sich dem Datenpunkt zu nähern, und Neuronen, die weiter entfernt sind, werden aktualisiert, um sich vom Datenpunkt zu entfernen. Diese Technik verstärkt den Kontrast und schärft die Merkmale auf der Karte. Da sie unterschiedliche Cluster hervorhebt, eignet sie sich gut für Aufgaben der Mustererkennung, bei denen eine klare Trennung von Clustern erwünscht ist.
• Dreieck: Diese Funktion definiert die Größe der Nachbarschaft als ein Dreieck, wobei das BMU den größten Einfluss hat. Sie nimmt linear mit der Entfernung von der BMU ab. Sie wird für das Clustern von Daten mit allmählichen Übergängen zwischen Clustern oder Merkmalen verwendet, z. B. bei Bild-, Sprach- oder Zeitreihendaten, bei denen benachbarte Datenpunkte ähnliche Merkmale aufweisen sollen. 
• Distanzfunktion (DISTANCE_FUNC): Um den Abstand zwischen Neuronen und Datenpunkten zu messen, können wir zwischen 4 Methoden wählen:
• Euklidischer Abstand (Standardeinstellung): Nützlich, wenn die Daten kontinuierlich sind und wir eine geradlinige Entfernung messen wollen. Sie eignet sich für die meisten allgemeinen Aufgaben, vor allem wenn die Datenpunkte gleichmäßig verteilt sind und in einem räumlichen Zusammenhang stehen.
• Kosinusabstand: Eine gute Wahl für Text oder hochdimensionale spärliche Daten, bei denen der Winkel zwischen Vektoren wichtiger ist als der Betrag. Sie ist nützlich, um die Richtungsabhängigkeit von Daten zu vergleichen.
• Manhattan Entfernung: Ideal, wenn die Datenpunkte in einem Gitternetz liegen (z. B. Häuserblocks). Diese Methode ist weniger anfällig für Ausreißer als der euklidische Abstand.
• Tschebyscheff-Abstand: Geeignet für Situationen, in denen die Bewegung in jede Richtung erfolgen kann (z. B. bei Schachbrettabständen). Sie ist nützlich für diskrete Räume, in denen wir die maximale Achsendifferenz priorisieren wollen.
• Topologie (TOPOLOGY): In einem Gitter können die Neuronen in einer sechseckigen oder rechteckigen Struktur angeordnet sein: 
• Rechteckig (Standard): Jedes Neuron hat 4 direkte Nachbarn. Das ist die richtige Wahl, wenn die Daten keinen klaren räumlichen Bezug haben. Sie ist auch rechnerisch einfacher. 
• Hexagonal: Jedes Neuron hat 6 Nachbarn. Dies ist die bevorzugte Option, wenn die Daten räumliche Beziehungen aufweisen, die mit einem sechseckigen Gitter besser dargestellt werden können. Dies ist bei kreisförmigen oder winkelförmigen Datenverteilungen der Fall.
• Anzahl der Trainingswiederholungen (N_ITERATIONS): Im Prinzip führen längere Trainingszeiten zu geringeren Fehlern und einer besseren Anpassung der Gewichte an die Eingabedaten. Die Leistung des Modells steigt jedoch asymptotisch mit der Anzahl der Iterationen. Nach einer bestimmten Anzahl von Iterationen ist die Leistungssteigerung durch nachfolgende Interaktionen also nur noch marginal. Um die richtige Anzahl von Iterationen zu bestimmen, musst du ein wenig experimentieren. In diesem Lernprogramm trainieren wir das Modell über 5000 Iterationen. 

Um die richtige Konfiguration der Hyperparameter zu ermitteln, empfehlen wir, mit verschiedenen Optionen auf einer kleineren Teilmenge der Daten zu experimentieren.

Fazit

Selbstorganisierende Karten sind ein robustes Werkzeug für unüberwachtes Lernen. Sie werden für das Clustering, die Dimensionalitätsreduktion, die Erkennung von Anomalien und die Datenvisualisierung verwendet. Da sie die topologischen Eigenschaften von hochdimensionalen Daten bewahren und sie auf einem niedrigdimensionalen Raster darstellen, erleichtern SOMs die Visualisierung und Interpretation komplexer Datensätze. 

In diesem Tutorium wurden die grundlegenden Prinzipien von SOMs besprochen und gezeigt, wie man ein SOM mit der MiniSom Python-Bibliothek implementiert. Außerdem wurde gezeigt, wie die Ergebnisse visuell analysiert werden können, und es wurden die wichtigen Hyperparameter erklärt, die zum Trainieren von SOMs und zur Feinabstimmung ihrer Leistung verwendet werden.