Fonction d'activation Softmax en Python : Un guide complet

Les fonctions d'activation sont l'épine dorsale des réseaux neuronaux. Ce sont des composants importants qui introduisent la non-linéarité et permettent à ces réseaux d'apprendre des modèles complexes. La fonction d'activation softmax est importante, en particulier lorsqu'il s'agit de problèmes de classification multi-classes.

Alors que des alternatives comme Sigmoid et ReLU ont leurs cas d'utilisation spécifiques, la softmax est meilleure pour gérer les situations où les résultats doivent être interprétés comme des probabilités pour des classes mutuellement exclusives.

La fonction d'activation softmax transforme un vecteur entier de nombres en une distribution de probabilité. Cette caractéristique unique le rend indispensable pour les tâches où nous devons classer les entrées dans l'une des catégories possibles.

Des systèmes de reconnaissance d'images qui identifient des milliers de catégories d'objets aux modèles de traitement du langage naturel qui prédisent le mot suivant dans une phrase, la softmax fournit la base mathématique permettant de prendre des décisions parmi de multiples possibilités.

Dans cet article, nous verrons ce qu'est la fonction d'activation softmax, comment elle fonctionne mathématiquement et quand vous devez l'utiliser dans votre réseaux neuronaux de réseaux neuronaux. Nous examinerons également les implémentations pratiques en Python.

Qu'est-ce que la fonction d'activation Softmax ?

La fonction d'activation Softmax est une fonction mathématique qui transforme un vecteur de sorties brutes du modèle est une fonction mathématique qui transforme un vecteur de sorties brutes du modèle, appelées logits, en une distribution de probabilité. En termes plus simples, il prend un ensemble de nombres et les convertit en probabilités dont la somme est égale à 1.

Contrairement à certaines fonctions d'activation qui opèrent sur des valeurs individuelles de manière indépendante, la softmax travaille sur un vecteur entier de valeurs, les transformant collectivement en une distribution de probabilité dont tous les éléments ont une somme égale à 1.

Dans le contexte des réseaux neuronaux, le softmax est généralement appliqué à la dernière couche d'un réseau conçu pour la classification multi-classes. Lorsque nous avons plusieurs catégories possibles et que notre modèle doit indiquer la probabilité de chaque catégorie, la fonction d'activation softmax est le choix standard.

Comment fonctionne la fonction softmax ?

Les sorties brutes de la dernière couche d'un réseau neuronal sont souvent appelées "logits". Ces valeurs peuvent varier de l'infini négatif à l'infini positif et n'ont pas d'interprétation probabiliste directe. La fonction d'activation softmax transforme ces logits en une forme plus facile à interpréter :

1. En prenant l'exponentielle de chaque valeur d'entrée (ce qui garantit que toutes les valeurs sont positives).
2. Diviser chaque exponentielle par la somme de toutes les exponentielles (ce qui garantit que la somme des résultats est égale à 1).

Cette transformation est cruciale car elle nous permet d'interpréter la sortie du réseau comme une distribution de probabilité. Par exemple, si un réseau neuronal classe des images en trois catégories (chat, chien, oiseau), la sortie softmax pourrait être [0,7, 0,2, 0,1], indiquant une probabilité de 70 % pour le chat, 20 % pour le chien et 10 % pour l'oiseau.

La fonction d'activation softmax joue un rôle essentiel dans la création de distributions de probabilités valides car :

• Il garantit que toutes les valeurs de sortie sont comprises entre 0 et 1.
• Il garantit que la somme de tous les résultats est exactement égale à 1.
• Il préserve le classement des valeurs d'entrée (les valeurs d'entrée les plus importantes se traduisent par des probabilités plus élevées).
• Il accentue les différences entre les grandes valeurs tout en supprimant les différences entre les petites valeurs.

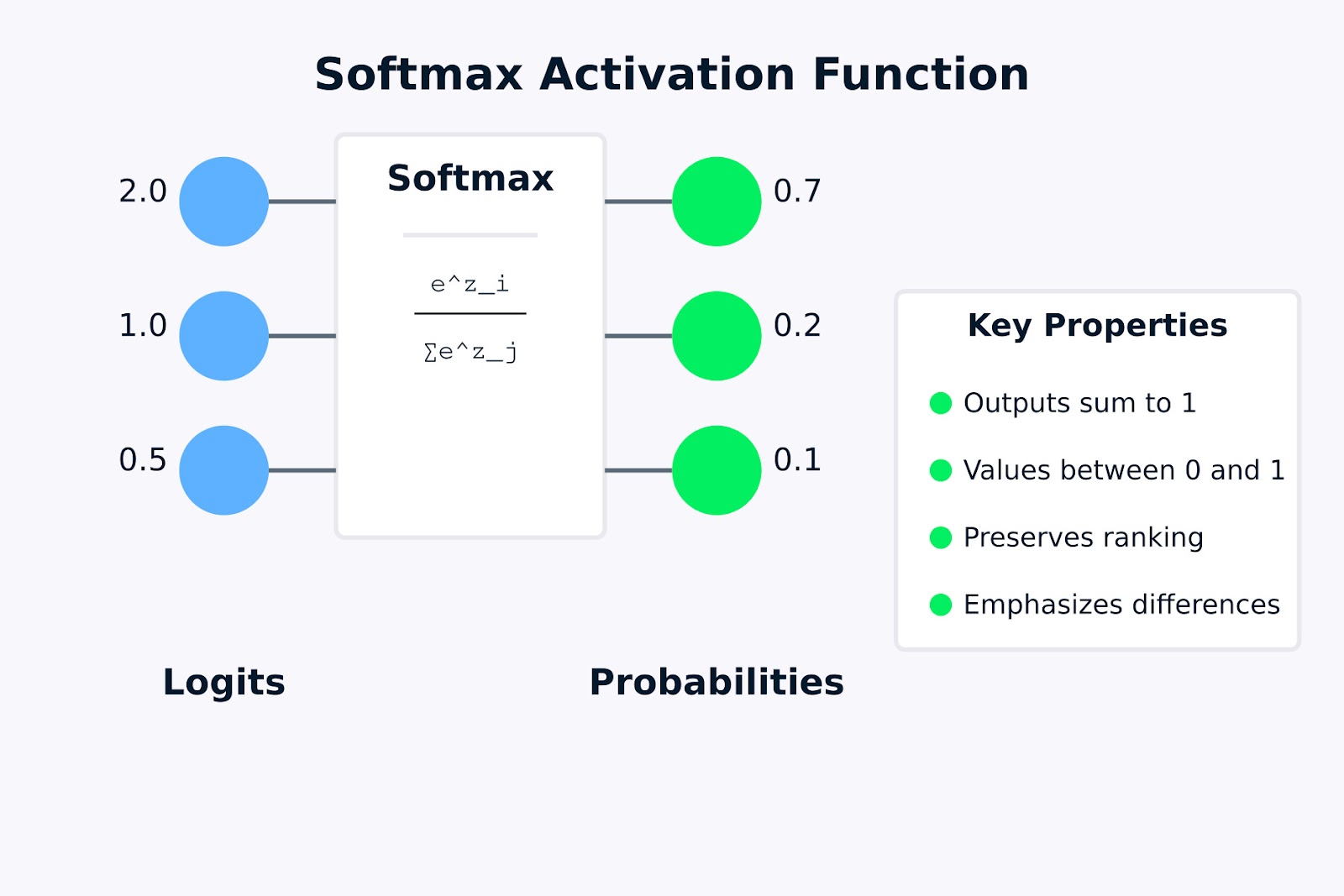
Fonction d'activation Softmax

La visualisation ci-dessus montre comment la fonction d'activation softmax transforme des logits bruts (les valeurs d'entrée 2,0, 1,0 et 0,5) en une distribution de probabilité (0,7, 0,2 et 0,1). La formule à l'intérieur de la boîte de softmax représente la manière dont chaque probabilité de sortie est calculée en prenant l'exponentielle d'une valeur d'entrée et en la divisant par la somme de toutes les exponentielles. 

Les propriétés clés mises en évidence sur la droite indiquent pourquoi la méthode softmax est utile pour les problèmes de classification multi-classes. Dans la section suivante, nous examinerons la formule mathématique et son fonctionnement.

Formule de la fonction d'activation Softmax et son fonctionnement

Maintenant que nous comprenons ce qu'est la fonction d'activation softmax, examinons sa formulation mathématique et la manière dont elle transforme les entrées en distributions de probabilités.

La formule de la fonction d'activation softmax peut être exprimée mathématiquement comme suit :

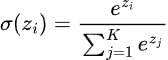
Où ?

• ​z_i est la valeur d'entrée (logit) pour la classe i
• e^z_i est la fonction exponentielle appliquée à z_i (également notée exp(z_i ​))
• K est le nombre total de classes
• Le dénominateur additionne les exponentielles de toutes les valeurs d'entrée, ce qui garantit que la somme des valeurs de sortie est égale à 1.

La fonction d'activation softmax suit ces étapes pour transformer un vecteur d'entrées en une distribution de probabilités :

1. Calculer les exponentielles: Tout d'abord, nous calculons l'exponentielle (e^x) de chaque valeur d'entrée. Cette étape permet de s'assurer que toutes les valeurs sont positives, car e^x > 0 pour tout nombre réel x
2. Additionnez les exponentielles: Nous calculons la somme de toutes les valeurs exponentielles de l'étape 1.
3. Normaliser: Nous divisons chaque valeur exponentielle par la somme calculée à l'étape 2. Cette normalisation garantit que toutes les sorties sont comprises entre 0 et 1 et que leur somme est exactement égale à 1.

Appliquons la formule de la fonction d'activation softmax à un exemple simple pour voir comment elle fonctionne en pratique.

Supposons que nous disposions d'un réseau neuronal avec trois neurones de sortie pour un problème de classification à trois classes (par exemple, identifier si une image contient un chat, un chien ou un oiseau). Après le calcul final, le réseau produit les logits suivants : z = [2.0, 1.0, 0.5].

Pour convertir ces logits en probabilités à l'aide de la fonction softmax :

1. Calculer les exponentielles:
• e^2.0 = 7.389
• e^1.0 = 2.718
• e^0.5 = 1.648
2. Somme des exponentielles:
• 7.389 + 2.718 + 1.648 = 11.755
3. Normaliser:
• P(classe 1) = 7,389 / 11,755 ≈ 0,628 ou 62,8%.
• P(classe 2) = 2,718 / 11,755 ≈ 0,231 ou 23,1%.
• P(classe 3) = 1,648 / 11,755 ≈ 0,140 ou 14,0%.

La distribution de distribution de probabilités résultante [0,628, 0,231, 0,140] est égale à 1, la probabilité la plus élevée étant attribuée à la classe correspondant à la valeur logit la plus élevée. Cet exemple montre comment la fonction d'activation softmax préserve le classement des valeurs d'entrée tout en les transformant en une distribution de probabilité valide.

Remarquez que les valeurs d'entrée initiales (2,0, 1,0, 0,5) ont conservé leur rang relatif dans les probabilités de sortie, mais que les différences entre elles ont été accentuées. Cette propriété fait de la softmax un outil particulièrement utile dans les tâches de classification où l'on souhaite identifier avec confiance la classe la plus probable.

Dans la section suivante, nous examinerons les différentes façons d'implémenter la fonction d'activation softmax à l'aide de Python.

Implémentation de la fonction d'activation Softmax en Python

Maintenant que nous comprenons la théorie derrière la fonction d'activation softmax, voyons comment la mettre en œuvre en Python. Nous commencerons par écrire une fonction softmax à partir de zéro en utilisant NumPy, puis nous verrons comment l'utiliser avec des frameworks d'apprentissage profond populaires comme TensorFlow/Keras et PyTorch.

Écrire softmax à partir de zéro en utilisant NumPy

Avant de plonger dans les cadres, il est important de comprendre comment mettre en œuvre la fonction d'activation softmax à partir de zéro. Cela permet de développer l'intuition de ce qui se passe sous le capot.

import numpy as np

def softmax(x):
    """
    Compute softmax values for each set of scores in x.
    
    Args:
        x: Input array of shape (batch_size, num_classes) or (num_classes,)
        
    Returns:
        Softmax probabilities of same shape as input
    """
    # For numerical stability, subtract the maximum value from each input vector
    # This prevents overflow when calculating exp(x)
    shifted_x = x - np.max(x, axis=-1, keepdims=True)
    
    # Calculate exp(x) for each element
    exp_x = np.exp(shifted_x)
    
    # Calculate the sum of exp(x) for normalization
    sum_exp_x = np.sum(exp_x, axis=-1, keepdims=True)
    
    # Normalize to get probabilities
    probabilities = exp_x / sum_exp_x
    
    return probabilities

Cette implémentation suit exactement la formule de la fonction d'activation softmax, avec un ajout important : nous soustrayons la valeur maximale de chaque vecteur d'entrée avant l'exponentiation. 

Cette opération de "décalage" ne modifie pas le résultat mathématique, mais permet d'éviter les débordements numériques, qui peuvent se produire lors du calcul d'exponentielles de grands nombres.

Testons notre mise en œuvre à l'aide d'un exemple simple :

# Sample logits from a neural network (batch of 2 examples, 3 classes each)
logits = np.array([
    [2.0, 1.0, 0.5],  # First example
    [3.0, 2.0, 1.0]   # Second example
])

probabilities = softmax(logits)
print("Logits:\n", logits)
print("\nSoftmax probabilities:\n", probabilities)
print("\nSum of probabilities (should be 1 for each example):", np.sum(probabilities, axis=1))

Sortie :

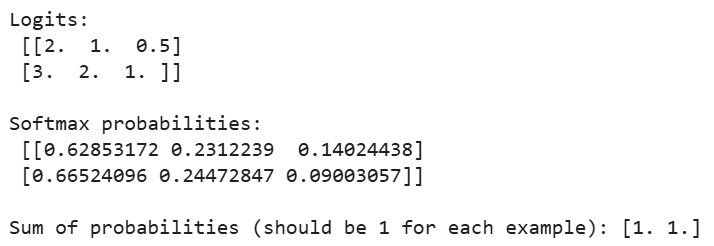
Lorsque nous exécutons le code ci-dessus, nous constatons que la somme des probabilités pour chaque exemple est égale à 1, ce qui confirme que notre implémentation de softmax produit des distributions de probabilités valides. Pour le premier exemple, la probabilité la plus élevée correspond au logit le plus élevé (2,0), et il en va de même pour le deuxième exemple.

Utilisation de softmax dans TensorFlow/Keras

TensorFlow et Keras facilitent l'utilisation de la fonction d'activation softmax dans vos réseaux neuronaux. Construisons pas à pas un classificateur simple pour l'ensemble de données MNIST.

Tout d'abord, importons les bibliothèques nécessaires et chargeons le jeu de données :

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Softmax
from tensorflow.keras.datasets import mnist
import matplotlib.pyplot as plt
import numpy as np

# Load and preprocess the MNIST dataset
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# Normalize pixel values to be between 0 and 1
x_train, x_test = x_train / 255.0, x_test / 255.0

# One-hot encode the labels
y_train_one_hot = tf.keras.utils.to_categorical(y_train, 10)
y_test_one_hot = tf.keras.utils.to_categorical(y_test, 10)

L'ensemble de données MNIST contient des images en niveaux de gris de 28x28 pixels de chiffres manuscrits (0-9). Nous normalisons les valeurs des pixels pour qu'elles soient comprises entre 0 et 1 afin d'améliorer la dynamique de l'apprentissage, et nous convertissons les étiquettes de classe en un encodage à un seul coup, qui est le format préféré pour les sorties softmax.

Créons maintenant un modèle de réseau neuronal avec une couche de sortie softmax :

# Method 1: Using softmax as the activation function in the final layer
model1 = Sequential([
    Flatten(input_shape=(28, 28)),  # Convert 28x28 images to 784-length vectors
    Dense(128, activation='relu'),   # Hidden layer with ReLU activation
    Dense(10, activation='softmax')  # Output layer with softmax activation
])

# Method 2: Using a separate Softmax layer
model2 = Sequential([
    Flatten(input_shape=(28, 28)),
    Dense(128, activation='relu'),
    Dense(10),  # Linear output (logits)
    Softmax()   # Separate softmax layer
])

Nous démontrons ici deux façons équivalentes d'incorporer la fonction d'activation softmax dans un réseau neuronal :

• Méthode 1: Spécifier directement "softmax" comme fonction d'activation dans la couche dense finale
• Méthode 2: Ajout d'une couche Softmax séparée après la couche Dense qui produit des logits bruts

Les deux approches produisent des résultats identiques, mais la seconde méthode rend la séparation entre logits et probabilités plus explicite, ce qui peut être utile dans certains scénarios.

Ensuite, compilons et entraînons le modèle :

# Compile the model
model1.compile(
    optimizer='adam',
    loss='categorical_crossentropy',  # This loss works well with softmax
    metrics=['accuracy']
)

# Print model summary
print("Model with softmax activation:")
model1.summary()

# Train the model
print("\nTraining the model...")
history = model1.fit(
    x_train, y_train_one_hot,
    epochs=5,
    batch_size=128,
    validation_split=0.1,
    verbose=1
)

Sortie:

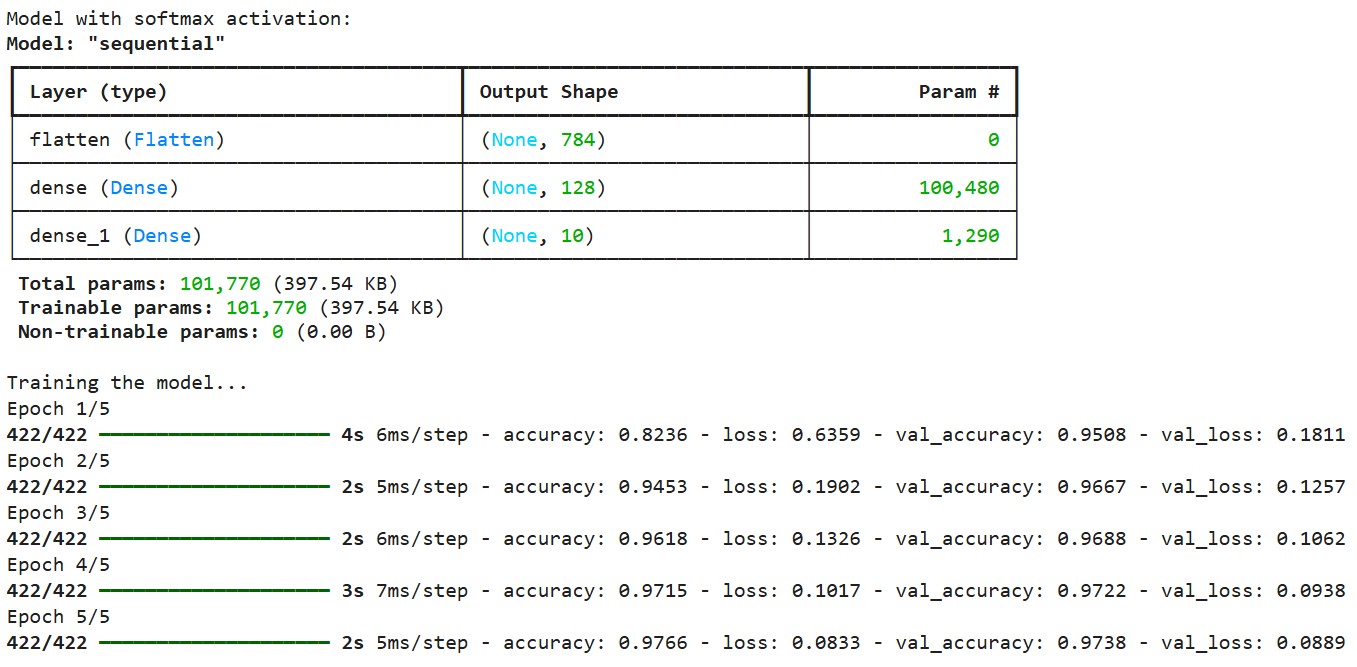Nous compilons le modèle à l'aide de la fonction de perte d'entropie croisée catégorielle, qui est conçue pour fonctionner avec des sorties softmax. Cette fonction de perte mesure la différence entre la distribution de probabilité prédite et les véritables étiquettes codées à une position. Nous utilisons l'optimiseur Adam, qui ajuste de manière adaptative le taux d'apprentissage pendant la formation.

Après l'entraînement, nous pouvons utiliser le modèle pour faire des prédictions et visualiser les résultats :

# Let's check predictions on a sample
sample_idx = 42
sample_image = x_test[sample_idx]
true_label = y_test[sample_idx]

# Get model predictions (probabilities across all classes)
predictions = model1.predict(sample_image[np.newaxis, ...])

# Visualize the results
plt.figure(figsize=(10, 4))

# Plot the image
plt.subplot(1, 2, 1)
plt.imshow(sample_image, cmap='gray')
plt.title(f"True label: {true_label}")
plt.axis('off')

# Plot the probability distribution
plt.subplot(1, 2, 2)
plt.bar(range(10), predictions[0])
plt.xticks(range(10))
plt.xlabel('Digit')
plt.ylabel('Probability')
plt.title('Softmax Probabilities')

Ce code sélectionne une image test, la fait passer par le modèle entraîné et visualise à la fois l'image et la distribution de probabilités résultant de la sortie de la softmax. La barre la plus haute du graphique de probabilité représente la prédiction du modèle.

Sortie:

TensorFlow fournit également une fonction intégrée permettant d'appliquer directement la méthode softmax :

# Demonstrate using a custom softmax function in TensorFlow
def custom_softmax(logits):
    """Custom implementation of softmax in TensorFlow"""
    exp_logits = tf.exp(logits - tf.reduce_max(logits, axis=-1, keepdims=True))
    return exp_logits / tf.reduce_sum(exp_logits, axis=-1, keepdims=True)

# Example usage of custom softmax
logits = tf.constant([[2.0, 1.0, 0.5], [3.0, 2.0, 1.0]])
custom_probs = custom_softmax(logits)
tf_probs = tf.nn.softmax(logits)

print("\nCustom softmax:", custom_probs.numpy())
print("TensorFlow softmax:", tf_probs.numpy())

Sortie:

Cet exemple compare une implémentation personnalisée de softmax avec la fonction intégrée de TensorFlow tf.nn.softmax(). Les deux devraient produire des résultats identiques. L'implémentation personnalisée inclut également l'astuce de stabilité numérique consistant à soustraire la valeur maximale avant l'exponentiation.

Utilisation de Softmax dans PyTorch

Mettons maintenant en œuvre un modèle similaire en utilisant PyTorch et l'ensemble de données CIFAR-10. Nous commencerons par importer les bibliothèques et configurer les données, comme indiqué ci-dessous :

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np

# Set the device
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")

# Load and preprocess the CIFAR-10 dataset
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))  # Normalize RGB channels
])

# Load a small subset of the CIFAR-10 dataset for demonstration
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64,
                                         shuffle=False, num_workers=2)

# Define the class names for CIFAR-10
classes = ('plane', 'car', 'bird', 'cat', 'deer',
           'dog', 'frog', 'horse', 'ship', 'truck')

Le code ci-dessus configure PyTorch pour qu'il utilise l'accélération GPU si elle est disponible, charge l'ensemble de données CIFAR-10 (qui contient des images couleur 32x32 réparties en 10 classes) et prépare les chargeurs de données pour l'entraînement et le test.

Définissons ensuite un réseau neuronal convolutif simple, comme indiqué ci-dessous :

# Define a simple convolutional neural network
class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        # Convolutional layers
        self.conv1 = nn.Conv2d(3, 16, 3, padding=1)
        self.conv2 = nn.Conv2d(16, 32, 3, padding=1)
        self.pool = nn.MaxPool2d(2, 2)
        
        # Fully connected layers
        self.fc1 = nn.Linear(32 * 8 * 8, 128)
        self.fc2 = nn.Linear(128, 10)  # 10 classes in CIFAR-10
        
        # Activation functions
        self.relu = nn.ReLU()
        
        # Note: We don't define softmax here as it will be applied with the loss function
    
    def forward(self, x):
        # Convolutional layers with ReLU and pooling
        x = self.pool(self.relu(self.conv1(x)))  # -> 16x16x16
        x = self.pool(self.relu(self.conv2(x)))  # -> 8x8x32
        
        # Flatten the output
        x = x.view(-1, 32 * 8 * 8)
        
        # Fully connected layers
        x = self.relu(self.fc1(x))
        x = self.fc2(x)  # Raw logits output
        
        # Note: No softmax here, as PyTorch's CrossEntropyLoss applies it internally
        return x

Ce CNN traite les images RVB 32x32 par le biais de couches convolutives, applique l'activation et le regroupement ReLU et termine par des couches entièrement connectées. Notamment, le modèle n'inclut pas de couche softmax dans sa passe avant. Au lieu de cela, il produit des logits bruts.

Il s'agit d'un schéma courant dans PyTorch, car la fonction CrossEntropyLoss utilisée pendant l'apprentissage applique en interne la méthode softmax avant de calculer la perte, ce qui est plus stable sur le plan numérique.

Nous verrons également comment inclure explicitement le softmax si nécessaire :

# Applying softmax within the model
class ModelWithSoftmax(nn.Module):
    def __init__(self):
        super(ModelWithSoftmax, self).__init__()
        self.features = SimpleCNN()
        self.softmax = nn.Softmax(dim=1)
    
    def forward(self, x):
        logits = self.features(x)
        probabilities = self.softmax(logits)
        return probabilities

Nous définissons deux variantes de modèle : SimpleCNN produit des logits bruts, tandis que ModelWithSoftmax applique explicitement la méthode softmax pour produire des probabilités. Pour la formation, nous utilisons SimpleCNN avec CrossEntropyLoss, qui est l'approche standard de PyTorch.

Définissons une fonction de formation :

# Create the model and move it to the device 
model = SimpleCNN().to(device) 
# Define loss function and optimizer 
criterion = nn.CrossEntropyLoss()  # Combines LogSoftmax and NLLLoss 
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# Train the model (only a few epochs for demonstration)
def train_model(epochs=2):
    for epoch in range(epochs):
        running_loss = 0.0
        for i, data in enumerate(trainloader, 0):
            inputs, labels = data[0].to(device), data[1].to(device)
            
            # Zero the parameter gradients
            optimizer.zero_grad()
            
            # Forward + backward + optimize
            outputs = model(inputs)  # These are logits (pre-softmax)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
            
            running_loss += loss.item()
            if i % 100 == 99:
                print(f'[{epoch + 1}, {i + 1}] loss: {running_loss / 100:.3f}')
                running_loss = 0.0
    
    print('Finished Training')

Enfin, créons une fonction permettant de visualiser les prédictions du modèle :

# Function to display predictions with softmax probabilities
def show_prediction_example():
    # Get a batch of test images
    dataiter = iter(testloader)
    images, labels = next(dataiter)
    
    # Select a single image
    img = images[0].to(device)
    label = labels[0]
    
    # Get the model's prediction (logits)
    with torch.no_grad():
        logits = model(img.unsqueeze(0))
    
    # Apply softmax to get probabilities
    probabilities = torch.nn.functional.softmax(logits, dim=1)
    
    # Plot the image and probabilities
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4))
    
    # Show the image
    img_np = img.cpu().numpy()
    img_np = np.transpose(img_np, (1, 2, 0))
    # Denormalize the image for display
    img_np = img_np * 0.5 + 0.5
    ax1.imshow(img_np)
    ax1.set_title(f"True label: {classes[label]}")
    ax1.axis('off')
    
    # Show the probabilities
    probs = probabilities[0].cpu().numpy()
    ax2.bar(range(10), probs)
    ax2.set_xticks(range(10))
    ax2.set_xticklabels(classes, rotation=45)
    ax2.set_xlabel('Class')
    ax2.set_ylabel('Probability')
    ax2.set_title('Softmax Probabilities')
    
    plt.tight_layout()

Cette fonction montre comment obtenir des probabilités de softmax à partir d'un modèle entraîné pendant l'inférence. Il fait passer une image par le modèle pour obtenir des logits, applique softmax manuellement à l'aide de torch.nn.functional.softmax(), puis visualise à la fois l'image et la distribution de probabilités résultante.

Entraînons maintenant le modèle :

train_model()

Sortie :

Prédisons et voyons comment les probabilités se présentent pour une image test :

show_prediction_example()

Sortie :

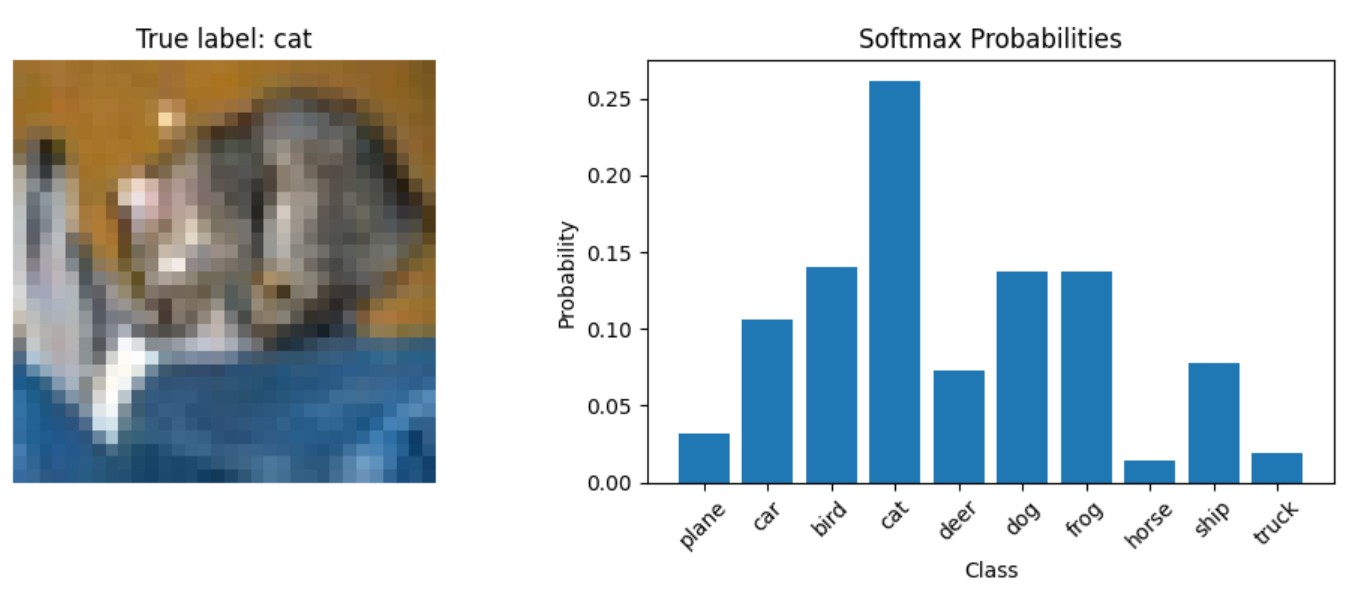
Dans la section suivante, nous examinerons les scénarios spécifiques dans lesquels la fonction d'activation softmax est le choix optimal, nous verrons quand la fonction d'activation softmax doit être utilisée et nous discuterons des applications du monde réel dans divers modèles d'apprentissage profond.

Quand utiliser la fonction d'activation Softmax ?

Pour concevoir des réseaux neuronaux efficaces, il est important de savoir quand utiliser la fonction d'activation softmax. La fonction d'activation softmax trouve sa principale application dans la couche de sortie des réseaux neuronaux conçus pour les tâches de classification.

Softmax pour la classification multi-classes

Softmax est le choix standard lorsque notre modèle doit classer les entrées dans l'une de plusieurs catégories mutuellement exclusives. Les exemples les plus courants sont les suivants :

• Classification d'images (identification d'objets dans des photos)
• Catégorisation des documents (attribution de thèmes au texte)
• Reconnaissance d'entités nommées (identification de noms de personnes, de lieux, etc.)
• Reconnaissance vocale (conversion du son en texte)

Interprétation probabiliste et indices de confiance

Lorsque nous avons besoin que notre modèle produise des probabilités plutôt que de simples prédictions de classe, softmax fournit une interprétation probabiliste de la confiance du modèle dans toutes les classes possibles.

Softmax dans l'apprentissage par renforcement et les mécanismes d'attention

Dans les problèmes d'apprentissage par renforcement et de décision séquentielle, le softmax peut être utilisé pour convertir les valeurs d'action en une distribution de probabilité pour la sélection des actions.

Architectures modernes architectures modernes à base de transformateurs utilisent la softmax pour répartir l'attention sur les différentes parties de la séquence d'entrée.

Le fondement mathématique solide et l'interprétation probabiliste intuitive font que la fonction d'activation softmax est particulièrement bien adaptée aux problèmes de classification où les classes s'excluent mutuellement.

Modèles d'apprentissage profond

Plusieurs architectures d'apprentissage profond utilisent la fonction d'activation softmax. 

Les réseaux de classification d'images tels que ResNet, VGG et Inception utilisent tous la méthode softmax dans leur couche finale pour classer les images dans des milliers de catégories. Par exemple, les modèles formés sur ImageNet comportent généralement une couche softmax de 1 000 unités correspondant à 1 000 catégories d'objets.

Dans la modélisation linguistique, les modèles basés sur les RNN utilisent la méthode softmax pour prédire le mot suivant dans une séquence à partir d'un vocabulaire qui peut contenir des dizaines de milliers de mots.

Les architectures NLP modernes telles que BERT, GPT et T5 utilisent la softmax dans plusieurs composants :

• Dans les mécanismes d'attention pour déterminer le degré d'attention à accorder aux différentes parties de l'entrée.
• Dans la couche de classification finale pour des tâches telles que l'analyse des sentiments ou la classification des documents

Autoencodeurs variationnels (VAE) et certains réseaux adversoriels génératifs (GAN) utilisent la softmax dans leurs composants discriminants ou pour la modélisation de variables latentes catégorielles.

Dans la section suivante, nous examinerons les différences entre la fonction d'activation softmax et la fonction d'activation sigmoïde.

Fonction d'activation softmax vs sigmoïde

La fonction sigmoïde, définie comme σ(x) = 1/(1+e^(-x)), transforme un seul nombre réel en une valeur comprise entre 0 et 1. En revanche, la fonction d'activation softmax opère sur un vecteur de nombres, qu'elle convertit en une distribution de probabilités.

Voici les différences fondamentales entre ces deux fonctions d'activation :

Dimensions des entrées et sorties

• Sigmoïde : Prend une entrée scalaire unique et produit une sortie scalaire unique entre 0 et 1.
• Softmax : Prend un vecteur de n entrées et produit un vecteur de n sorties dont la somme est égale à 1.

Interprétation des probabilités

• Sigmoïde : La sortie représente la probabilité d'un événement binaire unique (par exemple, "Ce courriel est-il du spam ?").
• Softmax : Les résultats représentent des probabilités pour plusieurs classes qui s'excluent mutuellement (par exemple, "Quel est ce chiffre de 0 à 9 ?").

Indépendance des résultats

• Sigmoïde : Lorsqu'elle est utilisée sur plusieurs neurones, chaque sortie est indépendante des autres. Les sorties multiples peuvent toutes être à l'état haut ou à l'état bas.
• Softmax : Les résultats sont interdépendants : si une probabilité augmente, les autres doivent diminuer pour que la somme reste égale à 1.

Relation mathématique

Il est intéressant de noter que la fonction sigmoïde est en fait un cas particulier de la fonction d'activation softmax lorsqu'il n'y a que deux classes. C'est pourquoi la sigmoïde est souvent appelée "softmax binaire".

Quand utiliser la softmax ou la sigmoïde ?

Le choix de la bonne fonction d'activation est crucial pour garantir qu'un réseau neuronal produise des prédictions significatives, et la décision entre softmax et sigmoïde dépend de la nature de la tâche de classification.

Utilisez le sigmoïde lorsque :

• Résolution de problèmes de classification binaire (deux classes)
• Chaque sortie doit être interprétée indépendamment
• Mise en œuvre d'une classification multi-labels dans laquelle une instance peut appartenir à plusieurs classes simultanément
• Création de mécanismes d'attention ou de portes dans les réseaux neuronaux récurrents

Utilisez softmax lorsque :

• Traitement des problèmes de classification multi-classes (plus de deux classes)
• Les classes s'excluent mutuellement (une entrée appartient à une seule classe).
• Vous avez besoin d'une distribution de probabilités appropriée pour tous les résultats possibles.
• Mise en œuvre de la couche finale de la plupart des réseaux de classification d'images

Par exemple, dans un réseau neuronal qui classe des images de chiffres manuscrits (0-9), la fonction d'activation softmax serait appropriée pour la couche de sortie puisque chaque image représente exactement un chiffre. En revanche, pour un réseau qui détecte plusieurs objets dans une image (par exemple, "contient une personne", "contient une voiture", "contient un arbre"), les activations sigmoïdes seraient plus appropriées puisque plusieurs objets peuvent être présents simultanément.

Voici un tableau de référence rapide comparant la fonction d'activation softmax et sigmoïde :

Il est essentiel de comprendre la distinction entre ces fonctions d'activation pour concevoir des réseaux neuronaux efficaces. Si la fonction d'activation softmax est le choix idéal pour les problèmes de classification multi-classes, la fonction sigmoïde reste utile pour la classification binaire et les problèmes nécessitant des probabilités indépendantes.

Dans la section suivante, nous examinerons les problèmes courants qui se posent et les considérations à prendre en compte lorsque vous travaillez avec des fonctions d'activation de type "softmax".

Questions et considérations communes

Lorsque vous travaillez avec la fonction d'activation softmax dans vos modèles d'apprentissage profond, plusieurs défis peuvent affecter les performances et la fiabilité du modèle. Comprendre ces problèmes et savoir comment les résoudre vous aidera à élaborer des modèles plus robustes.

Défis en matière de stabilité numérique

La stabilité numérique est une préoccupation essentielle lors de l'utilisation de la fonction d'activation softmax. L'opération exponentielle dans la formule de la fonction d'activation softmax peut entraîner un débordement ou un sous-débordement numérique si elle n'est pas gérée correctement.

Par exemple, lorsqu'il s'agit de très grandes valeurs d'entrée (comme 1000 ou plus), la fonction exponentielle produit des nombres extrêmement grands qui peuvent dépasser la valeur maximale représentable en virgule flottante dans votre système. Cela entraîne des erreurs de débordement, produisant des valeurs "infinies" qui font que l'opération de division finale donne des résultats indéfinis (NaN - Not a Number).

La solution standard, telle que mentionnée dans notre section sur la mise en œuvre, consiste à soustraire la valeur maximale de toutes les entrées avant d'appliquer la fonction exponentielle. Ce décalage ne modifie pas les proportions relatives après normalisation, mais maintient les valeurs dans une fourchette gérable. 

Les frameworks d'apprentissage profond modernes gèrent ce problème en interne, mais il est important de comprendre le problème lors de la mise en œuvre d'opérations personnalisées ou du débogage d'un comportement inattendu.

Softmax et excès de confiance dans les prédictions

Un autre problème courant avec la fonction d'activation softmax est que les réseaux neuronaux ont tendance à être trop confiants dans leurs prédictions, même lorsqu'elles sont erronées. Cet excès de confiance est dû au fait que

1. La nature exponentielle du softmax amplifie les petites différences de logits.
2. Les réseaux neuronaux profonds modernes sont suffisamment puissants pour mémoriser parfaitement les données d'entraînement.
3. La perte d'entropie croisée continue à pousser les probabilités vers 1 pour les classes correctes, même après qu'un modèle ait atteint une bonne précision.

Dans la pratique, cela signifie qu'un modèle peut attribuer une probabilité de 99 % à une prédiction qui est en fait incorrecte. Cela peut être problématique dans les applications critiques où une estimation fiable de l'incertitude est essentielle. Par exemple, un système de diagnostic médical trop confiant dans ses prédictions erronées pourrait conduire à des décisions de traitement inappropriées.

L'écart entre la confiance d'un modèle (à partir des probabilités softmax) et sa précision réelle est connu sous le nom d'erreur d'étalonnage. Les modèles bien calibrés produisent des scores de confiance qui correspondent à leurs taux de précision - si un modèle prédit des événements avec un taux de confiance de 80 %, ces événements devraient se produire environ 80 % du temps.

Techniques de régularisation pour améliorer les performances

Heureusement, plusieurs techniques permettent de résoudre ces problèmes avec la fonction d'activation softmax :

Mise à l'échelle de la température

La mise à l'échelle de la température introduit un paramètre T qui contrôle la "douceur" de la distribution de probabilité. En divisant les logits par ce paramètre de température avant d'appliquer softmax, vous pouvez ajuster le niveau de crête ou d'uniformité de la distribution résultante.

Des températures plus élevées (T > 1) produisent des distributions de probabilité plus douces avec moins de valeurs extrêmes, ce qui peut contribuer à réduire l'excès de confiance. Les températures plus basses (T < 1) font que la distribution est plus marquée par le pic de la valeur la plus élevée. La mise à l'échelle de la température est couramment utilisée comme technique de post-traitement après l'apprentissage pour calibrer la confiance du modèle sans affecter le classement des classes par le modèle.

Lissage des étiquettes

Le lissage des étiquettes remplace les vecteurs cibles durs à un coup par des distributions légèrement lissées. Au lieu d'entraîner le modèle à produire des zéros et des uns exacts, le lissage des étiquettes encourage le modèle à être légèrement moins confiant en ciblant des valeurs telles que 0,9 pour la classe correcte et 0,025 pour les classes incorrectes (dans un problème à 4 classes).

En s'entraînant avec ces étiquettes lissées, le modèle apprend à être moins confiant dans ses prédictions, ce qui améliore la généralisation et rend le modèle plus robuste au bruit des étiquettes. Cette technique est devenue une pratique courante dans de nombreux modèles de classification d'images de pointe.

Méthodes d'exclusion et d'ensemble

L'utilisation de l'exclusion pendant l'apprentissage et son maintien pendant l'inférence (une technique appelée exclusion de Monte Carlo) vous permet d'échantillonner plusieurs prédictions pour la même entrée et d'estimer l'incertitude. Si le modèle produit des prédictions cohérentes sur plusieurs passes avant avec différents schémas d'abandon, il est probablement plus sûr de sa prédiction.

De même, les méthodes d'ensemble combinent les prévisions de plusieurs modèles pour améliorer les performances et fournir de meilleures estimations de l'incertitude. Le désaccord entre les modèles d'un ensemble peut servir de mesure de l'incertitude.

Techniques d'étalonnage

L'échelle de Platt et d'autres méthodes d'étalonnage peuvent être appliquées après l'apprentissage afin de garantir que les scores de confiance obtenus avec Softmax correspondent réellement aux probabilités réelles. Ces méthodes utilisent généralement un ensemble de validation pour apprendre les paramètres qui transforment les sorties du modèle original en probabilités bien calibrées.

Par exemple, une simple approche de mise à l'échelle de la température (comme mentionné précédemment) peut être optimisée sur les données de validation afin de minimiser l'erreur d'étalonnage. Les approches plus complexes comprennent la régression isotonique et le binning bayésien.

Le goulot d'étranglement de la softmax

Des recherches récentes ont permis d'identifier une limitation fondamentale de la fonction softmax, connue sous le nom de "goulot d'étranglement softmax". Cela fait référence au fait que l'expressivité des modèles linguistiques basés sur la softmax est limitée par le rang de la matrice de poids dans la couche finale. Dans les contextes de langage naturel présentant des dépendances complexes, cela peut empêcher les modèles de capturer pleinement les distributions conditionnelles sous-jacentes.

Des architectures avancées telles que le mélange de softmax (MoS) ont été proposées pour remédier à cette limitation en utilisant une combinaison pondérée de plusieurs distributions de softmax.

En étant conscient de ces problèmes courants et en mettant en œuvre des solutions appropriées, vous pouvez améliorer la fiabilité et les performances des modèles qui utilisent la fonction d'activation softmax pour les tâches de classification.

Conclusion

La fonction d'activation softmax est un composant essentiel des réseaux neuronaux pour les problèmes de classification multi-classes, transformant les logits bruts en distributions de probabilité interprétables. Nous avons exploré ses fondements mathématiques, son implémentation en Python, sa comparaison avec la sigmoïde, ses cas d'utilisation pratiques et les techniques permettant de relever les défis courants tels que l'instabilité numérique et l'excès de confiance.

Prêt à approfondir votre compréhension des réseaux neuronaux ? 

• Découvrez notre Introduction aux fonctions d'activation ou plongez dans les cours spécifiques au cadre de travail sur Apprentissage profond avec Keras et PyTorch.
• Pour en savoir plus sur d'autres fonctions d'activation importantes, consultez notre article sur la fonction ReLU et commencez à construire des réseaux neuronaux plus efficaces dès aujourd'hui !