Softmax-Aktivierungsfunktion in Python: Ein vollständiger Leitfaden

Aktivierungsfunktionen sind das Rückgrat der neuronalen Netze. Sie sind wichtige Komponenten, die Nichtlinearität einführen und es diesen Netzen ermöglichen, komplexe Muster zu lernen. Die Softmax-Aktivierungsfunktion ist besonders wichtig, wenn es um Klassifizierungsprobleme mit mehreren Klassen geht.

Während Alternativen wie Sigmoid und ReLU ihre spezifischen Anwendungsfälle haben, eignet sich Softmax besser für Situationen, in denen die Ergebnisse als Wahrscheinlichkeiten für sich gegenseitig ausschließende Klassen interpretiert werden müssen.

Die Softmax-Aktivierungsfunktion wandelt einen ganzen Vektor von Zahlen in eine Wahrscheinlichkeitsverteilung um. Diese einzigartige Eigenschaft macht sie unverzichtbar für Aufgaben, bei denen wir die Eingaben in eine von mehreren möglichen Kategorien einordnen müssen.

Von Bilderkennungssystemen, die Tausende von Objektkategorien identifizieren, bis hin zu Modellen für die Verarbeitung natürlicher Sprache, die das nächste Wort in einem Satz vorhersagen, bietet Softmax die mathematische Grundlage für Entscheidungen über mehrere Möglichkeiten.

In diesem Artikel werden wir uns ansehen, was die Softmax-Aktivierungsfunktion ist, wie sie mathematisch funktioniert und wann du sie in deinem neuronalen Netz Architekturen verwenden solltest. Wir werden uns auch die praktischen Implementierungen in Python ansehen.

Was ist die Softmax-Aktivierungsfunktion?

Die Softmax Aktivierungsfunktion ist eine mathematische Funktion, die einen Vektor der rohen Modellausgaben, die so genannten Logits, in eine Wahrscheinlichkeitsverteilung umwandelt. Einfacher ausgedrückt: Er nimmt eine Reihe von Zahlen und wandelt sie in Wahrscheinlichkeiten um, die sich zu 1 summieren.

Im Gegensatz zu einigen Aktivierungsfunktionen, die unabhängig voneinander auf einzelne Werte wirken, arbeitet Softmax mit einem ganzen Vektor von Werten und wandelt sie gemeinsam in eine Wahrscheinlichkeitsverteilung um, bei der alle Elemente genau 1 ergeben.

Im Zusammenhang mit neuronalen Netzen wird Softmax in der Regel auf die letzte Schicht eines Netzes angewendet, das für die Klassifizierung in mehrere Klassen ausgelegt ist. Wenn wir mehrere mögliche Kategorien haben und unser Modell die Wahrscheinlichkeit für jede Kategorie angeben soll, ist die Softmax-Aktivierungsfunktion die Standardwahl.

Wie funktioniert die Softmax-Funktion?

Die Rohausgaben der letzten Schicht eines neuronalen Netzes werden oft als "Logits" bezeichnet. Diese Werte können von negativ unendlich bis positiv unendlich reichen und haben keine direkte probabilistische Interpretation. Die Softmax-Aktivierungsfunktion wandelt diese Logits in eine besser interpretierbare Form um:

1. Nimm den Exponentialwert jedes Eingabewerts (was sicherstellt, dass alle Werte positiv sind).
2. Dividieren jedes Exponentials durch die Summe aller Exponentiale (was sicherstellt, dass die Summe der Ergebnisse 1 ist).

Diese Umwandlung ist entscheidend, denn sie ermöglicht es uns, den Output des Netzwerks als Wahrscheinlichkeitsverteilung zu interpretieren. Wenn ein neuronales Netz beispielsweise Bilder in drei Kategorien (Katze, Hund, Vogel) klassifiziert, könnte die Softmax-Ausgabe [0,7, 0,2, 0,1] lauten, was einer Wahrscheinlichkeit von 70 % für Katze, 20 % für Hund und 10 % für Vogel entspricht.

Die Softmax-Aktivierungsfunktion spielt eine wichtige Rolle bei der Erstellung gültiger Wahrscheinlichkeitsverteilungen, denn:

• Sie stellt sicher, dass alle Ausgangswerte zwischen 0 und 1 liegen.
• Sie garantiert, dass die Summe aller Ausgaben genau 1 ist.
• Dabei wird die Rangfolge der Eingabewerte beibehalten (größere Eingaben führen zu größeren Wahrscheinlichkeiten).
• Sie hebt die Unterschiede zwischen größeren Werten hervor und unterdrückt die Unterschiede zwischen kleineren Werten.

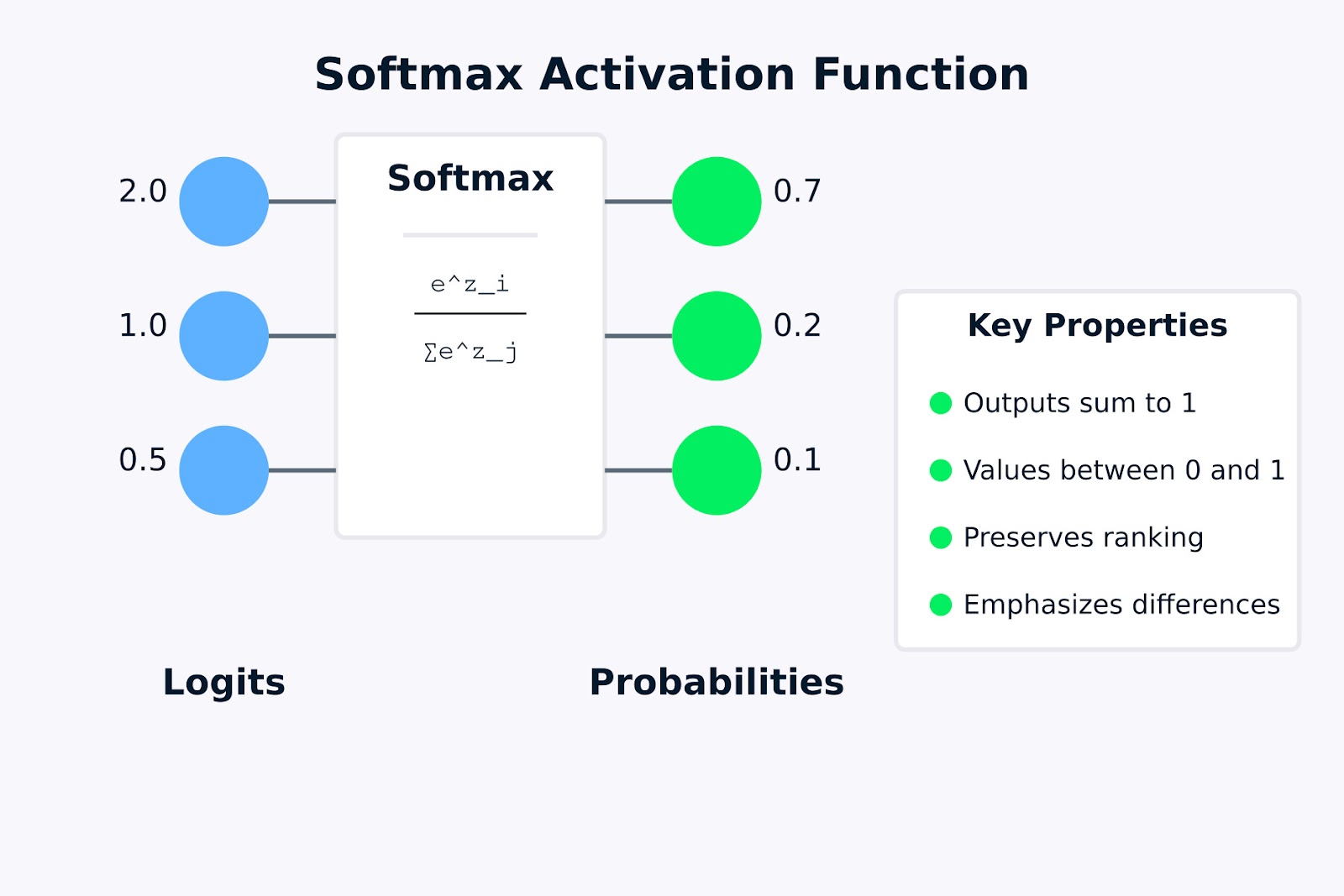
Softmax-Aktivierungsfunktion

Die obige Visualisierung zeigt, wie die Softmax-Aktivierungsfunktion rohe Logits (die Eingabewerte 2,0, 1,0 und 0,5) in eine Wahrscheinlichkeitsverteilung (0,7, 0,2 und 0,1) umwandelt. Die Formel in der Softmax-Box stellt dar, wie jede Ausgabewahrscheinlichkeit berechnet wird, indem der Exponentialwert eines Eingabewerts genommen und durch die Summe aller Exponentialwerte geteilt wird. 

Die auf der rechten Seite hervorgehobenen Schlüsseleigenschaften zeigen, warum Softmax für Mehrklassen-Klassifizierungsprobleme nützlich ist. Im nächsten Abschnitt schauen wir uns die mathematische Formel an und wie sie funktioniert.

Die Formel der Softmax-Aktivierungsfunktion und wie sie funktioniert

Da wir nun wissen, was die Softmax-Aktivierungsfunktion ist, wollen wir uns die mathematische Formulierung ansehen und wie sie Eingaben in Wahrscheinlichkeitsverteilungen umwandelt.

Die Formel der Softmax-Aktivierungsfunktion kann mathematisch wie folgt ausgedrückt werden:

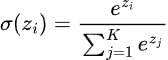
Wo:

• ​z_i ist der Eingangswert (Logit) für die Klasse i
• e^z_i ist die Exponentialfunktion, die auf z_i (auch geschrieben als exp(z_i ​))
• K ist die Gesamtzahl der Klassen
• Der Nenner summiert die Exponentiale aller Eingabewerte, so dass die Summe der Ausgabewerte 1 ergibt

Die Softmax-Aktivierungsfunktion folgt diesen Schritten, um einen Vektor von Eingaben in eine Wahrscheinlichkeitsverteilung umzuwandeln:

1. Berechne Exponentiale: Zunächst berechnen wir den Exponentialwert (e^x) jedes Eingabewerts. Dieser Schritt stellt sicher, dass alle Werte positiv sind, da e^x > 0 für jede reelle Zahl x
2. Addiere die Exponentiale: Wir berechnen die Summe aller Exponentialwerte aus Schritt 1.
3. Normalisieren: Wir teilen jeden Exponentialwert durch die in Schritt 2 berechnete Summe. Diese Normalisierung stellt sicher, dass alle Ausgaben zwischen 0 und 1 liegen und die Summe genau 1 ergibt.

Wenden wir die Formel der Softmax-Aktivierungsfunktion auf ein einfaches Beispiel an, um zu sehen, wie sie in der Praxis funktioniert.

Nehmen wir an, wir haben ein neuronales Netzwerk mit drei Ausgangsneuronen für ein Drei-Klassen-Klassifizierungsproblem (z. B. die Identifizierung, ob ein Bild eine Katze, einen Hund oder einen Vogel enthält). Nach der letzten Berechnung gibt das Netzwerk die folgenden Logits aus: z = [2,0, 1,0, 0,5].

Um diese Logits mit Hilfe der Softmax-Funktion in Wahrscheinlichkeiten umzuwandeln:

1. Exponentiale berechnen:
• e^2.0 = 7.389
• e^1.0 = 2.718
• e^0.5 = 1.648
2. Summe der Exponentiale:
• 7.389 + 2.718 + 1.648 = 11.755
3. Normalisieren:
• P(Klasse 1) = 7,389 / 11,755 ≈ 0,628 oder 62,8%
• P(Klasse 2) = 2,718 / 11,755 ≈ 0,231 oder 23,1%
• P(Klasse 3) = 1,648 / 11,755 ≈ 0,140 oder 14,0%

Die resultierende Wahrscheinlichkeitsverteilung [0,628, 0,231, 0,140] summiert sich zu 1, wobei die höchste Wahrscheinlichkeit der Klasse mit dem höchsten Logit-Wert zugeordnet ist. Dieses Beispiel zeigt, wie die Softmax-Aktivierungsfunktion die Rangfolge der Eingabewerte beibehält und sie gleichzeitig in eine gültige Wahrscheinlichkeitsverteilung umwandelt.

Beachte, dass die ursprünglichen Eingabewerte (2,0, 1,0, 0,5) ihre relative Rangfolge in den Ausgabewahrscheinlichkeiten beibehalten haben, aber die Unterschiede zwischen ihnen wurden hervorgehoben. Diese Eigenschaft macht Softmax besonders nützlich bei Klassifizierungsaufgaben, bei denen wir die wahrscheinlichste Klasse mit Sicherheit identifizieren wollen.

Im nächsten Abschnitt sehen wir uns die verschiedenen Möglichkeiten an, die Softmax-Aktivierungsfunktion mit Python zu implementieren.

Softmax-Aktivierungsfunktion in Python implementieren

Nachdem wir nun die Theorie hinter der Softmax-Aktivierungsfunktion verstanden haben, wollen wir sehen, wie man sie in Python implementiert. Wir beginnen damit, eine Softmax-Funktion von Grund auf mit NumPy zu schreiben, und sehen dann, wie man sie mit beliebten Deep-Learning-Frameworks wie TensorFlow/Keras und PyTorch verwendet.

Softmax von Grund auf mit NumPy schreiben

Bevor du dich mit den Frameworks beschäftigst, ist es wichtig zu verstehen, wie du die Softmax-Aktivierungsfunktion von Grund auf implementierst. Das hilft, ein Gespür dafür zu entwickeln, was unter der Haube passiert.

import numpy as np

def softmax(x):
    """
    Compute softmax values for each set of scores in x.
    
    Args:
        x: Input array of shape (batch_size, num_classes) or (num_classes,)
        
    Returns:
        Softmax probabilities of same shape as input
    """
    # For numerical stability, subtract the maximum value from each input vector
    # This prevents overflow when calculating exp(x)
    shifted_x = x - np.max(x, axis=-1, keepdims=True)
    
    # Calculate exp(x) for each element
    exp_x = np.exp(shifted_x)
    
    # Calculate the sum of exp(x) for normalization
    sum_exp_x = np.sum(exp_x, axis=-1, keepdims=True)
    
    # Normalize to get probabilities
    probabilities = exp_x / sum_exp_x
    
    return probabilities

Diese Implementierung folgt genau der Formel der Softmax-Aktivierungsfunktion, mit einem wichtigen Zusatz: Wir subtrahieren den Maximalwert von jedem Eingangsvektor vor der Potenzierung. 

Diese "Verschiebe"-Operation ändert das mathematische Ergebnis nicht, hilft aber, einen numerischen Überlauf zu verhindern, der bei der Berechnung von Exponentialen großer Zahlen auftreten kann.

Lass uns unsere Implementierung mit einem einfachen Beispiel testen:

# Sample logits from a neural network (batch of 2 examples, 3 classes each)
logits = np.array([
    [2.0, 1.0, 0.5],  # First example
    [3.0, 2.0, 1.0]   # Second example
])

probabilities = softmax(logits)
print("Logits:\n", logits)
print("\nSoftmax probabilities:\n", probabilities)
print("\nSum of probabilities (should be 1 for each example):", np.sum(probabilities, axis=1))

Ausgabe:

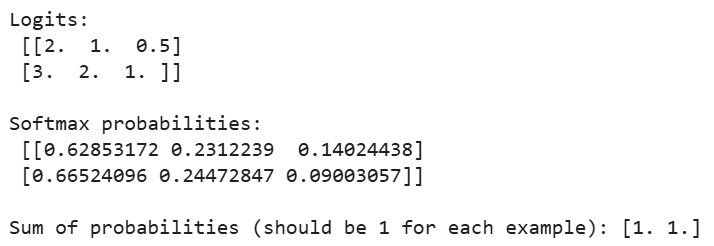
Wenn wir den obigen Code ausführen, sehen wir, dass die Summe der Wahrscheinlichkeiten für jedes Beispiel gleich 1 ist, was bestätigt, dass unsere Softmax-Implementierung gültige Wahrscheinlichkeitsverteilungen erzeugt. Für das erste Beispiel entspricht die größte Wahrscheinlichkeit dem größten Logit (2,0), und für das zweite Beispiel ist es ähnlich.

Softmax in TensorFlow/Keras verwenden

TensorFlow und Keras machen es einfach, die Softmax-Aktivierungsfunktion in deinen neuronalen Netzen zu verwenden. Lass uns Schritt für Schritt einen einfachen Klassifikator für den MNIST-Datensatz erstellen.

Zuerst importieren wir die notwendigen Bibliotheken und laden den Datensatz:

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Softmax
from tensorflow.keras.datasets import mnist
import matplotlib.pyplot as plt
import numpy as np

# Load and preprocess the MNIST dataset
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# Normalize pixel values to be between 0 and 1
x_train, x_test = x_train / 255.0, x_test / 255.0

# One-hot encode the labels
y_train_one_hot = tf.keras.utils.to_categorical(y_train, 10)
y_test_one_hot = tf.keras.utils.to_categorical(y_test, 10)

Der MNIST-Datensatz enthält 28x28 Pixel große Graustufenbilder von handgeschriebenen Ziffern (0-9). Für eine bessere Trainingsdynamik normalisieren wir die Pixelwerte auf einen Wert zwischen 0 und 1 und konvertieren die Klassenbezeichnungen in eine One-Hot-Kodierung, die das bevorzugte Format für Softmax-Ausgaben ist.

Jetzt wollen wir ein neuronales Netzmodell mit einer Softmax-Ausgabeschicht erstellen:

# Method 1: Using softmax as the activation function in the final layer
model1 = Sequential([
    Flatten(input_shape=(28, 28)),  # Convert 28x28 images to 784-length vectors
    Dense(128, activation='relu'),   # Hidden layer with ReLU activation
    Dense(10, activation='softmax')  # Output layer with softmax activation
])

# Method 2: Using a separate Softmax layer
model2 = Sequential([
    Flatten(input_shape=(28, 28)),
    Dense(128, activation='relu'),
    Dense(10),  # Linear output (logits)
    Softmax()   # Separate softmax layer
])

Hier zeigen wir zwei gleichwertige Möglichkeiten, die Softmax-Aktivierungsfunktion in ein neuronales Netz einzubauen:

• Methode 1: Direktes Festlegen von "softmax" als Aktivierungsfunktion in der letzten dichten Schicht
• Methode 2: Hinzufügen einer separaten Softmax-Schicht nach der Dense-Schicht, die rohe Logits ausgibt

Beide Ansätze führen zu identischen Ergebnissen, aber die zweite Methode macht die Trennung zwischen Logits und Wahrscheinlichkeiten deutlicher, was in bestimmten Szenarien nützlich sein kann.

Als Nächstes wollen wir das Modell kompilieren und trainieren:

# Compile the model
model1.compile(
    optimizer='adam',
    loss='categorical_crossentropy',  # This loss works well with softmax
    metrics=['accuracy']
)

# Print model summary
print("Model with softmax activation:")
model1.summary()

# Train the model
print("\nTraining the model...")
history = model1.fit(
    x_train, y_train_one_hot,
    epochs=5,
    batch_size=128,
    validation_split=0.1,
    verbose=1
)

Ausgabe:

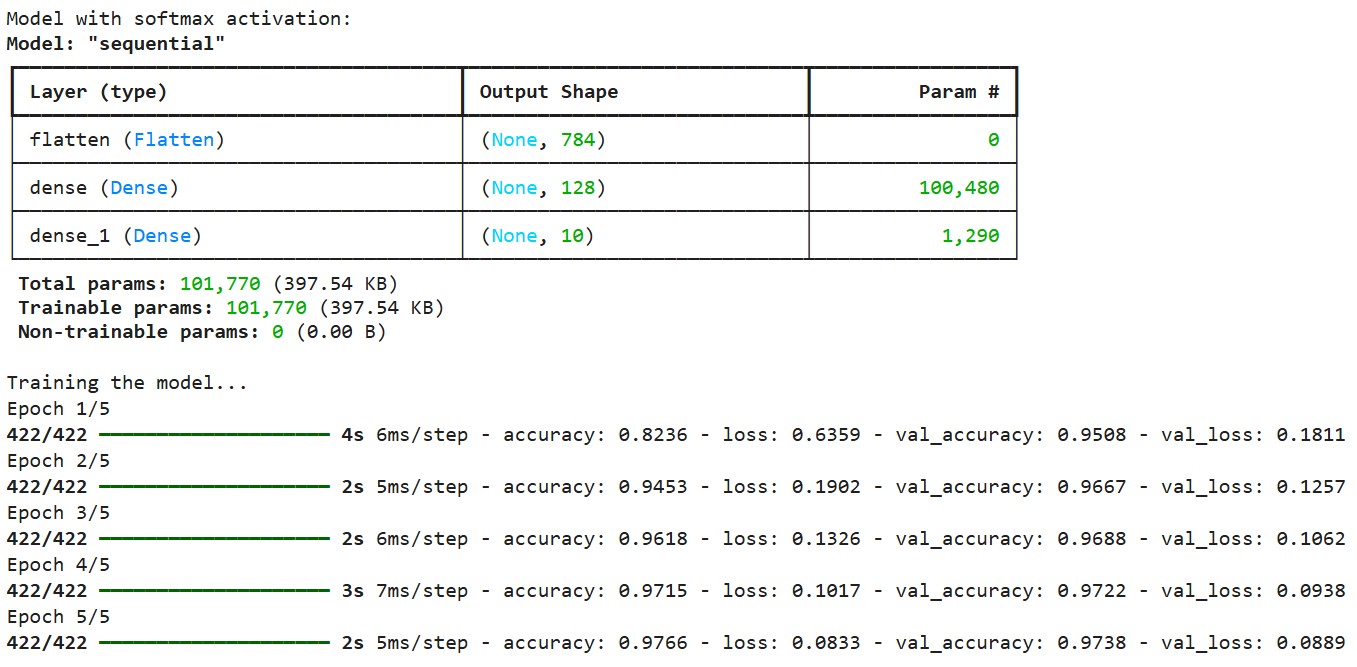Wir erstellen das Modell mit der kategorialen Cross-Entropie-Verlustfunktion, die für Softmax-Ausgaben konzipiert ist. Diese Verlustfunktion misst den Unterschied zwischen der vorhergesagten Wahrscheinlichkeitsverteilung und den wahren, mit einem Punkt kodierten Etiketten. Wir verwenden den Adam-Optimierer, der die Lernrate während des Trainings adaptiv anpasst.

Nach dem Training können wir das Modell nutzen, um Vorhersagen zu treffen und die Ergebnisse zu visualisieren:

# Let's check predictions on a sample
sample_idx = 42
sample_image = x_test[sample_idx]
true_label = y_test[sample_idx]

# Get model predictions (probabilities across all classes)
predictions = model1.predict(sample_image[np.newaxis, ...])

# Visualize the results
plt.figure(figsize=(10, 4))

# Plot the image
plt.subplot(1, 2, 1)
plt.imshow(sample_image, cmap='gray')
plt.title(f"True label: {true_label}")
plt.axis('off')

# Plot the probability distribution
plt.subplot(1, 2, 2)
plt.bar(range(10), predictions[0])
plt.xticks(range(10))
plt.xlabel('Digit')
plt.ylabel('Probability')
plt.title('Softmax Probabilities')

Dieser Code wählt ein Testbild aus, lässt es durch das trainierte Modell laufen und visualisiert sowohl das Bild als auch die resultierende Wahrscheinlichkeitsverteilung aus der Softmax-Ausgabe. Der höchste Balken in der Wahrscheinlichkeitsgrafik stellt die Vorhersage des Modells dar.

Ausgabe:

TensorFlow bietet auch eine eingebaute Funktion, um Softmax direkt anzuwenden:

# Demonstrate using a custom softmax function in TensorFlow
def custom_softmax(logits):
    """Custom implementation of softmax in TensorFlow"""
    exp_logits = tf.exp(logits - tf.reduce_max(logits, axis=-1, keepdims=True))
    return exp_logits / tf.reduce_sum(exp_logits, axis=-1, keepdims=True)

# Example usage of custom softmax
logits = tf.constant([[2.0, 1.0, 0.5], [3.0, 2.0, 1.0]])
custom_probs = custom_softmax(logits)
tf_probs = tf.nn.softmax(logits)

print("\nCustom softmax:", custom_probs.numpy())
print("TensorFlow softmax:", tf_probs.numpy())

Ausgabe:

Dieses Beispiel vergleicht eine eigene Implementierung von Softmax mit der in TensorFlow eingebauten Funktion tf.nn.softmax(). Beide sollten identische Ergebnisse liefern. Die benutzerdefinierte Implementierung enthält auch den numerischen Stabilitätstrick, bei dem der Maximalwert vor der Potenzierung abgezogen wird.

Softmax in PyTorch verwenden

Jetzt wollen wir ein ähnliches Modell mit PyTorch und dem CIFAR-10-Datensatz implementieren. Wir beginnen mit dem Import von Bibliotheken und dem Einrichten der Daten, wie unten gezeigt:

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np

# Set the device
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")

# Load and preprocess the CIFAR-10 dataset
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))  # Normalize RGB channels
])

# Load a small subset of the CIFAR-10 dataset for demonstration
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64,
                                         shuffle=False, num_workers=2)

# Define the class names for CIFAR-10
classes = ('plane', 'car', 'bird', 'cat', 'deer',
           'dog', 'frog', 'horse', 'ship', 'truck')

Der obige Code richtet PyTorch so ein, dass es die GPU-Beschleunigung nutzt, wenn sie verfügbar ist, lädt den CIFAR-10-Datensatz (der 32x32-Farbbilder in 10 Klassen enthält) und bereitet die Datenlader für Training und Test vor.

Als Nächstes wollen wir ein einfaches neuronales Faltungsnetzwerk definieren, wie unten gezeigt:

# Define a simple convolutional neural network
class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        # Convolutional layers
        self.conv1 = nn.Conv2d(3, 16, 3, padding=1)
        self.conv2 = nn.Conv2d(16, 32, 3, padding=1)
        self.pool = nn.MaxPool2d(2, 2)
        
        # Fully connected layers
        self.fc1 = nn.Linear(32 * 8 * 8, 128)
        self.fc2 = nn.Linear(128, 10)  # 10 classes in CIFAR-10
        
        # Activation functions
        self.relu = nn.ReLU()
        
        # Note: We don't define softmax here as it will be applied with the loss function
    
    def forward(self, x):
        # Convolutional layers with ReLU and pooling
        x = self.pool(self.relu(self.conv1(x)))  # -> 16x16x16
        x = self.pool(self.relu(self.conv2(x)))  # -> 8x8x32
        
        # Flatten the output
        x = x.view(-1, 32 * 8 * 8)
        
        # Fully connected layers
        x = self.relu(self.fc1(x))
        x = self.fc2(x)  # Raw logits output
        
        # Note: No softmax here, as PyTorch's CrossEntropyLoss applies it internally
        return x

Dieses CNN verarbeitet die 32x32 RGB-Bilder durch Faltungsschichten, wendet ReLU-Aktivierung und Pooling an und endet mit voll verknüpften Schichten. Bemerkenswert ist, dass das Modell keine Softmax-Schicht in seinem Vorwärtspass enthält. Stattdessen gibt sie rohe Logits aus.

Das ist ein häufiges Muster in PyTorch, weil die CrossEntropyLoss Funktion, die beim Training verwendet wird, intern Softmax anwendet, bevor sie den Verlust berechnet, was numerisch stabiler ist .

Wir wollen auch sehen, wie wir Softmax bei Bedarf explizit einbeziehen können:

# Applying softmax within the model
class ModelWithSoftmax(nn.Module):
    def __init__(self):
        super(ModelWithSoftmax, self).__init__()
        self.features = SimpleCNN()
        self.softmax = nn.Softmax(dim=1)
    
    def forward(self, x):
        logits = self.features(x)
        probabilities = self.softmax(logits)
        return probabilities

Wir definieren zwei Modellvarianten: SimpleCNN gibt rohe Logits aus, während ModelWithSoftmax explizit Softmax anwendet, um Wahrscheinlichkeiten zu erzeugen. Für das Training verwenden wir SimpleCNN mit CrossEntropyLoss, was der Standardansatz in PyTorch ist.

Lass uns eine Trainingsfunktion definieren:

# Create the model and move it to the device 
model = SimpleCNN().to(device) 
# Define loss function and optimizer 
criterion = nn.CrossEntropyLoss()  # Combines LogSoftmax and NLLLoss 
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# Train the model (only a few epochs for demonstration)
def train_model(epochs=2):
    for epoch in range(epochs):
        running_loss = 0.0
        for i, data in enumerate(trainloader, 0):
            inputs, labels = data[0].to(device), data[1].to(device)
            
            # Zero the parameter gradients
            optimizer.zero_grad()
            
            # Forward + backward + optimize
            outputs = model(inputs)  # These are logits (pre-softmax)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
            
            running_loss += loss.item()
            if i % 100 == 99:
                print(f'[{epoch + 1}, {i + 1}] loss: {running_loss / 100:.3f}')
                running_loss = 0.0
    
    print('Finished Training')

Zum Schluss erstellen wir eine Funktion zur Visualisierung der Modellvorhersagen:

# Function to display predictions with softmax probabilities
def show_prediction_example():
    # Get a batch of test images
    dataiter = iter(testloader)
    images, labels = next(dataiter)
    
    # Select a single image
    img = images[0].to(device)
    label = labels[0]
    
    # Get the model's prediction (logits)
    with torch.no_grad():
        logits = model(img.unsqueeze(0))
    
    # Apply softmax to get probabilities
    probabilities = torch.nn.functional.softmax(logits, dim=1)
    
    # Plot the image and probabilities
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4))
    
    # Show the image
    img_np = img.cpu().numpy()
    img_np = np.transpose(img_np, (1, 2, 0))
    # Denormalize the image for display
    img_np = img_np * 0.5 + 0.5
    ax1.imshow(img_np)
    ax1.set_title(f"True label: {classes[label]}")
    ax1.axis('off')
    
    # Show the probabilities
    probs = probabilities[0].cpu().numpy()
    ax2.bar(range(10), probs)
    ax2.set_xticks(range(10))
    ax2.set_xticklabels(classes, rotation=45)
    ax2.set_xlabel('Class')
    ax2.set_ylabel('Probability')
    ax2.set_title('Softmax Probabilities')
    
    plt.tight_layout()

Diese Funktion zeigt, wie man während der Inferenz Softmax-Wahrscheinlichkeiten aus einem trainierten Modell erhält. Es lässt ein Bild durch das Modell laufen, um Logits zu erhalten, wendet Softmax manuell mit torch.nn.functional.softmax() an und visualisiert dann sowohl das Bild als auch die resultierende Wahrscheinlichkeitsverteilung.

Jetzt lass uns das Modell trainieren:

train_model()

Ausgabe:

Schauen wir uns an, wie sich die Wahrscheinlichkeiten für ein Testbild darstellen:

show_prediction_example()

Ausgabe:

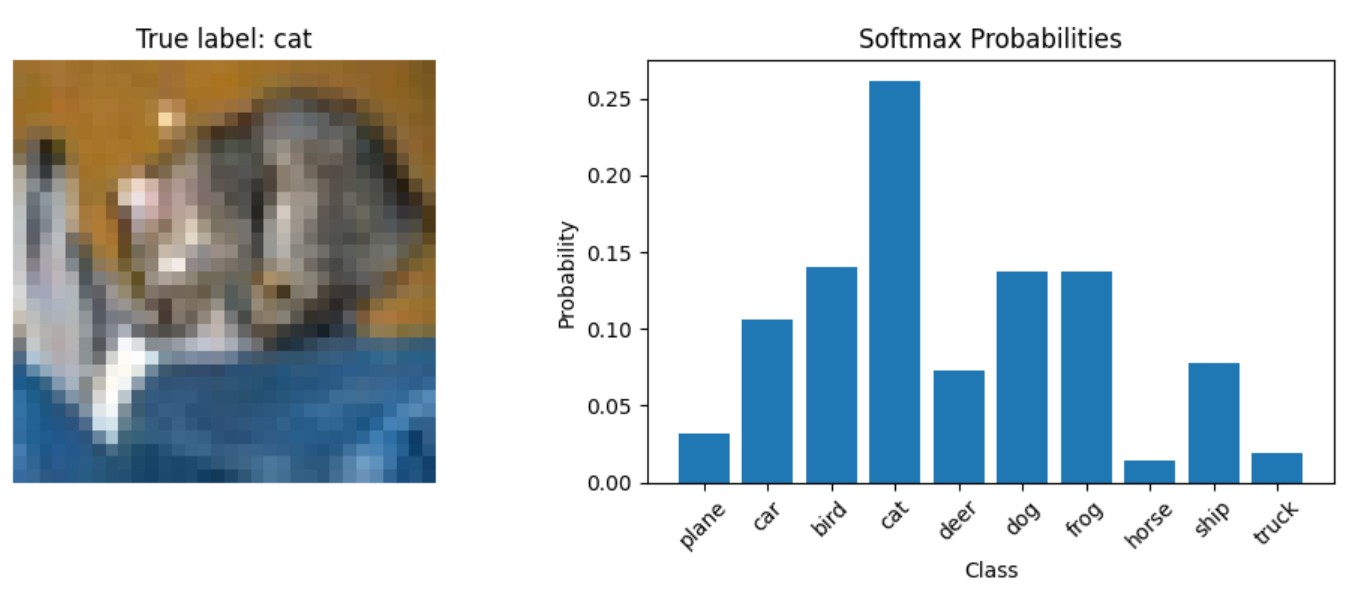
Im nächsten Abschnitt werden wir uns die spezifischen Szenarien ansehen, in denen Softmax die optimale Wahl ist, untersuchen, wann die Softmax-Aktivierungsfunktion verwendet werden sollte, und diskutieren reale Anwendungen in verschiedenen Deep Learning-Modellen.

Wann wird die Softmax-Aktivierungsfunktion verwendet?

Um effektive neuronale Netze zu entwerfen, ist es wichtig zu wissen, wann die Softmax-Aktivierungsfunktion verwendet werden sollte. Die Softmax-Aktivierungsfunktion wird vor allem in der Ausgabeschicht von neuronalen Netzen für Klassifizierungsaufgaben eingesetzt.

Softmax für Mehrklassen-Klassifizierung

Softmax ist die Standardwahl, wenn unser Modell die Eingaben in eine von mehreren sich gegenseitig ausschließenden Kategorien einordnen muss. Gängige Beispiele sind:

• Bildklassifizierung (Identifizierung von Objekten auf Fotos)
• Dokumentenkategorisierung (Zuweisung von Themen zu Texten)
• Named Entity Recognition (Erkennung von Personennamen, Orten usw.)
• Spracherkennung (Umwandlung von Audio in Text)

Probabilistische Interpretation und Vertrauenswerte

Wenn unser Modell Wahrscheinlichkeiten und nicht nur Klassenvorhersagen ausgeben soll, liefert Softmax eine wahrscheinlichkeitstheoretische Interpretation des Modellvertrauens über alle möglichen Klassen hinweg.

Softmax in Verstärkungslernen und Aufmerksamkeitsmechanismen

Beim Reinforcement Learning und bei sequentiellen Entscheidungsproblemen kann Softmax verwendet werden, um Aktionswerte in eine Wahrscheinlichkeitsverteilung für die Aktionsauswahl umzuwandeln.

Moderne Transformator-basierte Architekturen verwenden Softmax, um die Aufmerksamkeit auf verschiedene Teile der Eingangssequenz zu verteilen.

Aufgrund der starken mathematischen Grundlage und der intuitiven probabilistischen Interpretation eignet sich die Softmax-Aktivierungsfunktion besonders gut für Klassifizierungsprobleme, bei denen sich die Klassen gegenseitig ausschließen.

Deep Learning Modelle

Mehrere Deep Learning-Architekturen verwenden die Softmax-Aktivierungsfunktion. 

Bildklassifizierungsnetzwerke wie ResNet, VGG und Inception verwenden alle Softmax in ihrer letzten Schicht, um Bilder in Tausende von Kategorien zu klassifizieren. Modelle, die auf ImageNet trainiert werden, haben zum Beispiel eine Softmax-Schicht mit 1000 Einheiten, die 1000 Objektkategorien entspricht.

Bei der Sprachmodellierung verwenden RNN-basierte Modelle Softmax, um das nächste Wort in einer Sequenz aus einem Vokabular vorherzusagen, das Zehntausende von Wörtern enthalten kann.

Moderne NLP-Architekturen wie BERT, GPT und T5 verwenden Softmax in mehreren Komponenten:

• In Aufmerksamkeitsmechanismen, um zu bestimmen, wie viel Fokus auf verschiedene Teile des Inputs gelegt werden soll
• In der abschließenden Klassifizierungsschicht für Aufgaben wie Sentimentanalyse oder Dokumentenklassifizierung

Variationale Autoencoder (VAEs) und bestimmte Generative Adversarial Networks (GANs) verwenden Softmax in ihren Diskriminatorkomponenten oder für die Modellierung kategorialer latenter Variablen.

Im nächsten Abschnitt werden wir uns die Unterschiede zwischen der Softmax-Aktivierungsfunktion und der Sigmoid-Aktivierungsfunktion ansehen.

Softmax vs. Sigmoid-Aktivierungsfunktion

Die Sigmoidfunktion, definiert als σ(x) = 1/(1+e^(-x)), wandelt eine einzelne reelle Zahl in einen Wert zwischen 0 und 1 um. Im Gegensatz dazu arbeitet die Softmax-Aktivierungsfunktion mit einem Vektor von Zahlen und wandelt diese in eine Wahrscheinlichkeitsverteilung um.

Hier sind die grundlegenden Unterschiede zwischen diesen beiden Aktivierungsfunktionen:

Abmessungen von Eingang und Ausgang

• Sigmoid: Nimmt eine einzelne skalare Eingabe und erzeugt eine einzelne skalare Ausgabe zwischen 0 und 1.
• Softmax: Nimmt einen Vektor mit n Eingaben und erzeugt einen Vektor mit n Ausgaben, die sich zu 1 summieren.

Wahrscheinlichkeitsinterpretation

• Sigmoid: Die Ausgabe stellt die Wahrscheinlichkeit für ein einzelnes binäres Ereignis dar (z. B. "Ist diese E-Mail Spam?").
• Softmax: Die Ausgaben stellen Wahrscheinlichkeiten für mehrere sich gegenseitig ausschließende Klassen dar (z. B. "Welche Ziffer von 0-9 ist das?").

Unabhängigkeit der Ergebnisse

• Sigmoid: Wenn mehrere Neuronen verwendet werden, ist jede Ausgabe unabhängig von den anderen. Mehrere Ausgänge können alle hoch oder alle niedrig sein.
• Softmax: Die Ergebnisse sind voneinander abhängig - wenn eine Wahrscheinlichkeit steigt, müssen die anderen sinken, um die Summe von 1 zu erhalten.

Mathematische Beziehung

Interessanterweise ist die Sigmoid-Funktion eigentlich ein Spezialfall der Softmax-Aktivierungsfunktion, wenn es nur zwei Klassen gibt. Deshalb wird Sigmoid oft als "binäre Softmax" bezeichnet.

Wann Softmax und wann Sigmoid verwendet werden sollten

Die Wahl der richtigen Aktivierungsfunktion ist entscheidend dafür, dass ein neuronales Netz aussagekräftige Vorhersagen macht, und die Entscheidung zwischen Softmax und Sigmoid hängt von der Art der Klassifizierungsaufgabe ab.

Verwende das Sigmoid, wenn:

• Lösen von binären Klassifizierungsproblemen (zwei Klassen)
• Jede Ausgabe muss unabhängig interpretiert werden
• Implementierung einer Multi-Label-Klassifizierung, bei der eine Instanz gleichzeitig zu mehreren Klassen gehören kann
• Aufmerksamkeitsmechanismen oder Gates in rekurrenten neuronalen Netzen schaffen

Verwende Softmax, wenn:

• Umgang mit Mehrklassen-Klassifizierungsproblemen (mehr als zwei Klassen)
• Die Klassen schließen sich gegenseitig aus (eine Eingabe gehört zu genau einer Klasse)
• Du brauchst eine richtige Wahrscheinlichkeitsverteilung für alle möglichen Ergebnisse
• Implementierung der letzten Schicht der meisten Bildklassifizierungsnetzwerke

In einem neuronalen Netz, das Bilder von handgeschriebenen Ziffern (0-9) klassifiziert, wäre beispielsweise die Softmax-Aktivierungsfunktion für die Ausgabeschicht geeignet, da jedes Bild genau eine Ziffer darstellt. Für ein Netzwerk, das mehrere Objekte in einem Bild erkennt (z. B. "enthält eine Person", "enthält ein Auto", "enthält einen Baum"), wären sigmoidale Aktivierungen dagegen besser geeignet, da mehrere Objekte gleichzeitig vorhanden sein können.

Hier ist eine Tabelle, in der die Aktivierungsfunktion Softmax mit der Sigmoidfunktion verglichen wird:

Das Verständnis des Unterschieds zwischen diesen Aktivierungsfunktionen ist entscheidend für den Entwurf effektiver neuronaler Netze. Während die Softmax-Aktivierungsfunktion die erste Wahl für Mehrklassen-Klassifizierungsprobleme ist, bleibt die Sigmoid-Funktion für binäre Klassifizierung und Probleme, die unabhängige Wahrscheinlichkeiten erfordern, wertvoll.

Im nächsten Abschnitt befassen wir uns mit den häufigsten Problemen und den Überlegungen, die bei der Arbeit mit Softmax-Aktivierungsfunktionen angestellt werden müssen.

Allgemeine Probleme und Überlegungen

Wenn du mit der Softmax-Aktivierungsfunktion in deinen Deep Learning-Modellen arbeitest, können verschiedene Herausforderungen die Leistung und Zuverlässigkeit des Modells beeinträchtigen. Wenn du diese Probleme verstehst und weißt, wie du sie angehen kannst, kannst du robustere Modelle erstellen.

Herausforderungen bei der numerischen Stabilität

Die numerische Stabilität ist bei der Verwendung der Softmax-Aktivierungsfunktion ein wichtiger Aspekt. Die Exponentialoperation in der Formel der Softmax-Aktivierungsfunktion kann zu einem numerischen Über- oder Unterlauf führen, wenn sie nicht richtig behandelt wird.

Bei sehr großen Eingabewerten (z. B. 1000 oder mehr) erzeugt die Exponentialfunktion beispielsweise extrem große Zahlen, die den maximal darstellbaren Fließkommawert in deinem System überschreiten können. Dies führt zu Überlauffehlern, die "unendliche" Werte erzeugen, so dass die abschließende Divisionsoperation undefinierte Ergebnisse liefert (NaN - Not a Number).

Die Standardlösung, die wir in unserem Abschnitt über die Umsetzung erwähnt haben, besteht darin, den Maximalwert von allen Eingaben abzuziehen, bevor die Exponentialfunktion angewendet wird. Diese Verschiebung ändert die relativen Proportionen nach der Normalisierung nicht, sondern hält die Werte in einem überschaubaren Bereich. 

Moderne Deep Learning-Frameworks regeln dieses Problem intern, aber es ist wichtig, das Problem zu verstehen, wenn du eigene Operationen implementierst oder unerwartetes Verhalten debuggen willst.

Softmax und Übervertrauen in Vorhersagen

Ein weiteres Problem mit der Softmax-Aktivierungsfunktion ist, dass neuronale Netze dazu neigen, ihre Vorhersagen zu optimistisch zu gestalten, selbst wenn sie falsch sind. Diese Selbstüberschätzung entsteht, weil:

1. Die exponentielle Natur von Softmax verstärkt kleine Unterschiede in den Logits.
2. Moderne tiefe neuronale Netze sind so leistungsfähig, dass sie sich die Trainingsdaten perfekt merken können.
3. Der Cross-Entropie-Verlust drückt die Wahrscheinlichkeiten für die richtigen Klassen weiter in Richtung 1, selbst wenn ein Modell eine gute Genauigkeit erreicht.

In der Praxis bedeutet das, dass ein Modell einer Vorhersage, die eigentlich falsch ist, eine Wahrscheinlichkeit von 99 % zuweisen kann. Dies kann bei kritischen Anwendungen, bei denen eine zuverlässige Unsicherheitsabschätzung unerlässlich ist, problematisch sein. Ein medizinisches Diagnosesystem, das zu viele falsche Vorhersagen macht, könnte zum Beispiel zu unangemessenen Behandlungsentscheidungen führen.

Die Lücke zwischen dem Vertrauen in ein Modell (aus den Softmax-Wahrscheinlichkeiten) und seiner tatsächlichen Genauigkeit wird als Kalibrierungsfehler bezeichnet. Gut kalibrierte Modelle erzeugen Konfidenzwerte, die ihren Genauigkeitsraten entsprechen - wenn ein Modell Ereignisse mit einer Konfidenz von 80 % vorhersagt, sollten diese Ereignisse auch in etwa 80 % der Fälle eintreten.

Regularisierungstechniken zur Verbesserung der Leistung

Zum Glück gibt es verschiedene Techniken, die diese Probleme mit der Softmax-Aktivierungsfunktion lösen können:

Temperaturskalierung

Die Temperaturskalierung führt einen Parameter T ein, der die "Weichheit" der Wahrscheinlichkeitsverteilung steuert. Indem du die Logits durch diesen Temperaturparameter teilst, bevor du Softmax anwendest, kannst du einstellen, wie spitz oder gleichmäßig die resultierende Verteilung wird.

Höhere Temperaturen (T > 1) führen zu weicheren Wahrscheinlichkeitsverteilungen mit weniger extremen Werten, was dazu beitragen kann, dass das Übervertrauen reduziert wird. Bei niedrigeren Temperaturen (T < 1) wird die Verteilung zum höchsten Wert hin spitzer. Die Temperaturskalierung wird üblicherweise als Nachbearbeitungstechnik nach dem Training eingesetzt, um das Modellvertrauen zu kalibrieren, ohne die Klasseneinteilung des Modells zu beeinflussen.

Etikett glätten

Die Label-Glättung ersetzt harte One-Hot-Ziel-Vektoren durch leicht geglättete Verteilungen. Anstatt das Modell so zu trainieren, dass es exakte Nullen und Einsen ausgibt, ermutigt das Label Smoothing das Modell dazu, etwas weniger zuversichtlich zu sein, indem es Werte wie 0,9 für die richtige Klasse und 0,025 für falsche Klassen (bei einem 4-Klassen-Problem) anstrebt.

Durch das Training mit diesen geglätteten Bezeichnungen lernt das Modell, weniger Vertrauen in seine Vorhersagen zu haben, was die Generalisierung verbessert und das Modell robuster gegenüber Bezeichnungsstörungen macht. Diese Technik ist in vielen modernen Bildklassifizierungsmodellen zum Standard geworden.

Dropout- und Ensemble-Methoden

Wenn du während des Trainings Dropouts verwendest und sie während der Inferenz aktiviert lässt (eine Technik, die Monte-Carlo-Dropouts genannt wird), kannst du mehrere Vorhersagen für dieselbe Eingabe stichprobenartig überprüfen und die Unsicherheit abschätzen. Wenn das Modell bei mehreren Vorwärtsdurchläufen mit unterschiedlichen Dropout-Mustern konsistente Vorhersagen liefert, ist es wahrscheinlich sicherer in seiner Vorhersage.

Ähnlich verhält es sich mit Ensemble-Methoden, die Vorhersagen aus mehreren Modellen kombinieren, um die Leistung zu verbessern und bessere Unsicherheitsschätzungen zu liefern. Die Unstimmigkeit zwischen den Modellen in einem Ensemble kann als Maß für die Unsicherheit dienen.

Kalibrierungstechniken

Platt-Skalierung und andere Kalibrierungsmethoden können nach dem Training angewendet werden, um sicherzustellen, dass die Konfidenzwerte von Softmax tatsächlich den wahren Wahrscheinlichkeiten entsprechen. Diese Methoden verwenden in der Regel eine Validierungsmenge, um Parameter zu erlernen, die die ursprünglichen Modellergebnisse auf gut kalibrierte Wahrscheinlichkeiten abbilden.

Zum Beispiel kann eine einfache Temperaturskalierung (wie bereits erwähnt) anhand von Validierungsdaten optimiert werden, um den Kalibrierungsfehler zu minimieren. Zu den komplexeren Ansätzen gehören die isotonische Regression und das Bayes'sche Binning.

Der Softmax-Engpass

Neuere Forschungen haben eine grundlegende Einschränkung der Softmax-Funktion festgestellt, die als "Softmax-Engpass" bekannt ist. Dies bezieht sich auf die Tatsache, dass die Aussagekraft von Softmax-basierten Sprachmodellen durch den Rang der Gewichtsmatrix in der letzten Schicht begrenzt ist. In natürlichsprachlichen Kontexten mit komplexen Abhängigkeiten kann dies verhindern, dass die Modelle die zugrunde liegenden bedingten Verteilungen vollständig erfassen.

Fortgeschrittene Architekturen wie Mixture of Softmaxes (MoS) wurden vorgeschlagen, um diese Einschränkung durch die Verwendung einer gewichteten Kombination mehrerer Softmax-Verteilungen zu umgehen.

Wenn du dir dieser häufigen Probleme bewusst bist und geeignete Lösungen implementierst, kannst du die Zuverlässigkeit und Leistung von Modellen verbessern, die die Softmax-Aktivierungsfunktion für Klassifizierungsaufgaben verwenden.

Fazit

Die Softmax-Aktivierungsfunktion ist eine wesentliche Komponente neuronaler Netze für Mehrklassen-Klassifizierungsprobleme, die rohe Logits in interpretierbare Wahrscheinlichkeitsverteilungen umwandelt. Wir haben die mathematischen Grundlagen, die Implementierung in Python, den Vergleich mit dem Sigmoid, praktische Anwendungsfälle und Techniken zur Bewältigung gängiger Probleme wie numerische Instabilität und Overconfidence untersucht.

Bist du bereit, dein Wissen über neuronale Netze zu vertiefen? 

• Entdecken Sie unsere Einführung in Aktivierungsfunktionen Tutorial oder tauchen Sie ein in die Framework-spezifischen Kurse zu Deep Learning mit Keras und PyTorch.
• Wenn du mehr über andere wichtige Aktivierungsfunktionen erfahren möchtest, sieh dir unseren Artikel über ReLU und beginne noch heute mit dem Aufbau effektiver neuronaler Netze!