Função de ativação Softmax em Python: Um guia completo

As funções de ativação são a espinha dorsal das redes neurais. Eles são componentes importantes que introduzem a não linearidade e permitem que essas redes aprendam padrões complexos. A função de ativação softmax é importante, principalmente ao lidar com problemas de classificação multiclasse.

Enquanto alternativas como Sigmoid e ReLU tenham seus casos de uso específicos, o softmax é melhor para lidar com situações em que os resultados devem ser interpretados como probabilidades em classes mutuamente exclusivas.

A função de ativação softmax transforma um vetor inteiro de números em uma distribuição de probabilidade. Essa característica exclusiva o torna indispensável para tarefas em que precisamos classificar as entradas em uma das várias categorias possíveis.

De sistemas de reconhecimento de imagens que identificam milhares de categorias de objetos a modelos de processamento de linguagem natural que preveem a próxima palavra em uma frase, o softmax fornece a base matemática para a tomada de decisões em várias possibilidades.

Neste artigo, veremos o que é a função de ativação softmax, como ela funciona matematicamente e quando você deve usá-la em sua rede neural neurais. Também veremos as implementações práticas em Python.

O que é a função de ativação Softmax?

A função de ativação Softmax função de ativação é uma função matemática que transforma um vetor de saídas brutas do modelo, conhecido como logits, em uma distribuição de probabilidade. Em termos mais simples, ele pega um conjunto de números e os converte em probabilidades que somam 1.

Ao contrário de algumas funções de ativação que operam em valores individuais de forma independente, o softmax trabalha em um vetor inteiro de valores, transformando-os coletivamente em uma distribuição de probabilidade em que todos os elementos somam exatamente 1.

No contexto das redes neurais, o softmax é normalmente aplicado à camada final de uma rede projetada para classificação multiclasse. Quando temos várias categorias possíveis e precisamos que nosso modelo indique a probabilidade de cada categoria, a função de ativação softmax é a escolha padrão.

Como funciona a função softmax?

As saídas brutas da camada final de uma rede neural são geralmente chamadas de "logits". Esses valores podem variar de infinito negativo a infinito positivo e não têm uma interpretação probabilística direta. A função de ativação softmax transforma esses logits em uma forma mais interpretável:

1. Tomando o exponencial de cada valor de entrada (o que garante que todos os valores sejam positivos).
2. Dividir cada exponencial pela soma de todos os exponenciais (o que garante que a soma dos resultados seja 1).

Essa transformação é fundamental porque nos permite interpretar o resultado da rede como uma distribuição de probabilidade. Por exemplo, se uma rede neural estiver classificando imagens em três categorias (gato, cachorro, pássaro), a saída softmax poderá ser [0,7, 0,2, 0,1], indicando uma probabilidade de 70% para gato, 20% para cachorro e 10% para pássaro.

A função de ativação softmax desempenha um papel fundamental na criação de distribuições de probabilidade válidas porque:

• Ele garante que todos os valores de saída estejam entre 0 e 1.
• Ele garante que todas as saídas somem exatamente 1.
• Ele preserva a classificação dos valores de entrada (entradas maiores resultam em probabilidades maiores).
• Ele acentua as diferenças entre valores maiores e suprime as diferenças entre valores menores.

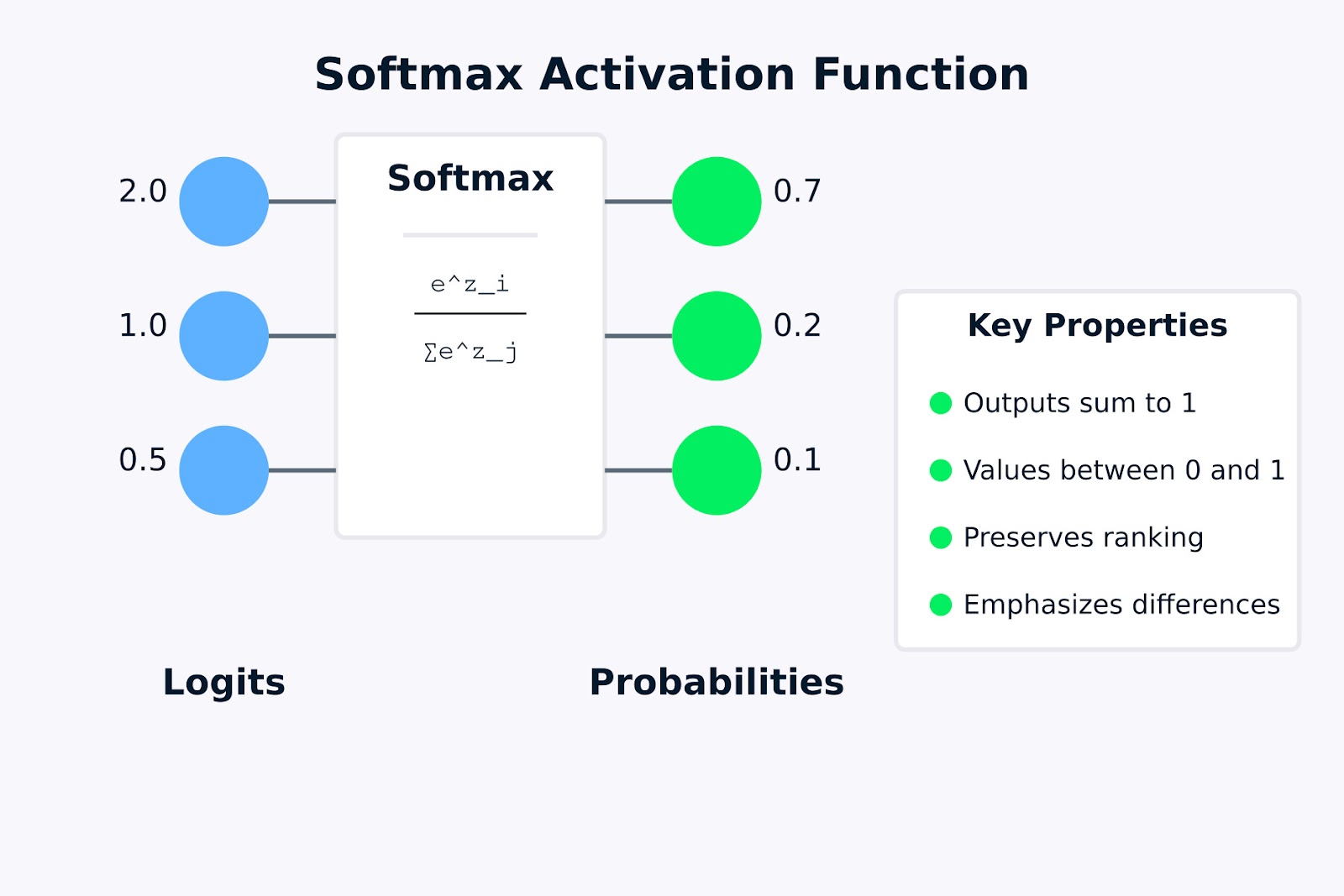
Função de ativação Softmax

A visualização acima mostra como a função de ativação softmax transforma logits brutos (os valores de entrada 2,0, 1,0 e 0,5) em uma distribuição de probabilidade (0,7, 0,2 e 0,1). A fórmula dentro da caixa de softmax representa como cada probabilidade de saída é calculada tomando o exponencial de um valor de entrada e dividindo-o pela soma de todos os exponenciais. 

As principais propriedades destacadas à direita indicam por que o softmax é útil para problemas de classificação multiclasse. Na próxima seção, veremos a fórmula matemática e como ela funciona.

Fórmula da função de ativação da Softmax e como ela funciona

Agora que entendemos o que é a função de ativação softmax, vamos examinar a formulação matemática e como ela transforma as entradas em distribuições de probabilidade.

A fórmula da função de ativação softmax pode ser expressa matematicamente como:

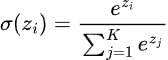
Onde:

• ​z_i é o valor de entrada (logit) para a classe i
• e^z_i é a função exponencial aplicada a z_i (também escrita como exp(z_i ​))
• K é o número total de classes
• O denominador soma os exponenciais de todos os valores de entrada, garantindo que os valores de saída somem 1

A função de ativação softmax segue essas etapas para transformar um vetor de entradas em uma distribuição de probabilidade:

1. Calcular exponenciais: Primeiro, calculamos o exponencial (e^x) de cada valor de entrada. Essa etapa garante que todos os valores sejam positivos, pois e^x > 0 para qualquer número real x
2. Some os exponenciais: Calculamos a soma de todos os valores exponenciais da etapa 1.
3. Normalize: Dividimos cada valor exponencial pela soma calculada na etapa 2. Essa normalização garante que todas as saídas estejam entre 0 e 1 e somem exatamente 1.

Vamos aplicar a fórmula da função de ativação softmax a um exemplo simples para ver como ela funciona na prática.

Suponha que tenhamos uma rede neural com três neurônios de saída para um problema de classificação de três classes (por exemplo, identificar se uma imagem contém um gato, um cachorro ou um pássaro). Após o cálculo final, a rede produz os seguintes logits: z = [2,0, 1,0, 0,5].

Para converter esses logits em probabilidades usando a função softmax:

1. Calcular exponenciais:
• e^2.0 = 7.389
• e^1.0 = 2.718
• e^0.5 = 1.648
2. Soma dos exponenciais:
• 7.389 + 2.718 + 1.648 = 11.755
3. Normalizar:
• P(classe 1) = 7,389 / 11,755 ≈ 0,628 ou 62,8%
• P(classe 2) = 2,718 / 11,755 ≈ 0,231 ou 23,1%
• P(classe 3) = 1,648 / 11,755 ≈ 0,140 ou 14,0%

A distribuição de probabilidade [0,628, 0,231, 0,140] soma 1, com a maior probabilidade atribuída à classe correspondente ao maior valor de logit. Esse exemplo demonstra como a função de ativação softmax preserva a classificação dos valores de entrada enquanto os transforma em uma distribuição de probabilidade válida.

Observe como os valores de entrada originais (2,0, 1,0, 0,5) mantiveram sua classificação relativa nas probabilidades de saída, mas as diferenças entre eles foram acentuadas. Essa propriedade torna o softmax particularmente útil em tarefas de classificação em que desejamos identificar a classe mais provável com confiança.

Na próxima seção, veremos as diferentes maneiras de implementar a função de ativação softmax usando Python.

Implementando a função de ativação Softmax em Python

Agora que entendemos a teoria por trás da função de ativação softmax, vamos ver como implementá-la em Python. Começaremos escrevendo uma função softmax do zero usando o NumPy e, em seguida, veremos como usá-la com estruturas populares de aprendizagem profunda, como TensorFlow/Keras e PyTorch.

Escrevendo softmax do zero usando NumPy

Antes de se aprofundar nas estruturas, é importante que você entenda como implementar a função de ativação softmax do zero. Isso ajuda a desenvolver a intuição sobre o que está acontecendo sob o capô.

import numpy as np

def softmax(x):
    """
    Compute softmax values for each set of scores in x.
    
    Args:
        x: Input array of shape (batch_size, num_classes) or (num_classes,)
        
    Returns:
        Softmax probabilities of same shape as input
    """
    # For numerical stability, subtract the maximum value from each input vector
    # This prevents overflow when calculating exp(x)
    shifted_x = x - np.max(x, axis=-1, keepdims=True)
    
    # Calculate exp(x) for each element
    exp_x = np.exp(shifted_x)
    
    # Calculate the sum of exp(x) for normalization
    sum_exp_x = np.sum(exp_x, axis=-1, keepdims=True)
    
    # Normalize to get probabilities
    probabilities = exp_x / sum_exp_x
    
    return probabilities

Essa implementação segue exatamente a fórmula da função de ativação softmax, com uma adição importante: subtraímos o valor máximo de cada vetor de entrada antes da exponenciação. 

Essa operação de "deslocamento" não altera o resultado matemático, mas ajuda a evitar o estouro numérico, que pode ocorrer ao calcular exponenciais de números grandes.

Vamos testar nossa implementação com um exemplo simples:

# Sample logits from a neural network (batch of 2 examples, 3 classes each)
logits = np.array([
    [2.0, 1.0, 0.5],  # First example
    [3.0, 2.0, 1.0]   # Second example
])

probabilities = softmax(logits)
print("Logits:\n", logits)
print("\nSoftmax probabilities:\n", probabilities)
print("\nSum of probabilities (should be 1 for each example):", np.sum(probabilities, axis=1))

Saída:

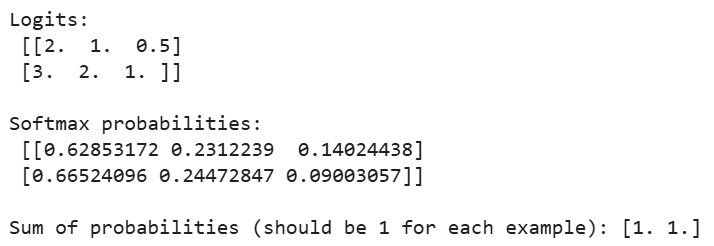
Quando executarmos o código acima, veremos que a soma das probabilidades de cada exemplo é igual a 1, confirmando que nossa implementação do softmax produz distribuições de probabilidade válidas. No primeiro exemplo, a maior probabilidade corresponde ao maior logit (2,0) e, da mesma forma, no segundo exemplo.

Usando softmax no TensorFlow/Keras

O TensorFlow e o Keras facilitam o uso da função de ativação softmax em suas redes neurais. Vamos criar um classificador simples para o conjunto de dados MNIST, passo a passo.

Primeiro, vamos importar as bibliotecas necessárias e carregar o conjunto de dados:

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Softmax
from tensorflow.keras.datasets import mnist
import matplotlib.pyplot as plt
import numpy as np

# Load and preprocess the MNIST dataset
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# Normalize pixel values to be between 0 and 1
x_train, x_test = x_train / 255.0, x_test / 255.0

# One-hot encode the labels
y_train_one_hot = tf.keras.utils.to_categorical(y_train, 10)
y_test_one_hot = tf.keras.utils.to_categorical(y_test, 10)

O conjunto de dados MNIST contém imagens em escala de cinza de 28x28 pixels de dígitos manuscritos (0-9). Normalizamos os valores de pixel para que fiquem entre 0 e 1, a fim de melhorar a dinâmica do treinamento, e convertemos os rótulos de classe em codificação de um ponto, que é o formato preferido para saídas softmax.

Agora, vamos criar um modelo de rede neural com uma camada de saída softmax:

# Method 1: Using softmax as the activation function in the final layer
model1 = Sequential([
    Flatten(input_shape=(28, 28)),  # Convert 28x28 images to 784-length vectors
    Dense(128, activation='relu'),   # Hidden layer with ReLU activation
    Dense(10, activation='softmax')  # Output layer with softmax activation
])

# Method 2: Using a separate Softmax layer
model2 = Sequential([
    Flatten(input_shape=(28, 28)),
    Dense(128, activation='relu'),
    Dense(10),  # Linear output (logits)
    Softmax()   # Separate softmax layer
])

Aqui, demonstramos duas maneiras equivalentes de incorporar a função de ativação softmax em uma rede neural:

• Método 1: Especificar diretamente "softmax" como a função de ativação na camada Dense final
• Método 2: Adição de uma camada Softmax separada após a camada Dense que produz logits brutos

Ambas as abordagens produzem resultados idênticos, mas o segundo método torna a separação entre logits e probabilidades mais explícita, o que pode ser útil em determinados cenários.

Em seguida, vamos compilar e treinar o modelo:

# Compile the model
model1.compile(
    optimizer='adam',
    loss='categorical_crossentropy',  # This loss works well with softmax
    metrics=['accuracy']
)

# Print model summary
print("Model with softmax activation:")
model1.summary()

# Train the model
print("\nTraining the model...")
history = model1.fit(
    x_train, y_train_one_hot,
    epochs=5,
    batch_size=128,
    validation_split=0.1,
    verbose=1
)

Saída:

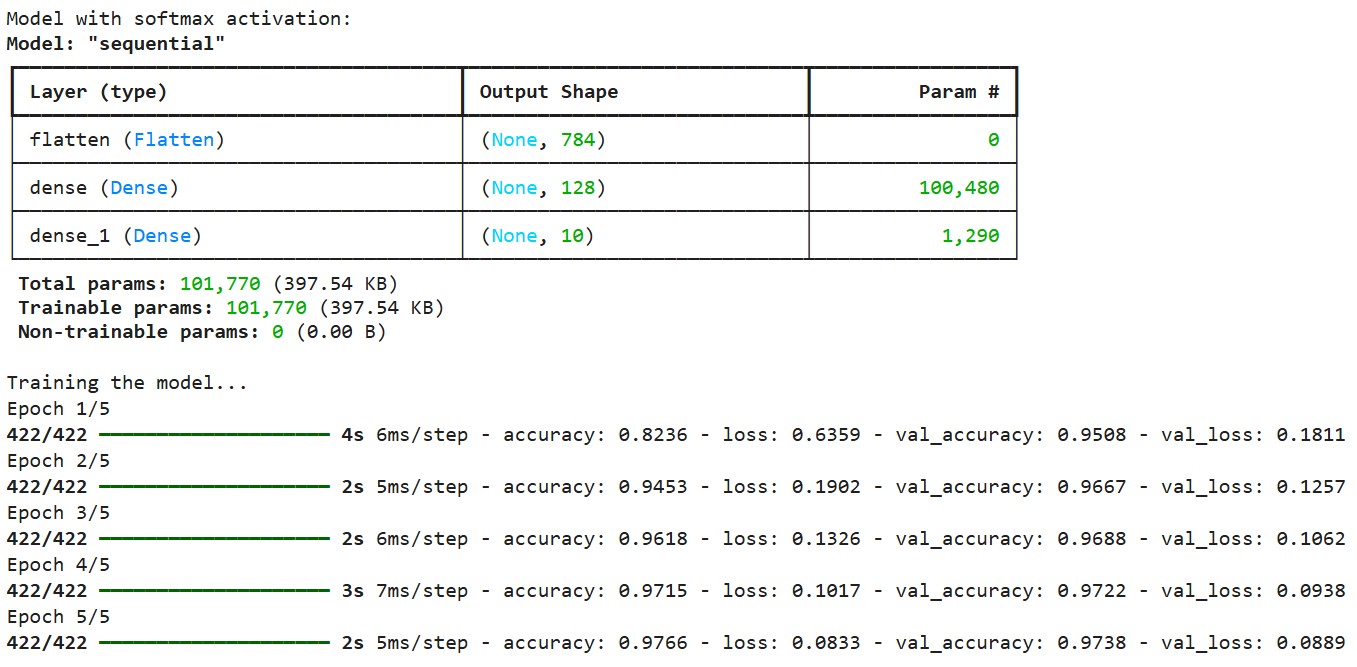Compilamos o modelo usando a função de perda de entropia cruzada categórica, que foi projetada para funcionar com saídas softmax. Essa função de perda mede a diferença entre a distribuição de probabilidade prevista e os rótulos verdadeiros codificados com um tiro. Usamos o otimizador Adam, que ajusta de forma adaptativa a taxa de aprendizado durante o treinamento.

Após o treinamento, podemos usar o modelo para fazer previsões e visualizar os resultados:

# Let's check predictions on a sample
sample_idx = 42
sample_image = x_test[sample_idx]
true_label = y_test[sample_idx]

# Get model predictions (probabilities across all classes)
predictions = model1.predict(sample_image[np.newaxis, ...])

# Visualize the results
plt.figure(figsize=(10, 4))

# Plot the image
plt.subplot(1, 2, 1)
plt.imshow(sample_image, cmap='gray')
plt.title(f"True label: {true_label}")
plt.axis('off')

# Plot the probability distribution
plt.subplot(1, 2, 2)
plt.bar(range(10), predictions[0])
plt.xticks(range(10))
plt.xlabel('Digit')
plt.ylabel('Probability')
plt.title('Softmax Probabilities')

Esse código seleciona uma imagem de teste, passa por ela por meio do modelo treinado e visualiza a imagem e a distribuição de probabilidade resultante da saída do softmax. A barra mais alta no gráfico de probabilidade representa a previsão do modelo.

Saída:

O TensorFlow também oferece uma função integrada para aplicar o softmax diretamente:

# Demonstrate using a custom softmax function in TensorFlow
def custom_softmax(logits):
    """Custom implementation of softmax in TensorFlow"""
    exp_logits = tf.exp(logits - tf.reduce_max(logits, axis=-1, keepdims=True))
    return exp_logits / tf.reduce_sum(exp_logits, axis=-1, keepdims=True)

# Example usage of custom softmax
logits = tf.constant([[2.0, 1.0, 0.5], [3.0, 2.0, 1.0]])
custom_probs = custom_softmax(logits)
tf_probs = tf.nn.softmax(logits)

print("\nCustom softmax:", custom_probs.numpy())
print("TensorFlow softmax:", tf_probs.numpy())

Saída:

Este exemplo compara uma implementação personalizada do softmax com a função tf.nn.softmax() integrada do TensorFlow. Ambos devem produzir resultados idênticos. A implementação personalizada também inclui o truque de estabilidade numérica de subtrair o valor máximo antes da exponenciação.

Usando o Softmax no PyTorch

Agora, vamos implementar um modelo semelhante usando o PyTorch e o conjunto de dados CIFAR-10. Começaremos importando as bibliotecas e configurando os dados, conforme mostrado abaixo:

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np

# Set the device
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")

# Load and preprocess the CIFAR-10 dataset
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))  # Normalize RGB channels
])

# Load a small subset of the CIFAR-10 dataset for demonstration
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64,
                                         shuffle=False, num_workers=2)

# Define the class names for CIFAR-10
classes = ('plane', 'car', 'bird', 'cat', 'deer',
           'dog', 'frog', 'horse', 'ship', 'truck')

O código acima configura o PyTorch para usar a aceleração de GPU, se disponível, carrega o conjunto de dados CIFAR-10 (que contém imagens coloridas de 32x32 em 10 classes) e prepara os carregadores de dados para treinamento e teste.

Em seguida, vamos definir uma rede neural convolucional simples, conforme mostrado abaixo:

# Define a simple convolutional neural network
class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        # Convolutional layers
        self.conv1 = nn.Conv2d(3, 16, 3, padding=1)
        self.conv2 = nn.Conv2d(16, 32, 3, padding=1)
        self.pool = nn.MaxPool2d(2, 2)
        
        # Fully connected layers
        self.fc1 = nn.Linear(32 * 8 * 8, 128)
        self.fc2 = nn.Linear(128, 10)  # 10 classes in CIFAR-10
        
        # Activation functions
        self.relu = nn.ReLU()
        
        # Note: We don't define softmax here as it will be applied with the loss function
    
    def forward(self, x):
        # Convolutional layers with ReLU and pooling
        x = self.pool(self.relu(self.conv1(x)))  # -> 16x16x16
        x = self.pool(self.relu(self.conv2(x)))  # -> 8x8x32
        
        # Flatten the output
        x = x.view(-1, 32 * 8 * 8)
        
        # Fully connected layers
        x = self.relu(self.fc1(x))
        x = self.fc2(x)  # Raw logits output
        
        # Note: No softmax here, as PyTorch's CrossEntropyLoss applies it internally
        return x

Essa CNN processa as imagens RGB 32x32 por meio de camadas convolucionais, aplica a ativação e o agrupamento ReLU e termina com camadas totalmente conectadas. Notavelmente, o modelo não inclui uma camada softmax em sua passagem direta. Em vez disso, ele gera logits brutos.

Esse é um padrão comum no PyTorch porque a função CrossEntropyLoss usada durante o treinamento aplica internamente o softmax antes de calcular a perda, que é numericamente mais estável .

Vamos ver também como incluir explicitamente o softmax, se necessário:

# Applying softmax within the model
class ModelWithSoftmax(nn.Module):
    def __init__(self):
        super(ModelWithSoftmax, self).__init__()
        self.features = SimpleCNN()
        self.softmax = nn.Softmax(dim=1)
    
    def forward(self, x):
        logits = self.features(x)
        probabilities = self.softmax(logits)
        return probabilities

Definimos duas variantes de modelo: SimpleCNN produz logits brutos, enquanto ModelWithSoftmax aplica explicitamente o softmax para produzir probabilidades. Para o treinamento, usamos o site SimpleCNN com CrossEntropyLoss, que é a abordagem padrão no PyTorch.

Vamos definir uma função de treinamento:

# Create the model and move it to the device 
model = SimpleCNN().to(device) 
# Define loss function and optimizer 
criterion = nn.CrossEntropyLoss()  # Combines LogSoftmax and NLLLoss 
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# Train the model (only a few epochs for demonstration)
def train_model(epochs=2):
    for epoch in range(epochs):
        running_loss = 0.0
        for i, data in enumerate(trainloader, 0):
            inputs, labels = data[0].to(device), data[1].to(device)
            
            # Zero the parameter gradients
            optimizer.zero_grad()
            
            # Forward + backward + optimize
            outputs = model(inputs)  # These are logits (pre-softmax)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
            
            running_loss += loss.item()
            if i % 100 == 99:
                print(f'[{epoch + 1}, {i + 1}] loss: {running_loss / 100:.3f}')
                running_loss = 0.0
    
    print('Finished Training')

Por fim, vamos criar uma função para visualizar as previsões do modelo:

# Function to display predictions with softmax probabilities
def show_prediction_example():
    # Get a batch of test images
    dataiter = iter(testloader)
    images, labels = next(dataiter)
    
    # Select a single image
    img = images[0].to(device)
    label = labels[0]
    
    # Get the model's prediction (logits)
    with torch.no_grad():
        logits = model(img.unsqueeze(0))
    
    # Apply softmax to get probabilities
    probabilities = torch.nn.functional.softmax(logits, dim=1)
    
    # Plot the image and probabilities
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4))
    
    # Show the image
    img_np = img.cpu().numpy()
    img_np = np.transpose(img_np, (1, 2, 0))
    # Denormalize the image for display
    img_np = img_np * 0.5 + 0.5
    ax1.imshow(img_np)
    ax1.set_title(f"True label: {classes[label]}")
    ax1.axis('off')
    
    # Show the probabilities
    probs = probabilities[0].cpu().numpy()
    ax2.bar(range(10), probs)
    ax2.set_xticks(range(10))
    ax2.set_xticklabels(classes, rotation=45)
    ax2.set_xlabel('Class')
    ax2.set_ylabel('Probability')
    ax2.set_title('Softmax Probabilities')
    
    plt.tight_layout()

Essa função demonstra como obter probabilidades softmax de um modelo treinado durante a inferência. Ele passa uma imagem pelo modelo para obter logits, aplica o softmax manualmente usando torch.nn.functional.softmax() e, em seguida, visualiza a imagem e a distribuição de probabilidade resultante.

Agora, vamos treinar o modelo:

train_model()

Saída:

Vamos fazer uma previsão e ver como as probabilidades aparecem em uma imagem de teste:

show_prediction_example()

Saída:

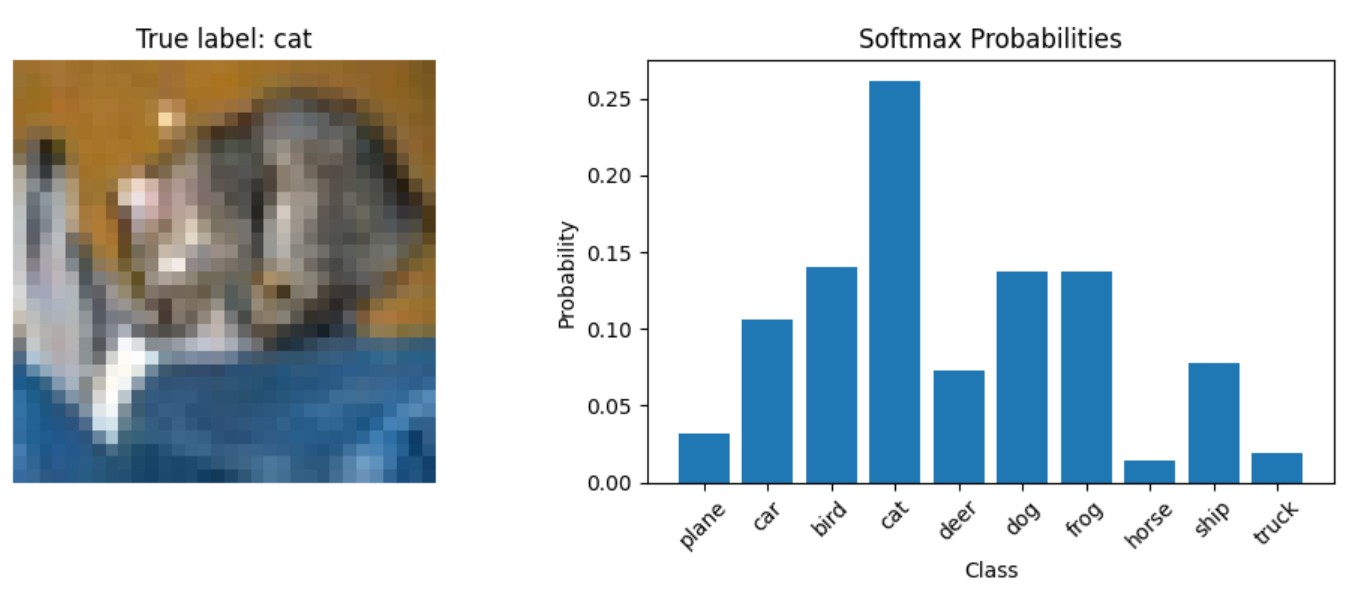
Na próxima seção, analisaremos os cenários específicos em que a softmax é a escolha ideal, examinaremos quando a função de ativação softmax deve ser usada e discutiremos as aplicações do mundo real em vários modelos de aprendizagem profunda.

Quando usar a função de ativação Softmax?

Entender quando usar a função de ativação softmax é importante para projetar redes neurais eficazes. A função de ativação softmax tem sua principal aplicação na camada de saída de redes neurais projetadas para tarefas de classificação.

Softmax para classificação multiclasse

O Softmax é a opção padrão quando nosso modelo precisa classificar as entradas em uma das várias categorias mutuamente exclusivas. Exemplos comuns incluem:

• Classificação de imagens (identificação de objetos em fotos)
• Categorização de documentos (atribuição de tópicos ao texto)
• Reconhecimento de entidades nomeadas (identificação de nomes de pessoas, locais, etc.)
• Reconhecimento de fala (mapeamento de áudio para texto)

Interpretação probabilística e escores de confiança

Quando precisamos que nosso modelo produza probabilidades em vez de apenas previsões de classe, o softmax fornece uma interpretação probabilística da confiança do modelo em todas as classes possíveis.

Softmax em mecanismos de aprendizagem por reforço e atenção

Em problemas de aprendizagem por reforço e de decisão sequencial, o softmax pode ser usado para converter valores de ação em uma distribuição de probabilidade para a seleção de ações.

Arquiteturas modernas arquiteturas modernas baseadas em transformadores usam o softmax para distribuir a atenção entre diferentes partes da sequência de entrada.

A sólida base matemática e a interpretação probabilística intuitiva tornam a função de ativação softmax particularmente adequada para problemas de classificação em que as classes são mutuamente exclusivas.

Modelos de aprendizagem profunda

Várias arquiteturas de aprendizagem profunda usam a função de ativação softmax. 

As redes de classificação de imagens, como ResNet, VGG e Inception, usam softmax em sua camada final para classificar imagens em milhares de categorias. Por exemplo, os modelos treinados no ImageNet normalmente têm uma camada softmax de 1.000 unidades correspondente a 1.000 categorias de objetos.

Na modelagem de linguagem, os modelos baseados em RNN usam softmax para prever a próxima palavra em uma sequência de um vocabulário que pode conter dezenas de milhares de palavras.

As arquiteturas modernas de NLP, como BERT, GPT e T5, usam softmax em vários componentes:

• Em mecanismos de atenção para determinar o grau de foco a ser colocado em diferentes partes da entrada
• Na camada de classificação final para tarefas como análise de sentimentos ou classificação de documentos

Autoencodificadores variacionais (VAEs) e algumas Redes Adversariais Generativas (GANs) usam softmax em seus componentes discriminadores ou para modelagem de variáveis latentes categóricas.

Na próxima seção, veremos as diferenças entre a função de ativação softmax e a função de ativação sigmoide.

Função de ativação Softmax vs. Sigmoid

A função sigmoide, definida como σ(x) = 1/(1+e^(-x)), transforma um único número real em um valor entre 0 e 1. Por outro lado, a função de ativação softmax opera em um vetor de números, convertendo-os em uma distribuição de probabilidade.

Aqui estão as diferenças fundamentais entre essas duas funções de ativação:

Dimensões de entrada e saída

• Sigmoide: Recebe uma única entrada escalar e produz uma única saída escalar entre 0 e 1.
• Softmax: Recebe um vetor de n entradas e produz um vetor de n saídas cuja soma é 1.

Interpretação de probabilidade

• Sigmoide: A saída representa a probabilidade de um único evento binário (por exemplo, "Este e-mail é spam?").
• Softmax: As saídas representam probabilidades em várias classes mutuamente exclusivas (por exemplo, "Qual dígito de 0 a 9 é este?").

Independência dos resultados

• Sigmoide: Quando usado em vários neurônios, cada saída é independente das outras. Várias saídas podem ser todas altas ou todas baixas.
• Softmax: Os resultados são interdependentes: se uma probabilidade aumenta, as outras devem diminuir para manter uma soma de 1.

Relação matemática

É interessante notar que a função sigmoide é, na verdade, um caso especial da função de ativação softmax quando há apenas duas classes. É por isso que o sigmoide é frequentemente chamado de "softmax binário".

Quando usar o softmax versus quando usar o sigmoide

A escolha da função de ativação correta é fundamental para garantir que uma rede neural produza previsões significativas, e a decisão entre softmax e sigmoide depende da natureza da tarefa de classificação.

Use o sigmoide quando:

• Solução de problemas de classificação binária (duas classes)
• Cada saída precisa ser interpretada de forma independente
• Implementação da classificação com vários rótulos, em que uma instância pode pertencer a várias classes simultaneamente
• Criação de mecanismos ou portas de atenção em redes neurais recorrentes

Use o softmax quando:

• Lidar com problemas de classificação multiclasse (mais de duas classes)
• As classes são mutuamente exclusivas (um input pertence exatamente a uma classe)
• Você precisa de uma distribuição de probabilidade adequada para todos os resultados possíveis
• Implementação da camada final da maioria das redes de classificação de imagens

Por exemplo, em uma rede neural que classifica imagens de dígitos manuscritos (0-9), a função de ativação softmax seria apropriada para a camada de saída, pois cada imagem representa exatamente um dígito. Por outro lado, para uma rede que detecta vários objetos em uma imagem (por exemplo, "contém pessoa", "contém carro", "contém árvore"), as ativações sigmoides seriam mais adequadas, pois vários objetos podem estar presentes simultaneamente.

Aqui você encontra uma tabela de referência rápida que compara a função de ativação softmax com a sigmoide:

Compreender a distinção entre essas funções de ativação é fundamental para projetar redes neurais eficazes. Embora a função de ativação softmax seja a escolha ideal para problemas de classificação multiclasse, a sigmoide continua valiosa para classificação binária e problemas que exigem probabilidades independentes.

Na próxima seção, veremos os problemas comuns que surgem e as considerações a serem feitas ao trabalhar com funções de ativação softmax.

Problemas e considerações comuns

Ao trabalhar com a função de ativação softmax em seus modelos de aprendizagem profunda, vários desafios podem afetar o desempenho e a confiabilidade do modelo. Compreender esses problemas e saber como resolvê-los ajudará você a criar modelos mais robustos.

Desafios de estabilidade numérica

A estabilidade numérica é uma preocupação fundamental ao usar a função de ativação softmax. A operação exponencial na fórmula da função de ativação softmax pode levar a um estouro ou subfluxo numérico se não for tratada adequadamente.

Por exemplo, ao lidar com valores de entrada muito grandes (como 1000 ou mais), a função exponencial produz números extremamente grandes que podem exceder o valor máximo de ponto flutuante representável em seu sistema. Isso leva a erros de estouro, produzindo valores "infinitos" que fazem com que a operação final de divisão produza resultados indefinidos (NaN - Not a Number).

A solução padrão, conforme mencionado em nossa seção de implementação, é subtrair o valor máximo de todas as entradas antes de aplicar a função exponencial. Essa mudança não altera as proporções relativas após a normalização, mas mantém os valores em uma faixa gerenciável. 

As estruturas modernas de aprendizagem profunda lidam com esse problema internamente, mas é importante que você entenda o problema ao implementar operações personalizadas ou depurar comportamentos inesperados.

Softmax e excesso de confiança nas previsões

Outro problema comum com a função de ativação softmax é que as redes neurais tendem a se tornar excessivamente confiantes em suas previsões, mesmo quando estão erradas. Esse excesso de confiança ocorre porque:

1. A natureza exponencial do softmax amplifica pequenas diferenças nos logits.
2. As redes neurais profundas modernas são poderosas o suficiente para memorizar perfeitamente os dados de treinamento.
3. A perda de entropia cruzada continua a empurrar as probabilidades em direção a 1 para as classes corretas, mesmo depois que um modelo atinge uma boa precisão.

Na prática, isso significa que um modelo pode atribuir uma probabilidade de 99% a uma previsão que, na verdade, está incorreta. Isso pode ser problemático em aplicações críticas em que a estimativa confiável da incerteza é essencial. Por exemplo, um sistema de diagnóstico médico que confia demais em previsões incorretas pode levar a decisões de tratamento inadequadas.

A diferença entre a confiança de um modelo (das probabilidades softmax) e sua precisão real é conhecida como erro de calibração. Modelos bem calibrados produzem pontuações de confiança que correspondem às suas taxas de precisão - se um modelo prevê eventos com 80% de confiança, esses eventos devem ocorrer aproximadamente 80% das vezes.

Técnicas de regularização para melhorar o desempenho

Felizmente, várias técnicas podem ajudar a resolver esses problemas com a função de ativação softmax:

Escala de temperatura

A escala de temperatura introduz um parâmetro T que controla a "suavidade" da distribuição de probabilidade. Ao dividir os logits por esse parâmetro de temperatura antes de aplicar o softmax, você pode ajustar o pico ou a uniformidade da distribuição resultante.

Temperaturas mais altas (T > 1) produzem distribuições de probabilidade mais suaves com valores menos extremos, o que pode ajudar a reduzir o excesso de confiança. Temperaturas mais baixas (T < 1) fazem com que a distribuição tenha mais picos em direção ao valor mais alto. A escala de temperatura é comumente usada como uma técnica de pós-processamento após o treinamento para calibrar a confiança do modelo sem afetar a classificação de classes do modelo.

Suavização de rótulos

A suavização de rótulos substitui os vetores de alvos rígidos e pontuais por distribuições ligeiramente suavizadas. Em vez de treinar o modelo para produzir zeros e uns exatos, a suavização de rótulos incentiva o modelo a ser um pouco menos confiante, visando valores como 0,9 para a classe correta e 0,025 para classes incorretas (em um problema de 4 classes).

Ao treinar com esses rótulos suavizados, o modelo aprende a ser menos confiante em suas previsões, o que melhora a generalização e torna o modelo mais robusto ao ruído do rótulo. Essa técnica tornou-se prática padrão em muitos modelos de classificação de imagens de última geração.

Métodos de abandono e de conjunto

Usar o dropout durante o treinamento e mantê-lo ativado durante a inferência (uma técnica chamada dropout de Monte Carlo) permite que você faça uma amostragem de várias previsões para a mesma entrada e estime a incerteza. Se o modelo produzir previsões consistentes em vários forward passes com diferentes padrões de desistência, é provável que você tenha mais certeza sobre sua previsão.

Da mesma forma, os métodos de conjunto combinam previsões de vários modelos para melhorar o desempenho e fornecer melhores estimativas de incerteza. A discordância entre os modelos em um conjunto pode servir como uma medida de incerteza.

Técnicas de calibração

O escalonamento de Platt e outros métodos de calibração podem ser aplicados após o treinamento para garantir que as pontuações de confiança do softmax realmente correspondam às probabilidades reais. Esses métodos normalmente usam um conjunto de validação para aprender parâmetros que mapeiam os resultados do modelo original para probabilidades bem calibradas.

Por exemplo, uma abordagem simples de escala de temperatura (conforme mencionado anteriormente) pode ser otimizada em dados de validação para minimizar o erro de calibração. Abordagens mais complexas incluem regressão isotônica e binning bayesiano.

O gargalo do softmax

Pesquisas recentes identificaram uma limitação fundamental da função softmax conhecida como "gargalo do softmax". Isso se refere ao fato de que a expressividade dos modelos de linguagem baseados em softmax é limitada pela classificação da matriz de peso na camada final. Em contextos de linguagem natural com dependências complexas, isso pode impedir que os modelos capturem totalmente as distribuições condicionais subjacentes.

Arquiteturas avançadas, como a Mixture of Softmaxes (MoS), foram propostas para resolver essa limitação usando uma combinação ponderada de várias distribuições de softmax.

Estando ciente desses problemas comuns e implementando soluções adequadas, você pode melhorar a confiabilidade e o desempenho dos modelos que usam a função de ativação softmax para tarefas de classificação.

Conclusão

A função de ativação softmax é um componente essencial das redes neurais para problemas de classificação multiclasse, transformando logits brutos em distribuições de probabilidade interpretáveis. Exploramos sua base matemática, a implementação em Python, a comparação com o sigmoide, casos de uso práticos e técnicas para lidar com desafios comuns, como instabilidade numérica e excesso de confiança.

Você está pronto para aprofundar seu conhecimento sobre redes neurais? 

• Explore nossa Introdução às funções de ativação ou mergulhe em cursos específicos de estrutura sobre Aprendizado profundo com Keras e PyTorch.
• Para saber mais sobre outras funções de ativação importantes, consulte nosso artigo sobre ReLU e comece a criar redes neurais mais eficazes hoje mesmo!