Función de activación Softmax en Python: Guía completa

Las funciones de activación son la columna vertebral de las redes neuronales. Son componentes importantes que introducen la no linealidad y permiten a estas redes aprender patrones complejos. La función de activación softmax es importante, sobre todo cuando se trata de problemas de clasificación multiclase.

Mientras que alternativas como Sigmoid y ReLU tienen sus casos de uso específicos, softmax es mejor para manejar situaciones en las que los resultados deben interpretarse como probabilidades entre clases mutuamente excluyentes.

La función de activación softmax transforma un vector entero de números en una distribución de probabilidad. Esta característica única lo hace indispensable para tareas en las que necesitamos clasificar entradas en una de varias categorías posibles.

Desde los sistemas de reconocimiento de imágenes que identifican miles de categorías de objetos hasta los modelos de procesamiento del lenguaje natural que predicen la siguiente palabra de una frase, softmax proporciona la base matemática para tomar decisiones entre múltiples posibilidades.

En este artículo, veremos qué es la función de activación softmax, cómo funciona matemáticamente y cuándo debes utilizarla en tu redes neuronales neuronales. También veremos las implementaciones prácticas en Python.

¿Qué es la función de activación Softmax?

La función de activación función de activación es una función matemática que transforma un vector de salidas brutas del modelo, conocidas como logits, en una distribución de probabilidad. En términos más sencillos, toma un conjunto de números y los convierte en probabilidades que suman 1.

A diferencia de algunas funciones de activación que operan sobre valores individuales de forma independiente, softmax trabaja sobre todo un vector de valores, transformándolos colectivamente en una distribución de probabilidad en la que todos los elementos suman exactamente 1.

En el contexto de las redes neuronales, softmax se aplica normalmente a la capa final de una red diseñada para la clasificación multiclase. Cuando tenemos varias categorías posibles y necesitamos que nuestro modelo indique la probabilidad de cada categoría, la función de activación softmax es la elección estándar.

¿Cómo funciona la función softmax?

Las salidas brutas de la capa final de una red neuronal suelen denominarse "logits". Estos valores pueden oscilar entre infinito negativo e infinito positivo y no tienen una interpretación probabilística directa. La función de activación softmax transforma estos logits en una forma más interpretable mediante:

1. Tomando la exponencial de cada valor de entrada (lo que garantiza que todos los valores son positivos).
2. Dividiendo cada exponencial por la suma de todos los exponenciales (lo que garantiza que los resultados suman 1).

Esta transformación es crucial porque nos permite interpretar la salida de la red como una distribución de probabilidad. Por ejemplo, si una red neuronal clasifica imágenes en tres categorías (gato, perro, pájaro), la salida softmax podría ser [0,7, 0,2, 0,1], lo que indica una probabilidad del 70% para el gato, del 20% para el perro y del 10% para el pájaro.

La función de activación softmax desempeña un papel vital en la creación de distribuciones de probabilidad válidas porque:

• Garantiza que todos los valores de salida estén entre 0 y 1.
• Garantiza que todas las salidas sumen exactamente 1.
• Conserva la clasificación de los valores de entrada (entradas mayores dan lugar a probabilidades mayores).
• Acentúa las diferencias entre valores mayores y suprime las diferencias entre valores menores.

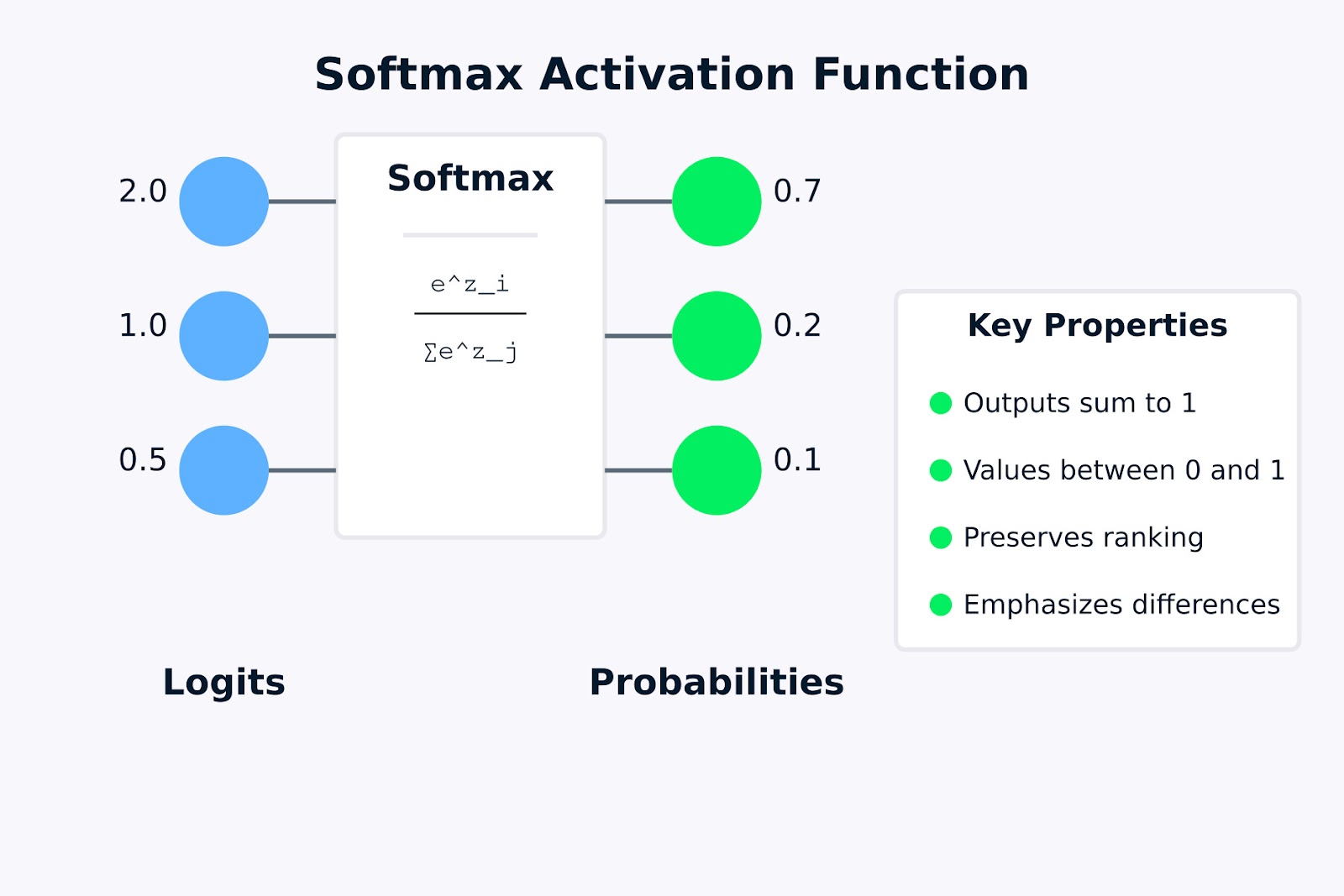
Función de activación Softmax

La visualización anterior muestra cómo la función de activación softmax transforma logits brutos (los valores de entrada 2,0, 1,0 y 0,5) en una distribución de probabilidad (0,7, 0,2 y 0,1). La fórmula dentro de la casilla softmax representa cómo se calcula cada probabilidad de salida tomando el exponencial de un valor de entrada y dividiéndolo por la suma de todos los exponenciales. 

Las propiedades clave resaltadas a la derecha indican por qué softmax es útil para los problemas de clasificación multiclase. En la siguiente sección, veremos la fórmula matemática y cómo funciona.

Fórmula de la función de activación Softmax y cómo funciona

Ahora que ya sabemos qué es la función de activación softmax, veamos su formulación matemática y cómo transforma las entradas en distribuciones de probabilidad.

La fórmula de la función de activación softmax puede expresarse matemáticamente como

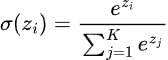
Dónde:

• ​z_i es el valor de entrada (logit) para la clase i
• e^z_i es la función exponencial aplicada a z_i (también escrita como exp(z_i ​))
• K es el número total de clases
• El denominador suma los exponenciales de todos los valores de entrada, garantizando que los valores de salida sumen 1

La función de activación softmax sigue estos pasos para transformar un vector de entradas en una distribución de probabilidad:

1. Calcula exponenciales: En primer lugar, calculamos el exponencial (e^x) de cada valor de entrada. Este paso garantiza que todos los valores sean positivos, ya que e^x > 0 para cualquier número real x
2. Suma los exponenciales: Calculamos la suma de todos los valores exponenciales del paso 1.
3. Normaliza: Dividimos cada valor exponencial por la suma calculada en el paso 2. Esta normalización garantiza que todas las salidas estén entre 0 y 1 y sumen exactamente 1.

Apliquemos la fórmula de la función de activación softmax a un ejemplo sencillo para ver cómo funciona en la práctica.

Supongamos que tenemos una red neuronal con tres neuronas de salida para un problema de clasificación de tres clases (por ejemplo, identificar si una imagen contiene un gato, un perro o un pájaro). Tras el cálculo final, la red produce los siguientes logits: z = [2,0, 1,0, 0,5].

Para convertir estos logits en probabilidades utilizando la función softmax:

1. Calcular exponenciales:
• e^2.0 = 7.389
• e^1.0 = 2.718
• e^0.5 = 1.648
2. Suma los exponenciales:
• 7.389 + 2.718 + 1.648 = 11.755
3. Normaliza:
• P(clase 1) = 7,389 / 11,755 ≈ 0,628 o 62,8%.
• P(clase 2) = 2,718 / 11,755 ≈ 0,231 ó 23,1%.
• P(clase 3) = 1,648 / 11,755 ≈ 0,140 ó 14,0%.

La distribución distribución de probabilidad [0,628, 0,231, 0,140] suma 1, asignando la probabilidad más alta a la clase correspondiente al valor logit más alto. Este ejemplo demuestra cómo la función de activación softmax conserva la clasificación de los valores de entrada al tiempo que los transforma en una distribución de probabilidad válida.

Observa cómo los valores de entrada originales (2,0, 1,0, 0,5) mantuvieron su clasificación relativa en las probabilidades de salida, pero se acentuaron las diferencias entre ellos. Esta propiedad hace que softmax sea especialmente útil en tareas de clasificación en las que queremos identificar la clase más probable con confianza.

En la siguiente sección, veremos las distintas formas de implementar la función de activación softmax utilizando Python.

Implementación de la función de activación Softmax en Python

Ahora que entendemos la teoría que hay detrás de la función de activación softmax, veamos cómo implementarla en Python. Empezaremos escribiendo una función softmax desde cero utilizando NumPy, y luego veremos cómo utilizarla con marcos de aprendizaje profundo populares como TensorFlow/Keras y PyTorch.

Escribir softmax desde cero con NumPy

Antes de sumergirte en los marcos, es importante entender cómo implementar la función de activación softmax desde cero. Esto ayuda a intuir lo que ocurre bajo el capó.

import numpy as np

def softmax(x):
    """
    Compute softmax values for each set of scores in x.
    
    Args:
        x: Input array of shape (batch_size, num_classes) or (num_classes,)
        
    Returns:
        Softmax probabilities of same shape as input
    """
    # For numerical stability, subtract the maximum value from each input vector
    # This prevents overflow when calculating exp(x)
    shifted_x = x - np.max(x, axis=-1, keepdims=True)
    
    # Calculate exp(x) for each element
    exp_x = np.exp(shifted_x)
    
    # Calculate the sum of exp(x) for normalization
    sum_exp_x = np.sum(exp_x, axis=-1, keepdims=True)
    
    # Normalize to get probabilities
    probabilities = exp_x / sum_exp_x
    
    return probabilities

Esta implementación sigue exactamente la fórmula de la función de activación softmax, con un añadido importante: restamos el valor máximo de cada vector de entrada antes de la exponenciación. 

Esta operación de "desplazamiento" no cambia el resultado matemático, pero ayuda a evitar el desbordamiento numérico, que puede producirse al calcular exponenciales de números grandes.

Vamos a probar nuestra aplicación con un ejemplo sencillo:

# Sample logits from a neural network (batch of 2 examples, 3 classes each)
logits = np.array([
    [2.0, 1.0, 0.5],  # First example
    [3.0, 2.0, 1.0]   # Second example
])

probabilities = softmax(logits)
print("Logits:\n", logits)
print("\nSoftmax probabilities:\n", probabilities)
print("\nSum of probabilities (should be 1 for each example):", np.sum(probabilities, axis=1))

Salida:

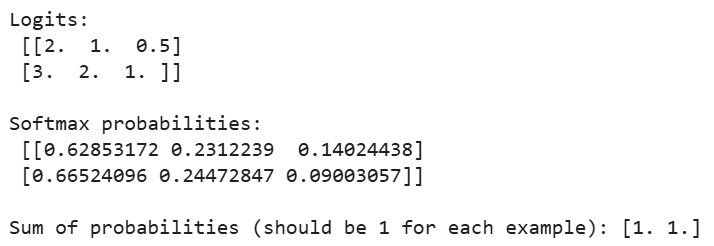
Cuando ejecutemos el código anterior, veremos que la suma de probabilidades de cada ejemplo es igual a 1, lo que confirma que nuestra implementación softmax produce distribuciones de probabilidad válidas. Para el primer ejemplo, la mayor probabilidad corresponde al mayor logit (2,0), y de forma similar para el segundo ejemplo.

Uso de softmax en TensorFlow/Keras

TensorFlow y Keras facilitan el uso de la función de activación softmax en tus redes neuronales. Construyamos paso a paso un clasificador sencillo para el conjunto de datos MNIST.

En primer lugar, vamos a importar las bibliotecas necesarias y a cargar el conjunto de datos:

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Softmax
from tensorflow.keras.datasets import mnist
import matplotlib.pyplot as plt
import numpy as np

# Load and preprocess the MNIST dataset
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# Normalize pixel values to be between 0 and 1
x_train, x_test = x_train / 255.0, x_test / 255.0

# One-hot encode the labels
y_train_one_hot = tf.keras.utils.to_categorical(y_train, 10)
y_test_one_hot = tf.keras.utils.to_categorical(y_test, 10)

El conjunto de datos MNIST contiene imágenes en escala de grises de 28x28 píxeles de dígitos manuscritos (0-9). Normalizamos los valores de los píxeles para que estén entre 0 y 1, para una mejor dinámica de entrenamiento, y convertimos las etiquetas de clase en codificación de un punto, que es el formato preferido para las salidas softmax.

Ahora, vamos a crear un modelo de red neuronal con una capa de salida softmax:

# Method 1: Using softmax as the activation function in the final layer
model1 = Sequential([
    Flatten(input_shape=(28, 28)),  # Convert 28x28 images to 784-length vectors
    Dense(128, activation='relu'),   # Hidden layer with ReLU activation
    Dense(10, activation='softmax')  # Output layer with softmax activation
])

# Method 2: Using a separate Softmax layer
model2 = Sequential([
    Flatten(input_shape=(28, 28)),
    Dense(128, activation='relu'),
    Dense(10),  # Linear output (logits)
    Softmax()   # Separate softmax layer
])

Aquí demostramos dos formas equivalentes de incorporar la función de activación softmax en una red neuronal:

• Método 1: Especificando directamente "softmax" como función de activación en la capa Densa final
• Método 2: Añadir una capa Softmax separada después de la capa Densa que produce logits brutos

Ambos enfoques producen resultados idénticos, pero el segundo método hace más explícita la separación entre logits y probabilidades, lo que puede ser útil en determinados escenarios.

A continuación, vamos a compilar y entrenar el modelo:

# Compile the model
model1.compile(
    optimizer='adam',
    loss='categorical_crossentropy',  # This loss works well with softmax
    metrics=['accuracy']
)

# Print model summary
print("Model with softmax activation:")
model1.summary()

# Train the model
print("\nTraining the model...")
history = model1.fit(
    x_train, y_train_one_hot,
    epochs=5,
    batch_size=128,
    validation_split=0.1,
    verbose=1
)

Salida:

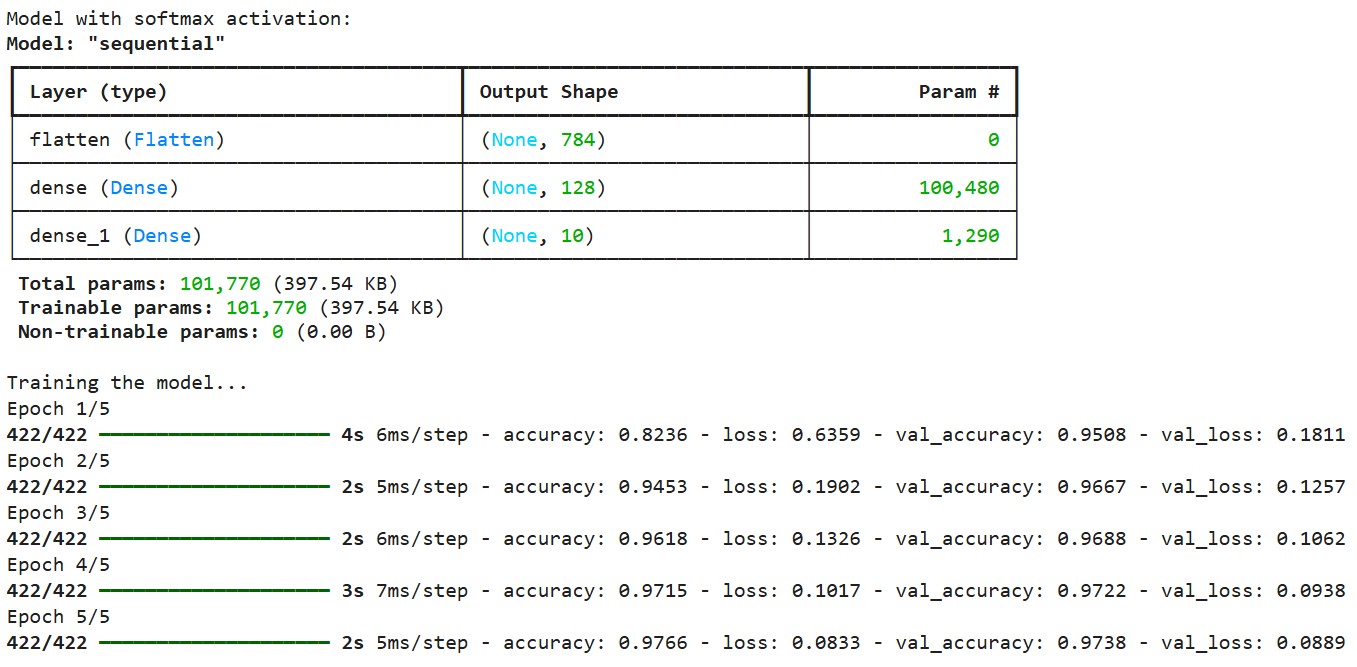Compilamos el modelo utilizando la función de pérdida de entropía cruzada categórica, que está diseñada para trabajar con salidas softmax. Esta función de pérdida mide la diferencia entre la distribución de probabilidad predicha y las verdaderas etiquetas codificadas en un punto. Utilizamos el optimizador Adam, que ajusta adaptativamente la tasa de aprendizaje durante el entrenamiento.

Tras el entrenamiento, podemos utilizar el modelo para hacer predicciones y visualizar los resultados:

# Let's check predictions on a sample
sample_idx = 42
sample_image = x_test[sample_idx]
true_label = y_test[sample_idx]

# Get model predictions (probabilities across all classes)
predictions = model1.predict(sample_image[np.newaxis, ...])

# Visualize the results
plt.figure(figsize=(10, 4))

# Plot the image
plt.subplot(1, 2, 1)
plt.imshow(sample_image, cmap='gray')
plt.title(f"True label: {true_label}")
plt.axis('off')

# Plot the probability distribution
plt.subplot(1, 2, 2)
plt.bar(range(10), predictions[0])
plt.xticks(range(10))
plt.xlabel('Digit')
plt.ylabel('Probability')
plt.title('Softmax Probabilities')

Este código selecciona una imagen de prueba, la hace pasar por el modelo entrenado y visualiza tanto la imagen como la distribución de probabilidad resultante de la salida softmax. La barra más alta del gráfico de probabilidad representa la predicción del modelo.

Salida:

TensorFlow también proporciona una función integrada para aplicar softmax directamente:

# Demonstrate using a custom softmax function in TensorFlow
def custom_softmax(logits):
    """Custom implementation of softmax in TensorFlow"""
    exp_logits = tf.exp(logits - tf.reduce_max(logits, axis=-1, keepdims=True))
    return exp_logits / tf.reduce_sum(exp_logits, axis=-1, keepdims=True)

# Example usage of custom softmax
logits = tf.constant([[2.0, 1.0, 0.5], [3.0, 2.0, 1.0]])
custom_probs = custom_softmax(logits)
tf_probs = tf.nn.softmax(logits)

print("\nCustom softmax:", custom_probs.numpy())
print("TensorFlow softmax:", tf_probs.numpy())

Salida:

Este ejemplo compara una implementación personalizada de softmax con la función incorporada de TensorFlow tf.nn.softmax(). Ambos deberían producir resultados idénticos. La implementación personalizada también incluye el truco de estabilidad numérica de restar el valor máximo antes de la exponenciación.

Utilizar Softmax en PyTorch

Ahora, pongamos en práctica un modelo similar utilizando PyTorch y el conjunto de datos CIFAR-10. Empezaremos importando bibliotecas y configurando los datos, como se muestra a continuación:

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np

# Set the device
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")

# Load and preprocess the CIFAR-10 dataset
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))  # Normalize RGB channels
])

# Load a small subset of the CIFAR-10 dataset for demonstration
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64,
                                         shuffle=False, num_workers=2)

# Define the class names for CIFAR-10
classes = ('plane', 'car', 'bird', 'cat', 'deer',
           'dog', 'frog', 'horse', 'ship', 'truck')

El código anterior configura PyTorch para que utilice la aceleración de la GPU si está disponible, carga el conjunto de datos CIFAR-10 (que contiene imágenes en color de 32x32 en 10 clases) y prepara los cargadores de datos para el entrenamiento y la prueba.

A continuación, vamos a definir una red neuronal convolucional sencilla, como se muestra a continuación:

# Define a simple convolutional neural network
class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        # Convolutional layers
        self.conv1 = nn.Conv2d(3, 16, 3, padding=1)
        self.conv2 = nn.Conv2d(16, 32, 3, padding=1)
        self.pool = nn.MaxPool2d(2, 2)
        
        # Fully connected layers
        self.fc1 = nn.Linear(32 * 8 * 8, 128)
        self.fc2 = nn.Linear(128, 10)  # 10 classes in CIFAR-10
        
        # Activation functions
        self.relu = nn.ReLU()
        
        # Note: We don't define softmax here as it will be applied with the loss function
    
    def forward(self, x):
        # Convolutional layers with ReLU and pooling
        x = self.pool(self.relu(self.conv1(x)))  # -> 16x16x16
        x = self.pool(self.relu(self.conv2(x)))  # -> 8x8x32
        
        # Flatten the output
        x = x.view(-1, 32 * 8 * 8)
        
        # Fully connected layers
        x = self.relu(self.fc1(x))
        x = self.fc2(x)  # Raw logits output
        
        # Note: No softmax here, as PyTorch's CrossEntropyLoss applies it internally
        return x

Esta CNN procesa las imágenes RGB de 32x32 a través de capas convolucionales, aplica activación ReLU y pooling, y termina con capas totalmente conectadas. En particular, el modelo no incluye una capa softmax en su paso hacia delante. En su lugar, produce logits brutos.

Este es un patrón común en PyTorch porque la función CrossEntropyLoss utilizada durante el entrenamiento aplica internamente softmax antes de calcular la pérdida, que es más estable numéricamente .

Veamos también cómo incluir explícitamente softmax si es necesario:

# Applying softmax within the model
class ModelWithSoftmax(nn.Module):
    def __init__(self):
        super(ModelWithSoftmax, self).__init__()
        self.features = SimpleCNN()
        self.softmax = nn.Softmax(dim=1)
    
    def forward(self, x):
        logits = self.features(x)
        probabilities = self.softmax(logits)
        return probabilities

Definimos dos variantes del modelo: SimpleCNN produce logits brutos, mientras que ModelWithSoftmax aplica explícitamente softmax para producir probabilidades. Para el entrenamiento, utilizamos SimpleCNN con CrossEntropyLoss, que es el enfoque estándar en PyTorch.

Definamos una función de entrenamiento:

# Create the model and move it to the device 
model = SimpleCNN().to(device) 
# Define loss function and optimizer 
criterion = nn.CrossEntropyLoss()  # Combines LogSoftmax and NLLLoss 
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# Train the model (only a few epochs for demonstration)
def train_model(epochs=2):
    for epoch in range(epochs):
        running_loss = 0.0
        for i, data in enumerate(trainloader, 0):
            inputs, labels = data[0].to(device), data[1].to(device)
            
            # Zero the parameter gradients
            optimizer.zero_grad()
            
            # Forward + backward + optimize
            outputs = model(inputs)  # These are logits (pre-softmax)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
            
            running_loss += loss.item()
            if i % 100 == 99:
                print(f'[{epoch + 1}, {i + 1}] loss: {running_loss / 100:.3f}')
                running_loss = 0.0
    
    print('Finished Training')

Por último, vamos a crear una función para visualizar las predicciones del modelo:

# Function to display predictions with softmax probabilities
def show_prediction_example():
    # Get a batch of test images
    dataiter = iter(testloader)
    images, labels = next(dataiter)
    
    # Select a single image
    img = images[0].to(device)
    label = labels[0]
    
    # Get the model's prediction (logits)
    with torch.no_grad():
        logits = model(img.unsqueeze(0))
    
    # Apply softmax to get probabilities
    probabilities = torch.nn.functional.softmax(logits, dim=1)
    
    # Plot the image and probabilities
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4))
    
    # Show the image
    img_np = img.cpu().numpy()
    img_np = np.transpose(img_np, (1, 2, 0))
    # Denormalize the image for display
    img_np = img_np * 0.5 + 0.5
    ax1.imshow(img_np)
    ax1.set_title(f"True label: {classes[label]}")
    ax1.axis('off')
    
    # Show the probabilities
    probs = probabilities[0].cpu().numpy()
    ax2.bar(range(10), probs)
    ax2.set_xticks(range(10))
    ax2.set_xticklabels(classes, rotation=45)
    ax2.set_xlabel('Class')
    ax2.set_ylabel('Probability')
    ax2.set_title('Softmax Probabilities')
    
    plt.tight_layout()

Esta función demuestra cómo obtener probabilidades softmax de un modelo entrenado durante la inferencia. Pasa una imagen por el modelo para obtener logits, aplica softmax manualmente utilizando torch.nn.functional.softmax(), y luego visualiza tanto la imagen como la distribución de probabilidad resultante.

Ahora, vamos a entrenar el modelo:

train_model()

Salida:

Hagamos una predicción y veamos cómo aparecen las probabilidades para una imagen de prueba:

show_prediction_example()

Salida:

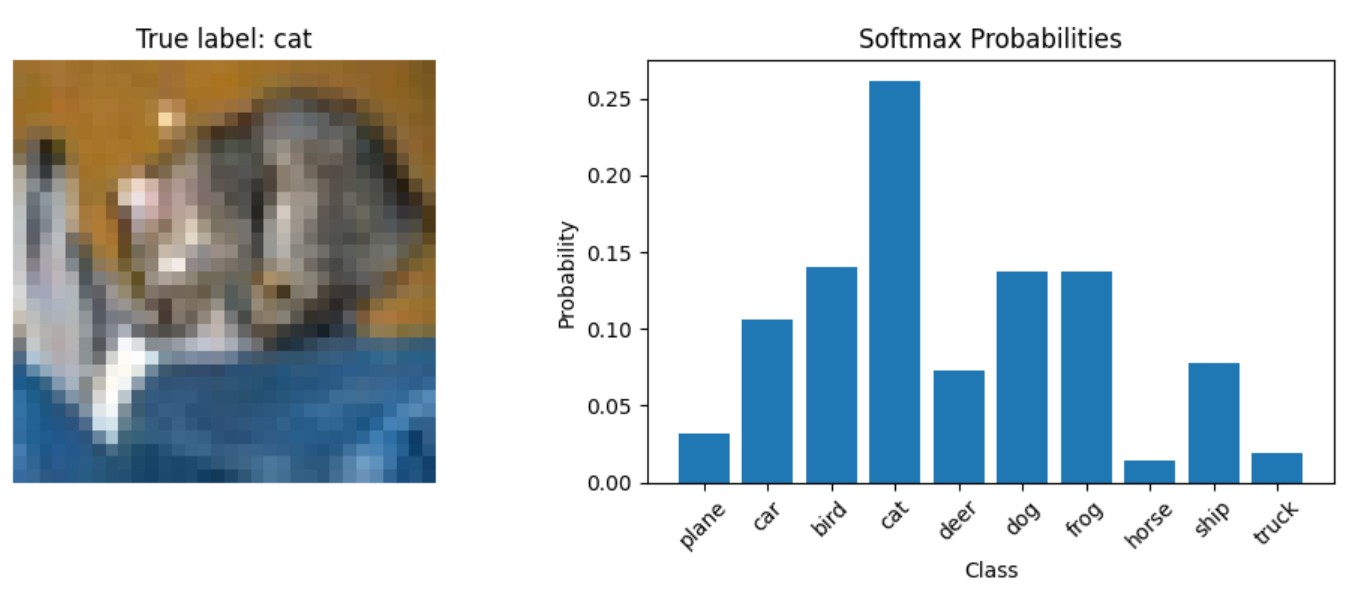
En la siguiente sección, veremos los escenarios específicos en los que softmax es la elección óptima, examinaremos cuándo debe utilizarse la función de activación softmax y analizaremos las aplicaciones del mundo real en varios modelos de aprendizaje profundo.

¿Cuándo utilizar la función de activación Softmax?

Entender cuándo utilizar la función de activación softmax es importante para diseñar redes neuronales eficaces. La función de activación softmax encuentra su principal aplicación en la capa de salida de las redes neuronales diseñadas para tareas de clasificación.

Softmax para clasificación multiclase

Softmax es la elección estándar cuando nuestro modelo necesita clasificar entradas en una de varias categorías mutuamente excluyentes. Algunos ejemplos comunes son:

• Clasificación de imágenes (identificar objetos en fotos)
• Categorización de documentos (asignar temas al texto)
• Reconocimiento de entidades con nombre (identificación de nombres de personas, lugares, etc.)
• Reconocimiento de voz (mapeo de audio a texto)

Interpretación probabilística y puntuaciones de confianza

Cuando necesitamos que nuestro modelo emita probabilidades en lugar de sólo predicciones de clase, softmax proporciona una interpretación probabilística de la confianza del modelo en todas las clases posibles.

Softmax en el aprendizaje por refuerzo y mecanismos de atención

En el aprendizaje por refuerzo y en los problemas de decisión secuencial, softmax puede utilizarse para convertir los valores de acción en una distribución de probabilidad para la selección de acciones.

Moderno arquitecturas basadas en transformadores utilizan softmax para distribuir la atención entre las distintas partes de la secuencia de entrada.

Su sólida base matemática y su intuitiva interpretación probabilística hacen que la función de activación softmax sea especialmente adecuada para los problemas de clasificación en los que las clases se excluyen mutuamente.

Modelos de aprendizaje profundo

Varias arquitecturas de aprendizaje profundo utilizan la función de activación softmax. 

Las redes de clasificación de imágenes como ResNet, VGG e Inception utilizan softmax en su capa final para clasificar las imágenes en miles de categorías. Por ejemplo, los modelos entrenados en ImageNet suelen tener una capa softmax de 1000 unidades correspondientes a 1000 categorías de objetos.

En el modelado del lenguaje, los modelos basados en RNN utilizan softmax para predecir la siguiente palabra de una secuencia a partir de un vocabulario que puede contener decenas de miles de palabras.

Las arquitecturas PNL modernas, como BERT, GPT y T5, utilizan softmax en varios componentes:

• En los mecanismos de atención para determinar cuánta atención se debe prestar a las distintas partes de la entrada
• En la capa de clasificación final, para tareas como el análisis de sentimientos o la clasificación de documentos

Autocodificadores variacionales (VAE) y algunas Redes Generativas Adversariales (GAN) utilizan softmax en sus componentes discriminadores o para el modelado de variables latentes categóricas.

En la siguiente sección, veremos las diferencias entre la función de activación softmax y la función de activación sigmoide.

Función de activación Softmax vs Sigmoide

La función sigmoidea, definida como σ(x) = 1/(1+e^(-x)), transforma un único número real en un valor comprendido entre 0 y 1. En cambio, la función de activación softmax opera sobre un vector de números, convirtiéndolos en una distribución de probabilidad.

He aquí las diferencias fundamentales entre estas dos funciones de activación:

Dimensiones de entrada y salida

• Sigmoide: Toma una única entrada escalar y produce una única salida escalar entre 0 y 1.
• Softmax: Toma un vector de n entradas y produce un vector de n salidas que suman 1.

Interpretación probabilística

• Sigmoide: La salida representa la probabilidad de un único suceso binario (por ejemplo, "¿Este correo electrónico es spam?").
• Softmax: Las salidas representan probabilidades a través de múltiples clases mutuamente excluyentes (por ejemplo, "¿Qué dígito del 0-9 es éste?").

Independencia de los resultados

• Sigmoide: Cuando se utiliza en varias neuronas, cada salida es independiente de las demás. Las salidas múltiples pueden ser todas altas o todas bajas.
• Softmax: Los resultados son interdependientes: si una probabilidad aumenta, las otras deben disminuir para mantener una suma de 1.

Relación matemática

Curiosamente, la función sigmoidea es en realidad un caso especial de la función de activación softmax cuando sólo hay dos clases. Por eso a menudo se llama a la sigmoide "softmax binaria".

Cuándo utilizar softmax frente a cuándo utilizar sigmoide

Elegir la función de activación adecuada es crucial para garantizar que una red neuronal produzca predicciones significativas, y la decisión entre softmax y sigmoide depende de la naturaleza de la tarea de clasificación.

Utiliza la sigmoidea cuando:

• Resolver problemas de clasificación binaria (dos clases)
• Cada salida debe interpretarse de forma independiente
• Implementación de la clasificación multietiqueta en la que una instancia puede pertenecer a varias clases simultáneamente
• Creación de mecanismos o puertas de atención en redes neuronales recurrentes

Utiliza softmax cuando:

• Tratar problemas de clasificación multiclase (más de dos clases)
• Las clases son mutuamente excluyentes (una entrada pertenece exactamente a una clase)
• Necesitas una distribución de probabilidad adecuada en todos los resultados posibles
• Implementación de la capa final de la mayoría de las redes de clasificación de imágenes

Por ejemplo, en una red neuronal que clasifica imágenes de dígitos manuscritos (0-9), la función de activación softmax sería adecuada para la capa de salida, ya que cada imagen representa exactamente un dígito. En cambio, para una red que detecta varios objetos en una imagen (por ejemplo, "contiene persona", "contiene coche", "contiene árbol"), las activaciones sigmoidales serían más adecuadas, ya que pueden estar presentes varios objetos simultáneamente.

Aquí tienes una tabla de referencia rápida que compara la función de activación softmax frente a la sigmoidea:

Comprender la distinción entre estas funciones de activación es fundamental para diseñar redes neuronales eficaces. Mientras que la función de activación softmax es la elección preferida para los problemas de clasificación multiclase, la sigmoide sigue siendo valiosa para la clasificación binaria y los problemas que requieren probabilidades independientes.

En la siguiente sección, veremos los problemas habituales que surgen y las consideraciones que hay que tener en cuenta al trabajar con funciones de activación softmax.

Cuestiones y consideraciones comunes

Cuando trabajas con la función de activación softmax en tus modelos de aprendizaje profundo, varios retos pueden afectar al rendimiento y la fiabilidad del modelo. Comprender estos problemas y saber cómo abordarlos te ayudará a construir modelos más sólidos.

Problemas de estabilidad numérica

La estabilidad numérica es una preocupación fundamental cuando se utiliza la función de activación softmax. La operación exponencial en la fórmula de la función de activación softmax puede provocar un desbordamiento o subdesbordamiento numérico si no se maneja adecuadamente.

Por ejemplo, cuando se trata de valores de entrada muy grandes (como 1000 o más), la función exponencial produce números extremadamente grandes que pueden superar el valor máximo representable en coma flotante de tu sistema. Esto provoca errores de desbordamiento, produciendo valores "infinitos" que hacen que la operación de división final produzca resultados indefinidos (NaN - Not a Number).

La solución estándar, como se menciona en nuestra sección de implementación, es restar el valor máximo de todas las entradas antes de aplicar la función exponencial. Este desplazamiento no cambia las proporciones relativas tras la normalización, pero mantiene los valores dentro de un rango manejable. 

Los marcos modernos de aprendizaje profundo manejan este problema internamente, pero es importante comprenderlo al implementar operaciones personalizadas o depurar comportamientos inesperados.

Softmax y el exceso de confianza en las predicciones

Otro problema habitual de la función de activación softmax es que las redes neuronales tienden a confiar demasiado en sus predicciones, incluso cuando se equivocan. Este exceso de confianza se produce porque

1. La naturaleza exponencial del softmax amplifica las pequeñas diferencias en los logits.
2. Las redes neuronales profundas modernas son lo bastante potentes como para memorizar perfectamente los datos de entrenamiento.
3. La pérdida de entropía cruzada sigue empujando las probabilidades hacia 1 para las clases correctas, incluso después de que un modelo alcance una buena precisión.

En la práctica, esto significa que un modelo puede asignar una probabilidad del 99% a una predicción que en realidad es incorrecta. Esto puede ser problemático en aplicaciones críticas en las que es esencial una estimación fiable de la incertidumbre. Por ejemplo, un sistema de diagnóstico médico que confíe demasiado en predicciones incorrectas podría llevar a decisiones terapéuticas inadecuadas.

La diferencia entre la confianza de un modelo (a partir de las probabilidades softmax) y su precisión real se conoce como error de calibración. Los modelos bien calibrados producen puntuaciones de confianza que coinciden con sus índices de precisión: si un modelo predice sucesos con un 80% de confianza, esos sucesos deberían ocurrir aproximadamente el 80% de las veces.

Técnicas de regularización para mejorar el rendimiento

Afortunadamente, varias técnicas pueden ayudar a resolver estos problemas con la función de activación softmax:

Escala de temperatura

La escala de temperatura introduce un parámetro T que controla la "suavidad" de la distribución de probabilidad. Dividiendo los logits por este parámetro de temperatura antes de aplicar softmax, puedes ajustar el grado de picos o de uniformidad de la distribución resultante.

Las temperaturas más altas (T > 1) producen distribuciones de probabilidad más suaves, con menos valores extremos, lo que puede ayudar a reducir el exceso de confianza. Las temperaturas más bajas (T < 1) hacen que la distribución tenga más picos hacia el valor más alto. El escalado de temperatura se suele utilizar como técnica de postprocesado tras el entrenamiento para calibrar la confianza del modelo sin afectar a la clasificación de clases del modelo.

Suavizado de etiquetas

El suavizado de etiquetas sustituye los vectores de objetivos duros de un solo golpe por distribuciones ligeramente suavizadas. En lugar de entrenar al modelo para que produzca ceros y unos exactos, el suavizado de etiquetas anima al modelo a ser ligeramente menos confiado, apuntando a valores como 0,9 para la clase correcta y 0,025 para las clases incorrectas (en un problema de 4 clases).

Al entrenarse con estas etiquetas suavizadas, el modelo aprende a ser menos confiado en sus predicciones, lo que mejora la generalización y hace que el modelo sea más robusto frente al ruido de las etiquetas. Esta técnica se ha convertido en una práctica habitual en muchos modelos de clasificación de imágenes de última generación.

Métodos de abandono y de conjunto

Utilizar el abandono durante el entrenamiento y mantenerlo activado durante la inferencia (una técnica llamada abandono de Montecarlo) te permite muestrear múltiples predicciones para la misma entrada y estimar la incertidumbre. Si el modelo produce predicciones consistentes a través de múltiples pases hacia delante con diferentes patrones de abandono, es probable que esté más seguro de su predicción.

Del mismo modo, los métodos de conjunto combinan predicciones de múltiples modelos para mejorar el rendimiento y proporcionar mejores estimaciones de la incertidumbre. El desacuerdo entre los modelos de un conjunto puede servir como medida de la incertidumbre.

Técnicas de calibración

El escalado de Platt y otros métodos de calibración pueden aplicarse después del entrenamiento para garantizar que las puntuaciones de confianza de softmax corresponden realmente a probabilidades verdaderas. Estos métodos suelen utilizar un conjunto de validación para aprender los parámetros que asignan las salidas del modelo original a probabilidades bien calibradas.

Por ejemplo, un enfoque simple de escalado de temperatura (como se ha mencionado antes) puede optimizarse sobre los datos de validación para minimizar el error de calibración. Otros enfoques más complejos son la regresión isotónica y el binning bayesiano.

El cuello de botella softmax

Investigaciones recientes han identificado una limitación fundamental de la función softmax conocida como "cuello de botella softmax". Esto se refiere al hecho de que la expresividad de los modelos lingüísticos basados en softmax está limitada por el rango de la matriz de pesos en la capa final. En contextos de lenguaje natural con dependencias complejas, esto puede impedir que los modelos capten plenamente las distribuciones condicionales subyacentes.

Se han propuesto arquitecturas avanzadas como la Mezcla de Softmaxes (MoS) para abordar esta limitación utilizando una combinación ponderada de múltiples distribuciones de softmaxes.

Si eres consciente de estos problemas comunes y aplicas las soluciones adecuadas, podrás mejorar la fiabilidad y el rendimiento de los modelos que utilizan la función de activación softmax para tareas de clasificación.

Conclusión

La función de activación softmax es un componente esencial de las redes neuronales para los problemas de clasificación multiclase, que transforma los logits brutos en distribuciones de probabilidad interpretables. Hemos explorado su fundamento matemático, su implementación en Python, su comparación con la sigmoidea, casos prácticos de uso y técnicas para abordar retos comunes como la inestabilidad numérica y el exceso de confianza.

¿Preparado para profundizar en tu comprensión de las redes neuronales? 

• Explora nuestra Introducción a las funciones de activación o sumérgete en cursos específicos sobre Aprendizaje profundo con Keras y PyTorch.
• Para conocer otras funciones de activación importantes, consulta nuestro artículo sobre ReLU y ¡empieza hoy mismo a construir redes neuronales más eficaces!