Regressão linear simples: Tudo o que você precisa saber

Toda história começa em algum lugar e, para o analista ou cientista de dados, o início da história costuma ser uma simples regressão linear. De fato, a regressão linear simples talvez seja o modelo mais fundamental de todos. Portanto, se você quer mesmo se tornar um analista ou cientista de dados, a regressão linear simples (e as regressões em geral) é um conhecimento absolutamente obrigatório.

O motivo pelo qual vale a pena aprender regressão não é apenas o fato de ela ser uma técnica inestimável para responder a perguntas urgentes em praticamente todos os campos, mas também porque ela abre as portas para uma compreensão mais profunda de uma enorme variedade de outras coisas, como testes de hipóteses, inferência causal e previsão. Portanto, faça nosso curso Introdução à regressão em R e nosso curso Introdução à regressão com modelos estatísticos em Python hoje mesmo.

O que é Regressão Linear Simples? 

A regressão linear simples é uma regressão linear com uma variável independente, também chamada de variável explicativa, e uma variável dependente, também chamada de variável de resposta. Na regressão linear simples, a variável dependente é contínua. 

Estimador de mínimos quadrados ordinários 

A maneira mais comum de fazer uma regressão linear simples é por meio da estimativa de mínimos quadrados ordinários (OLS). Como o OLS é, de longe, o método mais comum, a parte "mínimos quadrados ordinários" geralmente está implícita quando falamos de regressão linear simples.

Os mínimos quadrados comuns funcionam minimizando a soma das diferenças quadráticas entre os valores observados (os pontos de dados reais) e os valores previstos da linha de regressão. Essas diferenças são chamadas de resíduos, e elevá-las ao quadrado garante que os resíduos positivos e negativos sejam tratados igualmente. 

Como a regressão linear simples é usada

A regressão linear simples ajuda a fazer previsões e a entender as relações entre uma variável independente e uma variável dependente. Por exemplo, você pode querer saber como a altura de uma árvore (variável independente) afeta o número de folhas que ela tem (variável dependente). Ao coletar dados e ajustar um modelo de regressão linear simples, você poderia prever o número de folhas com base na altura da árvore. Essa é a parte de "fazer previsões". Mas essa abordagem também revela o quanto o número de folhas muda, em média, à medida que a árvore cresce, e é assim que a regressão linear simples também é usada para entender os relacionamentos.  

Equação de regressão linear simples

Vamos dar uma olhada na equação de regressão linear simples. Podemos começar analisando a forma de interceptação de uma reta usando a notação comum em livros didáticos de geometria ou álgebra. Ou seja, começaremos do início.

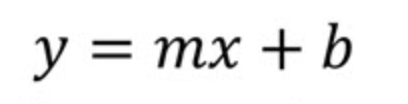
Aqui

• m é a inclinação da linha
• b é a interceptação

No contexto da ciência de dados, é mais provável que você veja essa equação: 

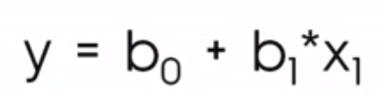
Onde

• b0 é o intercepto y 
• b1 é a inclinação

A notação envolvendo b0 e b1 nos ajuda a entender que estamos olhando para uma situação em que estamos fazendo uma previsão sobre ye é por isso que a chamamos de ŷou y-hat, já que não esperamos que nossa linha de regressão passe de fato por todos os pontos.

A visualização a seguir mostra a diferença conceitual entre a forma de interceptação de declive da linha, à esquerda, e a equação de regressão, à direita. Na linguagem da álgebra linear, diríamos que o sistema de equações lineares é sobredeterminado, o que significa que há mais equações (cerca de trinta) do que incógnitas (duas), portanto, não esperamos encontrar uma solução.

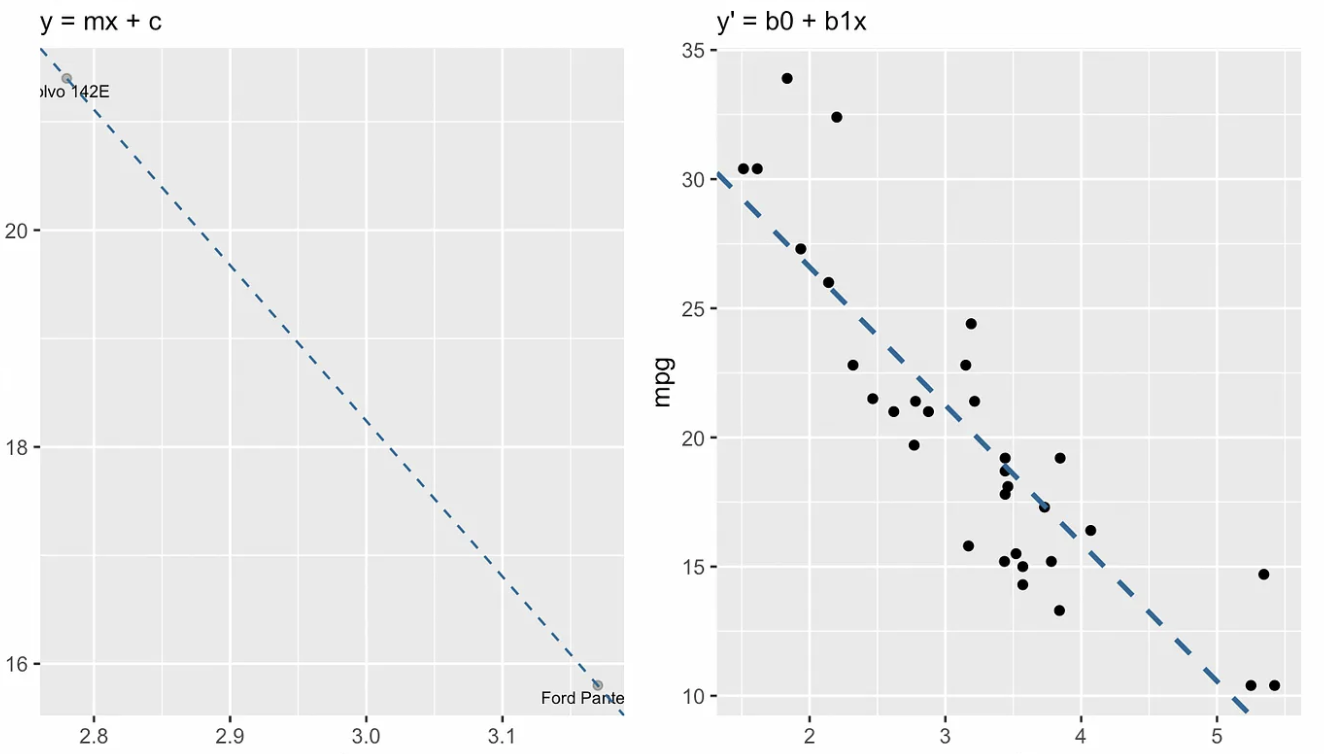Forma de interceptação de declive vs. equação de regressão linear simples. Imagem do autor

Coeficientes do modelo de regressão linear simples

Se estivéssemos usando apenas a equação de inclinação-interceptação, encontraríamos os valores de m (inclinação) e b (interceptação de y) calculando primeiro a inclinação como "subida sobre descida", ou seja, medindo a mudança em y sobre a mudança em x entre dois pontos na linha. Então, depois de encontrarmos a inclinação, encontraríamos o intercepto y b substituindo as coordenadas de um ponto da reta na equação e resolvendo para b. Essa etapa final fornece a você o ponto em que a linha cruza o eixo y.

Isso não funciona na regressão porque não há uma linha que passe por todos os pontos, e é por isso que, em vez disso, estamos encontrando a linha de melhor ajuste. Felizmente, existem equações simples e de forma fechada para você encontrar a inclinação e a interceptação. 

A inclinação pode ser calculada multiplicando-se a correlação r pelo quociente do desvio padrão de y sobre o desvio padrão de x. Isso faz sentido intuitivamente porque estamos essencialmente convertendo o coeficiente de correlação de volta em unidades das variáveis originais. Na equação abaixo, a se refere à inclinação e sy e sx se referem ao desvio padrão de y e ao desvio padrão de x, respectivamente.

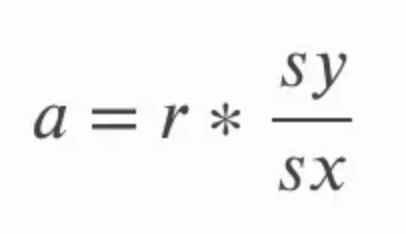
A interceptação da linha de melhor ajuste para regressão linear simples pode ser calculada depois de calcularmos a inclinação. Fazemos isso subtraindo o produto da inclinação e a média de x da média de y. Na equação abaixo, i refere-se à interceptação y e a linha reta sobre o ponto x e y é uma forma de se referir à média de x e y respectivamente; nos referimos a esses termos como x-bar e barra y.

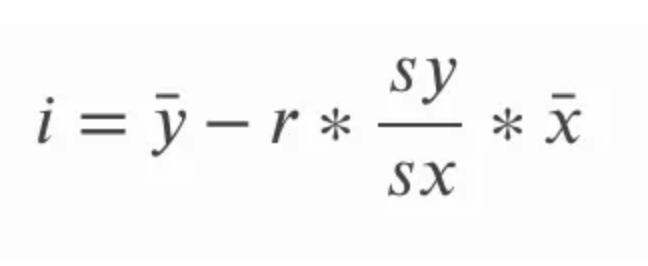
Para sermos minuciosos, podemos explorar formas alternativas de escrever essas equações. Lembre-se de que o desvio padrão é o mesmo que a raiz quadrada da variação, portanto, em vez de nos referirmos ao desvio padrão de y e ao desvio padrão de x, também poderíamos nos referir à raiz quadrada da variação de y e à raiz quadrada da variação de x. Lembramos que a variância em si é a média da soma dos quadrados. 

Na equação acima para a inclinação, a, também poderíamos escrever sy e sx em termos de desvio padrão, e também poderíamos escrever a equação de forma mais longa para a correlação r. Em seguida, podemos multiplicar e simplificar a equação removendo os termos comuns e obter o seguinte conjunto de equações para a inclinação e a interceptação. A questão aqui é menos mostrar como uma equação se transforma na outra e mais enfatizar que as duas equações são a mesma, pois você pode ver uma ou outra. 

Outra consequência interessante aqui é que a linha de regressão linear simples passará pelo ponto central, que é a média de x e a média de y. Em outras palavras, a regressão linear simples intercepta a média das variáveis independentes e dependentes, independentemente da distribuição dos pontos de dados, o que ajuda a dar à regressão linear simples uma espécie de propriedade de "equilíbrio".

Outras maneiras de encontrar os coeficientes do modelo de regressão linear simples 

Vimos como encontrar os coeficientes do modelo de regressão linear simples usando equações simples. Aqui, examinaremos mais detalhadamente alguns outros métodos que envolvem álgebra linear e cálculo. Os ambientes de programação, em particular, resolvem por meio de técnicas mais avançadas porque essas técnicas são mais rápidas e mais precisas (a questão de elevar ao quadrado para encontrar a variância pode reduzir a precisão).

• Álgebra Linear: Existem algumas técnicas de álgebra linear para encontrar os coeficientes de uma regressão linear simples. Podemos encontrar os coeficientes em um modelo de regressão linear simples resolvendo o que é conhecido como equação normal. A equação normal é interessante, mas um pouco desaconselhável com grandes conjuntos de dados porque envolve inversão de matriz, o que pode ser caro. Outra técnica de álgebra linear é resolver por meio da decomposição QR, que não requer inversão de matriz e também é conhecida por ser numericamente estável.
• Cálculo: Podemos encontrar a inclinação e a interceptação de um modelo de regressão linear simples tomando as derivadas parciais da soma dos erros quadráticos (SSE) em relação à inclinação e à interceptação e definindo-as como zero para resolver os coeficientes. Essa é uma opção. Outra opção ligada ao cálculo é a descida de gradiente, que é uma técnica de otimização iterativa que pode ser usada para minimizar o SSE e encontrar a inclinação e a interceptação. A descida de gradiente está intimamente ligada ao cálculo porque se baseia no gradiente, que é o vetor de derivadas parciais.

Premissas do modelo de regressão linear simples

Vamos dar uma olhada agora nas principais premissas do modelo de regressão linear simples. Se essas suposições forem violadas, talvez seja necessário considerar uma abordagem diferente. As três primeiras, em particular, são suposições fortes e não devem ser ignoradas.

1. Linearidade: A relação entre as variáveis independentes e dependentes deve ser linear. Se a relação não for linear, o modelo não a captará bem.
2. Independência de erros: Os resíduos devem ser independentes uns dos outros. Isso significa que não deve haver padrões ou correlações entre os resíduos. Isso é algo que você deve observar atentamente em dados ordenados por tempo.
3. Homocedasticidade: Os resíduos devem ter uma variação constante em todos os valores da variável independente. Se a variação mudar (heterocedasticidade), as previsões em determinados intervalos de x poderão se tornar menos precisas.
4. Normalidade dos resíduos: O ideal é que os resíduos sigam uma distribuição normal ou gaussiana. Isso é importante para testes estatísticos e para afirmar os níveis de confiança em nossa estimativa. Isso é menos importante para fazer previsões. 

Avaliação do modelo de regressão linear simples

Digamos que você tenha criado um modelo de regressão linear simples. Como saberemos se foi uma boa escolha? Para responder a isso, podemos examinar os gráficos de diagnóstico e as estatísticas do modelo. 

Gráficos de diagnóstico de regressão linear simples

Os gráficos de diagnóstico nos ajudam a ver se um modelo de regressão linear simples se ajusta bem e não viola nossas pressuposições. Quaisquer padrões ou desvios nesses gráficos sugerem problemas de modelo que precisam de atenção ou informações que não foram capturadas. Um gráfico de diagnóstico que é exclusivo da regressão linear simples é o gráfico de valores x versus resíduos, como você pode ver abaixo. Os gráficos adicionais incluem o gráfico Q-Q, o gráfico de localização em escala, o número de observações versus a distância do cozinheiro e outros. 

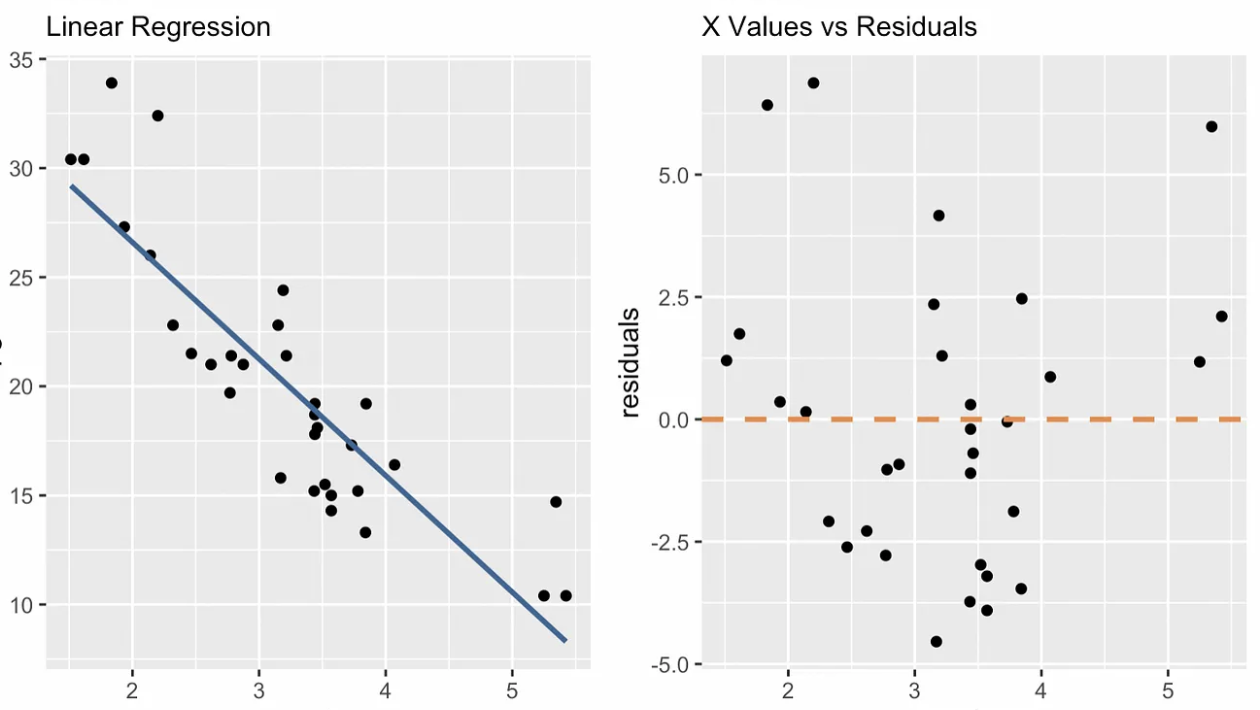valores x vs. gráfico de diagnóstico de resíduos. Imagem do autor

Estatísticas do modelo de regressão linear simples

As estatísticas do modelo, como R-quadrado e R-quadrado ajustado, quantificam o quanto a variável independente explica a variação na variável dependente. A estatística F testa a importância geral do modelo, e os valores p dos coeficientes nos informam sobre o impacto de preditores individuais. 

Como interpretar um modelo de regressão linear simples

Ao interpretar os resultados da regressão linear simples, devemos ter o cuidado de sermos exatos na forma como falamos sobre a relação entre a variável independente e a variável dependente.

Como interpretar a inclinação e a interceptação

Em particular, devemos ter cuidado ao falar sobre os dois componentes principais: a inclinação e a interceptação.

• O intercepto informa a você onde a linha de regressão cruza o eixo y. Em termos práticos, ele representa o valor da variável dependente quando a variável independente é zero. É importante que você saiba que o intercepto nem sempre é interpretável. Em nosso exemplo anterior com árvores, nosso modelo pode ter previsto um determinado número de folhas para árvores com altura zero. Não teria feito sentido tentar interpretar o intercepto nesse contexto. 
• A inclinação indica o quanto se espera que a variável dependente mude com um aumento de uma unidade na variável independente. Uma inclinação positiva sugere uma relação positiva, em que a variável dependente aumenta à medida que a variável independente aumenta. Uma inclinação negativa indica o oposto.

Um aspecto importante a ser considerado é que a correlação não é igual à causalidade. Os analistas que estão familiarizados com esse conceito ainda podem cometer erros ao interpretar uma regressão linear simples porque não têm prática com as palavras a serem usadas. Você não diria que a altura da árvore causa mais folhas, mas poderia dizer que um aumento de uma unidade na altura da árvore está associado a um aumento em um determinado número de folhas. 

Outra consideração importante é que a extrapolação para além do intervalo dos dados pode não gerar previsões confiáveis. Um modelo de regressão linear simples que prevê o número de folhas a partir da altura da árvore pode não ser muito preciso para árvores muito baixas ou muito altas, especialmente se as árvores baixas ou altas não foram consideradas na criação do nosso modelo. 

Como pensar em transformações

Os modelos lineares são chamados de modelos lineares porque são lineares em sua forma funcional. Especificamente, na regressão linear simples, a relação entre a variável de resposta y e a variável preditora x é modelada como uma combinação linear do preditor e de uma constante. Dito isso, você pode se surpreender com o que é possível fazer com uma regressão linear simples. Embora o modelo pressuponha uma relação linear entre as variáveis, você pode introduzir transformações para capturar relações não lineares.

Por exemplo, considere a relação não linear que representa o crescimento de ancestrais por geração, em que o número de ancestrais parece crescer exponencialmente a cada geração: dois pais, quatro avós, oito bisavós e assim por diante. Você não esperaria que um modelo linear captasse o crescimento exponencial, mas ao prever o log(y) em vez de y, você lineariza a relação .

Pensando melhor, no entanto, você percebe que não há um crescimento exponencial de antepassados por causa de algo chamado colapso do pedigree, que é quando a taxa de crescimento diminui drasticamente com o tempo porque antepassados distantes aparecem em vários lugares na árvore genealógica. Por esse motivo, você pode ter amplificado demais o nosso modelo usando o log(y). Agora, para amenizar isso, podemos criar uma nova variável que seja uma transformação de raiz quadrada em x e usá-la como nosso preditor. Agora, não estou dizendo que nenhum desses modelos está correto nem tentando interpretá-los totalmente, mas estou tentando mostrar como log(y) e raiz quadrada de x são transformações não lineares que entram na equação linearmente em relação aos coeficientes, de modo que ainda temos uma regressão linear simples.

Regressão linear simples em R e Python

Vamos considerar a regressão linear simples em R e Python.

Programação de R

O R é uma ótima opção para regressão linear simples.

Calcular manualmente a inclinação e a interceptação

Podemos encontrar os coeficientes por conta própria calculando a média e o desvio padrão de nossas variáveis. 

# Manually calculate the slope and intercept in R

# Sample data
X <- c(1, 2, 3, 4, 5)
y <- c(2, 4, 5, 4, 5)

# Calculate means
mean_X <- mean(X)
mean_y <- mean(y)

# Calculate standard deviations
sd_X <- sd(X)
sd_y <- sd(y)

# Calculate correlation
correlation <- cor(X, y)

# Calculate slope (b1) using the formula: b1 = (correlation * sd_y) / sd_X
slope <- (correlation * sd_y) / sd_X

# Calculate intercept (b0) using the formula: b0 = mean_y - slope * mean_X
intercept <- mean_y - slope * mean_X

# Print the slope and intercept
cat("Slope (b1):", slope, "\n")
cat("Intercept (b0):", intercept, "\n")

# Use the manually calculated coefficients to predict y values
y_pred <- intercept + slope * X
cat("Predicted values:", y_pred, "\n")

Usando a função lm()

No R, podemos criar uma regressão usando a função lm(), que pode ser acessada sem a necessidade de usar nenhuma biblioteca. 

# Fit the model 
model <- lm(y ~ X) 

# Print the summary of the regression 
summary(model)

Python

O Python é outra ótima opção para regressão linear simples. 

Calcular manualmente a inclinação e a interceptação

Aqui você encontra a média e o desvio padrão de cada variável. 

import numpy as np

# Sample data
X = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

# Calculate means
mean_X = np.mean(X)
mean_y = np.mean(y)

# Calculate standard deviations
sd_X = np.std(X, ddof=1)
sd_y = np.std(y, ddof=1)

# Calculate correlation
correlation = np.corrcoef(X, y)[0, 1]

# Calculate slope (b1) using the formula: b1 = (correlation * sd_y) / sd_X
slope = (correlation * sd_y) / sd_X

# Calculate intercept (b0) using the formula: b0 = mean_y - slope * mean_X
intercept = mean_y - slope * mean_X

# Print the slope and intercept
print(f"Slope (b1): {slope}")
print(f"Intercept (b0): {intercept}")

# Use the manually calculated coefficients to predict y values
y_pred = intercept + slope * X

print(f"Predicted values: {y_pred}")

Usando modelos estatísticos

statsmodels é uma opção para regressão linear simples.

import statsmodels.api as sm

# Adding a constant for the intercept
X = sm.add_constant(X)

# Fit the model
model = sm.OLS(y, X)
results = model.fit()

# Print the summary of the regression
print(results.summary())

Regressão linear simples, teste t e ANOVA

A regressão linear simples é usada no teste de hipóteses e é central nos testes t e na análise de variância (ANOVA). 

Regressão linear simples e teste t

Um teste t é frequentemente usado para determinar se a inclinação da linha de regressão é significativamente diferente de zero. Esse teste nos ajuda a entender se a variável independente tem um efeito estatisticamente significativo. Basicamente, formulamos uma hipótese nula afirmando que a inclinação da linha de regressão é igual a zero, o que significa que não há relação linear, e o teste t avalia isso. A regressão linear simples está relacionada aqui porque uma regressão linear simples com uma variável independente binária é o mesmo que uma diferença de médias, como vemos em um teste t.

Regressão linear simples e ANOVA

A análise de variância (ANOVA) é um método estatístico usado para avaliar o ajuste geral do modelo e determinar se a variável independente explica uma parte significativa da variância da variável dependente. O que fazemos é dividir a variação total da variável dependente em dois componentes: a variação explicada pelo modelo de regressão (entre grupos) e a variação devido a resíduos ou erros (dentro dos grupos). O teste F na ANOVA testa essencialmente se o modelo de regressão, como um todo, se ajusta melhor aos dados do que um modelo sem preditores. Por exemplo, em nosso exemplo de altura da árvore e contagem de folhas, a ANOVA ajudaria a determinar se a incorporação da altura da árvore melhora significativamente nossa capacidade de prever o número de folhas.

Alternativas ao OLS Regressão linear simples 

Dissemos que os mínimos quadrados ordinários são, de longe, o estimador mais comum na regressão linear simples, e nos concentramos no OLS neste artigo. No entanto, devemos considerar que o estimador de mínimos quadrados ordinários é sensível ou não é robusto em relação a valores discrepantes. Portanto, se você adicionar um ponto de dados altamente influente ou de alta alavancagem, poderá alterar drasticamente a inclinação e a interceptação da linha.  

Por esse motivo, existem opções não paramétricas. A visualização a seguir mostra os mínimos quadrados ordinários com três alternativas não paramétricas: desvio absoluto mediano (MAD), mínimos quadrados medianos (LMS) e Theil-Sen. Observe que a inclinação e o intercepto são diferentes para cada estimador. Se adicionássemos um ponto altamente influente, por exemplo, nas coordenadas x = 7 e y = 70, a linha de regressão dos mínimos quadrados comuns seria a mais alterada.

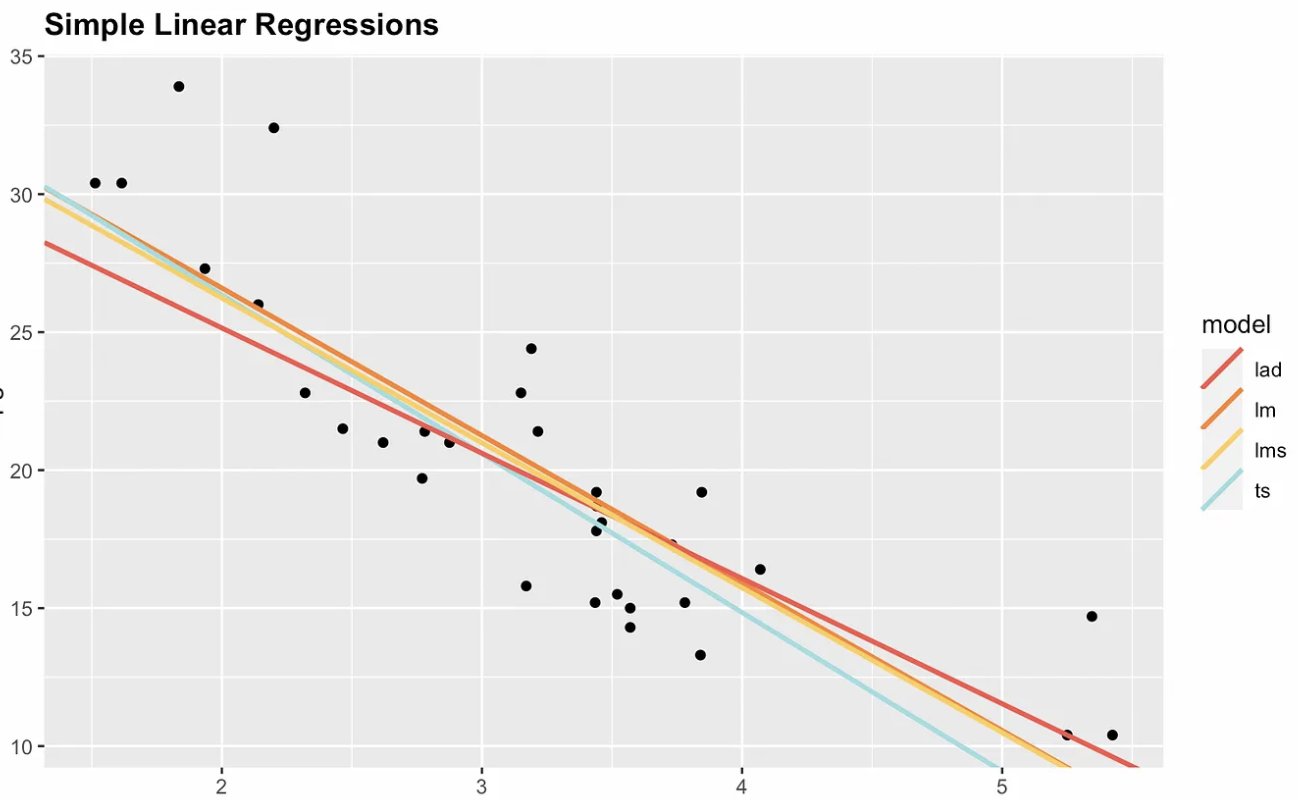Quatro opções de regressão linear simples. Imagem do autor

Considerações finais

A regressão linear simples é o ponto de partida para compreender relações mais complexas nos dados. Para ajudar, o DataCamp oferece tutoriais para que você possa continuar praticando, incluindo nosso tutorial Essentials of Linear Regression in Python, o tutorial How to Do Linear Regression in R e o Linear Regression in Excel: Um guia abrangente para iniciantes tutorial. Esses recursos guiarão você no uso de diferentes ferramentas para realizar a regressão linear e entender suas aplicações. Por fim, se você estiver pronto para expandir suas habilidades, consulte nosso site Multiple Linear Regression in R: Tutorial With Examples, que aborda modelos mais complexos envolvendo vários preditores.