Random Number Generator Using Numpy Tutorial

Numpy's random module, a suite of functions based on pseudorandom number generation. Random means something that can not be predicted logically.

np.random.seed() Function

In this example, you will simulate a coin flip. You will use the function np.random(), which draws a number between 0 and 1 such that all numbers in this interval are equally likely to occur.

If the number you draw is less than 0.5, which has a 50% chance of happening, you say heads and tails otherwise. This type of result where results are either True (Heads) or False (Tails) is referred to as Bernoulli trial.

The pseudorandom number works by starting with an integer called a seed and then generates numbers in succession. The same seed gives the same sequence of random numbers, hence the name "pseudo" random number generation. If you want to have reproducible code, it is good to seed the random number generator using the np.random.seed() function.

To do the coin flips, you import NumPy, seed the random number generator, and then draw four random numbers. You can specify how many random numbers you want with the size keyword.

import numpy as np
np.random.seed(42)
random_numbers = np.random.random(size=4)
random_numbers

array([0.3745012, 0.95071431, 0.73199394, 0.59865848])

The first number you get is less than 0.5, so it is heads while the remaining three are tails. You can show this explicitly using the less than operation, which gives you an array with boolean values, True for heads while False for tails.

heads = random_numbers < 0.5
heads

array([True, False, False, False], dtype=bool)

Finally, you can compute the number of heads by summing the array of booleans heads, because in numerical context, Python treats True as one and False as zero.

np.sum(heads)

1

Simulating Four Random Coin Flips

In the following example, we want to know the probability of getting four heads if we were to repeat the four flips of the coin over and over again. We can do this with a for loop.

We first initialize the count to zero. We then do repeat 10,000 repeats of the four-flip trials. If a given trial had four heads, we would increase the count.

So what is the probability of getting all four heads? It's the number of times you got all heads, divided by the total number of trials. The result is about 0.06.

n_all_heads = 0

# Initialize number of 4-heads trials
for _ in range(10000):
         heads = np.random.random(size=4) < 0.5
         n_heads = np.sum(heads)
         if n_heads == 4:
             n_all_heads += 1

n_all_heads / 10000

0.0621

Interactive Example of Generating Random Numbers

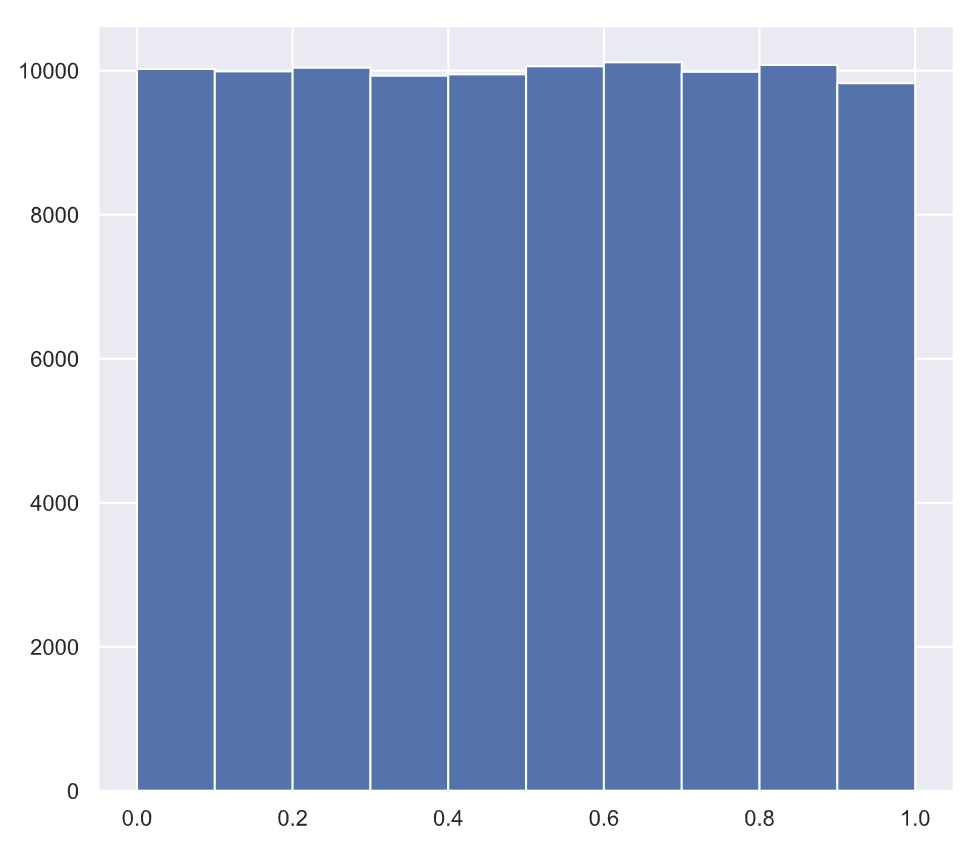
In this example, we'll generate lots of random numbers between zero and one, and then plot a histogram of the results. If the numbers are truly random, all bars in the histogram should be of (close to) equal height.

For this example you will need to:

• Seed the random number generator with np.random.seed using the seed 42.
• Initialize an empty array, random_numbers, of 100,000 entries to store the random numbers. Make sure you use np.empty(100000) to do this.
• Write a for loop to draw 100,000 random numbers using np.random.random(), storing them in the random_numbers array. To do so, loop over range(100000).
• Plot a histogram of random_numbers. It is not necessary to label the axes in this case because we are just checking the random number generator.

# Seed the random number generator
np.random.seed(42)

# Initialize random numbers: random_numbers
random_numbers = np.empty(100000)

# Generate random numbers by looping over range(100000)
for i in range(100000):
    random_numbers[i] = np.random.random()

# Plot a histogram
_ = plt.hist(random_numbers)

# Show the plot
plt.show()

When we run the above code, it produces the following result:

Try it for yourself.

To learn more about random number generators and hacker statistics, please see this video from our course Statistical Thinking in Python (Part 1).

This content is taken from DataCamp’s Statistical Thinking in Python (Part 1) course by Justin Bois.