Kurs
Die lineare Regression ist ein mächtiges Werkzeug in der Datenanalyse und Datenwissenschaft. Sie wird verwendet, um die Beziehung zwischen einer abhängigen Variable und einer oder mehreren unabhängigen Variablen zu quantifizieren. Wenn du mit der linearen Regression vertraut bist, kennst du vielleicht auch das gängige Anpassungsmaß r-Quadrat, das den Anteil der Varianz in der abhängigen Variable angibt, der durch die unabhängige(n) Variable(n) erklärt wird. Du bist aber vielleicht weniger vertraut mit dem bereinigten r-Quadrat, das oft bei komplexeren Modellen mit mehreren Prädiktoren verwendet wird.
Dieser Artikel vermittelt dir ein umfassendes Verständnis des bereinigten r-Quadrats, seiner Bedeutung für die Modellevaluation, seiner wichtigsten Unterschiede zum r-Quadrat und seiner Anwendungen in multiplen Regressionsszenarien, damit du diese Modellstatistiken vollständig beherrschen kannst. Für den Anfang empfehle ich dir den DataCamp-Kurs Einführung in die Regression mit Statistikmodellen in Python und unseren Kurs Einführung in die Regression in R, um mehr über Regressionsmodelle zu erfahren und zu lernen, wie man die verschiedenen Leistungskennzahlen, einschließlich des bereinigten r-Quadrats, interpretiert.
Was ist das bereinigte R-Quadrat?
Das R-Quadrat misst den Anteil der Varianz in der abhängigen Variable, der durch die unabhängige(n) Variable(n) des Modells erklärt wird. Das bereinigte r-Quadrat erklärt ebenfalls die Varianz, hat aber einen zusätzlichen Aspekt: Wie der Name schon sagt,passt den r-Quadrat-Wertan, indem er die Einbeziehung irrelevanter, d.h. stark kollinearer Variablen bestraft. Dabei werden sowohl die Anzahl der Prädiktoren als auch der Stichprobenumfang berücksichtigt.
Um das bereinigte r-Quadrat zu ermitteln, müssen wir zunächst das r-Quadrat bestimmen. Obwohl es verschiedene Möglichkeiten gibt, den r-Quadrat-Wert zu ermitteln, ist die folgende Formel eine der gängigsten:
Formel für r-Quadrat
Hier wird das r-Quadrat berechnet als eins minus dem Quotienten aus der Summe der Quadrate der Residuen und der Gesamtsumme der Quadrate.
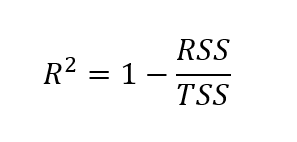
Wo:
- RSS = Summe der quadrierten Residuen (die Summe der quadrierten Unterschiede zwischen beobachteten und vorhergesagten Werten)
- TSS = Gesamtsumme der Quadrate (die Summe der quadrierten Differenzen zwischen beobachteten Werten und dem Mittelwert der beobachteten Werte)
Formel für das bereinigte r-Quadrat
Nachdem wir den r-Quadrat-Wert ermittelt haben, können wir das bereinigte r-Quadrat bestimmen. Dazu setzen wir unseren r-Quadrat-Wert in die untenstehende Formel ein.
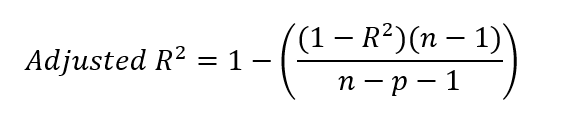
Wo:
- R² = r-Quadrat des Modells
- n = Anzahl der Beobachtungen (Datenpunkte)
- p = Anzahl der Prädiktoren (unabhängige Variablen)
Um das zu üben, können wir ein Beispiel ausprobieren. Stell dir folgendes Szenario vor: Wir haben einen Datensatz mit 30 Beobachtungen. Wir erstellen ein multiples lineares Regressionsmodell mit fünf Prädiktoren. Wir entdecken ein r-Quadrat von 0,8. Mit diesen Informationen können wir das bereinigte r-Quadrat ermitteln:

Du wunderst dich vielleicht über die -1 in der Gleichung, sowohl im Zähler als auch im Nenner. Zur Verdeutlichung: n-1 im Zähler berücksichtigt die Freiheitsgrade und korrigiert damit die Verwendung des Stichprobenmittelwerts bei der Berechnung der Varianz. Das liegt daran, dass wir bei der Berechnung der Varianz in der Regel den Stichprobenmittelwert als Schätzwert für den Populationsmittelwert verwenden. Da der Stichprobenmittelwert nicht dem wahren Mittelwert der Grundgesamtheit entspricht, wird die Varianz tendenziell unterschätzt. Um diese Verzerrung zu korrigieren, reduzieren wir die Freiheitsgrade um 1.
Im Nenner wird mit n-p-1 die Anzahl der Prädiktoren p im Modell angepasst , wobei p die Anzahl der unabhängigen Variablen ist. Die zusätzliche -1 im Nenner korrigiert die Schätzung des Achsenabschnitts des Modells, die ebenfalls einen Freiheitsgrad beansprucht. Wir müssen bedenken, dass wir in einem Regressionsmodell sowohl die Steigungskoeffizienten für die Prädiktoren als auch den Achsenabschnitt schätzen, um die gesamte Komplexität zu berücksichtigen.
Wie unterscheidet sich das bereinigte R-Quadrat vom R-Quadrat?
Obwohl sowohl das r-Quadrat als auch das bereinigte r-Quadrat die Leistung des Regressionsmodells bewerten, gibt es einen entscheidenden Unterschied zwischen den beiden Kennzahlen. Der r-Quadratwert steigt immer oder bleibt gleich, wenn weitere Prädiktoren zum Modell hinzugefügt werden, auch wenn diese Prädiktoren die Erklärungskraft des Modells nicht wesentlich verbessern. Dieses Problem kann einen falschen Eindruck von der Wirksamkeit des Modells vermitteln.
Das bereinigte r-Quadrat passt den r-Quadrat-Wert an die Anzahl der unabhängigen Variablen im Modell an. Der bereinigte r-Quadrat-Wert kann sinken, wenn ein neuer Prädiktor die Anpassung des Modells nicht verbessert, was ihn zu einem zuverlässigeren Maß für die Modellgenauigkeit macht. Aus diesem Grund kann das bereinigte r-Quadrat Datenanalysten bei der Entscheidung helfen, welche Prädiktoren sie einbeziehen sollten.
Wann wird das bereinigte R-Quadrat verwendet?
Um zuverlässige Modelle zu erstellen, ist es wichtig zu wissen, wann das bereinigte r-Quadrat dem r-Quadrat vorzuziehen ist. Im Folgenden sind Szenarien aufgeführt, in denen die Verwendung des bereinigten r-Quadrats zur Bewertung von Modellen sinnvoll ist.
- Multiple Regression: Im Allgemeinen ist das bereinigte r-Quadrat eine zuverlässigere Kennzahl, da es die Anzahl der Prädiktoren berücksichtigt und so eine bessere Bewertung der Leistung des Modells ermöglicht.
- Modellvergleich: Das bereinigte r-Quadrat ist nützlich, wenn du Modelle mit einer unterschiedlichen Anzahl von Prädiktoren vergleichst, um die besten Modelle auszuwählen.
- Um Overfitting zu verhindern: Das bereinigte r-Quadrat hilft, indem es die Einbeziehung irrelevanter Prädiktoren bestraft, um sicherzustellen, dass nur Prädiktoren einbezogen werden, die die Leistung des Modells verbessern.
Obwohl das bereinigte r-Quadrat in multiplen Regressionsmodellen im Allgemeinen dem r-Quadrat vorzuziehen ist, weil es die Anzahl der Prädiktoren berücksichtigt und das Hinzufügen irrelevanter Variablen bestraft, gibt es einige Szenarien, in denen die Verwendung des r-Quadrats dennoch angemessen sein kann:
- Einfache Vergleiche zwischen Modellen: Wenn du Modelle mit der gleichen Anzahl von Prädiktoren vergleichst, kann r-squared verwendet werden, um die allgemeine Anpassungsgüte zu messen, ohne dass du dir Sorgen über eine Überanpassung machen musst, da beide Modelle die gleiche Komplexität haben.
- Erläuternder Power Focus: Wenn dein Ziel lediglich darin besteht, zu verstehen, wie viel der Variation in der abhängigen Variable durch die unabhängigen Variablen erklärt wird, unabhängig von der Anzahl der Prädiktoren, kann das r-Quadrat eine einfachere Interpretation liefern.
Interpretation des bereinigten R-Quadrats in der Praxis
Betrachten wir ein Beispiel, bei dem die Nuancen zwischen r-Quadrat und bereinigtem r-Quadrat ins Spiel kommen. Angenommen, wir haben diese beiden Regressionsmodelle:
- Modell 1 hat ein r-Quadrat von 0,9 und ein bereinigtes r-Quadrat von 0,75.
- Modell 2 hat ein R-Quadrat von 0,85 und ein bereinigtes R-Quadrat von 0,8.
Man könnte sagen, dass Modell 1 mehr von der Gesamtvarianz in den Daten zu erklären scheint, weil es einen höheren r-Quadratwert hat. Wir müssen aber auch bedenken, dass Modell 2 möglicherweise mehr von der tatsächlichen Beziehung zwischen den Variablen erklärt, weil es irrelevante Prädiktoren berücksichtigt. Das höhere bereinigte r-Quadrat von Modell 2 deutet darauf hin, dass es eine zuverlässigere Anpassung bietet, indem es unnötige Komplexität bestraft, und es könnte auch weniger anfällig für eine Überanpassung sein. Ich persönlich würde mich in Ermangelung anderer Informationen für Modell 2 entscheiden.
Bereinigtes R-Quadrat in R und Python
Wir wollen uns praktische Beispiele für die Berechnung des bereinigten r-Quadrats in R und Python ansehen. Wir werden den Datensatz "Fischmarkt" von Kaggle verwenden, mit dem wir das Gewicht eines Fisches anhand seiner Art und physischen Maße schätzen können. Zur Vereinfachung runden wir die Ausgabe auf fünf Nachkommastellen.
Bereinigtes r-Quadrat in R
Lade den Datensatz herunter und speichere ihn in deinem Arbeitsverzeichnis. Verwende den folgenden Code, um ein lineares Modell zur Vorhersage des Fischgewichts in Abhängigkeit von verschiedenen Variablen zu erstellen: Length1, Height, Width und Length3, die sich jeweils auf die vertikale Länge des Fisches, die Höhe des Fisches, die diagonale Breite des Fisches und die Querlänge des Fisches beziehen.
# Load the dataset
data <- read.csv("data/Fish.csv")
# Remove rows with missing values
data <- na.omit(data)
# Model 1: Using 4 predictors ('Length1', 'Height', 'Width', 'Length3')
model1 <- lm(Weight ~ Length1 + Height + Width + Length3, data = data)Wenn wir nun die r-Quadrat-Werte und die bereinigten r-Quadrat-Werte überprüfen, ergibt sich folgendes Bild. Das bereinigte r-Quadrat kommt dem r-Quadrat-Wert sehr nahe, ist nur etwas langsamer.
r_squared_model1 <- round(summary(model1)$r.squared, 4)
r_squared_model1 <- round(summary(model1)$adj.r.squared, 4)0.88527
0.88229Was, wenn wir nun versuchen, ein anderes Modell zu erstellen, indem wir einen weiteren Prädiktor hinzufügen? Dieses Mal erstellen wir ein zweites Modell und fügen Length2 hinzu, das sich auf die diagonale Länge des Fisches bezieht. Auf dieselbe Weise wie zuvor können wir die r-squared- und bereinigten r-squared-Werte unseres neuen Modells überprüfen.
# Model 2: Adding one more predictor ('Length2')
model2 <- lm(Weight ~ Length1 + Height + Width + Length3 + Length2, data = data)r_squared_model2 <- round(summary(model1)$r.squared, 4)
r_squared_model2 <- round(summary(model1)$adj.r.squared, 4)0.88529
0.88154Bei Modell 2 können wir sehen, dass der r-Quadrat-Wert im Vergleich zu Modell 1 kaum gestiegen ist. Außerdem sehen wir, dass der bereinigte r-Quadrat-Wert gesunken ist, und der Rückgang des bereinigten r-Quadrats war größer als der Anstieg des r-Quadrat-Wertes. Das sagt uns, dass der Prädiktor, den wir hinzugefügt haben, nicht gut war.
Wenn wir darüber nachdenken, war Length2, das sich auf die diagonale Länge des Fisches bezieht, wahrscheinlich entweder mit den anderen Variablen im Modell oder einer linearen Kombination der anderen Variablen im Modell hoch korreliert. Insbesondere erwarten wir, dass die diagonale Länge des Fisches stark mit der Länge des Fisches und der Querlänge des Fisches korreliert ist. Wir sehen also, dass unsere neue Variable keine neuen, relevanten Informationen hinzugefügt hat.
Im Interesse der Gründlichkeit können wir auch zeigen, wie man das bereinigte r-Quadrat von Hand ermittelt. Wir verwenden den r-Quadrat-Wert und die Modellparameter und folgen der Formel, die wir zuvor gezeigt haben.
# Save R-squared as a variable
r_squared_model2 <- summary(model2)$r.squared
# Get the number of observations (n) for both models
n <- nrow(data) # Same for both models
# Get the number of predictors (excluding intercept) for each model
p_model1 <- length(coef(model1)) - 1
p_model2 <- length(coef(model2)) - 1
# Adjusted r-squared formula for Model 1
adjusted_r_squared_model1 <- 1 - ((1 - r_squared_model1) * (n - 1)) / (n - p_model1 - 1)
# Adjusted r-squared formula for Model 2
adjusted_r_squared_model2 <- 1 - ((1 - r_squared_model2) * (n - 1)) / (n - p_model2 - 1)
# Print R-squared values for both models
cat("R-Squared for Model 1:", r_squared_model1, "\n")
cat("R-Squared for Model 2:", r_squared_model2, "\n")
# Print the Adjusted R-Squared values for both models
cat("Adjusted R-Squared for Model 1:", adjusted_r_squared_model1, "\n")
cat("Adjusted R-Squared for Model 2:", adjusted_r_squared_model2, "\n")Bereinigtes r-Quadrat in Python
Der folgende Code zeigt eine Implementierung des gleichen Beispiels in Python.
# Import requied libraries
import pandas as pd
import statsmodels.api as sm
# Load the dataset
data = pd.read_csv('data/Fish.csv')
# Drop rows with missing values if any exist
data = data.dropna()
# Define predictors for Model 1 (4 variables)
X1 = data[['Length1', 'Height', 'Width', 'Length3']]
# Add a constant (intercept)
X1 = sm.add_constant(X1)
# Define the target variable 'Weight'
y = data['Weight']
# Fit Model 1
model1 = sm.OLS(y, X1).fit()
# Define predictors for Model 2 (5 variables)
X2 = data[['Length1', 'Height', 'Width', 'Length3', 'Length2']]
# Add a constant (intercept)
X2 = sm.add_constant(X2)
# Fit Model 2
model2 = sm.OLS(y, X2).fit()
# Save r-squared as a variable
r_squared_model1 = model1.rsquared # R-Squared for Model 1
r_squared_model2 = model2.rsquared # R-Squared for Model 2
# Get the number of observations
n = X1.shape[0] # Same for both models
# Get the number of predictors (excluding intercept) for each model
p_model1 = X1.shape[1] - 1 # Number of predictors for Model 1
p_model2 = X2.shape[1] - 1 # Number of predictors for Model 2
# Adjusted R-Squared formula for Model 1
adjusted_r_squared_model1 = 1 - ((1 - r_squared_model1) * (n - 1)) / (n - p_model1 - 1)
# Adjusted R-Squared formula for Model 2
adjusted_r_squared_model2 = 1 - ((1 - r_squared_model2) * (n - 1)) / (n - p_model2 - 1)
# Print R-squared for both models
print("R-Squared for Model 1:", r_squared_model1)
print("R-Squared for Model 2:", r_squared_model2)
# Print the Adjusted R-Squared values for both models
print("Adjusted R-Squared for Model 1:", adjusted_r_squared_model1)
print("Adjusted R-Squared for Model 2:", adjusted_r_squared_model2)Wir können auch Funktionen in Python verwenden, um die r-Quadrat- und bereinigten r-Quadrat-Werte der Regressionsmodelle zu ermitteln:
# Model 1
print("Model 1 R-Squared:", model1.rsquared)
print("Model 1 Adjusted R-Squared:", model1.rsquared_adj)
# Model 2
print("Model 2 R-Squared:", model2.rsquared)
print("Model 2 Adjusted R-Squared:", model2.rsquared_adj)Wenn du Probleme mit den obigen Codeabschnitten hattest, schau dir unsere Tutorien Essentials of Linear Regression in Python und How to Do Linear Regression in R an, um eine Schritt-für-Schritt-Anleitung zur Implementierung und Interpretation der verschiedenen Metriken des Regressionsmodells zu erhalten. Wenn Excel dein bevorzugtes Analysewerkzeug ist, schau dir unser Tutorial zu Lineare Regression in Excel an: A Comprehensive Guide For Beginners zu lernen, wie man lineare Regressionsmodelle in Excel implementiert und visualisiert.
Bereinigtes R-Quadrat, R-Quadrat und vorhergesagtes R-Quadrat
Wenn wir uns mit dem bereinigten r-Quadrat beschäftigen, sollten wir uns etwas Zeit nehmen, um unsere Begriffe zu klären. Es gibt einige Begriffe, die ähnlich erscheinen, aber unterschiedliche Zwecke haben. Hier habe ich eine Tabelle erstellt, die einige ähnlich klingende, aber unterschiedliche Begriffe vergleicht: r-Quadrat, bereinigtes r-Quadrat und vorhergesagtes r-Quadrat.
| Metrisch | Maßnahmen | Anwendungsfall | Stärken | Einschränkungen |
|---|---|---|---|---|
| R-Quadrat | Anteil der durch das Modell erklärten Varianz | Verstehen, wie gut das Modell zu den Trainingsdaten passt | Einfach zu interpretieren und liefert schnell eine Modellanpassung | Irreführend beim Vergleich von Modellen mit verschiedenen Prädiktoren, anfällig für Overfitting |
| Bereinigtes R-Quadrat | Anteil der erklärten Varianz, bereinigt um die Anzahl der Prädiktoren | Vergleich von Modellen mit einer unterschiedlichen Anzahl von Prädiktoren | Bestraft das Hinzufügen irrelevanter Variablen und verhindert eine Überanpassung | Gibt keinen Hinweis auf die Vorhersagekraft bei neuen Daten |
| Vorausgesagtes R-Quadrat | Wie gut das Modell neue Daten vorhersagt | Bewertung der Modellleistung bei ungesehenen Daten | Gibt an, wie gut sich das Modell auf neue Daten verallgemeinern lässt | Erfordert Kreuzvalidierung oder einen Holdout-Datensatz, rechenintensiv |
Häufige Missverständnisse über das bereinigte R-Quadrat
Zum Schluss wollen wir uns noch ein paar häufige Fehler ansehen, denn es gibt einige verbreitete Missverständnisse bei der Verwendung der Regression.
- Ein niedriges bereinigtes R-Quadrat bedeutet, dass das Modell schlecht ist: Ein niedriges bereinigtes r-Quadrat bedeutet nicht unbedingt, dass das Modell schlecht oder irrelevant ist. Der niedrige Wert kann darauf hindeuten, dass die unabhängigen Variablen im Modell keinen großen Anteil der Varianz in der abhängigen Variable erklären, aber je nach Thema ist das auch zu erwarten.
- Das bereinigte R-Quadrat darf nicht negativ sein: Das bereinigte r-Quadrat kann technisch gesehen negativ sein, wenn das Modell einen extrem niedrigen Anteil der Varianz in der abhängigen Variable erklärt und gleichzeitig viele Prädiktoren verwendet, was zu Strafen führt, die eine Situation mit negativem bereinigtem r-Quadrat schaffen.
- Das bereinigte R-Quadrat nimmt immer ab, wenn Variablen hinzugefügt werden: Das bereinigte r-Quadrat sinkt, wenn die neue Variable die Leistung des Modells nicht verbessert, aber es steigt, wenn die neue Variable einen echten Mehrwert für das Modell darstellt. Stell dir vor, du hast ein Modell mit einem schlechten Prädiktor und fügst dann einen guten hinzu: Das bereinigte r-Quadrat wird steigen.
Abschließende Überlegungen zum bereinigten R-Quadrat
Das bereinigte r-Quadrat ist eine wichtige Kennzahl für die Bewertung der Leistung von Regressionsmodellen, insbesondere wenn es um mehrere unabhängige Variablen geht. Im Vergleich zur r-Quadrat-Metrik bietet sie ein realistischeres und zuverlässigeres Maß für die Modellgenauigkeit, wenn mehrere Prädiktoren beteiligt sind.
Wenn du neugierig bist, wie R und Python die Koeffizienten von linearen Regressionsmodellen finden, schau dir die folgenden Tutorials an: Normal Equation for Linear Regression Tutorial und QR Decomposition in Machine Learning: Ein detaillierter Leitfaden.
Werde ein ML-Wissenschaftler
Bereinigtes R-Quadrat FAQs
Wie unterscheidet sich das bereinigte r-Quadrat vom r-Quadrat?
Das r-Quadrat misst den Anteil der Varianz in der abhängigen Variable, der durch die unabhängigen Variablen erklärt wird, und steigt immer, wenn mehr Prädiktoren hinzugefügt werden. Das bereinigte r-Quadrat wird um die Anzahl der Prädiktoren bereinigt und sinkt, wenn die zusätzlichen Variablen nicht zur Signifikanz des Modells beitragen.
Wann sollte ich das bereinigte r-Quadrat verwenden?
Das bereinigte r-Quadrat ist nützlich, wenn du die Anpassungsgüte von Regressionsmodellen mit einer unterschiedlichen Anzahl von Prädiktoren vergleichen willst oder wenn du dir Sorgen über eine Überanpassung machst.
Kann der bereinigte r-Quadrat-Wert negativ sein?
Das bereinigte r-Quadrat kann negativ sein, wenn das Modell nur sehr wenig Varianz in der abhängigen Variable erklärt und viele Prädiktoren enthält, was zu Strafen führt, die einen negativen Wert ergeben.
Warum ist der bereinigte r-Quadrat-Wert immer gleich oder niedriger als der r-Quadrat-Wert?
Das bereinigte r-Quadrat ist immer gleich oder niedriger als das r-Quadrat, weil es so konzipiert ist, dass es einen Abzug für das Hinzufügen unnötiger Prädiktoren zum Modell gibt.
Wann sollte ich das vorhergesagte r-Quadrat anstelle des bereinigten r-Quadrats verwenden?
Das vorhergesagte r-Quadrat ist nützlich, um zu beurteilen, wie gut das Modell bei neuen, ungesehenen Daten abschneidet.
Was ist der Unterschied zwischen dem bereinigten f-Quadrat und anderen Bewertungsmaßstäben für lineare Regressionsmodelle wie dem RMSE?
Das bereinigte r-Quadrat misst den Anteil der Varianz, der durch das Modell unter Berücksichtigung der Anzahl der Prädiktoren erklärt wird, während der RMSE (Root Mean Squared Error) die durchschnittliche Differenz zwischen beobachteten und vorhergesagten Werten quantifiziert. Mit anderen Worten: Der RMSE konzentriert sich auf den Vorhersagefehler, während das bereinigte r-Quadrat den Schwerpunkt auf die Modellanpassung legt.
Gilt das bereinigte r-Quadrat nur für lineare Regression?
Ja, das bereinigte r-Quadrat wird hauptsächlich mit multiplen linearen Regressionsmodellen in Verbindung gebracht. Für nicht-lineare Modelle wie exponentielle und logarithmische Funktionen werden in der Regel andere Metriken wie AIC oder BIC verwendet, um die Modellkomplexität zu bestrafen und die Anpassungsgüte zu bewerten.
Was bedeutet es, wenn das r-Quadrat und das bereinigte r-Quadrat eines linearen Regressionsmodells sehr unterschiedlich sind?
Ein großer Unterschied zwischen r-Quadrat und bereinigtem r-Quadrat deutet darauf hin, dass das Modell irrelevante Prädiktoren enthält. Das bereinigte r-Quadrat bestraft unnötige Variablen. Wenn du also einen großen Unterschied zwischen den beiden Werten siehst, hast du möglicherweise Prädiktoren, die stark korreliert sind.
Ist r-Quadrat und bereinigtes r-Quadrat bei einer einfachen linearen Regression dasselbe?
Bei einer einfachen linearen Regression, d.h. einer Regression mit einer abhängigen Variable und nur einer unabhängigen Variable, wären das r-Quadrat und das bereinigte r-Quadrat gleich groß.
