Curso
A regressão linear é uma ferramenta poderosa na análise de dados e na ciência de dados. É usado para quantificar a relação entre uma variável dependente e uma ou mais variáveis independentes. Se você estiver familiarizado com a regressão linear, talvez também conheça a medida comum de adequação chamada r-quadrado, que indica a proporção da variação na variável dependente que é explicada pela(s) variável(eis) independente(s). No entanto, você pode estar menos familiarizado com o r-quadrado ajustado, que é frequentemente usado em modelos mais complexos com vários preditores.
Este artigo lhe dará uma compreensão abrangente do r-quadrado ajustado, sua importância na avaliação do modelo, suas principais diferenças em relação ao r-quadrado e suas aplicações em cenários de regressão múltipla para que você possa ter um domínio completo dessas estatísticas de modelo. Para começar, recomendo que você faça o curso Introdução à regressão com modelos estatísticos em Python do DataCamp e nosso curso Introdução à regressão em R para aprender sobre modelos de regressão e como interpretar as diferentes métricas de desempenho, incluindo o r-quadrado ajustado.
O que é o R-quadrado ajustado?
O R-quadrado mede a proporção da variação na variável dependente explicada pela variável ou variáveis independentes do modelo. O r-quadrado ajustado também explica a variação, mas tem uma consideração adicional: Como o nome sugere, ele ajusta o valor r-quadrado penalizando a inclusão de variáveis irrelevantes, ou seja, altamente colineares. Isso é feito levando-se em conta o número de preditores e o tamanho da amostra.
Para encontrar o r-quadrado ajustado, primeiro temos que encontrar o r-quadrado. Embora existam diferentes maneiras de encontrar o valor r-quadrado, a fórmula abaixo é uma das mais comuns:
Fórmula para r-quadrado
Aqui, o r-quadrado é calculado como um menos o quociente da soma dos quadrados residuais sobre a soma total dos quadrados.
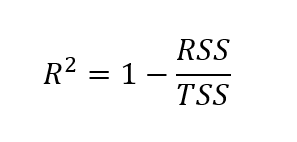
Onde:
- RSS = Soma dos resíduos ao quadrado (a soma das diferenças ao quadrado entre os valores observados e previstos)
- TSS = Soma total de quadrados (a soma das diferenças quadráticas entre os valores observados e a média dos valores observados)
Fórmula para o r-quadrado ajustado
Depois de encontrar o valor do r-quadrado, podemos encontrar o r-quadrado ajustado. Para isso, inserimos nosso valor de r-quadrado na fórmula abaixo.
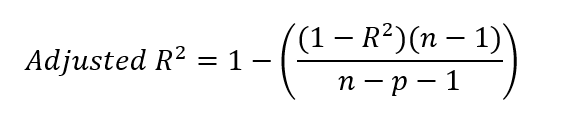
Onde:
- R² = r-quadrado do modelo
- n = número de observações (pontos de dados)
- p = número de preditores (variáveis independentes)
Para praticar, podemos tentar um exemplo. Considere este cenário: Temos um conjunto de dados com 30 observações. Criamos um modelo de regressão linear múltipla com cinco preditores. Descobrimos um r-quadrado de 0,8. Veja como podemos usar essas informações para encontrar o r-quadrado ajustado:

Você pode estar se perguntando sobre o -1 na equação, tanto no numerador quanto no denominador. Para esclarecer, n-1 no numerador representa os graus de liberdade, corrigindo o uso da média da amostra ao calcular a variação. Isso ocorre porque, ao calcular a variação, normalmente usamos a média da amostra como uma estimativa da média da população. Como a média da amostra não é a verdadeira média da população, a variação tende a ser subestimada. Para corrigir esse viés, reduzimos os graus de liberdade em 1.
No denominador, n-p-1 ajusta o número de preditores p no modelo, em que p é o número de variáveis independentes. O -1 adicional no denominador corrige a estimativa do intercepto do modelo, que também usa um grau de liberdade. É preciso lembrar que, em um modelo de regressão, estimamos os coeficientes de inclinação dos preditores e o intercepto para levar em conta toda a complexidade.
Como o R-quadrado ajustado difere do R-quadrado?
Embora tanto o r-quadrado quanto o r-quadrado ajustado avaliem o desempenho do modelo de regressão, existe uma diferença fundamental entre os dois indicadores. O valor do r-quadrado sempre aumenta ou permanece o mesmo quando mais preditores são adicionados ao modelo, mesmo que esses preditores não melhorem significativamente o poder explicativo do modelo. Esse problema pode criar uma impressão enganosa sobre a eficácia do modelo.
O r-quadrado ajustado ajusta o valor do r-quadrado para levar em conta o número de variáveis independentes no modelo. O valor r-quadrado ajustado pode diminuir se um novo preditor não melhorar o ajuste do modelo, tornando-o uma medida mais confiável da precisão do modelo. Por esse motivo, o r-quadrado ajustado pode ser usado como uma ferramenta pelos analistas de dados para ajudá-los a decidir quais preditores devem ser incluídos.
Quando usar o R-Squared ajustado
Entender quando usar o r-quadrado ajustado em vez do r-quadrado é importante para criar modelos confiáveis. A seguir, você encontrará cenários em que o uso do r-quadrado ajustado para avaliar modelos é apropriado.
- Regressão múltipla: De modo geral, o r-quadrado ajustado é uma métrica mais confiável porque leva em conta o número de preditores, garantindo uma melhor avaliação do desempenho do modelo.
- Comparação de modelos: O r-quadrado ajustado é útil ao comparar modelos com diferentes números de preditores para escolher os de melhor desempenho.
- Para evitar o ajuste excessivo: O r-quadrado ajustado ajuda a penalizar a inclusão de preditores irrelevantes para garantir que apenas os preditores que melhoram o desempenho do modelo sejam incluídos.
Em geral, embora o r-quadrado ajustado seja preferível ao r-quadrado em modelos de regressão múltipla porque ele leva em conta o número de preditores e penaliza a adição de variáveis irrelevantes, há alguns cenários em que o uso do r-quadrado ainda pode ser apropriado:
- Comparações simples entre modelos: Se você estiver comparando modelos com o mesmo número de preditores, o r-quadrado pode ser usado para medir a qualidade geral do ajuste sem se preocupar com o excesso de ajuste, já que ambos os modelos têm a mesma complexidade.
- Explanatory Power Focus: Se o seu objetivo for apenas entender o quanto da variação na variável dependente é explicada pelas variáveis independentes, independentemente do número de preditores, o r-quadrado pode fornecer uma interpretação mais direta.
Interpretação do R-Squared ajustado na prática
Vamos considerar um exemplo em que as nuances entre o r-quadrado e o r-quadrado ajustado entrariam em jogo. Suponha que tenhamos esses dois modelos de regressão:
- O modelo 1 tem um r-quadrado de 0,9 e um r-quadrado ajustado de 0,75.
- O modelo 2 tem um R-quadrado de 0,85 e um R-quadrado ajustado de 0,8.
Podemos dizer que o modelo 1 parece explicar mais a variação geral dos dados porque tem um valor r-quadrado mais alto. Mas também temos de considerar que o modelo 2 pode explicar mais da verdadeira relação subjacente entre as variáveis, porque ele leva em conta preditores irrelevantes. O r-quadrado ajustado mais alto do Modelo 2 sugere que ele oferece um ajuste mais confiável, penalizando a complexidade desnecessária, e também pode ser menos propenso a um ajuste excessivo. Pessoalmente, e na ausência de outras informações, eu escolheria o modelo 2.
R-quadrado ajustado em R e Python
Vamos explorar exemplos práticos de cálculo do r-quadrado ajustado em R e Python. Usaremos o conjunto de dados "Fish Market" do Kaggle, que é útil para estimar o peso de um peixe com base em sua espécie e medidas físicas. Para simplificar, arredondaremos o resultado para cinco casas decimais.
R-quadrado ajustado em R
Faça o download do conjunto de dados e salve-o em seu diretório de trabalho. Use o código a seguir para ajustar um modelo linear para prever o peso do peixe como uma função de algumas variáveis diferentes, incluindo Length1, Height, Width e Length3, que se referem ao comprimento vertical do peixe, à altura do peixe, à largura diagonal do peixe e ao comprimento transversal do peixe, respectivamente.
# Load the dataset
data <- read.csv("data/Fish.csv")
# Remove rows with missing values
data <- na.omit(data)
# Model 1: Using 4 predictors ('Length1', 'Height', 'Width', 'Length3')
model1 <- lm(Weight ~ Length1 + Height + Width + Length3, data = data)Agora, verificamos os valores de r-quadrado e r-quadrado ajustado, e vemos o seguinte. O r-quadrado ajustado é muito próximo do valor do r-quadrado, apenas um pouco mais lento.
r_squared_model1 <- round(summary(model1)$r.squared, 4)
r_squared_model1 <- round(summary(model1)$adj.r.squared, 4)0.88527
0.88229E se agora tentarmos criar outro modelo adicionando outro preditor? Desta vez, criamos um segundo modelo e adicionamos Length2, que se refere ao comprimento diagonal do peixe. Da mesma forma que antes, podemos verificar os valores de r-quadrado e r-quadrado ajustado do nosso novo modelo.
# Model 2: Adding one more predictor ('Length2')
model2 <- lm(Weight ~ Length1 + Height + Width + Length3 + Length2, data = data)r_squared_model2 <- round(summary(model1)$r.squared, 4)
r_squared_model2 <- round(summary(model1)$adj.r.squared, 4)0.88529
0.88154Para o modelo 2, podemos ver que o valor do r-quadrado quase não aumentou em comparação com o modelo 1. Além disso, vemos que o valor do r-quadrado ajustado diminuiu, e a diminuição do r-quadrado ajustado foi maior do que o aumento do valor do r-quadrado. Isso nos diz que o preditor que adicionamos não era bom.
Pensando nisso, Length2, que se refere ao comprimento diagonal do peixe, provavelmente estava altamente correlacionado com as outras variáveis do modelo ou com uma combinação linear das outras variáveis do modelo. Em particular, esperamos que o comprimento diagonal do peixe esteja altamente correlacionado com o comprimento do peixe e o comprimento transversal do peixe. Portanto, vemos que nossa nova variável não adicionou informações novas e relevantes.
Para sermos minuciosos, também podemos demonstrar como encontrar o r-quadrado ajustado manualmente. Usamos o valor r-quadrado e os parâmetros do modelo, e seguimos a fórmula que mostramos anteriormente.
# Save R-squared as a variable
r_squared_model2 <- summary(model2)$r.squared
# Get the number of observations (n) for both models
n <- nrow(data) # Same for both models
# Get the number of predictors (excluding intercept) for each model
p_model1 <- length(coef(model1)) - 1
p_model2 <- length(coef(model2)) - 1
# Adjusted r-squared formula for Model 1
adjusted_r_squared_model1 <- 1 - ((1 - r_squared_model1) * (n - 1)) / (n - p_model1 - 1)
# Adjusted r-squared formula for Model 2
adjusted_r_squared_model2 <- 1 - ((1 - r_squared_model2) * (n - 1)) / (n - p_model2 - 1)
# Print R-squared values for both models
cat("R-Squared for Model 1:", r_squared_model1, "\n")
cat("R-Squared for Model 2:", r_squared_model2, "\n")
# Print the Adjusted R-Squared values for both models
cat("Adjusted R-Squared for Model 1:", adjusted_r_squared_model1, "\n")
cat("Adjusted R-Squared for Model 2:", adjusted_r_squared_model2, "\n")R-quadrado ajustado em Python
O código a seguir mostra uma implementação do mesmo exemplo em Python.
# Import requied libraries
import pandas as pd
import statsmodels.api as sm
# Load the dataset
data = pd.read_csv('data/Fish.csv')
# Drop rows with missing values if any exist
data = data.dropna()
# Define predictors for Model 1 (4 variables)
X1 = data[['Length1', 'Height', 'Width', 'Length3']]
# Add a constant (intercept)
X1 = sm.add_constant(X1)
# Define the target variable 'Weight'
y = data['Weight']
# Fit Model 1
model1 = sm.OLS(y, X1).fit()
# Define predictors for Model 2 (5 variables)
X2 = data[['Length1', 'Height', 'Width', 'Length3', 'Length2']]
# Add a constant (intercept)
X2 = sm.add_constant(X2)
# Fit Model 2
model2 = sm.OLS(y, X2).fit()
# Save r-squared as a variable
r_squared_model1 = model1.rsquared # R-Squared for Model 1
r_squared_model2 = model2.rsquared # R-Squared for Model 2
# Get the number of observations
n = X1.shape[0] # Same for both models
# Get the number of predictors (excluding intercept) for each model
p_model1 = X1.shape[1] - 1 # Number of predictors for Model 1
p_model2 = X2.shape[1] - 1 # Number of predictors for Model 2
# Adjusted R-Squared formula for Model 1
adjusted_r_squared_model1 = 1 - ((1 - r_squared_model1) * (n - 1)) / (n - p_model1 - 1)
# Adjusted R-Squared formula for Model 2
adjusted_r_squared_model2 = 1 - ((1 - r_squared_model2) * (n - 1)) / (n - p_model2 - 1)
# Print R-squared for both models
print("R-Squared for Model 1:", r_squared_model1)
print("R-Squared for Model 2:", r_squared_model2)
# Print the Adjusted R-Squared values for both models
print("Adjusted R-Squared for Model 1:", adjusted_r_squared_model1)
print("Adjusted R-Squared for Model 2:", adjusted_r_squared_model2)Também podemos usar funções em Python para encontrar os valores de r-quadrado e r-quadrado ajustado dos modelos de regressão:
# Model 1
print("Model 1 R-Squared:", model1.rsquared)
print("Model 1 Adjusted R-Squared:", model1.rsquared_adj)
# Model 2
print("Model 2 R-Squared:", model2.rsquared)
print("Model 2 Adjusted R-Squared:", model2.rsquared_adj)Se você teve problemas com as seções de código acima, confira nossos tutoriais sobre Essentials of Linear Regression in Python e How to Do Linear Regression in R para aprender o guia passo a passo para implementar e interpretar diferentes métricas do modelo de regressão. Se você prefere usar o Excel como ferramenta de análise, confira nosso tutorial sobre Linear Regression in Excel: A Comprehensive Guide For Beginners para que você aprenda a implementar e visualizar modelos de regressão linear no Excel.
R-quadrado ajustado, R-quadrado e R-quadrado previsto
Ao considerarmos o r-quadrado ajustado, devemos reservar algum tempo para manter nossos termos claros. Há alguns termos que parecem semelhantes, mas têm finalidades diferentes. Aqui, criei uma tabela que compara algumas ideias que parecem semelhantes, mas distintas: r-quadrado, r-quadrado ajustado e r-quadrado previsto.
| Métrica | Medidas | Caso de uso | Pontos fortes | Limitações |
|---|---|---|---|---|
| R-quadrado | Proporção da variação explicada pelo modelo | Entender como o modelo se ajusta aos dados de treinamento | Simples de interpretar e fornece rapidamente o ajuste do modelo | Enganoso ao comparar modelos com preditores diferentes, vulnerável ao ajuste excessivo |
| R-quadrado ajustado | Proporção de variação explicada, ajustada para o número de preditores | Comparação de modelos com diferentes números de preditores | Penaliza a adição de variáveis irrelevantes, evitando o ajuste excessivo | Não indica o desempenho preditivo em novos dados |
| R-quadrado previsto | O grau de acerto do modelo na previsão de novos dados | Avaliação do desempenho do modelo em dados não vistos | Indica a capacidade de generalização do modelo para novos dados | Requer validação cruzada ou um conjunto de dados de espera, o que é computacionalmente caro |
Equívocos comuns sobre o R-Squared ajustado
Por fim, vamos analisar alguns erros comuns, pois há alguns mal-entendidos comuns sobre seu uso na regressão.
- Um R-Squared ajustado baixo significa que o modelo é ruim: Um r-quadrado ajustado baixo não significa necessariamente que o modelo seja ruim ou irrelevante. O valor baixo pode indicar que as variáveis independentes no modelo não explicam uma grande proporção da variação na variável dependente, mas, dependendo do assunto, isso pode ser esperado.
- O R-Squared ajustado não pode ser negativo: Tecnicamente, o r-quadrado ajustado pode ser negativo quando o modelo explica uma proporção extremamente baixa da variação na variável dependente e, ao mesmo tempo, usa muitos preditores, o que resulta em penalidades que criam uma situação com r-quadrado ajustado negativo.
- O R-quadrado ajustado sempre diminui quando você adiciona variáveis: O r-quadrado ajustado diminuirá se a nova variável não melhorar o desempenho do modelo, mas aumentará se a nova variável agregar valor genuíno ao modelo. Imagine um modelo com um preditor ruim e, em seguida, você adiciona um bom preditor; o r-quadrado ajustado aumentará.
Considerações finais sobre o R-Squared ajustado
O r-quadrado ajustado é uma métrica importante para avaliar o desempenho dos modelos de regressão, especialmente quando se lida com várias variáveis independentes. Em comparação com a métrica r-quadrado, ela fornece uma medida mais realista e confiável da precisão do modelo quando vários preditores estão envolvidos.
Se você estiver curioso para saber como o R e o Python encontram os coeficientes dos modelos de regressão linear, confira os tutoriais a seguir: Tutorial de Equação Normal para Regressão Linear e Decomposição QR em Aprendizado de Máquina: Um guia detalhado.
Torne-se um cientista de ML
Perguntas frequentes sobre o R-quadrado ajustado
Como o r-quadrado ajustado difere do r-quadrado?
Embora o r-quadrado meça a proporção da variação na variável dependente explicada pelas variáveis independentes, ele sempre aumenta quando mais preditores são adicionados. O r-quadrado ajustado ajusta o número de preditores e diminui se as variáveis adicionais não contribuírem para a significância do modelo.
Quando devo usar o r-quadrado ajustado?
O r-quadrado ajustado é útil ao comparar a qualidade do ajuste de modelos de regressão com diferentes números de preditores ou quando você está preocupado com o ajuste excessivo.
O valor r-quadrado ajustado pode ser negativo?
O r-quadrado ajustado pode ser negativo quando o modelo explica muito pouca variação na variável dependente e inclui muitos preditores, levando a penalidades que resultam em um valor negativo.
Por que o valor do r-quadrado ajustado é sempre igual ou inferior ao valor do r-quadrado?
O r-quadrado ajustado é sempre igual ou menor do que o r-quadrado porque foi projetado para adicionar uma penalidade pela adição de preditores desnecessários ao modelo.
Quando devo usar o r-quadrado previsto em vez do r-quadrado ajustado?
O r-quadrado previsto é útil para avaliar o desempenho do modelo em dados novos e não vistos.
Qual é a diferença entre o f-quadrado ajustado e outras métricas de avaliação de modelos de regressão linear, como o RMSE?
O r-quadrado ajustado mede a proporção da variação explicada pelo modelo, levando em conta o número de preditores, enquanto o RMSE (Root Mean Squared Error) quantifica a diferença média entre os valores observados e previstos. Em outras palavras, o RMSE se concentra no erro de previsão, enquanto o r-quadrado ajustado se concentra no ajuste do modelo.
O r quadrado ajustado se aplica somente à regressão linear?
Sim, o r-quadrado ajustado está associado principalmente a modelos de regressão linear múltipla. Para modelos não lineares, como funções exponenciais e logarítmicas, outras métricas, como AIC ou BIC, são normalmente usadas para penalizar a complexidade do modelo e avaliar a adequação do ajuste.
O que significa se os valores de r-quadrado e r-quadrado ajustado de um modelo de regressão linear forem muito diferentes?
Uma grande diferença entre o r-quadrado e o r-quadrado ajustado sugere que o modelo inclui preditores irrelevantes. O r-quadrado ajustado penaliza as variáveis desnecessárias; portanto, se você observar uma grande diferença entre os dois, é possível que os preditores estejam fortemente correlacionados.
O r-quadrado e o r-quadrado ajustado são iguais na regressão linear simples?
Na regressão linear simples, ou seja, na regressão com uma variável dependente e apenas uma variável independente, o r-quadrado e o r-quadrado ajustado seriam os mesmos.

